2차원 도형 그리기

직선 그리기

픽셀 공간에서 2개의 점을 잇는 선을 그리는 다양한 방법 중 Bresenham's line algorithm과 Wu's line algorithm이 있습니다.
간단하면서 가장 빠른 방법으로 Bresenham's line algorithm이 많이 사용되고 있고, Bresenham's line algorithm 대비 anti-aliasing을 지원하는 방법으로 Wu's line algorithm이 사용됩니다.

Bresenham’s line algorithm

내용: https://en.wikipedia.org/wiki/Bresenham%27s_line_algorithm
아래 그림은 Bresenham's line algorithm이 동작하는 방식입니다. 아래 그림과 같이 해당 영역의 픽셀을 선택함으로써 직선을 그리게 됩니다.

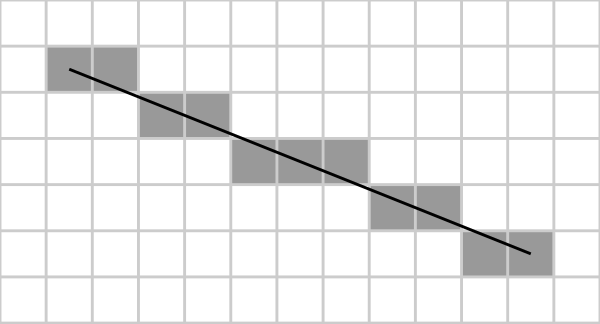
위 그림에서도 볼 수 있는 것과 같이 굉장히 심플하지만, 점유된 픽셀이 꺽여보이는 aliasing 현상이 발생합니다.

import numpy as np
import matplotlib.pyplot as plt

def bresenham_line(u1, v1, u2, v2):
    points = []
    du = abs(u2 - u1)
    dv = abs(v2 - v1)    
    u, v = u1, v1
    su = -1 if u1 > u2 else 1
    sv = -1 if v1 > v2 else 1
    if du > dv:
        err = du / 2.0
        while u != u2:
            points.append((u, v))
            err -= dv
            if err < 0:
                v += sv
                err += du
            u += su
    else:
        err = dv / 2.0
        while v != v2:
            points.append((u, v))
            err -= du
            if err < 0:
                u += su
                err += dv
            v += sv
    points.append((u, v))  # Include the last point
    return points

# Example usage:
u1, v1 = 10, 10
u2, v2 = 190, 190
line_points = bresenham_line(u1, v1, u2, v2)

board = np.zeros((200, 200))
for line_point in line_points:
    board[line_point[1]][line_point[0]] = 1

plt.imshow(board)

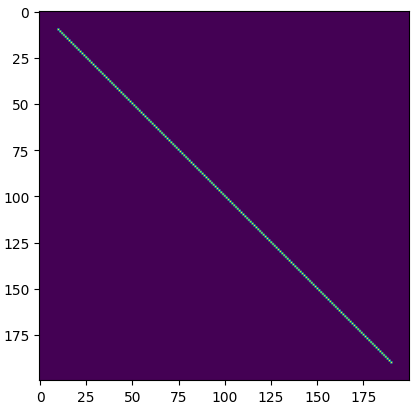
위 코드는 Bresenham's line algorithm을 이용하여 (10, 10) 과 (190, 190) 을 잇는 직선을 긋는 코드입니다.
앞에서 설명한 것과 같이 동작 방식은 매우 간단합니다. 확대해서 보면 계단 모양의 aliasing이 발생한 것을 볼 수 있습니다.
간단한 직선을 긋는 작업이 필요하면 Bresenham's line algorithm으로도 충분하며 조금 복잡하더라도 aliasing 개선이 필요하면 아래 Wu's line algorithm을 활용해 볼 수 있습니다.

Wu’s line algorithm

내용: https://en.wikipedia.org/wiki/Xiaolin_Wu%27s_line_algorithm

Wu's line algorithm은 위 그림과 같이 aliasing 문제를 개선하기 위해 aliasing 문제가 나타나는 부분에 픽셀을 추가적으로 선택하여 부드러운 선을 그릴 수 있도록 개선한 알고리즘 입니다.

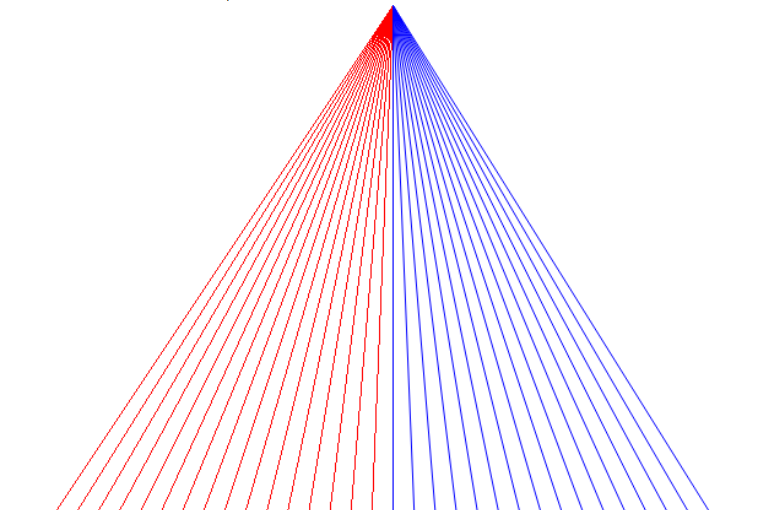
왼쪽의 빨간선이 Bresenham's line algorithm을 이용하여 그린 선이고 오른쪽의 파란선이 Wu's line algorithm을 이용하여 그린 선입니다. 오른쪽 선이 더 부드러운 것을 알 수 있습니다.

def wu_line(u1, v1, u2, v2):
    """Return the list of points and intensities for Xiaolin Wu's line algorithm."""
    from math import floor, ceil

    def ipart(x):
        return int(floor(x))

    def round(x):
        return int(floor(x + 0.5))

    def fpart(x):
        return x - floor(x)

    def rfpart(x):
        return 1 - fpart(x)

    points = []

    x0, y0 = u1, v1
    x1, y1 = u2, v2

    steep = abs(y1 - y0) > abs(x1 - x0)
    if steep:
        # Swap x and y
        x0, y0 = y0, x0
        x1, y1 = y1, x1

    if x0 > x1:
        # Swap start and end points
        x0, x1 = x1, x0
        y0, y1 = y1, y0

    dx = x1 - x0
    dy = y1 - y0
    gradient = dy / dx if dx != 0 else 1

    # Handle first endpoint
    xend = round(x0)
    yend = y0 + gradient * (xend - x0)
    xgap = rfpart(x0 + 0.5)
    xpxl1 = xend  # First pixel X-coordinate
    ypxl1 = ipart(yend)
    if steep:
        points.append((ypxl1, xpxl1, rfpart(yend) * xgap))
        points.append((ypxl1 + 1, xpxl1, fpart(yend) * xgap))
    else:
        points.append((xpxl1, ypxl1, rfpart(yend) * xgap))
        points.append((xpxl1, ypxl1 + 1, fpart(yend) * xgap))

    # First y-intersection for the main loop
    intery = yend + gradient

    # Handle second endpoint
    xend = round(x1)
    yend = y1 + gradient * (xend - x1)
    xgap = fpart(x1 + 0.5)
    xpxl2 = xend  # Last pixel X-coordinate
    ypxl2 = ipart(yend)
    if steep:
        points.append((ypxl2, xpxl2, rfpart(yend) * xgap))
        points.append((ypxl2 + 1, xpxl2, fpart(yend) * xgap))
    else:
        points.append((xpxl2, ypxl2, rfpart(yend) * xgap))
        points.append((xpxl2, ypxl2 + 1, fpart(yend) * xgap))

    # Main loop
    if steep:
        for x in range(xpxl1 + 1, xpxl2):
            y = ipart(intery)
            points.append((y, x, rfpart(intery)))
            points.append((y + 1, x, fpart(intery)))
            intery += gradient
    else:
        for x in range(xpxl1 + 1, xpxl2):
            y = ipart(intery)
            points.append((x, y, rfpart(intery)))
            points.append((x, y + 1, fpart(intery)))
            intery += gradient

    return points


# Define the start and end points
u1, v1 = 10, 10
u2, v2 = 190, 190

# Get the list of points with intensities
line_points = wu_line(u1, v1, u2, v2)

board = np.zeros((200, 200))
for line_point in line_points:
    board[line_point[1]][line_point[0]] = 1

plt.imshow(board)

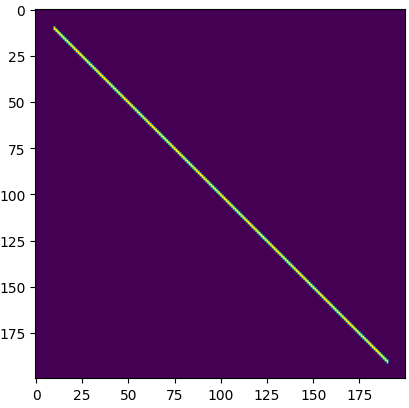
위 이미지는 Wu's line algorithm을 이용하여 (10, 10)과 (190, 190)을 잇는 선을 그린 것입니다. Bresenham's line algorithm에 비해 선이 부드러운 것을 알 수 있습니다.

Wu's line algorithm은 시각적으로 부드러운 선을 만들 수 있으나, 두 점을 이은 직선 상의 픽셀들을 이용해야 하는 다른 알고리즘의 중간 과정으로 사용해야 한다면 의도치 않게 많은 픽셀이 사용될 수 있습니다. 이러한 경우에는 Bresenham's line algorithm을 사용하는 것이 더 좋은 방법일 수 있습니다.

부채꼴 그리기

부채꼴을 그리기 위해서는 부채꼴의 중심 좌표, 반지름의 길이, 부채꼴의 시작 각도, 부채꼴의 끝 각도가 필요합니다.
아래 코드에서는 부채 꼴의 중심 좌표 \((u, v)\), 반지름의 길이 \(r\), 부채꼴의 시작 각도와 끝 각도인 \(\theta_{1}, \theta_{2}\) 를 입력으로 받아 부채꼴과 그 내부에 해당하는 픽셀 좌표값을 얻습니다.

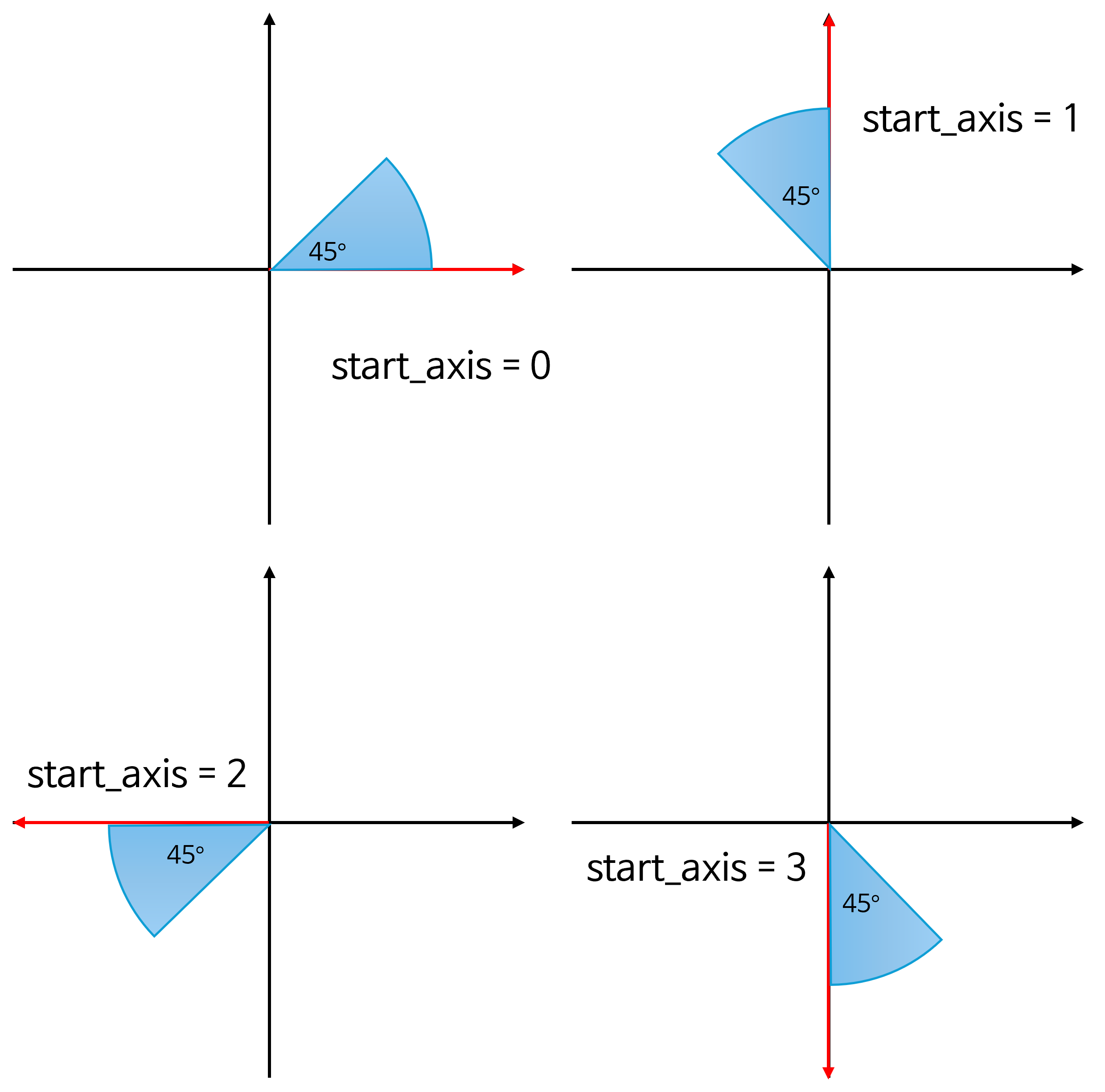
각도의 정의는 다음과 같습니다. 아래 사용될 코드의 fill_sector(u, v, r, theta1, theta2, start_axis)에서 start_axis의 기준에 따라 각도의 시작점이 달라집니다.
각도는 반 시계 방향으로 증가하며 아래 예시는 theta1 = 0 (degree), theta2 = 45 (degree) 기준의 예시를 보여 준 것입니다.

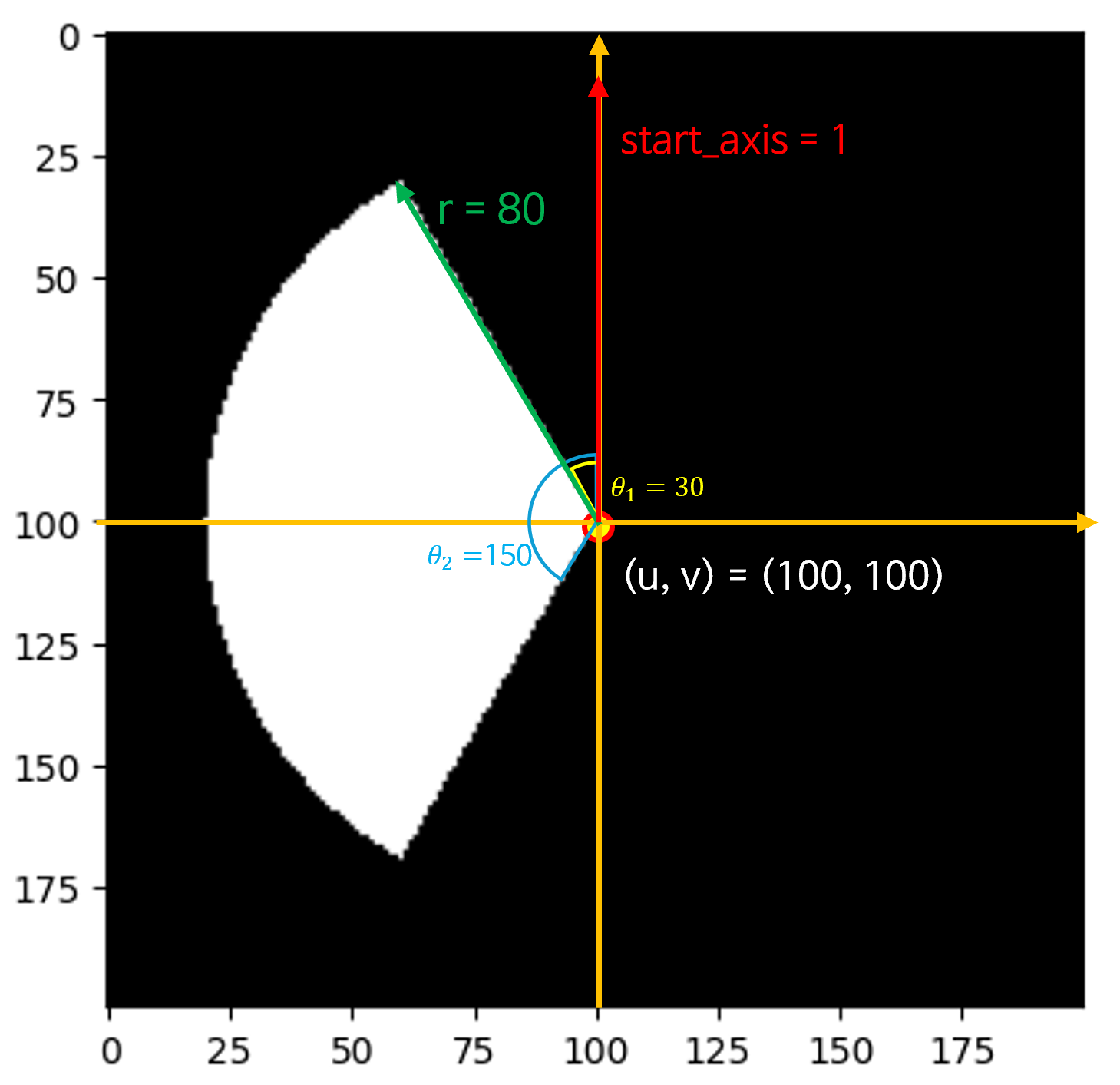
아래 코드 예시는 start_axis = 1 기준, \(r = 80 \text{ pixel}\), \(\theta_{1} = 30\), \(\theta_{2} = 150\) 인 예시입니다.

import numpy as np
import matplotlib.pyplot as plt

def calculate_angle(x, y, u, v, start_axis=0):
    """Calculate the angle with 0 degrees at 12 o'clock and increases counterclockwise."""
    if start_axis < 0 or start_axis > 3:
        print("start_line must be 0, 1, 2, 3.")
        exit()
        
    dx = x - u
    dy = v - y  # Reverse y because y increases downwards
    angle = np.arctan2(dy, dx)  # atan2 order to reflect the y-x plane
    angle = np.rad2deg(angle)  # Convert to degrees
    # Adjust to start from the top
    if angle < 0:
        angle += 360
    angle = (-90*start_axis + angle) % 360
    return angle

def fill_sector(u, v, r, theta1, theta2, start_axis):
    """Fill a circular sector given the center, radius, and angle range."""
    pixels_in_sector = set()

    # Define the bounding box of the circle
    x_min = u - r
    x_max = u + r
    y_min = v - r
    y_max = v + r

    for x in range(int(x_min), int(x_max) + 1):
        for y in range(int(y_min), int(y_max) + 1):
            if (x - u) ** 2 + (y - v) ** 2 <= r ** 2:  # Check if inside the circle
                angle = calculate_angle(x, y, u, v, start_axis)  # Calculate the angle
                # Check if the angle is within the sector's range
                if (theta1 <= angle <= theta2) or (theta2 < theta1 and (angle >= theta1 or angle <= theta2)):
                    pixels_in_sector.add((x, y))

    return pixels_in_sector

# Example usage
image_width = 200
image_height = 200
u, v = 100, 100
r = 80
theta1 =30
theta2 = 150
start_axis = 1

# Get the filled sector pixels
sector_pixels = fill_sector(u, v, r, theta1, theta2, start_axis)

# Plot the result
img = np.zeros((image_height, image_width), dtype=np.uint8)
for x, y in sector_pixels:
    if 0 <= x < img.shape[1] and 0 <= y < img.shape[0]:
        img[y, x] = 1

plt.imshow(img, cmap='gray')
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

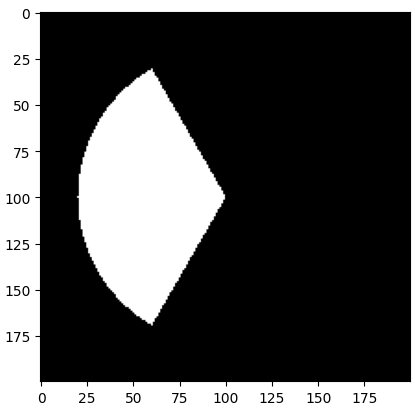
위 출력 결과를 입력인 \(u, v, r, \theta_{1}, \theta_{2}, \text{start_line}\) 으로 분석해 보면 다음과 같습니다.

원 그리기

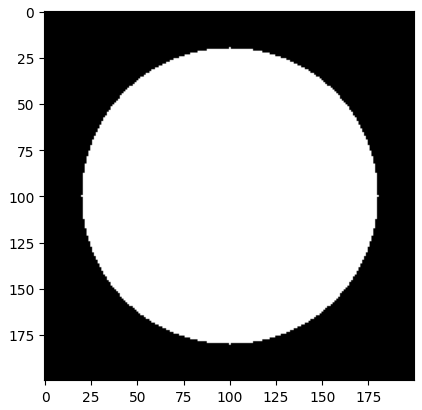
앞에서 사용한 부채꼴 그리기의 입력을 \(u, v, r, \theta_{1}=0, \theta_{2}=360, \text{start_line}\) 으로 지정하면 원을 그릴 수 있습니다.

image_width = 200
image_height = 200
u, v = 100, 100
r = 80
theta1 =0
theta2 = 360
start_axis = 0

# Get the filled sector pixels
sector_pixels = fill_sector(u, v, r, theta1, theta2, start_axis)

# Plot the result
img = np.zeros((image_height, image_width), dtype=np.uint8)
for x, y in sector_pixels:
    if 0 <= x < img.shape[1] and 0 <= y < img.shape[0]:
        img[y, x] = 1

plt.imshow(img, cmap='gray')
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

Vision 관련 글 목차