Homogeneous coordinate (동차 좌표계)

2022, Apr 01    

• 참조 : https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/geometry/homo-coor.html
• 참조 : https://blog.daum.net/shksjy/229
• 참조 : https://darkpgmr.tistory.com/78
• 참조 : Homogeneous Coordinates and Transformations ofthe Plane
• 참조 : The Homogeneous Perspective Transform

• Homogeneous coordinate는 Computer Vision에서 연산을 할 때 많이 사용하는 개념입니다. 그러면 Homogeneous coordinate가 무엇인 지, 왜 사용하는 지 등에 대한 개념을 알아보도록 하겠습니다.

목차

• Homogeneous coordinate의 의미와 사용 이유

• Homogeneous coordinate의 사용 예시

• Homogeneous coordinate 내용 정리

Homogeneous coordinate의 의미와 사용 이유

• 먼저 Homogeneous coordinate를 다루기 이전에 Affine Transformation에 대한 개념이 필요합니다. Affine Transformation의 상세 내용에 대한 내용을 확인하시길 바랍니다.
• Affine Transformation은 간단하게 선형 변환 + 이동으로 정의할 수 있습니다. 보통 어떤 벡터를 Transformation을 할 때, Transformation Matrix를 곱해주어서 변환하게 됩니다. 그런데 벡터라는 것은 크기와 방향을 가지게 되는데 벡터 자체만으로는 위치가 없기 때문에 이동 변환을 할 수 없습니다. 즉, 벡터를 Transformation Matrix를 곱하여 이동 변환을 바로 적용할 수 없다는 뜻입니다.

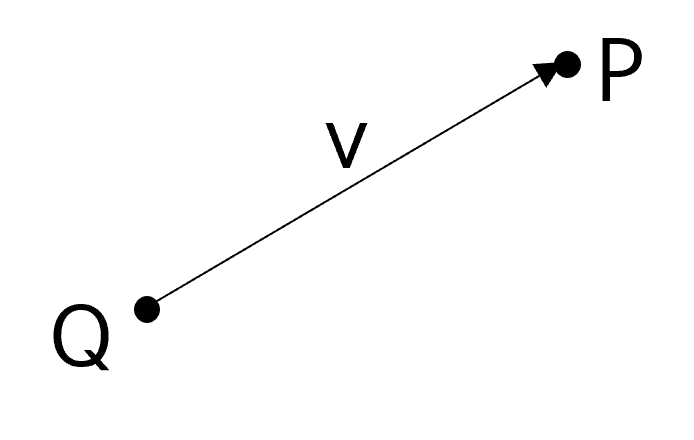
• 그러면 위 그림과 같이 벡터 \(v\) 에 포인트 개념을 추가하여 위치를 표현해 보도록 하겠습니다. 포인트 \(P, Q\) 가 있고 벡터 \(v\) 가 있을 때, 아래 식과 같이 정의 됩니다.

• \[v = P - Q \tag{1}\]
• \[P = Q + v \tag{2}\]

• 식(1)을 통하여 포인트 - 포인트는 벡터가 됨을 알 수 있고 식(2)를 통하여 포인트 더하기 벡터는 포인트가 됨을 알 수 있습니다.
• 단순히 벡터만 존재하는 벡터 공간 (Vector Space)에서 포인트를 도입하여 위치 정보가 추가되면 이 때부터 어파인 공간 (Affine Space)이라고 부르게 됩니다. 벡터 공간에서 발생하는 transformation은 linear transformation이고 어파인 공간에서 발생하는 transformation은 affine transformation인데 가장 큰 차이점은 앞에서 언급한 바와 같이 이동 성분입니다.

• \[y = Ax \tag{3}\]
• \[y = Ax + b \tag{4}\]

• 식 (3)과 같이 변환할 때 linear transformation이고 식 (4)와 같이 변환할 때 affine transformation입니다. 즉 \(b\) 라는 이동 성분으로 인하여 affine transformation이 되는 것입니다.

• 그런데 여기서 affine transfomation 조차 \(y = Ax\) 와 같이 표현할 수 있을까요? 즉, 단순히 벡터에 transformation matrix를 곱하여 affine transformation을 하는 방법이 있을까요? 이 방법을 적용하기 위해서 homogeneous coordinate를 도입해야 합니다. 다시 말하면 포인트의 transformation과 벡터의 transformation을 한번에 표현하는 transformation matrix를 구해야 합니다.

• \[v = \begin{bmatrix} v_{x} \\ v_{y} \\ v_{z} \\ 0 \end{bmatrix} \tag{5}\]
• \[p = \begin{bmatrix} p_{x} \\ p_{y} \\ p_{z} \\ 1 \end{bmatrix} \tag{6}\]

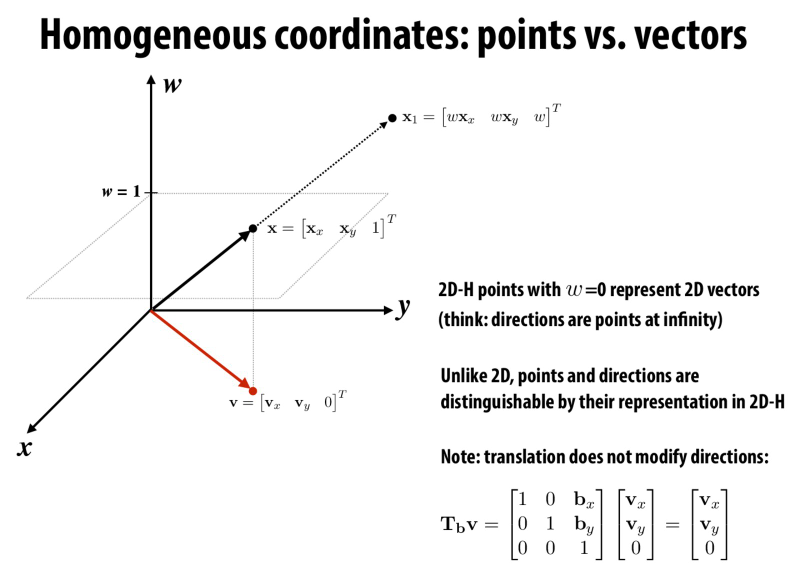
• 사용법을 먼저 다루고 상세 내용은 이후에 다루도록 하겠습니다. homogeneous coordinate의 사용 방법은 \(N\) 차원의 벡터와 포인트를 표현할 때, \(N + 1\) 차원의 벡터와 포인트를 사용하는 것입니다. 예를 들어 벡터의 경우 식 (5)와 같이 차원을 하나 추가하고 추가된 차원에는 0을 사용합니다. 반면 포인트의 경우 식 (6)과 같이 차원을 하나 추가하고 추가된 차원에는 1을 사용합니다.
• 예를 들어 2차원 실수 좌표계의 좌표값 \((x, y)\) 는 동차 좌표계에서 \((x, y, 1)\) 과 같이 표현되고 3차원 실수 좌표계의 좌표값 \((x, y, z)\) 는 동차 좌표계에서 \((x, y, z, 1)\) 과 같이 표현됩니다. 포인트를 나타날 때, 마지막 차원의 값이 0이 아닌 경우 모두 포인트 의미를 가지기 때문에 homogeneous 좌표 표현은 무한히 많이 존재하게 됩니다.
• 이와 같은 형태로 transformation matrix를 사용하게 되면 벡터와 포인트에 대하여 linear transformation과 translation을 하나의 transformation matrix로 표현할 수 있습니다.
• 만약 homogeneous coordinate에서 원래의 좌표를 구하려면 끝 자리가 1이 되도록 scale을 바꾼 후 1을 때어내면 됩니다. 예를 들어 homogeneous coordinate에서 \((x, y, \alpha) \to (x/\alpha, y/\alpha, 1)\) 로 바꾼 다음 2차원 실 수 좌표계에서는 \((x/\alpha, y/\alpha)\) 로 표현할 수 있습니다.

• 앞에서 설명한 내용을 다른 방식으로 한번 더 설명해 보도록 하겠습니다. 앞의 내용이 이해가 되셨으면 스킵하셔도 됩니다.
• homogeneous coordinate를 다루는 이유는 좌표계가 projection과 관련되어 있어 3차원에서 정의된 3차원 가상 공간 객체의 2차원에 투영된 이미지를 얻는 일과 관련되어 있기 때문이고 또 한가지 이유는 3차원 공간의 affine 변환들을 모두 4 x 4 행렬로 표현하기 위함입니다.
• 단순히 숫자 하나를 추가하여 표현한다면 2차원 공간의 좌표 \((x, y)\)는 \((x, y, 1)\)로 표현할 수 있습니다. 이와 같이 표현하면 보통 행벡터로 생각을 하고 열벡터로 표현할 경우 \([x, y]^{T}\) 또는 \([x, y, 1]^{T}\)로 표현합니다.
• 3차원 공간의 좌표를 표현하는 벡터 \([x, y, z]^{T}\) 는 homogeneous coordinate에서 \([x, y, z, 1]^{T}\) 로 표현할 수 있습니다. 보다 일반적인 형태는 마지막 숫자를 1이 아닌 다른 값도 가질 수 있도록 \(w\) 로 표현합니다.

• \[[x, y, w]^{T} \quad \text{2D homogeneous coordinate}\]
• \[[x, y, z, w]^{T} \quad \text{3D homogeneous coordinate}\]

• 위 그래프를 통해 homogeneous coordinate에 대한 직관적인 이해를 해보도록 하겠습니다. 위 그림에는 2개의 축이 있습니다. 하나는 \(x\) 축이고 다른 하나는 \(w\) 축입니다. homogeneous coordinate에서 마지막 원소 \(w\) 를 제외한 모든 성분은 이 \(x\) 축 값으로 보면 되고 마지막 원소는 \(w\) 축 값으로 생각하면 됩니다.
• \(x\) 축 위에 있지 않는 점 \(p\) 는 central projection 이라는 \(p'\) 를 가지게 되는데, central projection은 \(w = 1\) 의 직선 \(l\) 과 원점 \(o\)에서 \(p\) 를 연결한 직선의 교차점이 됩니다. 위 그래프에서 빨간색 선의 값들이 \(P'\) 값을 가지게 되는 과정을 central projection 이라고 합니다. (원점 \(o\) 는 center of projection (사영 중심)이라고 합니다.)
• 여기서 \(w\) 축과 \(x\) 축을 모두 포함한 차원의 공간을 이보다 한 차원 낮은 \(x\) 축 공간으로 떨어뜨릴 수 있는데 예를 들어 선분 \(\overline{op}\) 를 지나는 직선 위의 모든 점들이 \(p'\) 로 사영될 수 있습니다. 즉, \(p = (x, y) \to p' = (X, 1)\) 로 변경 가능합니다.
• 위 그림에서 삼각형 opq 와 op'q'를 이용하면 찾고자 하는 \(x\) 축 좌표 \(X\)는 \(\overline{oq'}\) 의 길이가 1이므로 이 길이와 \(\overline{p'q'}\) 길이의 비로 볼 수 있습니다.

• \[X = \frac{X}{1} = \frac{\vert p'q' \vert}{\vert oq' \vert}\]

• 닮은 삼각형의 성질을 이용하면 이것은 \(\vert pq \vert / \vert oq \vert\) 와 동일한 것을 알 수 있습니다. 그러므로 다음 식과 같이 바꿀 수 있습니다.

• \[X = \frac{X}{1} = \frac{\vert oq' \vert}{\vert p'q' \vert} = \frac{\vert oq \vert}{\vert pq \vert} = \frac{x}{w}\]

• 사영 기하에서 \(op\) 를 지나는 직선 위의 모든 점들은 \((x, w)\) 형태의 좌표로 표현할 수 있고, 이 모든 점들은 \(w = 1\) 인 평면으로 central projection을 수행하였을 때, \(w\) 좌표는 무의미해지면서 \((x/w)\) 의 좌표로 바뀌게 됩니다. 즉, 3차원 공간의 좌표를 표현하기 위해 homogeneous coordinate를 사용한다면 \([x, y, z, w]^{T}\) 의 형태가 되며, 이것은 위의 그림에서 \(w\) 축을 포함한 공간이 됩니다.
• 이와 같은 형태를 다시 3차원 좌표로 바꾸는 것은 central projection이 이루어지는 \(w = 1\) 평면으로 옮겨 놓는 것이고 이 때의 좌표는 \([x/w, y/w, z/w]^{T}\)가 되는 것입니다. 그리고 3차원 공간의 측면에서 보면 \(op\) 를 지나는 직선 위의 모든 점들이 동일한 점으로 간주됩니다.

• 다시 정리하면 3차원 좌표 \([x, y, z]^{T}\) 를 homogeneous coordinate 좌표로 바꾸는 간단한 방법은 \(w = 1\) 평면에서의 좌표인 \([x, y, z, 1]^{T}\) 로 옮기면 됩니다. 여기에 어떤 이점이 있을까요?
• 우선 단순한 좌표 표현에서는 구분할 수 없었던 좌표와 벡터의 구분이 가능해집니다. \([x, y, z]^{T}\) 가 3차원 좌표라면 이 좌표로 표현되는 지점은 3차원 공간내에 하나 밖에 없습니다. 하지만 이것이 벡터로 해석된다면 그것은 수많은 벡터를 표현하게 되며, 공간 내의 특별한 지점을 가리키지 않게 됩니다. 즉, 직교좌표계에서는 좌표(포인트)와 벡터는 분명히 다르지만 단순한 좌표 표현 방식으로는 구분이 불가능합니다.
• 하지만 homogeneous coordinate에서는 좌표와 벡터를 구분할 수 있습니다. 좌표는 \(w \ne 1\) 인 \([x, y, z, w]^{T}\) 입니다. 3차원 공간 좌표로의 변환은 앞에서 살펴본 바와 같이 \([x/w, y/w, z/w]^{T}\) 가 됩니다. 이 때, \(w\)에 \(k\) 를 곱한다면 \(x, y, z\) 에도 같은 \(k\) 를 곱해야 하므로 모두 같은 3차원 좌표라고 말할 수 있습니다.

• \[[kx, ky, kz, kw]^{T} = [x, y, z, w]^{T}\]

• 이 \(k\) 를 점점 0 에 접근시켜도 여전히 같은 값을 가지는데, \(k = 0\) 인 경우에는 전혀 다른 의미가 됩니다. 이제 \(w\) 좌표로 나누는 것이 불가능해 지는데 이렇게 \(w\) 축 값이 0인 경우에 벡터가 됩니다. \([x, y, z, 0]^{T}\) 는 위치를 가진 좌표 \([x, y, z]^{T}\) 가 아니라 위치가 없는 벡터 \([x, y, z]^{T}\) 가 됩니다.

• 앞에서 살펴본 바와 같이homogeneous coordinate의 실제 사용 측면에서의 이점은 이동 변환, 회전 변환와 같은 변환을 같은 차원의 행렬로 표현할 수 있다는 점입니다. 실세 사용 예시를 살펴보도록 하겠습니다.

Homogeneous coordinate의 사용 예시

• 그러면 homogeneous coodrdinate를 실제로 어떻게 사용하는 지 행렬곱을 통하여 알아보도록 하겠습니다.
• 먼저 이동 변환을 위한 translation matrix를 homogeneous coordinate 방식으로 나타내고 각각 homogeneous coordinate에서 벡터와 포인트에 각각 곱해보겠습니다.
• translation matrix를 이용하여 벡터 자체는 이동 할 수 없고 포인트는 이동할 수 있는 성질을 이용하여 homogeneous coordinate에서 translation matrix를 벡터와 포인트에 각각 곱하면 어떻게 되는지 살펴보겠습니다.

• \[\begin{bmatrix} 1 & 0 & 0 & d_{x} \\ 0 & 1 & 0 & d_{y} \\ 0 & 0 & 1 & d_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} v_{x} \\ v_{y} \\ v_{z} \\ 0 \end{bmatrix} = \begin{bmatrix} v_{x} \\ v_{y} \\ v_{z} \\ 0 \end{bmatrix} \tag{7}\]
• \[\begin{bmatrix} 1 & 0 & 0 & d_{x} \\ 0 & 1 & 0 & d_{y} \\ 0 & 0 & 1 & d_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_{x} \\ p_{y} \\ p_{z} \\ 1 \end{bmatrix} = \begin{bmatrix} p_{x} + d_{x} \\ p_{y} + d_{y} \\ p_{z} + d_{z} \\ 1 \end{bmatrix} \tag{8}\]

• 식 (7)에서 벡터는 이동 행렬을 곱하여도 변화가 없는 반면에 식 (8)에서 포인트는 이동 행렬을 곱하면 이동이 발생하는 것을 확인할 수 있습니다.
• 위 변환 행렬을 \(T_{d}\) 라고 하면 이동 변환은 다음과 같이 표현할 수 있습니다.

• \[p' = T_{d} p, \quad T_d \in \mathbb{R}^{4 x 4} \tag{9}\]

• 이동 변환 행렬 \(T_{d}\)의 역행렬은 어떻게 될까요? 역행렬은 이 행렬이 일으킨 변환을 원래대로 되돌려 놓는 것이므로 \(T_{-d}\) 로 표현할 수 있습니다.

• \[\begin{bmatrix} 1 & 0 & 0 & d_{x} \\ 0 & 1 & 0 & d_{y} \\ 0 & 0 & 1 & d_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix}^{-1} = \begin{bmatrix} 1 & 0 & 0 & -d_{x} \\ 0 & 1 & 0 & -d_{y} \\ 0 & 0 & 1 & -d_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \tag{10}\]

• 이번에는 회전 변환에 대하여 알아보도록 하겠습니다. homogeneous coodrdinate에서 회전변환을 어떻게 표현할 수 있는 지 생각해 보면 우선 3차원 공간에서 정의되었던 회전 변환을 \(R_{33}\) 이라고 하였을 때, homogeneous coodrdinate에서의 하나의 좌표가 4개의 성분을 가지므로 회전 행렬은 \(\mathbb{R}^{4 x 4}\)에 속해야 합니다. 이런 회전을 수행하는 회전 행렬을 \(R_{44}\) 라고 하겠습니다.
• homogeneous coodrdinate에서의 회전을 구하려면 3차원 좌표 \(p(x, y, z)\) 가 \(R_{33}\) 에 의해 \(p'(x', y', z')\) 로 옮겨질 때, homogeneous coodrdinate의 좌표 \(p(x, y, z, 1)\) 가 \(R_{44}\) 에 의해 회전하면 \(p'(x', y', z', 1)\) 로 옮겨지게 하면 됩니다.
• 원소가 모두 0인 3차원 열벡터를 \(O_{3}^{\text{col}}\) 이라 하고 원소가 모두 0인 행벡터를 \(O_{3}^{\text{row}}\) 라고 하면 \(R_{44}\) 를 다음과 같이 표현할 수 있습니다.

• \[R_{44} = \begin{bmatrix} R_{33} & O_{3}^{\text{col}} \\ O_{3}^{\text{row}} & 1 \end{bmatrix} \tag{11}\]

• homogeneous coodrdinate에서 \(x, y, z\) 축 기준 회전 행렬을 구하면 다음과 같습니다.

• \[R_{44}^{x} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos{(\theta)} & -\sin{(\theta)} & 0 \\ 0 & \sin{(\theta)} & \cos{(\theta)} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \tag{12}\]
• \[R_{44}^{y} = \begin{bmatrix} \cos{(\theta)} & 0 & \sin{(\theta)} & 0 \\ 0 & 1 & 0 & 0 \\ -\sin{(\theta)} & 0 & \cos{(\theta)} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \tag{13}\]
• \[R_{44}^{z} = \begin{bmatrix} \cos{(\theta)} & -\sin{(\theta)} & 0 & 0 \\ \sin{(\theta)} & \cos{(\theta)} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \tag{14}\]

• 지금까지 이동 변환과 회전 변환에 대하여 각각 다루어 보았습니다. 이제 변환 행렬은 이동 변환과 회전 변환을 계속 사용하면 변환을 누적하여 사용할 수 있습니다.
• 지금부터 다루어 볼 것은 이동 변환과 회전 변환을 한번에 표현하는 방법입니다. 먼저 ① 좌표 \(R_{44}\) 를 이용하여 회전하고 ② 이를 \(T_{d}\) 만큼 이동하는 변환을 생각해 보겠습니다. 이 변환은 어떤 점 \(p\) 가 있다면, 다음과 같이 \(p'\) 를 구하는 것입니다.

• \[p' = T_{d} R_{44}p \tag{15}\]

• 앞에서의 정의와 함께 3 x 3 크기의 항등 행렬을 \(I_{33}\) 이라고 하면 식 (15)를 다음과 같이 쓸 수 있습니다.

• \[p' = R_{44}T_{d} p = \begin{bmatrix} I_{33} & d \\ O_{3}^{\text{row}} & 1 \end{bmatrix} \begin{bmatrix} R_{33} & O_{3}^{\text{col}} \\ O_{3}^{\text{row}} & 1 \end{bmatrix} p = \begin{bmatrix} R_{33} & d \\ O_{3}^{\text{row}} & 1 \end{bmatrix} p \tag{16}\]

• homogeneous coodrdinate에서 어떤 변환이 회전과 이동으로만 이루어져 있다면 변환 행렬의 좌측 상단 3 x 3의 부분은 회전을 결정하고 최우측 열은 이동변환의 변위를 결정합니다.
• 식 (16)에 나타난 행렬의 역행렬은 어떻게 구할 수 있을까요? 가해진 변환을 역으로 수행할 것이므로 식 (16)의 반대 순서로 역행렬을 곱해주면 됩니다. 즉, 식 (16)에서 회전 변환 → 이동 변환 순으로 변환을 하였으므로 반대로 이동 역변환 → 회전 역변환 순으로 곱해주면 됩니다. 따라서 \(T_{-d}\) 의 이동을 먼저 수행하고 \(R_{33}^{-1}\) 의 회전을 수행하면 됩니다.
• 앞서 설명한 바와 같이 정규직교 행렬의 경우 전치 (transpose)가 역행렬이 되고 회정 행렬은 정규직교 행렬이기 때문에 \(R_{33}^{-1} = R_{33}^{T}\) 가 됩니다. 따라서 아래와 같이 회전 & 이동 행렬의 역행렬을 구할 수 있습니다.

• \[\begin{bmatrix} R_{33} & d \\ O_{3}^{\text{row}} & 1 \end{bmatrix}^{-1} = \begin{bmatrix} R_{33} & O_{3}^{\text{col}} \\ O_{3}^{\text{row}} & 1 \end{bmatrix}^{-1} \begin{bmatrix} I_{33} & d \\ O_{3}^{\text{row}} & 1 \end{bmatrix}^{-1} \tag{17}\]
• \[\begin{bmatrix} R_{33}^{T} & O_{3}^{\text{col}} \\ O_{3}^{\text{row}} & 1 \end{bmatrix} \begin{bmatrix} I_{33} & -d \\ O_{3}^{\text{row}} & 1 \end{bmatrix} = \begin{bmatrix} R_{33}^{T} & -R_{33}^{T}d \\ O_{3}^{\text{row}} & 1 \end{bmatrix} \tag{18}\]

• homogeneous coodrdinate에서 변환행렬이 있는데, 만약 \(R_{33}\) 부분이 정규직교가 아니라면, 이 행렬은 회전과 이동 이외에 크기변환 등이 추가되어 있는 형태로 유추할 수 있습니다.

• 이와 같은 복합 변환에 대하여 2가지 예제를 다루어 보겠습니다. ① \(y\) 축 회전과 이동에 대한 변환 예제, ② 좌표계 변환 예제 입니다.

y축 회전과 이동에 대한 변환 예제

• \[\begin{bmatrix} \cos{(\theta)} & 0 & \sin{(\theta)} & d_{x} \\ 0 & 1 & 0 & d_{y} \\ -\sin{(\theta)} & 0 & \cos{(\theta)} & d_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} v_{x} \\ v_{y} \\ v_{z} \\ 0 \end{bmatrix} = \begin{bmatrix} v_{x}\cos{(\theta)} + v_{z}\sin{(\theta)} \\ v_{y} \\ -v_{x}\sin{(\theta)} + v_{z}\cos{(\theta)} \\ 0 \end{bmatrix} \tag{9}\]
• \[\begin{bmatrix} \cos{(\theta)} & 0 & \sin{(\theta)} & d_{x} \\ 0 & 1 & 0 & d_{y} \\ -\sin{(\theta)} & 0 & \cos{(\theta)} & d_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} p_{x} \\ p_{y} \\ p_{z} \\ 1 \end{bmatrix} = \begin{bmatrix} p_{x}\cos{(\theta)} + p_{z}\sin{(\theta)} + d_{x} \\ p_{y} + d{y} \\ -p_{x}\sin{(\theta)} + p_{z}\cos{(\theta)} + d_{z} \\ 1 \end{bmatrix} \tag{10}\]

• 식 (9)와 식 (10) 에 사용된 transformation matrix는 모두 \(y\) 축에 대한 회전과 이동행렬을 적용한 것입니다.
• 식 (9)의 결과를 보면 벡터는 회전만 할 뿐 이동은 발생하지 않음을 알 수 있습니다.
• 반면 식 (10)의 결과를 보면 포인트는 원점에 대해 회전하고 이동함을 알 수 있습니다.

• 이와 같이 위 식들의 결과를 통해 homogeneous coordinate 상에서 transformation matrix를 만들면 벡터와 포인트 각각에 대하여 행렬곱 연산만으로 transformation을 할 수 있음을 알 수 있었습니다.

좌표계 변환 예제

• 어떤 점 \(p\) 가 좌표계 \(A\) 에서는 \(p_{A}\) 라고 정의된다고 가정하겠습니다. 이 점을 다른 좌표계 \(B\) 의 입장에서 보면 다른 좌표 \(p_{B}\)가 됩니다. 이렇게 좌표계가 달라질 때 바뀐 좌표계에 따라 새로운 좌표를 계산해야 합니다.
• 대표적인 경우가 가상 공간 내의 모든 객체의 위치를 하나의 기준으로 정의하는데에 필요한 global coordinate system이며, 다른 하나는 개별 객체 내에 정의된 local coordinate system입니다. 가상 공간에서 객체들이 이동, 회전 변환 등을 통해 위치와 방향이 바뀌어 있을 때, 이 객체를 구성하는 기하 정보의 좌표는 global coordinate system를 기준으로 변경됩니다. 하지만 이 객체가 변형을 일으키지 않는다면 local coordinate system을 기준으로 한 기하 정보는 언제나 일정하게 유지됩니다.
• 그러면 좌표계가 변경되었을 때 좌표가 어떻게 바뀌는 지 살펴보도록 하겠습니다.

• 아래는 좌표계의 이동을 나타냅니다.

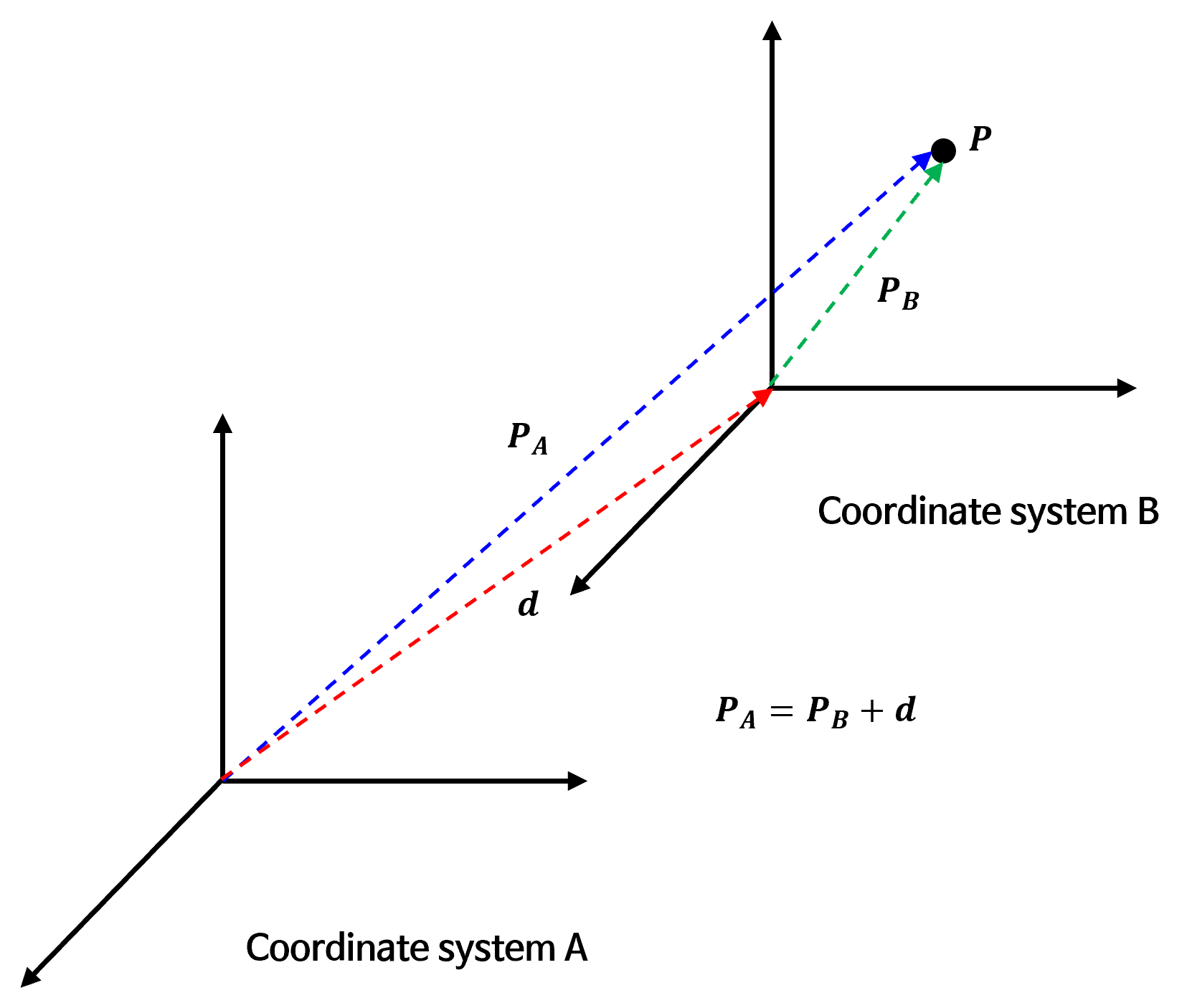
• 위 그림의 좌표계에서 나타난 바와 같이 일정한 변위 벡터 \(d\) 에 의해 좌표계 \(A\) 가 좌표계 \(B\) 로 이동했다고 가정하겠습니다. 이렇게 좌표계가 이동하였을 때 원래의 좌표계를 \(A\), 옮겨간 좌표계를 \(B\) 라고 하면 어떤 하나의 점 \(p\) 가 각각의 좌표계에서 같은 좌표를 \(p_{A}\) 와 \(p_{B}\) 라고 하겠습니다.
• 두 좌표의 관계는 \(p_{A} = p_{B} + d\) 로 표현할 수 있습니다. 행렬로 표현하면 좌표계를 옮겨 놓는 변환 행렬 \(T_{d}\) 와 좌표 \(p_{A}, p_{B}\) 는 다음과 같습니다.

• \[T_{d} = \begin{bmatrix} 1 & 0 & 0 & d_{x} \\ 0 & 1 & 0 & d_{y} \\ 0 & 0 & 1 & d_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \tag{11}\]
• \[p_{A} = T_{d} p_{B} \tag{12}\]
• \[p_{B} = T_{d}^{-1} p_{A} \tag{13}\]

• 아래는 좌표계의 회전을 나타냅니다.

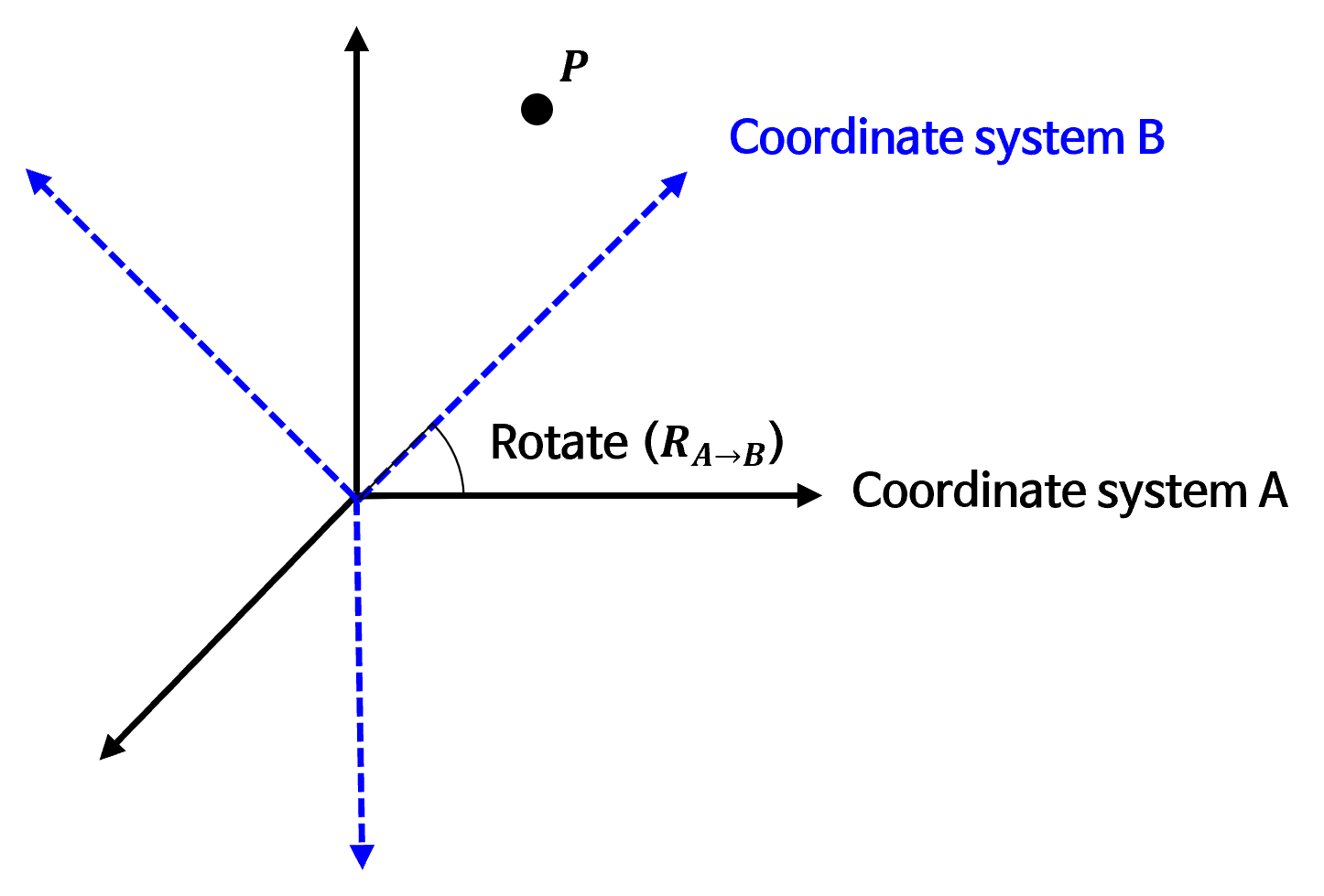
• 위 그림의 좌표계와 같이 회전 행렬 \(R_{A \to B}\) 에 의해 \(A\) 에서 \(B\) 로 회전되었다고 가정해 보겠습니다. 이 경우 각각의 좌표계를 기준으로 \(p\) 의 좌표를 정했을 때 얻어지는 좌표를 각각 \(p_{A}, p_{B}\) 라고 하겠습니다. 이 때, 두 좌표 사이에는 다음과 같은 관계가 존재합니다.

• \[p_{A} = R_{A \to B} p_{B} \tag{14}\]
• \[p_{B} = R_{A \to B}^{-1}p_{A} = R_{A \to B}^{T}p_{A} \tag{15}\]

• 회전 행렬이 정규 직교 (orthonormal) 이라는 것과 정규직교인 행렬의 역행렬은 전치를 이용하여 쉽게 구할 수 있다는 사실을 이용하여 식 (15)를 전개하였습니다.

• 아래는 좌표계의 회전과 이동이 동시 발생을 나타냅니다.

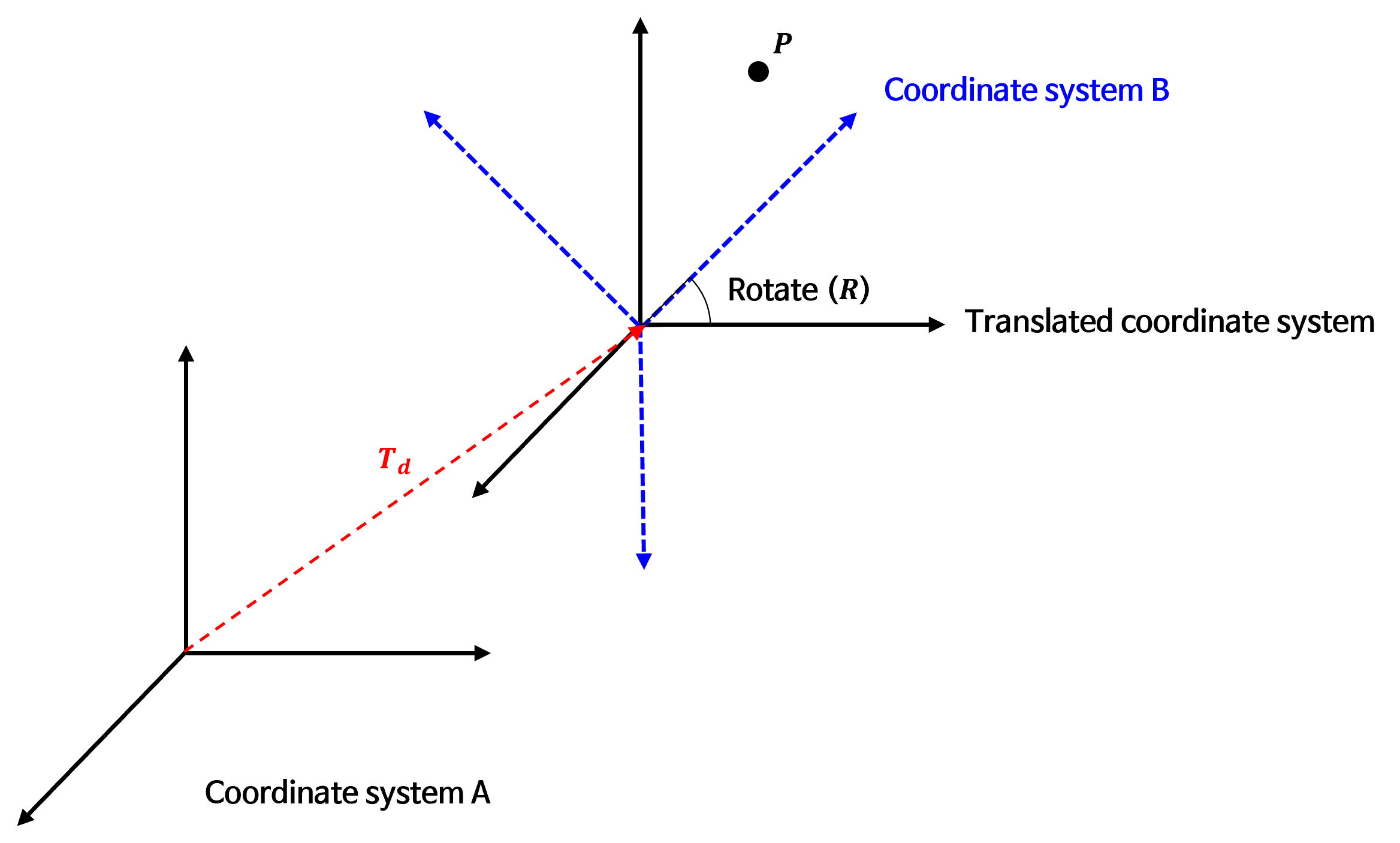
• 위 그림의 좌표계는 이동과 회전 두가지 변환이 함께 적용된 예시입니다. 먼저 회전 변환 행렬 \(R\) 로 회전한 다음에 이동 변환 행렬인 \(T_{d}\) 를 이용하여 이동한 것입니다.
• 회전 행렬 \(R\) 과 이동 변환 행렬 \(T_{d}\) 가 homogeneous coordinate에서 정의되는 4 x 4 행렬이라면 다음과 같이 표현할 수 있습니다.

• \[R = \begin{bmatrix} R_{33} & 0 \\ O_{3}^{\text{row}} & 1 \end{bmatrix} \tag{16}\]
• \[T_{d} = \begin{bmatrix} I_{33} & d \\ O_{3}^{\text{row}} & 1 \end{bmatrix} \tag{17}\]

• 회전이 먼저 이루어지고 이동이 그 다음에 수행되므로 복합 변환은 \(T_{d} R\) 이 됩니다.

• \[T_{d}R = \begin{bmatrix} R_{33} & d \\ O_{3}^{\text{row}} & 1 \end{bmatrix} \tag{18}\]

• 좌표 \(p\) 를 각각의 좌표계에서 표현하는 좌표 \(p_{A}\) 와 \(p_{B}\) 사이의 변환은 다음과 같습니다.

• \[p_{A} = \begin{bmatrix} R_{33} & d \\ O_{3}^{\text{row}} & 1 \end{bmatrix} p_{B} \tag{19}\]
• \[p_{B} = \begin{bmatrix} R_{33}^{T} & R_{33}^{T}d \\ O_{3}^{\text{row}} & 1 \end{bmatrix} p_{A} \tag{20}\]

• 좌표계 변환과 관련된 좀 더 자세한 내용을 확인하고 싶으시면 아래 링크를 참조하시기 바랍니다.
  • 링크 : https://gaussian37.github.io/vision-concept-calibration/

Homogeneous coordinate 내용 정리

• 지금까지 homogeneous coordinate의 의미와 사용 방법에 다루어 보았습니다. 그러면 이 좌표계를 왜 사용하는 것일까요? 가장 직접적인 이유는 projective transformation을 편리하게 다루기 위함입니다.
• 카메라 영상과 관련된 예제를 살펴보면 쉽게 설명할 수 있습니다. 예를 들어 카메라 영상은 3차원 공간에 있는 점들을 이미지 평면에 projection시킨 것입니다. 카메라 초점과 투영된 점을 연결하면 하나의 긴 projection ray가 나오게 되며 이 선 상에 있는 모든 점들은 모두 동일한 한 점으로 투영됩니다. 따라서 이미지 평면상의 한 점에 대한 homogeneous 좌표는 이 점으로 투영되는 projection ray 상의 모든 점들을 한꺼번에 표현하는 방법이 됩니다.

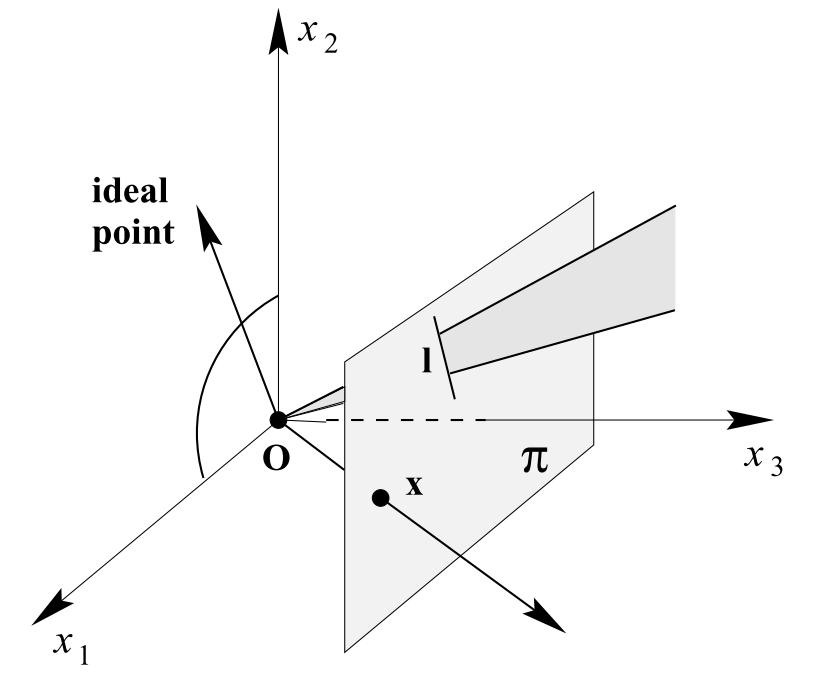
• 위 그림과 같이 3차원 좌표계에서 2차원 평면으로 투영을 한다고 가정해 보겠습니다. 이와 같은 투영을 projective transformation 통해 발생하게 되는데 원점으로부터 얼만큼 떨어져 있는 평면에 투영하느냐에 따라서 투영한 결과가 달라지게 됩니다.
• 물론 3차원 좌표계에서는 의미하는 점이 변하지 않지만 투영하고자 하는 평면에 따라서 평면 상에서의 값은 달라지게 됩니다.

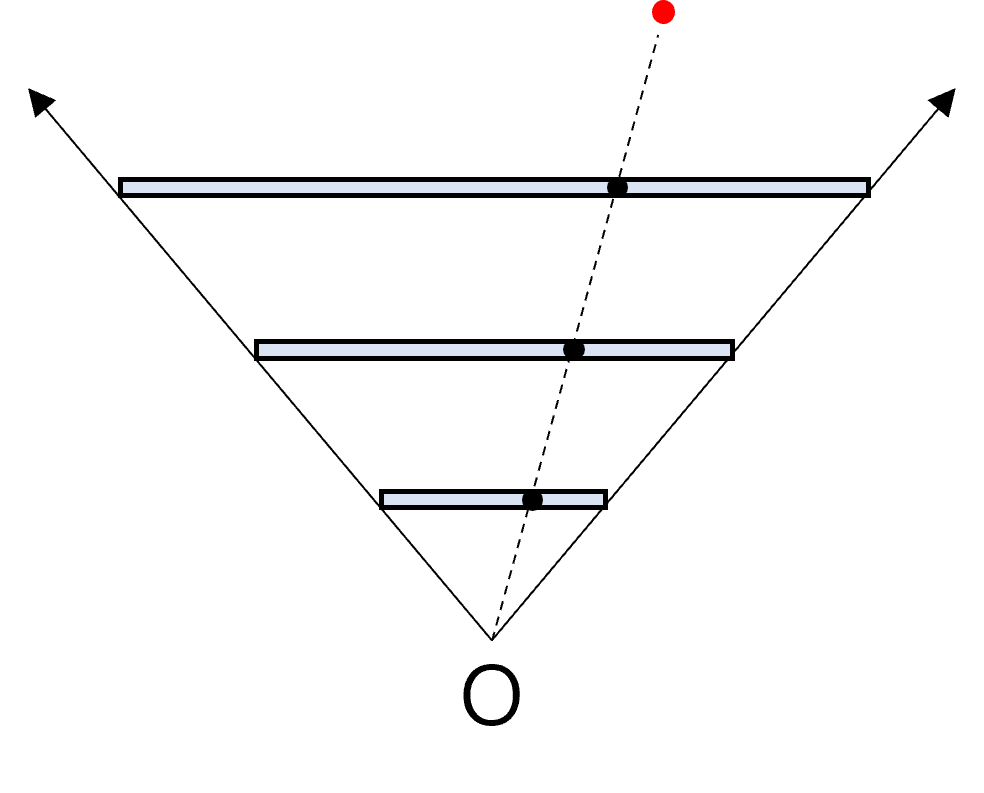
• 위 그림과 같이 3차원 상에서 빨간색 점이 존재하고 이 점을 2차원 평면에 투영한다고 하였을 때, 어떤 평면에 투영하는 지에 따라서 같은 점이 다른 좌표에 표현되게 됩니다.
• 그런데 같은 평면이 달라진다고 해서 값이 의미 없이 달라지는 것은 아니고 스케일에 비례하여 달라지는 것을 알 수 있습니다. (간단한 도형의 닮음을 이용하여 비례하는 것을 살펴보면 됩니다.)
• 이 때, 스케일을 의미하는 것이 앞에서 살펴본 추가된 차원의 값입니다. 추가된 차원을 \(w\) 라고 하겠습니다. (\(x, y, z\) 축과 별도로 \(w\) 축을 추가하였음)
• 앞에서 포인트의 경우 \(w = 1\) 을 적용하였습니다. 이것의 의미는 normalized 된 평면에 3차원 좌표의 어떤 점을 2차원 normalized 평면에 투영시킨 것을 의미합니다. 만약 \(w = 2\)가 된다면 normalized 평면보다 원점에 2배 가깝게 투영된 것입니다. 반대로 \(w = 0.5\)가 되면 normalized 평면보다 원점에서 2배 멀게 투영된 것입니다.
• 만약 \(w = 0\)이 된다면 어떻게 될까요? 이 경우 투영되는 평면이 무한대로 멀어지게 되어 단순히 평면에 투영되는 점이 아닌 무한대로 뻗어나아가는 벡터로 이해할 수 있습니다. 따라서 따로 무한대의 표현을 하지않고 \(w = 0\)을 사용하면 평면에 투영되는 특정 점이 아닌 벡터로 나타낼 수 있습니다.

• 지금 까지 내용을 다시 정리하면 동차 좌표계는 벡터와 포인트를 같이 표현할 수 있는 좌표계 라는 특성이 있고 이 특성을 이용하여 Projective Transformation 할 때, 포인트와 벡터가 서로 변환될 수 있는 관계임을 확인하였습니다. 이 성질로 인하여 Affine/Perspective Transform 형태를 행렬곱 형태 \(y = Ax\) (Linear Transformation)로 나타낼 수 있으므로 Affine/Perspective Transform이 연속적으로 발생하더라고 Linear Transformation형태로 나타낼 수 있다는 점이 동차 좌표계를 사용할 때 큰 이점이라고 말할 수 있습니다.