카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습

Vision 관련 글 목차

논문 : A Flexible New Technique for Camera Calibration

참조 : https://ms-neerajkrishna.medium.com/
참조 : https://darkpgmr.tistory.com/32
참조 : https://www.mathworks.com/help/vision/ug/camera-calibration.html
참조 : https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0165487
참조 : https://blog.immenselyhappy.com/post/camera-axis-skew/
참조 : https://youtu.be/-9He7Nu3u8s
참조 : 캘리브레이션 판 제작 샘플

이번 글에서는 컴퓨터 비전을 위한 카메라 내용 및 카메라 캘리브레이션 관련 내용과 파이썬을 이용하여 실습을 해보도록 하겠습니다.
먼저 카메라 캘리브레이션에서 사용되는 Intrinsic과 Extrinsic의 개념에 대하여 알아보고 마지막으로 A Flexible New Technique for Camera Calibration 또는 Zhang's Method라고 불리는 카메라 캘리브레이션 방법론에 대하여 살펴보도록 하겠습니다.
본 글에서는 Intrinsic, Extrinsic 설명의 편의를 위하여 Pinhole Camera를 가정하고 설명하였으나 실제 카메라 캘리브레이션을 다룰 때에는 Distortion까지 구해야 합니다. 따라서 카메라 캘리브레이션 내용을 읽기 이전에는 다음 글에서 렌즈 왜곡에 대한 개념을 먼저 숙지하시기 바랍니다.
- 카메라 모델과 렌즈 왜곡 (lens distortion)

이미지 형성과 핀홀 모델 카메라
Camera Extrinsic Matrix with Example in Python
Camera Extrinsic 변환 애니메이션
Camera Intrinsic Matrix with Example in Python
Camera Intrinsic 변환 애니메이션
Transformation 관점의 Camera Extrinsic과 Intrinsic
이미지 crop과 resize에 따른 intrinsic 수정 방법
OpenCV의 Zhang’s Method를 이용한 카메라 캘리브레이션 실습
Rotation, Translation을 이용한 카메라 위치 확인

이미지 형성과 핀홀 모델 카메라

이미지 형성의 기본 아이디어는 object에서 medium으로 반사되는 광선(Rays)을 포착하는 것에서 부터 시작합니다.
가장 단순한 방법은 object 앞에 medium을 놓고 반사되어 들어오는 광선을 캡쳐하면 됩니다. 하지만 단순히 이러한 방식으로 하면 필름 전체에 회색만 보일 수 있습니다. 왜냐하면 object의 다른 지점에서 나오는 광선이 필름에서 서로 겹쳐서 엉망이 되기 때문입니다.

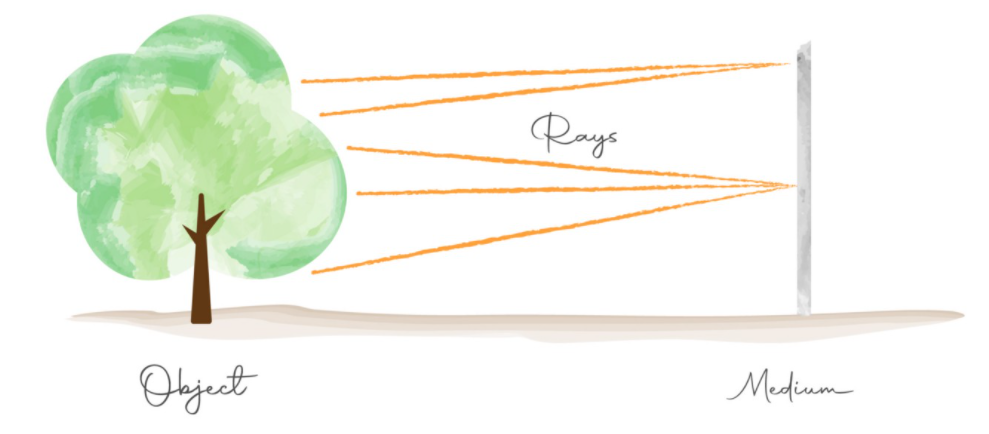
위 그림을 살펴보면 object에서 부터 반사되어 나온 광선이 medium의 같은 위치에서 수집될 수 있습니다. 이런 경우 object로 부터 반사되어 나온 위치의 형상을 정확히 알 수 없습니다.

Pinhole camera

반면 다음 그림과 같이 중간에 차단막이 생기고 차단막에 구멍을 만든 구조로 medium에 상을 맺히게 할 수 있습니다.

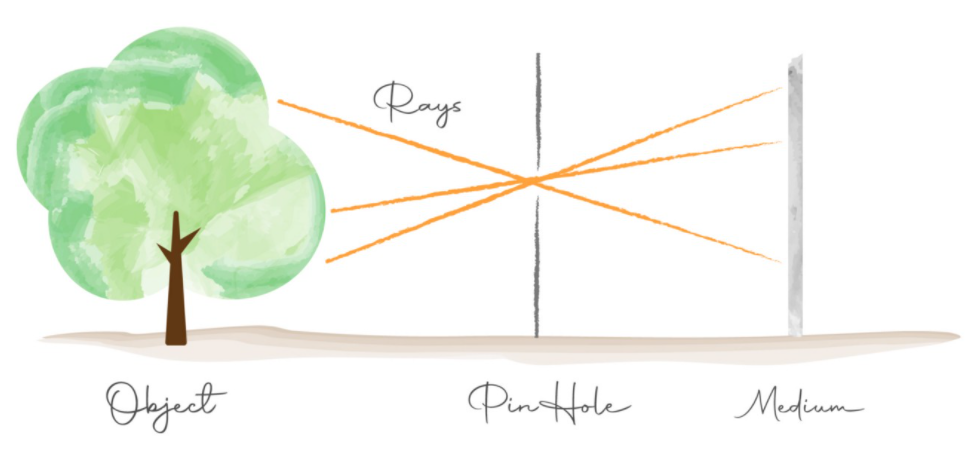
위 그림의 차단막에 생긱 구멍을 pinhole이라고 하며 pinhole 구조를 이용하면 object의 어떤 위치가 medium의 일대일 대응이 될 수 있도록 만들어 줄 수 있습니다. 이와 같은 방법을 이용하여 medium의 한 픽셀에 object의 여러 부분이 겹치는 문제를 개선할 수 있습니다.
이와 같이 pinhole을 이용하여 상을 맺히게 하는 방식의 카메라를 pinhole 카메라라고 합니다. 다음 영상을 참조하시면 더 쉽게 이해가 되실 것입니다.

pinhole 카메라에 상이 맺히는 것을 보면 다음과 같이 상이 뒤집혀서 맺혀지는 것을 확인할 수 있습니다. (위 영상에도 동일한 현상이 발생합니다.)

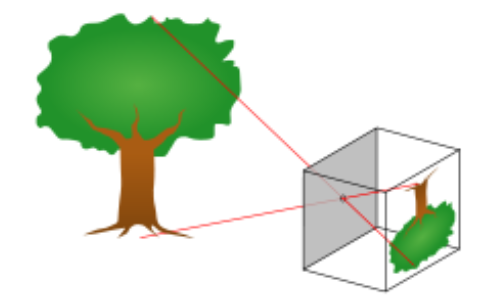
빛이 투영되는 원리를 이용하므로 이와 같은 현상이 발생하나 실제 이미지를 형성할 때에는 상하 반전되어 우리가 실제 보는 듯한 이미지로 만들어 주게 됩니다.

핀홀 카메라 모델은 대부분의 컴퓨터 비전 분야에서 기본적으로 사용됩니다. 왜냐하면 빛이 직진하여 들어온다는 조건이 물체의 위치와 관련된 다양한 알고리즘을 적용할 때 단순한 조건을 만족시키기 때문입니다.

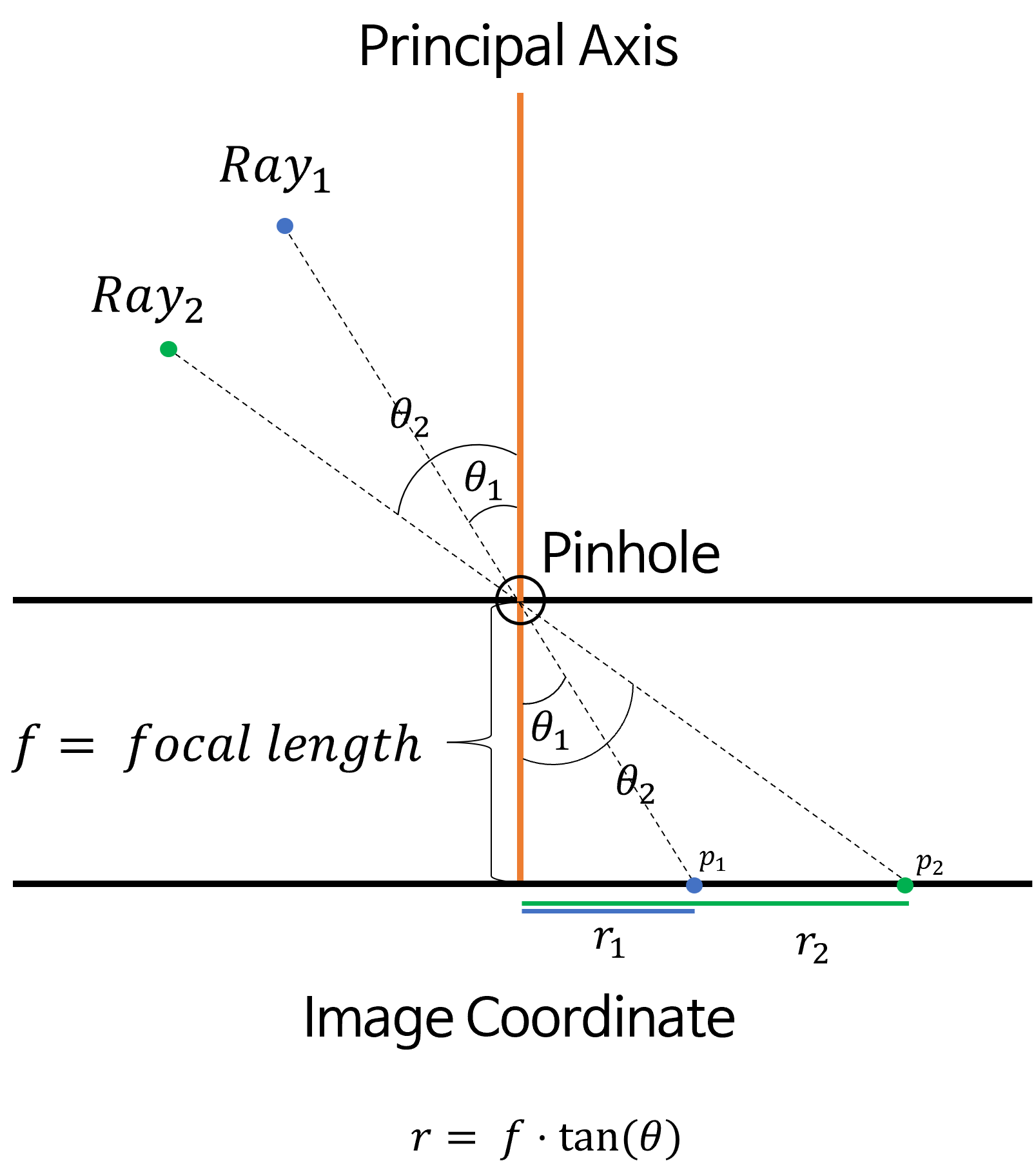
위 그림과 같이 빛이 들어오는 입사각 \(\theta\) 가 결정되면 빛이 이미지에 투영되는 위치 또한 \(r = f \cdot \tan{(\theta)}\) 로 결정이 됩니다.
여기서 \(f\) 는 focal length이고 \(r\) 은 principal point에서 부터 빛이 투영된 위치까지의 거리입니다. 이 내용은 뒷부분에서 살펴볼 예정입니다. 중요한 점은 \(f\) 는 상수이고 변수는 \(\theta\) 이므로 단순히 \(theta\) 만 결정되면 이미지에서의 위치가 정해지게 됩니다.

핀홀 카메라 모델은 이와 같은 간단한 원리로 구성이 되지만 빛의 양을 많이 모을 수 없어서 2가지 단점이 생기게 됩니다. ① 상이 흐리게 보이고 ② 넓은 영역을 (넓은 화각) 보기 어렵습니다.
따라서 넓은 영역의 빛을 많이 모으기 위하여 카메라 렌즈를 사용하는 것이 일반적입니다. 이와 같은 경우에는 빛이 직진해서 투영되지 않고 굴절되기 때문에 앞선 예시만큼 단순하지 않습니다. 관련 내용은 아래 링크에서 확인할 수 있습니다.
- 카메라 모델과 렌즈 왜곡 (lens distortion)

따라서 일반적으로 카메라 렌즈를 이용하여 넓은 화각의 선명한 영상을 확보하고 렌즈에 의해 발생한 왜곡을 보정하는 방법을 사용하여 핀홀 모델과 같이 만들어 줍니다. 이러한 방법을 왜곡 보정이라고 합니다. (이 부분은 본 글에서 다루고자 하는 범위를 넘기 때문에 다루지 않겠습니다.)

본 글의 내용을 다루기 이전에 몇 가지의 용어 정리를 하도록 하겠습니다.

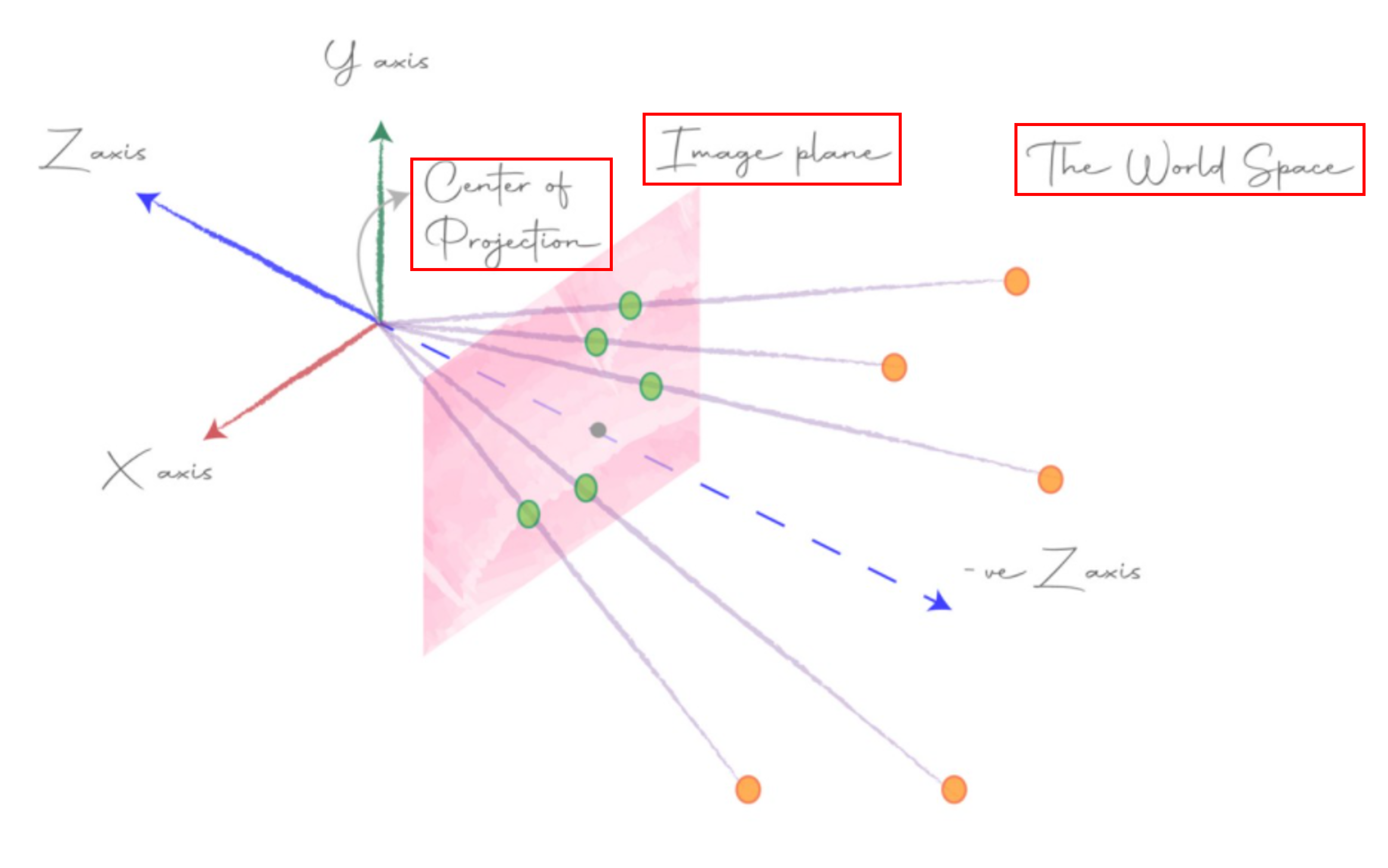
위 그림의 world space는 실제 3D 공간을 의미하며 노란색 점들은 world space에 존재하는 물체를 의미합니다.
노란색 점으로부터 center of projection 까지 이어진 선을 앞에서 다룬 ray 라고 합니다.
world space에서 부터 반사된 수많은 광선은 center of projection 또는 camera center라고 하는 지점으로 수렴됩니다.
이러한 가정을 이용하면 world space에 있는 물체들이 image plane에 투영되고 최종적으로 center of projection (camera center)로 수렴되는 구조로 이해할 수 있습니다.
image plane은 XY plane과 평행하고 center of projection과 일정 거리 떨어져 있습니다. 이 거리를 focal length라고 하며 이후에 다룰 예정입니다.
위 예시에서도 핀홀 카메라 모델로 가정하였기 때문에 빛이 직진으로 들어간 것으로 이해하시면 됩니다.

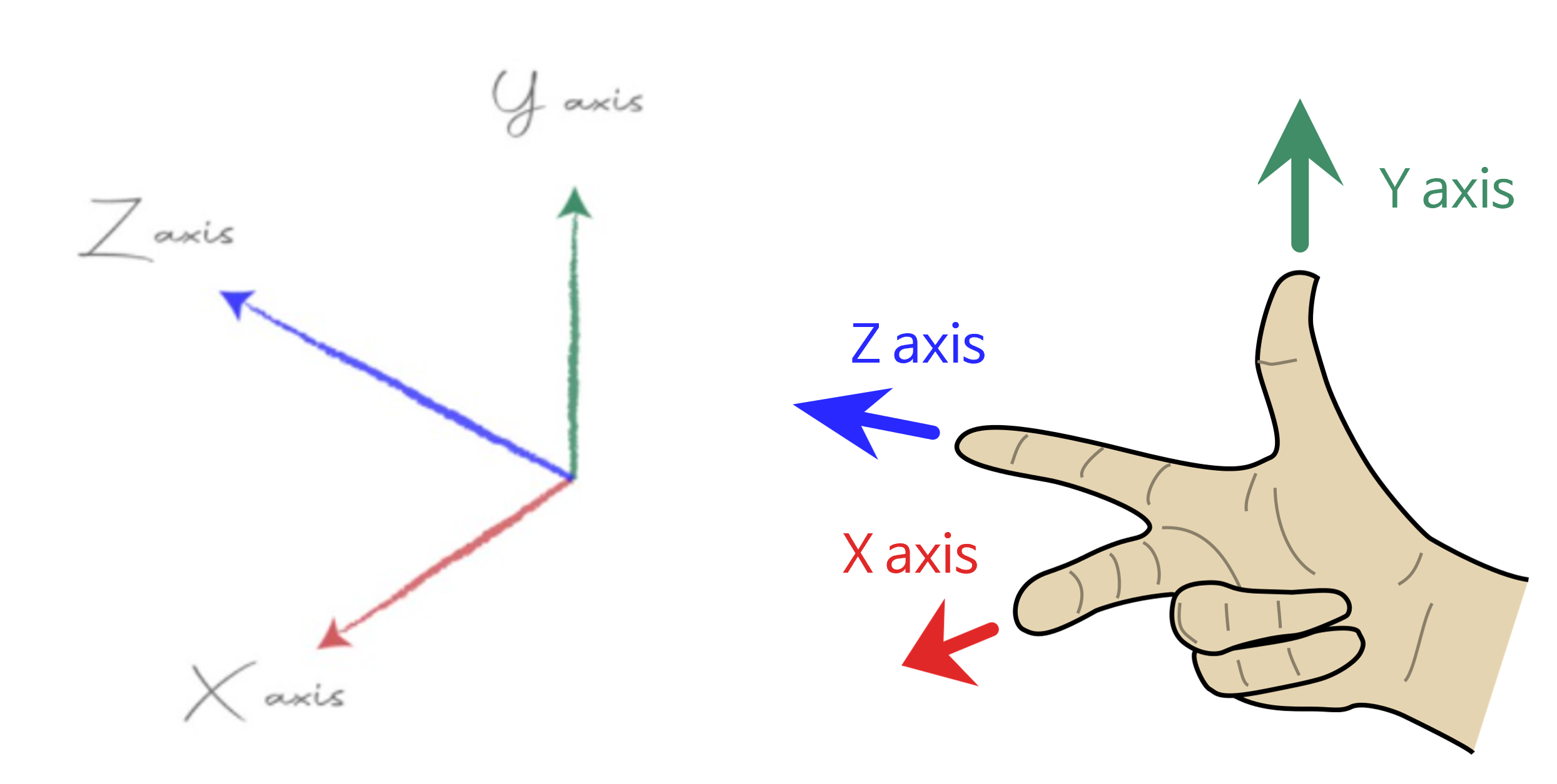
좌표계는 위 그림과 같으며 오른손으로 엄지, 검지, 중지로 나타내었을 때, 각각 y, z, x 축을 가리킵니다. 이를 참조하여 좌표계를 이해하시면 됩니다.

Geometric camera calibration

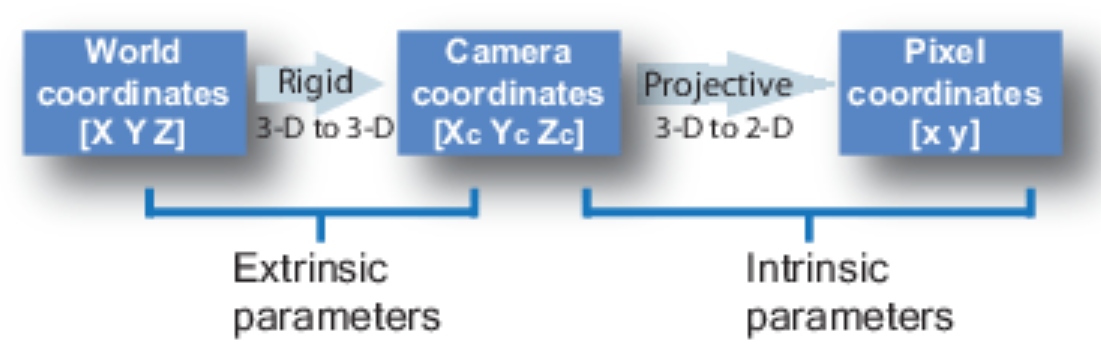
카메라는 어느 위치에나 장착될 수 있고 카메라가 보는 방향도 제각각 입니다. 여기서 해결해야 할 점은 world space에서 반사되어 들어오는 광선을 어떻게 image plane에 투영할 지 정해야 한다는 것입니다. 바꿔 말하면 world space와 image plane 간의 관계를 알아내어야 실제 이미지를 만들어 낼 수 있습니다.
이 관계는 world space → image plane으로 변환하는 행렬을 구해야 하며 이 때 필요한 2가지 행렬을 extrinsic, intrinsic 이라고 합니다.
extrinsic : world space의 좌표계를 world coordinate system이라고 하고 앞에서 \(X, Y, Z\) 축으로 표현한 좌표계를 camera coordinate system이라고 합니다. 이 때, world coordinate system → camera coordinate system으로 좌표계를 변환할 때 사용하는 행렬을 extrinsic이라고 합니다. 이 행렬은 카메라가 실제 장착된 위치 등의 환경과 관련이 있습니다.
intrinsic : camera coordinate system의 점들을 image plane의 좌표로 변환하는 행렬을 intrinsic이라고 합니다. 이 행렬은 카메라 내부 환경과 관련이 있습니다.
임의의 카메라에서 extrinsic과 intrinsic은 제공되는 경우도 있지만 대부분 직접 구해야 합니다. 이 값을 알아야 카메라와 3D 공간 상의 관계를 알 수 있기 때문입니다. 따라서 카메라의 extrinsic, intrinsic 정보를 구하는 것을 카메라 캘리브레이션이라고 합니다.

Camera Extrinsic Matrix with Example in Python

카메라가 설치되는 위치와 방향에 따라 world coordinate system에서 camera coordinate system으로 변형하기 위하여 extrinsic이 필요하다고 앞에서 설명하였습니다.
만약 물체 3D 좌표 기준이 camera coordinate system이라면 extrinsic은 필요하지 않으나 world coordinate system 상에서 물체의 3D 좌표가 형성되어 있다면 카메라 좌표계 기준으로 좌표값을 변경해야 합니다.

extrinsic은 world coordinate system와 camera coordinate system 간의 좌표 관계를 나타내기 때문에 extrinsic을 알기 위해서는 world coordinate system 대비 카메라의 방향과 위치를 알아야 합니다.
이것을 알기 위해서는 world coordinate system 대비 카메라의 ① rotation과 ② translation에 대한 변환이 어떻게 되어있는 지 알아야 합니다. world space 상에서의 좌표 기준이 있고 그 좌표계에서 카메라가 얼만큼 회전(rotation)이 되었는 지를 알고 카메라가 얼만큼 이동(translation)하였는 지 알면 카메라 좌표계 상에서의 위치 변화를 알 수 있습니다.

지금부터 살펴볼 내용은 rotation과 translation 각각에 대하여 좌표축 변환을 어떻게 하는 지 살펴보려고 합니다. 좌표축 변환을 확인하기 위하여 먼저 ① 같은 좌표축 내에서 점 \(P \to P'\) 로 rotation과 translation을 하는 방법에 대하여 알아보고 ② 좌표축1의 점 \(P\) 가 좌표축2에서는 어떤 좌표값을 가지는 지 살펴보도록 하겠습니다.
이와 같이 좌표축 변환을 통하여 좌표가 어떻게 바뀌는 지 알아보는 이유는 world space 상의 world coordinate system에서 camera coordinate system으로 좌표축 변환을 하기 위함입니다.

좌표 변환 (Change of coordinates) 을 이용한 회전 (Rotation)

점 \(P\)가 \(\theta\) 만큼 회전하였을 때 좌표를 구하기 위하여 다음 그림을 참조해 보도록 하겠습니다.

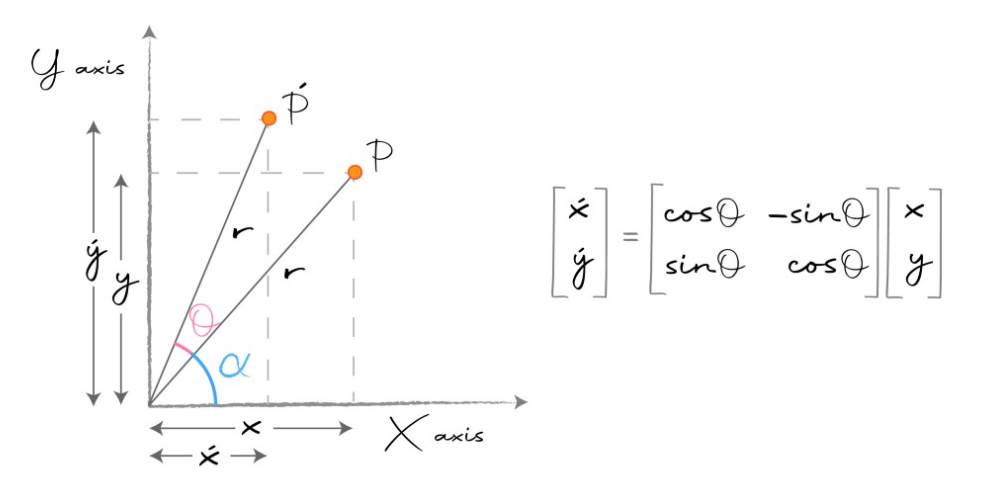
위 예시는 2차원 (\(\mathbb{R}^{2}\)) XY 평면에서 점 \(P\) 를 \(\theta\) 만큼 회전하여 \(P'\) 를 얻을 때 사용하는 행렬을 나타냅니다. 그러면 위 그래프를 기준으로 식을 전개해 보도록 하겠습니다.
먼저 \(\alpha\) 각도에 대하여 다루어 보도록 하곘습니다.

\[\sin{(\alpha)} = \frac{y}{r}, \cos{(\alpha)} = \frac{x}{r} \tag{1}\]

위 식에서 \(r\) 을 기준으로 등식을 만들어 정리하면 다음과 같이 두 식을 정리할 수 있습니다.

\[x\sin{(\alpha)} = y \cos{(\alpha)} \tag{2}\]

이번에는 \(\theta + \alpha\) 각도에 대하여 다루어 보도록 하겠습니다.

\[x' = r\cos{(\theta + \alpha)} \tag{3}\]
\[\cos{(\theta + \alpha)} = \cos{(\theta)}\cos{(\alpha)} - \sin{(\theta)}\sin{(\alpha)} \tag{4}\]

식(4)를 이용하여 식(3)을 전개해 보도록 하겠습니다.

\[\Rightarrow r\cos{(\theta + \alpha)} = r(\cos{(\theta)}\cos{(\alpha)} - \sin{(\theta)}\sin{(\alpha)}) \tag{5}\]
\[= r(\cos{(\theta)}\frac{x}{r} - \sin{(\theta)}\frac{y}{r}) = x\cos{(\theta)} - y\sin{(\theta)} \tag{6}\]
\[\therefore x' = x\cos{(\theta)} - y\sin{(\theta)} \tag{7}\]

이번에는 다른 식을 살펴보도록 하겠습니다.

\[y' = r\sin{(\theta + \alpha)} \tag{8}\]
\[\sin{(\theta + \alpha)} = \sin{(\theta)}\cos{(\alpha)} + \cos{(\theta)}\sin{(\alpha)} \tag{9}\]

식(7)을 전개하는 과정과 동일한 방식으로 식(8)을 식(9)를 이용하여 정리하면 다음과 같습니다.

\[y' = x\sin{(\theta)} + y\cos{(\theta)} \tag{10}\]

식 (7)과 식(10)을 묶어서 행렬로 나타내면 다음과 같습니다.

\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos{(\theta)} & -\sin{(\theta)} \\ \sin{(\theta)} & \cos{(\theta)} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \tag{11}\]

식(11)을 이용하면 점 \(P\)를 \(P'\) 로 변환할 수 있습니다.

위 예시는 2차원 평면에서의 회전 변환을 나타냅니다. 만약 3차원 평면에서의 회전이 발생하면 어떻게 될까요? 각 \(X, Y, Z\) 축 방향으로 회전 변환 행렬을 적용하면 됩니다. 변환 행렬은 다음과 같습니다.

\[R_{x}(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \text{cos}\theta & -\text{sin}\theta \\ 0 & \text{sin}\theta & \text{cos}\theta \end{bmatrix} \tag{12}\]
\[R_{y}(\theta) = \begin{bmatrix} \text{cos}\theta & 0 & \text{sin}\theta \\ 0 & 1 & 0 \\ -\text{sin}\theta & 0 & \text{cos}\theta \end{bmatrix} \tag{13}\]
\[R_{z}(\theta) = \begin{bmatrix} \text{cos}\theta & -\text{sin}\theta & 0 \\ \text{sin}\theta & \text{cos}\theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \tag{14}\]

전체 변환 행렬 \(R\) 은 \(R = R_{z}(\alpha)R_{y}(\beta)R_{x}(\gamma)\) 로 행렬 곱을 통해 나타낼 수 있습니다. \(\alpha, \beta, \gamma\) 각각은 각 축으로 회전한 각도를 의미합니다.

\[R = R_{z}(\alpha)R_{y}(\beta)R_{x}(\gamma) = \begin{bmatrix} \text{cos}\alpha & -\text{sin}\alpha & 0 \\ \text{sin}\alpha & \text{cos}\alpha & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \text{cos}\beta & 0 & \text{sin}\beta \\ 0 & 1 & 0 \\ -\text{sin}\beta & 0 & \text{cos}\beta \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \text{cos}\gamma & -\text{sin}\gamma \\ 0 & \text{sin}\gamma & \text{cos}\gamma \end{bmatrix} \tag{15}\]

\[R = \begin{bmatrix} \text{cos}\alpha \ \text{cos}\beta & \text{cos}\alpha \ \text{sin}\beta \ \text{sin}\gamma - \text{sin}\alpha \ \text{cos}\gamma & \text{cos}\alpha \ \text{sin}\beta \ \text{cos}\gamma + \text{sin}\alpha \ \text{sin}\gamma \\ \text{sin}\alpha \ \text{cos}\beta & \text{sin}\alpha \ \text{sin}\beta \ \text{sin}\gamma + \text{cos}\alpha \ \text{cos}\gamma & \text{sin}\alpha \ \text{sin}\beta \ \text{cos}\gamma - \text{cos}\alpha \ \text{sin}\gamma \\ -\text{sin}\beta & \text{cos}\beta \ \text{sin} \gamma & \text{cos}\beta \ \text{cos} \gamma \\ \end{bmatrix} \tag{16}\]

좌표축 변환 (Change of basis) 을 이용한 회전 (Rotation)

지금까지 살펴본 내용은 한 점 \(P\) 가 각 축의 방향으로 회전하였을 때 새로운 위치를 계산하는 방법에 대하여 알아보았습니다.
앞으로 살펴볼 내용은 좌표축이 회전할 때 각 좌표들이 어떻게 변경되는 지 살펴보도록 하겠습니다. 앞의 좌표 변환과 유사하지만 다소 차이점이 있으니 그 점을 유의해서 살펴보시면 됩니다.

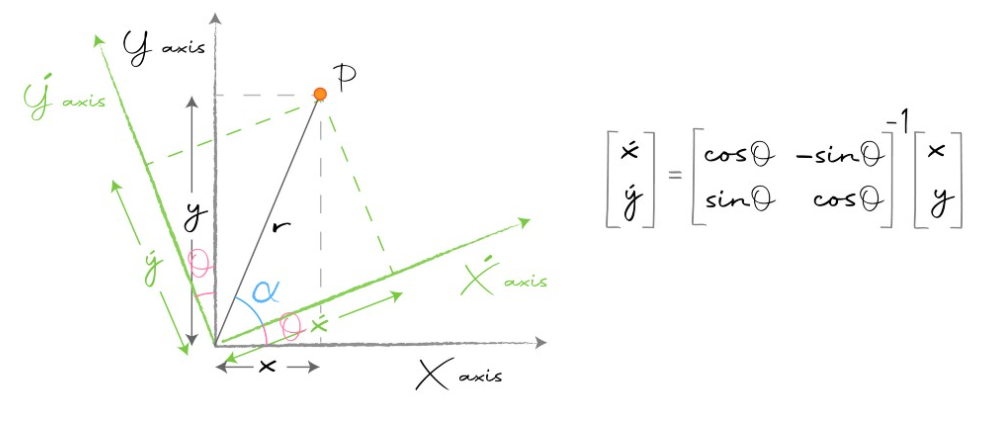
위 그래프를 살펴보면 기존의 \(X, Y\) 축이 이루는 평면을 \(X', Y'\) 평면이 이루는 축으로 변경을 해야 합니다.
XY 평면 상의 점 P가 X’Y’평면 상에서 어떤 좌표값을 가지는 지 알면 XY → X’Y’의 변환 관계를 알 수 있습니다.
결과는 위 그림의 행렬 식과 같이 회전 변환 행렬의 역행렬을 곱하면 됩니다.

\[\sin{(\alpha)} = \frac{y'}{r}, \cos{(\alpha)} = \frac{x'}{r} \tag{17}\]
\[\Rightarrow x'\sin{(\alpha)} = y'\cos{(\alpha)} \tag{18}\]
\[x = r\cos{(\theta + \alpha)} = \frac{x'}{\cos{(\alpha)}}\cos{(\theta + \alpha)} \tag{19}\]

식 (4)의 코사인 법칙을 이용하여 식을 전개합니다.

\[x = \frac{x'}{\cos{(\alpha)}}\cos{(\theta + \alpha)} = \frac{x'}{\cos{(\alpha)}}(\cos{(\theta)}\cos{(\alpha)} - \sin{(\theta)}\sin{(\alpha)}) \tag{20}\]
\[x = x'\cos{(\alpha)} - x'\sin{(\alpha)}\frac{\sin{(\theta)}}{\cos{(\alpha)}} \tag{21}\]

식 (21)에 식 (17)을 이용하여 \(x'\sin{(\alpha)}\) 을 \(y'\cos{(\alpha)}\) 로 대체한다.

\[x = x'\cos{(\alpha)} - y'\cos{(\alpha)}\frac{\sin{(\theta)}}{\cos{(\alpha)}} \tag{22}\]
\[x = x'\cos{(\alpha)} - y'\sin{(\theta)} \tag{23}\]

이 방법과 유사하게 아래 식 (24)를 식 (9)의 sin법칙과 식 (17)을 이용하여 전개하면 식 (25)와 같이 정리 됩니다.

\[y = r\sin{(\theta + \alpha)} = \frac{y'}{\sin{(\alpha)}}\sin{(\theta + \alpha)} \tag{24}\]
\[\Rightarrow x'\sin{(\theta)} + y'\cos{(\theta)} \tag{25}\]

따라서 basis를 회전하였을 때, 회전 변환 행렬은 다음과 같이 정리할 수 있습니다.

\[\begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \cos{(\theta)} & -\sin{(\theta)} \\ \sin{(\theta)} & \cos{(\theta)} \end{bmatrix} \begin{bmatrix} x' \\ y' \end{bmatrix} \tag{26}\]

변환의 최종 목적은 (x, y) → (x’, y’)로 변환하기 위한 행렬을 찾는 것이므로 아래와 같이 행렬식을 변경합니다.

\[\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos{(\theta)} & -\sin{(\theta)} \\ \sin{(\theta)} & \cos{(\theta)} \end{bmatrix}^{-1} \begin{bmatrix} x \\ y \end{bmatrix} \tag{27}\]

식 (27)과 같이 basis 행렬의 변환은 기존의 회전 변환 행렬을 역행렬 한 것으로 확인할 수 있습니다. 따라서 카메라의 extrinsic의 요소인 Rotation 정보를 안다면 역행렬을 이용하여 카메라 좌표계의 basis와 실제 세계의 basis 간의 변환을 할 수 있습니다.

지금까지 특정 점이 회전하는 경우와 좌표축이 회전하는 경우에 대하여 살펴보았습니다.
변환을 바라보는 관점에 따라 좌표 변환이 적합한 지 좌표축 변환이 적합한 지는 차이가 있을 수 있습니다. 물론 역관계를 가지기 때문에 어떤 변환을 적용해도 알맞게 적용하면 사용하는 데 문제는 없습니다.
보통 고정하고자 하는 지점이 어딘 지 따라서 어떤 변환을 적용하는 지 달라집니다.
예를 들어 camera coordinate system을 고정으로 두고 싶으면 좌표 변환을 하는 것이 일반적입니다. 기준을 camera coordinate system으로 정하였으니 world coordinate system에 있는 점들을 좌표 변환하여 camera coordinate system으로 옮기는 방법을 사용합니다.
반면 world coordinate system에 있는 점들을 고정으로 두고 싶으면 좌표계 변환을 사용하는 것이 일반적입니다. 왜냐하면 점들은 움직이지 않고 그대로 존재하기 때문에 좌표축을 바꾸어서 고정된 점들의 좌표를 새로운 좌표축 기준으로 생각해야 하기 때문입니다.
따라서 좌표 변환인 지 좌표축 변환인 지는 풀고자 하는 문제에 유리한 방향으로 생각하는 것이 좋습니다.

이번에는 특정 점이나 좌표축이 이동 (translation)하는 경우에 대하여 살펴보도록 하겠습니다.

좌표 변환 (Change of coordinates) 을 이용한 이동 (Translation)

먼저 translation에 의하여 특점 점의 좌표값이 바뀌는 경우에 대하여 살펴보도록 하겠습니다.

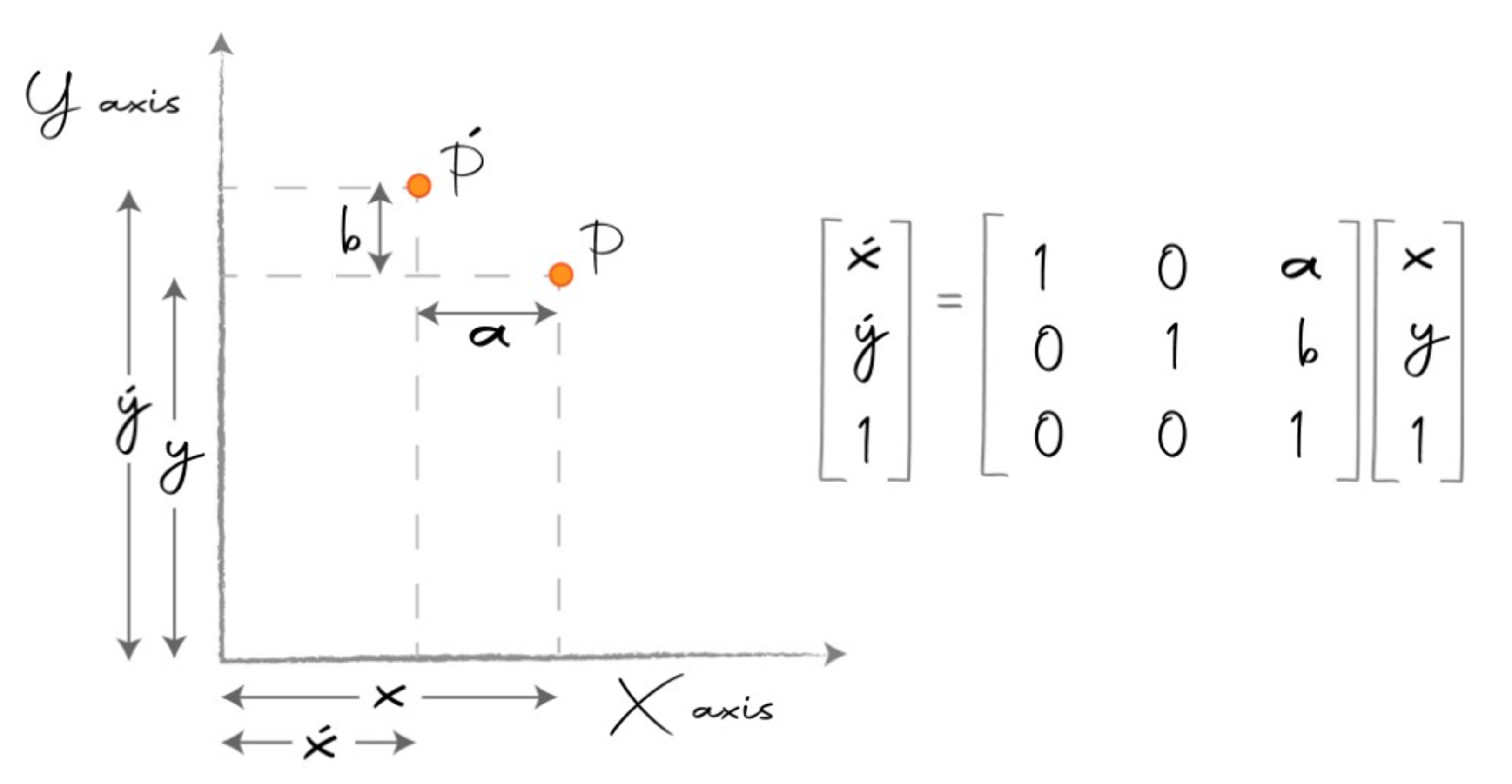
위 그림과 같이 점 \(P\) 가 점 \(P'\) 로 이동한 경우입니다. 아래 식과 같이 이동할 수 있습니다.

\[x' = x + a, y' = y + b \tag{28}\]

위 식을 행렬 곱으로 나타내려면 차원이 맞지 않기 때문에 차원을 하나 늘려주는 트릭을 통해 행렬의 곱으로 나타낼 수 있습니다. 이와 같이 행렬의 곱셈으로 나타내려는 이유는 앞에서 살펴본 rotation과 translation을 한번에 표현하기 위함입니다.

\[\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix}1 & 0 & a \\ 0 & 1 & b \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1\end{bmatrix} \tag{29}\]

위 식과 같이 차원을 추가하여 좌표를 표현한는 것을 homogeneous coordinates라고 합니다. 행렬의 곱으로만 표현된 형태를 뜻합니다.
homogeneous coordinate의 정확한 뜻을 알고 싶으면 아래 링크를 참조하시기 바랍니다.
- 링크 : https://gaussian37.github.io/vision-concept-homogeneous_coordinate/
만약 위 식에서 \(x, y\) 좌표값을 구하고 싶으면 다음과 같이 마지막 상수항을 나눠서 구할 수 있습니다.

\[\begin{bmatrix} x & y & 1 \end{bmatrix} \approx \begin{bmatrix} x/1 & y/1 \end{bmatrix} = \begin{bmatrix} x & y \end{bmatrix} \tag{30}\]

실제 연산을 할 때에는 homogeneous coordinate 상에서 연산을 하고 좌표를 구할 때에는 식 (30)을 이용하여 구합니다. 상세 내용은 글 이후에서 다룰 예정입니다.

좌표축 변환 (Change of basis) 을 이용한 이동 (Translation)

앞에서 다룬 것과 마찬가지로 XY 평면을 X’Y’ 평면으로 translation 하여 점 \(P\) 를 고정으로 둔 다음에 좌표가 어떻게 바뀌는 지 확인하여 살펴보겠습니다.

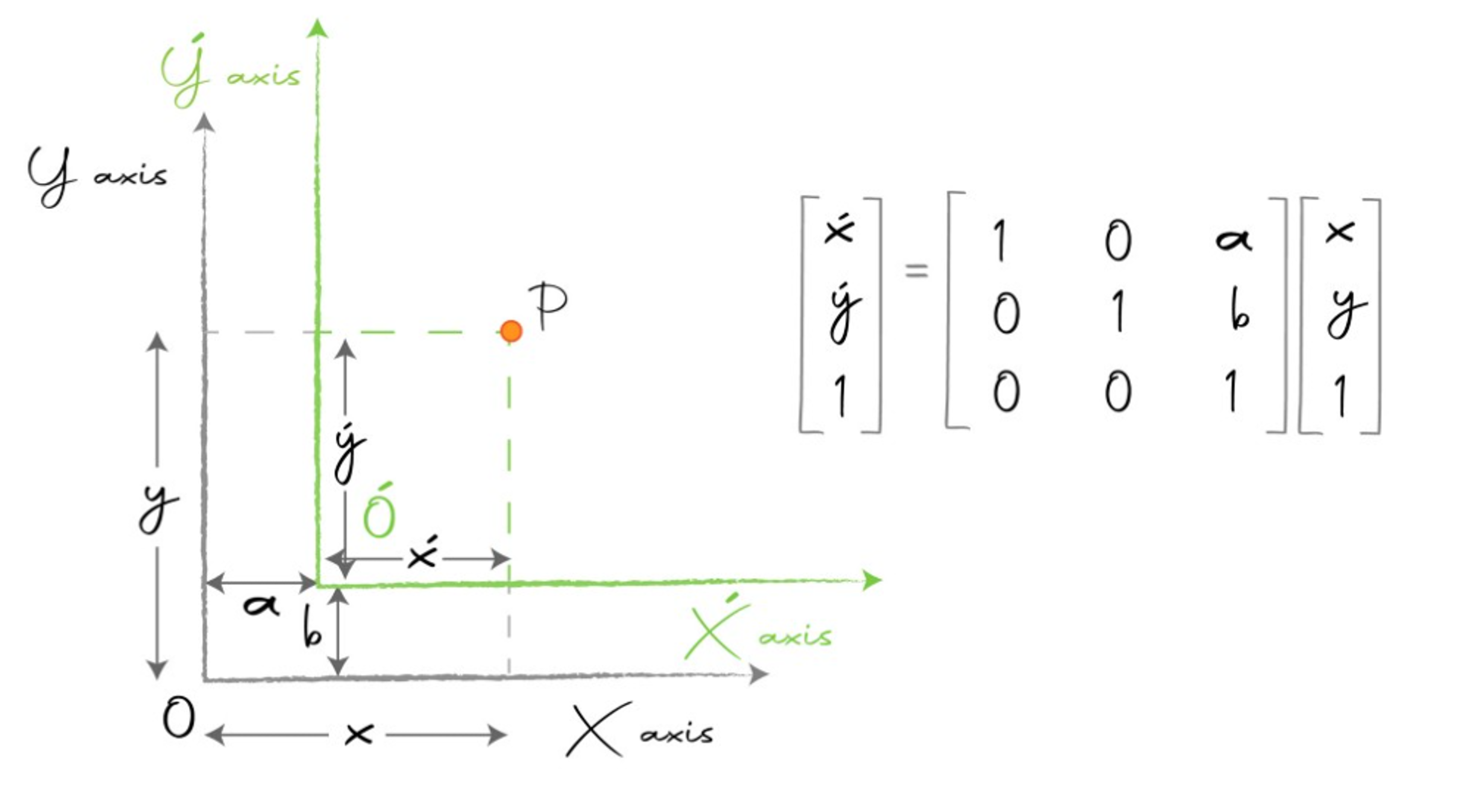
\[x' = x - a, y' = y - b \tag{31}\]
\[\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix}1 & 0 & -a \\ 0 & 1 & -b \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1\end{bmatrix} \tag{32}\]

식 (27)의 rotation에서 살펴보았듯이 좌표 위치 변환을 위한 linear transformation과 basis transformation 간에 역(inverse) 관계가 있었듯이 translation에서도 역관계가 있음을 확인할 수 있습니다.

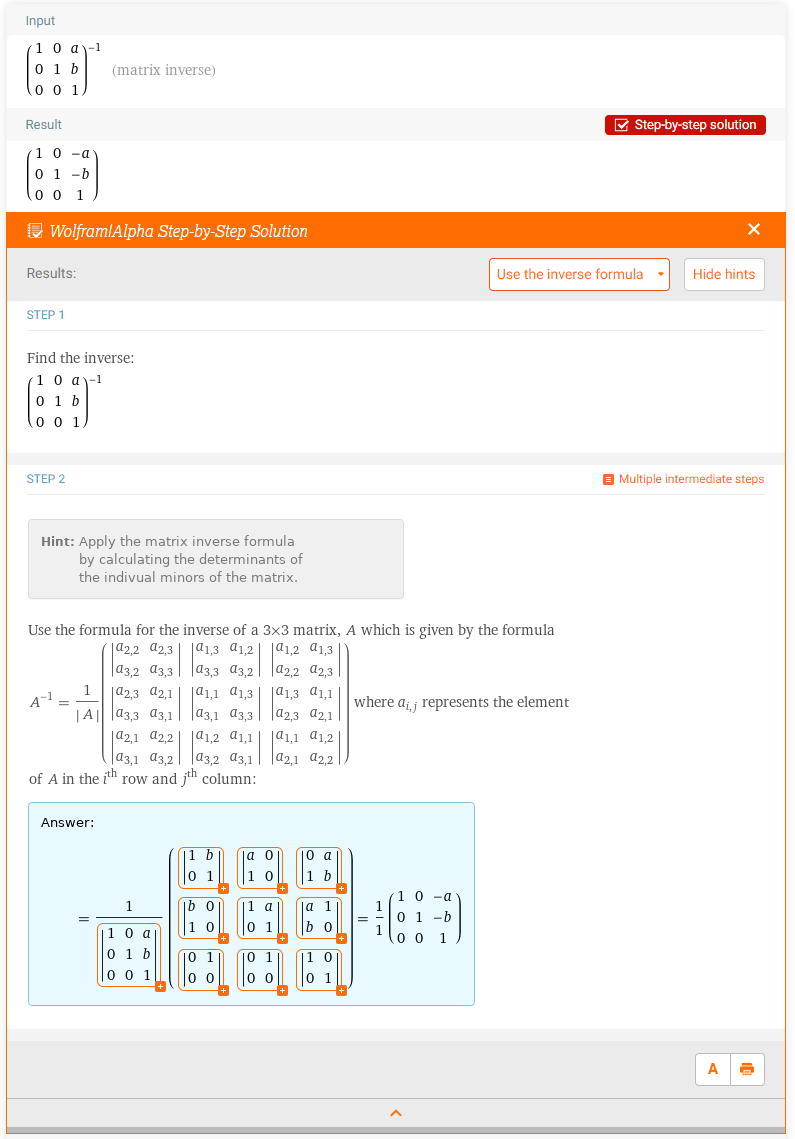
위 풀이 과정을 통하여 식 (29)의 우변의 행렬과 식 (32)의 우변의 행렬은 역행렬 관계임을 알 수 있습니다.
정리하면 rotation과 translation에서의 basis transformation과 coordinate transformation에는 역행렬 관계가 있습니다.

이와 같은 관계를 Active(Alibi)/Passive(Alias) Transformation 이라고 합니다.

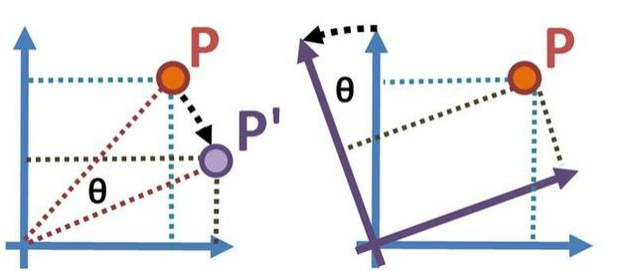
위 그림의 왼쪽과 같이 Active Transformation에서는 어떤 점 \(P\) 가 \(P'\) 로 \(\theta\) 만큼 시계 방향으로 회전합니다. 이 때 회전 기준은 점 \(P\) 가 존재하는 좌표계 기준입니다.
반면 위 그림의 오른쪽과 같이 Passive Transformation에서는 점 \(P\) 는 움직이지 않고 좌표계가 \(\theta\) 만큼 반시계 방향으로 회전합니다.
Active Transformation의 점 \(P'\) 와 Passive Transformation이 반영된 점 \(P\) 는 좌표계 기준으로 같은 좌표를 나타내는 것을 알 수 있습니다. 여기서 중요한 점은 방향까지 고려 하였을 때, Active Transformation에서는 \(-\theta\) 만큼 회전이 반영된 것이 Passive Transformation에서는 \(\theta\) 만큼 반영된 것입니다. 즉, 서로 inverse 관계를 가진다는 것입니다. 이와 같은 inverse 관계는 rotation 뿐만 아니라 다른 transformation에서도 적용됩니다.
수학에서는 주로 Active Transformation만 다루지만 물리 또는 공학에서는 두가지 모두를 다루게 되며 Computer Vision과 같은 좌표계 변환이 많은 분야에서는 Passive Transformation의 관점이 많이 다루어집니다. 예를 들어 어떤 강체 (rigid body)의 연속적인 움직임을 관측할 때에는 Active Transformation을 사용하는 반면 한 개의 물체를 두고 local coordinate와 global coordinate가 동시에 존재하는 상황에서는 Passive Transformation이 사용됩니다.

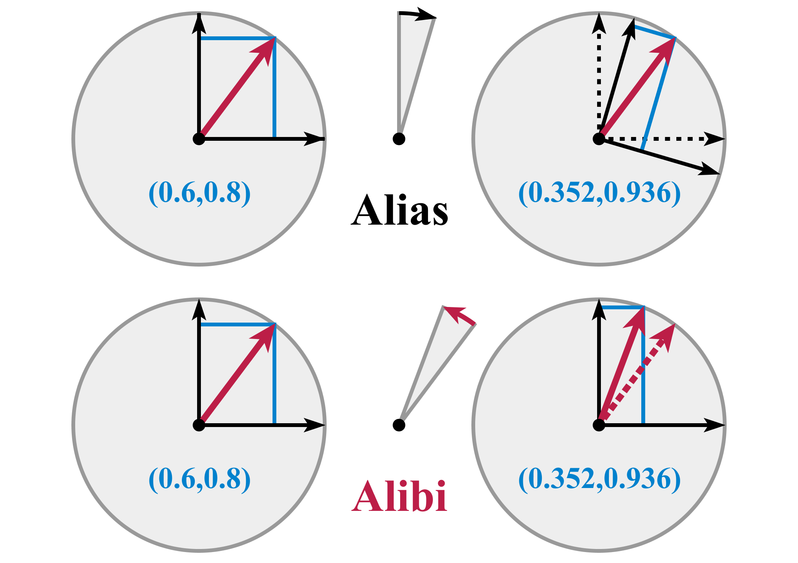
위 그림은 Rotation Matrix \(R\) 을 이용하여 Passive/Active Transformation을 한 그림입니다. 결국 최종 좌표계 기준으로 같은 점을 가리킨다는 것을 나타냅니다.

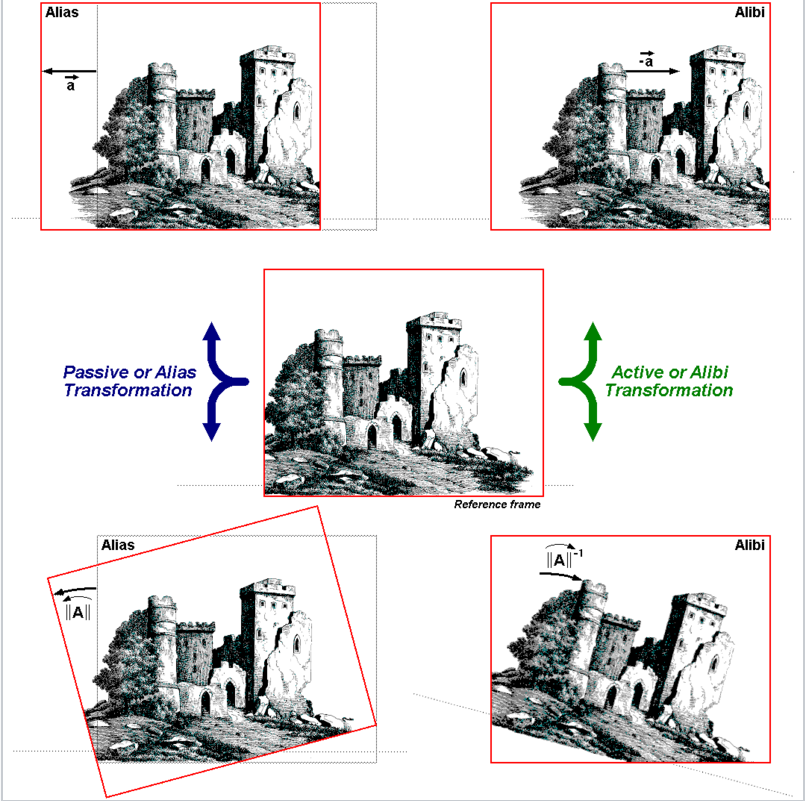
위 그림은 이미지 좌표계에서 Translation과 Rotation 각각의 Passiave/Active Transformation을 나타냅니다.

Extrinsic Camera Matrix

지금까지 rotation과 translation을 각각 살펴보았습니다. 그러면 homogeneous coordinate 형태로 나타내어 본 이유가 한번에 행렬곱으로 연산하기 위함이었듯이 행렬 곱으로 나타내어 보겠습니다.
아래 식을 어떤 점 \(P\) 를 \(P'\) 로 변환하기 위한 행렬식이라고 가정하겠습니다.

\[\begin{bmatrix} R & T \\ 0^{T} & 1 \end{bmatrix} = \begin{bmatrix} I & T \\ 0^{T} & 1 \end{bmatrix} \begin{bmatrix} R & 0 \\ 0^{T} & 1 \end{bmatrix} \tag{33}\]

위 식에서 \(R\) 은 rotation을 의미하고 \(T\) 는 translation을 의미합니다. \(R\) 은 (2, 2), (3, 3)과 같은 정사각행렬의 크기를 가집니다. 이 때 차원이 결정되면 \(R\)의 차원과 동일한 차원의 \(T\) 열벡터가 크기 2, 3과 같은 사이즈를 가지게 됩니다. \(0^{T}\) 는 열벡터를 행벡터 형태로 나타내기 위함입니다.
3차원 공간에서의 rotation과 translation을 위한 행렬에서 \(R\) 은 (3, 3)의 크기의 행렬을 가지고 \(T\) 는 (3, 1)의 크기의 열벡터를 가지므로 최종적으로 (4, 4) 크기의 행렬이 됩니다.
어떤 점 \(P \to P'\) 로 coordinate transform 할 때 사용한 행렬을 \(A\) 라고 하면 \(A^{-1}\) 은 basis transformation 이라고 하였습니다.
따라서 식 (33)의 행렬을 \(A\) 라고 하면 basis transformation 행렬은 \(A^{-1}\) 이 되고 world coordinate system을 camera coordinate system으로 변환하는 것을 extrinsic camera matrix \(E\) 라고 하기 때문에 \(A^{-1} = E\) 라고 정의하겠습니다.
만약 어떤 점 \(p\) 가 있고 world coordinate system에서는 \(p\) 를 좌표 \(p_{w}\) 의 값을 가지고 camera coordinate system에서는 좌표 \(p_{c}\) 를 가진다고 하면 좌표 기준으로 \(p_{w} \to p_{c}\) 로 변환하는 행렬을 구할 수 있습니다. 이 행렬을 앞의 예제와 같이 \(A\) 라고 한다면 반대로 world coordinate system 인 \(P^{W}\) 를 camera coordinate system 인 \(P^{C}\) 로 변환하는 행렬은 \(A^{-1} = E\) 가 됩니다.

\[P^{C} = E \times P^{W} \tag{34}\]

식 (34)와 같이 extrinsic camera matrix \(E\) 를 이용하여 world coordinate system에서 camera coordinate system으로의 좌표축 변환을 할 수 있습니다.

지금 까지 내용을 정리하면 coordinate system을 변환하는 행렬은 다음과 같은 순서로 구할 수 있습니다.
① 어떤 점 \(P\) 에 대하여 \(A\) 좌표계와 \(B\) 좌표계 각각에서 가지는 좌표값 \(P_{A}\) 와 \(P_{B}\) 를 구합니다.
② 한 좌표계의 점을 기준으로 삼습니다. 편의상 \(A\) 좌표계를 기준으로 삼겠습니다.
③ \(P_{A}\) 를 \(P_{B}\) 로 변환할 수 있는 변환 행렬 \(T\) 를 구합니다.
④ 변환 행렬 \(T\) 를 이용하여 \(T^{-1} \times A = B\) 또는 \(A = T \times B\) 형태로 좌표계 변환에 적용합니다.

지금 까지 살펴본 좌표 변환과 좌표계 변환의 관계를 아래 notation으로 다시 한번 살펴보며 정리하겠습니다.
아래 식의 기호의 의미는 다음과 같습니다.

\[R : \text{Rotation of Coordinate}\]
\[t : \text{Translation of Coordinate}\]
\[R_{c} : \text{Rotation of Coordinate System (Based on camera coordinate system)}\]
\[C : \text{Translation of Coordinate System (Based on camera coordinate system)}\]

위 표기에서 \(R_{c}\) 는 camera coordinate system을 기준으로 바라본 world coordinate system과의 rotation 차이를 나타낸 좌표계 변환입니다. \(C\) 또한 camera coordinate system을 기준으로 바라본 world coordinate system과의 translation 차이를 나타낸 좌표계 변환입니다. 따라서 \(R_{c}, C\) 는 좌표계 변환을 나타내며 앞에서 다룬 것과 같이 좌표 변환과 역관계를 나타냅니다.

\[\begin{align} \left[ \begin{array}{c|c} R & \boldsymbol{t} \\ \hline \boldsymbol{0} & 1 \\ \end{array} \right] \tag{35} &= \left[\begin{array}{c|c} R_c & C \\ \hline \boldsymbol{0} & 1 \\ \end{array} \right]^{-1} \\ &= \left[ \left[ \begin{array}{c|c} I & C \\ \hline \boldsymbol{0} & 1 \\ \end{array} \right] \left[ \begin{array}{c|c} R_c & 0 \\ \hline \boldsymbol{0} & 1 \\ \end{array} \right] \right]^{-1} & \text{(decomposing rigid transform)} \tag{36} \\ &= \left[ \begin{array}{c|c} R_c & 0 \\ \hline \boldsymbol{0} & 1 \\ \end{array} \right]^{-1} \left[ \begin{array}{c|c} I & C \\ \hline \boldsymbol {0} & 1 \\ \end{array} \right]^{-1} & \text{(distributing the inverse)} \tag{37} \\ &= \left[ \begin{array}{c|c}R_c^T & 0 \\ \hline \boldsymbol{0} & 1 \\ \end{array} \right] \left[ \begin{array}{c|c} I & -C \\ \hline \boldsymbol{0} & 1 \\ \end{array} \right] & \text{(applying the inverse)} \tag{38} \\ &= \left[ \begin{array}{c|c} R_c^T & -R_c^TC \\ \hline \boldsymbol{0} & 1 \\ \end{array} \right] & \text{(matrix multiplication)} \tag{39} \end{align}\]

\[R = R_{c}^{T} \tag{40}\]
\[t = -R_{c}^{T} C \tag{41}\]

Degrees of Freedom

지금까지 살펴본 Extrinsic Camera matrix를 선언할 때, 필요한 파라미터는 6가지가 있었습니다. X, Y, Z 축으로 얼만큼 회전하였는 지와 X, Y, Z 축으로 부터 얼마 만큼의 translation이 발생하였는 지 입니다.
이 필요한 파라미터를 DoF(Degree of Freedom)이라고 하며 따라서 Extrinsic을 구할 때에는 6개의 DoF가 필요하다고 말합니다.

앞에서 살펴본 내용을 파이썬으로 실습해 보도록 하겠습니다. 아래 링크의 예제는 world coordinate system → camera coordinate system으로 좌표축 변환이 되었을 때, \(y\) 축으로 45도 회전과 -8만큼 translation이 발생하였다고 가정하고 변환하였습니다.
그래프 출력 결과는 colab에서 생성이 안되어 local의 jupyter notebook에서 실행하시길 바랍니다.

colab 링크 : Image formation and camera extrinsics

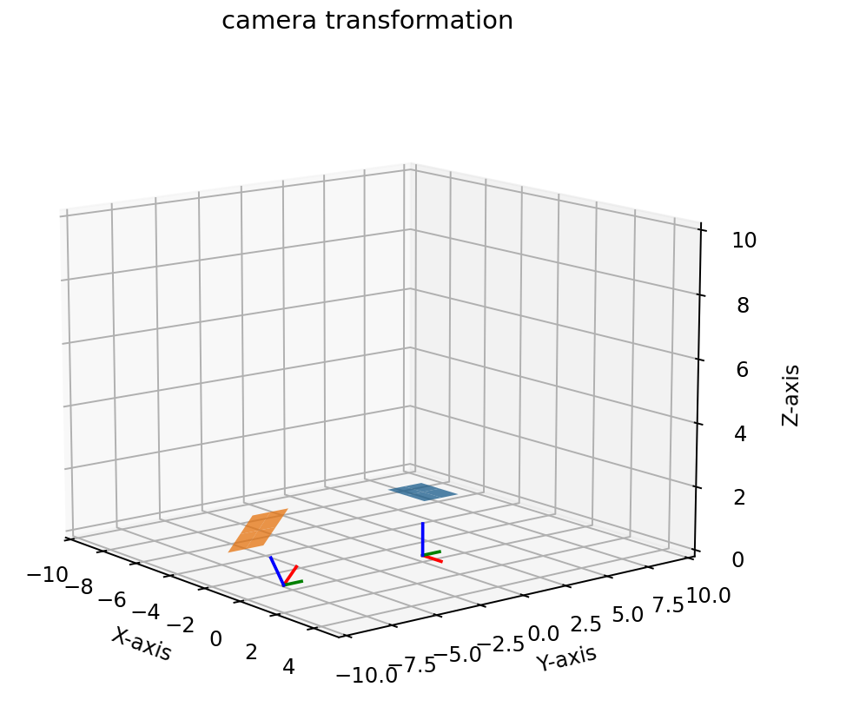
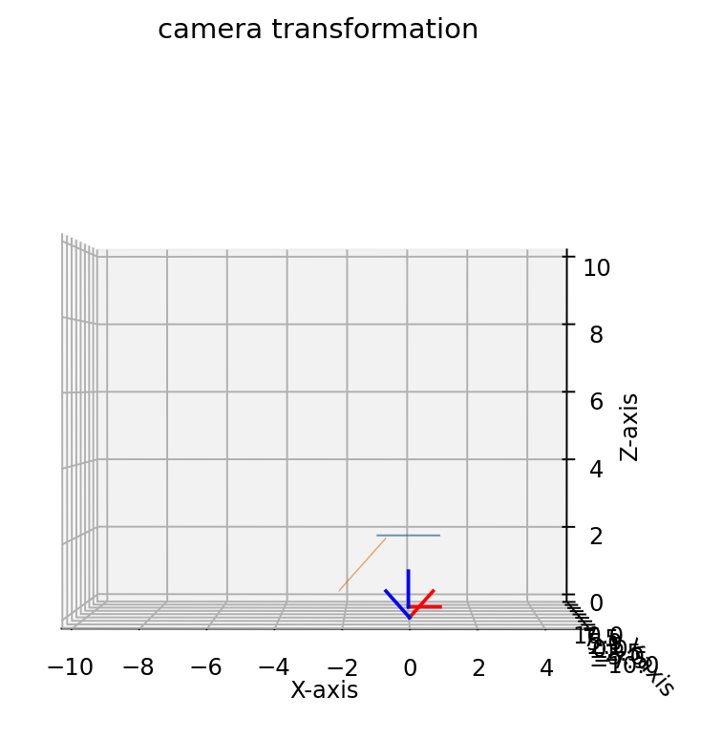
먼저 결과부터 살펴보면 기존의 파란색 평면 (world 좌표계)이 Y축 (초록색 축)을 기준으로 45도 rotation과 Y축 기준으로 -8 만큼 translation이 발생한 것을 확인할 수 있습니다.
파란색 평면 아래에 있는 좌표 축이 위 좌표계의 기준 축입니다. X, Y, Z 축의 원점이 (0, 0, 0)에 있는 것을 확인할 수 있습니다. 이것을 편의상 world coordinate system이라고 하겠습니다.
반면에 주황색 평면 아래에 있는 좌표 축은 새로운 좌표축이며 편의상 camera coordinate system이라고 하겠습니다.
파란색 평면과 주황색 평면은 좌표의 집합입니다. 즉, 파란색 평면을 주황색 평면으로 변환하는 것은 좌표를 변환하는 것과 같습니다.

위 코드 부분에서 R과 T는 각각 Y축 방향으로 45도 회전과 -8만큼 translation이 발생함을 나타낸 것입니다. 즉, 파란색 평면을 주황색 평면으로 변환하기 위한 것이고 이것은 좌표를 변환하는 것과 같습니다.
R_과 T_는 homogeneous coordinate로 표현하기 위하여 나타낸 것이며 이렇게 표현하면 R_과 T_의 행렬 곱을 통하여 rotation과 translation을 한번에 표현할 수 있습니다.
따라서 주황색 평면은 파란생 평면에에 비하여 Y축 방향으로 +45도 회전과 -8만큼의 translation이 발생한 것을 확인할 수 있습니다.

# create an image grid
xx, yy, Z = create_image_grid(f, img_size)
# convert the image grid to homogeneous coordinates
pt_h = convert_grid_to_homogeneous(xx, yy, Z, img_size)
# transform the homogeneous coordinates
pt_h_transformed = R_ @ T_ @ pt_h
# convert the transformed homogeneous coordinates back to the image grid
xxt, yyt, Zt = convert_homogeneous_to_grid(pt_h_transformed, img_size)

위 코드에서 xx, yy, Z는 (3, 3) 평면을 만들기 위한 코드이며 pt_h는 (4, 9)의 크기를 가지는 행렬입니다. 여기서 행 사이즈인 4의 의미는 X, Y, Z 방향에서의 값과 homogeneous를 만들기 위한 dummy 차원 1개를 의미하며 열 사이즈는 (3, 3) 크기 행렬에 속한 값들을 의미합니다.
위 코드에서 pt_h_transformed = R_ @ T_ @ pt_h을 보면 world coordinate system상에서 파란색 평면을 주황색 평면 위치로 변환하는 역할을 합니다.

# define axis and figure
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111,projection='3d')

# set limits
ax.set(xlim=(-10, 5), ylim=(-10, 10), zlim=(0, 10))

# plot the global basis and the transformed camera basis
ax = pr.plot_basis(ax)
ax = pr.plot_basis(ax, R, T)

# plot the original and transformed image plane
ax.plot_surface(xx, yy, Z, alpha=0.75)
ax.plot_surface(xxt, yyt, Zt, alpha=0.75)

ax.set_title("camera transformation")
ax.set_xlabel("X-axis")
ax.set_ylabel("Y-axis")
ax.set_zlabel("Z-axis")

위 그래프를 생설할 때, 주황색 평면 아래 좌표축은 ax = pr.plot_basis(ax, R, T)을 통해서 만든 것입니다. 즉, 기존 R, T를 이용하여 world coordinate system을 camera coordinate system로 변환시킨 것임을 알 수 있습니다.

앞에서 설명한 바와 같이 rotation과 translation을 하나의 homogeneous 형태로 만든 R_T_의 역행렬이 좌표축 즉, 좌표계를 변환하는 행렬임을 확인하였습니다. 따라서 위 식의 E = np.linalg.inv(R_ @ T_)를 world coordinate system좌표계를 camera coordinate system 좌표계로 변환하는 extrinsic 행렬 E를 구할 수 있습니다.

(4, 4) 행렬의 E의 마지막 행을 삭제하여 (3, 4) 크기의 행렬을 만들면 왼쪽 (3, 3)은 Rotation을 의미하고 가장 오른쪽 (3, 1) 크기의 열벡터는 Translation을 의미하게 됩니다.
이 과정의 의미는 homogeneous coordinate (동차 좌표계)를 다시 cartesian coordinate (직교 좌표계)로 표현한 것입니다.

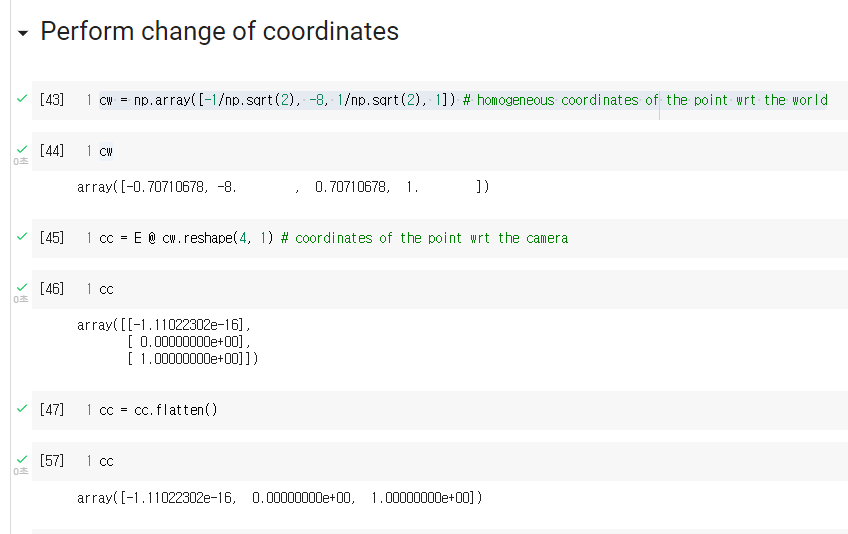
위 코드의 cw는 world coordinate system에서의 좌표를 의미하고 cc는 camera coordinate system의 좌표를 의미합니다.
앞에서 선언한 E를 이용하여 cw → cc로 변환하고자 합니다. 여기서 중요한 것은 cw와 cc 모두 같은 한 점을 의미하지만 좌표계가 다르기 때문에 다른 값을 가진다는 것입니다.
world coordinate system에서는 약 (X = -0.7, Y = -8, Z = 0.7)을 가지지만 camera coordinate system에서는 (X = -1, Y = 0, Z = 1)을 가짐을 코드 또는 그래프를 통해서 확인할 수 있습니다.

지금까지 살펴본 예제가 Camera Extrinsic을 의미하며 이와 같은 원리로 사용됩니다.

Camera Extrinsic 변환 애니메이션

애니메이션 링크 : http://ksimek.github.io/perspective_camera_toy.html

앞에서 살펴본 extrinsic의 좌표 변환과 좌표계 변환을 애니메이션을 통해 살펴보도록 하겠습니다.

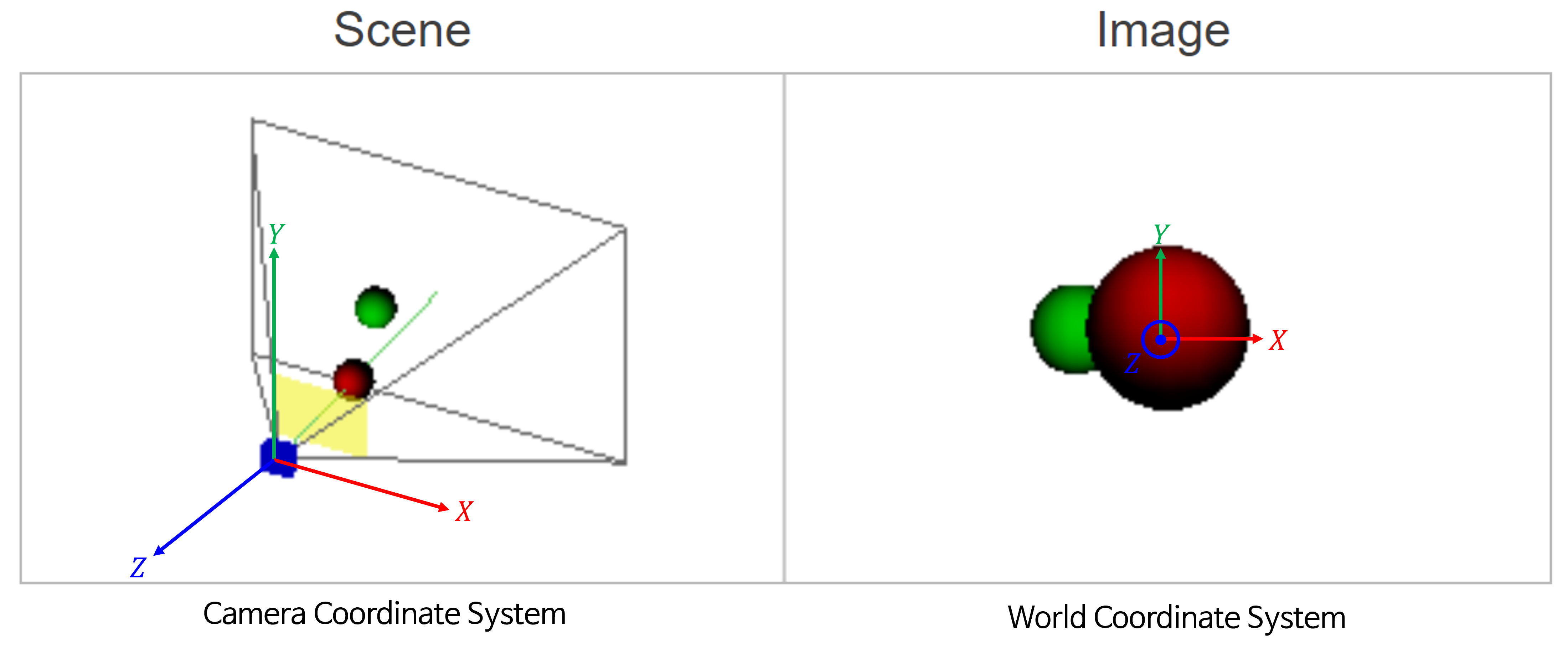
위 그림은 좌측의 카메라가 두 개의 공을 바라볼 때 형성되는 이미지를 캡쳐하여 우측에 표현한 것입니다.
좌측 이미지의 축은 camera coordinate system에서의 좌표축을 나타내며 각 축의 방향이 양의 방향입니다. 좌측 이미지에서 공 방향으로 뻗은 초록색 선은 Principal Axis를 뜻합니다. (관련 내용은 본 글의 뒷부분에 설명되어 있습니다.)
우측 이미지의 공은 world coordinate system을 따릅니다.

먼저 world coordinate 기준으로 translation을 적용해 보도록 하겠습니다. world coordinate에서 각 축의 양의 방향으로 공이 움직이면 camera coordinate system 기준에서는 반대로 음의 방향으로 카메라가 움직여야 합니다. 이 부분을 주의깊게 보시면 됩니다.

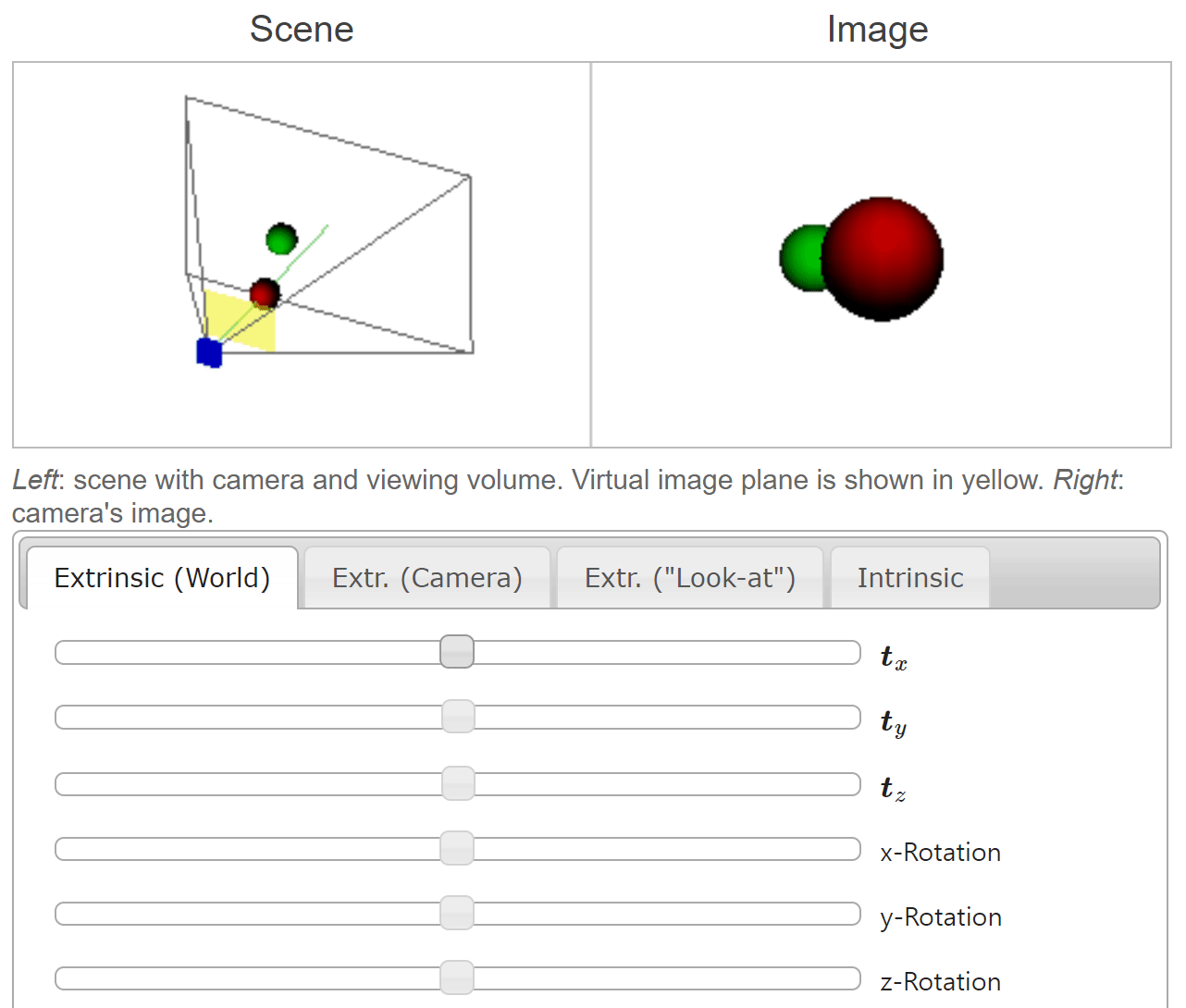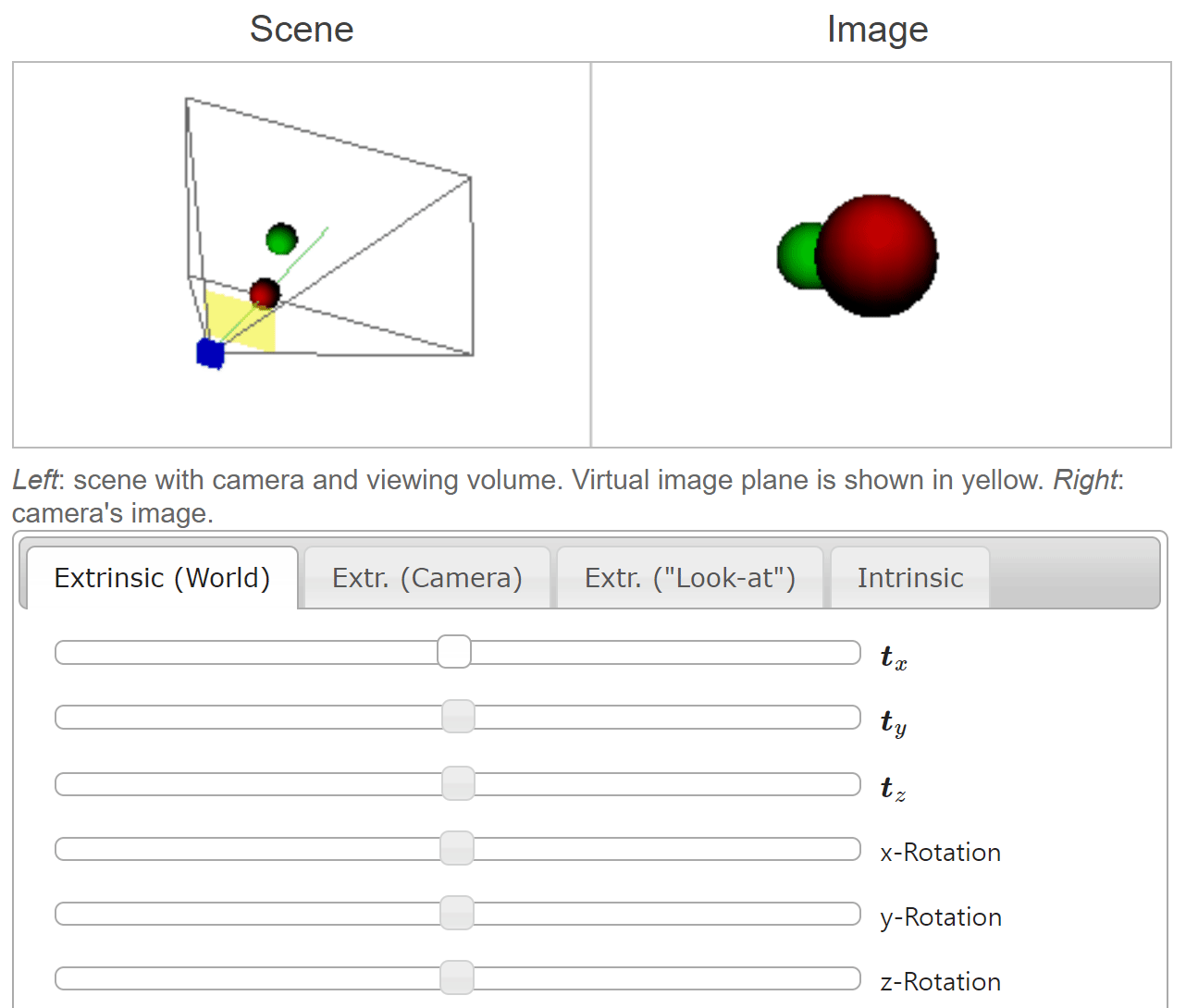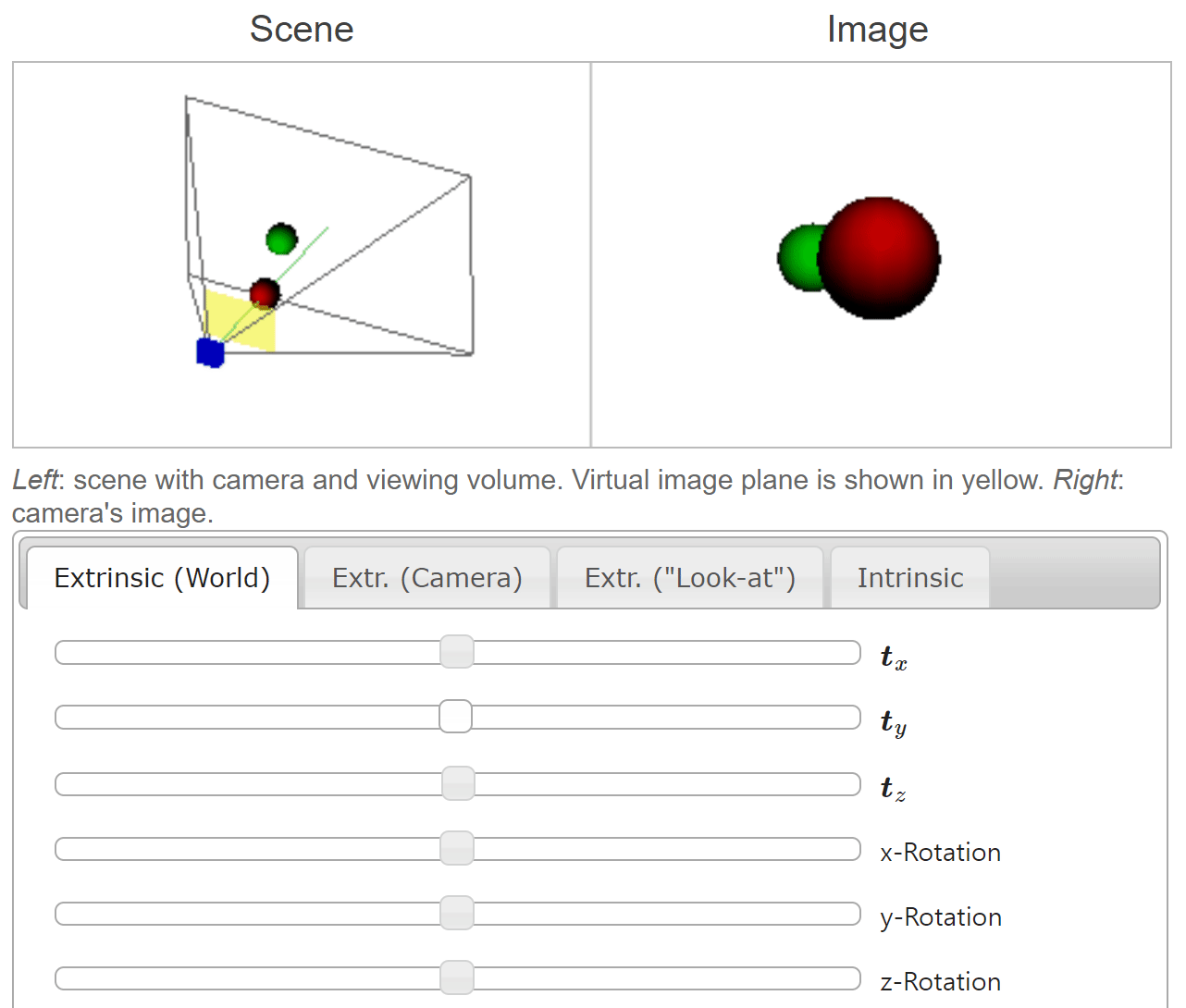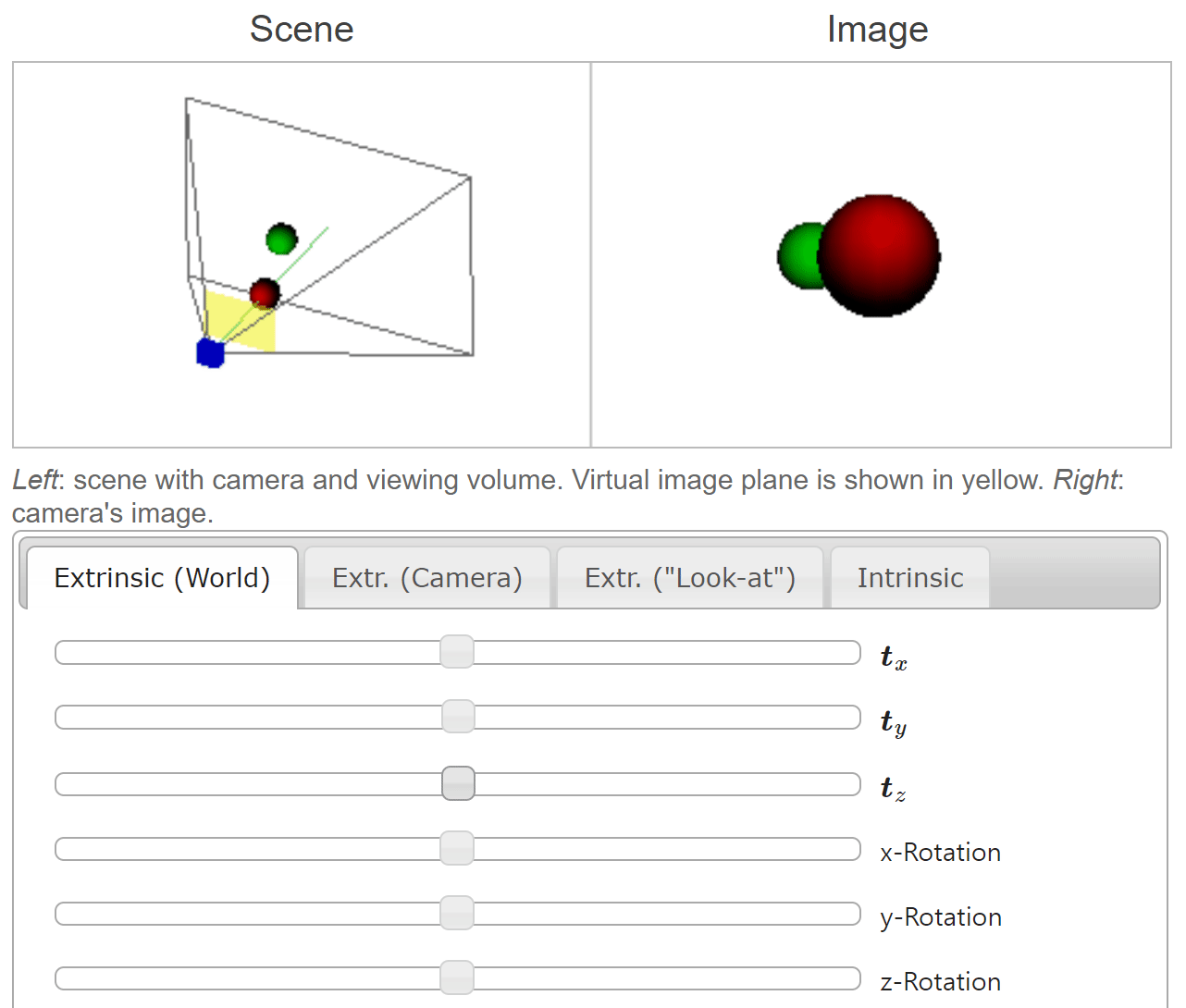
위 애니메이션에서 \(t_{x}, t_{y}, t_{z}\) 의 슬라이더 바를 오른쪽으로 움직일수록 world coordinate의 각 축의 양의 방향으로 움직임을 나타냅니다.
world coordinate에서 양의 방향으로 움직일 때, camera coordinate에서는 반대 방향으로 움직이게 되는 것을 볼 수 있습니다.

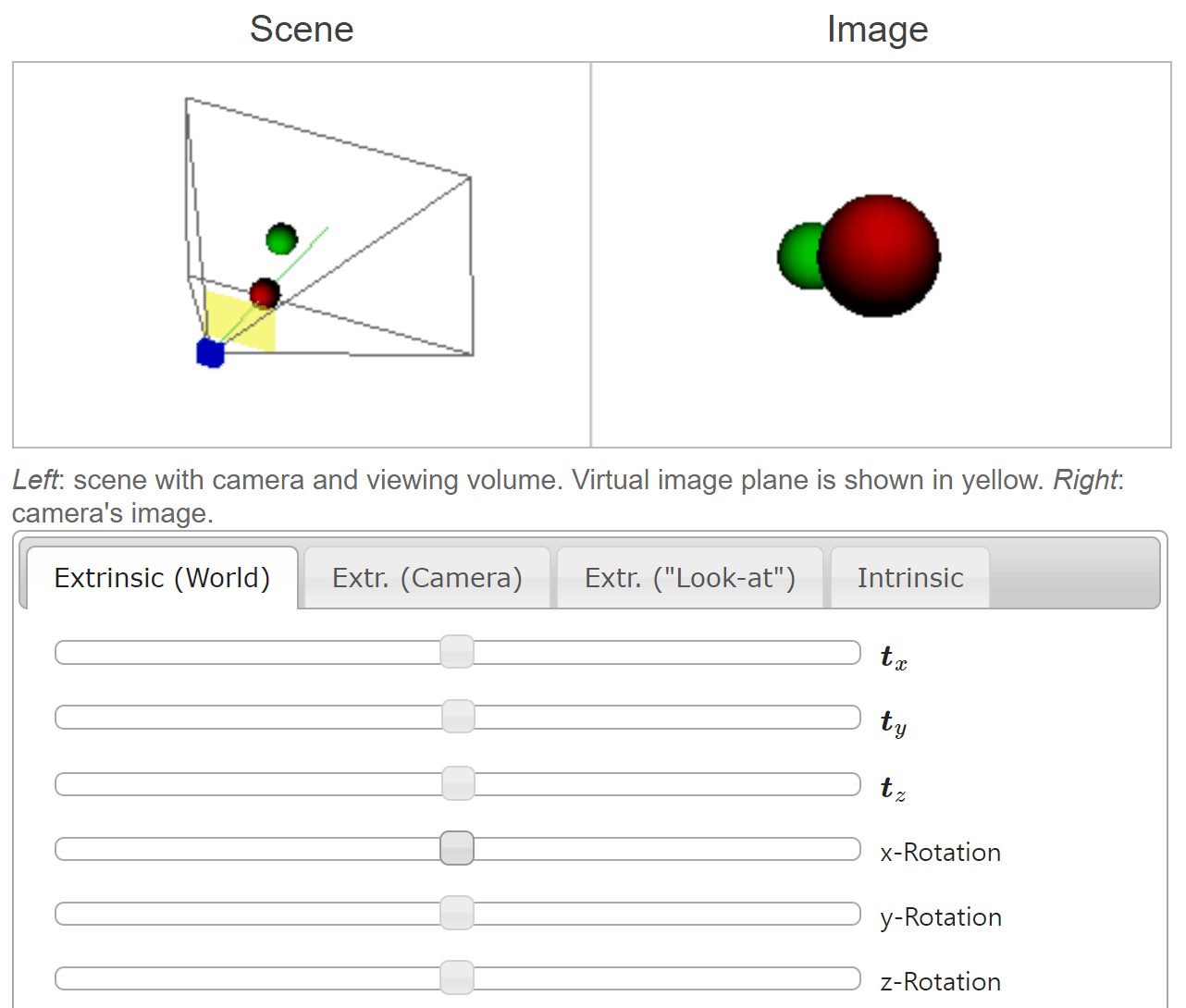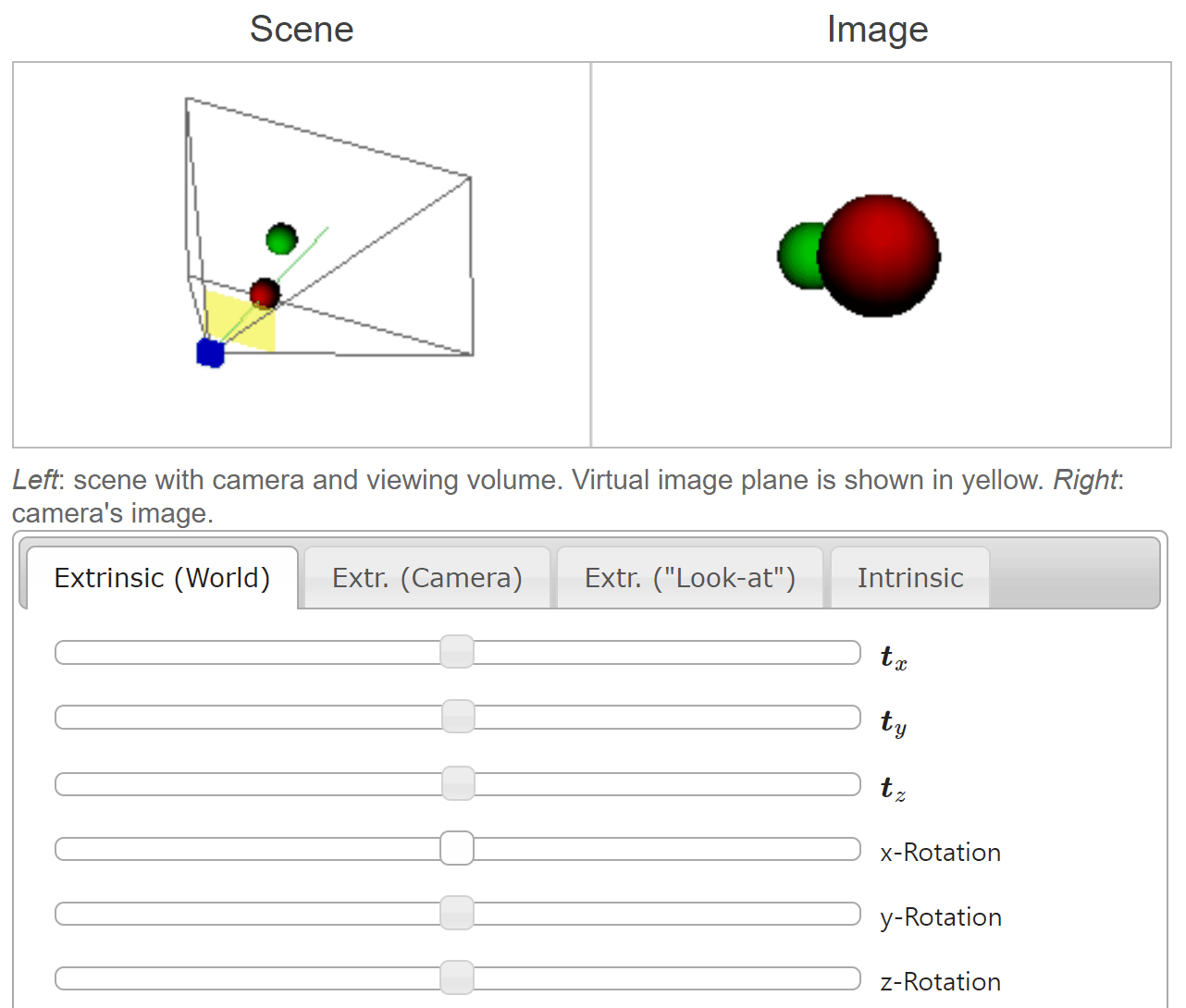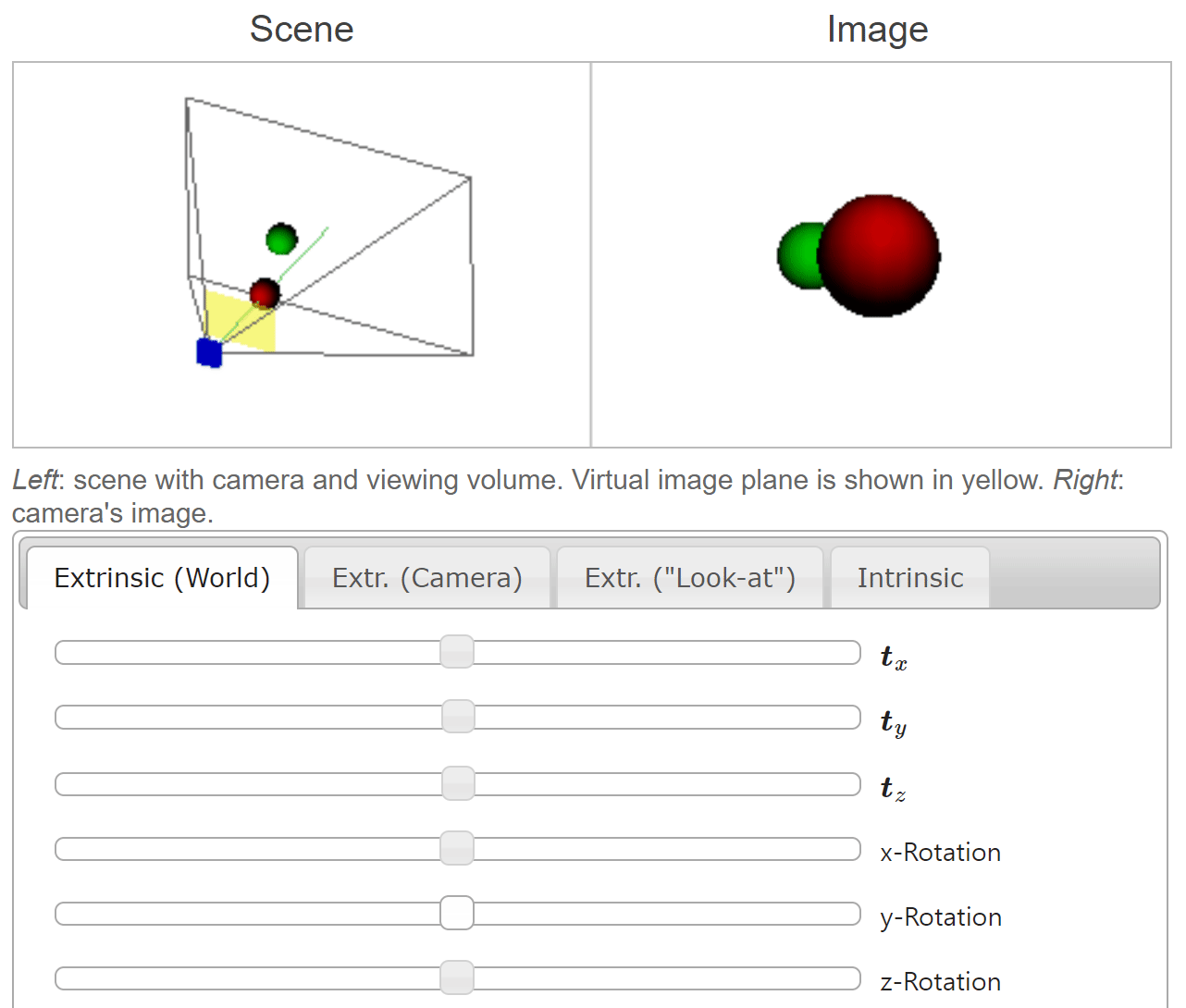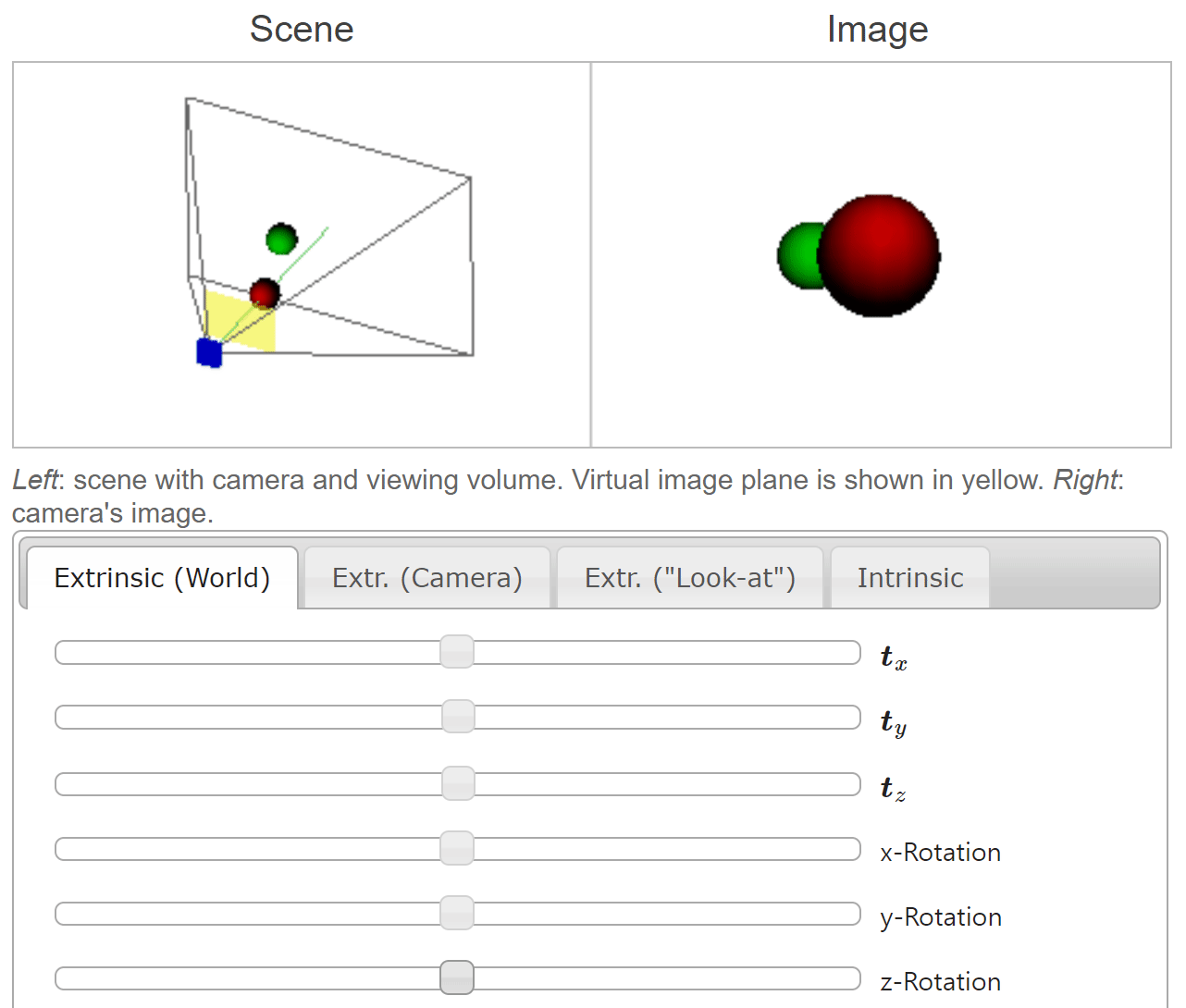
이번에는 rotation을 적용해 보도록 하겠습니다. 앞의 예시와 동일하게 world coordinate와 camera coordinate 간의 관계를 잘 살펴보시면 됩니다. 참고로 \(Z\) 축에 대한 회전은 반시계 방향이 양의 방향 회전이며 시계 방향 회전의 음의 방향 회전입니다.

이번에는 좌표계 변환 관점에서 translation과 rotation을 적용해 보도록 하겠습니다.

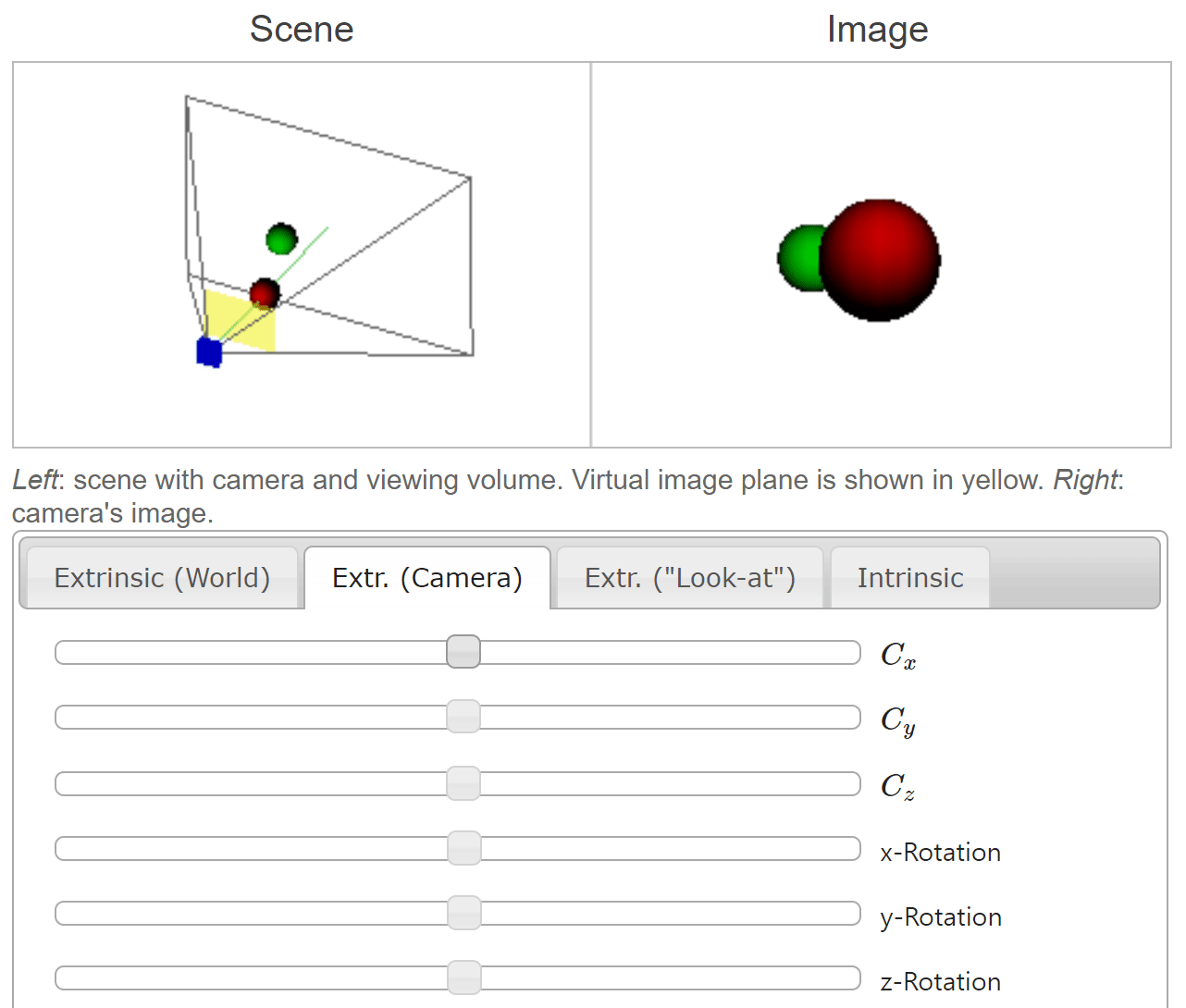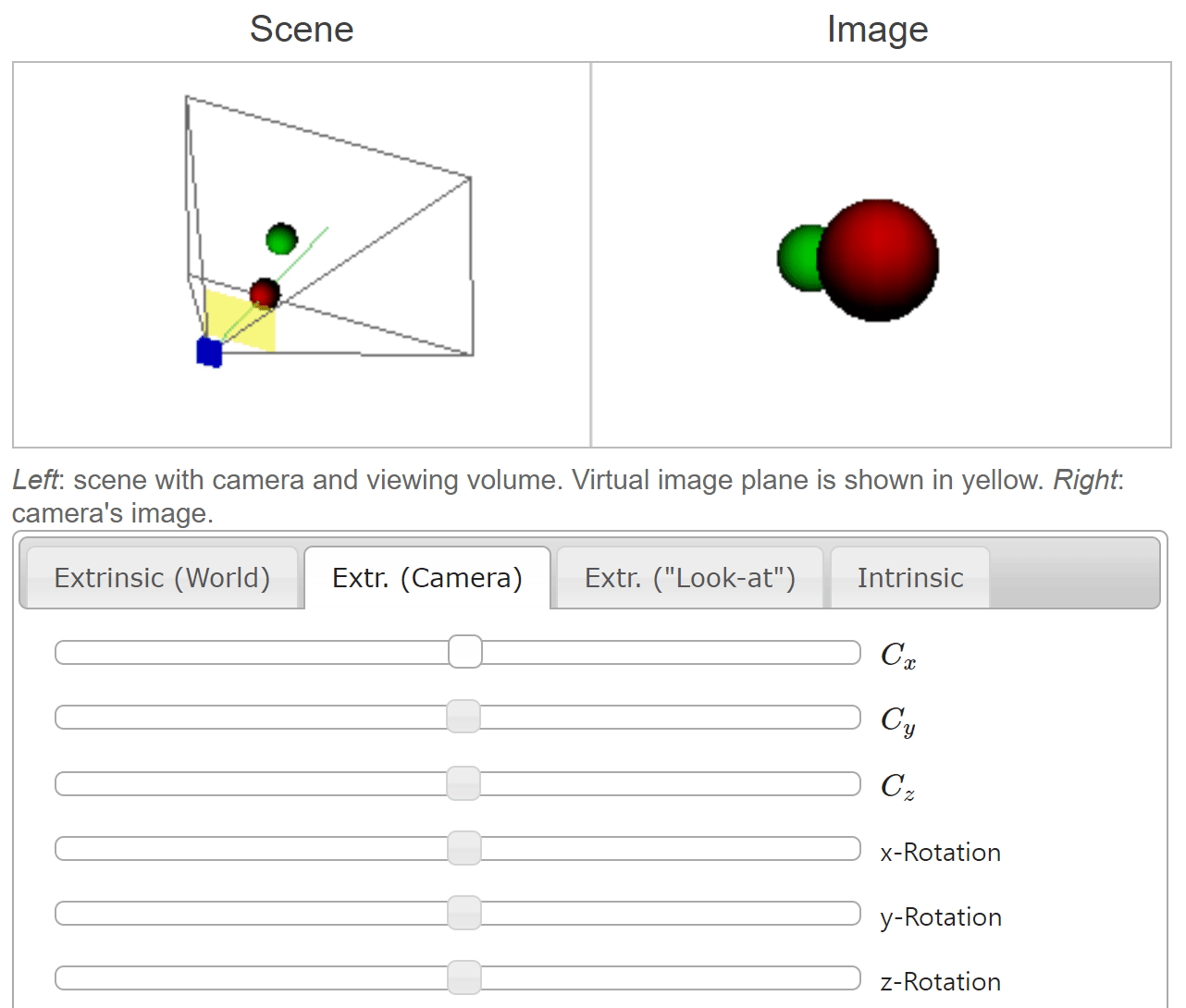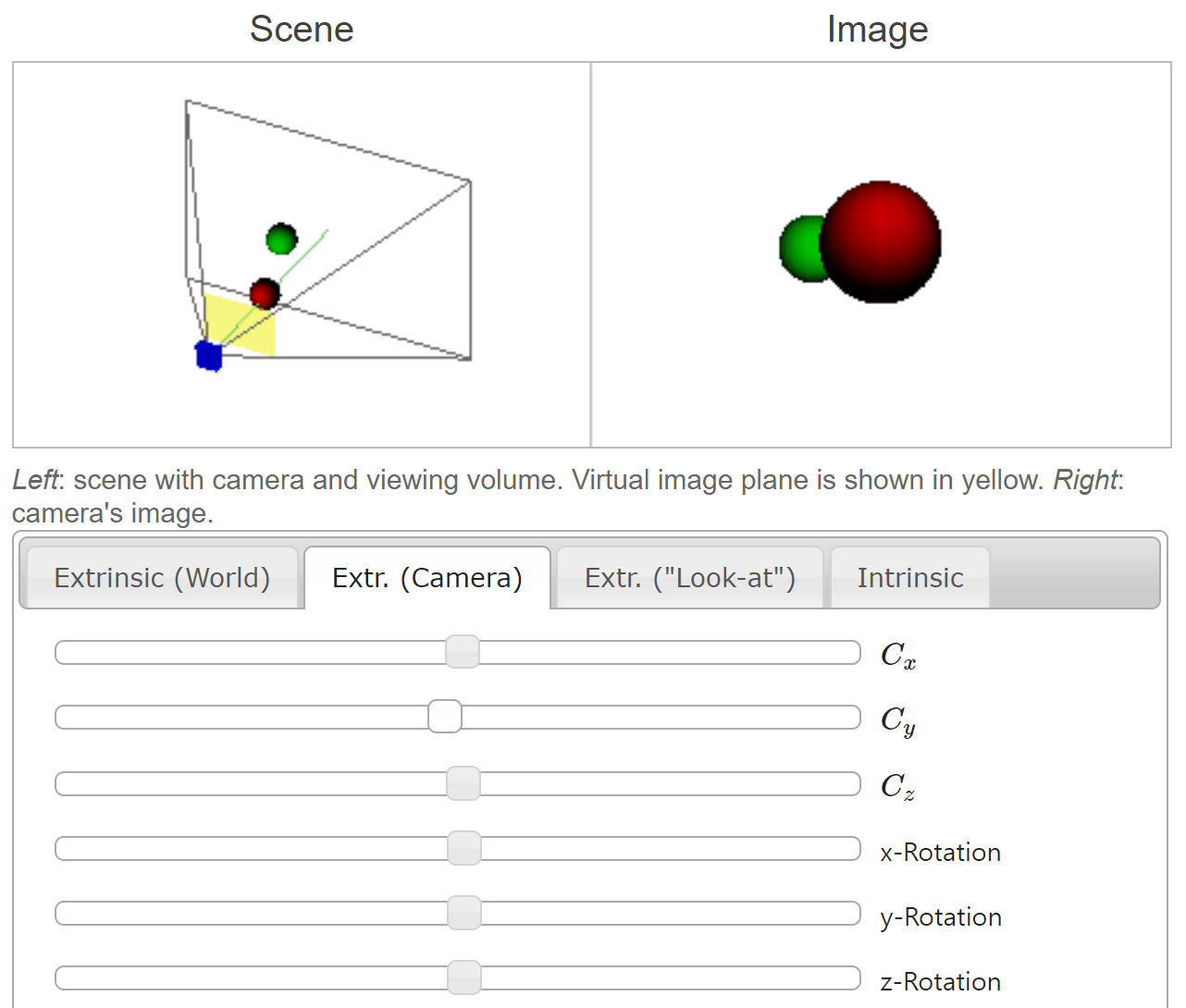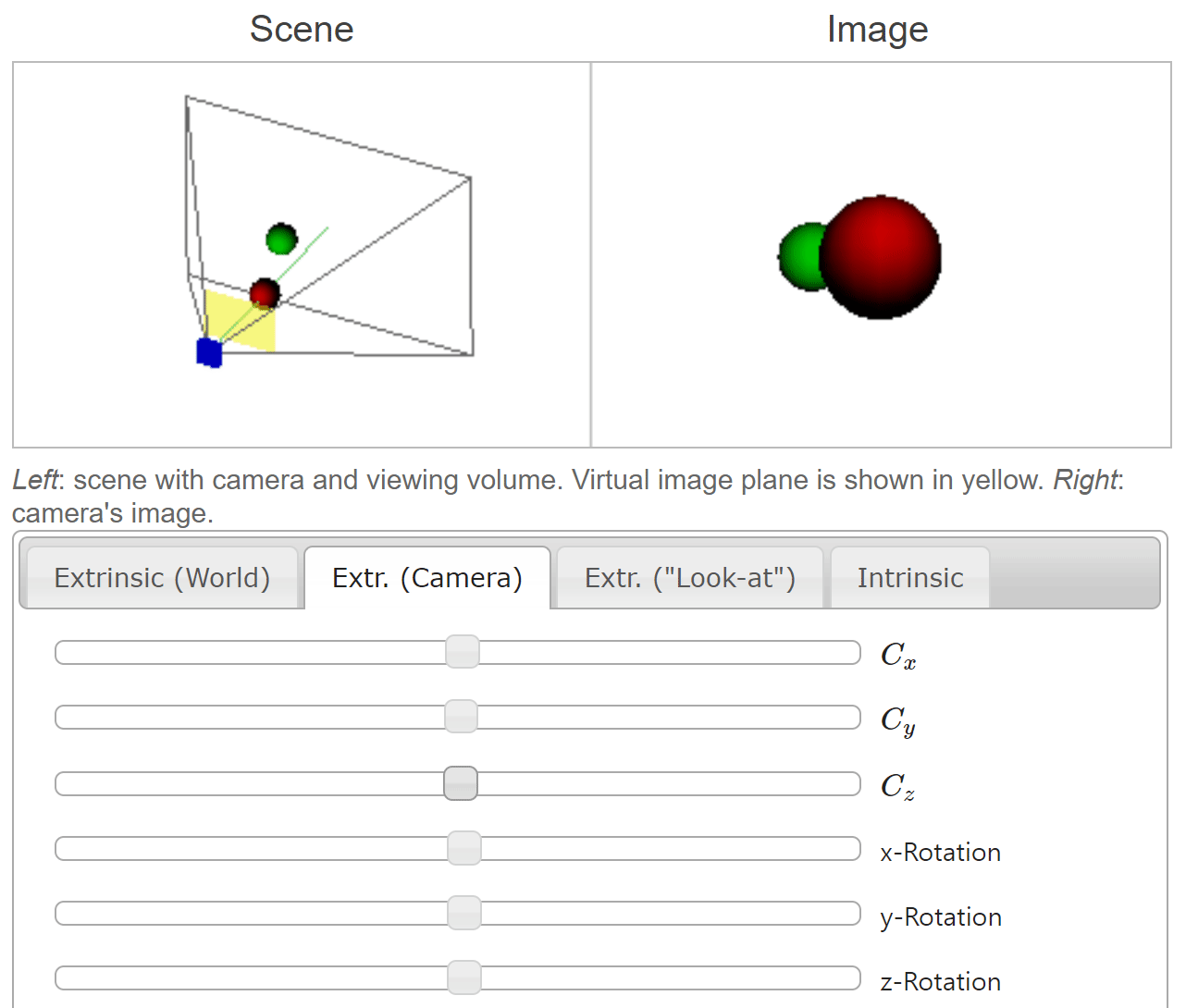
위 애니메이션에서는 \(C_{x}, C_{y}, C_{z}\) 가 카메라의 translation과 관련되어 있습니다. 이번 예시에서는 카메라의 좌표축에 따라 translation이 발생한 것이고 공의 좌표는 이와 반대로 움직이는 것을 확인할 수 있습니다.

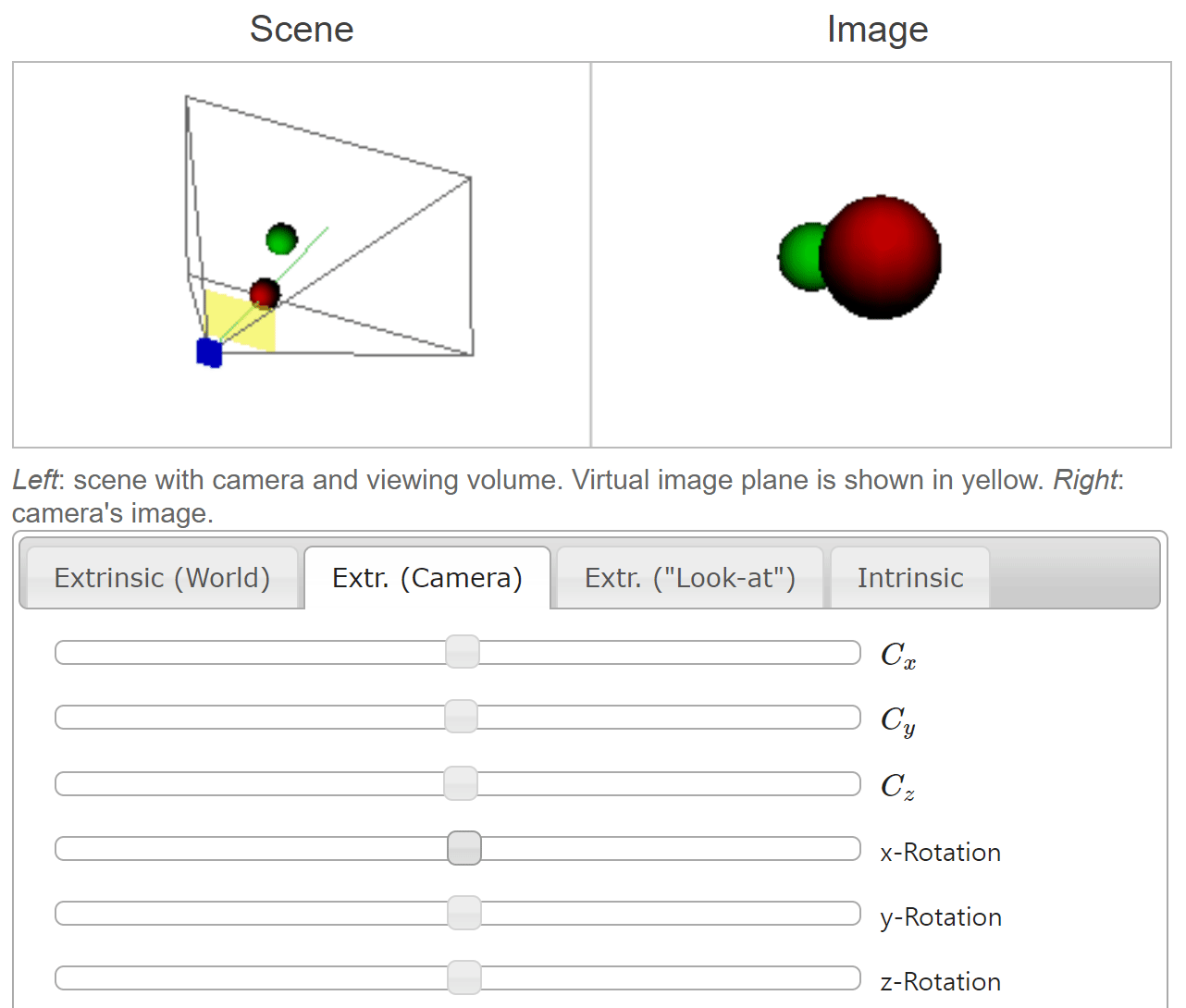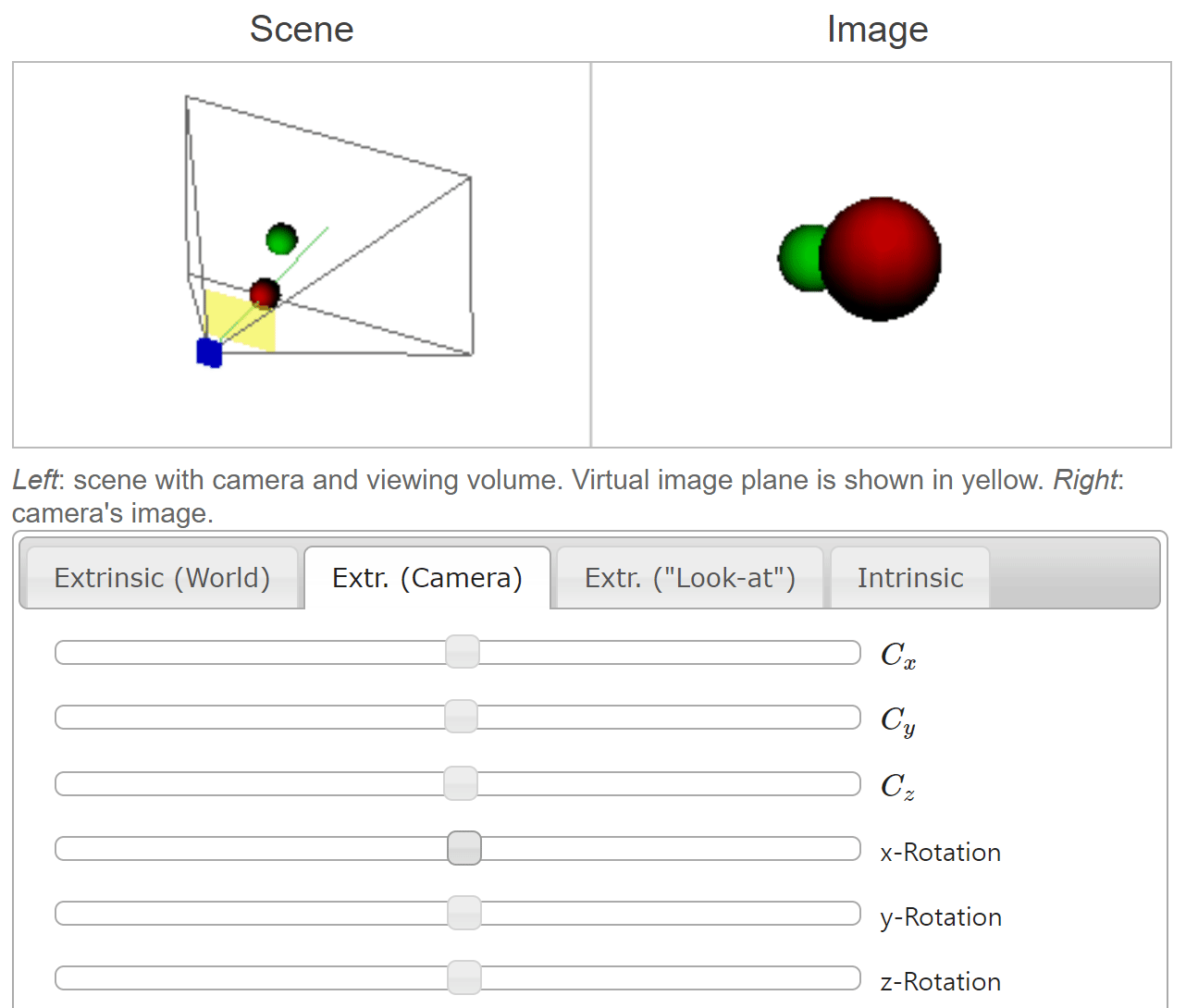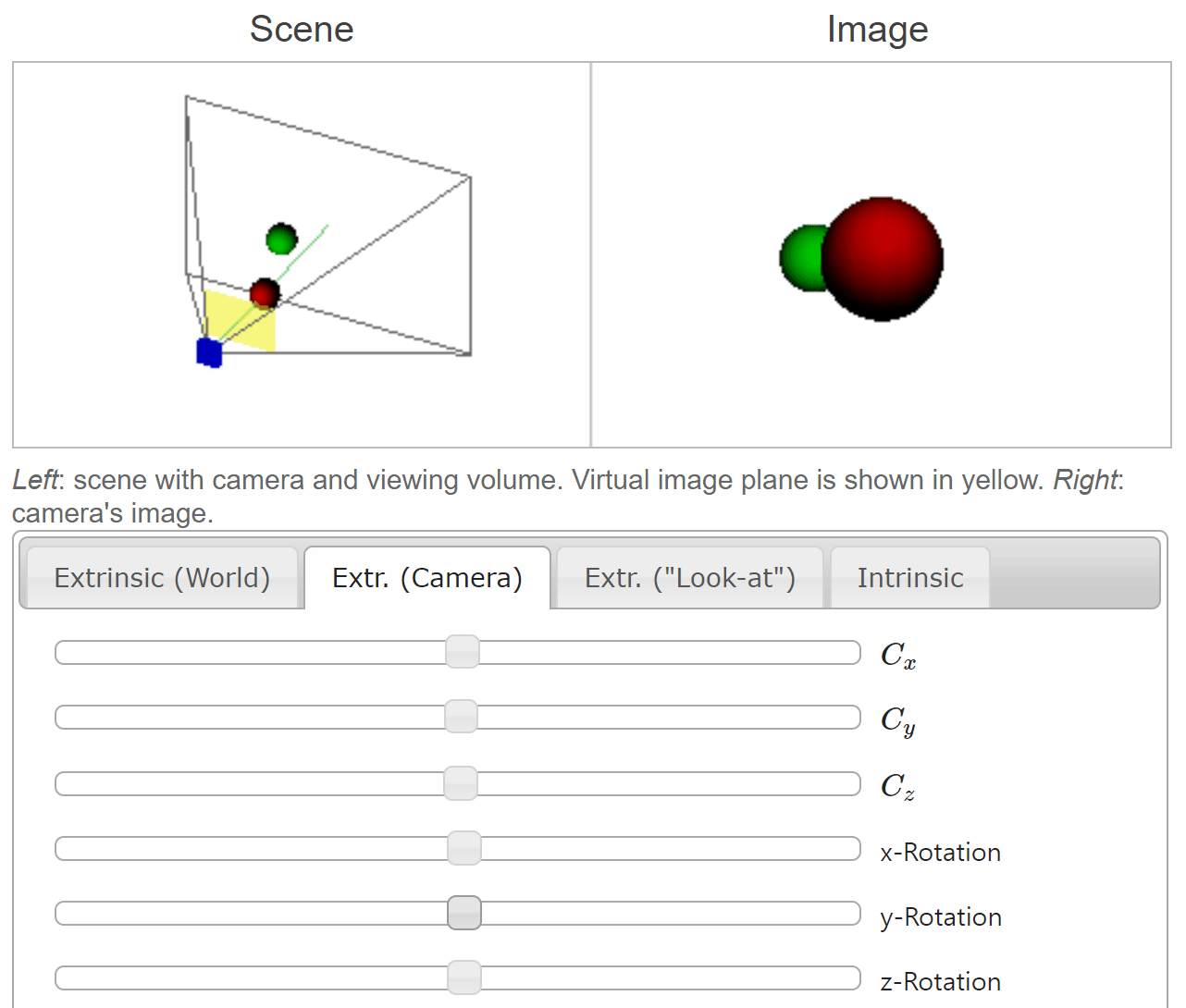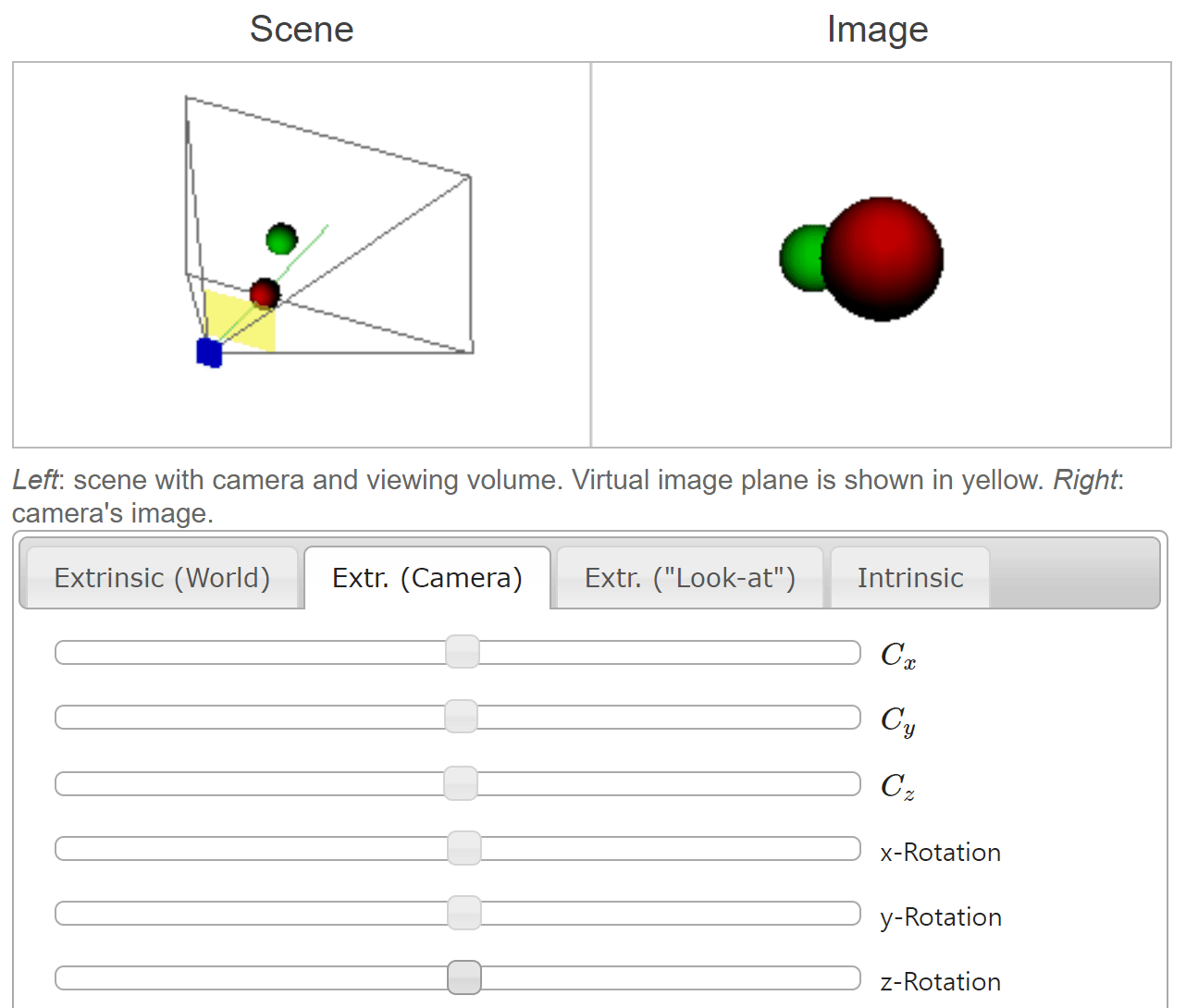
앞선 예시와 동일하게 카메라 좌표축 기준으로 rotation이 적용되었습니다.

지금까지 살펴본 예시들을 통해 좌표 변환과 좌표축 변환 시 어떤 관계를 가지는 지 살펴볼 수 있었으며 이 관계를 extrinsic 행렬에 어떻게 표현하는 지 살펴보았습니다.

Camera Intrinsic Matrix with Example in Python

앞으로 살펴볼 내용은 카메라 intrinsic 파라미터 입니다. 일반적으로 카메라 파라미터로 사용하는 값들이 extrinsic, intrinsic, distortion coefficient입니다. 앞에서 extrinsic은 살펴보았고 intrinsic은 본 글에서 다룰 내용입니다. 단, intrinsic의 내용에 집중하기 위하여 본 글에서 다루는 카메라는 핀홀 카메라 모델을 사용할 예정이므로 distortion coefficient는 무시합니다.
distortion coefficient의 내용을 살펴보려면 다음 링크를 참조하시면 됩니다.
- 카메라 모델과 렌즈 왜곡 (lens distortion)

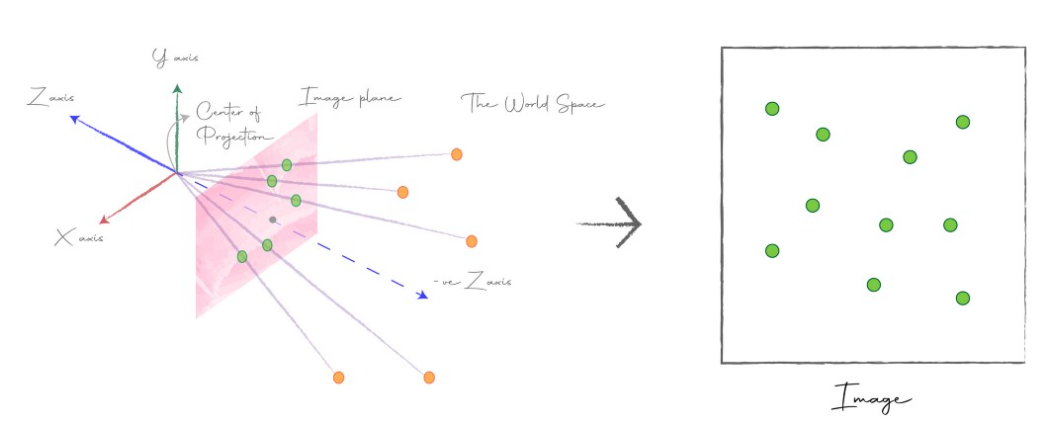
지금까지 world coordinate system에서 camera coordinate system으로 변환하는 방법을 camera extrinsic을 통하여 알아보았습니다. 지금부터는 camera coordinate system에서 image plane으로 어떻게 변환이 되는지를 통하여 intrinsic에 대하여 알아보도록 하겠습니다. 위 그림의 초록색 점들이 표현된 곳이 image plane입니다.

Projection of a point

이미지 형성을 위한 기본적인 아이디어는 물체로 반사되어 온 빛을 image plane에 projection 하는 것입니다. 이 때, image plane은 물체로 부터 반사된 빛을 캡쳐한다는 관점에서 필름과 같이 이해할 수 있습니다. 그리고 이미지에서의 각 픽셀은 image plane에서의 각 위치와 대응이 됩니다.

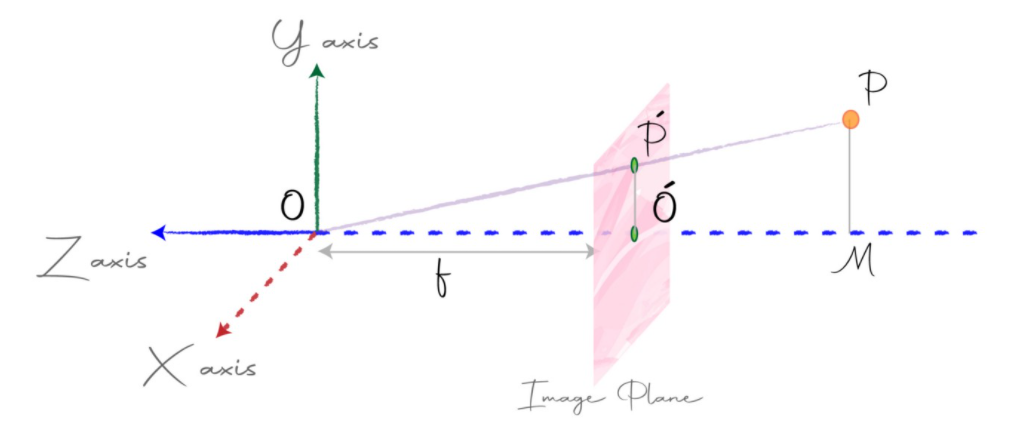
위 그림에서 원점은 앞에서 계속 명시하였던 center of projection으로 물체로부터 반사되어 온 빛을 projection 하였을 때 한 곳으로 모이는 점이 됩니다.
image plane은 원점으로부터 Z축 방향으로 \(f\) 만큼 떨어져 있다고 가정합니다. 여기서 \(f\) 를 focal length라고 합니다.
물체 \(P\) 가 image plane에 projection되었을 때, image plane상에서의 점을 \(P'\) 라고 하곘습니다. 그러면 위 그림의 \(X, Y, Z\) 축 기준으로 \(P\) 의 좌표는 \((x, y, z)\) 인 반면 \(P'\)의 좌표는 \((x', y', f)\) 가 됩니다. 여기서 목표는 \(P'\) 좌표를 알아내는 것 입니다.
위 그림에서 \(\Delta \text{OMP}\) 와 \(\Delta \text{OO'P}\) 가 닮은꼴 삼각형임을 이용하여 \(P'\) 좌표를 추정하면 다음과 같습니다.

\[\frac{x'}{x} = \frac{y'}{y} = \frac{f}{z} \tag{42}\]
\[x' = x \frac{f}{z} \tag{43}\]
\[y' = y \frac{f}{z} \tag{44}\]

식 (43), 식 (44)를 이용하여 \(x', y'\) 은 알 수 있으며 \(z' = f\) 로 고정됩니다.
만약 \(P\) 가 카메라로 부터 점점 더 멀어진다면 image plane에 projection된 물체의 좌표값인 \(P'\) 는 점점 작아질 것입니다. 왜냐하면 물체가 카메라로부터 멀어지면 \(f\) 는 고정이나 \(z\) 값이 커져서 \(x', y'\) 는 작아지기 때문입니다.

projection 된 이미지 상의 좌표를 구하고 싶다면 식 (43), (44)를 이용하여 \(x', y'\) 좌표를 구하고 \(z'\) 좌표는 버리면 됩니다. 예를 들어 \(P' = (xf/z, yf/z, f)\) 에서 마지막 \(z' = f\) 제외하면 됩니다. 이렇게 구한 좌표를 image coordinate 라고 하며 \((u, v)\) 로 표현합니다.

\[(u, v) = (\frac{xf}{z}, \frac{yf}{z}) \tag{45}\]

식 (45)를 이용하면 camera coordinate system → image coordinate로 변경할 수 있습니다. 하지만 현실적으로 image plane이 XY plane과 평행하지 않을 수 있고, image plane이 Z축과 많이 벗어날 수 있고 심지어 image plane 자체가 기울어져 있을 수도 있습니다. 카메라 제작 상황에 따라서 이 부분은 바뀔 수 있습니다.
따라서 정확하게 camera coordinate system → image coordinate로 좌표축을 변경하기 위한 행렬을 intrinsic 이라고 합니다.
intrinsic에는 크게 5가지 DoF가 있으며 이 값에 따라서 어떻게 image coordinate가 형성되는 지 달라집니다. 지금부터는 이 값을 이용하여 어떻게 intrinsic matrix를 만드는 지 살펴보도록 하겠습니다. 살펴볼 요소는 크게 4가지로 Scale, Rectangular Pixels, Offset, Skew 입니다.

Scale

카메라를 구입하면 카메라의 상세 스펙으로 adjustable focal length라는 부분이 있습니다. 이 수치는 주로 mm와 같은 길이 수치로 되어 있습니다. 이 값은 앞에서 설명한 \(f\)에 해당합니다.

\[(u, v) = (\alpha \frac{x}{z}, \alpha \frac{y}{z}) \tag{46}\]

위 예시에서 \(u, v\) 를 구하기 위하여 동일한 \(\alpha\) 를 썻다는 것 또한 이상적인 환경입니다. 만약 image plane의 픽셀의 크기가 정사각형이 아니라 직사각형 형태이면 어떻게 될까요?
이상적인 환경에서 픽셀의 크기는 정사각형이지만 실제로는 height와 width의 크기가 다른 직사각형 형태인 경우가 많습니다. 따라서 앞의 \(u, v\) 좌표를 다음과 같이 표현하도록 하겠습니다.

\[(u, v) = (\alpha \frac{x}{z}, \beta \frac{y}{z}) \tag{47}\]

식 (47)에서 \(\alpha\)는 width 방향으로의 scaling factor이고 \(\beta\) 는 height 방향으로의 scaling factor입니다.

식 (47) 에서 표현한 \((\alpha \frac{x}{z}, \beta \frac{y}{z})\) 에서는 근본적인 원리를 설명하기 위하여 모두 분해하여 나타내었습니다.
하지만 앞에서 언급하였듯이, 실제로 카메라에 기입된 스펙에는 focal length 1개가 mm 단위로 나타내어져 있습니다. 이상적인 환경에서는 실제 픽셀에 해당하는 이미지 센서의 각 셀의 크기가 정사각형이어야 하지만 현실적으로 직사각형일 수 있으므로 \(f_{x}, f_{y}\) 표기법으로 나타내면 다음과 같습니다.
\[\alpha = f_{x} \propto \frac{f}{\text{sensor cell width (e.g. mm)}} \times \text{ image width (in pixels)}\]
\[\beta = f_{y} \propto \frac{f}{\text{sensor cell height (e.g. mm)}} \times \text{ image height (in pixels)}\]

카메라 intrinsic에서 사용하는 \(f_{x}, f_{y}\) 는 실제 하드웨어 값인 focal length에 비례하고 각 방향의 이미지 해상도 크기에 비례합니다. 따라서 이미지 해상도를 크게 표현할수록 \(f_{x}, f_{y}\) 는 커집니다.

정리하면 \(fx, fy\) 를 결정하는 데 영향을 주는 값은 focal length인 \(f\), 센서셀의 가로/세로 크기 그리고 이미지 해상도 임을 확인할 수 있습니다.
여기서 센서셀의 가로/세로 크기는 완전히 고정된 상수값이므로 \(fx, fy\) 의 값을 조정할 때, 무시할 수 있습니다. 반면 원하는 \(fx, fy\) 를 결정하는 데 focal length \(f\) 와 이미지 해상도는 변경할 수 있습니다.
먼저 focal length \(f\) 는 사용하는 렌즈에 따라 조절이 가능한 값입니다. 하나의 카메라에 대하여 focal length를 큰 카메라 렌즈 환경을 구성할 수 있고 focal length가 작은 카메라 렌즈 환경도 구성할 수 있기 때문입니다. 이 값에 따라 보고자 하는 영역이 달라집니다. 대표적으로 원거리 영상을 확대해서 촬영하는 대포카메라 같은 경우에 focal length가 큰 렌즈 환경입니다.
그리고 이미지 해상도를 크게 할수록 이미지 width/height 방향의 픽셀 갯수가 많아지기 때문에 이 공간을 표현하기 위해서 \(fx, fy\) 값 또한 커져야 함을 알 수 있습니다.
따라서 \(fx, fy\) 와 연관된 값을 정리하면 다음과 같습니다.
- ① Focal Length ( \(f\) ) : Variable. 렌즈 셋팅 환경에 따라 변경될 수 있습니다.
- ② Sensor Cell Size : Constant. 센서의 물리적인 값으로 고정된 값입니다.
- ③ Image Size : Variable. 카메라 환경이나 Post-Processing 측면에서 변경될 수 있습니다.
- ④ \(fx, fy\) : Variable. focal length와 image size/resolution에 의하여 결정되는 값입니다.

따라서 (cell width/height size 사이즈가 같고) focal length의 크기가 같은 두개의 이미지의 \(f_{x}, f_{y}\) 의 크기 차이가 난다면 \(f_{x}, f_{y}\) 크기가 더 큰 이미지의 해상도가 더 크다는 의미를 가지며 3D 공간의 정보를 좀 더 세세하게 표현하고 접근할 수 있다는 것을 의미합니다.
반면 이미지의 해상도가 같은 두개의 이미지의 \(f_{x}, f_{y}\) 의 크기 차이가 난다면 focal length가 다르다고 해석할 수 있으며 focal length가 큰 이미지는 화각은 좁지만 멀리까지 선명하게 볼 수 있고 focal length가 작은 이미지는 넓은 영역을 볼 수 있지만 가까운 영역만 선명하게 볼 수 있다는 차이가 있습니다.

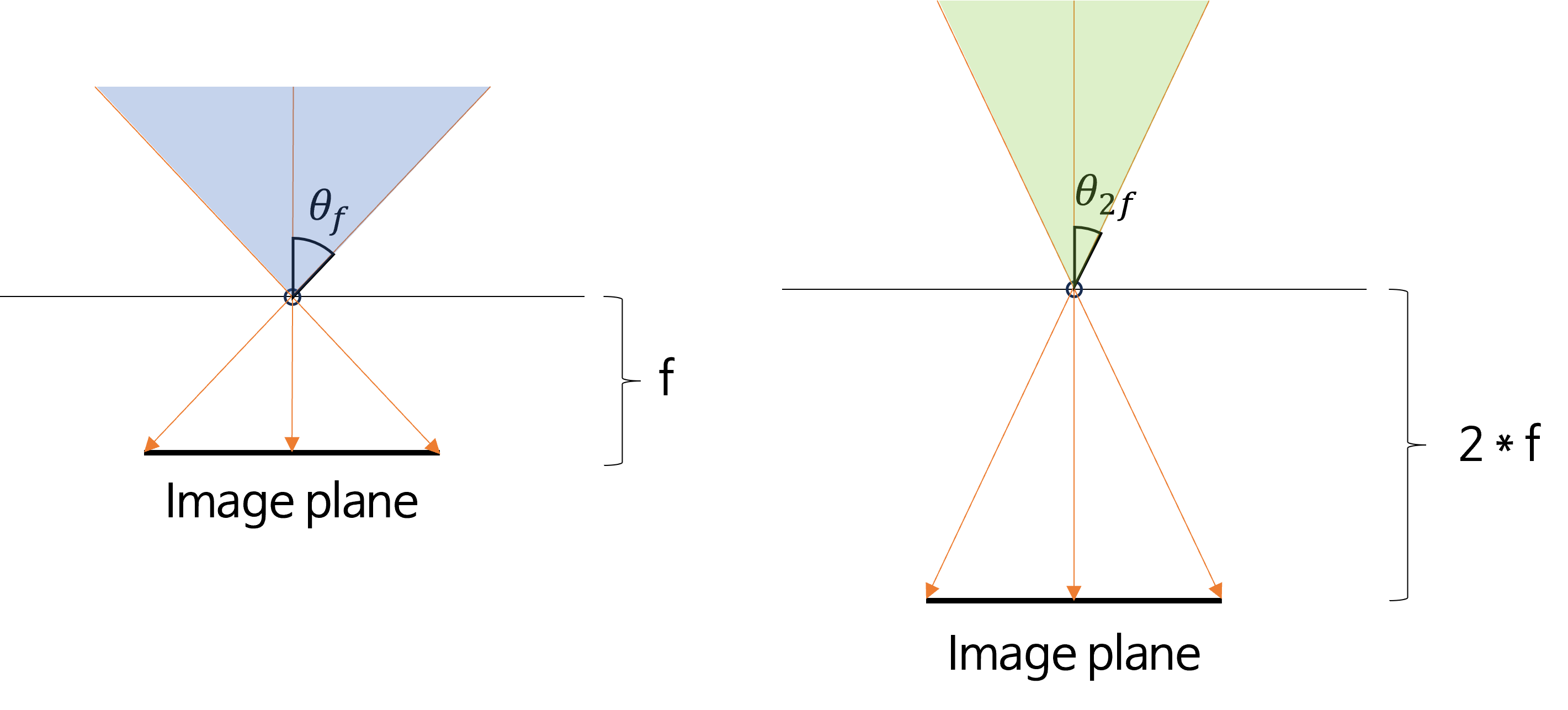
위 그림을 살펴보면 같은 크기의 image plane을 사용한 것을 통해 이미지의 해상도는 같다는 설정을 확인할 수 있고 focal length \(f\) 의 길이를 2배 차이나도록 하였습니다.
왼쪽 이미지는 focal length \(f\) 를 가지게 되고 고정된 이미지 해상도에 파란색 영역을 모두 투영시킬 수 있습니다. 반면 오른쪽 이미지는 focal length \(2f\) 를 가지게 되고 파란색 영역보다 좁은 초록색 영역만 투영시킬 수 있습니다. 따라서 즉 \(\theta_{f} \gt \theta_{2f}\) 가 됩니다.
반면 image plane의 크기가 같기 때문에 픽셀 별 대응해야 할 3D 공간의 크기는 동일해야 하므로 파란색 영역과 초록색 영역의 밀도는 같아져야 합니다. 따라서 초록색 영역은 화각 ( \(\theta_{2f}\) )이 좁기 때문에 더 먼 영역까지 픽셀 정보가 빽빽하게 존재할 수 있습니다. 이러한 이유로 \(f\) 가 클수록 화각은 좁지만 멀리까지 선명하게 볼 수 있습니다.

Offset

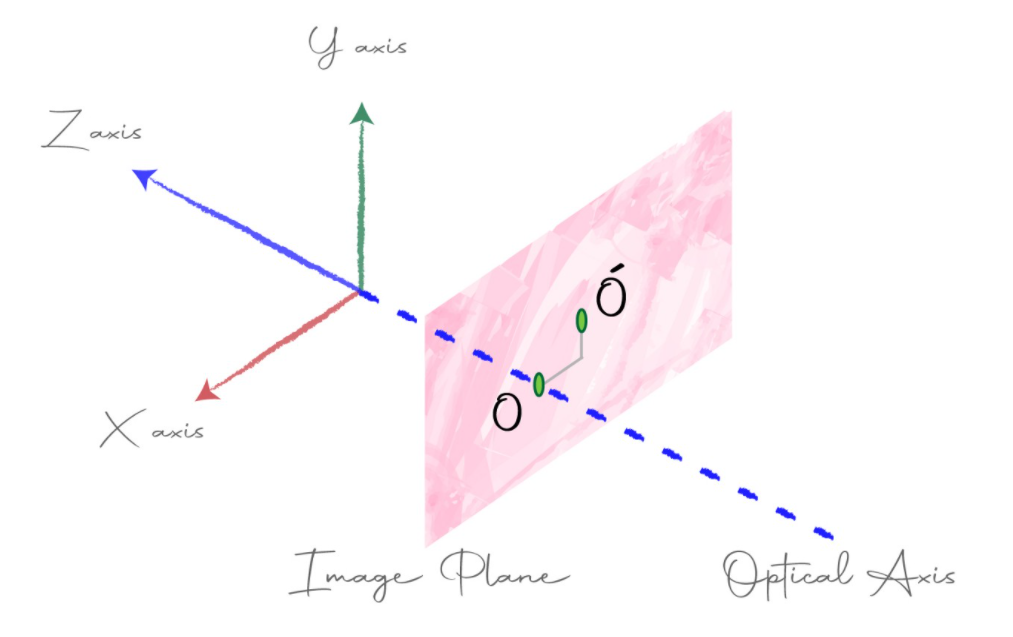
camera center와 image plane 의 수직선을 optical axis라고 합니다. 이상적인 환경에서는 optical center와 image plane의 origin은 서로 일치하지만, 실제 카메라 환경에서는 차이가 발생할 수 있습니다. 이 차이를 보상해 주는 것을 Offset 이라고 합니다.
Offset은 위 그림에서 \(O\) 와 \(O'\) 간의 image plane에서의 차이를 뜻하며 \(O\) 는 optical axis와 image plane의 수직선이 만나는 부분이고 \(O'\) 는 image plane의 중심점을 뜻합니다.

\[(u, v) = (\alpha \frac{x}{z} + x_{0}, \beta \frac{y}{z} + y_{0}) \tag{48}\]

따라서 식 (48)과 같이 \(x_{0} , y_{0}\) 를 통하여 \((u, v)\) 를 보정하여 구합니다.

실제 이미지를 사용할 때, 이미지 좌표계의 원점은 좌상단을 \((0, 0)\) 원점으로 잡습니다. 식 (48)의 원리를 이용하면 offset을 이미지 좌상단이 원점이 되도록 만들 수 있습니다. 이 내용은 intrinsic 마지막 부분에서 다루도록 하겠습니다.

Skew

지금까지 image plane은 직사각형 형태를 가지고 있음을 가정하였습니다. 하지만 실제 image plane이 기울어져서 평행사변형 형태인 경우도 있습니다.

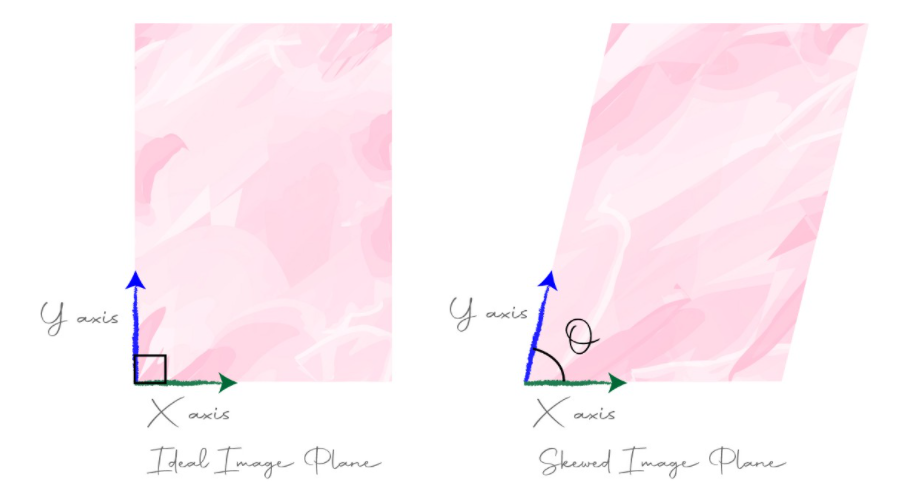
왼쪽 그림은 이상적인 image plane이고 X, Y 축은 직각 관계를 가집니다. 반면 오른쪽 그림은 기울어직 image plane입니다. 지금부터 왼쪽 image plane과 오른쪽 image plane 간의 관계를 파악하고 image plane을 변환하는 방법에 대하여 살펴보도록 하겠습니다.

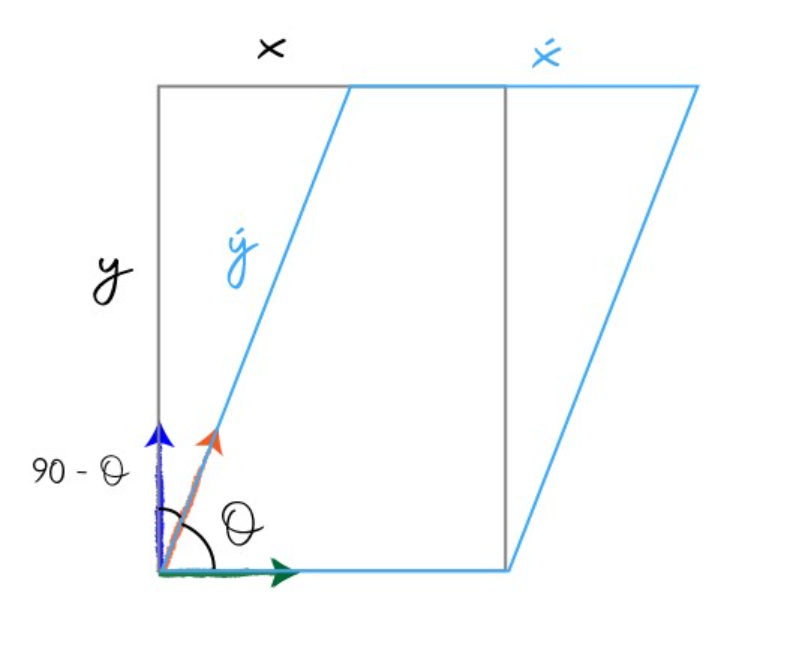
지금부터 \(x'\)와 \(x\) 의 관계식과 \(y'\)와 \(y\) 의 관계식을 각각 알아보고 검정색 \(xy\) 평면을 하늘색 \(x'y'\) 평면으로 변환하는 식을 정의해 보겠습니다.

\[\cos{(90 - \theta)} = \frac{y}{y'} \tag{49}\]
\[\sin{(\theta)} = \frac{y}{y'} \tag{50}\]
\[y = y'\sin{(\theta)} \tag{51}\]
\[\therefore y' = \frac{y}{\sin{(\theta)}} \tag{52}\]

\[\sin{(90 - \theta)} = \frac{(x - x')}{y'} \tag{53}\]
\[y'\cos{(\theta)} = x - x' \tag{54}\]
\[x' = x - y'\cos{\theta} \tag{55}\]
\[y' = \frac{y}{\sin{(\theta)}} \tag{56}\]
\[x' = x - \frac{y\cos{(\theta)}}{\sin{(\theta)}} \tag{57}\]
\[\therefore x' = x - y\cot{(\theta)} \tag{58}\]

식(58)을 통하여 \(x'\) 의 관계식을 찾았고 식 (52)를 통하여 \(y'\) 의 관계식을 찾았습니다. 식 (58)과 식 (52)를 식 (48)에 대입하여 기울어진 평면 위의 좌표인 \((u, v)\) 를 정의해 보겠습니다.

\[u = \alpha \frac{x'}{z} + x_{0} = \alpha \frac{x - y\cot{(\theta)}}{z} + x_{0} \tag{59}\]
\[v = \beta \frac{y'}{z} + y_{0} = \beta \frac{\frac{y}{\sin{(\theta)}}}{z} + y_{0} = \beta \frac{y}{z\sin{(\theta)}} + y_{0} \tag{60}\]

위 식에서 skew가 전혀 없다면 \(\theta = \pi / 2\) 가 됩니다. skew 값이 존재하더라도 미세한 값이므로 \(\theta\) 가 \(\pi/4 \sim \pi/2\) 의 범위에서 \(u\) 에 영향을 끼치는 \(-\cot{(\theta)}\) 와 \(v\) 에 영향을 끼치는 \(1/\sin{(\theta)}\) 의 변경 범위를 살펴보면 다음과 같습니다.

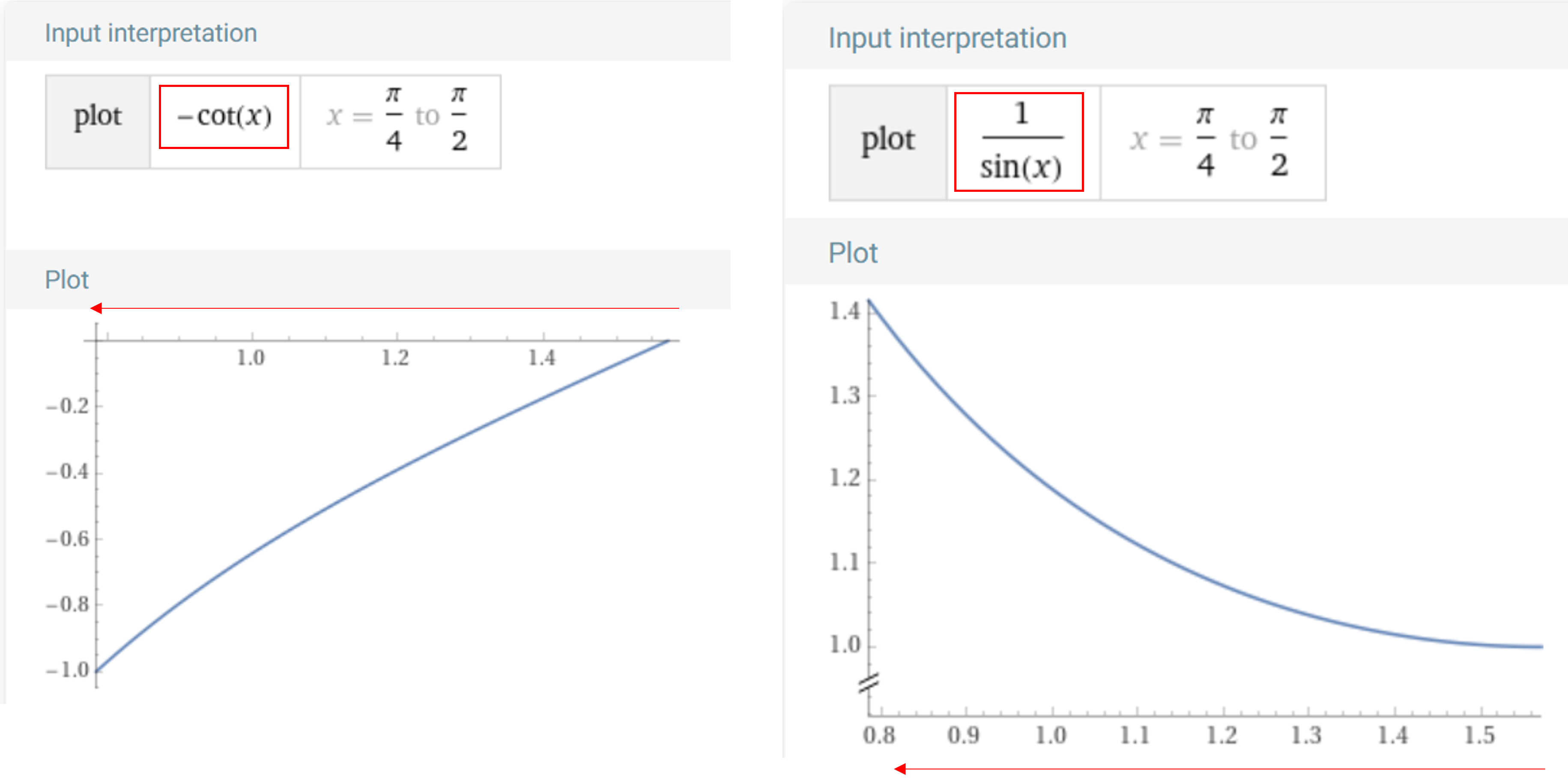
위 그래프와 같이 \(\theta\) 값이 증가할수록 \(-\cot{(\theta)}\) 값은 음의 방향으로 커지게 됩니다. 따라서 \(u\) 의 값은 작아지게 됩니다. (좌측 방향으로 이동)
반면 \(\theta\) 값이 증가할수록 \(1/\sin{(\theta)}\) 의 값은 양의 방향으로 커지게 되어 \(v\) 값은 커지게 됩니다. (아래 방향으로 이동)
따라서 \(\theta\) 값이 증가할수록 전체 좌표값은 좌측 하단 방향으로 기울어진 형태를 가지게 됩니다. shear transformation을 생각하면 됩니다.
위 그림의 \(\theta\) 기울기는 우측 상단 방향으로 image plane이 기울어진 반면 좌표 결과는 좌측 하단 방향으로 반대로 기울어진 이유는 image plane이 기울어진 것은 좌표계가 shear transformation이 적용된 것이므로 좌표는 반대로 적용되기 때문입니다.

Camera Intrinsic Matrix

식 (59), (60)을 이용하여 image plane의 scale, offset, skew를 고려한 \(u, v\) 좌표를 구하는 방법에 대하여 알아보았습니다. 다시 좌표 형태로 표현하면 다음과 같습니다.

\[(u, v) = (\frac{\alpha}{z}x - \frac{\alpha\cot{(\theta)}} {z}y + x_{0}, \frac{\beta}{z\sin{(\theta)}}y + y_{0}) \tag{61}\]

앞에서 extrinsic을 구할 때, homogeneous coordinates 형태의 행렬 곱으로 나타낸 것과 같이 intrinsic을 구할 때에도 이와 같은 형태를 사용해 보도록 하겠습니다.
앞으로의 식 전개를 위해 식 (61)의 \(x /z\) 와 \(y / z\) 는 \(x_{n}\) 과 \(y_{n}\) 표기로 사용하겠습니다. \(n\) 은 normalized의 약자로 관련 내용은 뒷편에서 설명할 예정입니다.

\[(u, v) = (\alpha x_{n} -\alpha \cot{(\theta)}y_{n} + x_{0}, \frac{\beta}{\sin{(\theta)}}y_{n} + y_{0}) \tag{62}\]

아래와 같은 행렬 연산식인 식(63)을 정의해 보겠습니다. 식 (63)에 추가 연산을 통하여 최종 좌표를 구할 수 있습니다.

\[\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha & -\alpha\cot{(\theta)} & x_{0} \\ 0 & \frac{\beta}{\sin{(\theta)}} & y_{0} \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_{n} \\ y_{n} \\ 1 \end{bmatrix} \tag{63}\]

식 (63)의 우변의 3 x 3 행렬을 camera intrinsic matrix 라고하며 \(K\) 라고 나타냅니다. 따라서 \(P_{c}\) 인 camera coordinate system에서의 좌표가 \(K\) 인 camera intrinsic matrix와 곱해지면 이미지 상의 좌표인 \(P'\) 로 구해집니다.

\[P' = K \frac{1}{z}P_{c} \tag{64}\]
\[P' : \text{Homogeneous coordinates of the point in the image}\]
\[K : \text{Camera Intrinsic Matrix}\]
\[P_{c} : \text{Homogeneous Coordinates of the point in the camera coordinate system}\]

식 (64)를 풀어서 적으면 다음과 같습니다.

\[P' = K \frac{1}{z} P_{c} = K \frac{1}{z}\begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = \begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix} \tag{65}\]
\[K = \begin{bmatrix} \alpha & -\alpha\cot{(\theta)} & x_{0} \\ 0 & \frac{\beta}{\sin{(\theta)}} & y_{0} \\ 0 & 0 & 1 \end{bmatrix}\]

최종적으로 식 (65) 과정을 거치면 image plane 상의 pixel 위치인 \(u, v\) 를 구할 수 있습니다.
지금까지 알아본 내용을 통하여 camera coordinate system에서 intrinsic을 곱하여 image plane으로 좌표를 변환할 수 있었습니다.
지금까지 내용을 바탕으로 실질적으로 사용하는 형태의 intrinsic 행렬을 정리하려면 다음 내용을 고려하여 정리할 수 있습니다.
① 이미지 센서 셀 생산 기술의 발달로 이미지 센서가 기울어지지 않게 생산됩니다. 즉, skew 값의 \(\theta = \frac{\pi}{2}\) 로 둘 수 있습니다. 따라서 \(\cot{(\frac{\pi}{2})} = 0, \sin^{-1}{(\frac{\pi}{2})} = 1\) 로 사용할 수 있습니다.
② \(x_{0}, y_{0}\) 은 단순히 offset을 보상하는 개념 뿐 아니라 image coordinate에서 좌상단을 원점으로 만들어주는 역할을 합니다. 따라서 이상적인 환경에서는 \(x_{0}, y_{0}\) 각각이 이미지 width/2, height/2가 됩니다.

위 ①, ② 조건을 만족하도록 intrinsic을 다시 구성해보도록 하겠습니다.

\[K = \begin{bmatrix} \alpha & -\alpha\cot{(\theta)} & x_{0} \\ 0 & \beta\sin^{-1}{(\theta)} & y_{0} \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} \alpha & 0 & x_{0} \\ 0 & \beta & y_{0} \\ 0 & 0 & 1 \end{bmatrix} \tag{66}\]

따라서 camera coordinate system의 임의의 점 \((X_{c}, Y_{c}, Z_{c})\) 는 다음과 같이 image coordinate의 \((u, v)\) 좌표로 변환될 수 있습니다.

\[\begin{bmatrix} u \\ v \end{bmatrix} = \begin{bmatrix} \alpha & 0 & x_{0} \\ 0 & \beta & y_{0} \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X_{c} / Z_{c} \\ Y_{c} / Z_{c} \end{bmatrix} \tag{67}\]
\[u = \alpha ( X_{c} / Z_{c} ) + x_{0} \tag{68}\]
\[v = \beta ( Y_{c} / Z_{c} ) + y_{0} \tag{69}\]

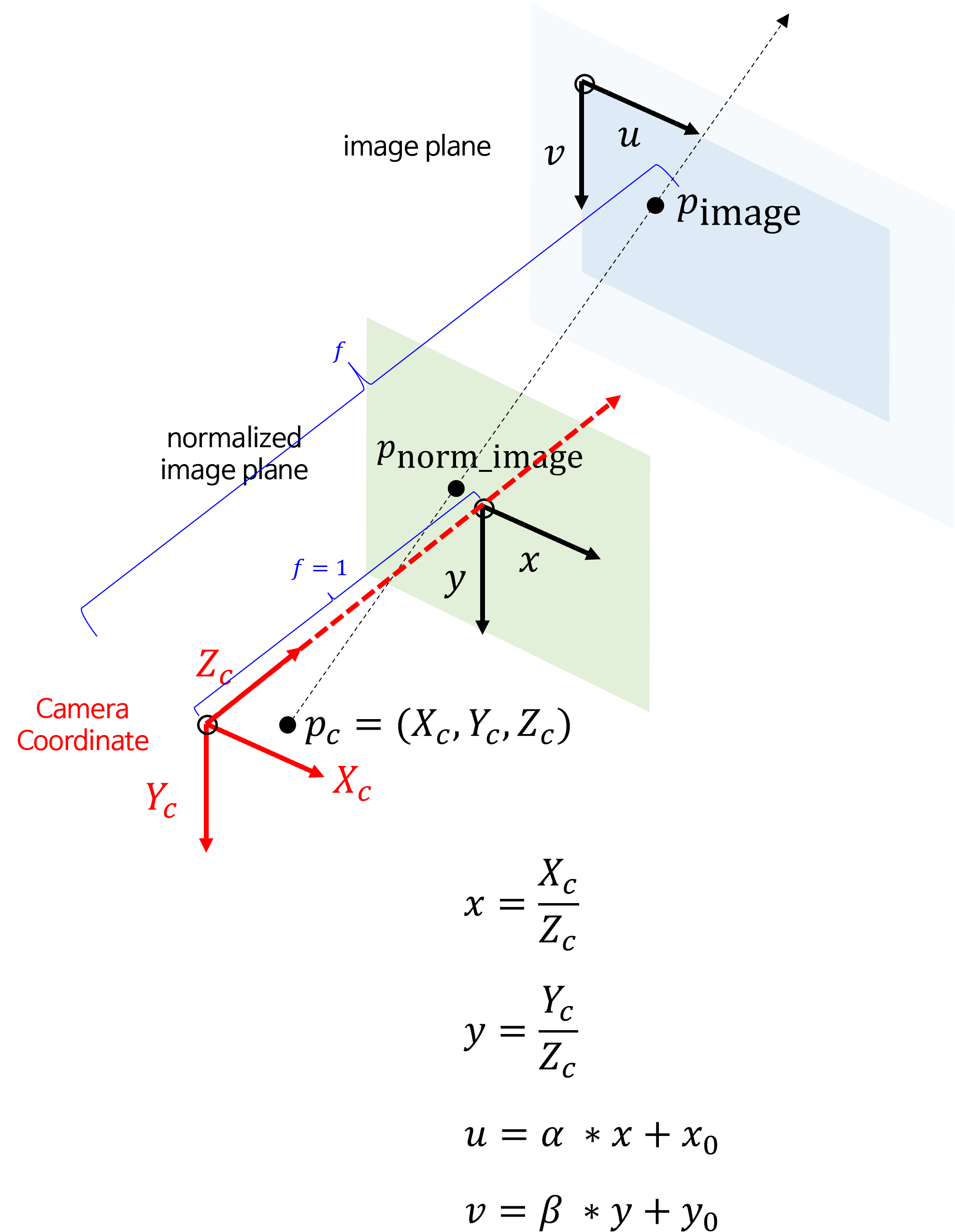
식 (68), (69)에 사용된 \(\alpha, \beta\) 는 focal length의 크기와 이미지 해상도 등에 영향을 받으므로 값은 항상 0보다 큰 값입니다. 즉, \((X_{c} / Z_{c}), (Y_{c} / Z_{c})\) 값을 scale 조절하여 최종적으로 image coordinate에 대응 시키는 역할을 합니다.
위 그림에서 \(x = X_{c}/Z_{c}, y = Y_{c}/Z_{c}\) 에 해당하며 이 때 focal length는 1이 되는 것을 확인할 수 있습니다. \(Z_{c}\) 로 값을 나누어서 scale=1로 normalize 시켜주었기 때문에 \(Z_{c} = 1\) 인 공간을 normalized image plane이라고 합니다.
normalized image plane의 값에 \(\alpha, \beta\) 를 곱해주면 image plane에 대응되는 scale의 값으로 투영됩니다.
여기 까지가 \(\alpha * X_{c}/Z_{c}\), \(\beta * Y_{c}/Z_{c}\) 까지 연산한 것입니다.

scale이 조정된 후 \(x_{0}, y_{0}\) 이 더해져서 값이 이동하게 됩니다. 이 때 \(x_{0}, y_{0}\) 의 역할이 scale이 조정된 값을 image coordinate 기준인 좌상단을 원점으로 좌표값을 이동시켜주는 역할을 한다고 보면 됩니다. 만약 camera center와 image plane의 수직선인 optical axis가 이미지의 정중앙에 위치한다면 \(x_{0}, y_{0}\) 가 optical axis를 보정하는 역할은 하지 않고 image coordinate로의 변환을 위한 이동의 의미만을 가지게 됩니다.
optical axis가 정중앙에 위치할 때, \(x_{0}, y_{0}\) 가 image coordinate로의 이동을 의미하려면 다음 값을 가져야 합니다.

\[x_{0} = \frac{\text{width}}{2}\]
\[y_{0} = \frac{\text{height}}{2}\]

이러한 이유로 intrinsic의 값 중 \(x_{0}, y_{0}\) 은 각각 width, height의 중간값 부근에서 값을 가지게 됩니다. (완전히 중간값을 가지지 않는 경우는 그만큼 optical axis가 이동되어 보정 역할 까지 한 것으로 볼 수 있습니다.)
따라서 scale 조정 이후에 image plane의 좌표축에 맞도록 좌표 이동을 해준 것이 식 (68), (69)가 됩니다.

저는 개인적으로 카메라 intrinsic을 망원경에 종종 비유합니다.

3D 공간 상에 물체 및 배경은 존재하고 내가 어떻게 바라보는 지 따라서 보이는 형태가 다르기 때문입니다.
내가 보고싶은 영역을 돋보기를 평행이동하면서 보는 것을 \(x_{0}, y_{0}\) 로 표현하고 돋보기의 배율을 \(\alpha, \beta\) 로 표현할 수 있기 때문입니다. 돋보기의 배율이 높아지면 멀리까지 볼 수 있지만 볼 수 있는 영역이 좁아지는 것도 앞에서 살펴본 \(\alpha, \beta\) 의 의미와 일맥상통합니다.

Camera Intrinsic 변환 애니메이션

애니메이션 링크 : http://ksimek.github.io/perspective_camera_toy.html

앞에서 다룬 focal length와 \(x_{0}\), \(y_{0}\) 의 변화에 따라서 이미지가 어떻게 변화하는 지 살펴보도록 하겠습니다.
먼저 focal length의 변화를 적용해 보면 다음과 같습니다.

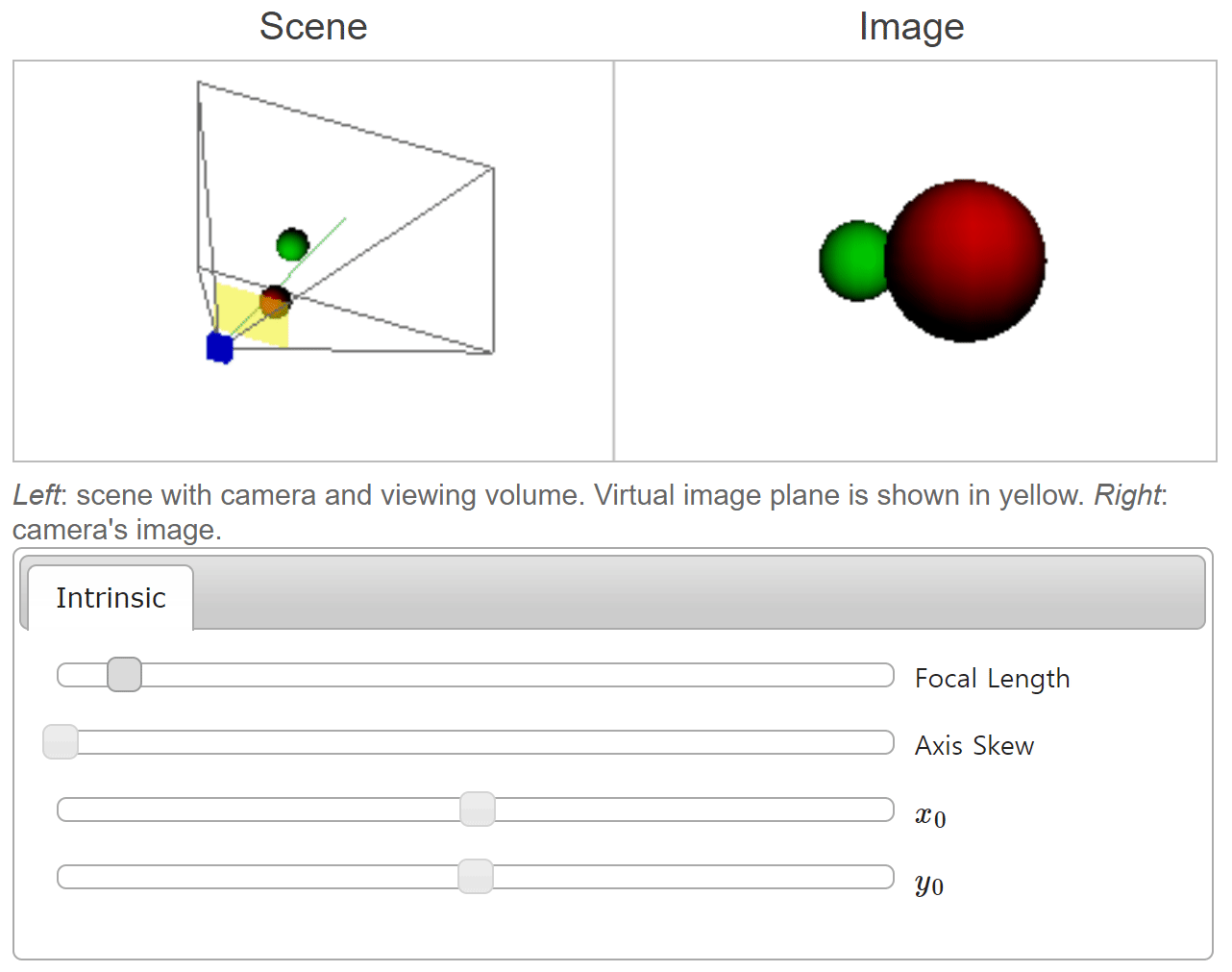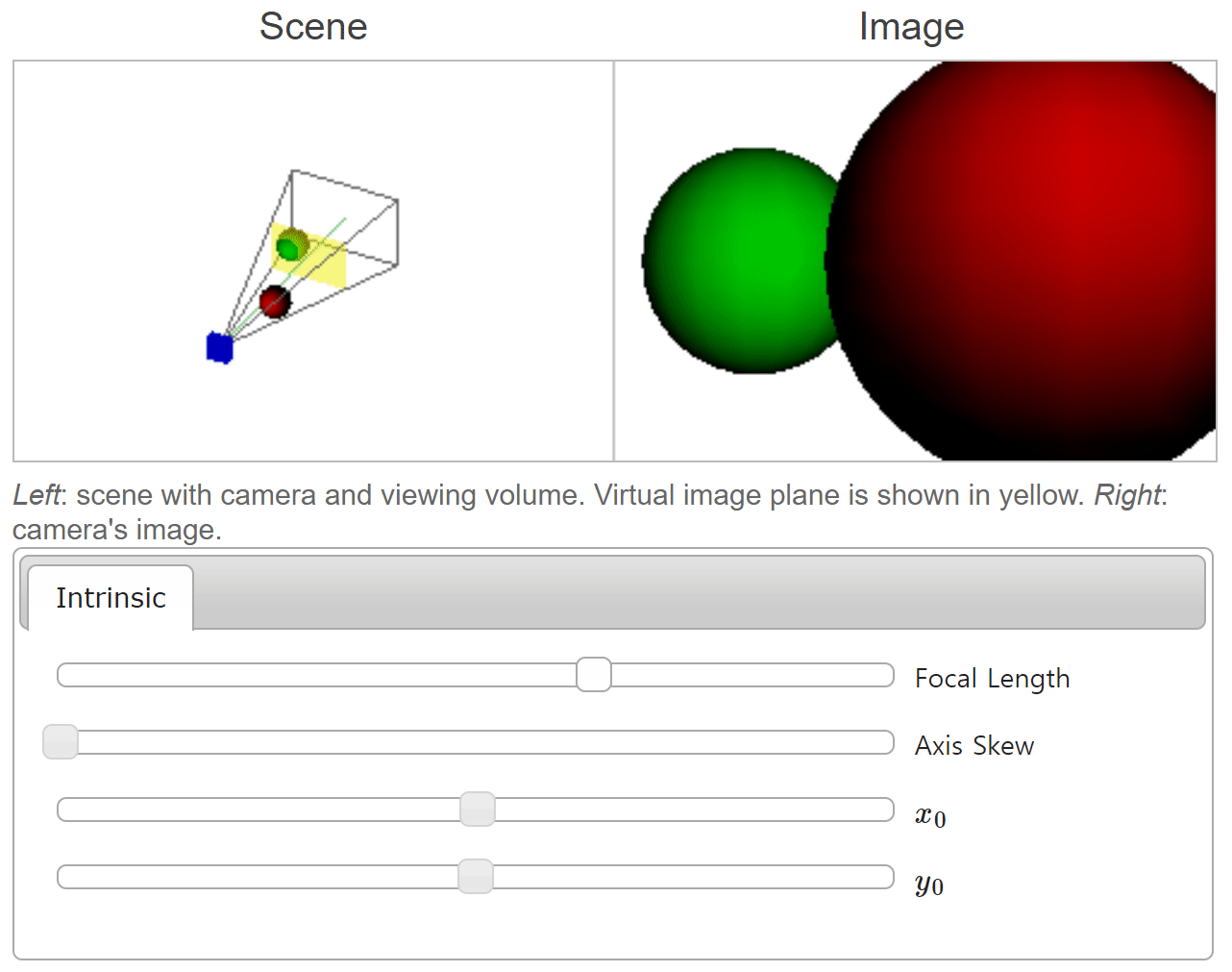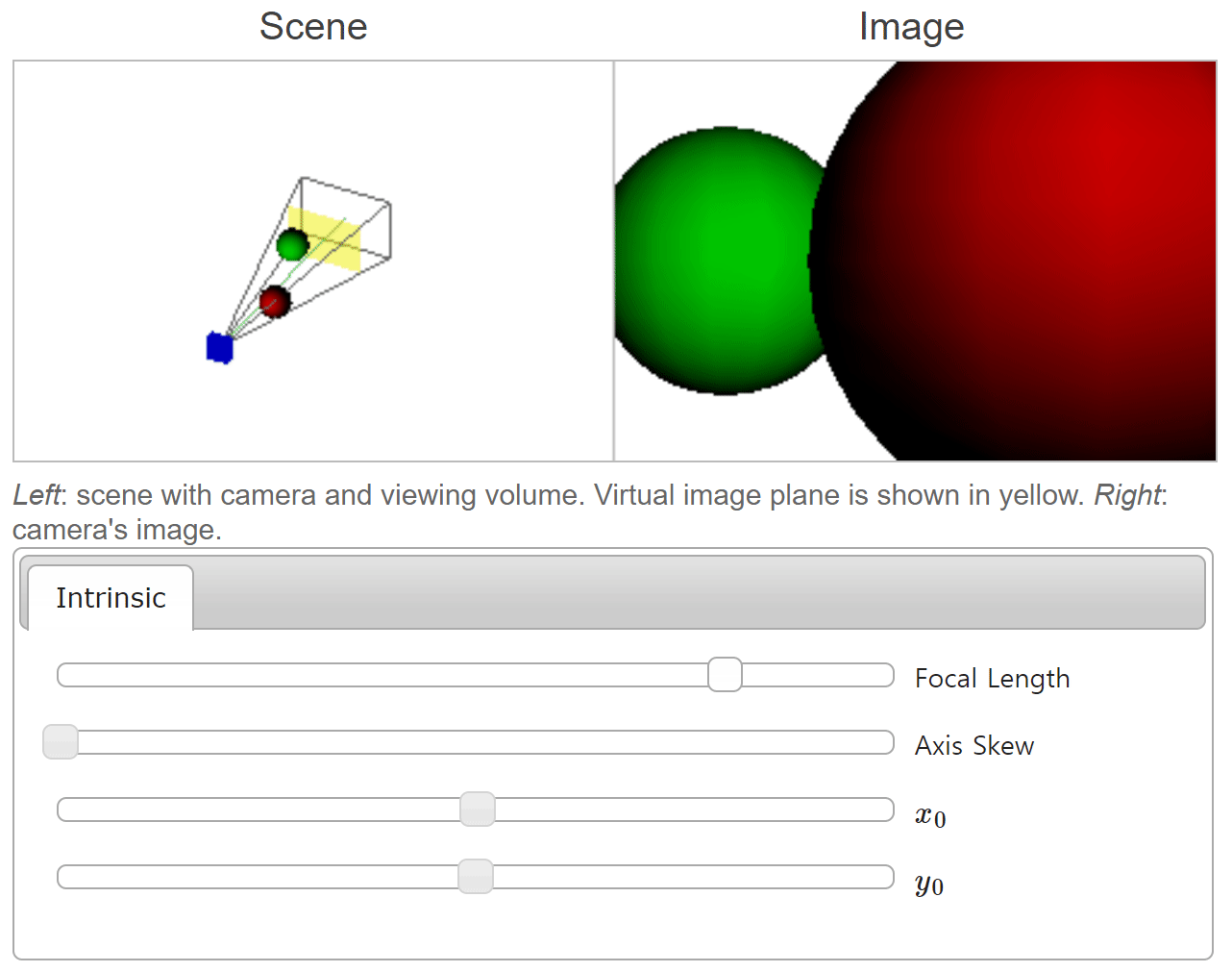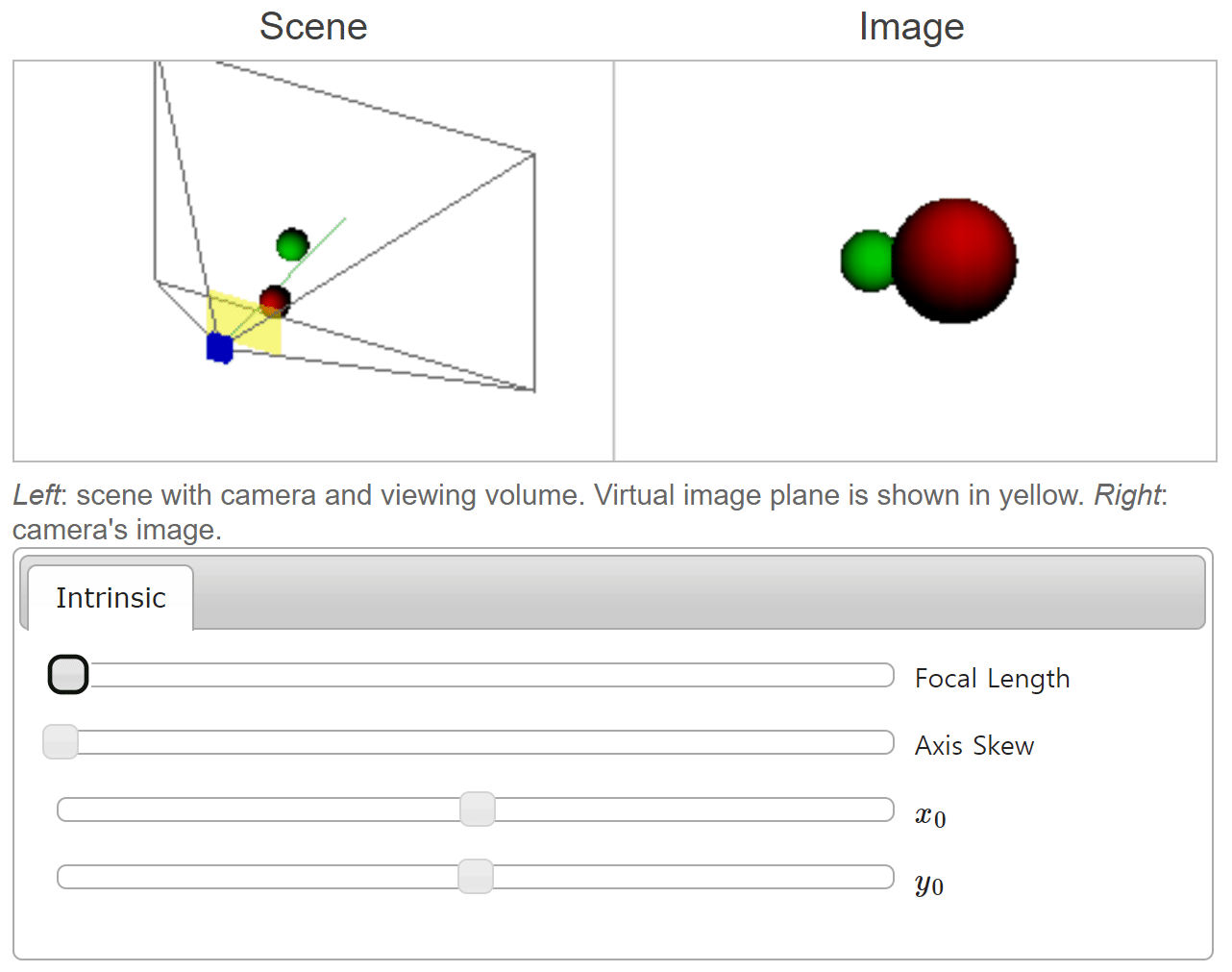
focal length가 커질수록 화각은 좁아지는 대신에 확대되어 보이는 것을 확인할 수 있습니다. 반대로 focal length가 작아질수록 화각은 넓어지면서 같은 물체의 크기가 작아지는 것을 볼 수 있습니다. 이와 관련된 내용은 scale 부분에서 설명하였습니다.

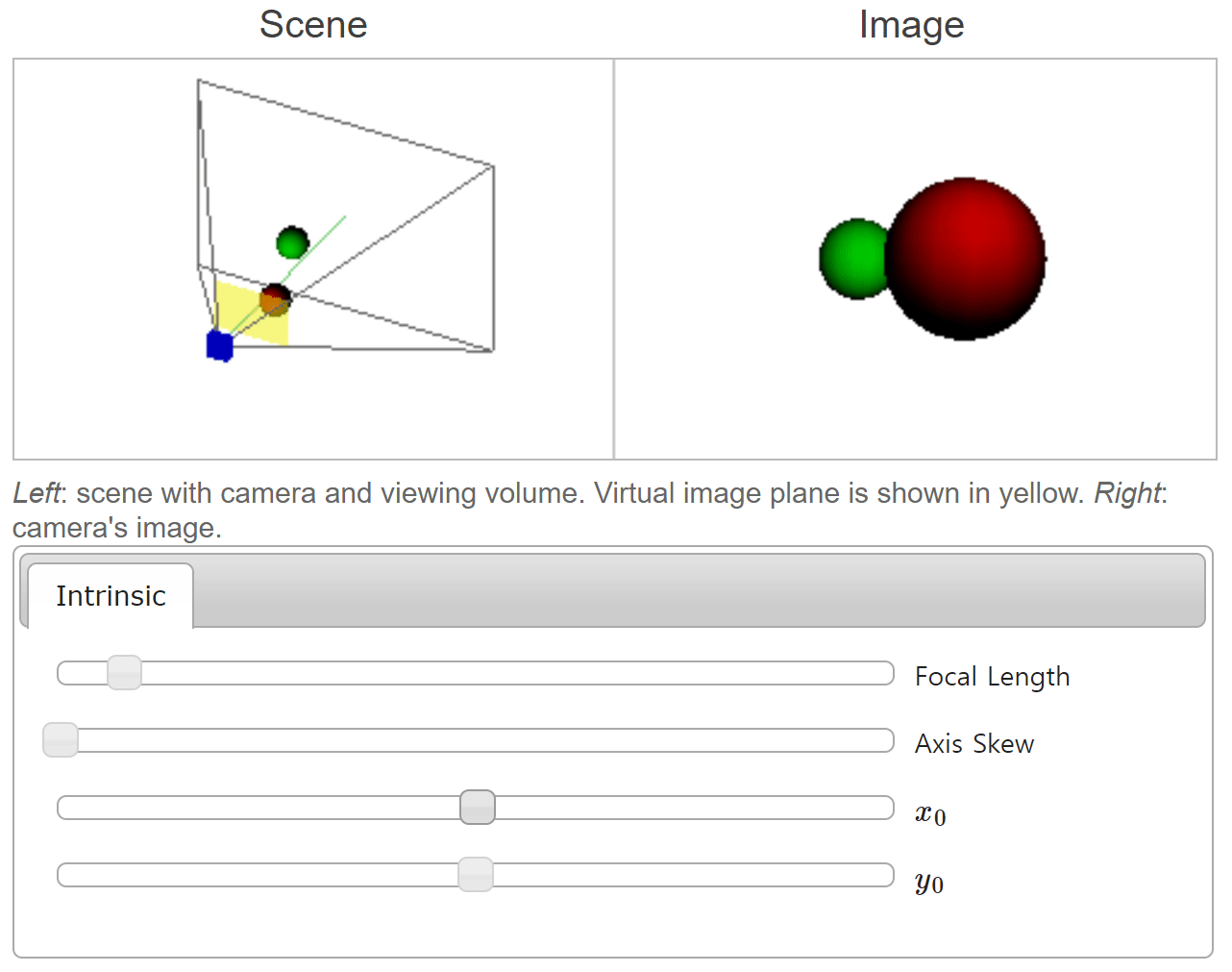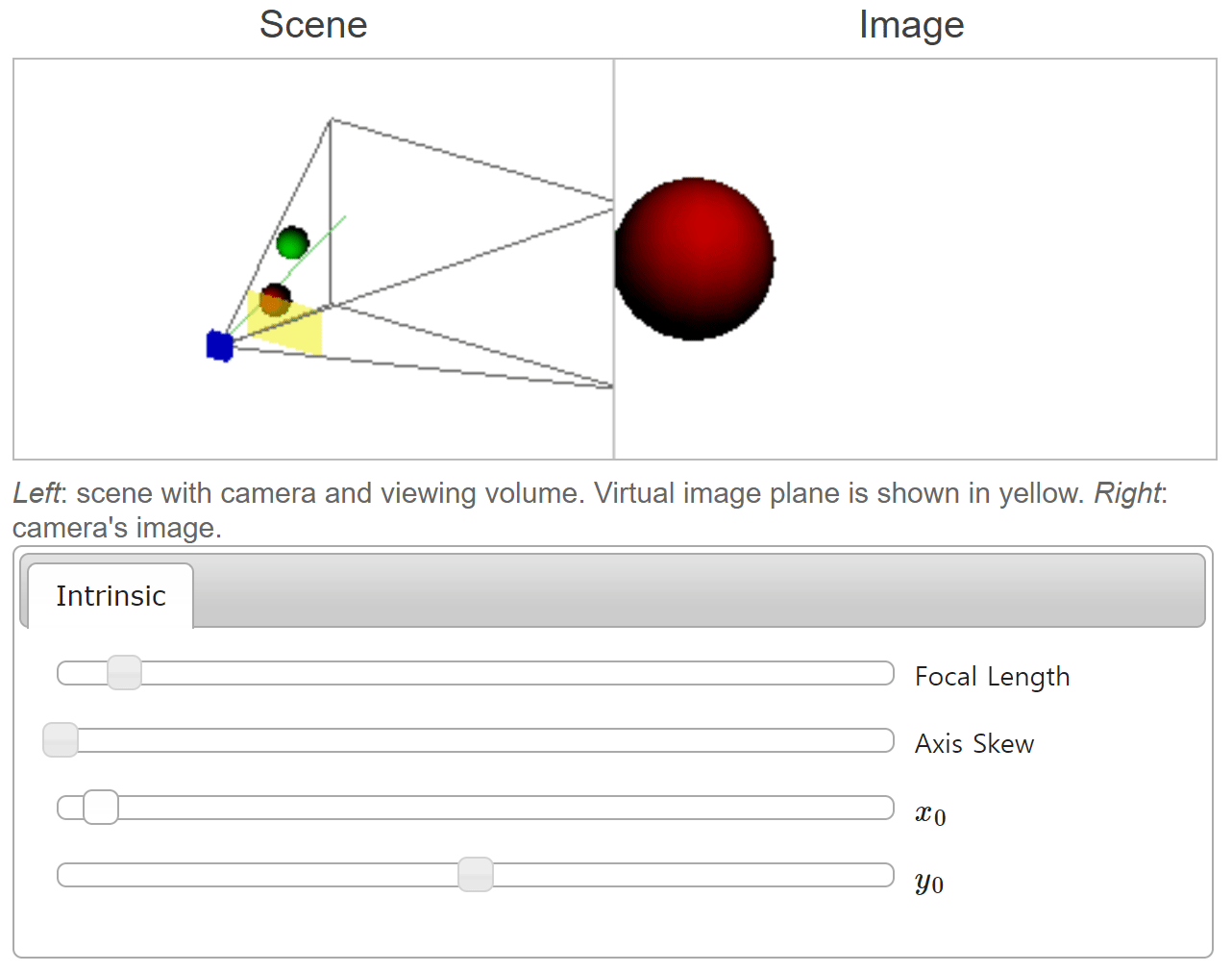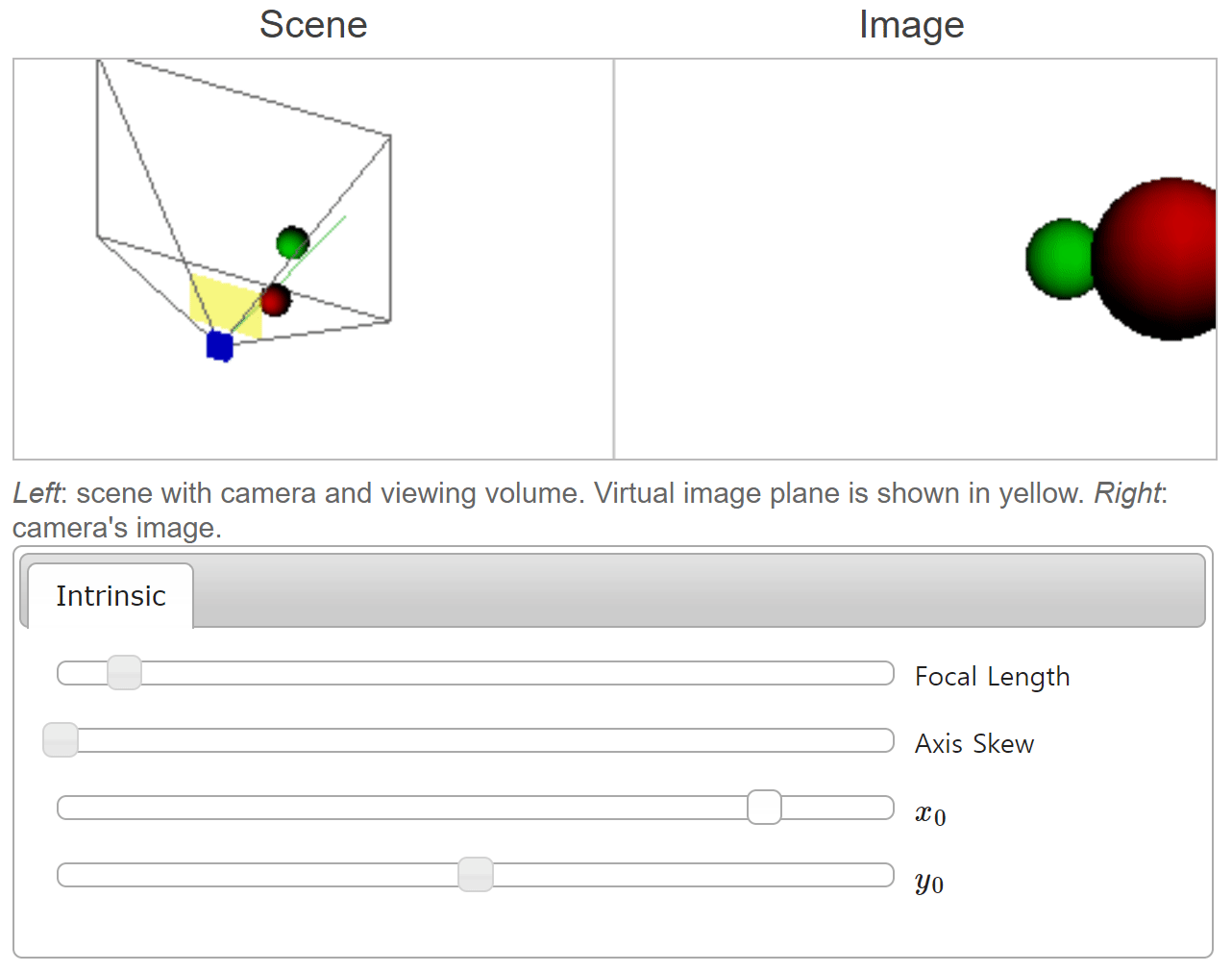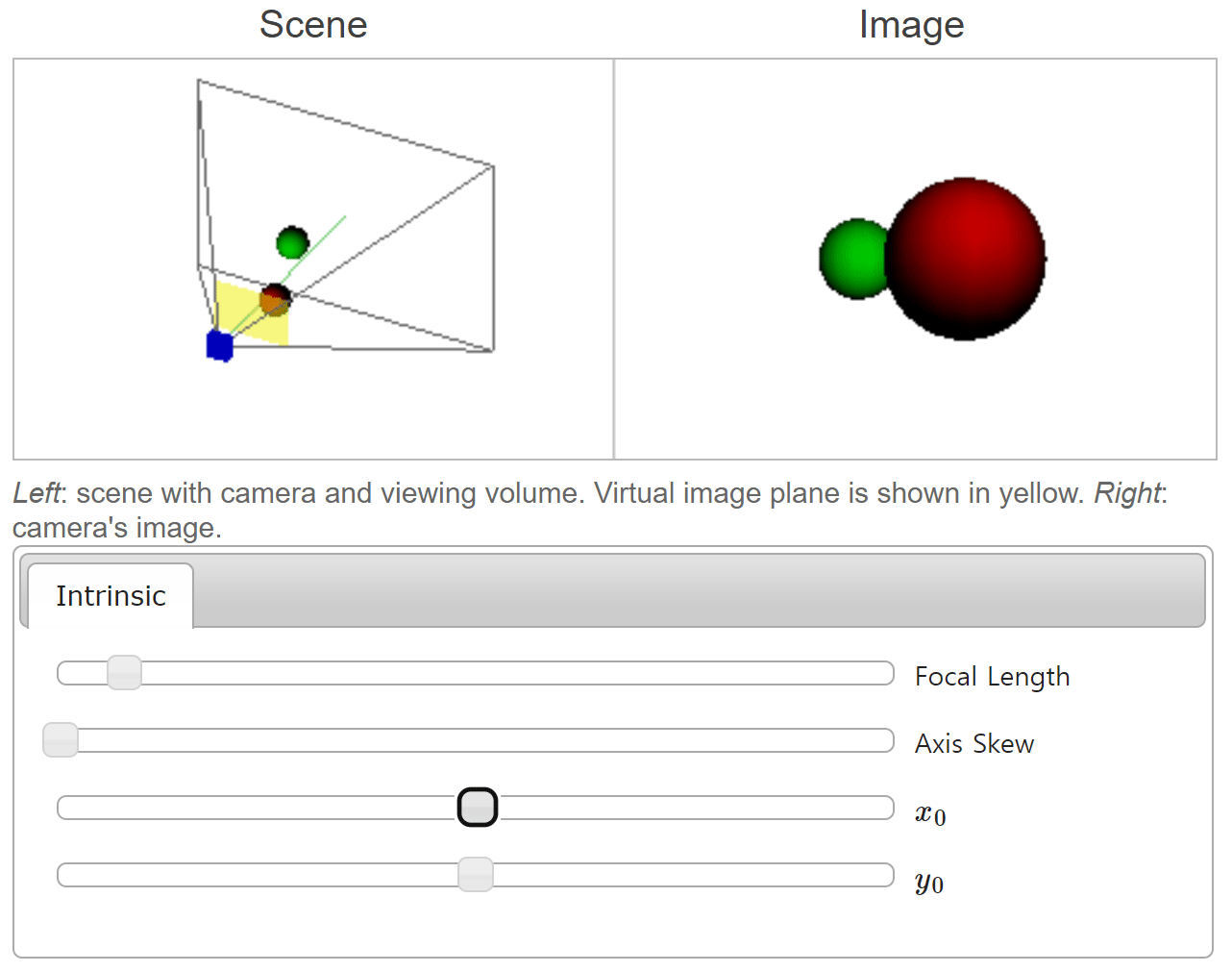
위 그림에서는 \(x_{0}\) 값 변경에 따라 물체가 이미지의 어느 위치에 형성되는 지 확인할 수 있습니다. \(x_{0}\) 의 크기 변화에 따라 카메라의 방향이 어떻게 바뀌는 지 살펴보는 것도 이해하는 데 도움이 됩니다.

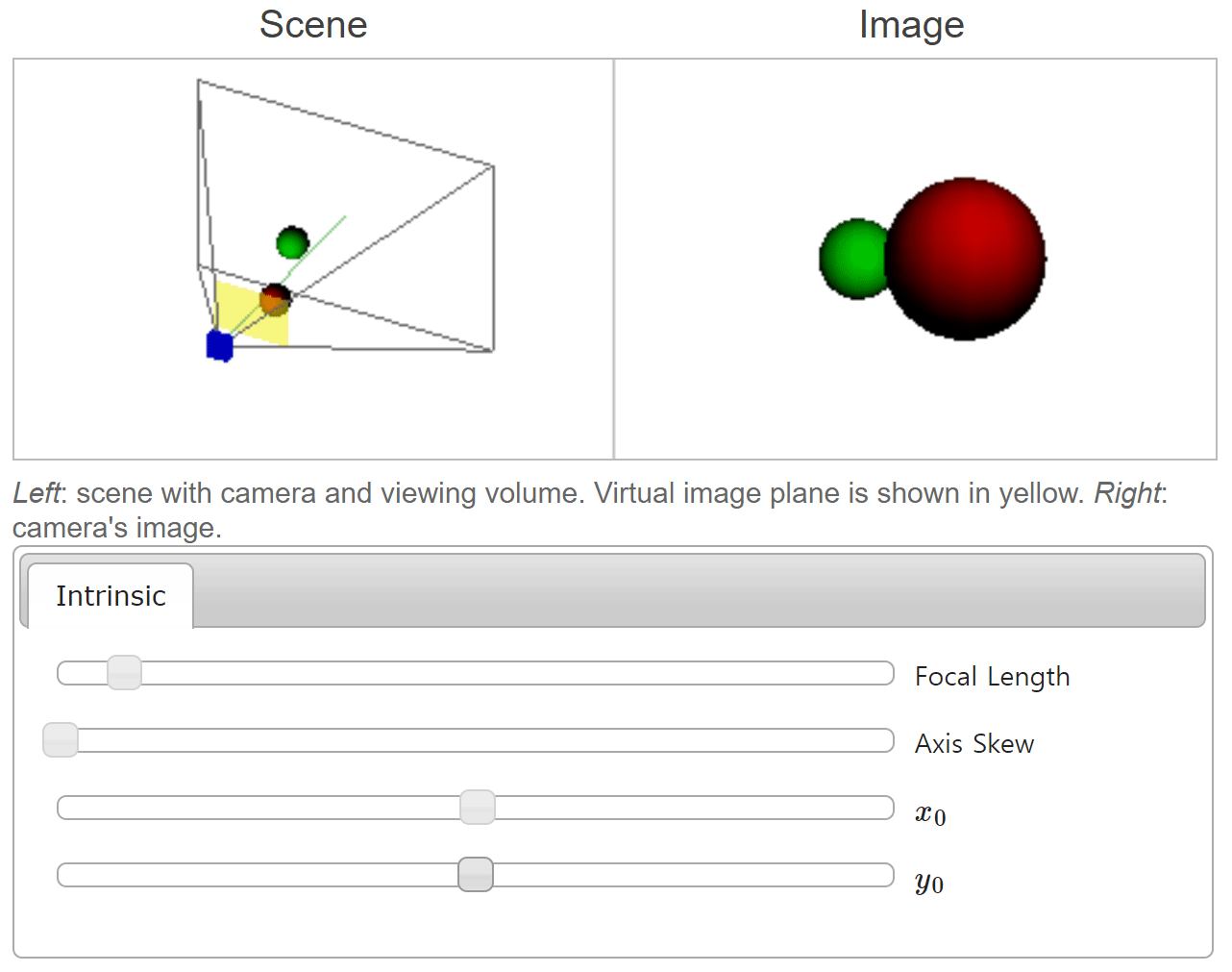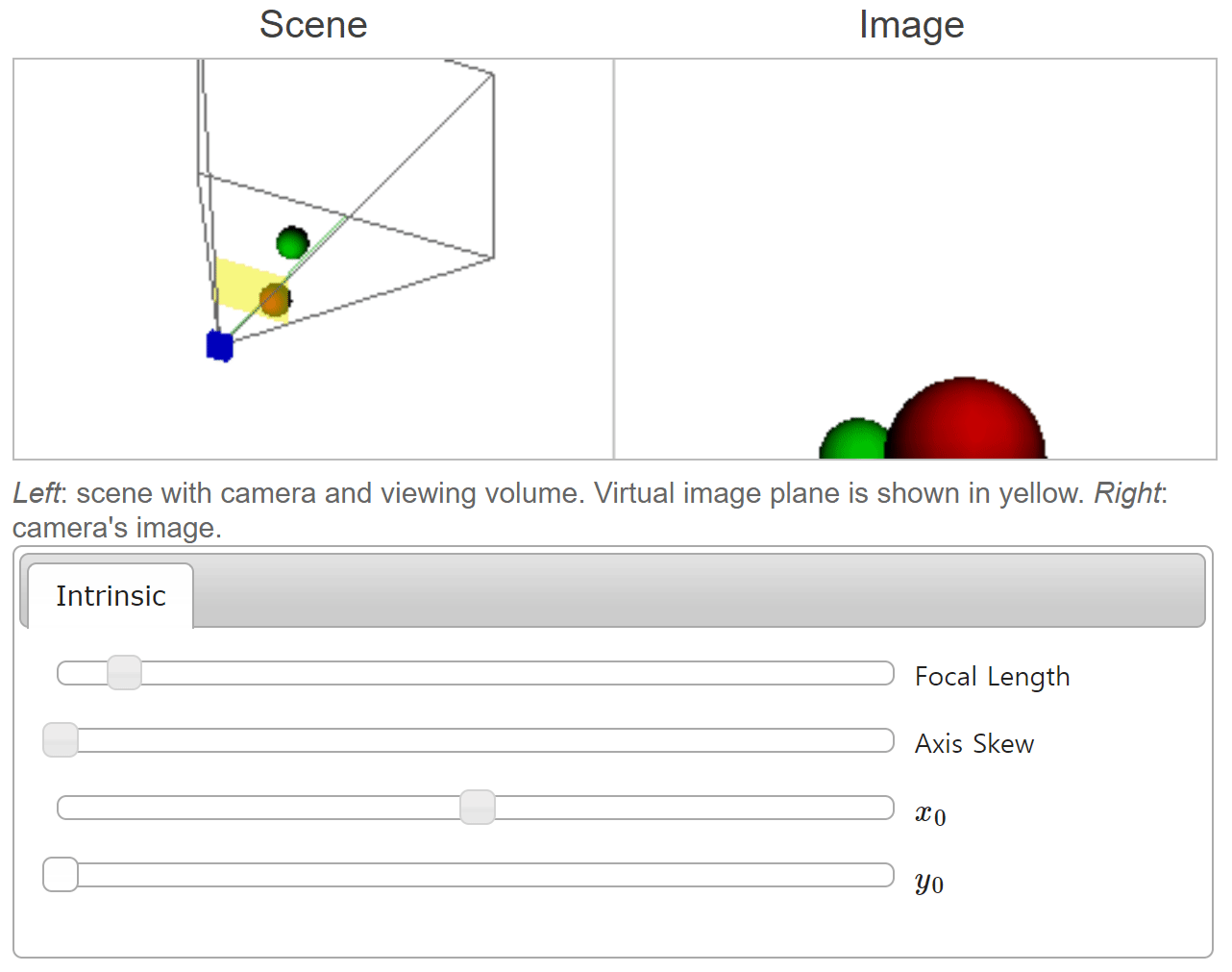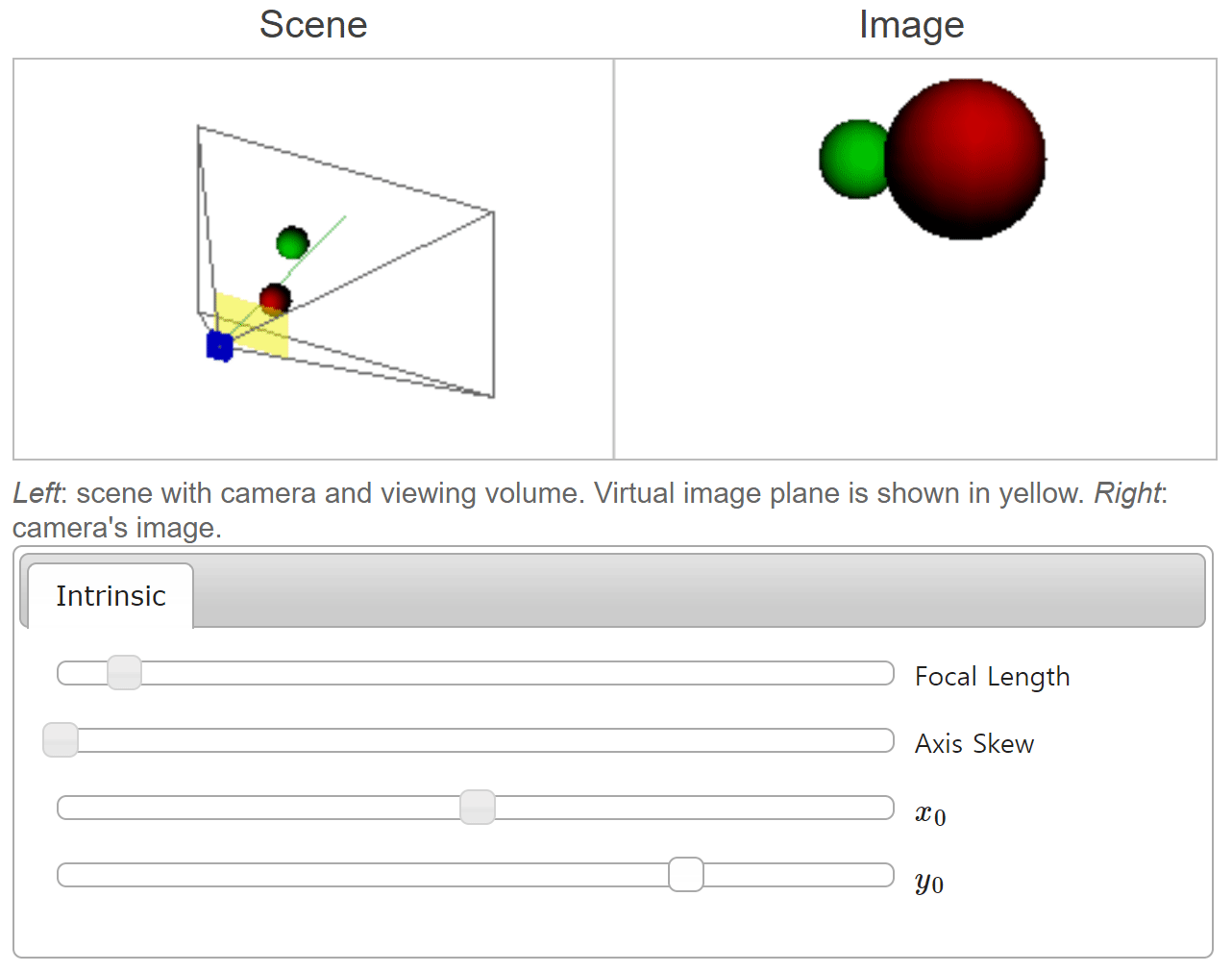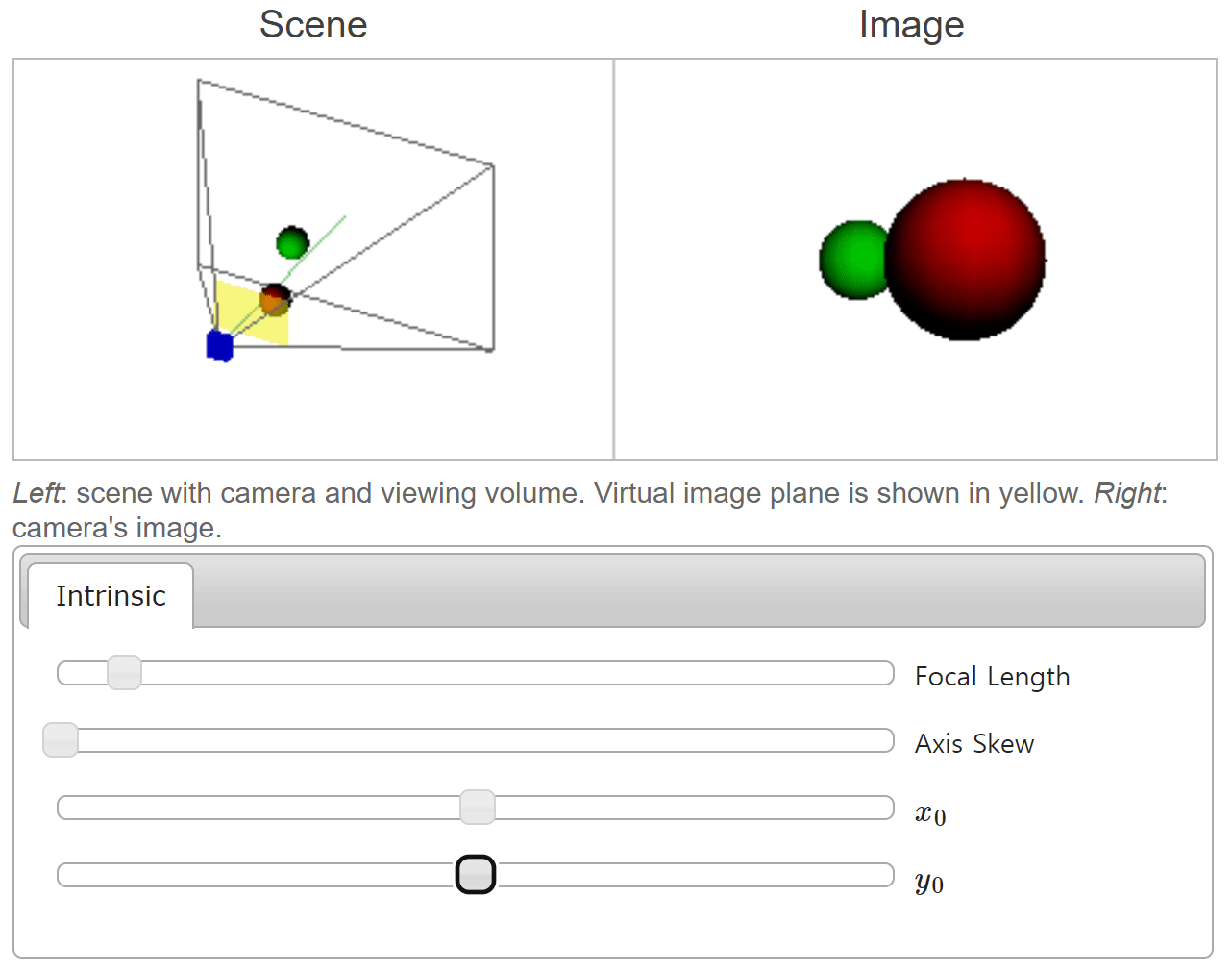
위 그림에서는 \(y_{0}\) 값 변경에 따라 물체가 이미지의 어느 위치에 형성되는 지 확인할 수 있습니다. 앞선 \(x_{0}\) 케이스와 동일한 원리로 적용되는 것을 확인할 수 있습니다.

Transformation 관점의 Camera Extrinsic과 Intrinsic

핀홀 카메라 모델에서는 extrinsic과 intrinsic 파라미터를 연속적인 행렬곱으로 나타낼 수 있습니다. 핀홀 카메라 모델에서는 비선형 관계가 없기 떄문에 단순히 선형 관계만으로도 image coordinate와 world coordinate의 관계를 나타낼 수 있습니다.
앞에서 사용한 기호인 \(\alpha, \beta\) 는 \(f_{x}, f_{y}\) 로 바꿔서 표현하겠습니다. 그리고 skew는 간단히 \(s\) 로 표현하였습니다. extrinsic은 좌표 변환 관계를 이용하였습니다.

\[\begin{align} P &= \overbrace{K}^\text{Intrinsic Matrix} \times \overbrace{[R \mid \mathbf{t}]}^\text{Extrinsic Matrix} \\[0.5em] &= \overbrace{ \underbrace{ \left ( \begin{array}{ c c c} 1 & 0 & x_0 \\ 0 & 1 & y_0 \\ 0 & 0 & 1 \end{array} \right ) }_\text{2D Translation} \times \underbrace{ \left ( \begin{array}{ c c c} f_x & 0 & 0 \\ 0 & f_y & 0 \\ 0 & 0 & 1 \end{array} \right ) }_\text{2D Scaling} \times \underbrace{ \left ( \begin{array}{ c c c} 1 & s & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right ) }_\text{2D Shear}}^\text{Intrinsic Matrix} \times \overbrace{ \underbrace{ \left( \begin{array}{c | c} I & \mathbf{t} \end{array}\right)}_\text{3D Translation} \times \underbrace{ \left( \begin{array}{c | c} R & 0 \\ \hline 0 & 1 \end{array}\right)}_\text{3D Rotation} }^\text{Extrinsic Matrix} \end{align} \tag{70}\]

위 식을 살펴 보았을 때, intrinsic은 2D 상에서의 Translation, Scaling, Shear 관점으로 Transformation한 것이고 extrinsic은 3D 상에서의 Rotation과 Translation 관점의 Transformation 한 것을 확인할 수 있습니다.

이미지 crop과 resize에 따른 intrinsic 수정 방법

이번 내용은 어떤 이미지를 crop과 resize를 하였을 때, intrinsic이 어떻게 변하는 지 살펴보도록 하겠습니다.
intrinsic에서 사용되는 유효한 값은 fx, fy, cx, cy로 가정하겠습니다.

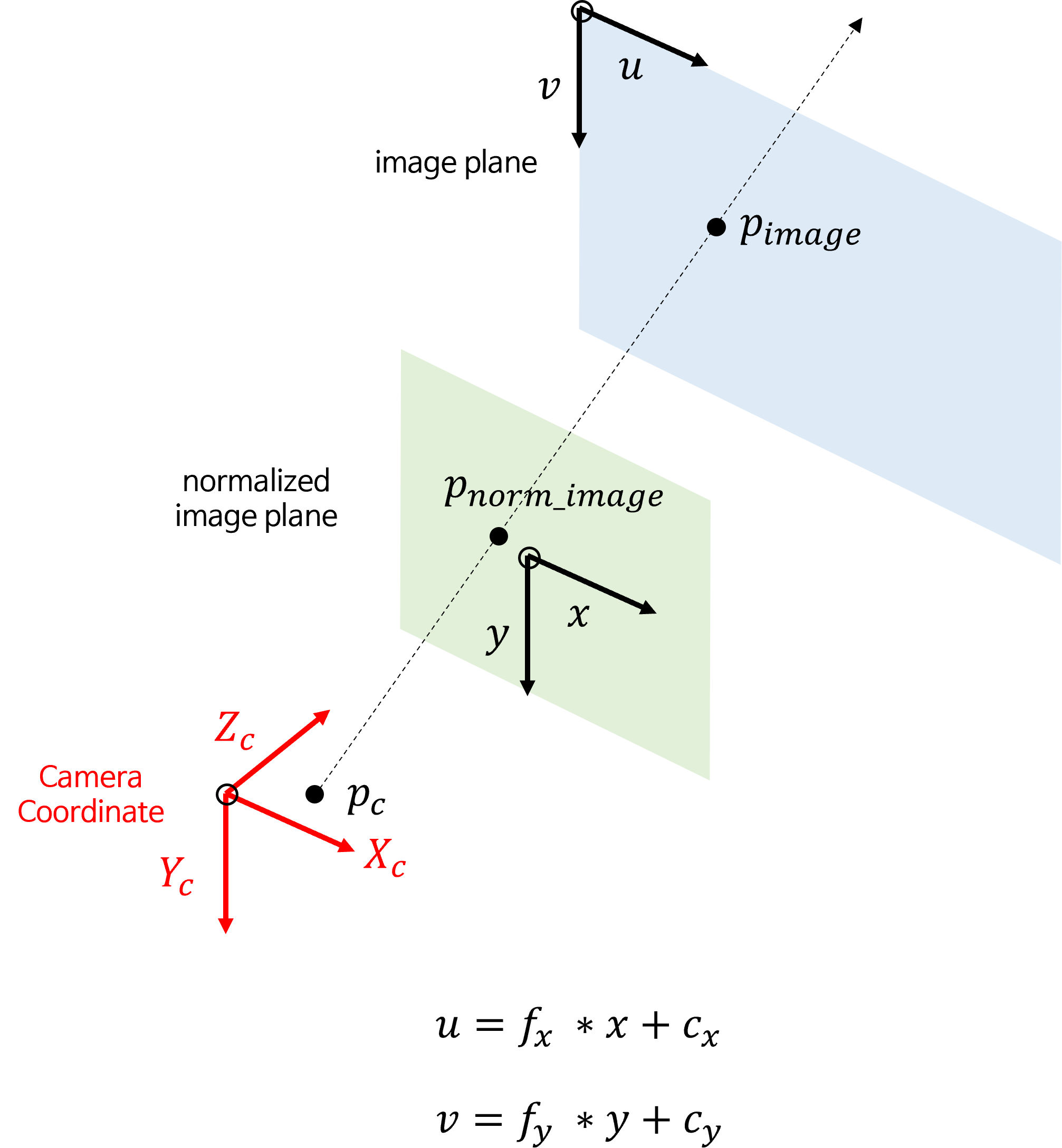
intrinsic은 normalized image plane에서 image plane에 영상을 대응하기 위하여 사용하는 값입니다.
위 그림에서 \(X_{c}, Y_{c}, Z_{c}\) 는 카메라 좌표계를 의미하고 \(x = X_{c} / Z_{c}\), \(y = Y_{C} / Z_{C}\) 를 이용하여 normalized image plane으로 \((x, y)\) 좌표로 좌표값을 변경합니다.
마지막으로 아래와 같은 intrinsic값을 이용하여 image plane으로 픽셀 값에 대응 시킵니다.

\[\text{intrinsic} = \begin{bmatrix} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{bmatrix}\]

이번 글에서는 기존의 intrinsic 파라미터가 있는 상황에서 image plane의 image의 크기가 달라졌을 때, intrinsic을 어떻게 변경해야 하는 지 확인합니다.
먼저 image plane의 축인 (0, 0) 부근의 width와 height 방향으로 crop이 발생 시 intrinsic의 변화를 살펴보면 다음과 같습니다.

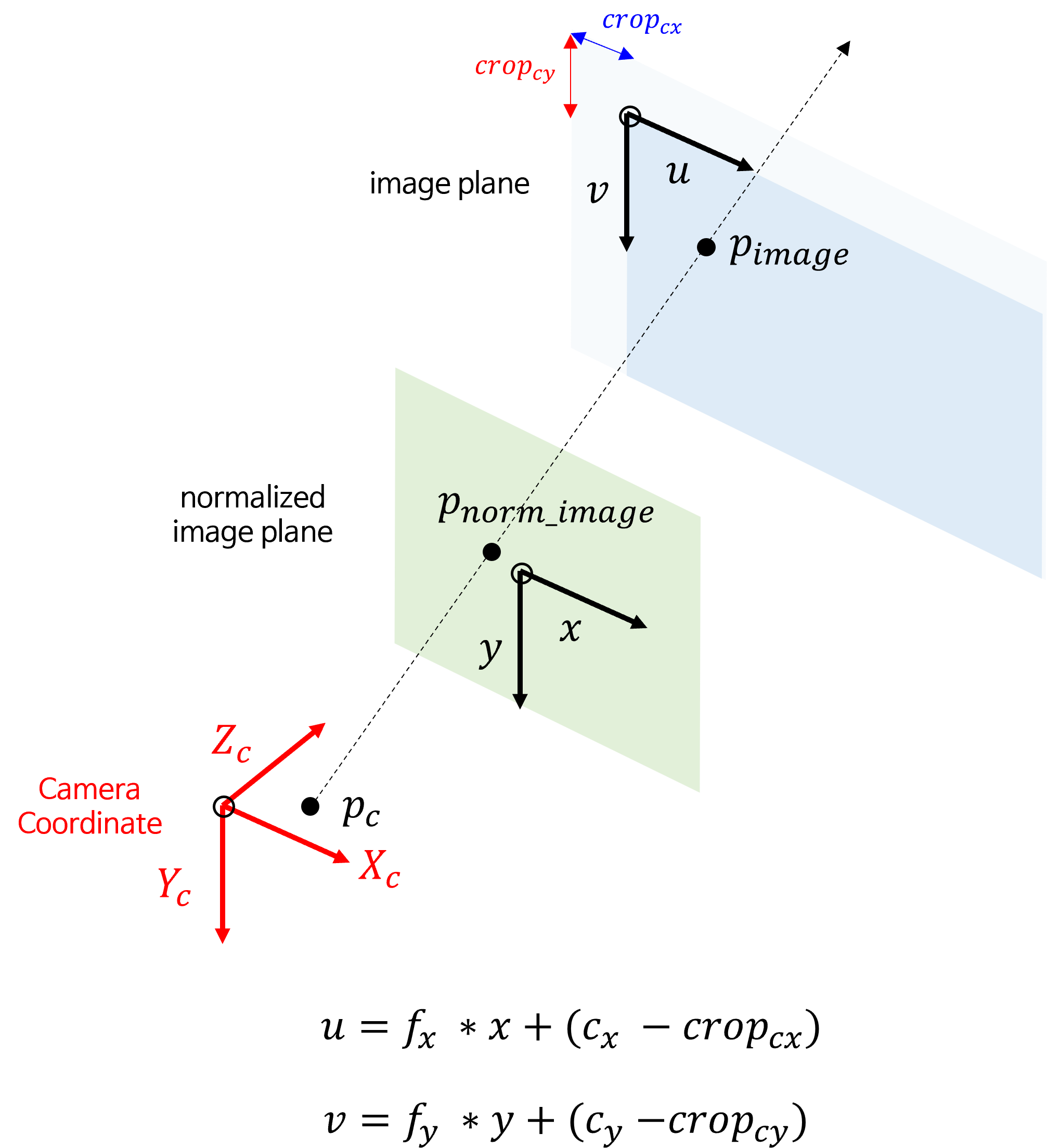
위 그림과 같이 image plane의 (0, 0) 부근에서 crop이 발생하면 normalized image plane → image plane 으로 대응되는 점의 위치가 달라집니다. \(P_{\text{image}}\) 의 위치가 crop으로 인하여 width, height 방향으로 좌표 값이 각각 감소한 것을 알 수 있습니다.

위 그림과 같이 crop으로 인한 좌표 값의 상대적인 변화를 알 수 있습니다. 이 변화를 적용하기 위하여 실제 crop된 크기 만큼 \(c_{x}, c_{y}\) 에 반영해 주면 됩니다. 앞의 intrinsic 연산 수식에서 \(c_{x}, c_{y}\) 는 translation 역할을 하기 때문에 줄어든 값 만큼 아래와 같이 반영하면 됩니다.

\[u = f_{x} x + (c_{x} - \text{crop}_{c_{x}})\]
\[v = f_{y} y + (c_{y} - \text{crop}_{c_{y}})\]

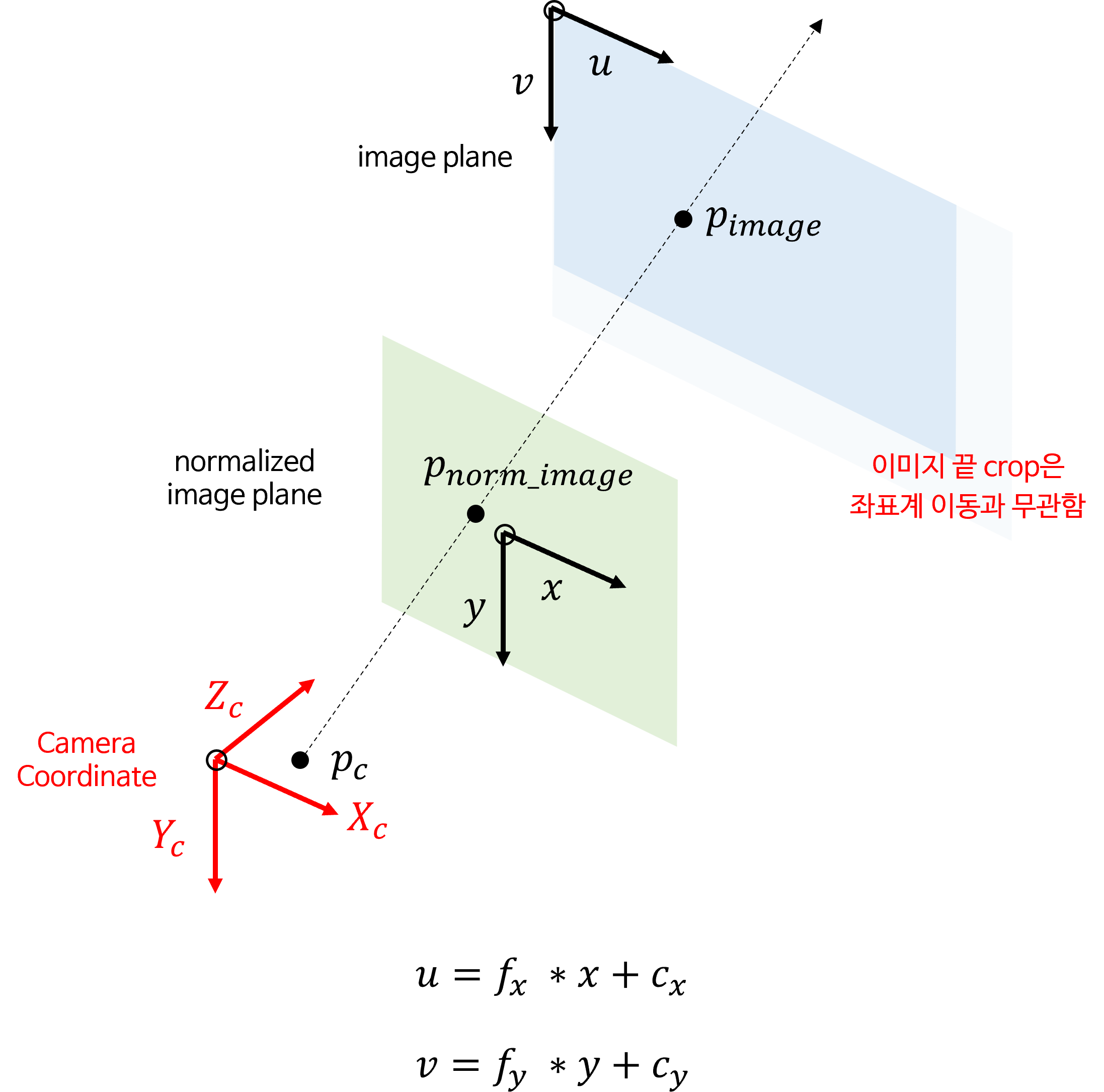
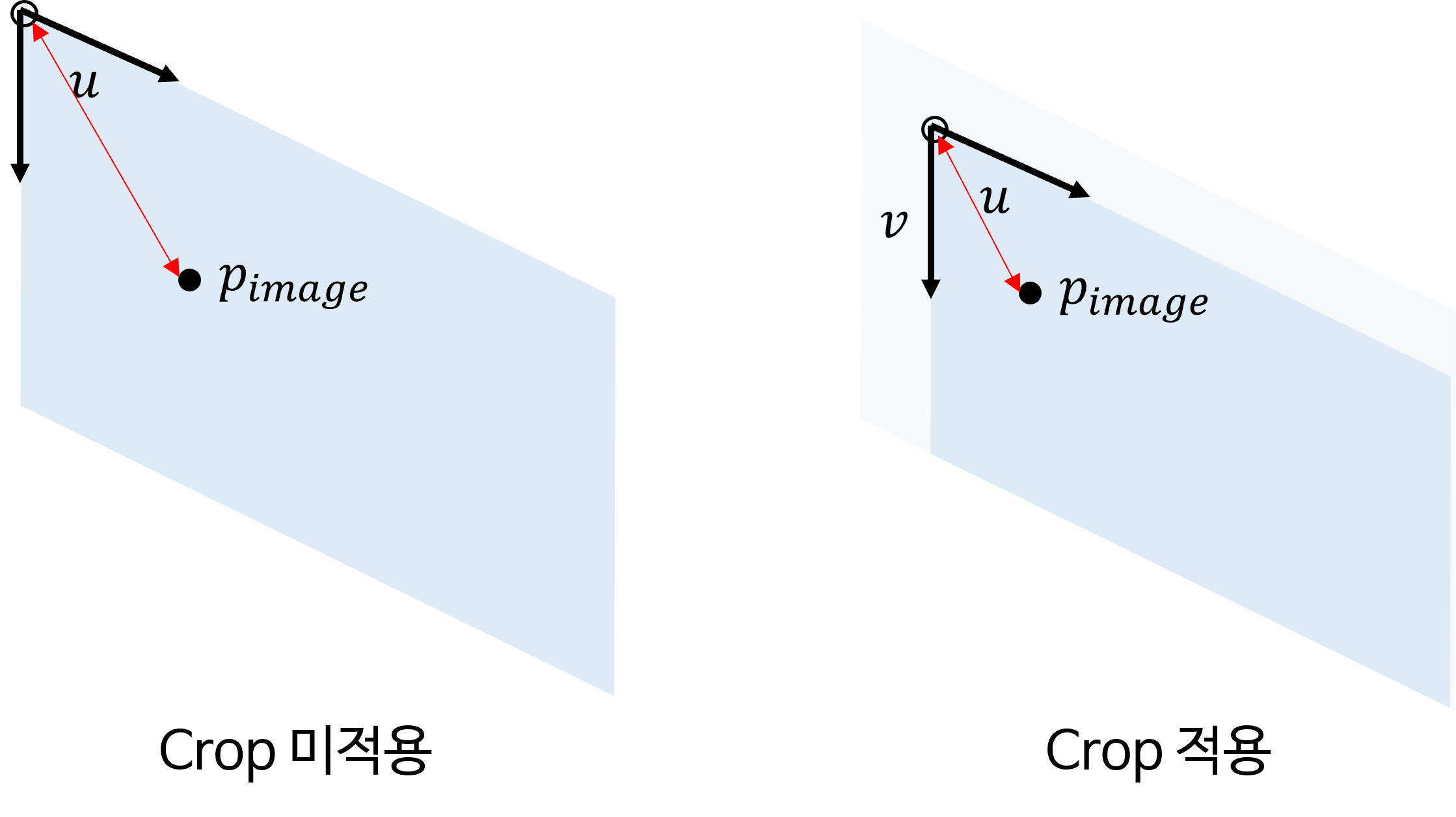
반면 위 그림과 같이 이미지 좌표계의 시작인 왼쪽 상단이 아닌 우측 하단에서 crop이 발생한 경우 intrinsic에 변화가 없는 것을 확인할 수 있습니다. 이미지 끝 쪽 crop은 image plane 에서의 좌표계 이동과 무관하기 때문입니다.

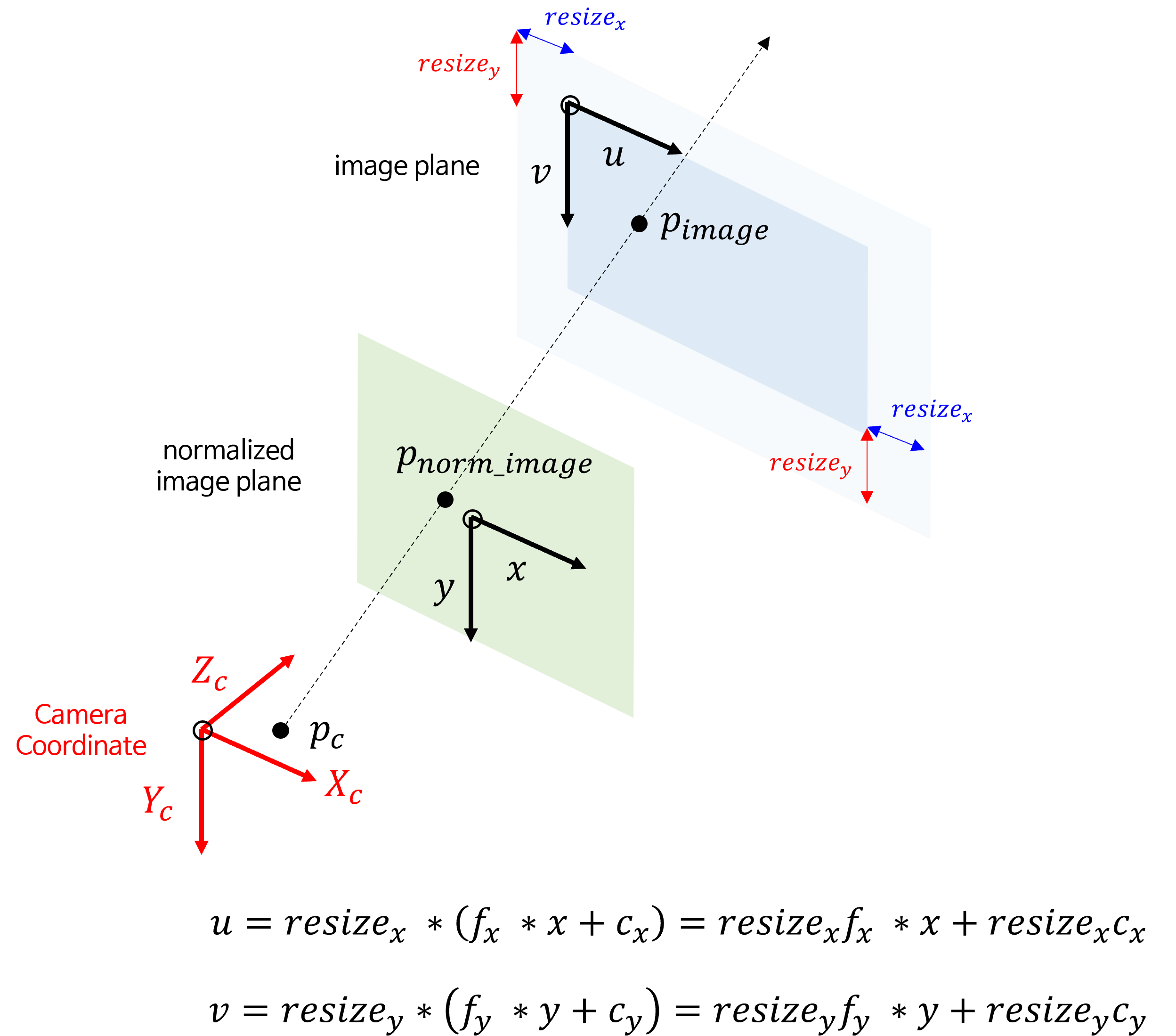
이번에는 resize가 발생하였을 때, intrinsic의 변화를 살펴보겠습니다. 적용되는 수식은 위 그림과 같습니다.
resize는 crop과 다르게 \(f_{x}, c_{x}\) 또는 \(f_{y}, c_{y}\) 모두에 영향을 끼칩니다. resize 라는 배율에 따라서 normalized image plane의 좌표와 곱해지는 \(f_{x}, f_{y}\) 뿐만 아니라 translation 역할을 하는 \(c_{x}, c_{y}\) 값 또한 그 배율만큼 조정되어야 하기 때문입니다. 간단하게 전체적으로 scale과 translation 모두 resize가 반영되었다고 보면 됩니다.
따라서 resize에 대한 결과는 다음과 같습니다.

\[u = \text{resize}_{x} (f_{x}x + c_{x}) = \text{resize}_{x}f_{x}x + \text{resize}_{x}c_{x}\]
\[u = \text{resize}_{y} (f_{y}y + c_{y}) = \text{resize}_{y}f_{y}y + \text{resize}_{y}c_{y}\]

일반적으로 crop과 resize를 할 때에는 crop을 먼저하여 원하는 부분만 선택한 다음에 resize를 적용하여 원하는 사이즈의 이미지를 구합니다. 따라서 다음 순서를 따릅니다.

① 이미지 좌측 상단에서 width, height 방향으로 각각 crop할 사이즈를 정한 뒤 crop을 적용합니다.
- \[c_{x} -= \text{crop}_{x}\]
- \[c_{y} -= \text{crop}_{y}\]
② resize 비율에 맞게 아래와 같이 resize를 적용합니다.
- \[f_{x} *= \text{resize}_{x} f_{x}\]
- \[f_{y} *= \text{resize}_{y} f_{y}\]
- \[c_{x} *= \text{resize}_{x} c_{x}\]
- \[c_{y} *= \text{resize}_{y} c_{y}\]

위 내용을 파이썬 코드로 적용하면 아래와 같습니다.

def get_cropped_and_resized_intrinsic(
    fx, fy, cx, cy, crop_cx, crop_cy, resize_fx, resize_fy):
    '''
    crop_cx : crop size of u axis orientation in image plane
    crop_cy : crop size of v axis orientation in image plane
    resize_fx : resize ratio of width orientation in image plane
    resize_fy : resize ratio of height orientation in image plane    
    '''

    cx -= crop_cx
    cy -= crop_cy

    fx *= resize_fx
    fy *= resize_fy

    cx *= resize_fx
    cy *= resize_fy

    return fx, fy, cx, cy

OpenCV의 Zhang’s Method를 이용한 카메라 캘리브레이션 실습

이번에는 앞에서 다룬 Intrinsic, Extrinsic 파라미터를 직접 구하는 방법을 다루어 보도록 하겠습니다.
카메라 캘리브레이션을 하기 위해서는 일반적으로 Zhang's Method라고 불리는 카메라 캘리브레이션 방법을 사용합니다. 논문의 제목은 A Flexible New Technique for Camera Calibration이며 아래 링크에서 상세 내용 및 구현 방법을 확인할 수 있습니다.
- 링크: A Flexible New Technique for Camera Calibration (Zhang’s Method)
사용한 카메라 모델은 Generic Camera Model입니다.
본 글에서는 실습 데이터와 Zhang's Method를 구현한 OpenCV 함수들을 이용하여 카메라 캘리브레이션을 하는 방법에 대하여 살펴보겠습니다. 카메라 캘리브레이션 관련 코드는 아래 링크를 통해 참조할 수 있습니다.
- 링크: https://github.com/gaussian37/generic_camera_calibration

실습 데이터

실습에 사용될 카메라 모델과 체커보드 패턴은 다음과 같습니다.

카메라 모델 : ELP-USB16MP01-BL180을 이용하여 width=2048, height=1536으로 취득하였습니다.
체커보드 패턴 : 각 정사각형의 크기가 5cm이고 교점의 갯수가 가로 15개 세로 10개인 체커보드 패턴을 이용하였습니다.

Intrinsic 파라미터를 구하기 위한 체커보드 패턴의 이미지셋과 Extrinsic 파라미터를 구하기 위한 데이터 셋은 다음 링크에서 확인할 수 있습니다.
- 데이터셋 링크 : https://drive.google.com/file/d/1ri4Go75UWQ3JHmRZwWVW35ms3xYosmgf/view?usp=sharing
- 캘리브레이션 결과 파일 : https://drive.google.com/file/d/1ri4Go75UWQ3JHmRZwWVW35ms3xYosmgf/view?usp=sharing
위 데이터셋의 파일명은 ELP-USB16MP01-BL180-2048x1536.zip이고 ELP-USB16MP01-BL180은 카메라 모델명이고 2048 x 1536은 영상의 해상도를 의미합니다.
파일의 압축을 풀면 Intrinsic과 Extrinsic 폴더가 있으며 폴더 구조는 다음과 같습니다.

Intrinsic
- ORIGIN
  - 000.png
  - 001.png
  - …
- REPROJECTION (출력물)
  - 000_reprojection_error.png
  - 001_reprojection_error.png
  - …
- intrinsic.json (출력물)
Extrinsic
- 카메라 모델명_EXTRINSIC.png
- 카메라 모델명
  - points.csv
  - points.png
카메라 모델명_calibration.json (출력물)

# Example of Dataset

base_path
├─ELP-USB16MP01-BL180-2048x1536_calibration.json
├─Extrinsic
│  │  ELP-USB16MP01-BL180-2048x1536_EXTRINSIC.png
│  │
│  └─ELP-USB16MP01-BL180-2048x1536
│          points.csv
│          points.png
│
└─Intrinsic
    │  intrinsic.json
    │
    ├─ORIGIN
    │      000.png
    │      001.png
    │      002.png
    │      003.png
    │	   ...
    │
    └─REPROJECTION
            000_0.0678.png
            001_0.0568.png
            002_0.0576.png
            003_0.0553.png
            ...

Intrinsic 폴더 내부의 ORIGIN 폴더의 각 파일은 위에서 설명한 체커보드 패턴을 들고 찍은 사진들이며 영상에서 체커보드 패턴이 다양한 위치 또는 다양한 크기로 나타날 수 있도록 다양한 이미지 (약 250여장)를 구성하였습니다. 아래는 대표 사진 예시입니다.

Intrinsic 폴더 내부의 REPROJECTION 폴더의 각 파일은 ORIGIN 폴더의 각 이미지를 캘리브레이션하여 R(Rotation), t(Translation), K(Intrinsic), D(Distortion)을 구한 뒤 패턴의 좌표를 Reprojection한 결과를 저장하였습니다. 아래는 대표 사진 예시입니다. 저장된 파일명의 접미사로 각 이미지의 Reprojection Error를 같이 기입하였습니다. Reprojection Error가 클수록 캘리브레이션 결과에 이상이 있음을 나타냅니다.

Extrinsic의 points.csv는 카메라를 아래와 같이 설치해 놓고 World 좌표계의 원점 (0, 0, 0)을 정한 뒤 ① 이미지 좌표계의 (u, v) 좌표와 그 좌표에 해당하는 ② World 좌표계의 (X, Y, Z) 좌표를 대응시켜 놓은 파일입니다. 이 때, (u, v) 좌표와 (X, Y, Z)를 대응시키기 위하여 체크보드 패턴을 사용하였으며 원본 이미지 파일 카메라 모델명_EXTRINSIC.png을 통하여 points.csv를 구하고 이 결과를 다시 검증한 것이 points.png가 됩니다.
World 좌표계를 설정한 방식은 다음과 같습니다.

카메라 모델명_EXTRINSIC.png 이미지를 이용하여 points.csv와 points.png를 추출하는 코드는 아래 코드를 이용하였습니다. 아래 코드를 이용하면 체크보드가 있는 이미지에서 (u, v) 좌표를 쉽게 추출할 수 있습니다. 물론 각 (u, v) 좌표에 해당하는 (X, Y, Z) 좌표는 사전에 알고 있어야 합니다. 데이터셋의 (u, v)는 아래 코드를 이용하여 구하였고 (X, Y, Z) 좌표는 사전에 그 위치에 해당하는 체크보드 패턴의 크기를 이용하여 구해 놓았습니다.
- 코드: https://github.com/gaussian37/generic_camera_calibration/blob/main/manual_checkboard_points_extractor.py
- 코드 설명: https://gaussian37.github.io/vision-opencv-manual_checkboard_points_extractor/

카메라 모델명_EXTRINSIC.png과 위 코드를 통해 구한 points.csv의 파일 형식과 points.png의 결과물은 다음과 같습니다.

카메라 모델명_EXTRINSIC.png:

points.csv:
아래 표에서 Z 가 0.04인 이유는 패턴 아래에 손잡이가 있어서 0.04m 만큼 바닥에서 떨어져 있기 때문입니다.
아래 표의 한 행을 해석하면 다음과 같습니다.

points.png:

조금 더 확대해 보면 아래 노란색 점의 좌표는 (X, Y, Z) = (0, 0, 0.04)이 됩니다.

마지막으로 Intrinsic과 Extrinsic의 모든 캘리브레이션 작업을 마치면 최종 카메라 모델명_calibration.json 파일이 생성됩니다. calibration 값을 읽어보면 다음과 같은 Key 값들을 확인할 수 있습니다.
- Position : World 좌표계 상의 카메라의 위치를 나타냅니다. 각 좌표값은 World 좌표계 상의 X, Y, Z 값을 순서대로 나타냅니다.
- Intrinsic:
  - K : Intrinsic을 의미합니다.
  - D : Radial Distortion을 의미합니다.
  - ReprojectionError : 캘리브레이션에 사용된 모든 이미지의 평균 Reprojection Error를 의미합니다.
- Extrinsic
  - From (ex. World)
    - To (ex. Camera)
      - R : From → To 로의 Active Transform 변환을 위한 Rotation을 의미합니다.
      - t : From → To 로의 Active Transform 변환을 위한 translation을 의미합니다.

Rotation, Translation을 이용한 카메라 위치 확인

앞에서 구한 카메라 캘리브레이션 결과 값을 이용하면 World 좌표 기준으로 카메라의 위치를 추정할 수 있습니다. 추정하고자 하는 World 좌표에서의 카메라 위치를 \(\mathbf{X} = [x, y, z]^{T}\) 라고 가정해 보겠습니다.
Extrinsic 파라미터를 이용하여 \(\mathbf{X}\) 의 위치를 World → Camera로 변환하면 Camera 좌표에서는 원점이 됩니다. \(\mathbf{X}\) 가 카메라 위치로 가정하였기 때문입니다. 아래 식과 같습니다. (아래 식의 \(R, t\) 는 Active Transformation입니다.)

\[R_{\text{world } \to \text{ Camera}} \mathbf{X} + t_{\text{world } \to \text{ Camera}} = 0\]
\[\Rightarrow R_{\text{world } \to \text{ Camera}} \mathbf{X} = -t_{\text{world } \to \text{ Camera}}\]
\[\Rightarrow \mathbf{X} = -R_{\text{world } \to \text{ Camera}}^{T}t_{\text{world } \to \text{ Camera}}\]

결과 확인을 위하여 캘리브레이션 결과 파일을 이용하겠습니다.

import numpy as np
import json

calib = json.load(open("path/to/the/../ELP-USB16MP01-BL180-2048x1536_calibration.json", "r"))
R = np.array(calib["ELP-USB16MP01-BL180-2048x1536"]["Extrinsic"]["World"]["Camera"]["R"]).reshape(3, 3)
t = np.array(calib["ELP-USB16MP01-BL180-2048x1536"]["Extrinsic"]["World"]["Camera"]["t"]).reshape(3, 1)

camera_position = -R.T @ t
print(f"X:{camera_position[0]}, Y: {camera_position[1]}, Z: {camera_position[2]}")
# X:[-0.23686769], Y: [-0.00676988], Z: [0.52936941]

캘리브레이션 값을 통해 추정한 값과 캘리브레이션 환경에서 실제 측정한 값을 비교해 보도록 하겠습니다.
먼저 \(X\) 의 경우 실측은 -0.25m 인 반면 추정값은 약 -0.236m 입니다. 약 1.4 cm 정도의 오차를 가지는 것을 알 수 있습니다. 다음으로 \(Y\) 의 경우 실측과 추정값 모두 0m에 가까운 값으로 1cm 이하의 오차를 가지는 것을 확인할 수 있습니다. 마지막으로 \(Z\) 의 경우 실측은 0.53m이고 추정값은 약 0.529m로 1cm 이하의 오차를 가지는 것을 확인할 수 있습니다.
이와 같이 카메라의 위치를 캘리브레이션 결과를 이용하여 역으로 추정해 볼 수 있으며 캘리브레이션 결과가 정확한 지 확인하는 방법으로도 이용해 볼 수 있습니다.

다음은 A2D2 데이터셋을 이용하여 센서 장착 위치를 살펴보도록 하겠습니다. A2D2 데이터는 아우디에서 공개한 자율주행 인식 관련 데이터셋입니다.

A2D2 데이터셋은 위 그림과 같이 아우디 차량에 6개의 카메라를 장착하고 뒷바퀴 중심을 원점으로 잡아서 카메라 캘리브레이션을 진행하였습니다.
아래 링크에서 캘리브레이션 결과를 확인할 수 있으며 캘리브레이션 값을 어떻게 사용하는 지 확인할 수 있습니다.
- https://www.a2d2.audi/a2d2/en/download.html
- https://aev-autonomous-driving-dataset.s3.eu-central-1.amazonaws.com/cams_lidars.json
- https://aev-autonomous-driving-dataset.s3.eu-central-1.amazonaws.com/tutorial.ipynb

아래 코드는 A2D2 데이터셋의 캘리브레이션 값을 Vehicle → Camera의 Rotation과 Translation으로 정리하는 코드입니다.

import json
import cv2
import numpy as np
import numpy.linalg as la
import matplotlib.pyplot as plt

EPSILON = 1.0e-10 # norm should not be small

def get_origin_of_a_view(view):
    return view['origin']

def get_axes_of_a_view(view):
    x_axis = view['x-axis']
    y_axis = view['y-axis']
     
    x_axis_norm = la.norm(x_axis)
    y_axis_norm = la.norm(y_axis)
    
    if (x_axis_norm < EPSILON or y_axis_norm < EPSILON):
        raise ValueError("Norm of input vector(s) too small.")
        
    # normalize the axes
    x_axis = x_axis / x_axis_norm
    y_axis = y_axis / y_axis_norm
    
    # make a new y-axis which lies in the original x-y plane, but is orthogonal to x-axis
    y_axis = y_axis - x_axis * np.dot(y_axis, x_axis)
 
    # create orthogonal z-axis
    z_axis = np.cross(x_axis, y_axis)
    
    # calculate and check y-axis and z-axis norms
    y_axis_norm = la.norm(y_axis)
    z_axis_norm = la.norm(z_axis)
    
    if (y_axis_norm < EPSILON) or (z_axis_norm < EPSILON):
        raise ValueError("Norm of view axis vector(s) too small.")
        
    # make x/y/z-axes orthonormal
    y_axis = y_axis / y_axis_norm
    z_axis = z_axis / z_axis_norm
    
    return x_axis, y_axis, z_axis

def get_transform_to_global(view):
    # get axes
    x_axis, y_axis, z_axis = get_axes_of_a_view(view)
    
    # get origin 
    origin = get_origin_of_a_view(view)
    transform_to_global = np.eye(4)
    
    # rotation
    transform_to_global[0:3, 0] = x_axis
    transform_to_global[0:3, 1] = y_axis
    transform_to_global[0:3, 2] = z_axis
    
    # origin
    transform_to_global[0:3, 3] = origin
    
    return transform_to_global

def get_transform_from_global(view):
   # get transform to global
   transform_to_global = get_transform_to_global(view)
   trans = np.eye(4)
   rot = np.transpose(transform_to_global[0:3, 0:3])
   trans[0:3, 0:3] = rot
   trans[0:3, 3] = np.dot(rot, -transform_to_global[0:3, 3])
    
   return trans

def transform_from_to(src, target):
    transform = np.dot(get_transform_from_global(target), \
                       get_transform_to_global(src))
    
    return transform

with open ('cams_lidars.json', 'r') as f:
    config = json.load(f)
    
vehicle_to_camera_dict = {}
src_view = config['vehicle']['view']
for camera_name in config['cameras'].keys():
    target_view = config['cameras'][camera_name]['view']
    trans = transform_from_to(src_view, target_view)
    
    R = trans[:3, :3]
    t = trans[:3, -1]

    vehicle_to_camera_dict[camera_name] = {}
    vehicle_to_camera_dict[camera_name]["R"] = R
    vehicle_to_camera_dict[camera_name]["t"] = t

앞에서 확인한 -R.T @ t를 이용하여 Vehicle (World)에서의 카메라 위치를 추정해 보면 다음과 같습니다. 아래 코드에서는 BEV 형태로 \(X, Y\) 축으로 나타낸 결과 입니다.

# Parameters
vehicle_x_max = 3
vehicle_x_min = -1
vehicle_y_max = 2
vehicle_y_min = -2

vehicle_x_interval = 0.01  # meters per pixel
vehicle_y_interval = 0.01  # meters per pixel

# Calculate the output image size in pixels
output_width = int(np.ceil((vehicle_y_max - vehicle_y_min) / vehicle_y_interval))
output_height = int(np.ceil((vehicle_x_max - vehicle_x_min) / vehicle_x_interval))

def vehicle_coord_to_bev_coord(x, y):
    """
    Convert vehicle coordinates (x, y) to BEV image coordinates (u, v).
    
    x, y : Vehicle coordinates in meters
    Returns:
    u, v : BEV image coordinates in pixels
    """
    # u = (y - vehicle_y_min) / vehicle_y_interval
    # v = (x - vehicle_x_min) / vehicle_x_interval
    u = (vehicle_y_max - y) / vehicle_y_interval
    v = (vehicle_x_max - x) / vehicle_x_interval
    return int(np.round(u)), int(np.round(v))

def bev_coord_to_vehicle_coord(u, v):
    """
    Convert BEV image coordinates (u, v) to vehicle coordinates (x, y).
    Adjust to the center of the grid.
    
    u, v : BEV image coordinates in pixels
    Returns:
    x, y : Vehicle coordinates in meters
    """
    x = u * vehicle_x_interval + vehicle_x_min + vehicle_x_interval / 2
    y = v * vehicle_y_interval + vehicle_y_min + vehicle_y_interval / 2
    return x, y

topview_image = np.zeros((output_height, output_width, 3)).astype(np.uint8)
u_bev, v_bev = vehicle_coord_to_bev_coord(0, 0)
cv2.circle(topview_image, (u_bev, v_bev), radius=3, color=(255, 255, 0))
cv2.putText(topview_image, "origin", (u_bev - 10, v_bev + 20), cv2.FONT_HERSHEY_SIMPLEX, 0.3, (255, 255, 255))        

for camera_name in vehicle_to_camera_dict.keys():
    R = vehicle_to_camera_dict[camera_name]["R"]
    t = vehicle_to_camera_dict[camera_name]["t"]
    camera_position = -R.T @ t

    x_veh, y_veh = np.round(camera_position[0], 4), np.round(camera_position[1], 4)
    u_bev, v_bev = vehicle_coord_to_bev_coord(x_veh, y_veh)

    print(f"{camera_name}: (x_veh={x_veh}, y_veh={y_veh}), (u_bev={u_bev}, v_bev={v_bev})")
    
    cv2.circle(topview_image, (u_bev, v_bev), radius=3, color=(255, 0, 0))
    if camera_name == 'front_center':
        cv2.putText(topview_image, camera_name, (u_bev - 20, v_bev - 20), cv2.FONT_HERSHEY_SIMPLEX, 0.3, (255, 255, 255))
    else:
        cv2.putText(topview_image, camera_name, (u_bev - 20, v_bev + 20), cv2.FONT_HERSHEY_SIMPLEX, 0.3, (255, 255, 255))       

plt.figure(figsize=(10, 8))
plt.imshow(topview_image)

# >> front_left: (x_veh=1.711, y_veh=0.58, z_veh=0.9431), (u_bev=142, v_bev=129)
# >> front_right: (x_veh=1.711, y_veh=-0.58, z_veh=0.9431), (u_bev=258, v_bev=129)
# >> front_center: (x_veh=1.711, y_veh=-0.0, z_veh=0.9431), (u_bev=200, v_bev=129)
# >> side_left: (x_veh=0.651, y_veh=0.58, z_veh=0.9431), (u_bev=142, v_bev=235)
# >> side_right: (x_veh=0.651, y_veh=-0.58, z_veh=0.9431), (u_bev=258, v_bev=235)
# >> rear_center: (x_veh=-0.409, y_veh=0.0, z_veh=0.9431), (u_bev=200, v_bev=341)

뒷 바퀴 축의 중심이 원점이었을 때, 각 카메라의 장착 위치를 캘리브레이션 결과를 통해 살펴보면 위 주석 처리된 출력과 같습니다.
Z 값이 모두 동일한 것으로 보아 의도적으로 카메라들을 같은 높이로 장착한 것으로 보입니다.

BEV 형태로 나타내보면 위 그림과 같습니다. 원점의 위치와 6개의 카메라의 위치를 확인할 수 있습니다.

홈페이지에 실제 장착된 위치를 살펴보면 같은 결과를 얻은 것을 확인할 수 있습니다.

Vision 관련 글 목차