단안 카메라와 객체와의 거리 구하는 방법
2022, Sep 30
- 이번 글에서는 단안 카메라로 물체와의 거리를 추정하는 방법에 대한 간단한 방법에 대하여 다루어 보도록 하겠습니다.
- 이번 글의 실험 조건은 카메라 또는 물체 중 하나가 움직이는 상황이며 움직임의 양을 알아야 합니다.
- 또는 카메라가 고정이고 물체가 움직인다면 물체가 움직인 양을 알아야 하고 물체가 고정이고 카메라가 움직인다면 카메라가 움직인 양을 알아야 합니다.
- 두번째 실험 조건은 핀홀 카메라 모델을 사용하였습니다. 렌즈 왜곡이 있는 카메라면 렌즈 왜곡을 적용해 주어야 합니다.

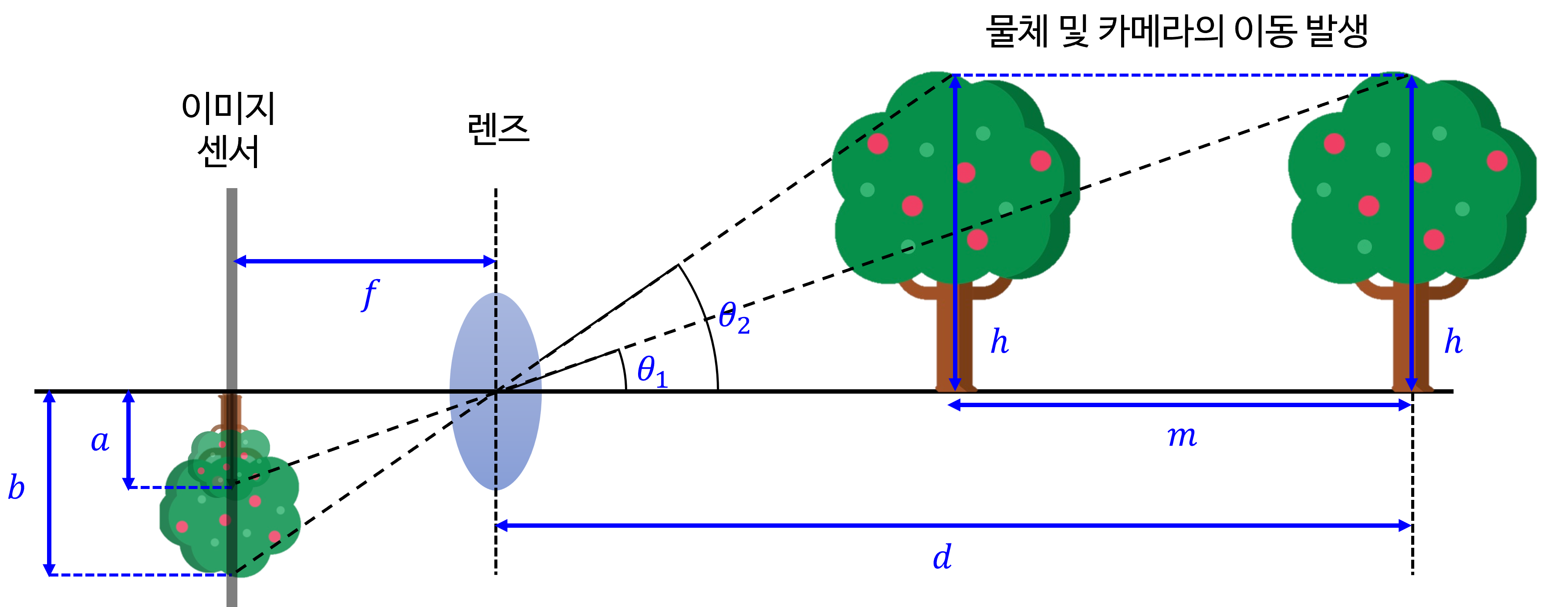
- 위 그림은 카메라의
이미지 센서,렌즈가 있을 때, 이미지 상에 관측되는 객체의 크기를 이용하여 렌즈와 객체 사이의 거리인d를 구할 수 있는 방법입니다. - 먼저 필요한 수식을 나열해 보도록 하겠습니다.
- \[\frac{a}{f} = \tan{(\theta_{1})} = \frac{h}{d} \tag{1}\]
- \[\frac{b}{f} = \tan{(\theta_{2})} = \frac{h}{d - m} \tag{2}\]
- 위 수식 (1)과 (2) 를 이용하여 이미지 상의 물체의 크기 비율을 통해 카메라와 물체와의 거리를 구할 수 있습니다.
- \[\frac{a}{b} = \frac{h}{d} \times \frac{d-m}{h} = \frac{d - m}{d} = 1 - \frac{m}{d} \tag{3}\]
- \[d = \frac{m}{1 - \frac{a}{b}} \tag{4}\]
- 따라서 식 (4)와 같이 \(d\) 를 구하려면 두개의 이미지에서 이미지 좌표 상에서 같은 물체의 특정 길이인 \(a, b\) 와 움직인 카메라의 거리를 알아야 합니다. 상대적인 거리를 이용하기 때문에 \(f\) 는 필요 없습니다.

- 실험에 사용된 카메라는 일반 PC용 웹캠이며 보시는 바와 같이 렌즈 왜곡이 없어 보입니다. (있어도 영향은 없을 것으로 추정합니다.) 움직인 거리 측정을 위하여 자를 사용하였습니다.
- 물체는 책을 사용하였고 책의 가로 길이를 사용 하도록 하겠습니다. 처음 그림에서는 나무의 높이를 사용하였습니다. 그 나무의 높이에 해당하는 것이 현재 책의 가로 길이이며 다른 길이를 써도 상관없습니다.

- 책의 길이는 약
26cm입니다.

- 책과 카메라 시작점 까지의 거리는
80cm입니다.
- 실험은 첫 이미지를 기준으로 물체는 고정한 상태에서 카메라를 물체 방향으로
5cm,10cm,15cm,20cm더 가까이 가도록 하곘습니다.

- 왼쪽 이미지를 기준으로 물체는 고정한 체 카메라의 위치만 이동하면서 촬영을 하였습니다.
- 각 이미지의 크기는 height : 360, width : 640 입니다.
- 픽셀의 좌표 확인은 아래 사이트를 사용하였습니다.
- 링크 : https://pixspy.com/

- 책의 가로 길이는 위 노란색 사각형의 모서리와 같은 선 상의 책 끝점의 길이를 이용하였고 측정 결과는 다음과 같습니다. (y, x)에서 x 좌표 기준으로 (왼쪽 끝 좌표, 오른쪽 끝 좌표, 좌표 길이 순서) 로 작성 하였습니다.
- 좌표를 측정하는 기준은 Bounding Box를 그리는 관점으로 수동으로 작업하였으며 픽셀이 흐릿하여 오차가 있습니다.
- 기준 (카메라 이동 없음) : 259, 512,
253 - 기준 (책 방향으로 카메라 5cm 이동) : 261, 532,
271 - 기준 (책 방향으로 카메라 10cm 이동) : 245, 536,
291 - 기준 (책 방향으로 카메라 15cm 이동) : 238, 553,
315 - 기준 (책 방향으로 카메라 20cm 이동) : 243, 589,
346
- 카메라가 책에 점점 더 가까워 지기 때문에 픽셀에서의 길이도 점점 길어지는 것을 확인할 수 있습니다.
- 식 (6)을 이용하여 구한 결과 아래와 같습니다.

- 위 식의 결과의 각 열은 원리를 설명 할 때 사용한 기호와 같습니다.
- 카메라를 5 cm 앞으로 이동하였을 때에는 상당히 정확한 거리를 추정하였지만 나머지의 경우 오차가 큰 것을 확인할 수 있습니다. 마지막
ratio열을 보았을 때, ratio를 보면 흔히 Depth Estimation을 할 때, True Positive (1.25 이하)로 간주할 수 있는 수준의 오차를 보입니다.
- 위 실험을 통해 카메라의 이동 (또는 실험 조건을 바꿔서 물체를 이동시킬 수 있습니다.)을 통해 물체와의 거리를 구할 수 있었습니다.
- 만약 자동으로 물체의 위치를 Bounding Box를 그릴 수 있고 카메라의 이동 거리 (또는 물체의 이동 거리)를 구할 수 있으면 Bounding Box를 Tracking하여 이전, 이후 Frame 간 박스의 크기를 비교하고 이동 거리를 알 수 있다면 자동으로 거리를 추정할 수 있습니다.