옵티컬 플로우 (Optical Flow) 알아보기 (Luckas-Kanade w/ Pyramid, Horn-Schunck, FlowNet 등)

참조 : 컴퓨터 비전 (오일석 저)
참조 : https://powerofsummary.tistory.com/35
참조 : https://learnopencv.com/optical-flow-in-opencv/
참조 : Introduction to Computer Vision
참조 : http://www.cse.psu.edu/~rtc12/CSE486/lecture30.pdf
참조 : https://www.ri.cmu.edu/pub_files/pub3/baker_simon_2002_3/baker_simon_2002_3.pdf
참조 : http://www.cs.cmu.edu/~16385/s17/Slides/14.3_OF__HornSchunck.pdf

이번 글에서는 object의 움직임과 관련된 개념 중 하나인 optical flow에 대하여 알아보도록 하겠습니다.

연속 영상에 관한 지식

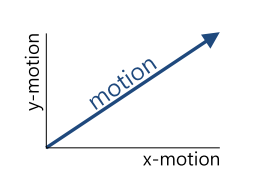
먼저 연속된 영상이 입력될 때 사용되는 용어로 Frame이 있습니다. Frame은 연속 영상 (동영상)을 구성하는 각각의 영상을 뜻하며 시간 축 $t$를 가지게 됩니다.

위 그림과 같이 기존에 이미지 좌표계인 $y, x$ 이외의 $t$ 축이 더 추가되며 1 초당 몇 번의 Frame을 다루는 지에 따라서 FPS(Frame Per Second)라는 단위를 사용합니다. 예를 들어 30 fps는 30 frame / sec 즉, 1초당 30개의 이미지를 다룬다는 뜻입니다.
동영상에서 다루는 fps는 어떤 영상을 다루는 지에 따라서 다르게 설정됩니다. 예를 들어 일반 웹캡이나 감시 카메라 등은 일반적으로 10 ~ 30 fps를 사용합니다.

일반적으로 연속된 Frame이 들어올 떄, 영상은 영상 일관성(coherence)이라는 성질을 가집니다.

예를 들어 어떤 픽셀 (y, x)의 색이 빨간색이라면, 주변 픽셀의도 유사한 색을 띌 가능성이 높다는 것입니다.

연속된 Frame에서의 또 다른 성질 중 하나는 시간 일관성입니다.

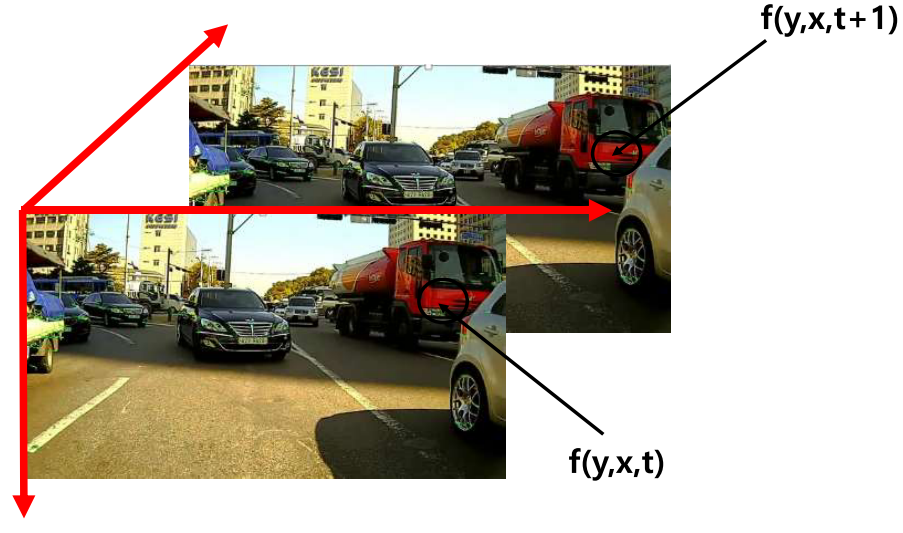
즉, $t$ 순간의 픽셀 값 $f(y, x, t)$는 다음 순간 $f(y, x, t + 1)$과 비슷할 가능성이 높습니다. 만약 픽셀값의 변경량이 거의 없다면 그 만큼 이동량이 작다고 직관적으로 생각할 수 있습니다.

보통 가장 직관적인 방법으로 두 Frame 간의 픽셀값의 차이를 통하여 변화를 확인하는 방법이 있습니다.
예를 들어 $r$번째 Frame과 $t$ 번째 Frame의 픽셀 값의 차이를 계산한다고 가정해 보겠습니다.

\[f(n) = \begin{cases} 1, & \vert f(y, x, t) - f(y, x, r) \vert > \tau \\[2ex] 0, & \text{else} \end{cases}\]

위 식을 이용하여 영상 간의 차이를 구하면 영상에서의 움직임을 구할 수 있습니다. 이 경우는 굉장히 간단하지만 한계점도 명확히 있습니다.
먼저, 위치가 고정된 카메라에서만 적용 가능하고 배경과 물체의 색상이나 명암에 큰 변화가 있는 경우 사용할 수 없습니다.
따라서 두 영상의 차이를 구하는 한계를 개선하기 위하여 실제 영상에서 움직이는 물체를 찾을 필요가 있습니다.

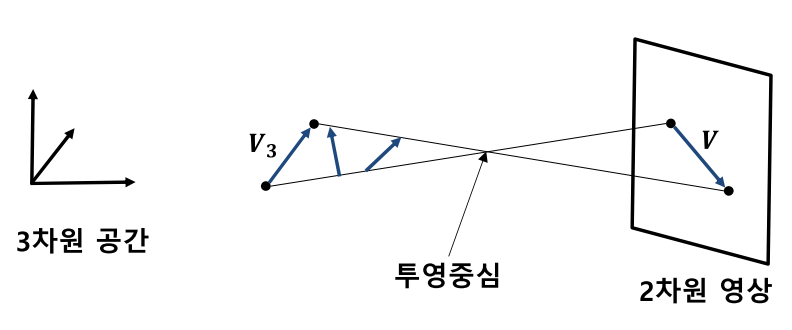
물체의 이동이 발생할 때, 3차원 실제 공간에서 일어나는 물체의 움직임은 2차원 영상 공간에 투영됩니다. 이 때, 차원이 축소되면서 투영되기 때문에 3차원 공간의 무수히 많은 벡터가 2차원 영상 공간 상의 벡터로 투영될 수 있습니다.

여기서 motion field라는 개념이 필요합니다.

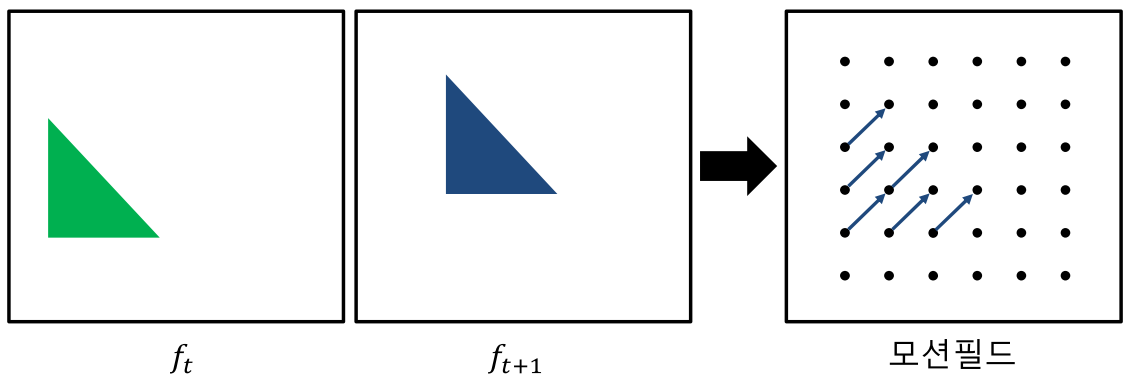
motion field는 움직임이 발생한 모든 점의 모션 벡터로 얻어낸 2차원 모션맵을 뜻합니다.
위 그림을 보면 초록색 삼각형( $t$ )이 파란색 삼각형($t+1$)과 같이 이동하였을 떄, 픽셀들이 일관성 있게 이동한 것을 확인할 수 있습니다. 따라서 위 그림과 같은 상황에서는 이상적으로 motion field를 구할 수 있습니다.

motion field를 구하여 분석하면 위 그림과 같이 움직인 픽셀에 대한 정보를 추정할 수 있습니다.

물론 근본적으로 현실 이미지에서는 위 그림 예시들과 같은 motion field를 정확하게 구하기는 어려울 수 있습니다. 대표적으로 구체 회전과 광원 회전과 같은 어려움이 있습니다.

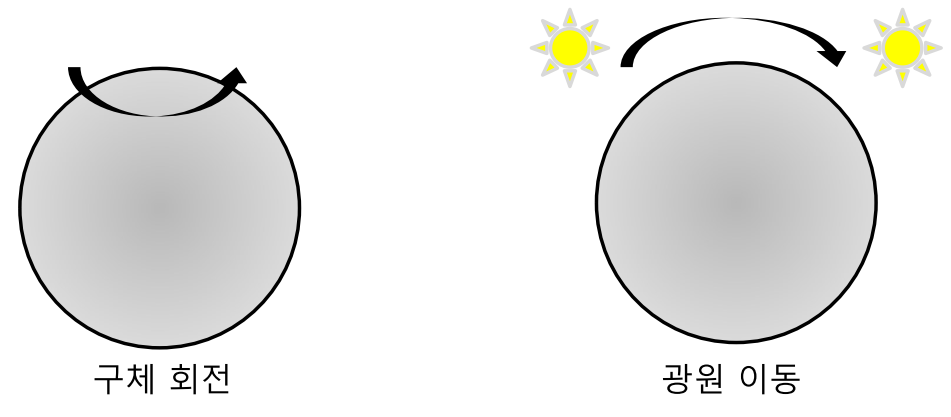
구의 texture가 단조로운 상태에서 회전이 발생한다면 모션 벡터가 발생함에도 불구하고 영상에는 아무런 변화가 발생하지 않습니다.
반면 구가 회전하지 않지만 광원이 움직이는 경우에는 모션 벡터가 0이어야 하지만 영상에는 변화가 발생합니다.
즉, 실질적으로 움직였지만 모션 벡터가 발생하지 않는 경우와 움직임이 발생하지 않았지만 모션 벡터가 발생하는 오인식 경우가 문제가 되곤 합니다.

따라서 Temporal Feature를 구하는 것이 중요합니다. 이는 시간의 흐름에 따라 변하는 특징을 나타내며 움직이는 물체의 경우 잘 나타납니다.

앞에서 설명하였듯이, 픽셀의 움직임을 motion이라고 합니다. motion을 나타낼 떄에는 대표적으로 ① motion의 크기, ② X방향, Y방향의 모션, ③ Dominant Motion등을 나타냅니다.

Optical flow의 의미와 추정 원리

앞에서 설명한 Motion field를 Optical field라고도 합니다. Optical Field는 수식으로 나타낼 수 있고 이 내용은 글의 뒷부분에서 다룰 예정입니다.
Optical flow는 Optical field를 구하기 위하여 이전 프레임과 현재 프레임의 차이를 이용하고 픽셀값과 주변 픽셀들과의 관계를 통해 각 픽셀의 이동(motion)을 계산하여 추출합니다. 이를 통하여 움직임을 구별해 낼 수 있습니다.

Optical flow를 사용하면 위 그림 예시와 같이 차량의 움직임을 나타낼 수 있습니다. 그 결과 Optical flow가 좌측으로 발생하게 되는 것을 확인할 수 있습니다.

따라서 Optical flow 문제를 정의하면 위 그림과 같이 각 픽셀 별로 $I(x, y, t) \to I(x, y, t+1)$ 를 어떻게 추정하는 지 구하는 문제가 됩니다.

지금부터 살펴 볼 optical flow는 인접한 두 장의 영상에 나타나는 명암 변화만을 고려합니다. optical flow 추정의 단계에서는 물체를 검출하거나 검출한 물체의 움직임을 반영하려는 시도를 하지 않게 때문에 물체와는 독립적인 추정 방식입니다.
optical flow는 계산 과정에서 개별 물체의 움직임을 명시적으로 반영하지는 않지만 물체가 움직이면 그에 따른 명암 변화가 발생하므로 암시적으로 물체의 움직임인 motion field를 반영한다고 말할 수 있습니다. (물론 구체 회전이나 광원 이동과 같은 한계 상황에서는 여전히 어려움이 있습니다.)

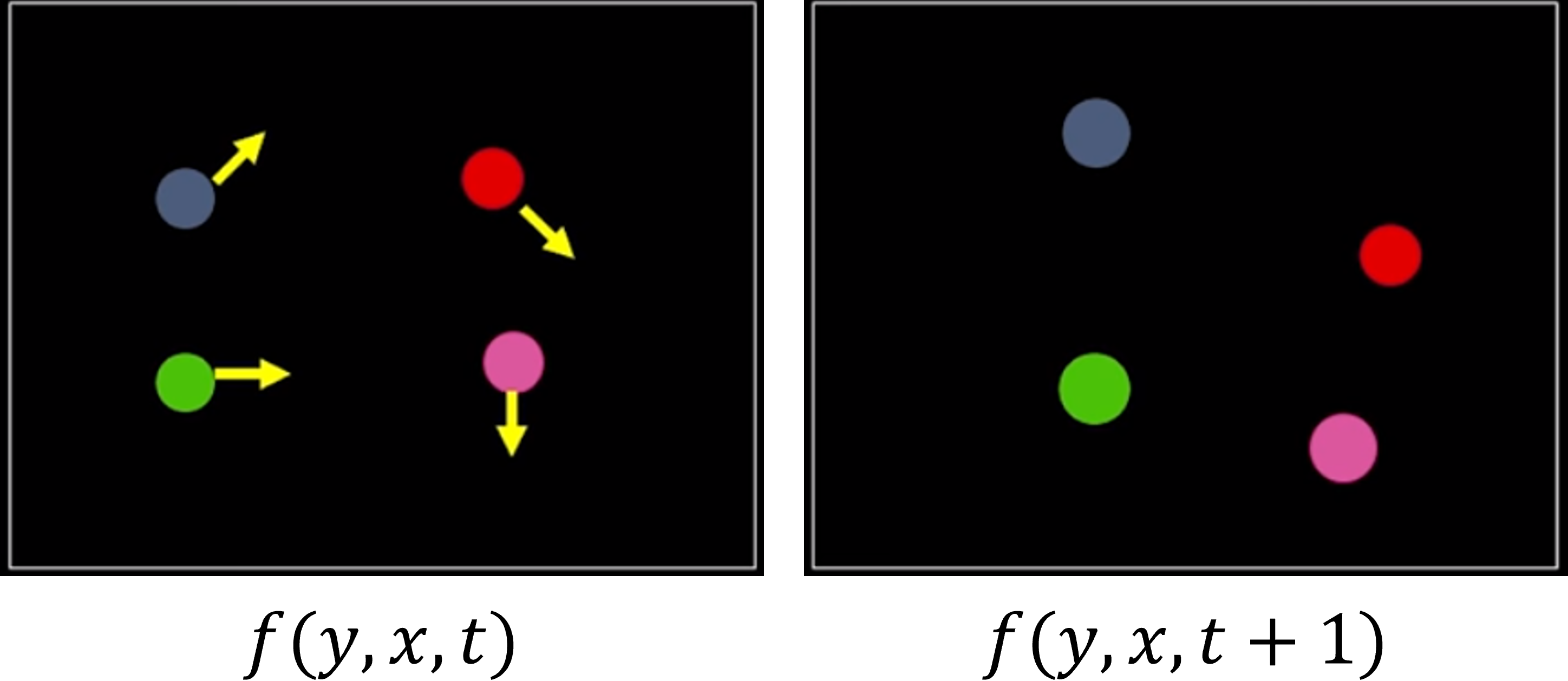
이와 같이 optical flow는 인접한 두 영상의 명암 변화를 분석하여 움직임 정보를 추정합니다. $t$라는 순간의 영상 $f(y, x, t)$와 짧은 시간이 흐른 후의 인접 영상 $f(y, x, t+1)$이 주어졌다고 가정해 보겠습니다.

위 그림과 같이 optical flow 알고리즘이 추정해야 할 motion vector인 $\vec{v} = (v, u)$는 위 그림과 같습니다. 여기에서 $v, u$는 각각 $y, x$방향의 이동량에 해당합니다.
초록색의 $t$ 순간의 삼각형이 파란색의 $t+1$ 순간의 삼각형으로 이동하면서 영상에서의 그에 대응하는 픽셀도 이동하게 됩니다. 그 내용을 위 오른쪽 그림에서 살펴볼 수 있습니다. 하지만 $t$ Frame의 어떤 픽셀이 $t + 1$의 어떤 픽셀과 대응이 되는 지 알아야 motion vector를 구할 수 있습니다. 이 문제가 optical flow 추정의 핵심입니다.
optical flow 추정 알고리즘은 카메라가 고정되지 않는 상황에서도 적용할 수 있어야 합니다.
만약 카메라가 고정되어 있는 상황이라면 optical flow에 등장하는 움직임은 모두 물체의 움직임으로 봐야 하고, 물체가 고정된 상황이라면 optical flow를 카메라 움직임으로 해석해야 합니다.

optical flow를 추정하기 위해서는 현실을 훼손하지 않는 범위 내에서 적절하게 가정을 세웁니다. optical flow의 전제 조건 2가지는 다음과 같습니다.
- ① color/brightness constancy : 어떤 픽셀과 그 픽셀의 주변 픽셀의 색/밝기는 같음을 가정으로 세웁니다.
- ② small motion : Frame 간 움직임이 작아서 어떤 픽셀 점은 멀리 움직이지 않는 것을 가정으로 세웁니다.

앞의 그림을 다시 살펴 보면 $f(y, x, t)$ 와 $f(y, x, t+1)$ 의 4가지 픽셀은 $t \to t+1$ 로 변경되더라도 색/밝기 항상성은 유지된다는 것과 움직임 또한 크지 않고 근처에 있음을 알 수 있습니다.
이 중 첫번째 전제 조건인 밝기 항상성은 optical flow의 가장 중요한 가정입니다. 연속한 두 영상에 나타난 물체의 같은 점은 명암값이 같거나 비슷하다는 뜻입니다.

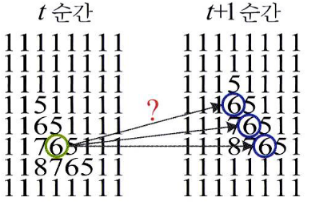
위 이미지에서 $t$ 순간의 영상에서 동그라미로 표시된 픽셀은 6이라는 명암을 가지므로 $t + 1$ 순간의 영상에서도 이 픽셀은 6 또는 6과 아주 유사한 값을 가져야 한다는 조건입니다. 밝기 항상성에는 조명의 변화가 없어야 한다는 전제가 내표되어 있습니다. 또한 물체 표면과 광원이 이루는 각에 따라 변하는 명암 차이를 무시한다는 사실도 포함됩니다.
현실적으로 밝기 항상성은 실제 세계에 정확히 들어맞지는 않습니다. 외부 환경도 변할 뿐 아니라 물체의 법선 벡터와 광원이 이루는 각에 따라 명암값이 변하기 때문입니다. 하지만 이 가정이 없이는 알고리즘을 설계하기가 매우 어렵습니다. 다행인 점은 실제 실험 결과를 살펴보면 이 가정이 받아들일 수 있는 정도의 오차 이내에 들어 맞는다은 사실을 확인할 수 있습니다. 이러한 이유로 ① 전제 조건인 밝기 항상성이라는 전제 조건을 사용합니다.

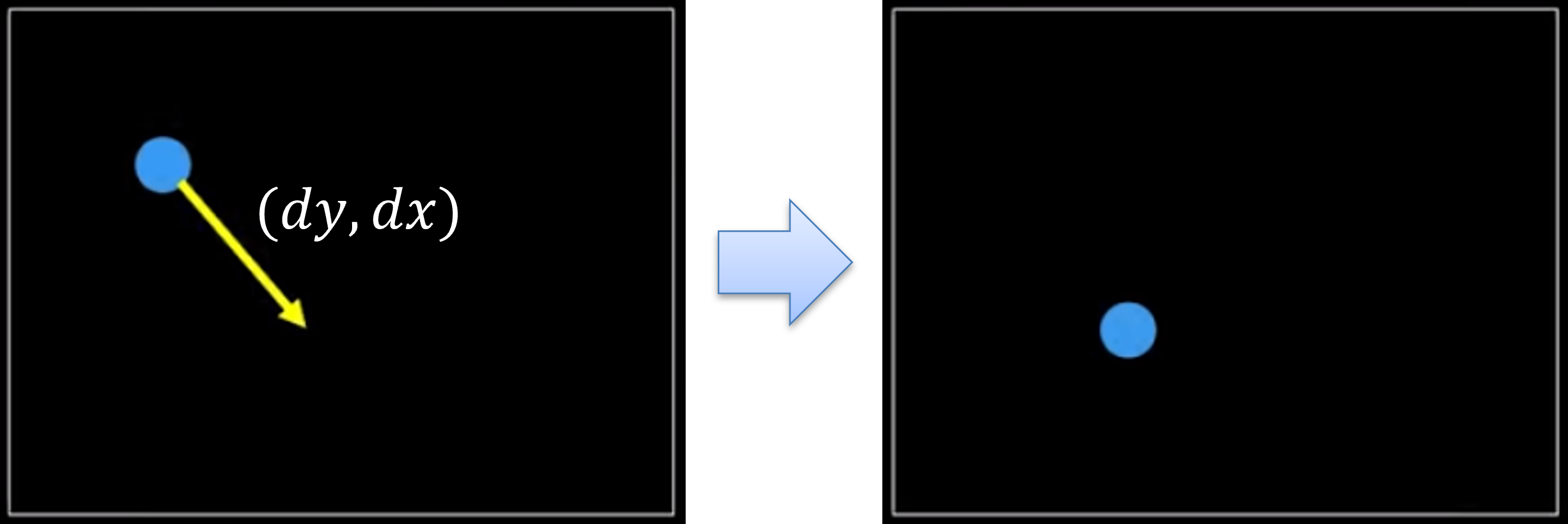
다시 한번 식으로 나타내면 다음과 같습니다. 함수 식으로 나타내기 위하여 $f$로 사용하겠습니다.

\[f(y, x, t) = f(y + dy, x + dx, t + dt)\]
\[f(y + dy, x + dx, t + dt) - f(y, x, t) = 0\]

위 식에서 ② 전제 조건인 small motion을 적용해 보겠습니다. 즉, $dy, dx$ 가 굉장히 작은 값을 가진다는 것이 small motion을 의미합니다. 인접한 두 영상의 시간 차이 $dt$가 충분히 작아서 small motion 조건을 만족한다면 테일러 급수에 따라 다음과 같이 식을 정리할 수 있습니다.

\[f(y + dy, x + dx, t + dt) = f(y, x, t) + \frac{\partial f}{\partial y}dy + \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial t}dt + \cdots\]

테일러 급수의 생략된 항은 2차 이상의 항이며 이 값은 1차 항에 비하여 영향이 작기 때문에 생략하였습니다.
위 식에서 $dt$는 fps에 따라 다르며 초당 30 프레임을 획득하는 fps=30인 비디오 영상의 경우 $dt = 1/30$이 됩니다. $dt$가 충분히 작다는 말은 시간이 짧아야 한다는 뜻이 아니라 물체 이동 거리를 몇 개 픽셀 정도로 작게 유지할 수 있을 정도의 시간을 뜻합니다. 즉, 이동 거리량이 작아야 된다는 뜻입니다.

따라서 $dt$가 작다는 가정에 따라, 물체의 움직임을 나타내는 $dy, dx$도 작으므로 2차 이상의 항을 무시해도 큰 오차가 발생하지는 않습니다.
밝기 항상성 가정에 따르면 $dt$라는 시간 동안 $(dy, dx)$만큼 움직여 형성된 새로운 점의 $f(y + dy, x + dx, t + dt)$는 원래 점의 $f(y, x, t)$와 같습니다. 따라서 테일러 급수에 해당하는 term을 밝기 항상성 가정에 의해 0으로 둘 수 있습니다.

\[\frac{\partial f}{\partial y}dy + \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial t}dt = 0\]

위 식에서 양변을 $dt$로 나누어 보겠습니다.

\[\frac{\partial f}{\partial y}\frac{dy}{dt} + \frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial t} = 0\]

위 식에서 $\frac{\partial f}{\partial y}, \frac{\partial f}{\partial x}, \frac{\partial f}{\partial t}$의 의미를 살펴보겠습니다.
이 값들은 영상 $f(y, x, t)$를 각각 매개변수 $y, x, t$로 편미분한 값입니다.
먼저 $\biggl( \frac{\partial f}{\partial y}, \frac{\partial f}{\partial x} \biggr)$는 gradient vector를 의미합니다. 반면 $\frac{dy}{dt}, \frac{dx}{dt}$는 시간 $dt$ 동안 $y$와 $x$ 방향으로의 이동량을 뜻하므로 motion vector에 해당합니다. 따라서 $\frac{dy}{dt} = v, \frac{dx}{dt} = u$를 뜻하며 최종적으로 다음과 같이 정리할 수 있습니다.

\[\frac{\partial f}{\partial y}v + \frac{\partial f}{\partial x}u + \frac{\partial f}{\partial t} = 0\]

이 식은 미분 방정식으로 optical flow constraint equation 또는 gradient constraint equation 이라고 부릅니다. 미분을 이용하는 대부분의 optical flow 추정 알고리즘은 이 방정식을 풀어 motion vector를 구합니다. 앞으로 살펴 볼 Lucas-Kanade 알고리즘과 Horn-Schunck 알고리즘이 이 식을 사용합니다.
이 식을 살펴보면 gradient를 구성하는 세 개의 값 $\frac{\partial f}{\partial y}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial t}$를 모두 구했다 하더라도 $v, u$ 즉, motion vector를 유일한 값으로 결정할 수 없음을 알 수 있습니다. 방정식은 하나인데 구해야 할 값은 $v, u$ 두개 이기 때문입니다.
바로 뒤에서 살펴 볼 2가지 알고리즘 (Lucas-Kanade, Horn-Shunck) 각각에서는 조건을 추가하여 방정식의 해를 찾아 motion vector $v, u$를 구합니다.

optical flow constraint equation의 의미를 구체적인 예시를 통하여 좀 더 자세하게 알아보도록 하겠습니다. 먼저 위에서 정의한 식만을 이용해서 optical flow를 추정해 보겠습니다.

위 이미지에서 편도 함수 값은 다음과 같이 이웃한 점과의 차이로 구한다고 가정해 보겠습니다.

\[\frac{\partial f}{\partial y} = f(y + 1, x, t) - f(y, x, t)\]
\[\frac{\partial f}{\partial x} = f(y, x + 1, t) - f(y, x, t)\]
\[\frac{\partial f}{\partial t} = f(y, x, t + 1) - f(y, x, t)\]

위 그림의 초록색 동그리미로 표시한 픽셀의 좌표가 $(5, 3, t)$이고 이 값에 대하여 편도 함수 값을 계산해 보면 다음과 같습니다.

\[\frac{\partial f}{\partial y} = f(5 + 1, 3, t) - f(5, 3, t) = 7 - 6 = 1\]
\[\frac{\partial f}{\partial x} = f(5, 3 + 1, t) - f(5, 3, t) = 5 - 6 = -1\]
\[\frac{\partial f}{\partial t} = f(5, 3, t + 1) - f(5, 3, t) = 8 - 6 = 2\]

계산한 값을 $\frac{\partial f}{\partial y}v + \frac{\partial f}{\partial x}u + \frac{\partial f}{\partial t} = 0$에 적용하면 다음과 같은 방정식을 얻습니다.

\[v - u + 2 = 0\]

구한 식을 그래프로 나타내면 위 그래프와 같습니다. 이 식을 해석해 보면 구하려면 motion vector $(v, u)$는 이 직선 상에 놓여야 하는데 유일한 점으로 결정한 수는 없는 상태입니다. 따라서 앞으로 알아볼 optical flow 추정 방법을 통하여 밝기 항상성 이외에 또 다른 가정을 추가하여 유일한 해를 찾아보도록 하곘습니다.

Lucas-Kanade 알고리즘

먼저 지역적 방법으로 optical flow의 유일한 해를 찾는 방법으로 Lucas-Kanade 알고리즘이 있습니다. 이 알고리즘은 픽셀 $(y, x)$를 중심으로 하는 윈도우 영역 $N(y, x)$의 optical flow는 같다라고 가정합니다. 따라서 Lucas-Kanade 알고리즘의 전제조건은 다음 3가지입니다.
- ① 밝기 향상성 (brightness constancy)
- ② Frame 간 움직임이 작다.
- ③ 픽셀 $(y, x)$를 중심으로 하는 윈도우 영역 $N(y, x)$의 optical flow는 같다

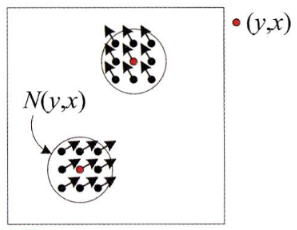
이 의미를 그림으로 살펴보면 위와 같습니다. 이웃 영역에 속하는 모든 픽셀 $(y_{i}, x_{i}), i=1, 2, \cdots, n$은 같은 motion vector $\vec{v} = (v, u)$를 가져야 합니다. 여기서 $n$은 영역 $N()$ 에 속하는 픽셀의 갯수로 위 그림에서 $n = 9$가 됩니다.
물론 이 픽셀은 모두 $\frac{\partial f}{\partial y}v + \frac{\partial f}{\partial x}u + \frac{\partial f}{\partial t} = 0$을 만족해야 하며 추가적으로 다음과 같이 식을 정리할 수 있습니다.

\[\frac{\partial f(y_{i}, x_{i})}{\partial y}v + \frac{\partial f(y_{i}, x_{i})}{\partial x}u + \frac{\partial f(y_{i}, x_{i})}{\partial t} = 0, \ \ (y_{i}, x_{i}) \in N(y, x)\]

위 식을 행렬 형태로 바꾸어 표현해 보곘습니다.

\[A\vec{v}^{T} = b\]
\[A = \begin{pmatrix} \frac{\partial f(y_{1}, x_{1})}{\partial y} & \frac{\partial f(y_{1}, x_{1})}{\partial x} \\ \cdots & \cdots \\ \frac{\partial f(y_{n}, x_{n})}{\partial y} & \frac{\partial f(y_{n}, x_{n})}{\partial x} \end{pmatrix}\]
\[\vec{v} = (v, u)\]
\[b = \begin{pmatrix} -\frac{\partial f(y_{1}, x_{1})}{\partial t} \\ \cdots \\ -\frac{\partial f(y_{n}, x_{n})}{\partial t} \end{pmatrix}\]

위 식에서 미지수는 $(v, u)$ 두 개이지만 식은 $n$개로 식이 더 많은 상황입니다. 따라서 least square를 이용하여 미지수 $v, u$를 구합니다.
위 식을 $A^{T}A\vec{v}^{T} = A^{T}b$와 같이 바꿔 쓴 후, 아래와 같이 $\vec{v}$로 정리합니다.

\[\vec{v}^{T} = (A^{T}A)^{-1}A^{T}b\]

위 식에서 $(A^{T}A)^{-1}$과 $A^{T}b$를 분리하여 생각하면 $(A^{T}A)^{-1}$은 2X2 행렬이고 $A^{T}b$는 2X1 행렬입니다.

\[\vec{v}^{T} = \begin{pmatrix} v \\ u \end{pmatrix} = (A^{T}A)^{-1}A^{T}b = \begin{pmatrix} \sum_{i=1}^{n} \biggl( \frac{\partial f(y_{i}, x_{i})}{\partial y} \biggr)^{2} & \sum_{i=1}^{n} \frac{\partial f(y_{i}, x_{i})}{\partial y}\frac{\partial f(y_{i}, x_{i})}{\partial x} \\ \sum_{i=1}^{n} \frac{\partial f(y_{i}, x_{i})}{\partial y}\frac{\partial f(y_{i}, x_{i})}{\partial x} & \sum_{i=1}^{n} \biggl( \frac{\partial f(y_{i}, x_{i})}{\partial x} \biggr)^{2} \end{pmatrix}^{-1} \begin{pmatrix} -\sum_{i=1}^{n} \frac{\partial f(y_{i}, x_{i})}{\partial y}\frac{\partial f(y_{i}, x_{i})}{\partial t} \\ -\sum_{i=1}^{n} \frac{\partial f(y_{i}, x_{i})}{\partial x}\frac{\partial f(y_{i}, x_{i})}{\partial t} \end{pmatrix}\]

위 식의 첫번째 항은 $\partial t$를 포함하지 않으므로 $t$ 순간의 영상만 있으면 모든 계산이 가능합니다. 두번째 항은 $t$ 순간과 $t+1$ 순간의 영상을 둘 다 사용합니다.
위 식은 윈도우 영역 $N()$에 속한 모든 픽셀을 같은 비중으로 취급합니다. 그런데 윈도우의 중앙에 있는 픽셀 $(y, x)$에 가깡루수록 큰 비중을 두는 식으로 바꾸면 보다 나은 품질의 motion vector를 구할 수 있습니다.

\[A^{T} W A v^{T} = A^{T} W b\]
\[\vec{v}^{T} = (A^{T} W A)^{-1} A^{T} W b\]

따라서 중앙 픽셀에 가중치를 주기 위하여 $W$를 도입하고 $W$는 보통 가우시안을 사용합니다. 따라서 아래와 같이 $w_{i}$가 추가된 $\vec{v}$를 구할 수 있습니다.

\[\vec{v}^{T} = \begin{pmatrix} v \\ u \end{pmatrix} = (A^{T}WA)^{-1}A^{T}Wb = \begin{pmatrix} \sum_{i=1}^{n}w_{i} \biggl( \frac{\partial f(y_{i}, x_{i})}{\partial y} \biggr)^{2} & \sum_{i=1}^{n} w_{i} \frac{\partial f(y_{i}, x_{i})}{\partial y}\frac{\partial f(y_{i}, x_{i})}{\partial x} \\ \sum_{i=1}^{n} w_{i} \frac{\partial f(y_{i}, x_{i})}{\partial y}\frac{\partial f(y_{i}, x_{i})}{\partial x} & \sum_{i=1}^{n} w_{i} \biggl( \frac{\partial f(y_{i}, x_{i})}{\partial x} \biggr)^{2} \end{pmatrix}^{-1} \begin{pmatrix} -\sum_{i=1}^{n} w_{i} \frac{\partial f(y_{i}, x_{i})}{\partial y}\frac{\partial f(y_{i}, x_{i})}{\partial t} \\ -\sum_{i=1}^{n} w_{i} \frac{\partial f(y_{i}, x_{i})}{\partial x}\frac{\partial f(y_{i}, x_{i})}{\partial t} \end{pmatrix}\]

위 식이 optical flow를 추정하는 Lucas-Kanade 알고리즘의 핵심입니다.

이러한 이유로 Lucas-Kanade optical flow 방식은 다음과 같은 장단점을 가집니다.
장점 : Lucas-Kanade algorithm은 sparse optical flow에 속하여 코너와 같이 두드러지는 특징 점을 사용하여 optical flow를 추적하기 때문에 연산량이 적다는 장점이 있다.
단점 : 좁은 지역의 윈도우를 사용하기 때문에 이 윈도우보다 큰 움직임이 발생하였을 경우 움직임을 계산하지 못한다는 단점이 있고, 특징 점을 사용하여 optical flow를 얻기 때문에 dense optical flow에 비해서 정확도가 낮은 편이다.

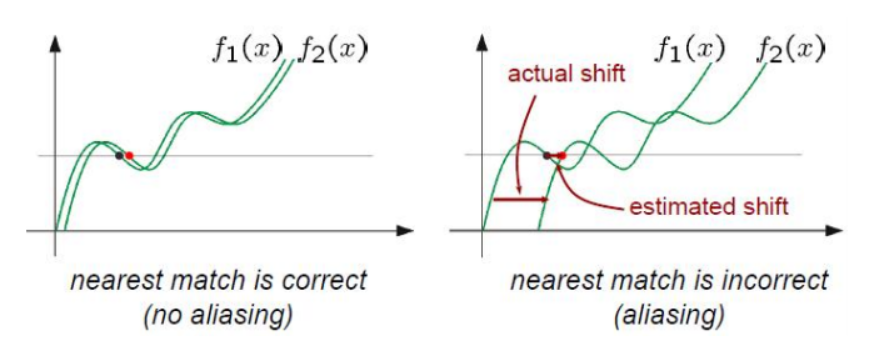
Luckas-Kanade 알고리즘은 위와 같은 장단점을 가집니다. 단점을 통해 알 수 있듯이 motion vector를 가지는 작은 window에 대하여 적용하는 알고리즘이므로 만일 영상내의 object가 큰 움직임의 motion vector를 가진다면 aliasing이 발생한다.

또한 지역적 방법의 옵티컬 플로우를 찾는 방식의 주요한 문제점 중 하나는 aperture problem이라고 불리는 문제입니다. aperture는 작은 구멍이라는 뜻을 가지는 단어입니다. 아래 그림을 살펴보겠습니다.

위 그림의 왼쪽과 같이 어떤 edge 성분이 왼쪽 → 오른쪽으로 이동했다고 가정하겠습니다. 이 때, edge 전체의 움직임을 보고 판단하였을 떄, edge가 오른쪽으로 이동했다고 판단합니다.
반면 구멍 안의 edge 성분의 이동을 살펴보면 오른쪽 상단으로 이동한 것으로 판단됩니다.

반면 위 그림처럼 투명하게 살펴보았을 경우 edge 성분이 오른쪽으로 이동한 것을 알 수 있습니다. 이와 같이 edge를 투명하게 본다는 것은 지역적 방법이 아닌 전역적 방법을 뜻합니다.
이처럼 지역적 방법에는 aperture problem으로 인하여 옵티컬 플로우 추정이 불확실하게 나타날 수 있습니다.

이와 같은 문제를 해결하기 위하여 Pyramid 방식의 Lucas-Kanade 알고리즘이 도입되었습니다.

추가적으로 살펴본 Lucas-Kanade method with pyramids 방법에 대하여 장단점을 정리하면 다음과 같습니다.

원리 : Lukas-Kanade 방법에서 큰 움직임을 계산하지 못하는 단점을 개선하기 위해 고안되어진 방법으로 원본 영상으로부터 영상 스케일에 따른 영상 피라미드를 구성한다.
장점 : 영상 피라미드의 상위계층에서 하위계층으로 추적하면서 다양한 스케일의 이미지를 탐색하기 때문에 커다란 움직임도 찾아낼 수 있다.
단점 : 몇 개의 특징점을 추출하고 그 특징 점에 대하여 optical flow를 얻으므로 dense optical flow algorithm 보다는 정확성이 떨어진다는 단점이 있다.

Horn-Schunck 알고리즘

Lucas-Kanade 알고리즘은 윈도우 영역 내부를 고려하는 지역적 방식을 사용하였습니다. 반면 Horn-Schunk 알고리즘은 영상 전체를 한꺼번에 고려하는 전역적 방식을 사용합니다.
Horn-Shunk 알고리즘에서 전역적 방식을 사용하기 위해서 한가지 전제 조건이 추가로 필요합니다. optical flow는 균일해야 한다. 입니다. 따라서 Horn-Schunk 알고리즘은 다음 3가지 전제 조건이 필요합니다.
- ① 밝기 향상성 (brightness constancy)
- ② Frame 간 움직임이 작다.
- ③ optical flow는 균일해야 한다.

optical flow 맵의 균일한 정도는 아래 식을 사용하여 추정합니다.

\[\Vert \nabla v \Vert^{2} + \Vert \nabla u \Vert^{2} = \biggl( \frac{\partial v}{\partial y} \biggr)^{2} + \biggl( \frac{\partial v}{\partial x} \biggr)^{2} + \biggl( \frac{\partial u}{\partial y} \biggr)^{2} + \biggl( \frac{\partial u}{\partial x} \biggr)^{2}\]

위 식에서 $\nabla v = \biggl(\frac{\partial v}{\partial y}, \frac{\partial v}{\partial x} \biggr)$로 $v$를 $y$와 $x$ 방향으로 미분한 gradient 입니다. $\nabla u$도 동일하게 정의됩니다.
만약 gradient가 작다면 이 뜻은 이웃한 화소의 $v$와 $u$가 비슷하다는 뜻입니다.

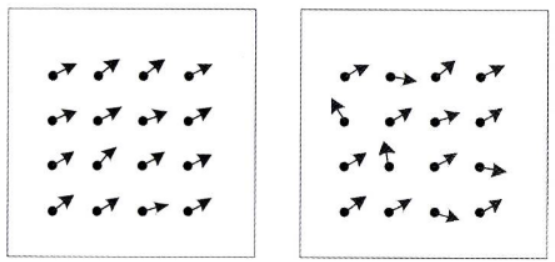
위 두 optical flow 맵을 살펴보면 왼쪽은 optical flow가 균일합니다. 반면 오른쪽은 optical flow가 균일하지 않습니다.
gradient가 작다면 왼쪽 그림과 같이 optical flow가 균일하다고 할 수 있습니다. 반면 오른쪽 그림과 같이 optical flow가 균일하지 않다면 벡터의 방향이 크게 변하는 지점에서 gradient 값일 클 것입니다.
따라서 $\Vert \nabla v \Vert^{2} + \Vert \nabla u \Vert^{2}$를 작게하여 gradient 값이 작도록 해야 합니다.

뿐만 아니라 Horn-Schunk 알고리즘은 기존의 optical flow의 밝기 항상성 조건식인 $\frac{\partial f}{\partial y}v + \frac{\partial f}{\partial x}u + \frac{\partial f}{\partial t} = 0$ 식도 만족해야 합니다. 정리하면 다음과 같습니다.

\[\frac{\partial f}{\partial y}v + \frac{\partial f}{\partial x}u + \frac{\partial f}{\partial t} = 0\]
\[\text{Minimize } \Vert \nabla v \Vert^{2} + \Vert \nabla u \Vert^{2} = \biggl( \frac{\partial v}{\partial y} \biggr)^{2} + \biggl( \frac{\partial v}{\partial x} \biggr)^{2} + \biggl( \frac{\partial u}{\partial y} \biggr)^{2} + \biggl( \frac{\partial u}{\partial x} \biggr)^{2}\]

Horm-Schunk 알고리즘은 영상 전체에 대해 이들 값을 최소로 하는 해를 찾는 전략을 취합니다.
이러한 전략을 반영한 것이 다음 식입니다.

\[E = \int\int \biggl(\biggl(\frac{\partial f(y, x)}{\partial y}v + \frac{\partial f(y, x)}{\partial x}u + \frac{\partial f(y, x)}{\partial t} \biggr)^{2} + \alpha^{2}( \Vert \nabla v(y, x) \Vert^{2} + \Vert \nabla u(y, x) \Vert^{2} ) \biggr)dydx\]

위 식에서 적분 식 속에 있는 첫번째 항은 optical flow의 밝기 항상성 조건식이고 두번째 항은 전역적 방식을 위한 식입니다. 이 때, $\alpha$는 어느 것에 더 큰 비중을 둘 것인 지 결정해 주는 가중치입니다. 이와 같은 두번째 항을 regularization term 이라고 합니다. 이와 같이 정규화 항을 이용하여 균일한 optical flow의 해를 구하는 방법을 정규화 기법 이라고 합니다.

위 식은 Error이므로 Error를 최소로 하는 optical flow 맵, 즉 모든 픽셀 $(y, x)$에 대한 $$ v(y, x)

이러한 이유로 Horn-Shunk optical flow 방식은 다음과 같은 장단점을 가집니다.
장점 : 영상 모든 픽셀을 탐색하는 알고리즘으로써 다른 알고리즘보다 정확하다는 장점이 있습니다.
단점 : 대표적인 dense optical flow 로써 영상 내부의 모든 픽셀의 속도를 계산하므로 느리다는 단점이 있습니다.

Optical flow 알고리즘 성능 동향

지금까지 설명한 바와 같이 Lucas-Kanade (LK) 알고리즘은 지역적이로, Horn-Schunck (HS) 알고리즘은 전역적입니다. 이러한 특성 때문에 LK는 optical flow 값이 정해지지 않는 영역이 군데군데 발생할 수 있는데, 특히 명암 변화가 적은 곳에서 잘 나타납니다. 반대로 HS는 반복하는 과정에서 명암 변화가 적은 영역에도 정보가 파급되므로 모든 픽셀이 motion vector를 가지는 밀집된 optical flow 맵을 생성해 줍니다. 이는 일종의 interpolation 효과로 볼 수 있습니다.
LK나 HS 모두 미분으로 얻은 도함수를 기반으로 작동하는 optical flow 알고리즘입니다. 이와 같은 알고리즘을 미분 기반 방법이라고 합니다.
미분 기반 방법 이외에도 optical flow를 추정하는 다양한 방법들이 있습니다. 예를 들어 블록 매칭 방법, 에너지 방법, 위상 방법 등이 있는데, Performance of optical flow techniques (Barron94] J. L. Barron, D. J. Fleet, and S. S. Beauchemin, International Journal of Computer Vision, Vol. 12，No .l, pp.43-77.)에 따르면 미분을 사용하는 Luckas-Kanade 알고리즘이 가장 우수하다는 결론을 이끌어 냈습니다.

2000년 이후에 발표된 방법까지 포함하여 가장 성능이 좋다고 알려진 "Lucas/Kanade meets Horn/Schunck : combining local and global optic flow methods"(Andres Bruhn, Joachim Weickert, and Christoph Schnorr, International Journal of Computer Vision, Vol.61, No.3)이 가장 우수하다는 결론을 도출하였습니다.

실질적으로 optical flow를 활용할 때에는 정확도와 효율성을 고려하여 Luckas-Kanade with Pyramid 알고리즘을 사용하기를 추천드립니다.

Optical flow의 활용

optical flow 알고리즘을 이용하여 다음과 같은 optical flow 맵을 얻게 되면 물체 추적이나 인식같은 컴퓨터 비전 처리에 필요한 feature들을 얻을 수 있습니다.

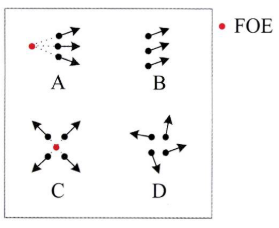
위 그림은 optical flow로 부터 얻은 motion vector의 형상을 간단하게 표현해 보았습니다. 실제로 motion vector는 알고리즘의 한계와 다양한 노이즈로 인하여 많은 오차를 포함하기 때문에 위 그림과 같이 깔끔하게 나타나지는 않습니다.
A와 같은 형태의 motion vector를 가지게 되면 물체가 오른쪽으로 이동함과 동시에 카메라에 가까워지는 상황임을 추정할 수 있습니다. 이 때, motion vector가 모이는 한 점을 FOE (Factor of Expansion) 이라고 합니다.
B는 카메라와 일정한 거리를 유지하면서 오른쪽 위로 이동하는 물체를 나타냅니다.
C는 물체가 광축 방향을 따라 카메라에 다가오는 상황을 나타냅니다.
D는 제자리에서 회전하는 물체를 나타냅니다.

위 그림에서는 optical flow를 통하여 객체를 인식하고 각 객체의 motion vector를 시각화 하여 나타낸 것입니다. motion vector의 방향을 통하여 인식한 객체의 이동 방향을 추정할 수 있습니다.
이 예제는 글 아래에서 OpenCV를 통하여 살펴볼 예정입니다.

위 예시와 같이 motion vector를 이용하여 주변 물체의 상태를 확인할 수 있을 뿐 아니라, 카메라가 고정되어 있을 때, 로봇이나 자동차의 현재 자신의 위치인 ego motion을 추정하는 문제에도 활용할 수 있습니다.
뿐만 아니라 motion vector를 feature로 이용하고 이 feature들과 SVM과 같은 classifier 이용하여 다양한 분류 문제에도 활용할 수 있습니다.

위 그림과 같이 비디오에서 Shout boundary detection의 용도로도 옵티컬 플로우를 사용할 수 있습니다. 아래 그림과 같이 같은 비디오에서는 옵티컬 플로우 추정이 가능하므로 영상이 완전히 바뀌게 되면 옵티컬 플로우를 추정할 수 없게 되므로 영상이 바뀐 시점을 확인할 수 있습니다.

또 다른 사용 방법으로 배경을 제거하는 방법이 있습니다. 움직이는 물체의 옵티컬 플로우를 추정하면 물체와 배경을 구분할 수 있으므로 위 그림과 같이 사용할 수 있습니다.
반대로 말하면 움직이는 물체의 Motion만을 분리 즉, Motion Segmentation Task에도 사용할 수 있습니다.

OpenCV를 이용한 Optical Flow 예제

딥러닝을 이용한 Optical Flow 구하기

지금까지 살펴본 Lucas-Kanade, Horn-Schunck과 같은 옵티컬 플로우를 구하는 알고리즘은 딥러닝과 무관하게 사용가능한 고전적인 컴퓨터 비전 방법에 해당합니다. 현재까지도 앞에서 다룬 방식의 옵티컬 플로우가 오랜 시간 동안 최적화가 잘 되어 있기 때문에, 효율적으로 잘 사용되고 있습니다.
최근에는 컴퓨터 비전에 해당하는 대부분의 Task들을 딥러닝을 통해 해결하고자 하며 옵티컬 플로우 또한 2015년의 FlowNet을 시작으로 다양한 모델이 나타나기 시작하였습니다.
이번 글에서 모든 딥러닝 모델을 다루기는 글이 길어지므로 딥러닝 모델과 관련된 글은 별도로 다루겠습니다. 아래 링크에서 레퍼런스가 되는 옵티컬 플로우 목적의 딥러닝 모델의 내용을 확인하실 수 있습니다.

옵티컬 플로우 (Optical Flow) 알아보기 (Luckas-Kanade w/ Pyramid, Horn-Schunck, FlowNet 등)

목차

연속 영상에 관한 지식

Optical flow의 의미와 추정 원리

Lucas-Kanade 알고리즘

Hierarchical Lucas-Kanade 알고리즘

Horn-Schunck 알고리즘

Optical flow 알고리즘 성능 동향

Optical flow의 활용

OpenCV를 이용한 Optical flow 예제

딥러닝을 이용한 Optical Flow 구하기

연속 영상에 관한 지식

Optical flow의 의미와 추정 원리

Lucas-Kanade 알고리즘

Horn-Schunck 알고리즘

Optical flow 알고리즘 성능 동향

Optical flow의 활용

OpenCV를 이용한 Optical Flow 예제

딥러닝을 이용한 Optical Flow 구하기