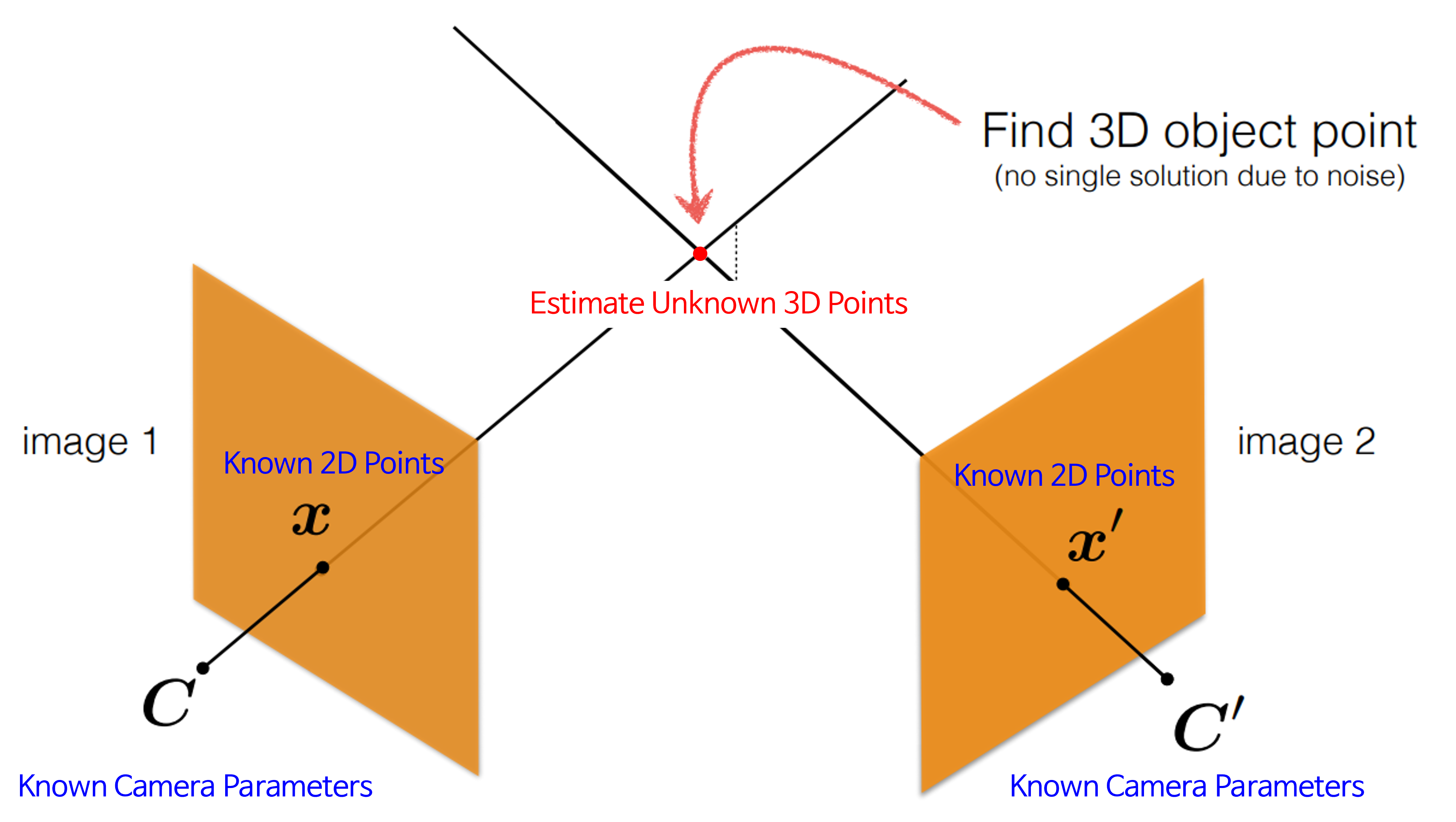
Triangulation

• 참조 : https://www.cs.cmu.edu/~16385/s17/Slides/

• 사전 지식 : Direct Linear Transformation
• 사전 지식 : 특이값 분해 (Singular Value Decomposition)
• 사전 지식 : 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습

목차

• Triangulation 개념

• Python 실습

Triangulation 개념

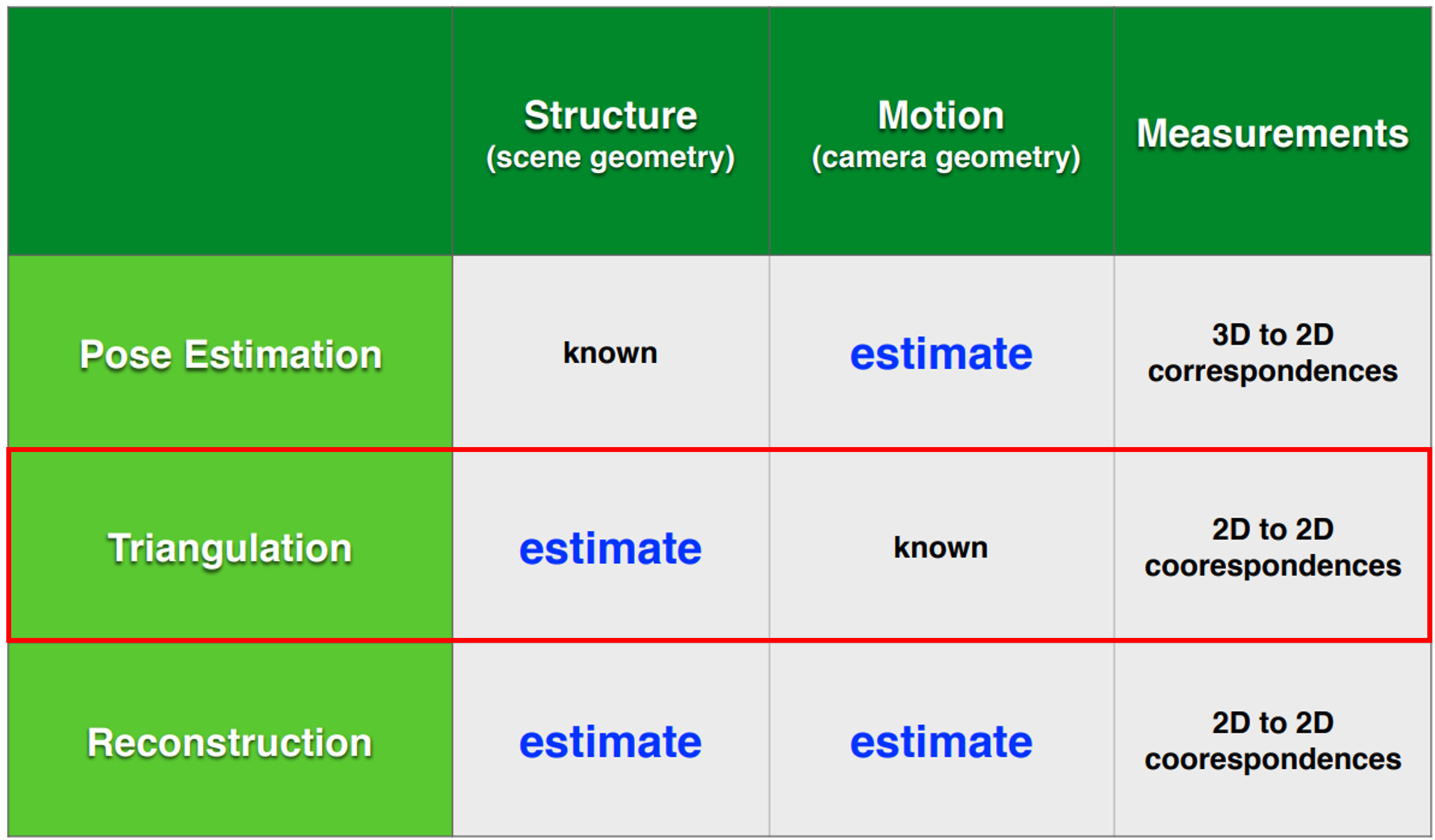
• 위 표의 3가지 항목인 Pose Estimation, Triangulation, Reconstruction 중 이번 글에서 다룰 내용은 Triangulation이며 이 태스크는 도표의 분류와 같이 Pose Estimation 또는 Reconstruction과 차이가 있음을 알 수 있습니다. 그 내용에 대하여 좀 더 자세하게 살펴보겠습니다.

• Triangulation은 2개의 이미지에서 같은 지점을 가리키는 2D point 셋과 카메라 파라미터가 있을 때, 2D point의 실제 3D point를 추정하는 작업을 의미합니다.
• 2D Point는 보통 Feature Extraction & Matching 작업 등과 같은 방식을 통하여 얻기 때문에 일부 오차가 있음을 가정합니다. 또한 Triangulation에서는 이미지의 왜곡 보정이 반영되어 있음을 가정합니다.
• 이번 글에서는 다음과 같이 용어 및 기호를 통일하여 사용하도록 하겠습니다.

• \[\text{Given a set of (noisy) matched points: } x = (u, v), x' = (u', v') \tag{1}\]
• \[\text{Camera projection matrices: } P, P' \tag{2}\]
• \[\text{Estimated 3D points: } \mathbf{X}^{T} = \begin{bmatrix} X & Y & Z \end{bmatrix} \tag{3}\]

• 식 (1)에서 \(x, x'\) 각각은 이미지 상에서 서로 같은 지점의 이미지 좌표를 의미합니다.
• 식 (2)에서 \(P\) 는 Camera Extrinsic Matrix와 Camera Intrinsic Matrix를 모두 반영한 Camera Projection Matrix를 의미합니다. 상세 내용은 글 상단의 카메라 캘리브레이션 링크를 참조해 보시기 바랍니다.
• 식 (3)의 \(\mathbf{X}\) 는 식 (1)의 이미지 2D points인 \(x, x'\) 가 이미지에 투영되기 이전의 3D points를 의미하며 최종 추정하고자 하는 값이 됩니다.

• \[x = P\mathbf{X} \tag{4}\]

• 식 (4)에서 3D points인 \(\mathbf{X}\) 를 Camera Projection Matrix를 통해 이미지에 투영하면 \(x\) 가 됩니다.
• 이 때, \(\mathbf{X}\) 를 알고 싶으나 \(\mathbf{X}\) 의 후보가 되는 값은 무수히 많이 있습니다. 관련 내용은 아래 링크를 참조하시면 됩니다.
  • 동차좌표계 : https://gaussian37.github.io/vision-concept-homogeneous_coordinate/

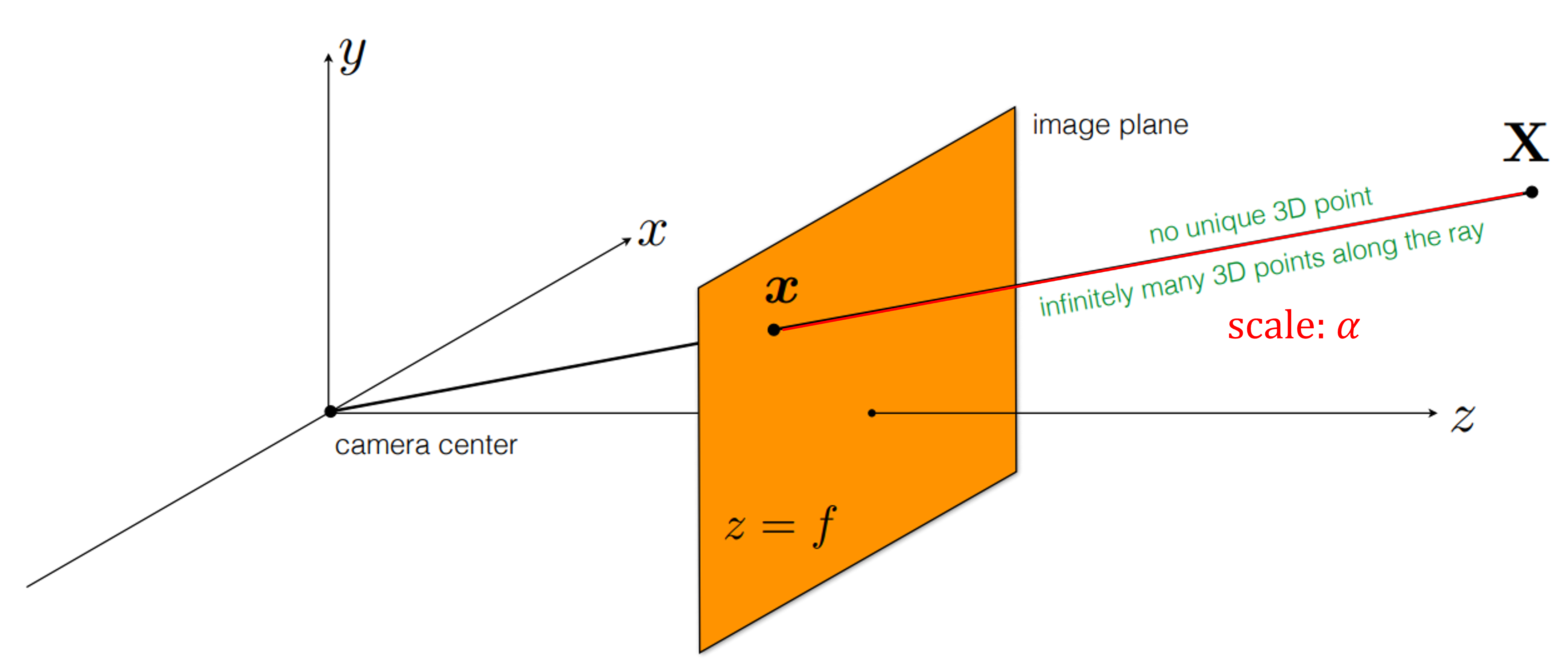
• 위 그림과 같이 빨간색 선인 Ray에 대응되는 모든 점들이 \(\mathbf{X}\) 가 될 수 있으므로 유일한 해를 결정할 수 없습니다. scale \(\alpha\) 값에 따라 빨간색 선의 어떤 점으로도 대응될 수 있기 때문에 1개의 카메라 만을 이용하면 무수히 많은 해를 가지게 됩니다.

• 반면 이상적인 상황에서 2개의 카메라에서 생성한 Ray의 교점을 이용하여 \(X\) 의 좌표를 구하는 방법을 사용해 볼 수 있습니다. 이 경우에는 다음과 같은 식을 이용합니다.

• \[\begin{cases} x = P\mathbf{X} \\ x' = P'\mathbf{X} \end{cases} \tag{5}\]

• 앞에서 가정한 바와 같이 \(x, x'\) 의 matched points는 노이즈를 포함할 수 밖에 없음을 가정하였습니다. 따라서 식(5)에서 완벽히 일치하는 해 \(X\) 를 찾기는 어렵습니다. 대신에 가장 적합한 해를 찾는 최적화 방법을 이용해야 합니다.
• 한 개의 점 \(\mathbf{X} = \{X, Y, Z\}\) 에 대하여 찾고자 하는 값은 3개이므로 최소 3개식을 이용해야 \(X, Y, Z\) 를 추정할 수 있습니다.

• 식을 구하기 위하여 2개의 Ray \(\alpha x\) 와 \(P\mathbf{X}\) 가 서로 평행하다는 조건을 이용하도록 하겠습니다. 2개의 Ray가 평행하다면 cross product가 0이 되기 때문에 이 값을 이용하면 식을 구할 수 있습니다.

• 먼저 아래와 같이 \(\alpha x = P \mathbf{X}\) 를 전개해 보도록 하겠습니다.

• \[x = P\mathbf{X} \tag{6}\]
• \[\Rightarrow \begin{align} \alpha \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} \\ &= \begin{bmatrix} P_{1}^{T} \\ P_{2}^{T} \\ P_{3}^{T}\end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} \end{align} \tag{7}\]
• \[\begin{cases} P_{1}^{T} = \begin{bmatrix} p_{11} & p_{12} & p_{13} & p_{14} \\ \end{bmatrix} \\ P_{2}^{T} = \begin{bmatrix} p_{21} & p_{22} & p_{23} & p_{24} \\ \end{bmatrix} \\ P_{3}^{T} = \begin{bmatrix} p_{31} & p_{32} & p_{33} & p_{34} \\ \end{bmatrix}\end{cases} \tag{8}\]

• 2개의 Ray \(\alpha x\) 와 \(P\mathbf{X}\) 가 평행하기 때문에 다음 식을 만족합니다. scale factor \(\alpha\) 는 아래 식에 영향이 없으므로 제거 할 수 있습니다.

• \[x \times P\mathbf{X} = 0 \tag{9}\]

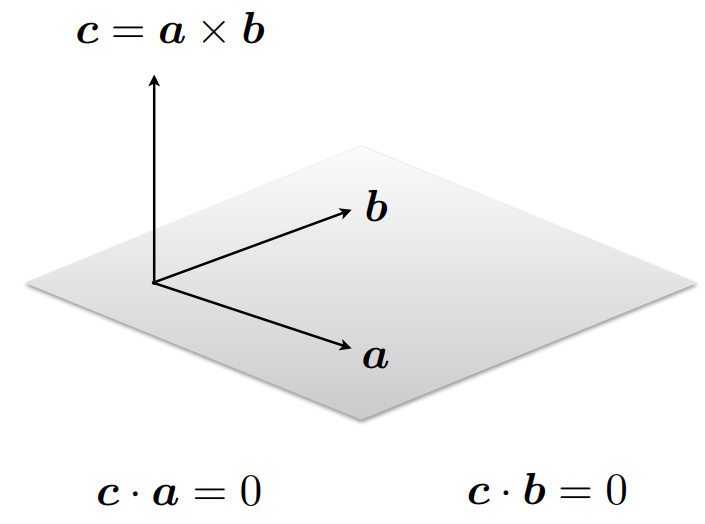
• \[a^{T} = \begin{bmatrix} a_{1} & a_{2} & a_{3} \end{bmatrix} \tag{10}\]
• \[b^{T} = \begin{bmatrix} b_{1} & b_{2} & b_{3} \end{bmatrix} \tag{11}\]
• \[a \times b = \begin{bmatrix} a_{2}b_{3} - a_{3}b_{2} \\ a_{3}b_{1} - a_{1}b_{3} \\ a_{1}b_{2} - a_{2}b_{1} \end{bmatrix} \tag{12}\]
• \[\text{Cross product of two vectors in the same direction is zero: } a \times a = 0\]

• 식 (7)을 이용하여 전개하면 다음과 같습니다.

• \[\alpha \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} P_{1}^{T} \\ P_{2}^{T} \\ P_{3}^{T}\end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix} = \begin{bmatrix} P_{1}^{T}\mathbf{X} \\ P_{2}^{T}\mathbf{X} \\ P_{3}^{T}\mathbf{X} \end{bmatrix} \tag{13}\]
• \[\alpha \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} P_{1}^{T}\mathbf{X} \\ P_{2}^{T}\mathbf{X} \\ P_{3}^{T}\mathbf{X} \end{bmatrix} \tag{14}\]

• 앞에서 설명한 바와 같이 \(\alpha\) 를 제거하겠습니다. 식 (14)에서 좌변의 \(\alpha\) 는 scale에 해당하므로 cross proudct 식을 적용할 때, normalized scale인 1 로 두어도 cross product 식 전개에는 영향이 없습니다. 따라서 다음과 같이 식을 전개할 수 있습니다.

• \[\begin{bmatrix} u \\ v \\ 1 \end{bmatrix} \times \begin{bmatrix} P_{1}^{T}\mathbf{X} \\ P_{2}^{T}\mathbf{X} \\ P_{3}^{T}\mathbf{X} \end{bmatrix} = \begin{bmatrix} v P_{3}^{T}\mathbf{X} - P_{2}^{T}\mathbf{X} \\ P_{1}^{T}\mathbf{X} - u P_{3}^{T}\mathbf{X} \\ uP_{2}^{T}\mathbf{X} - vP_{1}^{T}\mathbf{X}\end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \tag{15}\]

• 식 (15)에서 3행은 1행과 2행의 선형 결합으로 이루어져 있습니다. (1행에 \(x\) 를 곱하고 2행에 \(y\) 를 곱하여 더하면 3행이 도출됩니다.) 따라서 1행과 2행의 식만 이용할 수 있습니다. 즉, 식 (15)를 통해 2개의 2D point와 3D point 간의 대응 관계를 구할 수 있습니다.

• \[\begin{bmatrix} v P_{3}^{T}\mathbf{X} - P_{2}^{T}\mathbf{X} \\ P_{1}^{T}\mathbf{X} - u P_{3}^{T}\mathbf{X} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \tag{16}\]
• \[\begin{bmatrix} v P_{3}^{T} - P_{2}^{T} \\ P_{1}^{T} - u P_{3}^{T} \end{bmatrix} \mathbf{X} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \tag{17}\]

• 같은 방식으로 \(x' \times P'\mathbf{X} = 0\) 을 이용한 후 식(17)의 좌변 행렬에 누적시키면 다음과 같이 식을 구성할 수 있습니다.

• \[\begin{bmatrix} v P_{3}^{T} - P_{2}^{T} \\ P_{1}^{T} - u P_{3}^{T} \\ v' P_{3}^{'T} - P_{2}^{'T} \\ P_{1}^{'T} - u' P_{3}^{'T}\end{bmatrix} \mathbf{X} = \begin{bmatrix} 0 \\ 0 \\0 \\ 0 \end{bmatrix} \tag{18}\]

• 식 (18)의 좌변을 간단히 다음과 같이 나타낼 수 있습니다.

• \[A\mathbf{X} = 0 \tag{19}\]

• 식 (19)에서 \(\mathbf{X}\) 이 trivial solution이 아닌 해를 구하려면 특이값 분해 (Singular Value Decomposition)를 이용하여 구할 수 있습니다. 상세 내용은 아래 링크에서 확인할 수 있습니다.
  • 링크 : SVD 활용

Python 실습

• 아래 예제에서는 앞에서 배운 내용을 바탕으로 Triangulation을 적용하는 코드를 다루었습니다. Triangulated 3D point와 X_true의 값이 동일한 것을 통해 개념에서 배운 내용이 유효한 것을 확인할 수 있습니다.

import numpy as np

def triangulate_point(x, P, x_prime, P_prime):
    u, v, _ = x
    u_prime, v_prime, _ = x_prime
    P_1 = P[0, :]
    P_2 = P[1, :]
    P_3 = P[2, :]

    P_prime_1 = P_prime[0, :]
    P_prime_2 = P_prime[1, :]
    P_prime_3 = P_prime[2, :]

    A = np.array([
        v * P_3 - P_2,
        P_1 - u * P_3,
        v_prime * P_prime_3 - P_prime_2,
        P_prime_1 - u_prime * P_prime_3
    ])

    # Perform SVD on matrix A
    _, _, Vt = np.linalg.svd(A)
    X = Vt[-1]

    # Convert from homogeneous to inhomogeneous coordinates
    X = X / X[-1]
    return X

# Define the true 3D point in homogeneous coordinates
X_true = np.array([45, -35, 150, 1])

# Define the camera matrices
P1 = np.array([[700, 120, 320, 80],
               [60, 650, 230, -50],
               [0.5, 0.3, 1, 0.1]])

P2 = np.array([[650, -100, 310, -140],
               [-80, 700, 240, 90],
               [0.4, -0.2, 1, 0.2]])

# Project the 3D point onto the image planes to get x and x'
x = P1 @ X_true
x = x / x[-1]  # Normalize to get inhomogeneous coordinates

x_prime = P2 @ X_true
x_prime = x_prime / x_prime[-1]  # Normalize to get inhomogeneous coordinates

# Triangulate the 3D point using the projections
X_triangulated = triangulate_point(x, P1, x_prime, P2)
print(f"Triangulated 3D point: {X_triangulated} Vs. X true: {X_true}.")
# Triangulated 3D point: [ 45. -35. 150.   1.] Vs. X true: [ 45 -35 150   1].

# Reproject the 3D point back to 2D to check
x_reprojected = P1 @ X_triangulated
x_reprojected = x_reprojected / x_reprojected[-1]

x_prime_reprojected = P2 @ X_triangulated
x_prime_reprojected = x_prime_reprojected / x_prime_reprojected[-1]

print(f"Original x: {x} Vs. Reprojected x: {x_reprojected}.")
print(f"Original x_prime: {x_prime} Vs. Reprojected x_prime: {x_prime_reprojected}.")
# Original x: [465.02159161  88.83405305   1.        ] Vs. Reprojected x: [465.02159161  88.83405305   1.        ].
# Original x_prime: [451.54109589  45.60502283   1.        ] Vs. Reprojected x_prime: [451.54109589  45.60502283   1.        ].