(멀티플 뷰 지오메트리) Lecture 0. Multiple View Geometry 용어 둘러보기
2022, Apr 20
- 참조 : Multiple View Geometry in Computer Vision
- 이번 글에서는 Multiple View Geometry 책의 서론에 해당하는 부분을 요약하였습니다.
- 강의에 따로 포함되어 있지는 않기 때문에 책 내용을 요약하였고 전체 내용을 한번 소개하는 부분임에도 불구하고 중요한 개념이 많이 수록되어 있습니다.
- 추가적으로 Multiple View Geometry 책 전체에 걸쳐서 필요한 용어들을 추가적으로 정리합니다.
목차
-
Introduction and Basic Concepts
-
Affine and Euclidean Geometry
-
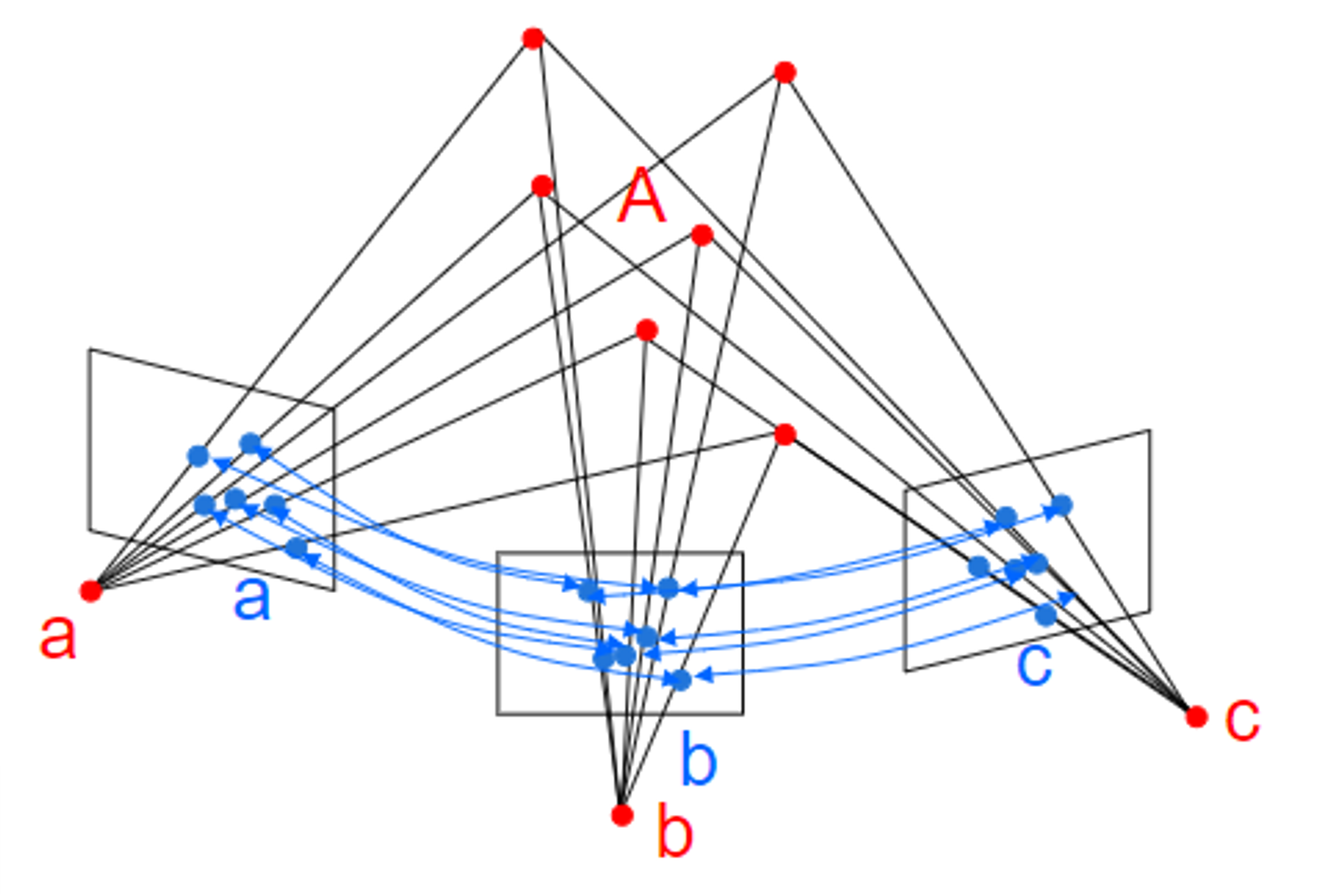
Camera projections
-
Reconstruction from more than one view
-
Three-view geometry
-
Four view geometry and n-view reconstruction
-
Transfer
-
Euclidean reconstruction
-
Auto-calibration
-
3D graphical models
-
video augmentation
Introduction and Basic Concepts
euclidean geometry는 물체의 각도와 모양을 서술하는 기하입니다. 일반적인 공간에서 흔히 사용하는 기하학입니다.euclidean geometry에서 두 선은 교차한다는 성질을 이용하고 싶지만 평행하는 선에 대한 예외를 두어야 하는데 이 부분을 예외로 두지 않고 평행선은 무한에서 만난다고 가정하여 사고를 확장하고자 합니다. 이 때 두 평행선이 만나는 점을point at infinity라고하며euclidiean geometry→projective geometry로 개념이 확장 됩니다.
- 무한이라는 공간을 표현하기 위하여
projective geometry에서는 좌표 형식을homogeneous coordinate로 변환을 하고자 합니다. - 2D euclidean space에서는 (x, y)로 나타내었던 좌표를 (x, y, 1)로 나타내고자 합니다. 마지막 좌표인 1은 스케일 값 형태로 나타낸다면 (kx, ky, k)같은 형태로 나타낼 수 있으며 따라서 (x, y, 1)과 (kx, ky, k)는
equivalent class라고 표현합니다. 두 값 모두 (x/1, y/1) = (kx/k, ky/k) = (x, y)로 나타낼 수 있기 때문입니다. - 이 때, (x, y, 0)은
equivalent class로 나타내어 지지 않습니다. x/0, y/0이 정의되어 지지 않기 때문입니다. 따라서 마지막 차원의 값이 0인homogeneous coordinate상의 좌표를point at infinity라고 정의합니다.
- 이와 같은 방식으로 euclidean space \(\mathbb{R}^n\) 의 점을 \(\mathbb{P}^{n}\) 공간으로 확장할 수 있으며 \(\mathbb{P}^{2}\) 에서 무한대에 있는 점은
line at infinity라고 불리는 선을 만들 수 있고 \(\mathbb{P}^{3}\) 에서는plane at infinity를 만들 수 있습니다.
- 어떤 점을 좌표로 표현하기 위해서는 특정 한 점을 원점으로 선택해야 합니다. 즉, 다른 점을 원점으로 이용한다면 기존의 좌표값은 달라지게 됩니다.
- 어떤 원점을 다른 위치로 이동하고 회전하는 방식을 통하여 euclidean space의 좌표를 변경할 수 있습니다. 이 때, euclidean space에서 발생하는 이동 및 회전에 관한 변환을
euclidean transformation이라고 합니다. euclidean transformation은 \(\mathbb{R}^{n}\) 에 선형 변환을 적용한 후 공간의 원점을 이동하는 것을 의미하는 반면 공간을 다른 방향의 다른 비율로 선형적으로 움직이거나 회전 및 늘리는 방법을affine transformation이라고 합니다.affine(euclidean 포함) transformation을 적용하면point at infinity는 여전히 무한대에 존재합니다. 하지만projective transformation을 적용하면point at infinity는 더 이상 무한대에 존재하지 않으며 다른 점과 차이가 없어집니다. 즉, \(\mathbb{R}^{n}\) 공간 상에서의point at infinity는 \(\mathbb{P}^{n}\) 에서 임의의 다른 점으로 변환되며 아래 식과 같이 나타내 집니다.
- \[X' = H_{(n+1) \times (n+1)} X\]
- 컴퓨터 비전에서는
projective space는 3D 세계를 표현하는 방법으로 사용됩니다. 즉, 2D 상의 이미지를 2D projective space에 놓인 것으로 생각하고 이것을 3D로 생각하며point at infinity,line at infinity등을projective space에서 다른 점 또는 선과 동일하게 취급하는 방식을 사용합니다.
Affine and Euclidean Geometry
- 무한대 공간에 선 또는 면을 추가하여
euclidean space에서projective space로 확장한 것을 살펴보았습니다. euclidean space\(\mathbb{R}^{n}\) 에서 사용하는 기하학을euclidean geometry라고 하고projective space\(\mathbb{P}^{n}\) 에서 사용하는 기하학을projective geometry라고 정의하면affine geometry는 어떤 의미를 가질까요?
- 먼저
projective geometry와affine geometry를 구분해 보겠습니다. affine geometry의 정의는projective geometry+line at infinity로 정의할 수 있고 한 공간에서의line at infinity를 다른 공간에서의line at infinity로projective transformation하는 것으로 이 방식을affine transformation이라고 말할 수 있습니다.- 기존의
projective geometry와affine geometry의 차이점은line at infinity가 무한에 있는 것인 지의 차이점입니다.projective geometry의line at infinity는 유한한 공간에 존재하여 실제 평면 상에 평행선이 교차하는 반면에affine geometry에서는line at infinity가 무한한 공간에 존재하여 실제 평면 상에 평행선이 존재하지 않습니다.
- 따라서 지금 까지 내용을 정리하면 다음과 같습니다.
