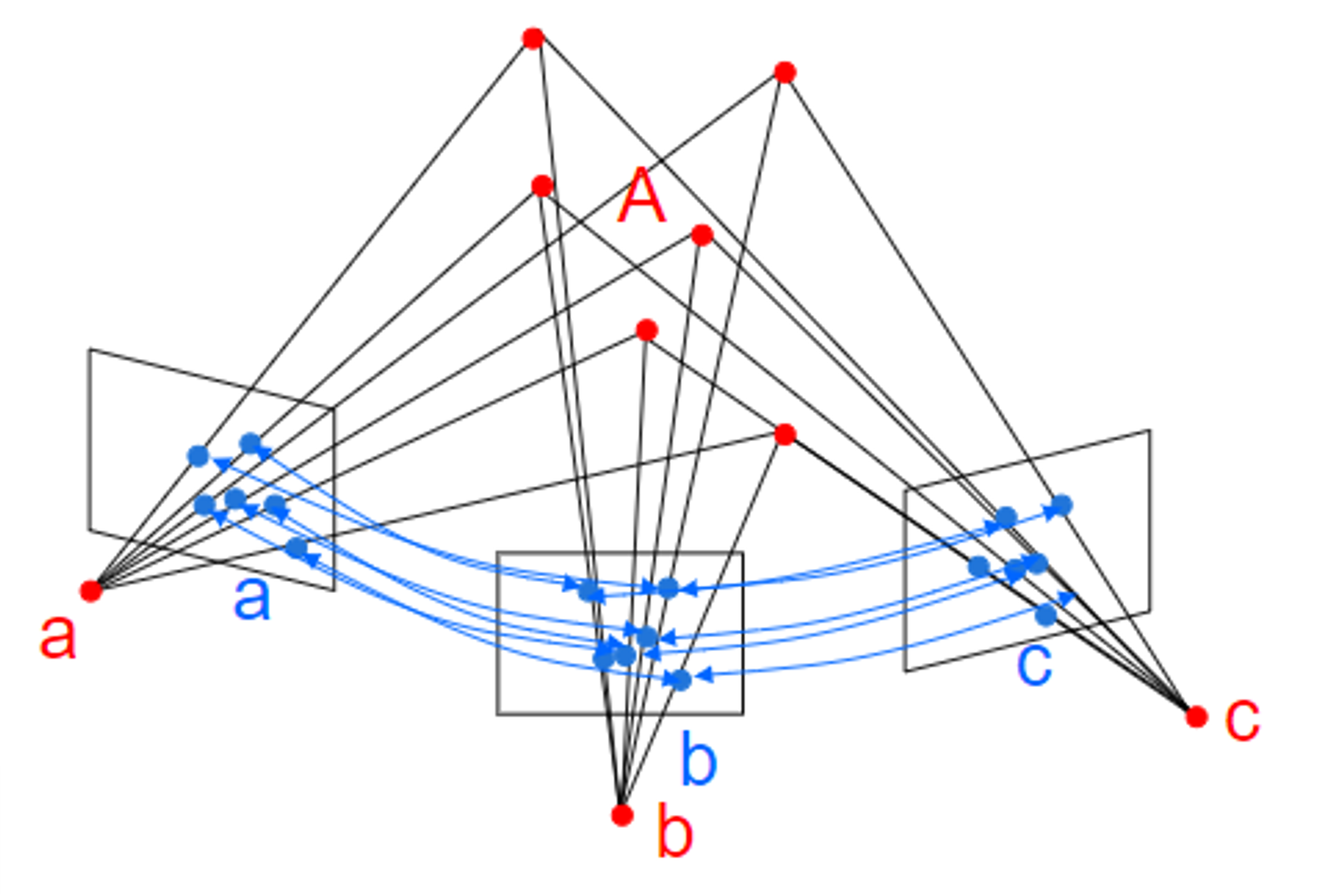
(멀티플 뷰 지오메트리) Lecture 11. Two-view and multi-view stereo

2022, Apr 20    

Multiple View Geometry 글 목차

• 참조 : https://youtu.be/OpZs7kfjFPA?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : https://youtu.be/N_iECTqZtQQ?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : https://youtu.be/hfQR7X8eH9s?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : https://youtu.be/YgOC9DjHyJs?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : Multiple View Geometry in Computer Vision

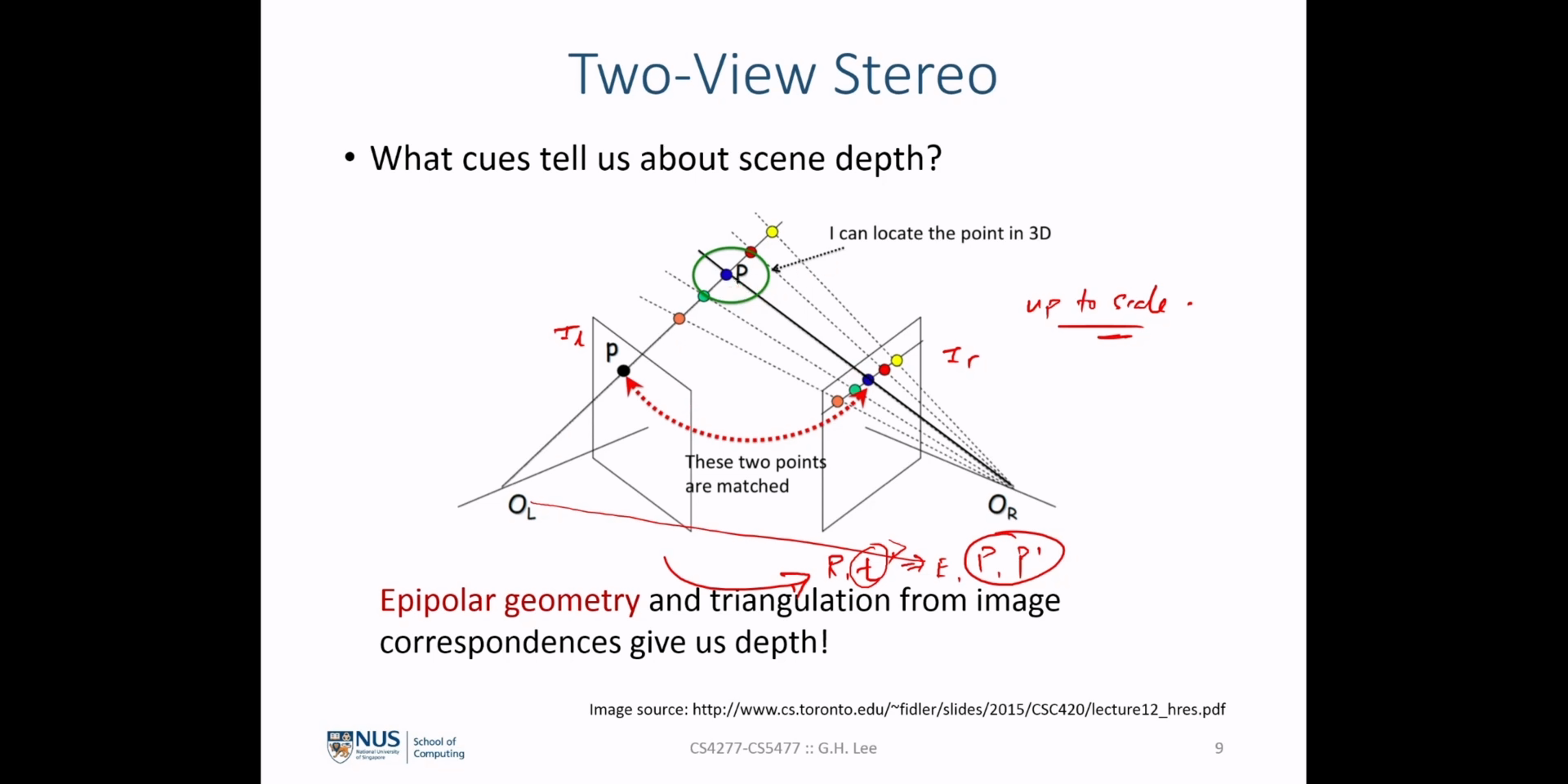
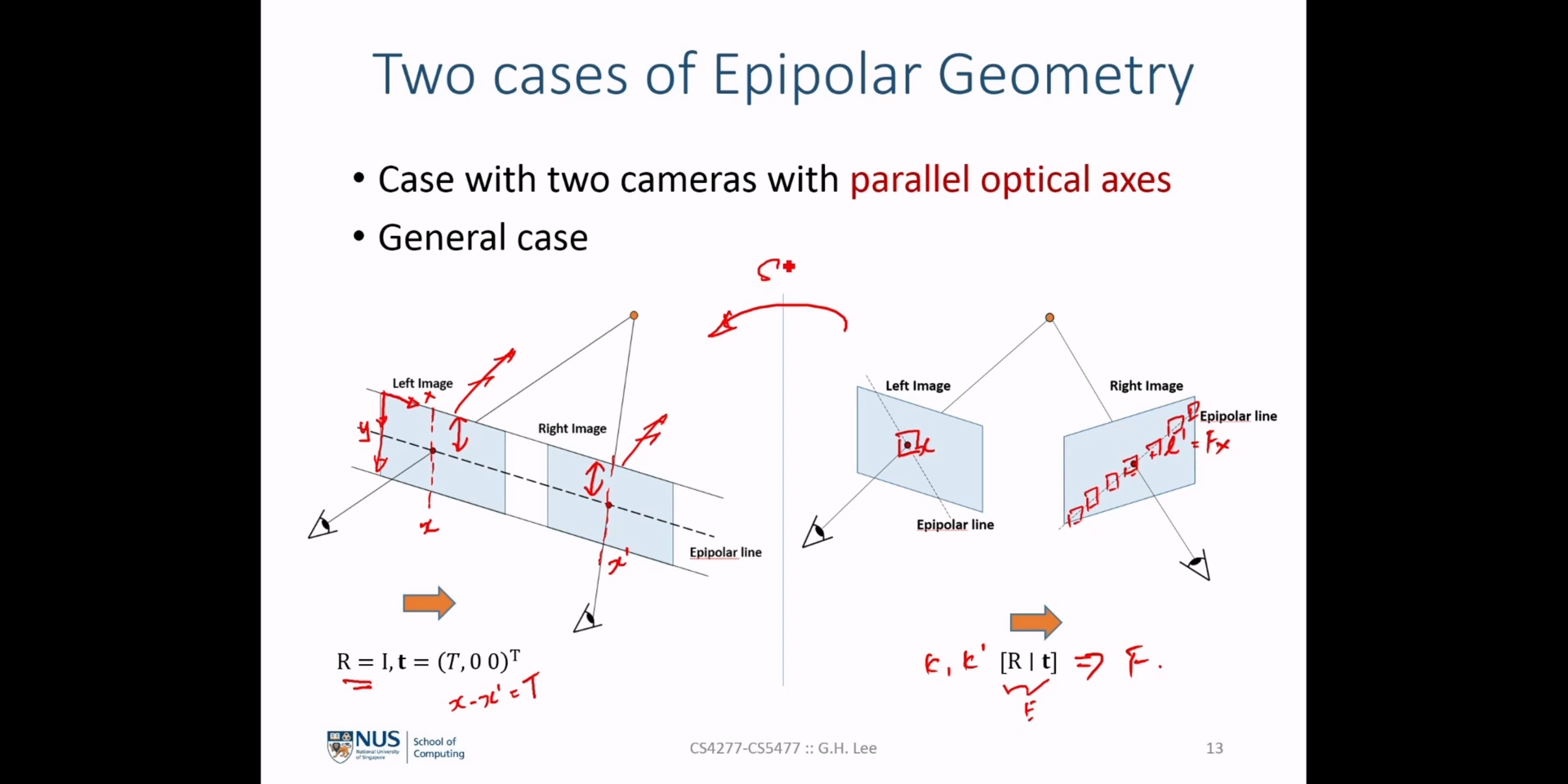
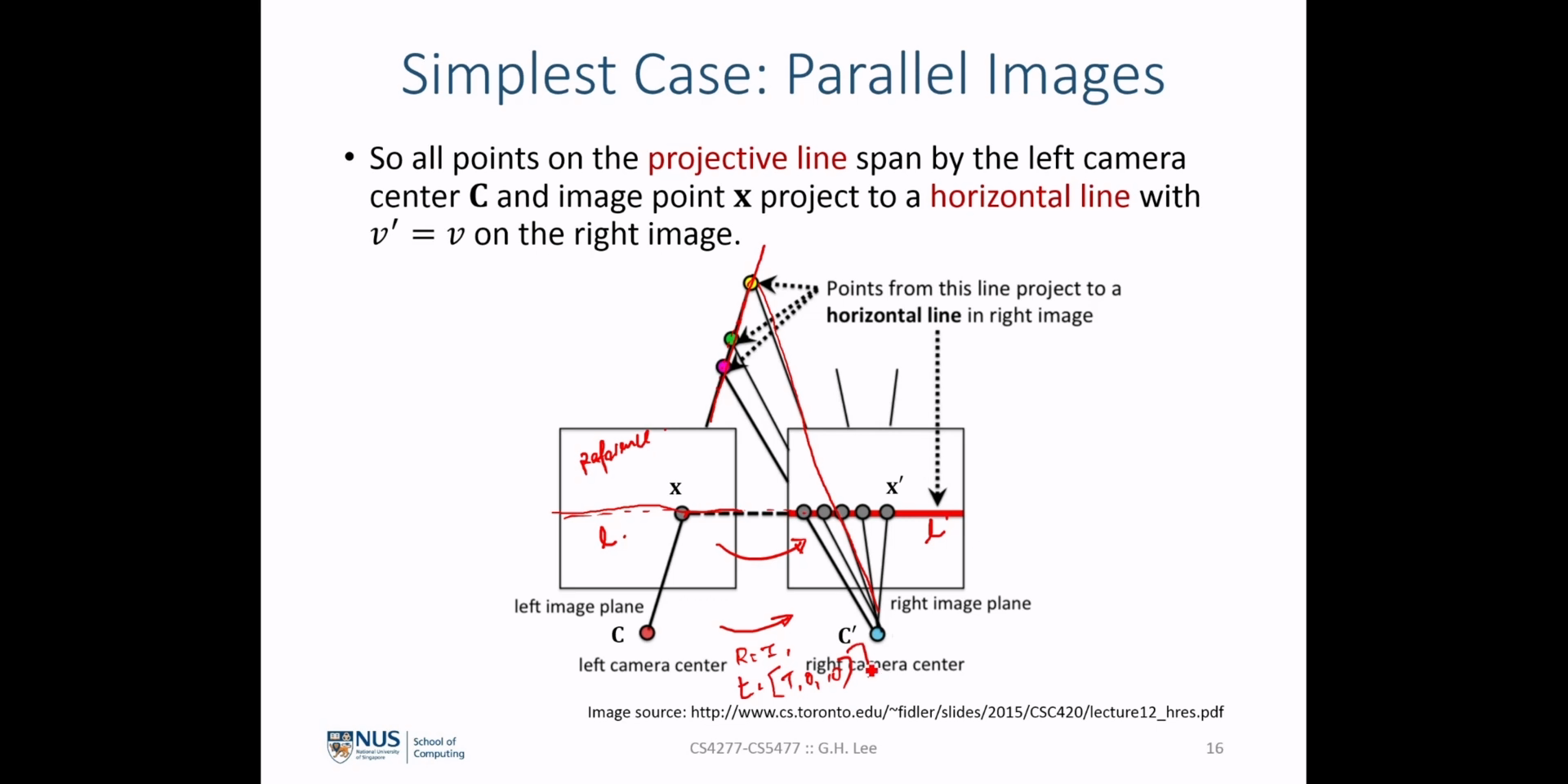
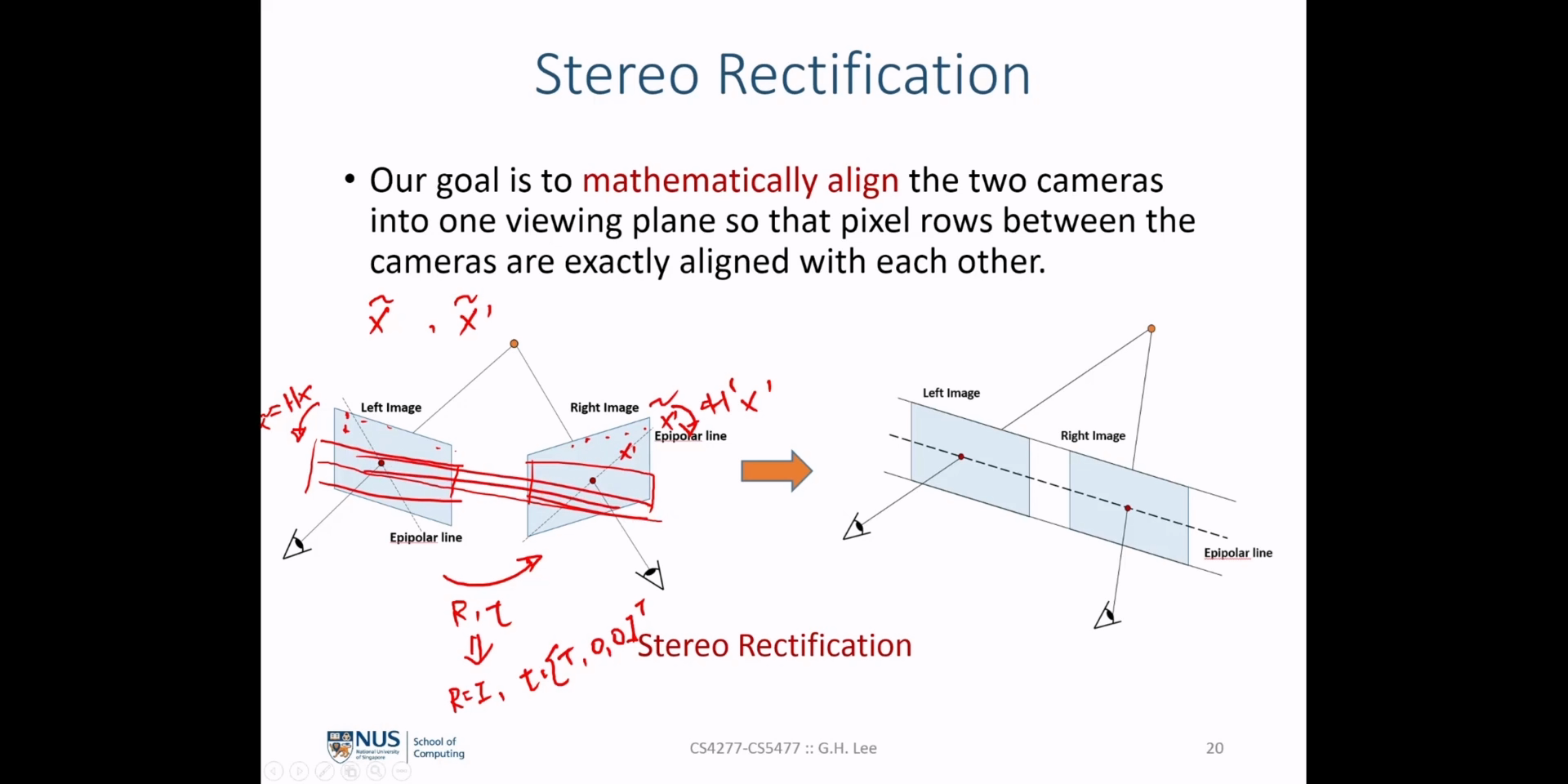
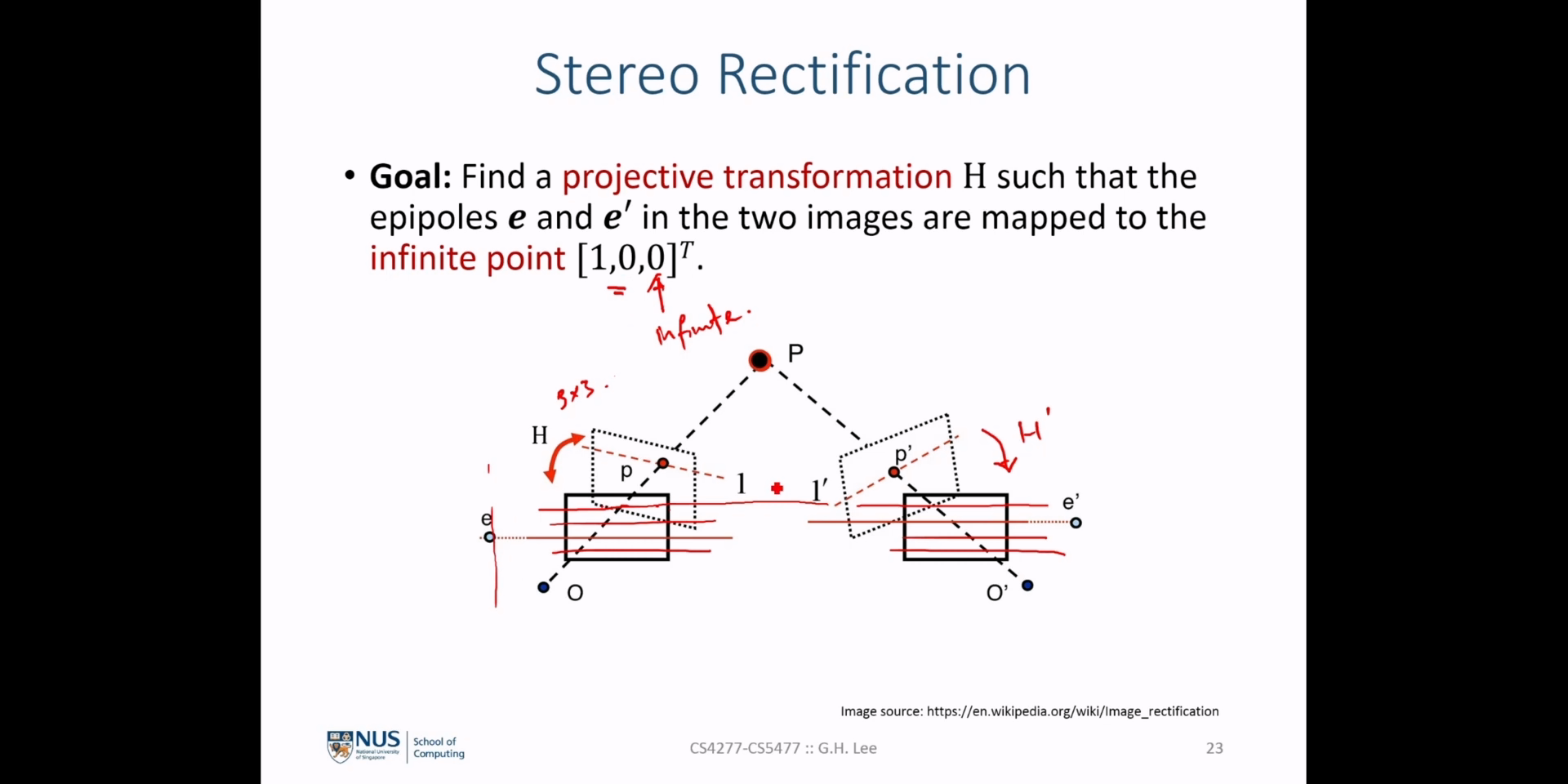
• $$\text{Reference Camera Projection Matrix: } P_{\text{ref}} = K_{text{ref}}[I \vert 0]$$
• $$\text{Camera k Projection Matrix: } P_{k} = K_{k}[R_{k}^{T} \vert -R_{k}^{T}C_{k}]$$

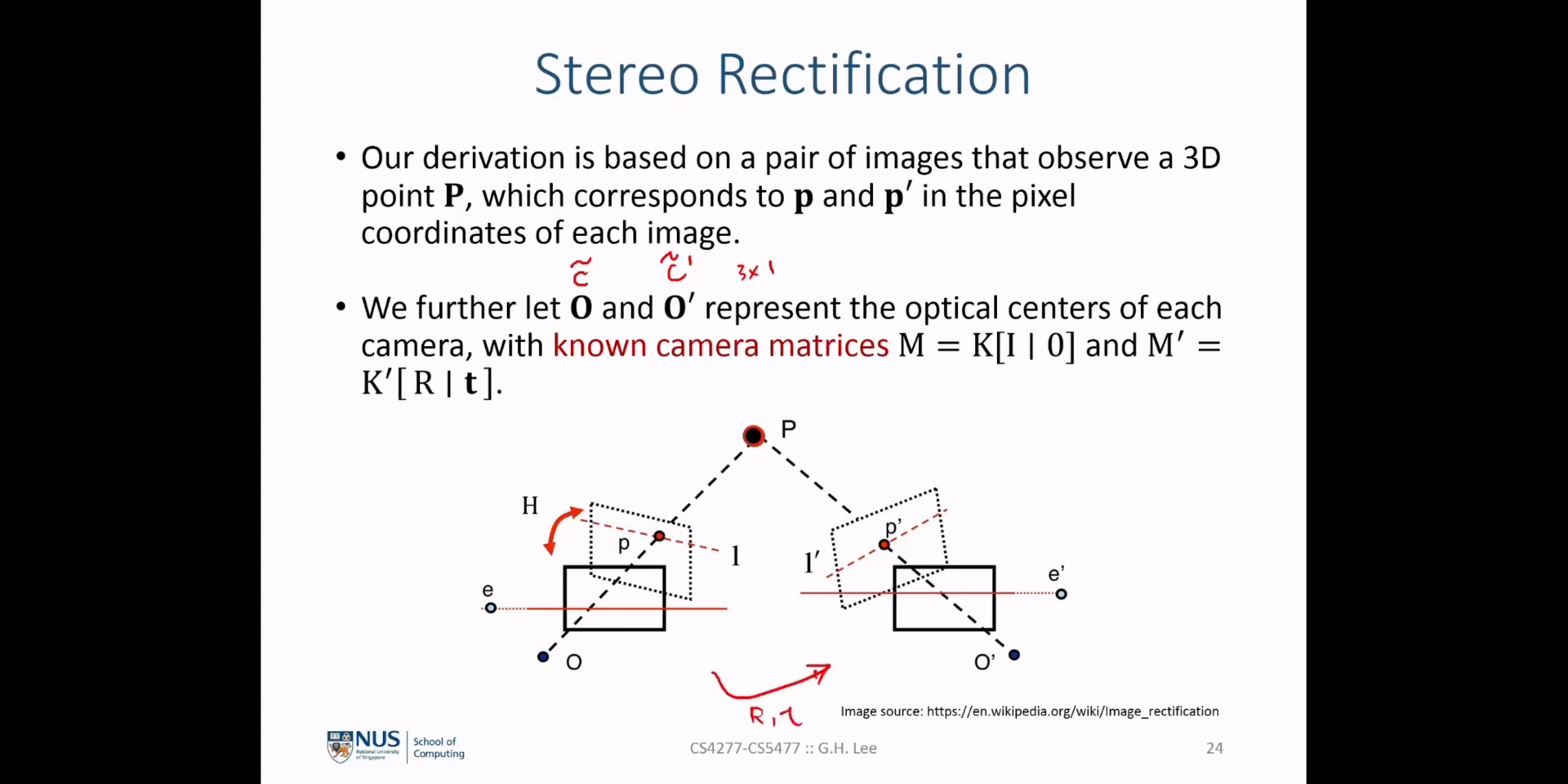
• reference camera의 image plane으로 부터 카메라 $k$ 의 image plane으로 매핑하는 homography를 구해보도록 하겠습니다.
• reference camera image plane 상의 임의의 점을 $x_{\text{ref}}$ 라고 하고 이에 대응되는 $k$ 카메라의 image plane 상의 점을 $x_{k}$ 라고 하겠습니다.

• $$X \text{: A point on the } \Pi_{m} \text{ plane in homogeneous coordinates.}$$
• $$n_{m}^{T}X - d_{m} = 0$$

• Point $X$ 를 $x_{\text{ref}}$ 와 $x_{k}$ 로 투영하면 다음과 같습니다.

• $$\text{Reference Camera: } x_{\text{ref}} = P_{\text{ref}} X = K_{\text{ref}} X$$
• $$\text{Camera K: } x_{k} = P_{k}X = K_{k}(R_{k}^{T}X - R_{k}^{T}C_{k})$$

• 위 $x_{\text{ref}}, x_{k}$ 식을 변형하면 다음과 같습니다.

• $$X = K_{\text{ref}}^{-1} x_{\text{ref}}$$
• $$n_{m}^{T}X = d_{m}$$
• $$n_{m}^{T}K_{\text{ref}}^{-1} x_{\text{ref}} = d_{m}$$
• $$\frac{n_{m}^{T}K_{\text{ref}}^{-1} x_{\text{ref}}}{d_{m}} = 1 \text{ : This term will be used below.}$$
• $$\begin{align} \color{red}{x_{k}} &= K_{k}(R_{k}^{T}K_{\text{ref}}^{-1}x_{\text{ref}} - R_{k}^{T}C_{k}) \\ &= K_{k}R_{k}^{T}K_{\text{ref}}^{-1}x_{\text{ref}} - K_{k}R_{k}^{T}C_{k} \\ &= K_{k}R_{k}^{T}K_{\text{ref}}^{-1}x_{\text{ref}} - K_{k}R_{k}^{T}C_{k} \cdot \frac{n_{m}^{T}K_{\text{ref}}^{-1} x_{\text{ref}}}{d_{m}} \quad (\because \frac{n_{m}^{T}K_{\text{ref}}^{-1} x_{\text{ref}}}{d_{m}} = 1) \\ &= \color{blue}{K_{k}\left( R_{k}^{T} + \frac{R_{k}^{T}C_{k}n_{m}}{d_{m}} \right)K_{\text{ref}}^{-1}} \color{green}{x_{\text{ref}}} \end{align}$$

• 즉, $x_{\text{ref}}$ 를 $x_{k}$ 로 변환하는 Homography인 $H_{\Pi_m, P_k}$ 는 위 파란색 식으로 정의될 수 있습니다.

• $$H_{\Pi_m, P_k} = K_{k}\left( R_{k}^{T} + \frac{R_{k}^{T}C_{k}n_{m}}{d_{m}} \right)K_{\text{ref}}^{-1}$$

Multiple View Geometry 글 목차