(멀티플 뷰 지오메트리) Lecture 12. Generalized cameras

2022, Apr 20    

Multiple View Geometry 글 목차

• 참조 : https://youtu.be/PUgr2VKlNbc?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : https://youtu.be/HuxLHhvdBLY?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : https://youtu.be/E-YXFI5xzNM?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : Multiple View Geometry in Computer Vision

• plucker vector 설명: https://en.wikipedia.org/wiki/Pl%C3%BCcker_coordinates

• 위 그림에서 $d$ 는 direction vector이고 $m$ 은 moment vector를 의미합니다.

• Plucker Vector의 Rigid Transformation을 적용하면 direction vector $q$ 와 moment vector $q'$ 는 다음과 같이 변환될 수 있습니다.

• $$p' = Rp + t$$
• $$q_{\text{transformed}} = Rq$$
• $$\begin{align} q'_{\text{transformed}} &= p' \times q_{\text{transformed}} \\ &= (Rp + t) \times (Rq) \\ &= (Rp) \times (Rq) + t \times (Rq) \\ &= R(p \times q) + t \times (Rq) = Rq' + t \times Rq \\ &= Rq' + [t]_{\times} Rq \end{align}$$

• 따라서 위 슬라이드의 행렬과 같이 표현할 수 있습니다.

• $$\begin{bmatrix} R & 0 \\ [t]_{\times} R & R \end{bmatrix} \begin{bmatrix} q_{1} \\ q'_{1} \end{bmatrix} = \begin{bmatrix} Rq_{1} \\ [t]_{\times} Rq_{1} + Rq'_{1} \end{bmatrix}$$

• 한 쌍의 선이 교차할 때의 필요 충분 조건에 대하여 다루어 보도록 하겠습니다. 필요 충분 조건에 대한 수식 증명을 위해서는 아래 식을 증명해야 합니다.

• $$q_{b}^{T}q'_{a} + q_{b}'^{T}q_{a} = 0$$

• 위 식을 증명하기 위하여 두 선 $L_{a}$ 와 $L_{b}$ 를 다음과 같이 표현해 보겠습니다.

• $$L_{a} = p_{a} + t_{a}q_{a} \quad (t_{a} \text{ is scalar.})$$
• $$L_{b} = p_{b} + t_{b}q_{b} \quad (t_{b} \text{ is scalar.})$$

• 이 때, 두 선 $L_{a}, L_{b}$ 가 교차한다면 다음과 같이 식을 적을 수 있습니다.

• $$p_{a} - p_{b} = t_{b}q_{b} - t_{a}q_{a}$$

• 따라서 벡터 $p_{a} - p_{b}$ 는 $q_{a}, q_{b}$ 벡터의 span된 plane 상에 존재함을 알 수 있습니다.

• 지금부터 $q_{b}^{T}q'_{a} + q_{b}'^{T}q_{a} = q_{a}(q'_{b})^{T} + q_{b}^{T}q'_{a} = 0$ 식에 대한 유도를 진행해 보도록 하겠습니다.

• $$q'_{a} = p_{a} \times q_{a}$$
• $$q'_{b} = p_{b} \times q_{b}$$
• $$q_{a}(q'_{b})^{T} + q_{b}^{T}q'_{a} = q_{a} \cdot (p_{b} \times q_{b}) + q_{b} \cdot (p_{a} \times q_{a})$$

• 스칼라 삼중적 성질을 이용하면 $a \cdot (b \times c) = b \cdot (c \times a)$ 이므로 위 식을 다음과 같이 변형할 수 있습니다.

• $$\begin{align} q_{a}(q'_{b})^{T} + q_{b}^{T}q'_{a} &=q_{a} \cdot (p_{b} \times q_{b}) + q_{b} \cdot (p_{a} \times q_{a}) \\ &= p_{b} \cdot (q_{b} \times q_{a}) + p_{a} \cdot (q_{a} \times q_{b}) \\ &= p_{b} \cdot (q_{b} \times q_{a}) - p_{a} \cdot (q_{b} \times q_{a}) \\ &= (p_{b} - p_{a}) \cdot (q_{b} \times q_{a}) \end{align}$$

• 이 때, $p_{a} - p_{b}$ 는 $q_{a}, q_{b}$ 의 선형 결합으로 span 된 평면 상에 존재하는 벡터임을 앞에서 확인하였습니다. 그리고 $q_{b} \times q_{a}$ 는 $q_{a}, q_{b}$ 에 의해 만들어진 평면과 직교합니다.
• 따라서 $p_{a} - p_{b}$ 는 $q_{a}, q_{b}$ 에 형성되는 평면상에 존재하고 $(q_{b} \times q_{a})$ 는 평면과 직교하므로 $p_{a} - p_{b}$ 와 $(q_{b} \times q_{a})$ 또한 직교합니다. 따라서 다음 식을 만족해야 합니다.

• $$q_{a}(q'_{b})^{T} + q_{b}^{T}q'_{a} = (p_{b} - p_{a}) \cdot (q_{b} \times q_{a}) = 0$$

• 앞에서 두 선이 교차한다는 조건인 $p_{a} - p_{b} = t_{b}q_{b} - t_{a}q_{a}$ 식을 사용하였으므로 두 선이 교차할 때, $q_{a}(q'_{b})^{T} + q_{b}^{T}q'_{a} = 0$ 이 만족함을 확인할 수 있습니다.

• 선들이 교차하는 경우, 선 위의 점들 사이의 벡터는 direction vector에 의해 형성되는 평면에 있기 때문에 스칼라 삼중곱은 0이 되어야 합니다. 따라서 필요 조건을 만족함을 확인하였습니다. 반대로 $q_{a}q'_{b} + q_{b}^{T}q'_{a} = 0$ 인 경우에 앞에서 보인 바와 같이 선들이 교차하므로 충분 조건을 만족합니다. 따라서 필요 충분 조건을 만족함을 알 수 있습니다.

• 앞에서 유도한 식을 이용하여 위 슬라이드의 식을 전개해 보도록 하겠습니다.

• $$q_{a}(q'_{b})^{T} + q_{b}^{T}q'_{a} = q_{b}^{T}q'_{a} + q_{a}(q'_{b})^{T} \Rightarrow q_{2}^{T}q'_{1} + q_{1}(q'_{2})^{T} = 0$$
• $$\Rightarrow q_{2}^{T}([t]_{\times} Rq_{1} + Rq'_{1}) +(q'_{2})^{T}q_{1} = 0 \quad (\because q'_{1} = [t]_{\times} Rq_{1} + Rq'_{1})$$
• $$\therefore \quad q_{2}^{T}[t]_{\times} Rq_{1} + q_{2}^{T}Rq'_{1} + (q'_{2})^{T}q_{1} = 0$$

• 따라서 행렬로 표현하면 다음과 같이 표현할 수 있습니다.

• $$\begin{bmatrix}q_{2} \\ q'_{2} \end{bmatrix}^{T} \begin{bmatrix} E & R \\ R & 0 \end{bmatrix} \begin{bmatrix} q_{1} \\ q'_{1} \end{bmatrix} = 0$$

• 이전 슬라이드에서 유도된 식을 Generalized epipolar geometry라고 하며 이 식의 의미와 형태는 앞선 강의에서 다룬 Epipolar geometry와 일치합니다.
• 이와 같은 이유로 $\begin{bmatrix} E & R \\ R & 0 \end{bmatrix}$ 는 generalized essential matrix로 불립니다.
• 다음 슬라이드의 내용과 연결 짓기 위하여 Generalized epipolar geometry의 식을 아래와 같이 풀어서 써보겠습니다.

• $$q_{1} = \begin{bmatrix} q_{11} \\ q_{12} \\ q_{13} \end{bmatrix}$$
• $$q'_{1} = \begin{bmatrix} q'_{11} \\ q'_{12} \\ q'_{13} \end{bmatrix}$$
• $$\therefore \begin{bmatrix} q_{1} \\ q'_{1} \end{bmatrix} = \begin{bmatrix} q_{11} \\ q_{12} \\ q_{13} \\ q'_{11} \\ q'_{12} \\ q'_{13} \end{bmatrix}$$
• $$\begin{bmatrix} E & R \\ R & 0 \end{bmatrix} = \begin{bmatrix}e_{11} & e_{12} & e_{13} & r_{11} & r_{12} & r_{13} \\ e_{21} & e_{22} & e_{23} & r_{21} & r_{22} & r_{23} \\ e_{31} & e_{32} & e_{33} & r_{31} & r_{32} & r_{33} \\ r_{11} & r_{12} & r_{13} & 0 & 0 & 0 \\ r_{21} & r_{22} & r_{23} & 0 & 0 & 0 \\ r_{31} & r_{32} & r_{33} & 0 & 0 & 0 \end{bmatrix}$$
• $$\begin{align} \begin{bmatrix} q_{2} \\ q'_{2} \end{bmatrix}^{T} \begin{bmatrix} E & R \\ R & 0 \end{bmatrix} \begin{bmatrix} q_{1} \\ q'_{1} \end{bmatrix} &= \begin{bmatrix} q_{21} & q_{22} & q_{23} & q'_{21} & q'_{22} & q'_{23} \end{bmatrix} \begin{bmatrix}e_{11} & e_{12} & e_{13} & r_{11} & r_{12} & r_{13} \\ e_{21} & e_{22} & e_{23} & r_{21} & r_{22} & r_{23} \\ e_{31} & e_{32} & e_{33} & r_{31} & r_{32} & r_{33} \\ r_{11} & r_{12} & r_{13} & 0 & 0 & 0 \\ r_{21} & r_{22} & r_{23} & 0 & 0 & 0 \\ r_{31} & r_{32} & r_{33} & 0 & 0 & 0 \end{bmatrix}\begin{bmatrix} q_{11} \\ q_{12} \\ q_{13} \\ q'_{11} \\ q'_{12} \\ q'_{13} \end{bmatrix} \\ &= q'_{1 1} q_{2 1} r_{11} + q'_{1 1} q_{2 2} r_{21} + q'_{1 1} q_{2 3} r_{31} + q'_{1 2} q_{2 1} r_{12} \\ &+ q'_{1 2} q_{2 2} r_{22} + q'_{1 2} q_{2 3} r_{32} + q'_{1 3} q_{2 1} r_{13} + q'_{1 3} q_{2 2} r_{23} \\ &+ q'_{1 3} q_{2 3} r_{33} + q'_{2 1} q_{1 1} r_{11} + q'_{2 1} q_{1 2} r_{12} + q'_{2 1} q_{1 3} r_{13} \\ &+ q'_{2 2} q_{1 1} r_{21} + q'_{2 2} q_{1 2} r_{22} + q'_{2 2} q_{1 3} r_{23} + q'_{2 3} q_{1 1} r_{31} \\ & + q'_{2 3} q_{1 2} r_{32} + q'_{2 3} q_{1 3} r_{33} + e_{11} q_{1 1} q_{2 1} + e_{12} q_{1 2} q_{2 1} \\ & + e_{13} q_{1 3} q_{2 1} + e_{21} q_{1 1} q_{2 2} + e_{22} q_{1 2} q_{2 2} + e_{23} q_{1 3} q_{2 2} \\ &+ e_{31} q_{1 1} q_{2 3} + e_{32} q_{1 2} q_{2 3} + e_{33} q_{1 3} q_{2 3} \end{align}$$

• 이전 슬라이드에서 $q_{1}, q'_{1}, q_{2}, q'_{2}$ 는 알고 있는 값인 반면 $\begin{bmatrix} E & R \\ R & 0 \end{bmatrix}$ 에 정의된 $E, R$ 의 각 원소는 미지수인 상황입니다. 이전 강의에서 살펴본 바와 같이 Epipolar Geometry에서 Essential Matrix의 값을 추정해야 하는 상황이거나 Levenberg-Marquardt 알고리즘을 이용하여 R 값을 추정하는 내용등을 상기시키면 이해가 될 것입니다.
• 17 페이지 슬라이드에서 최종적으로 풀어쓴 식에서 $r_{ij}$ 또는 $e_{ij}$ 가 미지수이고 이 미지수에 곱해진 계수들을 분리하여 식을 정리해 보고자 합니다. 이 때, 계수들은 $a$ 로 표시하고 미지수는 $g$ 로 표시하겠습니다. 다음과 같습니다.

• $$a = \begin{bmatrix}q_{1 1} q_{2 1} \\ q_{1 2} q_{2 1} \\ q_{1 3} q_{2 1} \\ q_{1 1} q_{2 2} \\ q_{1 2} q_{2 2} \\ q_{1 3} q_{2 2} \\ q_{1 1} q_{2 3} \\ q_{1 2} q_{2 3} \\ q_{1 3} q_{2 3} \\ q'_{1 1} q_{2 1} + q'_{2 1} q_{1 1} \\ q'_{1 2} q_{2 1} + q'_{2 1} q_{1 2} \\ q'_{1 3} q_{2 1} + q'_{2 1} q_{1 3} \\ q'_{1 1} q_{2 2} + q'_{2 2} q_{1 1} \\ q'_{1 2} q_{2 2} + q'_{2 2} q_{1 2} \\ q'_{1 3} q_{2 2} + q'_{2 2} q_{1 3} \\ q'_{1 1} q_{2 3} + q'_{2 3} q_{1 1} \\ q'_{1 2} q_{2 3} + q'_{2 3} q_{1 2} \\ q'_{1 3} q_{2 3} + q'_{2 3} q_{1 3} \end{bmatrix}, \quad g = \begin{bmatrix}e_{11}\\ e_{12}\\ e_{13}\\ e_{21}\\ e_{22}\\ e_{23}\\ e_{31}\\ e_{32}\\ e_{33}\\ r_{11}\\ r_{12}\\ r_{13}\\ r_{21}\\ r_{22}\\ r_{23}\\ r_{31}\\ r_{32}\\ r_{33}\end{bmatrix}$$

• 위 식에서 $\begin{bmatrix} q_{2} \\ q'_{2} \end{bmatrix}^{T} \begin{bmatrix} E & R \\ R & 0 \end{bmatrix} \begin{bmatrix} q_{1} \\ q'_{1} \end{bmatrix} = a^{T}g = 0$ 을 만족해야 하므로 아래의 식과 같이 적을 수 있습니다.

• $$\begin{align} a^{T}g &= \begin{bmatrix}q_{1 1} q_{2 1} \\ q_{1 2} q_{2 1} \\ q_{1 3} q_{2 1} \\ q_{1 1} q_{2 2} \\ q_{1 2} q_{2 2} \\ q_{1 3} q_{2 2} \\ q_{1 1} q_{2 3} \\ q_{1 2} q_{2 3} \\ q_{1 3} q_{2 3} \\ q'_{1 1} q_{2 1} + q'_{2 1} q_{1 1} \\ q'_{1 2} q_{2 1} + q'_{2 1} q_{1 2} \\ q'_{1 3} q_{2 1} + q'_{2 1} q_{1 3} \\ q'_{1 1} q_{2 2} + q'_{2 2} q_{1 1} \\ q'_{1 2} q_{2 2} + q'_{2 2} q_{1 2} \\ q'_{1 3} q_{2 2} + q'_{2 2} q_{1 3} \\ q'_{1 1} q_{2 3} + q'_{2 3} q_{1 1} \\ q'_{1 2} q_{2 3} + q'_{2 3} q_{1 2} \\ q'_{1 3} q_{2 3} + q'_{2 3} q_{1 3} \end{bmatrix}^{T}\begin{bmatrix}e_{11}\\ e_{12}\\ e_{13}\\ e_{21}\\ e_{22}\\ e_{23}\\ e_{31}\\ e_{32}\\ e_{33}\\ r_{11}\\ r_{12}\\ r_{13}\\ r_{21}\\ r_{22}\\ r_{23}\\ r_{31}\\ r_{32}\\ r_{33}\end{bmatrix} \\ &= q'_{1 1} q_{2 1} r_{11} + q'_{1 1} q_{2 2} r_{21} + q'_{1 1} q_{2 3} r_{31} + q'_{1 2} q_{2 1} r_{12} \\ &+ q'_{1 2} q_{2 2} r_{22} + q'_{1 2} q_{2 3} r_{32} + q'_{1 3} q_{2 1} r_{13} + q'_{1 3} q_{2 2} r_{23} \\ &+ q'_{1 3} q_{2 3} r_{33} + q'_{2 1} q_{1 1} r_{11} + q'_{2 1} q_{1 2} r_{12} + q'_{2 1} q_{1 3} r_{13} \\ &+ q'_{2 2} q_{1 1} r_{21} + q'_{2 2} q_{1 2} r_{22} + q'_{2 2} q_{1 3} r_{23} + q'_{2 3} q_{1 1} r_{31} \\ & + q'_{2 3} q_{1 2} r_{32} + q'_{2 3} q_{1 3} r_{33} + e_{11} q_{1 1} q_{2 1} + e_{12} q_{1 2} q_{2 1} \\ & + e_{13} q_{1 3} q_{2 1} + e_{21} q_{1 1} q_{2 2} + e_{22} q_{1 2} q_{2 2} + e_{23} q_{1 3} q_{2 2} \\ &+ e_{31} q_{1 1} q_{2 3} + e_{32} q_{1 2} q_{2 3} + e_{33} q_{1 3} q_{2 3} \end{align}$$

• 따라서 $\begin{bmatrix} q_{2} \\ q'_{2} \end{bmatrix}^{T} \begin{bmatrix} E & R \\ R & 0 \end{bmatrix} \begin{bmatrix} q_{1} \\ q'_{1} \end{bmatrix} = a^{T}g$ 가 됨을 알 수 있습니다.

• 16 페이지의 식을 참조하면 위 슬라이드의 GEC (Generalized Epipolar Geometry Contraints)를 정의할 수 있습니다.

• $$q_{2}^{T}[t]_{\times} Rq_{1} + q_{2}^{T}Rq'_{1} + (q'_{2})^{T}q_{1} = 0$$
• $$\Rightarrow q_{2}^{T} E q_{1} + q_{2}^{T}Rq'_{1}+ (q'_{2})^{T}q_{1} = 0$$
• $$\Rightarrow x_{i}^{T} E x'_{i} + x_{i}^{T}R(v'_{i} \times x'_{i})+ (v_{i} \times x_{i})^{T}x'_{i} = 0$$

• 만약 $E = 0, R = I$ 라면 다음과 같이 GEC의 해를 만족합니다.

• $$\begin{align} x_{i}^{T} (v_{i} \times x'_{i}) + (v_{i} \times x_{i})^{T} x'_{i} &= (x'_{i})^{T}(x_{i} \times v_{i}) + (v_{i} + x_{i})^{T}x'_{i} \quad (\because a \cdot (b \times c) = c \cdot (a \times b)) \\ &= -(x'_{i})^{T} (v_{i} \times x_{i}) + (v_{i} \times x_{i})^{T} x'_{i} \quad (\because a \times b = -b \times a) \\ &= 0 \end{align}$$

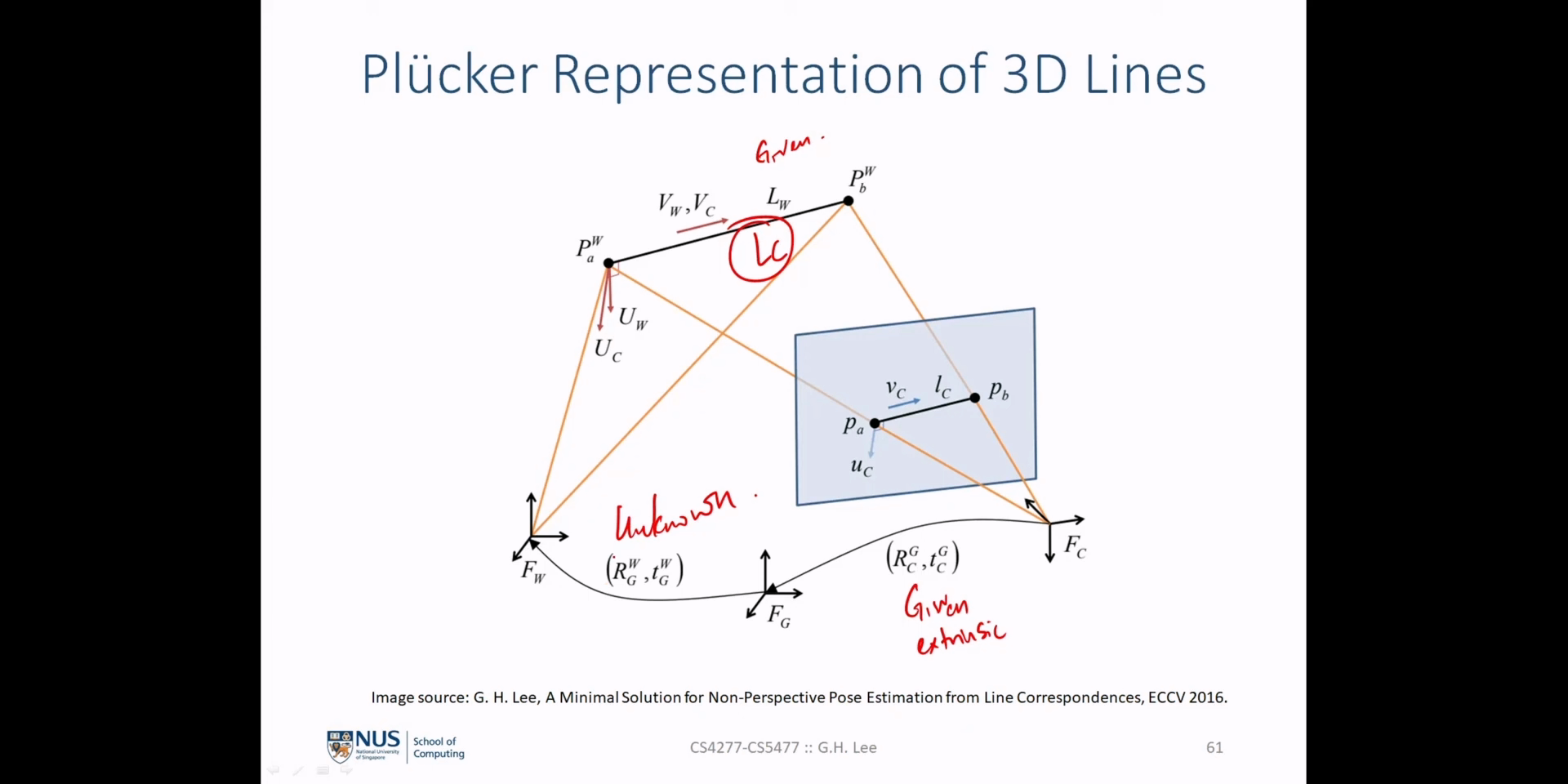
• 위 슬라이드에서 $L_{C} = \tau_{W}^{C}L_{W}$ 를 변환할 때, $\tau_{W}^{C}$ 는 $L_{W} = [U_{W}^{T} V_{W}^{T}]$ 를 $L_{C} = [U_{C}^{T} V_{C}^{T}]$ 로 변환하기 위해 다음과 같이 정의 됩니다.

• $$P_{C} = R_{W}^{C} P_{W} + t_{W}^{C}$$
• $$\begin{align} U_{C} &= P_{C} \times V_{C} \\ &= (R_{W}^{C} P_{W} + t_{W}^{C}) \times (R_{W}^{C}V_{W}) \\ &= (R_{W}^{C}P_{W}) \times (R_{W}^{C}V_{W}) + t_{W}^{C} \times (R_{W}^{C}V_{W}) \\ &= (R_{W}^{C})(P_{W} \times V_{W}) + t_{W}^{C} \times (R_{W}^{C}V_{W}) \\ &= R_{W}^{C} U_{W} + t_{W}^{C} \times (R_{W}^{C} V_{W}) \\ &= R_{W}^{C} U_{W} + (\lfloor t_{W}^{C} \rfloor_{\times}R_{W}^{C})V_{W} \end{align}$$
• $$V_{C} = R_{W}^{C}V_{W}$$
• $$\therefore L_{C} = \tau_{W}^{C}L_{W} = \begin{bmatrix} R_{W}^{C} & \lfloor t_{W}^{C} \rfloor_{\times}R_{W}^{C} \\ 0_{3 \times 3} & R_{W}^{C} \end{bmatrix} L_{W}$$

Multiple View Geometry 글 목차