(멀티플 뷰 지오메트리) Lecture 4. Robust homography estimation
2022, Apr 20
- 참조 : https://youtu.be/W8vgVoQdwAM?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
- 참조 : https://youtu.be/v3322cNhCTk?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
- 참조 : Multiple View Geometry in Computer Vision
- 이번 강의를 이해하기 위해 아래 사전 지식이 필요합니다.
least squrares: https://gaussian37.github.io/math-la-least_squares/rank: https://gaussian37.github.io/math-la-rank/SVD (Singular Value Decomposition): https://gaussian37.github.io/math-la-svd/
























- 안정적인
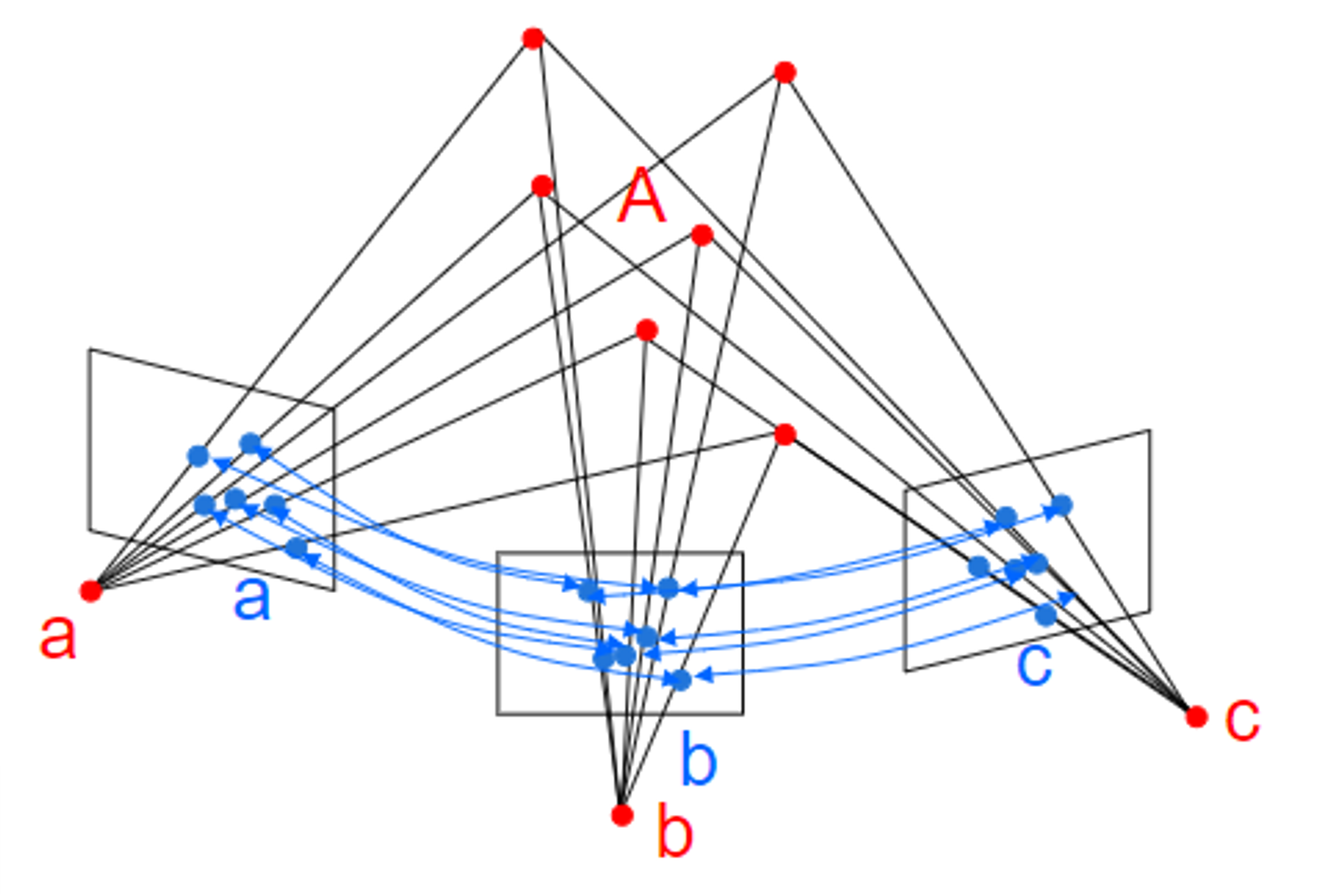
DLT알고리즘을 구현하기 위하여Nomalied DLT알고리즘을 필수적으로 사용하기를 권장하며 전체적인 알고리즘의 순서는 위 표와 같습니다. - 4개 이상의 2D 포인트 간의 대응 \(x_{i} \leftrightarrow x_{i}'\) 이 주어지면
2D homography행렬 \(H\) 를 구할 수 있으며 구 역할은 \(x_{i}' = H x_{i}\) 와 같습니다.
normalized DLT알고리즘은 다음과 같습니다.
- ① 각 대응된 포인트 \(x_{i} \leftrightarrow x_{i}'\) 를 \(T_{\text{norm}}\) 과 \(T_{\text{norm}}'\) 각각을 이용하여
normalize를 적용합니다. \(T_{\text{norm}}\) 은 \(x_{i}\) 를normalize하는 변환 행렬이며 \(T_{\text{norm}}'\) 는 \(x_{i}'\) 를normalize합니다. 즉, 각2D image coordinate에서 각 포인트 값에 맞게normalize하게 됩니다. 변환 행렬은 다음과 같이 구성됩니다.
- \[T_{\text{norm}} = \begin{bmatrix} s & 0 & -s c_{x} \\ 0 & s & -s c_{y} \\ 0 & 0 & 1 \end{bmatrix}\]
- \[c = (c_{x}, c_{y}) = \text{centroid of all data points}\]
- \[s = \frac{\sqrt{2}}{\bar{d}}\]
- \[\bar{d} = \text{mean distance of all points from centroid}\]
- 위 식에서 \(s\) 는 평균
distance를 \(sqrt{2} = \sqrt{ (1 - 0)^{2} + (1 - 0)^{2} }\) 에 나눔으로써 \(x, y\) 방향으로 거리가 1이고 원점으로 부터distance가 \(sqrt{2}\) 인 공간으로normalization하는scale값으로 사용 되었습니다. - 따라서 \(T_{\text{norm}}\) 를 이용하여
scale변화와centroid까지의 이동 까지 반영하여normalize할 수 있습니다.
- ② 앞에서 다룬 방식과 동일하게
DLT알고리즘을 사용하여 \(\tilde{x}_{i} \leftrightarrow \tilde{x}_{i}'\) 간 변환을 하는homography\(\tilde{H}\) 를 구할 수 있습니다.normalize된 공간에서의homography이기 때문에 \(\tilde{H}\) 로 표현합니다.
- ③ 실제 사용해야 하는
homography는image coordinate의homography인 \(H\) 이므로 다음과 같이 구할 수 있습니다.
- \[H = T_{\text{norm}}'^{-1} \tilde{H} T_{\text{norm}}\]
- \[T_{\text{norm}} : \text{image space} \to \text{normalized space}\]
- \[\tilde{H} : \text{normalized space homography}\]
- \[T_{\text{norm}}'^{-1} : \text{normalized space} \to \text{image space}\]
- 따라서 \(H\) 는
image space에서 적용하는homography가 되며 그 내부 과정을 살펴보면image space → normalized space → normalized space homography → image space순서로 변환 과정이 누적됩니다.








- 어떤 함수 \(f(x)\) 를
테일러 급수로 근사화 하면 다음과 같이 나타낼 수 있습니다. 아래 \(p_{n}(x)\) 가 \(n\) 차항 까지 근사화 한 것이고 \(n \to \infty\) 가 되면 \(f(x) = p_{\infty}(x)\) 를 만족하는 것이테일러 급수의 성질입니다.
- \[f(x) = p_{\infty}(x)\]
- \[\begin{align} f(x) &= p_{n}(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x-a)^{2} + \cdots + \frac{f^{n}(a)}{n!}(x-a)^{n} \\ &= \sum_{k=0}^{n} \frac{f^{k}(a)}{k!}(x-a)^{k} \end{align}\]
테일러 급수를 변화량 \(h\) 와 함께 표현하면 다음과 같이 나타낼 수 있으며 위 식과 표현에 차이만 있을 뿐 의미는 같습니다.
- \[\begin{align} f(a + h) &= f(a) + f'(a)h + \frac{f^{2}(a)}{2!}h^{2} + \frac{f^{3}(a)}{3!}h^{3} + \cdots + \frac{f^{n}(a)}{n!}h^{n} \\ &= \sum_{k=0}^{n} \frac{f^{k}(a)}{k!}h^{k} \end{align}\]



