(멀티플 뷰 지오메트리) Lecture 5. Camera models and calibration
2022, Apr 20
- 참조 : https://youtu.be/sae97GVUXcg?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
- 참조 : https://youtu.be/oyGCk4idsaU?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
- 참조 : https://youtu.be/77kpTQUfIBg?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
- 참조 : Multiple View Geometry in Computer Vision
- 이번 강의에서는 카메라 모델과 카메라 캘리브레이션에 관한 내용을 다루어 보도록 하겠습니다.




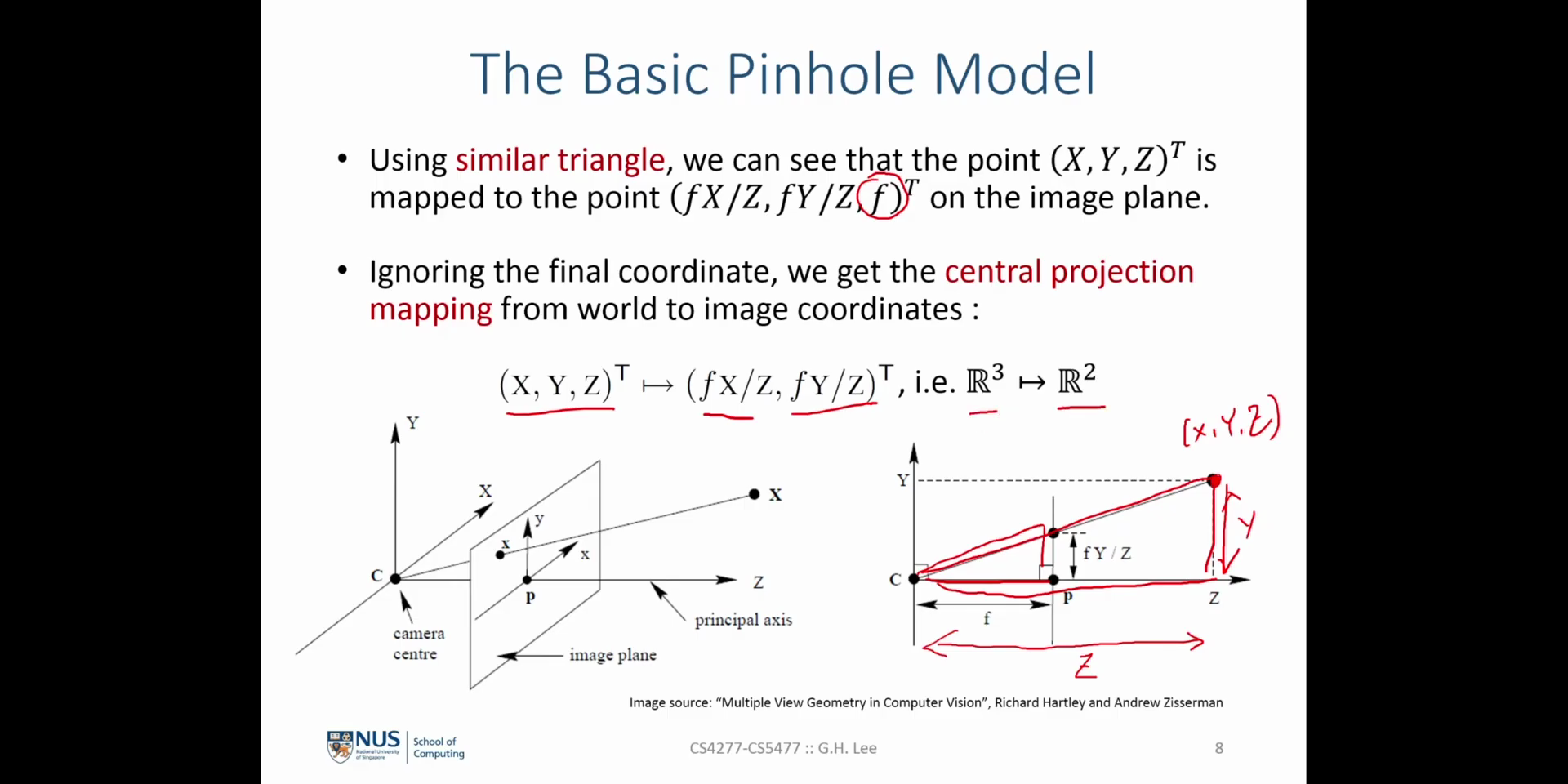
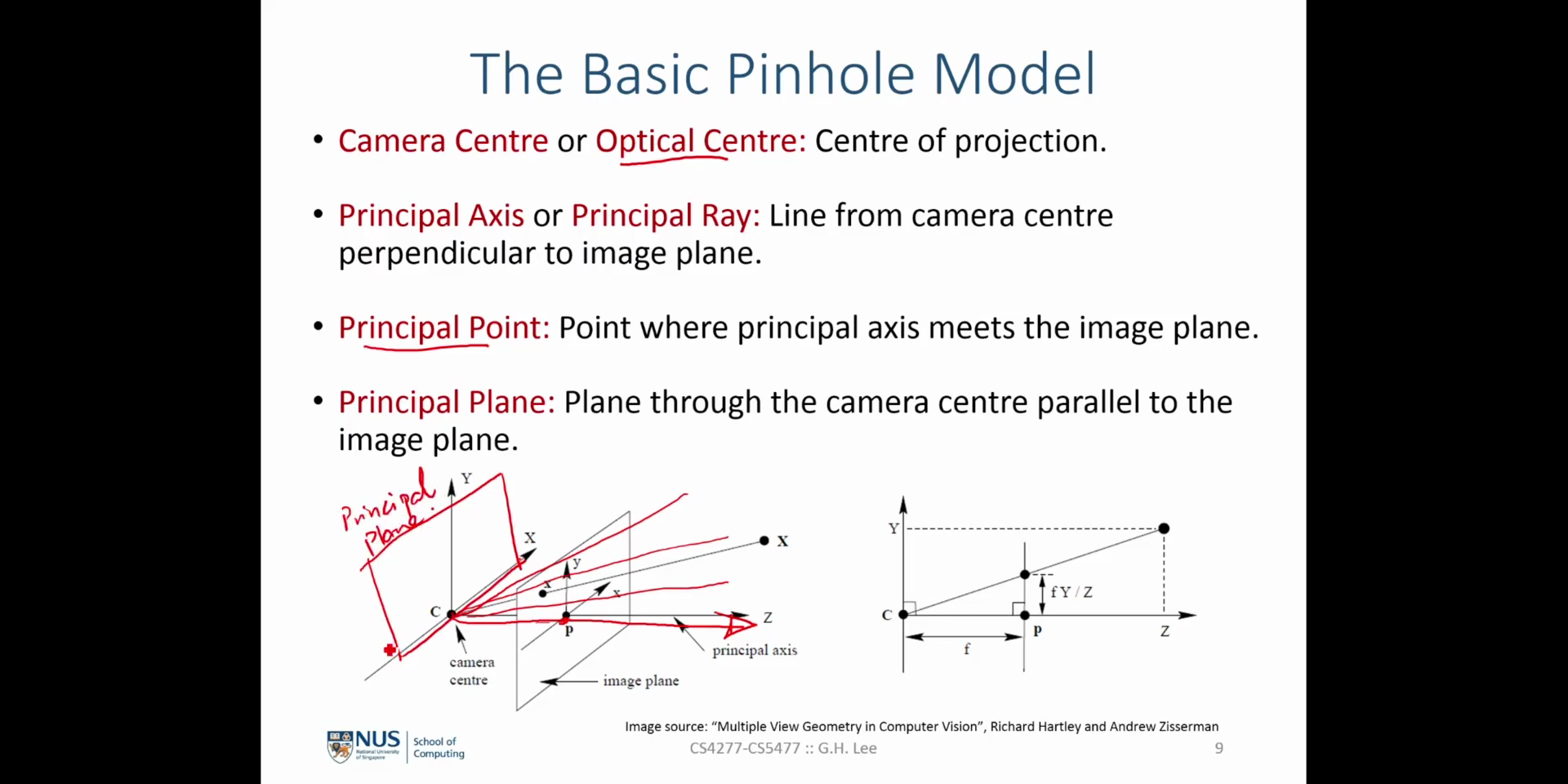




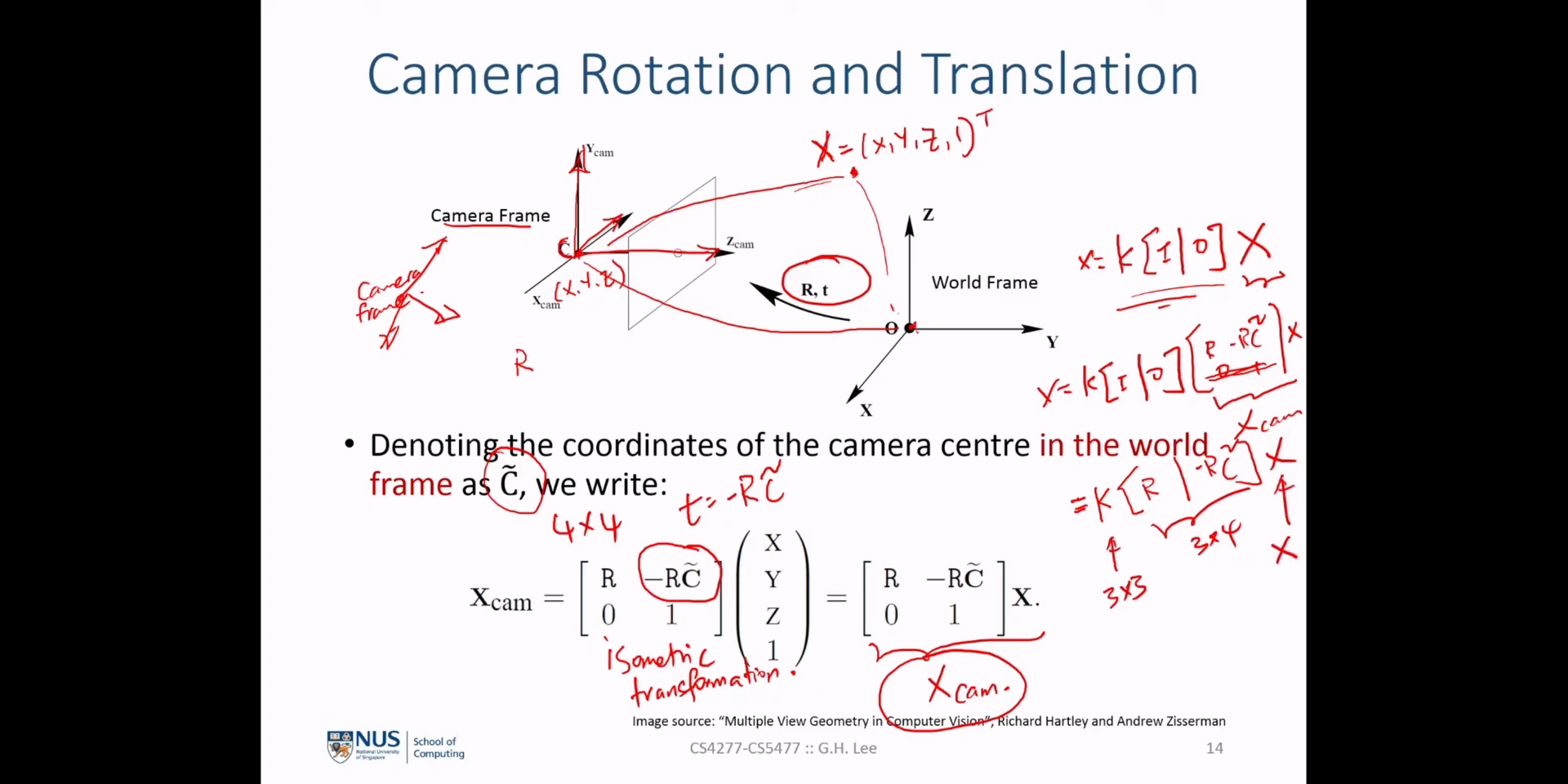
- 위 슬라이드에서 \(\tilde{C}\) 는
world 좌표계기준에서camera 좌표계의 중점을 나타냅니다. 따라서world 좌표계의 중점에서camera 좌표계중점까지의 관계를 나타내는 벡터는 \(0 - \tilde{C} = -\tilde{C}, \quad (\text{world_coordinate} \to \text{camera_coordinate})\) 로 나타낼 수 있습니다.


































orthographic projection에 대한 이해를 위하여 아래 링크에서의 그림 자료를 참조 하였습니다.- 링크 : https://cvlearnblog.notion.site/Perspective-projection-orthographic-projection-glm-perspective-3638c48333ad4ce4b4c26787272e6424
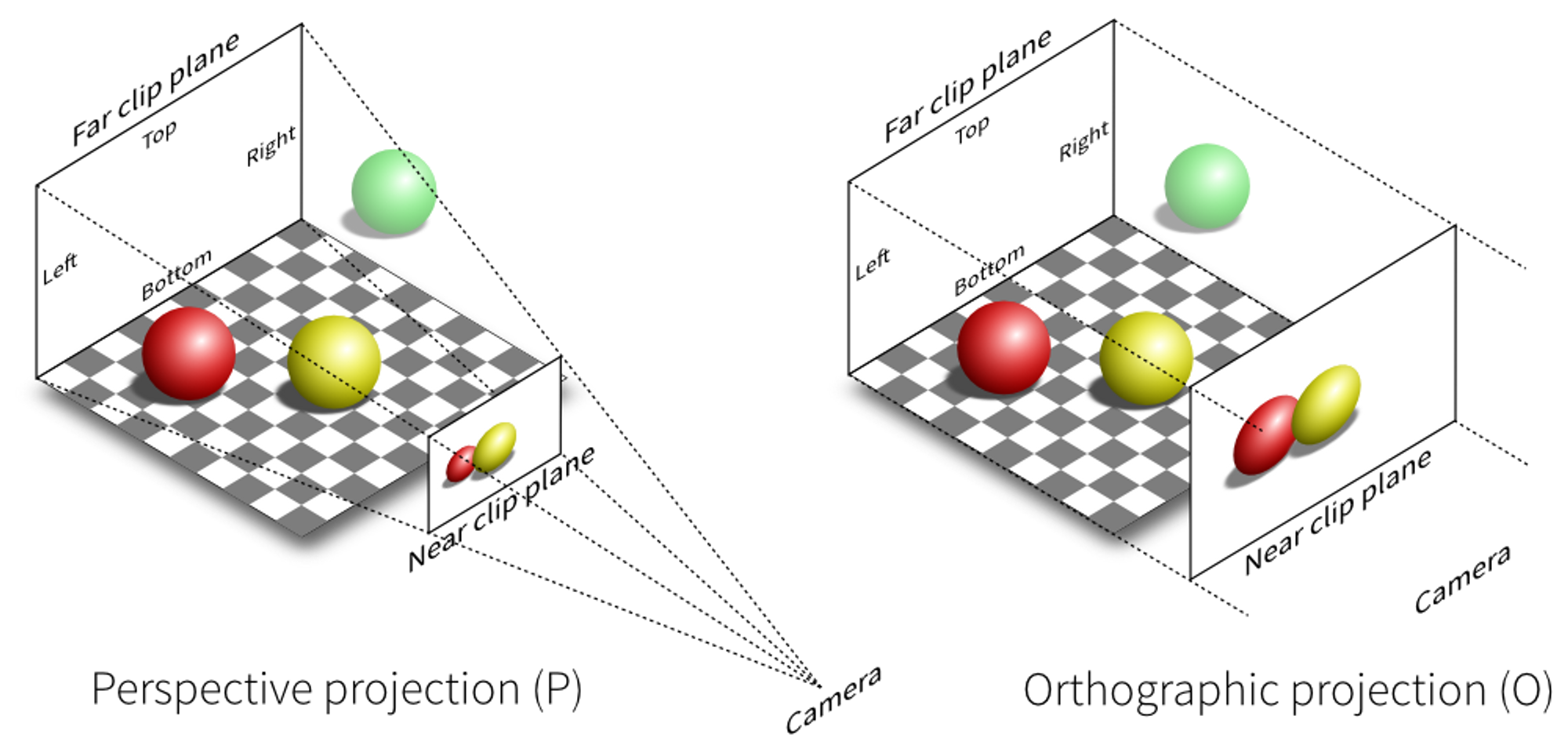
- 위 그림의 왼쪽은
Perspective Projection의 예시로 흔히 많이 보는 이미지의 형상입니다. 빨간색 공과 노란색 공의 크기가 같으나 노란색 공이 카메라에 더 가깝게 위치해 있기 때문에 노란색 공이 더 크게 보입니다. 반면 오른쪽은Orthographic Projection으로 3차원을 2차원에 그대로 투영하기 때문에 빨간색 공과 노란색 공의 크기가 같게 표현됩니다. 이와 같은 방식은 3D 모형을 2D 도면으로 나타낼 때 많이 사용합니다.