(멀티플 뷰 지오메트리) Lecture 6. Single view metrology

2022, Apr 20    

Multiple View Geometry 글 목차

• 참조 : https://youtu.be/D6Pm5id_LK4?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : https://youtu.be/XSflleJr4qM?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : https://youtu.be/9TuPY67JBpo?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : Multiple View Geometry in Computer Vision

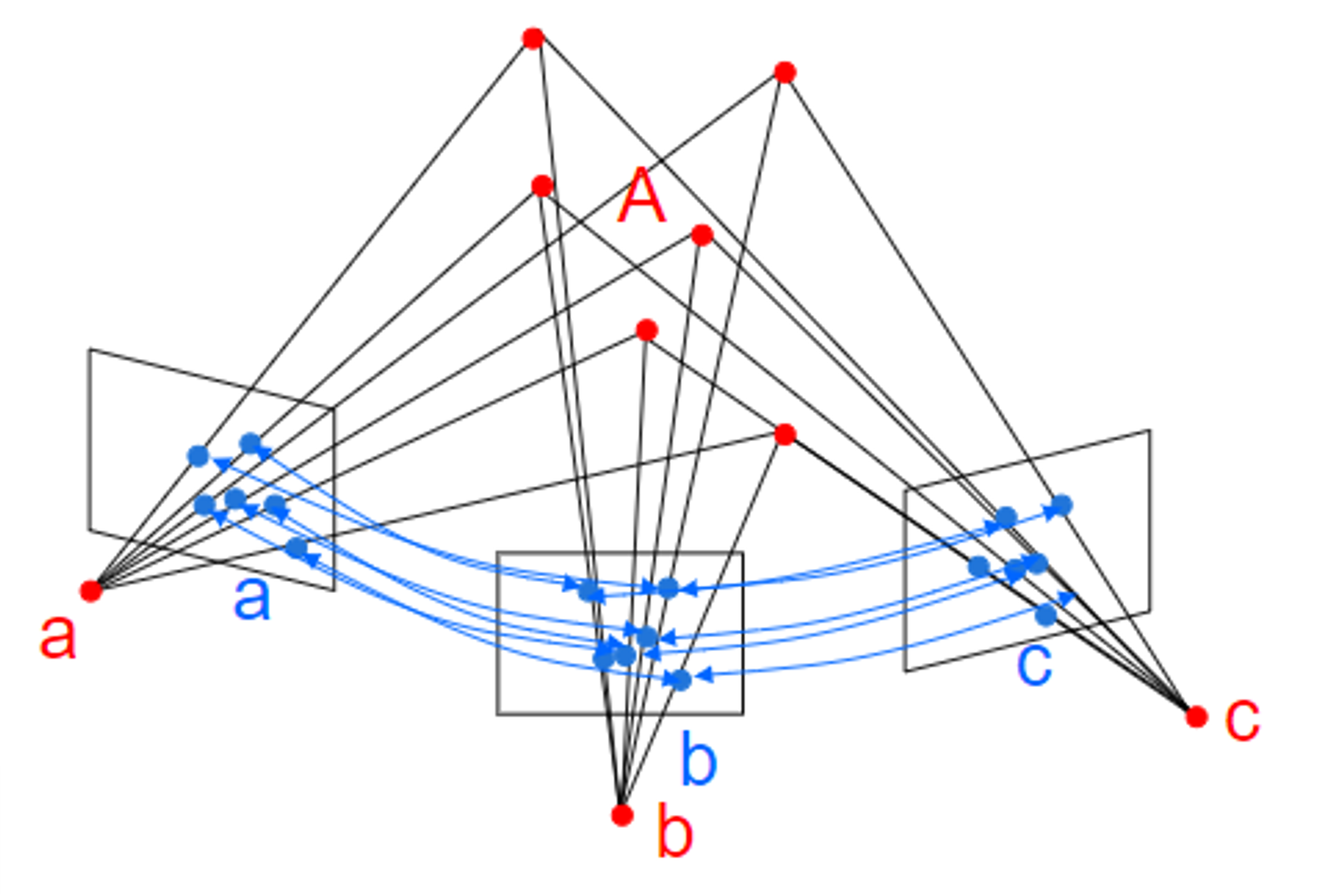
• 이번 챕터의 이름은 The Importance of the Camera Centre로 카메라 센터점에 관하여 다룹니다.
• 앞에서 다룬 cone은 이상적인 기하 형태의 cone을 나타내므로 하나의 꼭지점과 매끈한 면을 가진을 cone을 생각하게 할 수 있습니다.
• 반면 위 슬라이드에서 보여주는 형태의 cone은 실제 이미지가 형성되는 형태와 연관되어 있습니다.
• 카메라 센터점 $C$ 를 꼭지점으로 시작하여 ray를 쏘았을 때, 형성되는 cone과 같은 형태를 위 슬라이드에서는 cone of rays라고 표현하며 위 슬라이드의 그림과 같습니다. cone of rays는 실제 object가 존재하는 위치 까지 형성됩니다.
• 이 때, 이미지는 cone of rays에서 어떤 위치에 어떤 방향으로 교차하도록 평면을 위치시키면 ray들이 평면에 투영되는 데, 그 결과를 이미지 라고 볼 수 있습니다.
• 위 슬라이드에서 표시된 것 처럼 같은 cone of rays에 표시되어 있으나 focal length의 차이를 통하여 물체를 점점 더 확대하여 표현할 수 있음을 보여줍니다.

• 같은 카메라 센터점을 통하여 얻어진 이미지들은 어떤 평면에서 다른 평면으로의 projective transformation (Homography) 관계를 가집니다. 예를 들어 이전 슬라이드에서 집 형태의 물체를 다양한 위치 및 방향으로 평면을 집어 넣어서 조금씩 다른 형상의 집 형태의 상이 맺히도록 이미지를 형성하였습니다.
• 이 때, 서로 다른 형태의 집은 projective transformation 관계를 가지게 되고 그 관계만 알 수 있다면 같은 형태로 만들 수 있습니다. projective transformation 관계이기 때문에 line은 그대로 line으로 유지됩니다.
• 서로 다른 평면의 이미지 간에는 projective transformation 관계를 가지므로 projective properties는 유지 됩니다. 이와 관련된 속성으로는 incidence, cross ratio, conic section이 있습니다. (이전 글에서 다룬 내용입니다.)
  • incidence는 2개의 점이 하나의 선에 있었다면 projective transformation을 하더라도 2개의 점은 같은 하나의 선에 있다는 것입니다. 즉, 선은 그대로 선으로 유지됨을 의미합니다.
  • cross ratio : 4개의 동일 선상에 존재하는 점들 간의 거리 비율은 projective transformation을 하더라도 유지됨을 의미합니다.
  • conic section : 어떤 이미지 상에서의 conic section은 projective transformation을 하더라도 conic section으로 유지된다는 점입니다. 물론 어떤 변환 관계인 지에 따라서 다른 형태의 conic section이 됩니다.

• 같은 카메라 센터점에서 촬영한 2개의 이미지 $I$ 와 $I'$ 에 대하여 projective transformation 즉, homography 관계를 가짐을 앞에서 살펴보았습니다. 이번 슬라이드에서는 이 부분에 대하여 좀 더 수식적으로 살펴봅니다.
• 위 슬라이드에서 $K$ 는 intrinsic parameter ( $3 \times 3$ 크기의 행렬)을 의미하고 $R$ 은 extrinsic parameter ( $3 \times 3$ 크기의 행렬)을 의미합니다. $-\tilde{C}$ 는 원점에서 카메라 중점 까지의 거리를 나타냅니다. (translation의미로 이 부분도 이전 강의에서 다루었습니다.)
• 같은 카메라 중점을 고려하기 때문에 $P$ 와 $P'$ 모두 $-\tilde{C}$ 을 사용하였습니다. 나머지 $K, R$ 은 서로 다른 카메라를 고려하였기 때문에 $K, R$ 과 $K', R'$ 로 구분하였습니다.

• 이미지에 표현된 3D 공간 상에서의 점 $X$ 는 위 슬라이드에 있는 식을 통하여 2개의 카메라에서 다음과 같은 관계로 표현됩니다.

• $$x' = P'X = (K'R')(KR)^{-1}PX = (k'R')(KR)^{-1}x$$

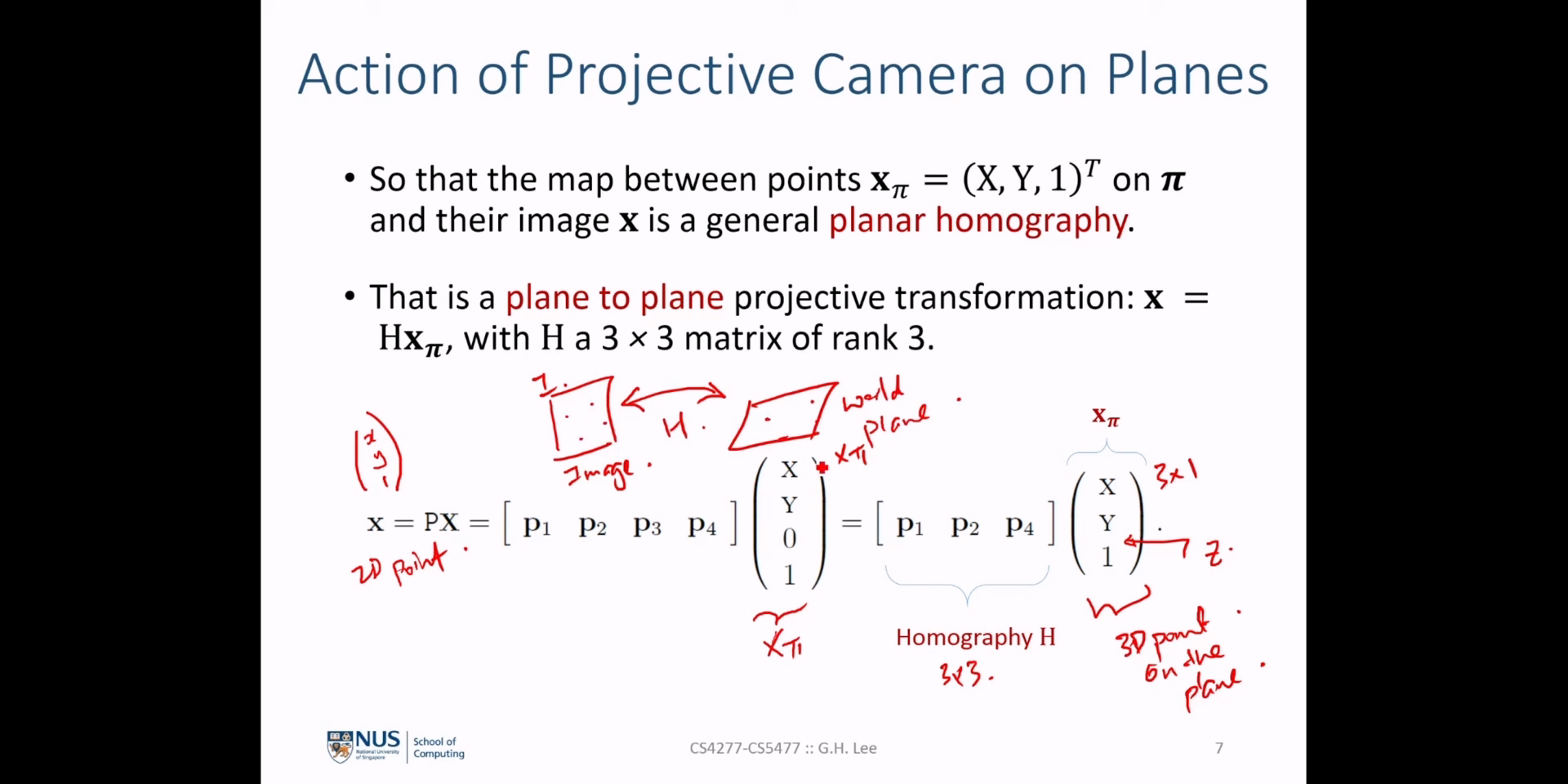
• 따라서 앞에서 언급한 homography $H$ 는 $H = (K'R')(KR)^{-1}$ 로 정의할 수 있습니다.
• 3D 공간 상의 점들을 변환하는 관계이지만 2D 이미지 상에서 변환이 발생하므로 planar homography라는 용어로 표현합니다.

• 이번 슬라이드에서는 focal length의 증가에 따라서 이미지 평면에서의 변화와 관련된 내용을 다룹니다.

• 슬라이드의 $K'K^{-1}$ 의 행렬에서 $(1 - k)\tilde{x}_{0}$ 가 사용된 이유를 살펴보면 다음과 같습니다.

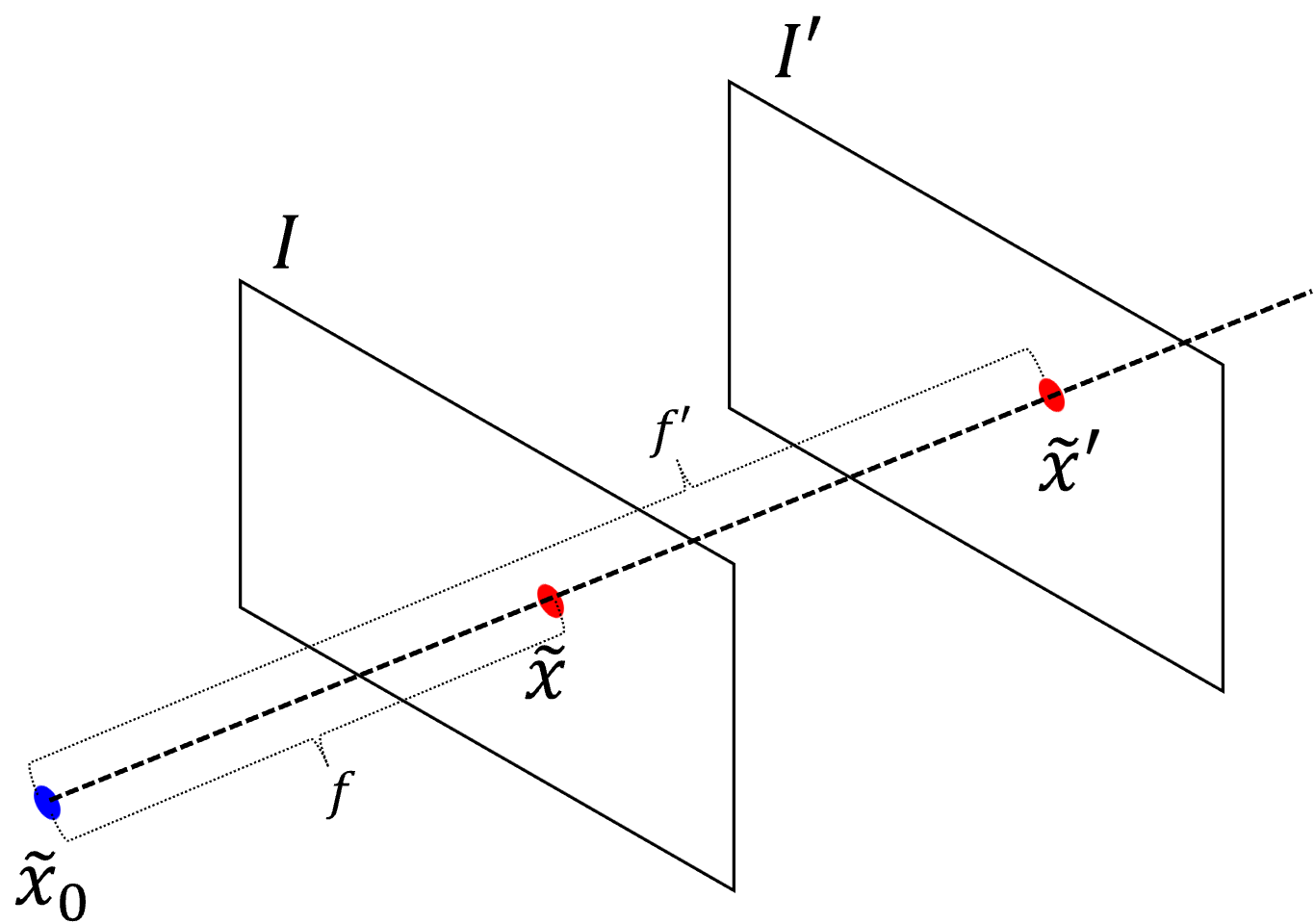
• 위 그림과 같이 $\tilde{x}_{0}$ 는 principal point를 뜻하고 magnification factor인 $k = f'/f$ 가 됩니다.
• 위 그림에서 $\tilde{x}'$ 는 다음과 같이 정의할 수 있습니다.

• $$\begin{align} \tilde{x}' &= \frac{f'}{f}(\tilde{x} - \tilde{x}_{0}) + \tilde{x}_{0} \\ &= \frac{f'}{f}\tilde{x} + (1 - \frac{f'}{f})\tilde{x}_{0} \\ &= k\tilde{x} + (1 - k)\tilde{x}_{0} \end{align}$$

• 따라서 $\tilde{x}' = k\tilde{x} + (1-k)\tilde{x}_{0}$ 로 표현할 수 있음을 확인하였습니다. 즉, $I$ 이미지에서의 점 $\tilde{x}$ 를 $I'$ 이미지의 점 $\tilde{x}'$ 로 변환하기 위해서는 $k$ 배를 한 후 $(1-k)\tilde{x}_{0}$ 만큼 이동해 주면 됩니다.
• 이 내용을 이미지의 $u, v$ 방향에 대하여 모두 적용해 주면 focal length의 차이를 반영하는 행렬 $K'K^{-1}$ 은 다음과 같이 정의할 수 있습니다.

• $$K'K^{-1} = \begin{bmatrix} k & 0 & (1-k)c_{x} \\ 0 & k & (1-k)c_{y} \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} kI & (1-k)\tilde{x}_{0} \\ 0^{T} & 1 \end{bmatrix}$$

• 이전 강의에서는 카메라의 센터점이 동일한 상태에서의 서로 다른 상태로 취득한 이미지에 대하여 homography를 이용하면 이론적으로 이미지들을 서로 복원할 수 있음을 확인하였습니다.
• 이번 슬라이드에서 부터는 그 이론적인 내용을 이용하여 적용할 수 있는 대표적인 Application인 Synthetic Views와 Planar Panoramic Mosaicing입니다.

• 먼저 Synthetic Views는 위 그림과 같이 source image로 부터 planar homography를 이용하여 새로운 형태의 target image로 생성하는 것을 의미합니다. planar homography를 이용한 이미지 변환은 카메라 센터점은 고정한 상태에서 카메라의 촬영 방향을 변화하는 효과를 줄 수 있도록 할 수 있습니다.
• planar homography는 3 x 3 크기의 행렬로 어떤 이미지의 점들을 다른 이미지의 점들로 변환할 수 있도록 하며 3 x 3 행렬의 성분을 통하여 rotation, translation, scale 및 perspective distortion이 이미지 변환 시 어떻게 바뀌는 지 설명해 줄 수 있습니다.
• systhetic view를 생성하기 위해서는 기본적으로 다음의 절차를 따릅니다.
• ① source image와 target image에 서로 대응되는 (같은 위치를 가리키는) 점들을 확인합니다.
• ② 이 점들 쌍을 이용하여 homograpy matrix를 계산합니다.
• ③ homography를 적용하여 source image를 target image로 생성합니다. (synthetic view)

• 앞에서 설명한 바와 같이 source image에서 임의의 사각형을 지정하고 target image에서 이 사각형이 어디에 위치해 있는 지 알 수 있으면 homography를 계산할 수 있습니다. homography를 계산하는 일반적인 방법은 source image와 target image에 대응되는 점들의 쌍을 선형 방정식의 해를 푸는 방식으로 구합니다. 자세한 내용은 아래 글을 참조하시면 됩니다.
  • 참조 : image transformation
  • 참조 : direct linear transformation

• 이와 같은 방법은 통해 $H$ 를 구하면 source image 에서 $x$ 점을 target image에서 $x' = Hx$ 로 변환할 수 있으며 필요한 영역의 모든 점을 이와 같이 변환하면 필요한 영역의 이미지를 구할 수 있습니다. 이와 같은 작업은 warping 이라고 하기도 합니다.

• 이번에는 카메라 캘리브레이션을 통해 어떤 정보를 얻을 수 있는 지 살펴보도록 하겠습니다.
• 이전 강의에서 다루었듯이 카메라 캘리브레이션을 통하여 카메라의 intrinsic와 extrinsic 파라미터를 얻을 수 있었고 intrinsic 파라미터를 통해 focal length, optical center, lens distortion 등을 구할 수 있으며 extrinsic 파라미터를 통하여 카메라와 world의 관계를 구할 수 있었습니다.
• 이전 강의에서는 이와 같은 의미를 가지는 intrinsic과 extrinsic 파라미터를 이용하여 2D 이미지와 3D 공간 상의 정보를 변환하는 projection matrix를 구하여 사용하였고 이 행렬은 $3 \times 4$ 크기를 가졌습니다. 또한 projection matrix를 역으로 분해를 하면 intrinsic과 extrinsic을 구할 수 있었습니다.

• 위 슬라이드에서의 $\tilde{X} = \lambda d$ 는 카메라 좌표계 상의 3D 점을 의미하고 $d$ 는 카메라 센터점으로 부터 뻗어나가는 방향 벡터에 해당하며 $\lambda$ 는 그 방향의 depth를 의미합니다.
• 위 슬라이드의 $x = K[I \vert 0] ( \lambda d^{T}, 1) ^{T} = Kd$ 식은 카메라 좌표계의 3D 포인트가 어떻게 2D 이미지에 투영되는 지 나타냅니다. 여기서 $K$ 는 카메라 intrinsic 파라미터이고 $[I \vert 0]$ 은 extrinsic 파라미터를 나타내며 여기서는 world의 원점에서 간단히 z 축을 바라보는 카메라를 의미하도록 하여 간략하게 나타내었습니다.
• 식 $d = K^{-1} x$ 를 통하여 이미지의 점 $x$ 는 다시 $d$ 벡터로 나타낼 수 있으며 이와 관련된 내용은 앞선 강의에서 다루었습니다. homogeneous 좌표계로 나타내고 있기 때문에 $d$ 는 반드시 unit vector일 필요는 없으며 scale은 달라질 수 있습니다.
• 정리하면 카메라 캘리브레이션 정보는 2D 이미지와 3D 공간 상의 정보를 연결해 주는 역할을 하고 있으며 이 정보는 다양한 task에 사용될 수 있습니다.

• 2D 이미지의 두 점 $x_{1}, x_{2}$ 는 $d_{1} = K^{-1}x_{1}$ 과 $d_{2} = K^{-1}x_{2}$ 로 변형하여 두 벡터 간의 사이각을 구할 수 있습니다. 다음과 같습니다.

• $$\begin{align} \cos{\theta} &= \frac{d_{1}^{T} d_{2} }{ \sqrt{d_{1}^{T}d_{1}} \sqrt{d_{2}^{T}d_{2}} } \\ &= \frac{ (K^{-1}x_{1})^{T}(K^{-1}x_{2}) }{ \sqrt{ (K^{-1}x_{1})^{T}(K^{-1}x_{1}) } \sqrt{ (K^{-1}x_{2})^{T}(K^{-1}x_{2}) } } \\ &= \frac{ x_{1}^{T} (K^{-T}K^{-1})x_{2} } { \sqrt{ x_{1}(K^{-T}K^{-1})x_{1} } \sqrt{ x_{2}^{T}(K^{-T}K^{-1})x_{2} } } \end{align}$$

• 이 방법은 두 카메라 간의 상대적인 pose를 구하거나 multiple view를 고려한 3D 점의 triangulation을 구할 때 사용되곤 합니다.

• 카메라 캘리브레이션을 통하여 카메라 intrinsic 파라미터 $K$ 를 알게 되었다면 $K^{-T}K^{-1}$ 또한 알 수 있습니다.
• 이 값은 꽤 유용하게 사용될 수 있는데 이 값을 통하여 이미지의 점들을 3D 공간 상의 ray로 보낼 수 있으며 반대로도 적용할 수 있습니다.
• 정리하면 파라미터 $K$ 만 알 수 있으면 이미지 상의 점들 만으로도 3D 공간 상의 ray의 방향 또한 알 수 있고 이미지 점들 사이의 각도 또한 알 수 있습니다.

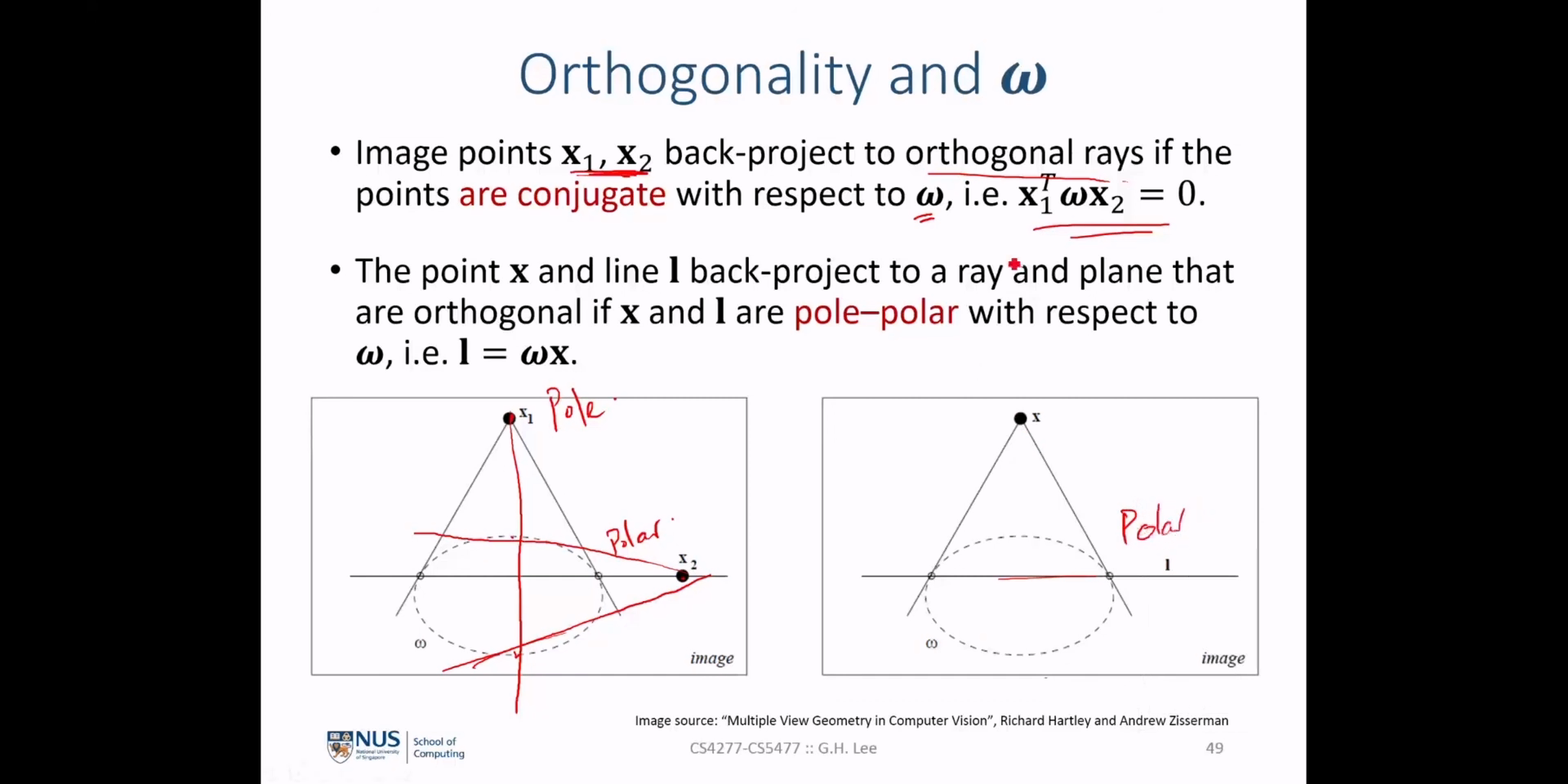
• 위 슬라이드에서는 이미지 상의 선 $l$ 을 구성하기 위해 카메라 센터 $c$ 로 부터 나온 ray인 $d$ 전체와 직교한 방향의 벡터 $n$ 은 $n = K^{T} l$ 로 정의 됨을 보여줍니다.

• 먼저 앞에서 살펴본 바와 같이 이미지 상의 선 $l$ 의 점을 $x$ 는 다음과 같이 back-project 됩니다.

• $$d = K^{-1}x$$

• ray $d$ 는 위 그림과 같이 $n$ 벡터에 직교하므로 다음과 같이 전개할 수 있습니다. 아래 식은 직교한 벡터의 dot product는 0임을 이용한 것입니다.

• $$d^{T}n = x^{T}K^{-T}n = 0$$

• 선 $l$ 상에 존재하는 점 $x$ 에 대하여 $x^{T}l = 0$ 을 만족합니다. 따라서 식을 다음과 같이 전개할 수 있습니다.

• $$x^{T}K^{-T}n = x^{T}l = 0$$
• $$K^{-T}n = l$$
• $$\therefore n = K^{T}l$$

• 따라서 2D 이미지에서 선을 찾았을 때, 그 선을 구성하는 ray 전체와 직교하는 3D 공간상의 normal vector를 찾는 데 $K$ 를 사용할 수 있음을 확인하였습니다. 이와 같은 정보를 이용하면 2D 이미지 상의 선을 통해 3D 공간 상의 기하 정보를 추정할 수 있습니다.

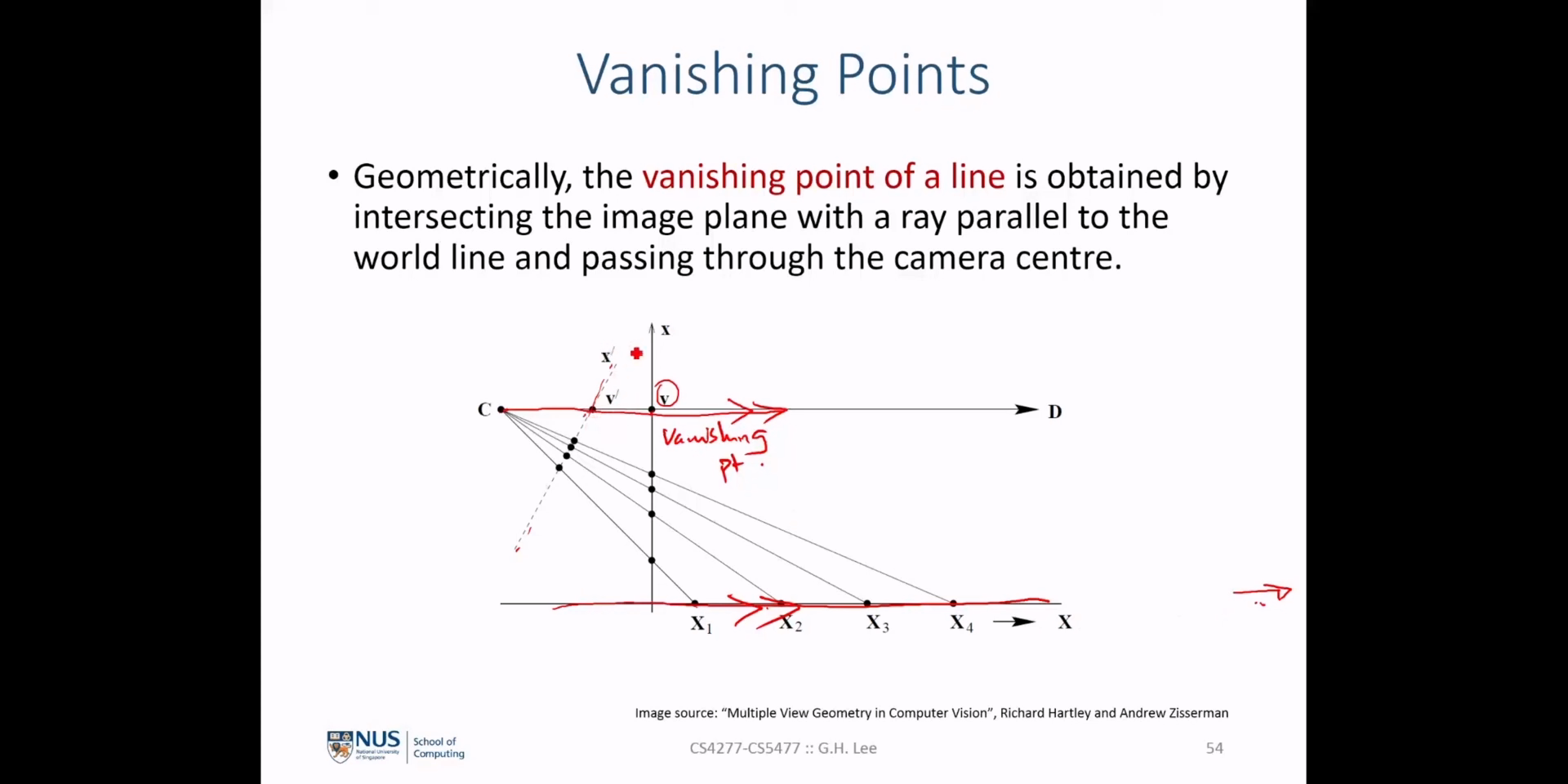
• 지금부터는 Vanishing Points와 Vanishing Lines에 대하여 살펴보도록 하겠습니다.
• 위 그림에서 $C$ 는 카메라의 중심으로 $C$ 의 위치는 움직이지 않고 카메라가 바라보는 방향만 위 아래로 움직이는 것을 나타냅니다.
• 또한 위 그림에서 가로 방향의 $X$ 축은 world 상의 3D 공간 좌표를 의미하고 $D$ 축은 2D 공간 상의 무한 (infinity) 평면에 해당합니다.
• world 상의 점 $X_{1}, X_{2}, X_{3}, X_{4}$ 는 동일한 간격을 두고 점점 멀어지도록 표현되어 있습니다.
• 위 그림에서 $X$ 와 직교하는 실선의 세로 축과 비스듬한 점선의 세로 축 2개가 표현되어 있습니다. 카메라 중심 $C$ 로부터 $X_{1}, X_{2}, X_{3}, X_{4}$ 까지 뻗은 직선과 세로 축의 교점들이 이미지에서의 $X_{1}, X_{2}, X_{3}, X_{4}$ 의 위치를 나타냅니다. world 상에서 $X_{1}, X_{2}, X_{3}, X_{4}$ 는 등간격으로 나타내어진 반면에 이미지 상에서는 점점 간격이 좁아지게 되는데 이는 원근법(Perspective View)이 적용되었기 때문입니다. 따라서 world 상에서 멀리 존재하는 점들이 빽빽하게 모여있게 됩니다.
• vanishing point는 world 상의 점 $X_{\infty}$ 가 무한히 먼 곳에 존재할 때 이미지에 대응되는 점을 의미합니다. 위 그림에서는 $v$ 와 $v'$ 가 각각 vanishing point에 해당합니다.
• 위 그림에서 주목할 점은 같은 점이라도 카메라가 바라보는 방향에 따라 vanishing point의 위치가 다르다는 점입니다.

• vanishing point는 위 그림과 같이 direction of a line에 의해 영향을 받는 것이지 line의 위치 (position)와는 무관합니다.

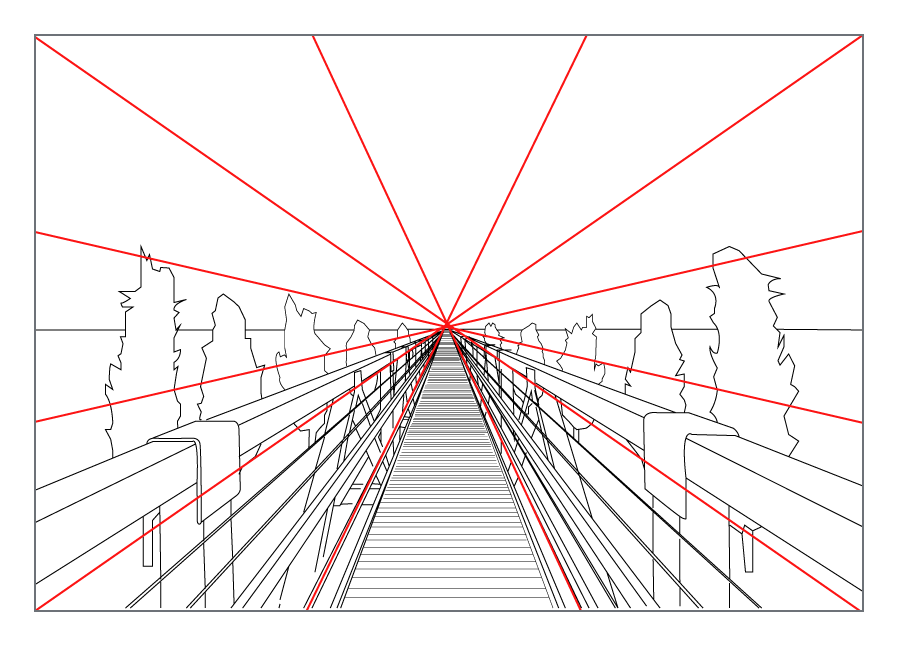
• 위 그림과 같이 line의 위치는 다르더라도 line이 world 상에서 모두 평행하다면 같은 vanishing point를 가지게 됨을 알 수 있습니다.
• 54 페이지에서는 같은 world 상에서의 점에 대해서 카메라가 바라보는 위치가 달라지면 vanishing point의 위치가 바뀌는 것을 보여주었고 55 페이지에서는 평행한 선의 vanishing point가 모두 같은것을 보여주었습니다. 둘 다 같은 의미를 다른 방식으로 보여준 것이며 중요한 것은 vanishing point의 direction of a line에 의해 결정된다는 것입니다.
• 55 페이지에서의 $l$ 은 vanishing line을 의미합니다. 2개의 vanishing point를 구하면 그 점을 이용하여 vanishing line을 구할 수 있습니다.

• 이번 슬라이드에서는 대수적으로 vanishing point에 대한 정의를 내려 보도록 하겠습니다.
• 위 그림에서 $C$ 는 카메라의 중심이고 3D 공간상의 어떤 점 $X(\lambda)$ 는 $X(\lambda) = A + \lambda D$ 로 정의 됩니다. 임의의 점 $A$ 에서 $D$ 의 방향과 크기 만큼 이동하였을 때 생기는 점을 의미합니다.
• 위 식에서 $D = (d^{T}, 0)^{T}$ 에서 $d$ 는 3D 벡터를 의미합니다. homogeneous coordinate에서 벡터를 나타내므로 마지막 차원의 값이 0이 되어 homogeneous 상의 벡터로 나타낼 수 있습니다.
• 따라서 임의의 3D 상의 점 $X(\lambda) = A + \lambda D$ 로 나타낼 수 있습니다.

• 앞에서 정의한 $X(\lambda)$ 에 Projection Matrix인 $P$ 를 적용해 보도록 하겠습니다.
• 앞에서 다루온 바와 같이 $P = K[I \vert 0]$

회전행렬의 자유도는 3이므로 2개 이상의 vanishing point 쌍을 사용하면 회전행렬을 복원할 수 있습니다.

• metric rectification은 이미지에서 perspective view로 인하여 수직 성분이 왜곡되어 이미지 상에서 형성된 것을 다시 수직 형태로 복원하는 과정을 의미합니다.

• 앞에서 다룬 그림을 다시 살펴보겠습니다. 위 그림에서 (b), (c)가 (a)를 metric rectification 하여 수직 성분을 복원한 예시입니다. 그림에서도 (b), (c)를 Front-Parallel로 표현할 것을 확인할 수 있습니다.

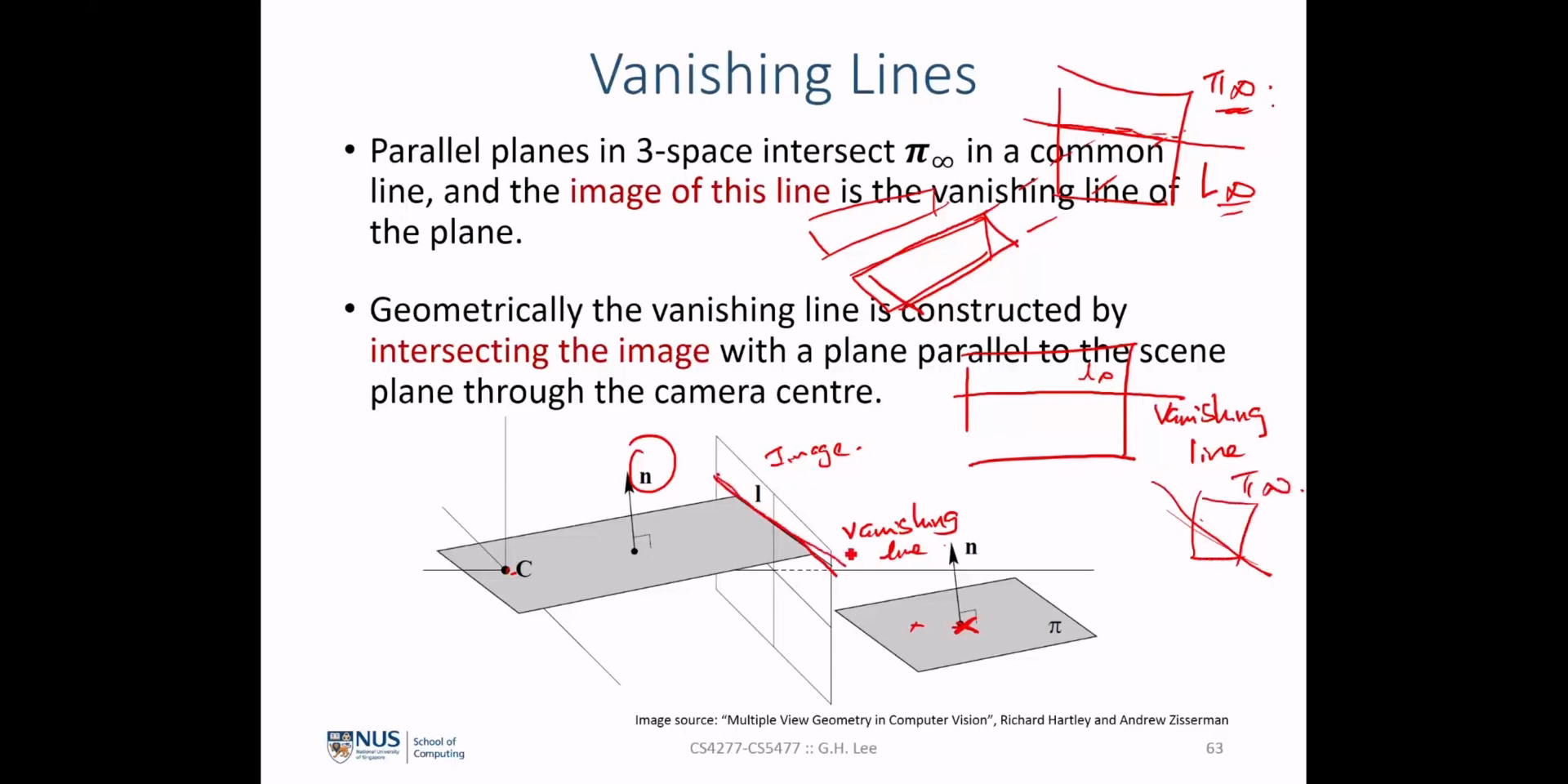
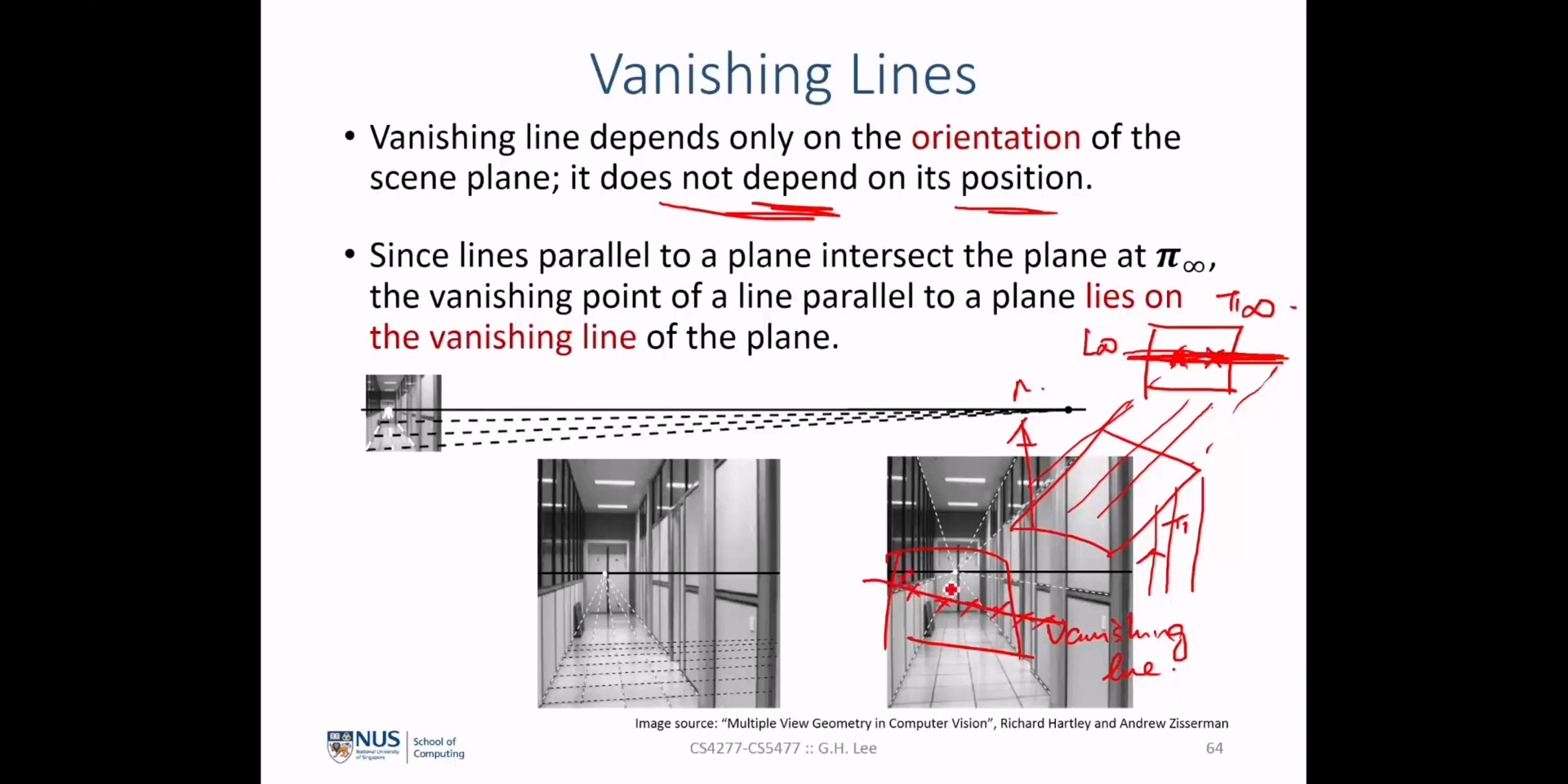
• 지금까지 살펴본 vanishing point와 vanishing line에 대하여 정리해 보면 다음과 같습니다.
• vanishing point와 vanishing line 3D 공간 상의 위치와는 무관하고 방향에만 관계가 있습니다.
• vanishing point는 3D 공간 상의 평행한 선들 (parallel scene lines)을 알 수 있으면 이미지 상에서 구할 수 있습니다. vanishing point를 활용하는 대표적인 예시로 ① intrinsic이 같은 2개의 카메라의 Rotation을 구하는 것과 ② 2개의 scene lines 사이의 각을 구하는 것이 있었습니다.
• vanishing lines은 2개의 vanishing point를 연결하여 구할 수 있고 ( $l = v_{1} \times v_{2}$) 또는 3D 공간 상의 평면과 $\pi_{\infty}$ 의 교차선을 통하여 구할 수도 있습니다.
• 특히 두번째 방법에서 3D 공간 상의 평면인 scene plane의 normal vector인 $n$ 을 $n = K^{T}l$ 으로 구할 수 있습니다. 이 때, 어떤 $n$ 값을 가지는 scene plane들 중에서 카메라 센터를 통과하는 scene plane이 이미지와 교차하는 선이 vanishing line이 되는 것을 확인하였습니다.
• vanishing line을 이용하면 ① vanishing line을 생성하는 scene plane의 normal vector를 알 수 있다는 것과 ② metric rectification을 하는 데 이용할 수 있다는 점, ③ 2개의 scene plane 사이의 각도를 확인할 때 사용할 수 있다는 것을 확인하였습니다.

• 75p의 슬라이드 하단의 이미지를 아래 좀 더 선명하게 표현하도록 하였습니다.

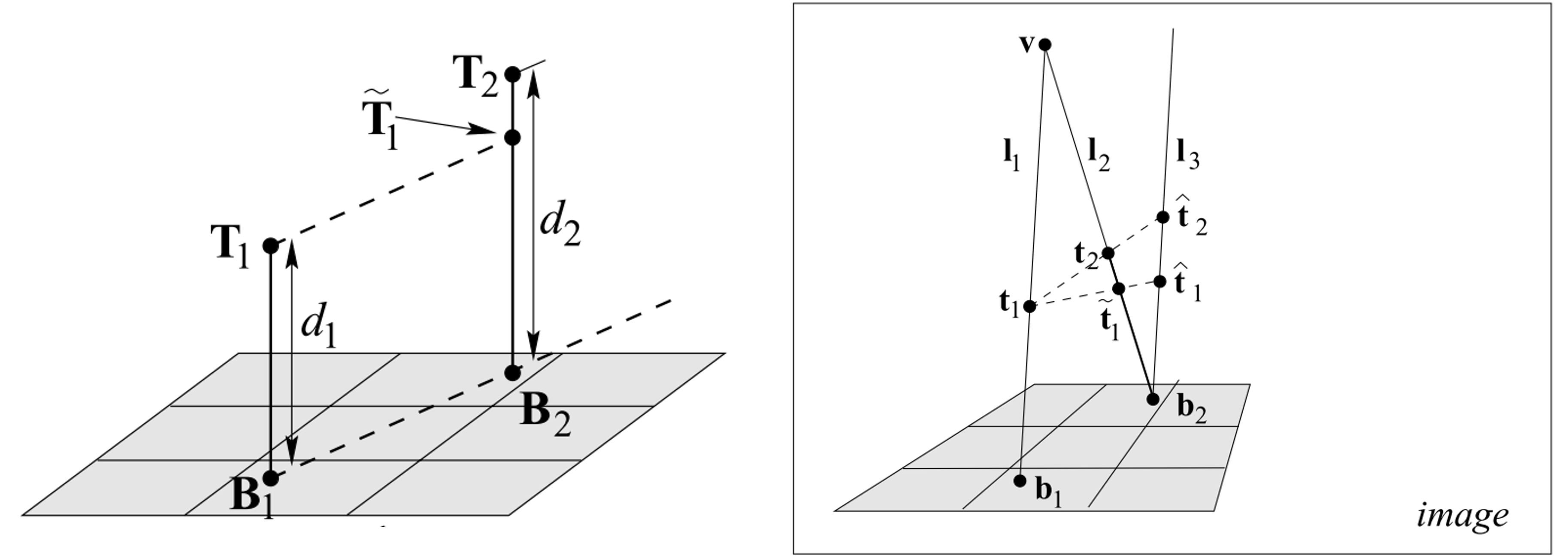
• 위 슬라이드에서는 $H_{2 \times 2}$ 를 이용하여 오른쪽의 image에 존재하는 $\tilde{t}_{1}$ 와 $t_{2}$ 를 왼쪽의 스케일 변환된 3D space에서의 $\tilde{T}_{1}$ 와 $T_{2}$ 로 대응 시키는 내용을 설명합니다.
• 74p에서 정의된 $H_{2 \times 2}$ 를 이용하면 이미지 상의 $0 \approx v$ 범위의 높이 값을 3D space 상에서 $0 ~ 1$ 사이의 값으로 스케일 변환하여 대응시킬 수 있습니다. 즉 image의 지면 점 $b_{2}$ 는 그대로 스케일 변환된 3D 공간 상에서 $0$ 이 되고 image 상의 무한이 높이 있는 점 $v$ 는 스케일 변환된 3D 공간 상에서 $1$ 이 됩니다.
• 따라서 image 상의 점 $\tilde{t}_{1}$ 과 $H_{2 \times 2}$ 를 통해 스케일 변환된 3D space에서의 $\tilde{T}_{1}$ 의 값과 $t_{2}$ 와 $H_{2 \times 2}$ 를 통하여 스케일 변환된 3D space에서의 $T_{2}$ 의 값을 구하면 다음과 같습니다.

• $$\tilde{T}_{1} = \begin{bmatrix} 1 & 0 \\ 1 & -v \end{bmatrix} \begin{bmatrix} \tilde{t}_{1} \\ 1 \end{bmatrix} = \begin{bmatrix} \tilde{t}_{1} \\ \tilde{t}_{1} - v \end{bmatrix}$$
• $$T_{2} = \begin{bmatrix} 1 & 0 \\ 1 & -v \end{bmatrix} \begin{bmatrix} t_{2} \\ 1 \end{bmatrix} = \begin{bmatrix} t_{2} \\ t_{2} - v \end{bmatrix}$$

• 위 결과에서 $\tilde{T}_{1}$ 과 $T_{2}$ 는 지면에서 (스케일 변환된) 수직으로 뻗은 위치입니다. 따라서 inhomogeneous로 변환하면 (스케일 변환된) distance가 됩니다. 다음과 같습니다.

• $$d_{1} = \frac{\tilde{t}_{1}}{(\tilde{t}_{1} - v)}$$
• $$d_{2} = \frac{t_{2}}{(t_{2} - v)}$$

• 따라서 distance ratio를 구하면 다음과 같습니다.

• $$d_{1} \text{ : } d_{2} = \frac{\tilde{t}_{1}}{(\tilde{t}_{1} - v)} \text{ : } \frac{t_{2}}{(t_{2} - v)}$$
• $$\therefore \frac{d_{1}}{d_{2}} = \frac{\tilde{t}_{1}(v - t_{2})}{t_{2}(v - \tilde{t}_{1})}$$

Multiple View Geometry 글 목차