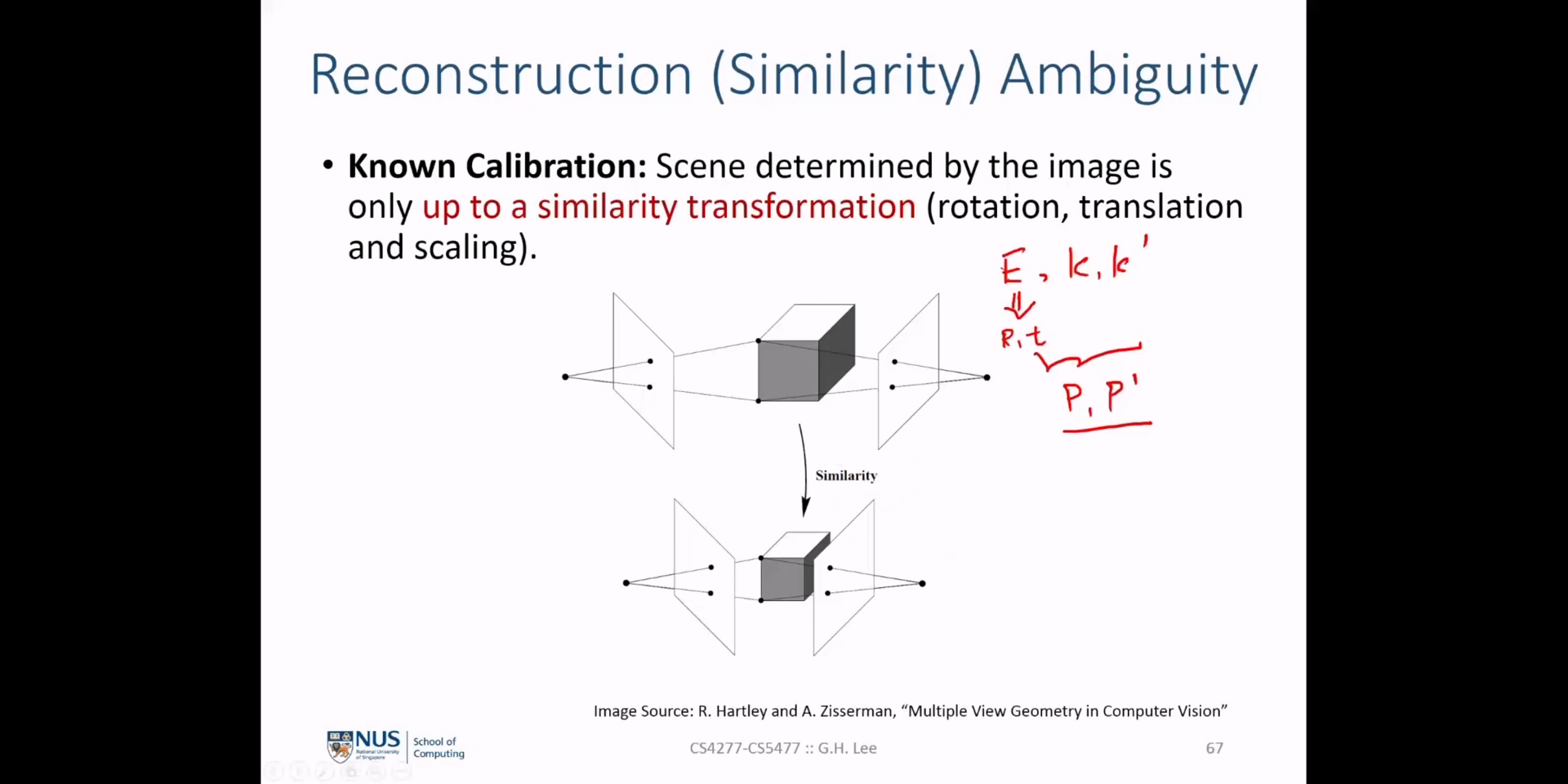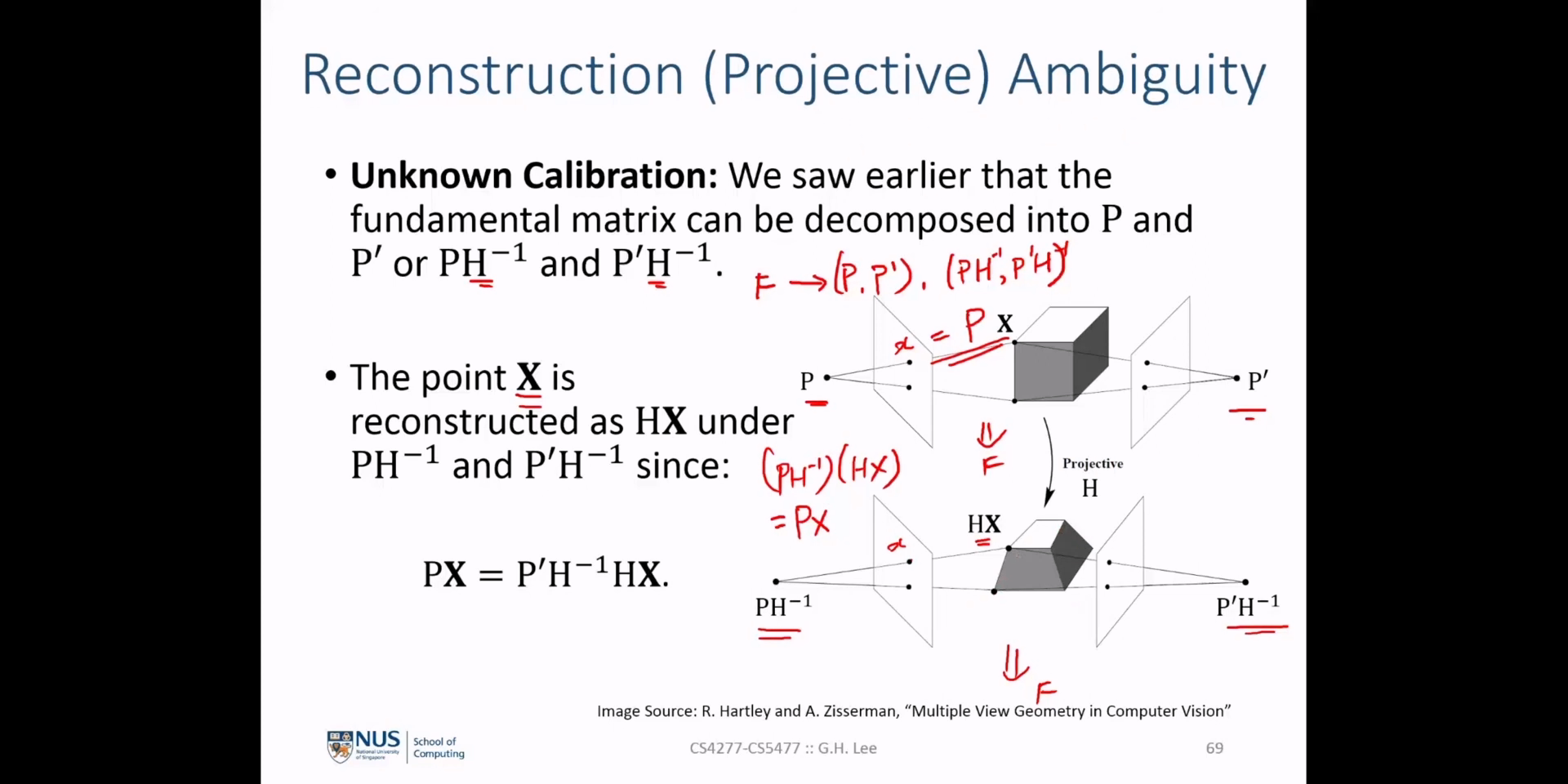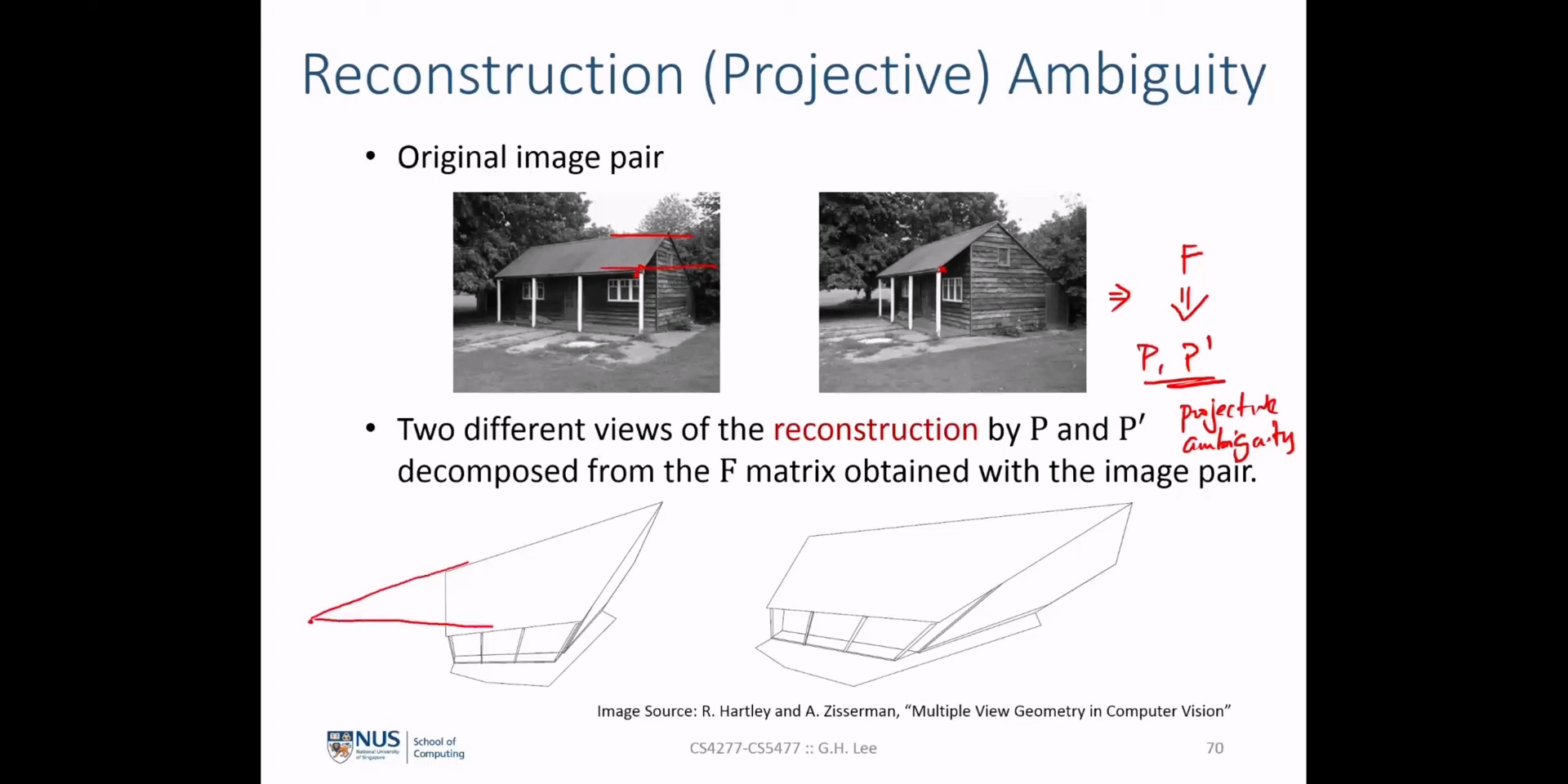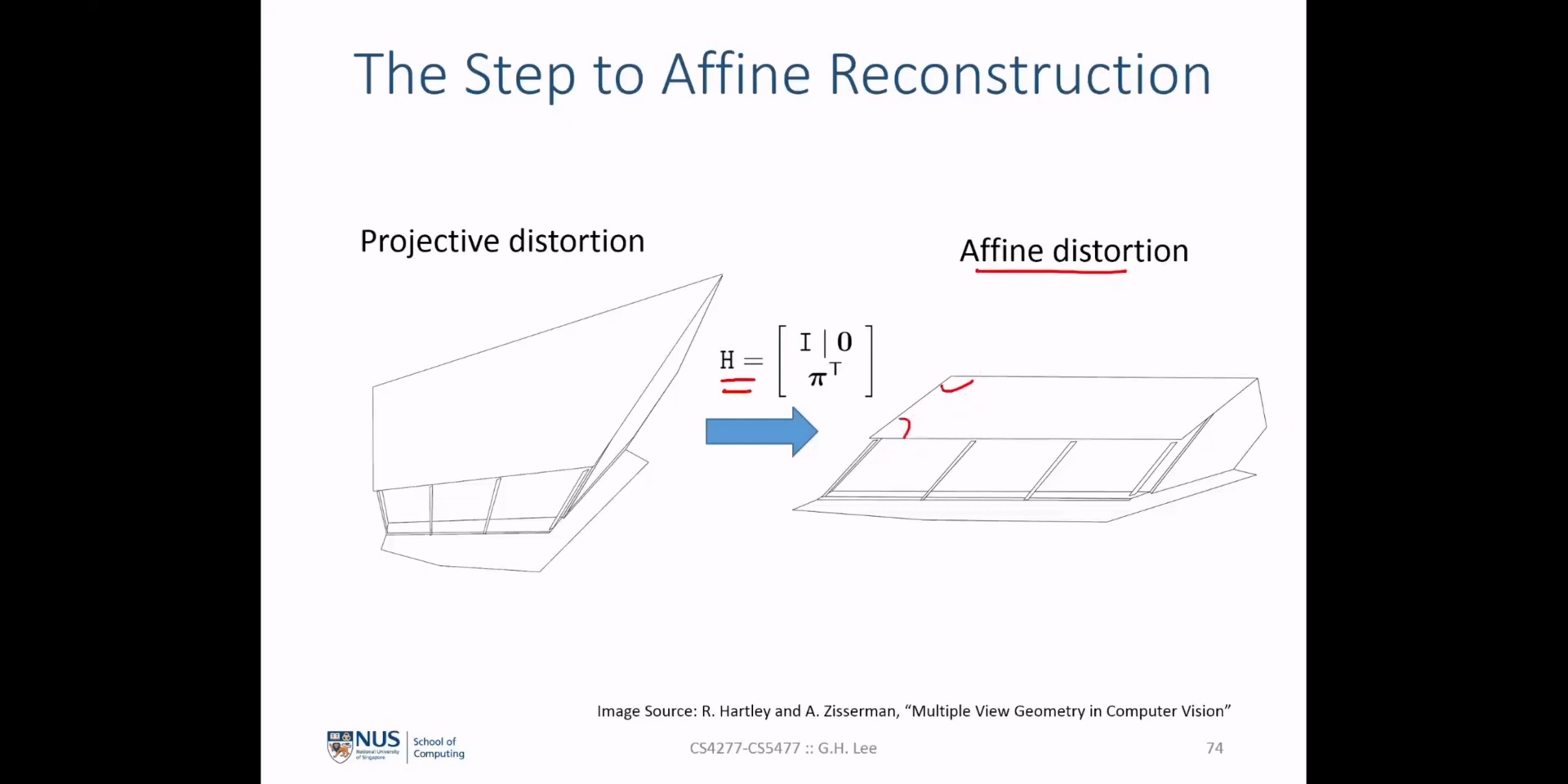
(멀티플 뷰 지오메트리) Lecture 7. The fundamental and essential matrices

Multiple View Geometry 글 목차

참조 : https://youtu.be/eJnG1vwGJkE?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : https://youtu.be/mNThwULGR-g?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : https://youtu.be/7QYq7qNkmtg?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : https://youtu.be/WQvJICS3Ecc?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : Multiple View Geometry in Computer Vision

Lecture 7에서는 fundamental matrix와 essential matrix 내용을 다룹니다. 이 개념들을 통하여 카메라 간의 관계를 정의하기 위한 기본적인 개념을 익힐 수 있습니다.

먼저 본 강의 내용에 앞서 다음 내용을 간략히 숙지하면 이해하는 데 도움이 됩니다.

epipolar geometry란 2개이상의 카메라에서 카메라 간의 관계를 추정하는 것으로 생각할 수 있습니다.
만약 카메라가 2개라면 스테레오 비전 또는 2-view라고 하며 스테레오 비전에서의 두 카메라의 관계를 epipolar geometry로 표현할 수 있습니다. 아래 그림과 같습니다.

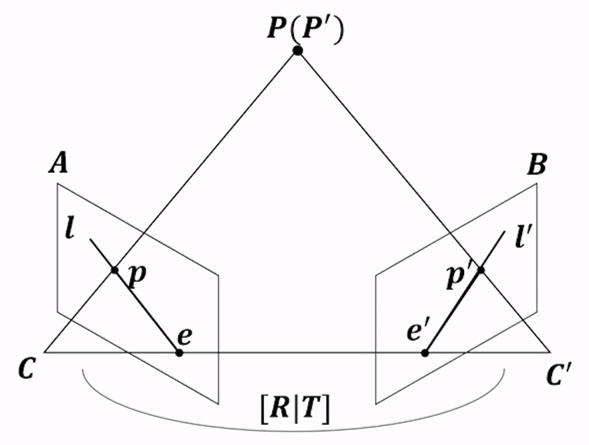
위 그림에서 동일한 3차원의 점인 \(P\) 를 서로 다른 두 카메라에서 획득하였을 때, 매칭 쌍 \((p, p')\) 사이의 기하학적 관계를 다룹니다. 먼저 위 그림에 각 기호에 대한 설명을 하면 다음과 같습니다.
　\(P(P')\) : 이미지 상에 맺힐 3차원 공간 상의 점을 의미합니다.
　\(C, C'\) : 각 영상의 카메라 센터점을 의미합니다.
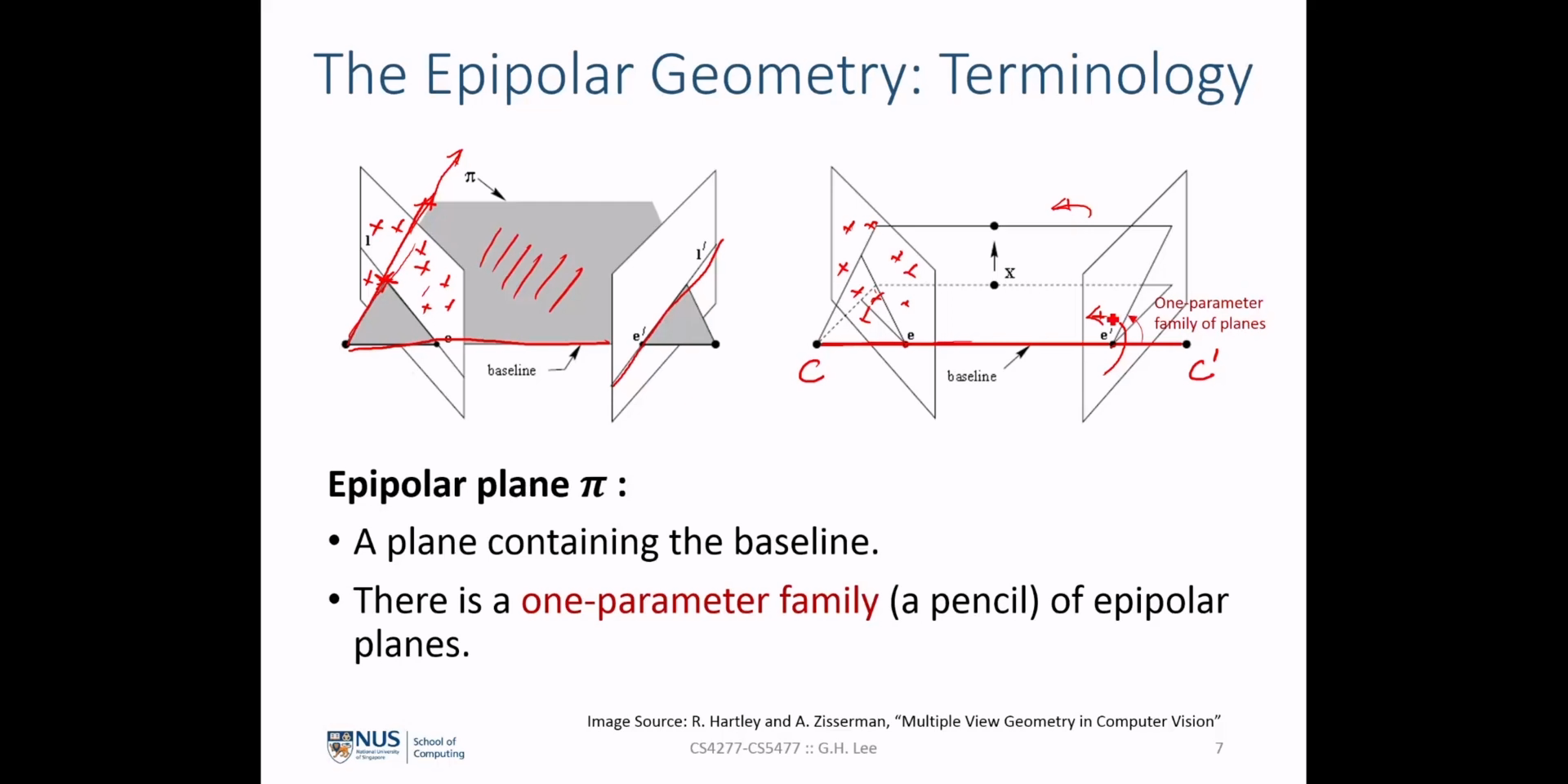
　\(\text{base line}\) : 카메라의 센터점을 이은 선을 base line이라고 합니다. \(C, C'\) 의 거리가 가까운 경우를 narrow base line이라고 하고 거리가 먼 경우를 wide base line이라고 합니다.
　\(p, p'\) : 각 영상에서 \(P(P')\) 가 투영된 점을 의미합니다.
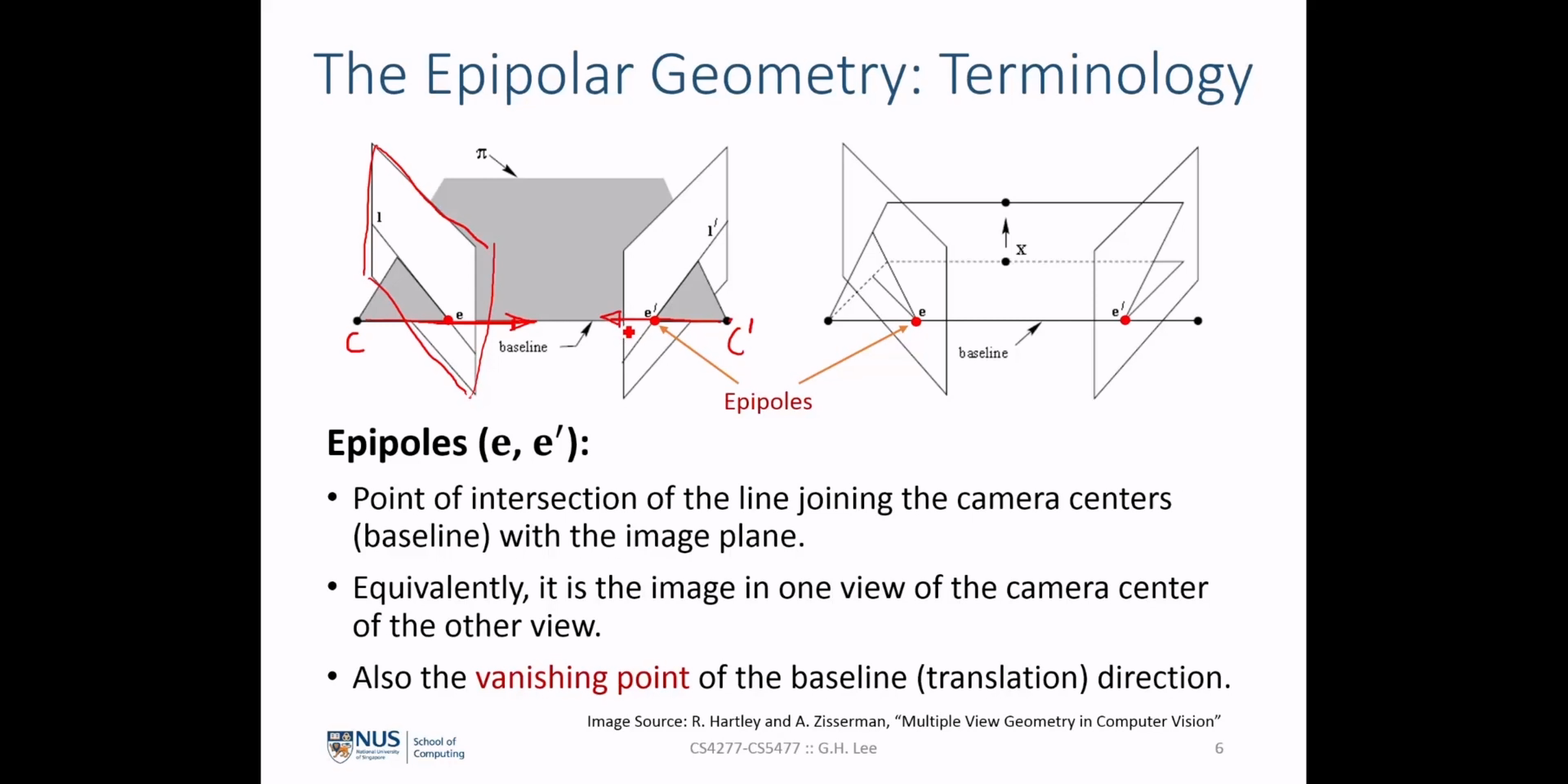
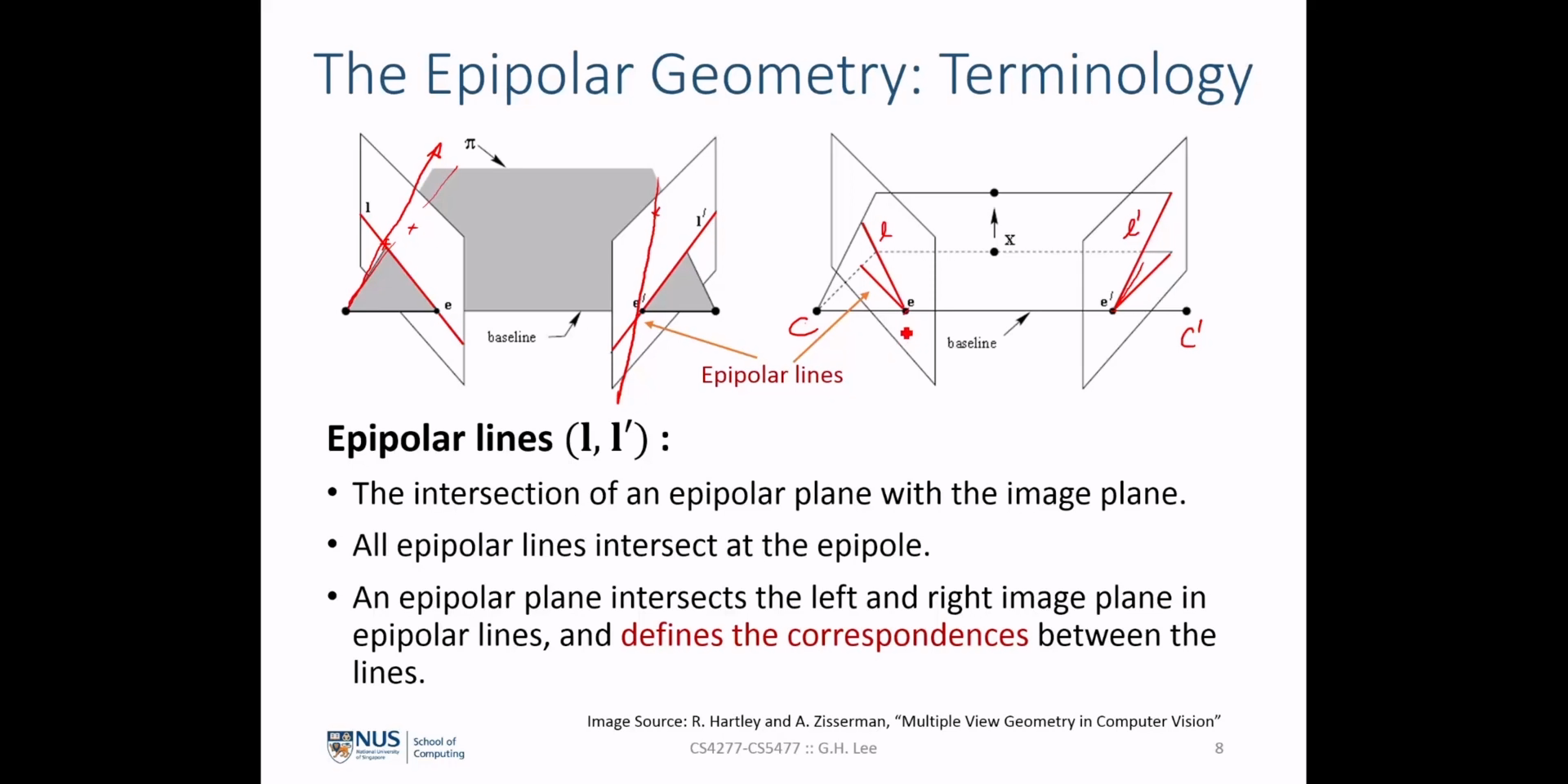
　\(e, e'\) : 반대 영상의 카메라 센터점에서 해당 영상의 이미지 상에 맺힌 점을 의미합니다. 이 점을 epipole 이라고 합니다.
　\(l, l'\) : 각 영상에서 epipole ( \(e, e'\) )과 이미지 상의 점 ( \(p, p'\) )를 이은 선을 의미합니다. 이 선을 epolar line 이라고 합니다.

위 그림에서 \(C\) 와 \(C'\) 간의 3차원 위치 관계인 \([R \vert T]\) 와 \(p\) 를 알더라도 3차원 공간 상의 점 \(P\) 에 대한 실제 깊이 (depth) 를 알지 못하면 유일한 \(p'\) 를 결정하지 못합니다.
반면에 \(P\) 는 \(C\) 와 \(p\) 를 잇는 ray 상에 존재하므로 이 선이 반대 영상에 투영된 epipolar line \(l'\) 은 유일하게 존재합니다.
이 때, \(A\) 이미지에서 \(B\) 이미지로 대응되는 epipolar line ( \(l'\) ) 의 관계를 나타내는 행렬이 \(F, E\) 이며 각각 Fundamental Matrix, Essential Matrix라고 합니다.

Essential Matrix \(E\) 는 normalized image plane 에서의 매칭쌍들 사이의 기하학적 관계를 설명하는 행렬을 의미하고 Fundamental Matrix \(F\) 는 카메라 파라미터 까지 포함한 두 이미지의 실제 픽셀 좌표 사이의 기하학적 관계를 표현하는 행렬을 의미합니다. 따라서 \(E\) 는 \(F\) 의 특수한 형태라고 생각할 수 있습니다.

두 이미지 평면 간의 기하학적 관계가 \(E, F\) 가 주어지고 두 이미지 평면상의 매칭쌍 \(p, p'\) 가 주어질 때, 3D 공간 상의 좌표 \(P\) 를 결정할 수 있습니다. 따라서 스테레오 비전에서의 깊이 (‘depth’)를 구할 수 있습니다.

상세 내용은 본 강의 내용을 통하여 자세하게 살펴보도록 하겠습니다.

이번 슬라이드에서는 Fundamental Matrix를 유도하기 위하여 필요한 각 요소 값들을 소개합니다. 필요한 값은 \(P, P', P^{+}, C, x\) 의 의미입니다. 3차원 좌표 \(X(\lambda)\) 를 \(P, P', P^{+}, C, x\) 값을 이용하여 표현함으로써 각 성분의 의미를 먼저 이해해 보도록 하겠습니다.
위 식에서 Projection Matrix \(P, P'\) 는 각각 임의의 3D 포인트 \(X\) 를 이미지 \(I, I'\) 에 투영하는 \(3 \times 4\) 크기의 행렬을 의미합니다.
반면 \(P^{+}\) 는 \(P\) 의 Pseudo-Inverse 행렬을 의미하며 \(3 \times 4\) 행렬의 역행렬을 구하기 위하여 Pseudo-Inverse를 이용하여 구합니다. 따라서 \(P^{+}\) 는 \(4 \times 3\) 크기의 행렬이며 이미지 좌표 \(x\) 를 역투영 (back-project) 하는 역할을 합니다.
3차원 상에서의 카메라 원점을 의미하는 \(C\) 는 \(X(\lambda)\) 를 표현할 때, 방향 벡터 형태로 사용됩니다. homogeneous coordinate에서 \((X_{C}, Y_{C}, Z_{C}, 1)\) 형태로 back-project 시 방향 벡터로 사용되며 그 스케일은 \(\lambda\) 를 이용하여 조절합니다.
정리하면 \(P^{+}x\) 점을 시작 (origin) 으로 하여 카메라 원점에서 뻣어나가는 방향의 ray \(C\) 를 \(\lambda\) 만큼 뻣어나간 것이 3D 포인트 점 \(X(\lambda)\) 가 됩니다.

하나의 3D 물체를 두 이미지에 각각 투영하여 얻은 점을 \(x, x'\) 라고 하였을 때, 지금까지 살펴본 Fundamental Matrix \(F\) 와 \(x, x'\) 를 이용하여 다음과 같은 식을 나타낼 수 있습니다.

\[x'^{T} F x = 0\]

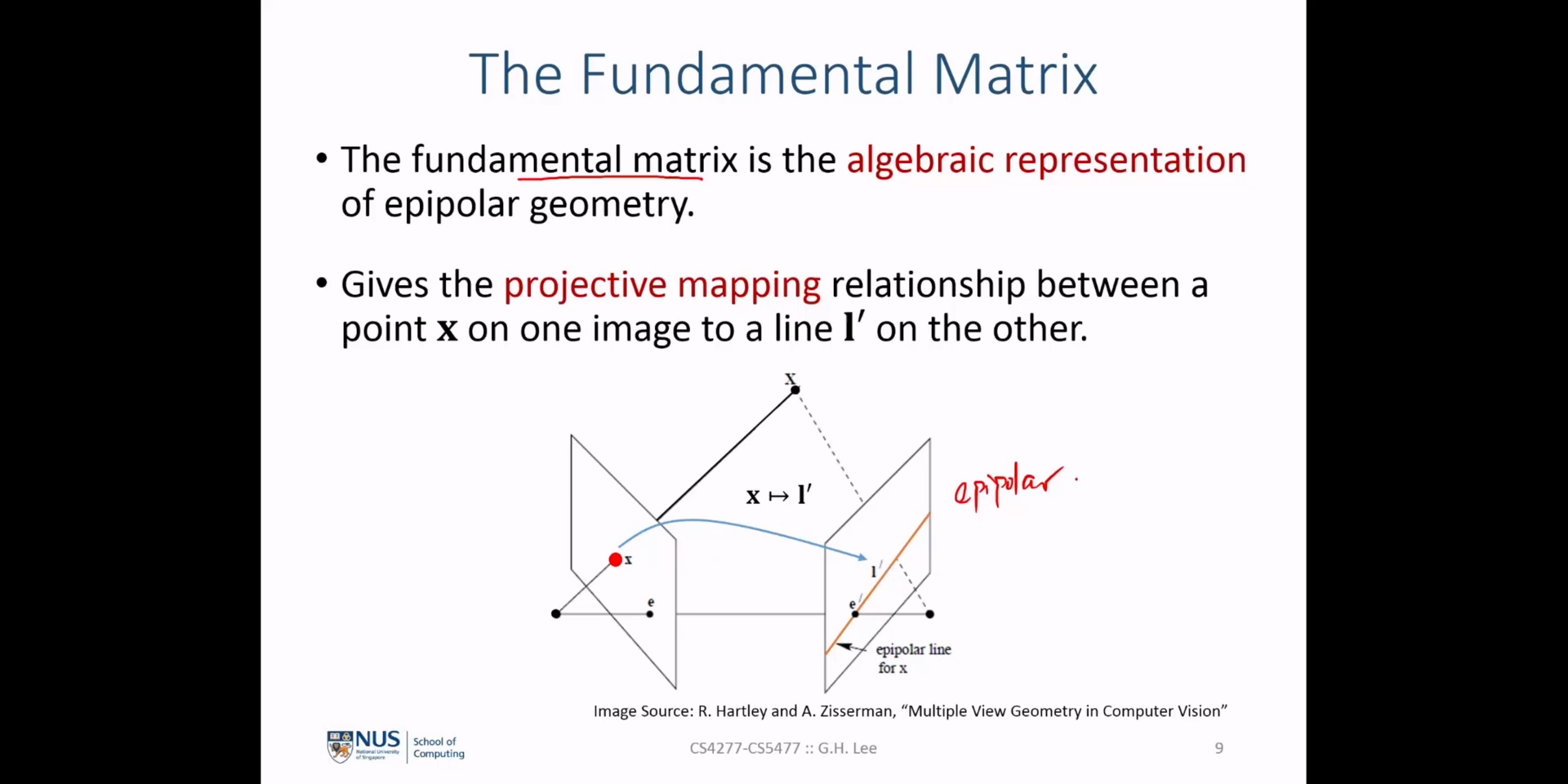
이와 같이 Fundamental Matrix를 통하여 위 식과 같은 조건을 만족하면 \(x, x'\) 를 corresponding points 관계라고 말할 수 있습니다. 위 식이 만족하는 이유는 슬라이드의 Proof 부분을 보면 쉽게 이해할 수 있습니다. 위 관계를 성립하기 위하여 \(l' = Fx\) epipolar line을 이용합니다. 간략히 살펴보면 다음과 같습니다.

① Definition of \(l'\): 두번째 이미지에서의 epipolar line \(l'\) 는 첫번째 이미지의 포인트 \(x\) 와 \(F\) 행렬을 통해 만들어집니다. \(l' = Fx\)
② Point on the Line : \(x'\) 는 \(x\) 의 corresponding point 이기 때문에 반드시 epipolar line \(l'\) 상에 있어야 합니다. homogeneous coordinate에서 \(x'\) 가 \(l'\) 상에 있으면 \(x'^{T}l' = 0\) 으로 표현할 수 있습니다.
③ Substitue \(l'\) : \(x'^{T}l' = x'^{T}(Fx) = 0\)

식 \(x'^{T} F x = 0\) 은 epipolar constraint 라고도 불립니다. epipolar constraint는 첫번째 이미지에서의 임의의 점 \(x\) 와 \(F\) 가 두번째 이미지에서 만들어내는 epipolar line 상에 두번째 이미지에서 \(x\) 와 corresponding point 관계인 \(x'\) 가 존재한다는 조건입니다.
epipoelar constraint는 multiple view geometry의 가장 기본적이면서도 중요한 개념입니다. corresponding points를 이용하여 Stereo Matching, 3D reconstruction과 같은 분야를 접근할 수 있기 때문입니다.

epipolar constraint \(x'^{T} F x = 0\) 의 관계를 구하기 위해서는 Fundamental Matrix \(F\) 를 알아야 합니다. \(F\) 를 알기 위해서는 카메라 파라미터 정보와 상관 없이 corresponding points인 \(x, x'\) 의 관계들만을 필요로 합니다.
그러면 Fundamental matrix \(F\) 를 구하기 위하여 필요한 corresponding points의 갯수에 대하여 간략히 알아보겠습니다. 상세 내용은 본 글의 뒷부분에서 다룰 예정입니다.

참조 : https://stackoverflow.com/questions/49763903/why-does-fundamental-matrix-have-7-degrees-of-freedom

Fundamental Matrix \(F\) 는 \(3 \times 3\) 크기를 가지는 행렬이므로 9 개의 값을 가집니다. 따라서 9개의 자유도를 가지기 때문에 9 개의 corresponding points가 필요한 것으로 보이지만 Fundamental Matrix는 7개의 자유도인 7-DOF를 가지므로 7개의 corresponding points를 필요로 합니다.
7개의 자유도를 가지는 이유는 Fundamental Matrix의 scale ambiguity와 rank-2 constraint와 연관되어 있습니다.
scale ambiguity는 스케일 값에 무관함을 나타내며 \(F\) 와 \(\alpha F (\alpha \ne 0 )\) 가 같은 의미를 가지는 행렬이므로 이러한 scale ambiguity가 발생합니다. 이 컨셉은 homogeneous coordinate에서 충분히 많이 다룬 개념입니다. 수식으로 좀 더 자세히 살펴보면 다음과 같습니다.

\[x = \begin{bmatrix} u & v & 1 \end{bmatrix}^{T}\]
\[x' = \begin{bmatrix} u' & v' & 1 \end{bmatrix}^{T}\]
\[F = \begin{bmatrix} f_{1} & f_{2} & f_{3} \\ f_{4} & f_{5} & f_{6} \\ f_{7} & f_{8} & f_{9} \end{bmatrix}\]
\[x'^{T} F x = 0\]

위 식을 풀어서 정리해 보면 다음과 같습니다.

\[uu'f_{1} + vu'f_{2} + u'f_{3} + uv'f_{4} + vv'f_{5} + v'f_{6} + uf_{7} + vf_{8} + f_{9} = 0\]

위 식을 \(AF = 0\) 형태로 나타내면 \(A\) 와 \(F\) 는 다음과 같습니다.

\[AF = 0\]
\[A = \begin{bmatrix} uu' & vu' & u' & uv' & vv' & v' & u & v & 1 \end{bmatrix}\]
\[F = \begin{bmatrix} f_{1} & f_{2} & f_{3} & f_{4} & f_{5} & f_{6} & f_{7} & f_{8} & f_{9} \end{bmatrix}\]

행렬 \(A\) 를 살펴보면 8개의 미지수가 있고 위 예시에서는 1이라는 상수가 한개 있습니다. 이 값이 1이기 때문에 이미 미지수를 풀 수 있는 하나의 정보는 주어졌고 이 정보가 scale에 관한 정보입니다. 1은 \(f_{9}\) 와 곱해지고 \(f_{9}\) 가 scale에 해당합니다.
만약 1이 아니라 \(\alpha\) 라는 값이 적용 된다면 \(A\) 의 모든 원소에 \(\alpha\) 를 곱하여 \(AF = 0\) 을 만족시킬 수 있습니다. 따라서 이 값을 통해 scale ambiguity의 성질을 만족시킬 수 있습니다.

두번째로 rank-2 constraint에 관한 것입니다. \(l' = Fx\) 를 통하여 임의의 점 \(x\) 에 \(F\) 를 곱하면 선 형태인 epipolar line을 얻을 수 있음을 확인하였습니다. 즉, \(F\) 는 모든 column 또는 row 성분이 independent 한 full rank 행렬이 아니기 때문에 점이 선으로 변환될 수 있습니다. (만약 full rank 행렬이면 \(l' = Fx\) 를 얻을 수 없고 \(Fx\) 는 포인트가 되어야 합니다.)
full rank가 아닌 행렬은 determinant가 0이 되기 때문에 다음과 같이 식을 전개해 볼 수 있습니다.

\[F = \begin{bmatrix} f_{1} & f_{2} & f_{3} & f_{4} & f_{5} & f_{6} & f_{7} & f_{8} & f_{9} \end{bmatrix}\]
\[\text{det}(F) = (f_{1}*f_{5}*f_{8})+(f_{2}*f_{6}*f_{7})+(f_{3}*f_{4}*f_{8})-(f_{3}*f_{5}*f_{7})-(f_{2}*f_{4}*f_{9})-(f_{1}*f_{6}*f_{8}) = 0 \quad \text{by determinant formula}\]

식 \(\text{det}(F) = 0\) 에서 단 하나의 미지수를 제외하고 다른 미지수의 해를 구하면 나머지 하나의 미지수는 자동으로 결정되기 때문에 자유도가 하나 줄어들게 됩니다.
따라서 scale ambiguity로 인하여 \(f_{9}\) 의 결정이 필요 없어져서 자유도가 1 감소되는 것과 \(\text{det}(F) = 0\) 조건으로 인한 자유도 1 감소로 Fundamental Matrix는 7 DoF를 가지게 됩니다.

추가적으로 rank 2가 가지는 의미와 rank 1을 가지면 epipolar constraint을 만족할 수 없음을 보이면 다음과 같습니다.

먼저 rank 2가 가지는 기하학적인 의미입니다.
① Point-to-Line Mapping
② Epipolar Constraint

다음으로 rank 2가 가지는 대수적인 의미입니다.
① Rank Deficiency
② Null Vectors
③ Non-Invertibility

다음으로 rank 1을 가지면 epipolar constraint을 만족할 수 없는 이유를 설명하겠습니다.
① Rank Deficiency : \(3 \times 3\) 행렬이 rank-1을 가지면 column (또는 row) 들 중 하나만 의미가 있으며 나머지는 linear combination을 통해 만들어 지는 것은 의미합니다. 따라서 단일 선 (single line) 만을 span할 수 있습니다.
② Point-to-Point Mapping : 3차원에서 rank-1 행렬은 모든 포인트들을 단일 선에 매핑되도록 축소시킵니다. Fundamental Matrix 와 관련하여, rank-1 행렬의 의미는 한 이미지의 모든 점이 다른 이미지의 단일 점으로 매핑되는 것을 의미하므로 적합하지 않습니다.
③ Loss of Epipolar Constarint : rank-1 행렬에서 epipolar constraint \(x'^{T} F x = 0\) 식은 만족하지만 기하학적인 의미는 만족하지 못합니다. 왜냐하면 이미지의 모든 점들에 대하여 고정된 epipolar line만 존재하기 때문에 실제 사용하고자 하는 3D 조건에 부합하지 못합니다.

지금까지 살펴본 Fundamental Matrix의 성질에 대하여 몇가지 살펴보도록 하겠습니다.

먼저 Transpose 성질에 대하여 살펴보도록 하겠습니다. \(F\) 는 \((P, P')\) 와 \((P', P)\) 양쪽에 모두 적용될 수 있습니다. \((P, P')\) 에 대한 관계를 \(F\) 로 나타날 때, \((P', P)\) 는 \(F^{T}\) 로 나타낼 수 있습니다. 이러한 대칭 관계가 성립하는 이유는 epipolar geometry에서 두 이미지 간의 역 관계가 성립하기 때문입니다. 역관계를 살펴보면 다음과 같습니다.

\[x'^{T} F x = 0\]
\[(x'^{T} F x)^{T} = 0\]
\[(x'^{T} F x)^{T} = x^{T} F^{T} x' = 0\]

다음으로 Epipolar lines 성질에 대하여 살펴보도록 하겠습니다. 관련 내용은 앞에서 다룬 내용입니다. \(l' = Fx\) 로 정의되는 epipolar line은 두번째 이미지에 형성되며 첫번째 이미지의 포인트 \(x\) 에 대응됩니다.
반대 방향으로 \(l = F^{T} x'\) 로 식을 적용할 수 있습니다. \(l\) 은 첫번째 이미지에 형성되는 epipolar line이고 두번째 이미지의 포인트 \(x'\) 에 대응됩니다.
2가지 방향 모두 아래 식과 같이 epipolar constrain을 통해 정의될 수 있습니다.

\[x'^{T} F x = (x'^{T}) (F x) = (x'^{T}) l' = 0\]
\[x^{T} F^{T} x' = (x^{T}) (F^{T} x') = (x^{T}) l = 0\]

다음으로 Epipole 성질에 대하여 살펴보도록 하겠습니다.
두번째 이미지의 임의의 epipolar line \(l' = Fx\) 은 epipole \(e'\) 를 포함하고 있습니다. 왜냐하면 두번째 이미지의 epipole은 첫번째 이미지를 촬영한 카메라의 센터점이기 때문에 \(l'\) 는 항상 \(e'\) 에 수렴하게 되어있습니다. 이 원리는 반대 방향도 동일하게 적용됩니다.
다음으로 Epipole과 Fundamental Matrix의 관계를 살펴보면 다음과 같습니다. 다음 수식을 살펴보겠습니다.

\[e'^{T} (Fx) = (e'^{T}F)(x) = 0\]

epipole \(e'\) 는 epipolar line \(l'\) 상에 있기 때문에 위 식과 같이 적을 수 있습니다. 그리고 \(x\) 는 영벡터가 아닌 유효한 이미지 포인트이기 때문에 \((e'^{T}F) = 0\) 를 만족해야 위 식을 만족시킬 수 있습니다.
따라서 \(e'\) 는 \(F\) 에 대하여 left null-vector가 됩니다.

반대 방향으로 적용하면 다음과 같습니다.

\[e^{T} F^{T} x' = x'^{T} F e = x'^{T} (F e) = 0\]

같은 논리로 \(e\) 는 \(F\) 에 대하여 right null-vector가 됩니다.

앞에서 설명한 바와 같이 \(F\) 는 7-DOF를 가집니다. 9개의 elements 중 scale ambiguity와 Rank-2 constraint로 2개의 DOF가 제외되어 최종적으로 7-DOF를 가지게 됩니다.

Fundamental Matrix는 임의의 포인트 \(x\) 를 epipolar line \(l'\) 로 변환하는 행렬입니다. 즉, 점을 선으로 매핑하는 관계를 가지게 됩니다.
첫번째 카메라에서 형성되는 \(l\) 과 두번째 카메라에서 형성되는 \(l'\) 은 corresponding epipolar lines 라고 부르며 \(l\) 선상에 있는 임의의 점 \(x\) 를 \(F\) 통해 매핑하였을 때, \(l'\) 선상에 위치하게 됩니다. 물론 그 반대 관계도 성립합니다.
이와 같은 점 → 선으로의 매핑 관계를 가지므로 역관계는 가질 수 없습니다. (1:1 대응이 되지 않기 때문입니다.) 이와 같은 조건이 \(F\) 가 full rank가 될 수 없는 이유이기도 합니다.

지금까지 살펴본 Fundamental Matrix 내용을 살펴보면 위 표와 같습니다.

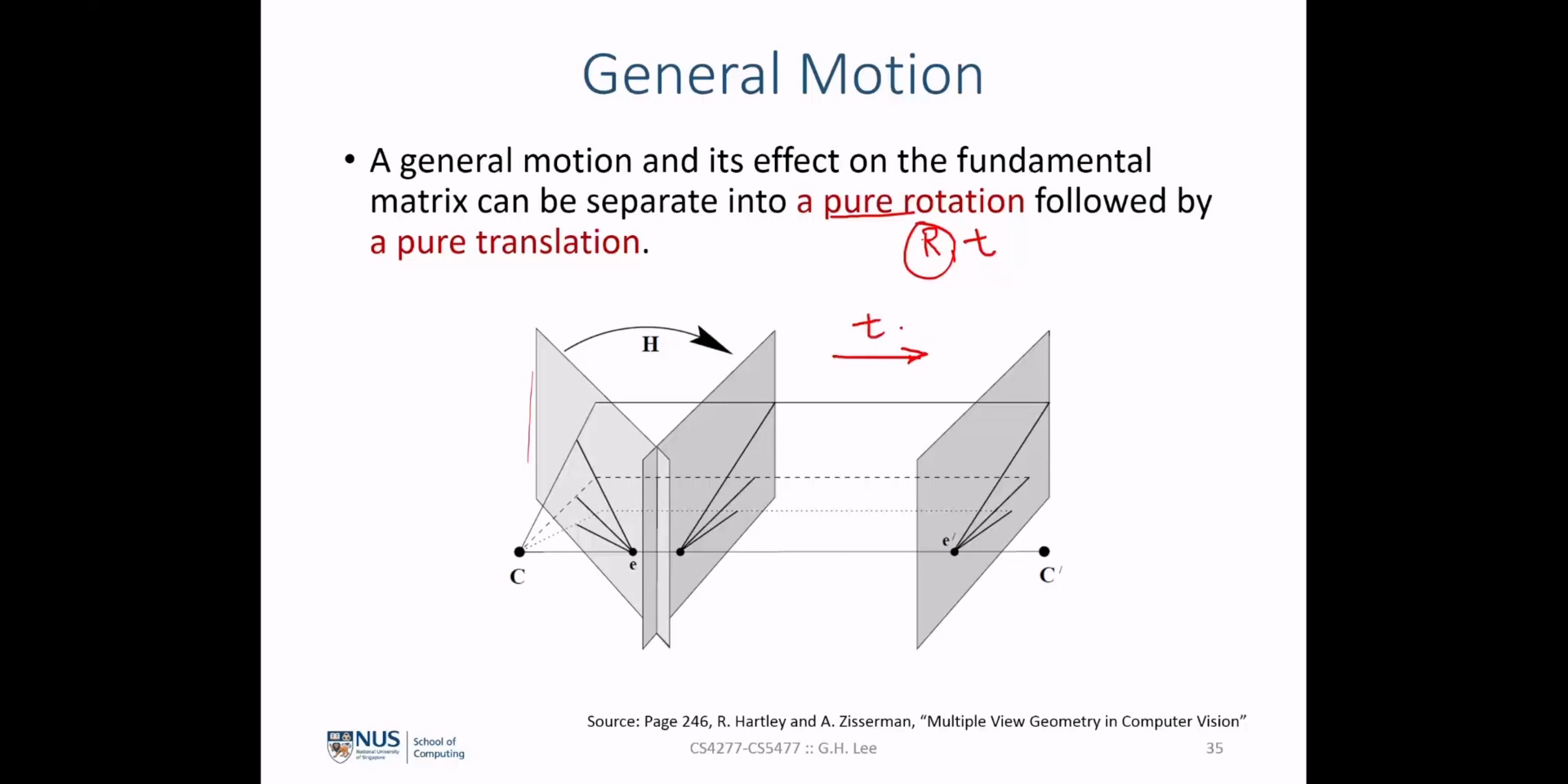
이번 강의에서는 앞의 강의에서 다룬 Fundamental Matrix를 이용하여 개념을 좀 더 확장해 보도록 하겠습니다.
먼저 Epipolar Line의 관계를 정의하는 Epipolar Line Homography 부터 다루어 보도록 하겠습니다.

corresponding epipolar line인 \(l\) 과 \(l'\) 가 있고 epipole \(e\) 를 통과하지 않는 임의의 선 \(k\) 가 있다고 가정하겠습니다. 이 때, \(l' = F[k]_{\times}l\) 을 만족하며 \(F[k]_{\times}\) 는 \(l\) 과 \(l'\) 사이의 관계를 정의하는 homography 역할을 합니다.
대칭 관계를 이용하면 \(l = F^{T}[k']_{\times} l'\) 을 만족합니다.

이 관계가 성립하는 이유는 간단히 \([k]_{\times} l = k \times l = x\) 가 성립하기 때문입니다. 즉 epipolar line과 임의의 선 \(k\) 의 cross product를 통해 교차점에서 \(x\) 를 도출해 낼 수 있습니다. (교차점이기 때문에 \(x\) 는 \(l\) 상에 존재합니다.)
따라서 \(F[k]_{\times}l = Fx = l'\) 를 만족하며 그 결과 \(x\) 와 \(l\) 에 대응되는 epipolar line \(l'\) 가 됨을 알 수 있습니다.

따라서 \(l\) 과 \(l'\) 간의 변환 관계인 homography는 \(F[k]_{\times}\) 와 \(F^{T}[k']_{\times}\) 가 됨을 알 수 있었습니다.

위 그림과 같이 \(l_{i}\) 는 \(l'_{i}\) 와 대응되는 관계입니다. 앞에서 이러한 관계를 correspondence 라고 언급하였었습니다. 대응되는 epipolar lines는 각각의 이미지에서 epipole \(e\) 와 \(e'\) 를 공통적인 교점으로 가지고 있습니다. 이와 같이 하나의 공통 요소를 가지고 있는 집합을 pencil 이라고 부릅니다. 따라서 위 그림은 pencil of epipolar lines를 나타냅니다.
epipolar line \(l_{i}\) 와 \(l'_{i}\) 그리고 base line을 통해 plane을 만들 수 있습니다. 각 대응되는 epipolar line을 통해 다양한 plane을 만들 수 있고 공통 요소인 base line을 가지므로 이렇게 만들어진 plane을 pencil of planes라고 합니다. 물론 공통 요소는 base line이 됩니다.

base line 상의 임의의 점 \(p\) 를 중심으로 두 이미지 \(I, I'\) 에 대하여 선을 긋는 상황을 살펴보도록 하겠습니다.
pencil of epipolar lines과 epipole \(e\) 를 통과하지 않는 임의의 선 \(k\) 와 교차하는 점을 이미지 \(I, I'\) 에 검은 점으로 표현하였습니다. 점 \(p\) 에서 부터 \(I, I'\) 의 검은 점을 연결하는 직선을 그엇다고 가정하겠습니다.
두 이미지 \(I, I'\) 간의 점들이 homography (Perspective Transform) 변환 관계이므로 점들 간의 cross-ratio는 만족함을 알 수 있습니다.

슬라이드에서 1D homography는 다음을 만족하는 homography를 의미합니다.

\[l' = H_{ll'} l\]
\[l = [a, b, c]^{T} = e + td\]
\[l' = [a', b', c']^{T} = e' + t'd'\]
\[t \text{ : scale parameter}\]
\[d \text{ : direction vector}\]

이번에는 Pure Translation이 발생하였을 때의 Fundamental Matrix를 살펴보도록 하겠습니다. Pure Translation이라고 하면 하나의 카메라를 이동시켰을 때, Rotation은 발생하지 않고 단순히 Translation만 발생한 경우를 의미합니다. 카메라 하나를 이용한 2개의 이미지 이므로 intrinsic \(K\) 는 하나입니다.
20p 슬라이드 내용을 통하여 Fundamental Matrix \(F\) 를 다음과 같이 정의할 수 있었습니다.

\[F = [e']_{\times} K' R K^{-1}\]

여기서 \(R = I\) 가 되고 \(K'=K\) 이므로 식을 다음과 같이 정리할 수 있습니다.

\[F = [e']_{\times} K' R K^{-1} = [e']_{\times} K I K^{-1} = [e']_{\times}\]

skew-symmetric 형태의 \([e']_{\times}\) 는 epipole의 값에 의해 결정됩니다. epipole \(e'\) 는 \((x', y', 1)\) 의 좌표값을 가지므로 2-DOF를 가지게 됩니다. 즉, \(e'\) 좌표값에 의해 Fundamental Matrix가 결정됩니다.

\[F = [e']_{\times} = \begin{bmatrix} 0 & -1 & y' \\ 1 & 0 & -x' \\ -y' & x' & 0 \end{bmatrix}\]

skew-symmetric \(n \times n\) 행렬에서 \(n\) 의 크기가 홀수이면 최대 rank는 \(n-1\) 임이 알려져 있습니다.
skew-symmetric 행렬의 정의는 다음과 같습니다.
- ① \(A = -A^{T}\)
- ② \(\text{All diagonal elements are zero.}\)
따라서 행렬 \(A\) 는 다음과 같이 determinant를 적용할 수 있습니다.

\[\text{det}(A) = \text{det}(-A^{T}) = (-1)^{n}\text{det}(A)\]
\[\text{det}(A) = -\text{det}(A) \quad (\because n = 3 \text{ is odd.})\]
\[\therefore \text{det}(A) = 0\]

위 식과 같이 \(\text{det}(A) = 0\) 를 만족하므로 최대 rank는 \(n - 1\) 이 되고 앞에서 다룬 바와 같이 Fundamental Matrix의 rank \(3 - 1 = 2\) 를 만족하게 됩니다.

Pure Translation 조건에서 다음 조건이 만족함을 확인할 수 있습니다.

\[l' = Fx = [e']_{\times}x\]

그리고 \(x'\) 는 \(l'\) 상에 존재하므로 다음과 같이 식을 적을 수 있습니다.

\[x'^{T}[e']_{\times}x = 0\]

위 식을 해석하면 \(x'\) 와 \(e'\) 는 같은 선상에 있고 (epipolar line) 심지어 \(x\) 또한 같은 선상에 있으므로 \(x, x', e=e'\) 가 같은 선상에 있는 것으로 이해할 수 있습니다. 따라서 collinear 관계임을 확인할 수 있습니다.

참조 : https://www.geeksforgeeks.org/python-opencv-epipolar-geometry/

현재 다루고 있는 Pure Translation의 경우 위 그림과 같이 2개의 이미지가 평행한 상태입니다.
위 그림과 같이 두 이미지 평면이 평행할 때 두 카메라 중심을 연결하는 기준선이 이미지 평면과 평행하므로 epipole \(e\) 와 \(e'\) 는 무한대에 위치하고 epipolar line은 각 이미지 평면의 \(u\) 축과 평행합니다.
이전 강의에서 무한대에 존재하는 점을 point at infinity라고 하였으며 vanishing point라는 이름으로 다루기도 하였습니다. 즉, 평행하는 두 이미지의 epipole은 vanishing point가 됩니다.

위 예시는 Pure Translation을 가정한 예시입니다. 카메라는 고정인 상태로 세상만 \(-t\) 만큼 translation 하였다는 가정입니다.
앞의 슬라이드에서 다루었듯이 Pure Translation 상태에서는 \(x, x', e\) 가 모두 collinear 함을 확인하였습니다. 따라서 두 직육면체의 대응되는 점들을 이어서 선을 만들었을 때, 그 선이 모이는 지점의 vanishing point가 epipole \(e\) 가 됩니다. \(e\) 에서 pencil of epipolar lines가 형성되는 것을 볼 수 있습니다.

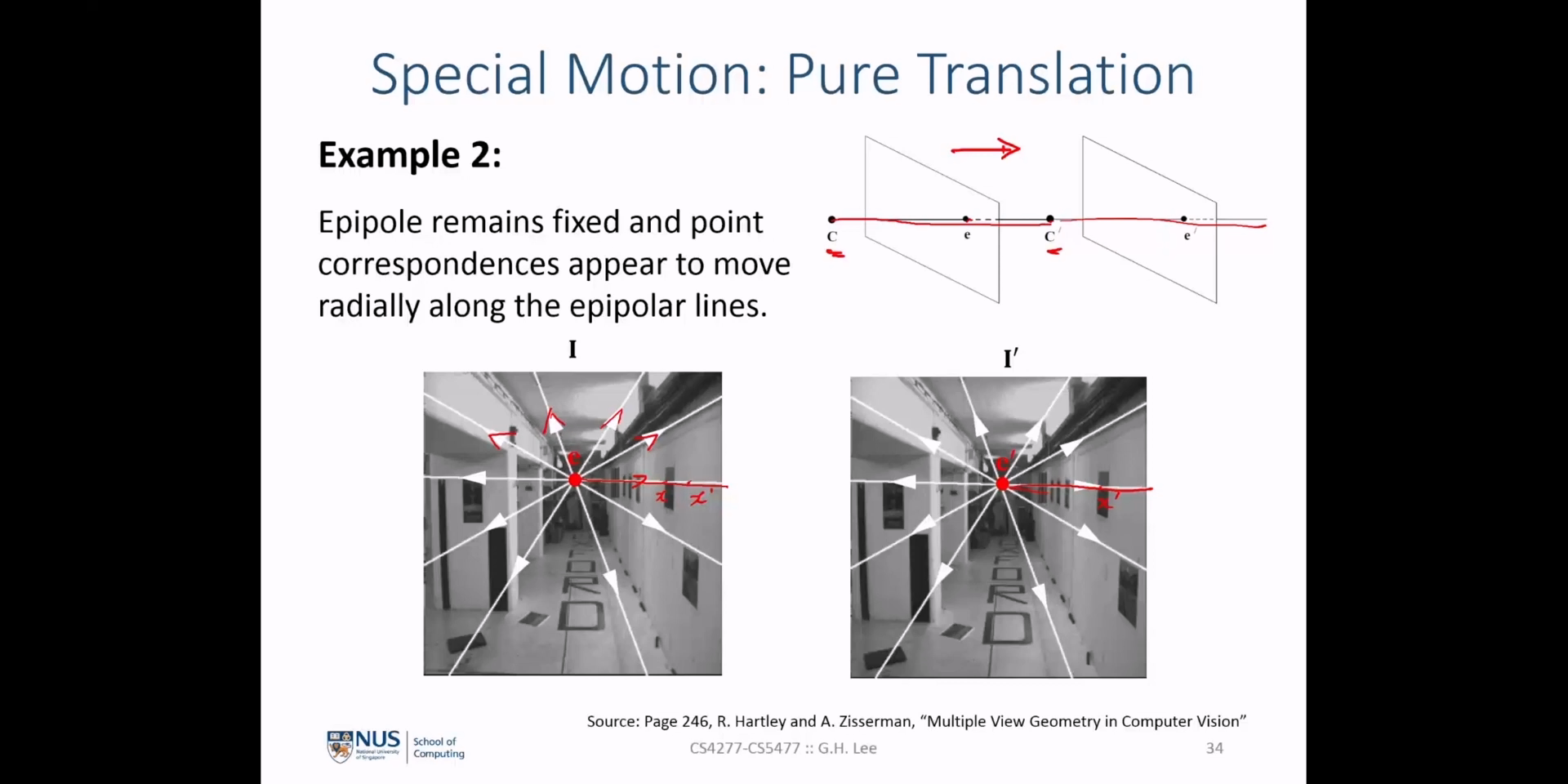
두번째 예시에서도 Pure Translation임을 가정합니다. 따라서 카메라 이동 발생 시 카메라 중점 \(C\) 의 위치는 collinear 한 상태로 이동하게 됩니다. 따라서 \(e = e'\) 를 만족합니다.
Pure Translation이 발생하였으므로 epipolar line 또한 그대로 유지됩니다. 하지만 \(x, x'\) 는 카메라의 움직임 때문에 실제 이미지 상의 위치는 옮겨질 것입니다. 따라서 correspondent point인 \(x, x'\) 는 Pure Translation 시 이미지 상의 위치 이동은 발생하되 epipolar line을 따라서 움직이게 되어 epipolar line은 그대로 유지됩니다.

40p에서 보여준 바와 같이 canonical form 형태의 행렬 \(P\) 와 그에 대응되는 행렬 \(P'\) 를 이용할 때, \(F = [a]_{\times} A\) 가 됨을 확인하였습니다. 같은 논리로 \(F = [\tilde{a}]_{\times} \tilde{A}\) 또한 만족합니다.
그리고 벡터 \(a\) 의 cross product \(a \times a = 0\) 이기 때문에 다음과 같이 식이 유도될 수 있습니다.

\[a^{T}F = a^{T}[a]_{\times}A = 0\]
\[\tilde{a}^{T}F = \tilde{a}^{T}[\tilde{a}]_{\times}\tilde{A} = 0\]

Fundamental Matrix \(F\) 는 앞에서 살펴본 바와 같이 rank가 2이므로 null-space를 가집니다.
따라서 \(a^{T}F = \tilde{a}^{T}F = 0\) 에서 \(a, \tilde{a}\) 각각은 같은 \(F\) 에 대한 null-space를 가지므로 \(\tilde{a} = ka\) 와 같이 dependent하게 표현할 수 있습니다.
또는 \(\tilde{a}^{T}F = \tilde{a}^{T}[a]_{\times}A = 0\) 을 항상 만족하기 위해서는 \(\tilde{a}^{T}[a]_{\times}\) 가 항상 \(0\) 을 만족해야 하므로 이 조건을 만족하기 위해서는 cross proudct가 0이 되는 \(\tilde{a} = ka\) 조건을 만족해야 하는 것으로도 해석할 수 있습니다.
따라서 \(\tilde{a} = ka\) 를 이용하면 다음과 같이 식을 전개할 수 있습니다.

\[[a]_{\times}A = [\tilde{a}]_{\times}\tilde{A}\]
\[[a]_{\times}(k\tilde{A} - A) = 0\]

위 식을 만족하려면 \([a]_{\times}\) 와 \(a\) 의 cross product 연산을 통해 항상 0 벡터가 만들어 질 수 있도록 구성해야 합니다. 따라서 \(k\tilde{A} - A = av^{T}\) 로 정의할 수 있습니다. 이 때, \(v\) 는 임의의 벡터입니다. 정리하면 \(\tilde{A}\) 는 다음과 같습니다.

\[\tilde{A} = k^{-1}(A + av^{T})\]

앞의 21p 슬라이드를 살펴보면 \(F = [e']_{\times}P'P^{+} = K'^{-T} [t]_{\times} R K^{-1}\) 을 전개하는 방법에 대하여 다루었습니다. 따라서 49p의 슬라이드에 해당하는 내용을 다음과 같이 전개할 수 있습니다.

\[F = K'^{-T} E K^{-1} = K'^{-T} [t]_{\times} R K^{-1}\]
\[E = [t]_{\times} R\]

앞에서 살펴본 바와 같이 Essential Matrix를 결정하기 위해서는 \(R\) 과 \(t\) 만 결정되면 됩니다. \(R\) 의 경우 scale이 없으며 각 축의 방향으로의 회전량이 정해지면 되기 때문에 3개의 자유도를 가집니다.
반면 \(t\) 의 경우 움직임에 해당하는 Translation이므로 scale과 연관되어 있습니다. 하지만 scale이 정해질 수 없는 scale ambiguity 상황에서는 자유도가 1개 빠지게 되어 2개의 자유도만을 가질 수 있습니다. \(t\) 의 경우 \(s \cdot \hat^{t}\) 으로 표현할 수 있습니다. 여기서 \(s\) 는 scale로 임의의 상수로 가정한 것이고 \(\hat{t}\) 는 normalized vector를 의미합니다. 즉, 방향값만 가지고 있는 벡터라고 보면 됩니다. 식으로 나타내면 다음과 같습니다.

\[\hat{t} = (\hat{t}_{x}, \hat{t}_{y}, \hat{t}_{z}) = \frac{(t_{x}, t_{y}, t_{z})}{\sqrt(t_{x}^{2} + t_{y}^{2} + t_{z}^{2})}\]

이 때, normalized vector는 \(\hat{t}_{x}^{2} + \hat{t}_{y}^{2} + \hat{t}_{z}^{2} = 1\) 의 조건을 만족해야 하므로 \((\hat{t}_{x}, \hat{t}_{y}, \hat{t}_{z})\) 중 2개만 만족하면 나머지 하나는 결정됩니다. 따라서 \(s \cdot \hat^{t}\) 에서 결정되어야 하는 것은 2개이므로 \(t\) 를 구할 때 DoF는 2개가 됩니다.

따라서 \(R\) 을 구할 때 3 DoF와 \(t\) 를 구할 때 2 DoF로 Essential Matrix는 5 DoF를 가집니다.

위 식에서 \(E = [t]_{\times} R\) 의 각 성분을 SVD를 적용하면 다음과 같습니다.

\[[t]_{\times} = U Z U^{T}\]
\[R = UXV^{T}\]

Skew-symmetric matrix인 \([t]_{\times}\) 인 경우 다음과 같은 이유로 SVD 시 같은 orthogonal matrix( \(U\) ) 로 분해 됩니다.

\[A = U \Lambda V^{T}\]
\[A^{T}A = V \Lambda U^{T}U \Lambda V^{T} = V \Lambda^{2} V^{T}\]

따라서 Skew-symmetric matrix를 SVD 하였을 때, \(U, V\) 는 같은 값으로 분해됩니다.

반면 \(R\) 을 SVD 하였을 때, \([t]_{\times}\) 에서 분해된 \(U\) 가 \(R\) 에도 사용되었습니다. 이와 같이 \(U\) 가 같이 사용됨으로 인하여 \(E = [t]_{\times} R\) 로 묶일 수 있도록 수식이 전개됩니다.
기하적으로는 동일한 \(U\) 를 사용하면 Translation 및 Rotation이 동일한 좌표계에 표시됩니다. SVD의 \(U\Lambda V^{T}\) 에서 \(U, V\) 는 basis의 회전으로 나타내고 \(\Lambda\) 는 basis의 스케일 변화를 나타냅니다. (참조 : SVD 의미 해석)
따라서 최종 \(R\) 을 적용하였을 때, basis가 \(U\) 에 의해 회전되고 \(t\) 또한 basis가 \(U\) 에 의해 회전되도록 구성되어야 기하학적으로 일관성이 있기 때문에 \([t]_{\times} R\) 값이 의미를 가지게 됩니다.

위 슬라이드에서 설명하는 Frobenius norm은 행렬의 크기 및 사이즈 등을 측정하는 척도이며 벡터의 크기를 측정하는 방법과 유사합니다. 대표적으로 사용하는 Frobenius norm의 수학적인 정의는 다음과 같습니다.

\[\Vert A \Vert_{F} = \sqrt{\sum_{i}\sum_{j} \vert a_{ij} \vert^{2} }\]

위 식은 행렬 \(A\) 에 대하여 square root of sum of absolute squares를 나타냅니다.
이와 같은 방법으로 크기를 정하는 것은 벡터의 Euclidean (L2) norm을 구하는 방식과 같으며 단지 행렬에 적용한 것으로 보면 됩니다.
반면에 Singular Value를 이용하는 방법도 존재합니다. singular value가 \(\sigma_{1}, \sigma_{2}, ... , \sigma_{n}\) 일 때, Frobenius norm은 다음과 같습니다.

\[\Vert A \Vert_{F} = \sqrt{\sigma_{1}^{2} + \sigma_{2}^{2} + ... + \sigma_{n}^{2}}\]

이와 같이 Frobenius norm을 계산하는 방법은 여러가지가 있고 다음과 같은 조건을 만족하면 Frobenius norm이라고 합니다.
① Frobenius norm은 항상 0 또는 양수이어야 합니다. (non-negative)
② Frobenius norm이 0이면 행렬은 항상 영행렬 이어야 하며 그 역도 성립합니다.
③ triangle inequality가 성립합니다. \(\Vert A + B \Vert_{F} \le \Vert A \Vert_{F} + \Vert B \Vert_{F}\)
④ orthogonal transformation에 대하여 불변해야 합니다. \(\Vert Q A U \Vert_{F} = \Vert A \Vert_{F} \quad (Q, U \text{ are orthogonal matrices.})\)