(멀티플 뷰 지오메트리) Lecture 8. Absolute Pose Estimation from Points or Lines

2022, Apr 20    

Multiple View Geometry 글 목차

• 참조 : https://youtu.be/C5L7LnNL4oo?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : https://youtu.be/8Nh1UeuD9-k?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : https://youtu.be/9peph2zvSyY?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
• 참조 : Multiple View Geometry in Computer Vision

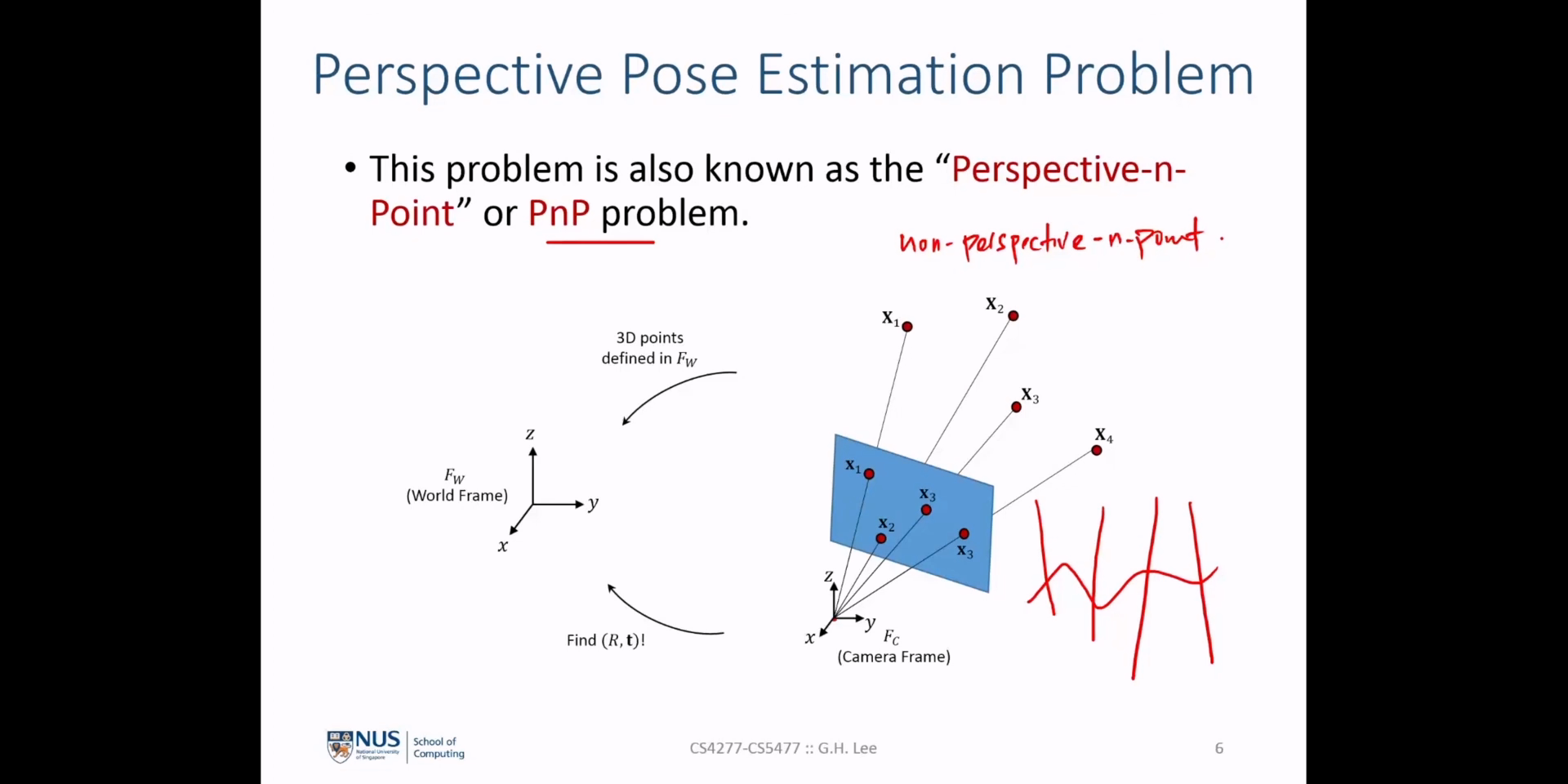
• Lecture 8에서는 Camera Pose Estimation 문제를 풀기 위한 PnP(Perspective-n-point) 문제를 정의하고 카메라의 calibration 정보를 사용하는 경우와 그렇지 않은 경우에 대하여 Pose Estimation을 하는 방법에 대하여 알아보도록 하겠습니다.

• Companion Matrix의 정의

• 참조 : https://youtu.be/N1aCvzFll6Q?t=1769
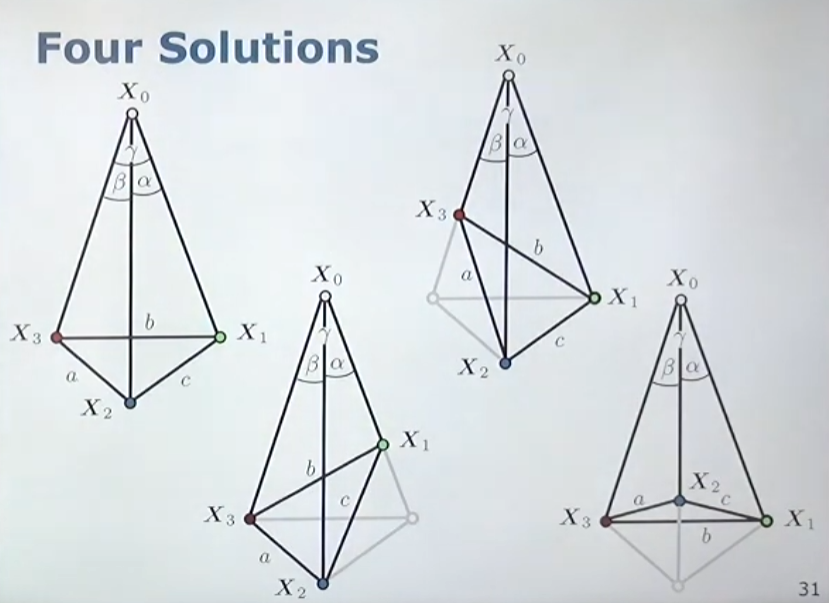
• 앞에서 설명한 Companion Matrix 또는 다차 방정식의 해를 구하는 방법을 통하여 4차 방정식을 풀면 4가지의 해를 구할 수 있습니다. 따라서 4가지의 해 중 실제 해에 해당하는 값을 구할 수 있어야 합니다.
• 예를 들면 위 그림과 같이 4가지 경우의 해를 구할 수 있기 때문에 추가적인 정보를 이용하여 특정 상황을 결정해 주어야 합니다. 이 경우 4번째 점인 $X_{4}$ 에 대한 정보를 추가적으로 이용하여 depth를 구하였을 때에도 동일한 값이 나오는 경우를 선택하면 실제 해를 구할 수 있습니다. (또는 다른 추가적인 센서 값을 이용할 수도 있습니다.)

• 앞의 슬라이드 과정에서 unknown depth인 $s_{s1}, s_{2}, s_{3}$ 를 구하면 카메라 좌표 기준의 3D 포인트의 좌표인 $p'_{1}, p'_{2}, p'_{3}$ 를 알 수 있습니다.
• 현재 최종적으로 구하고자 하는 목표인 absolute orientation는 $p'_{1}, p'_{2}, p'_{3}$ 을 $p_{1}, p_{2}, p_{3}$ 로 변환하기 위한 $(R, t)$ 값을 구하는 것이며 다음 식을 만족하는 $(R, t)$ 값을 구하는 것이 목표가 됩니다.

• $$\text{argmin}_{R, t} \sum_{i=1}^{i=n} \Vert p_{i} - (Rp_{i} + t) \Vert$$

• 이 때, $n \ge 3$ 을 만족해야 문제를 풀 수 있는 조건이 됩니다.

• 먼저 위 슬라이드의 식과 같이 $p_{i}$ 와 $p'_{i}$ 각각의 중앙점인 centroid인 $\bar{p}_{i}, \bar{p}'_{i}$ 를 평균값을 이용하여 구합니다.
• 그 다음 $r_{i} = p_{i} - \bar{p}_{i}$ 와 $r'_{i} = p'_{i} - \bar{p}'_{i}$ 를 구합니다. 이 값은 기존 각 좌표의 기준점이 각 카메라의 원점인 상태를 좌표들의 중앙점으로 바꾼 것입니다. 이 치환식의 정의에 따르면 $r_{i}, r'_{i}$ 각각은 각 점 $p_{i}, p'_{i}$ 가 centroid인 $\bar{p}_{i}, \bar{p}'_{i}$ 로 부터 얼만큼 떨어져 있는 지 나타냅니다.
• 이와 같이 사용하는 이유는 두 점군들의 관계를 $t$ 와 상관없이 $R$ 로만 나타낼 수 있기 때문입니다. 기존에는 하나의 원점을 기준으로 두 점군의 좌표 값이 나타내어졌다면 centroid를 이용하면 각 점군이 centroid로 부터 얼만큼 떨어져 있는 지 나타내기 때문에 centroid 기준의 좌표계를 가지게 됩니다. 따라서 각 점의 좌표는 centroid 와의 거리 차이를 나타내는 벡터가 되고 각 벡터 $r_{i}, r'_{i}$ 의 회전 차이인 $R$ 만 구하면 되는 문제로 바뀌게 됩니다. 따라서 이와 같은 방법을 사용합니다.

• Roatation 행렬 $R$ 을 구하기 위하여 먼저 다음과 같은 행렬 $M$ 을 먼저 계산합니다. $M$ 은 sum of outer product를 나타내며 각 $r_{i}, r'_{i}$ 의 각 좌표축 별 상관관계를 나타냅니다.

• $$M = \sum_{i=1}^{n} r'_{i}r_{i}^{T}$$

• 만약 $r'_{i} = (x'_{i}, y'_{i}, z'_{i})^{T}$, $r_{i} = (x_{i}, y_{i}, z_{i})^{T}$ 라고 하면 $i$ 인덱스에 대한 행렬 연산의 결과는 다음과 같습니다.

• $$r'_{i}r_{i}^{T} = \begin{bmatrix} x'_{i}x_{i} & x'_{i}y_{i} & x'_{i}z_{i} \\ y'_{i}x_{i} & y'_{i}y_{i} & y'_{i}z_{i} \\ z'_{i}x_{i} & z'_{i}y_{i} & z'_{i}z_{i} \end{bmatrix}$$

• 위 행렬은 두 벡터의 correlation을 의미합니다. 각 $i$ 번 째 벡터 간의 연산을 outer product한 다음 생성된 행렬을 element-wise sum을 하면 원하는 행렬인 $M$ 을 얻을 수 있습니다. $M$ 은 두 점군의 전체 correlation의 누적된 정보를 의미합니다. 직관적으로 $M$ 은 변환된 점이 상대 위치와 방향 측면에서 원래 점과 어떻게 관련되어 있는지 나타냅니다. 행렬 $M$ 의 의미를 정리하면 다음과 같습니다.

• 행렬 $M$ 의 대각 요소는 해당 원래 점을 기준으로 변환된 점의 $x, y, z$ 구성 요소의 분산을 나타냅니다.
• 행렬 $M$ 의 비대각 요소는 변환된 점의 $x, y, z$ 구성 요소와 해당 원래 점 사이의 공분산을 나타냅니다.

• 행렬 $M$ 에 의해 정의된 correlation 정보는 위 슬라이드의 행렬 $Q$ 를 통하여 normalized 하여 두 점 군을 가장 잘 정렬하는 회전 행렬 $R$ 을 유도하는 데 사용 됩니다.
• 아래 내용 전개 시, 특이값 분해 내용이 사용되므로 관련 내용은 아래 링크를 참조하시면 됩니다.
  • 특잇값 분해

• $$M = U \Sigma V^{T} \text{, Singular Value Decomposition}$$
• $$Q = M^{T}M = (U \Sigma V^{T})^{T}(U \Sigma V^{T}) = (V \Sigma^{T} U^{T})(U \Sigma V^{T}) = V(\Sigma^{2})V^{T}$$
• $$Q^{-1/2} = V(\Sigma^{2})V^{T} = V\Sigma^{-1}V^{T}$$
• $$MQ^{-1/2} = (U \Sigma V^{T})(V\Sigma^{-1}V^{T}) = U(\Sigma\Sigma^{-1})V^{T} = UV^{T}$$

• 마지막으로 구한 $UV^{T}$ 는 orthogonal matrix이며 행렬 $M$ 의 rotation을 의미합니다. 위 식에서 $M$ 에 $Q^{-1/2}$ 를 곱함으로써 scaling 및 shearing 요소들을 제거하여 순수하게 rotation 정보만을 얻을 수 있었습니다.
• 행렬 $Q = (M^{T}M)^{-1/2}$ 이기 때문에 normzalization을 위한 스케일 값만을 제거해주는 역할을 하는 것을 식을 통해서도 알 수 있습니다.

• 다음과 같이 특이값 분해의 본연의 성질을 시각화한 것을 살펴보면 앞의 설명을 이해하실 수 있을 것입니다.
  

• 따라서 지금까지 식의 전개 내용을 살펴보면 다음과 같습니다.
• ① 각 좌표를 centroid를 기준으로 centroid와의 거리 차이를 나타내는 벡터로 표현합니다.
• ② 두 점군의 벡터 $r_{i}, r'_{i}$ 의 correlation을 나타내는 행렬 $M$ 을 구합니다. $M$ 은 rotation 정보 뿐 아니라 scaling, shearing 등의 정보 또한 포함하고 있습니다. 따라서 $MQ^{-1/2} = M(M^{T}M)^{-1/2}$ 을 통해 Normalization을 적용합니다.
• ③ 순수한 rotation 정보만을 추출하기 위하여 $MQ^{-1/2}$ 에 특이값 분해를 적용하여 rotation 정보를 추출합니다.

• 마지막 ③ 과정에서 특이값 분해 과정을 좀 더 자세하게 살펴보면 다음과 같습니다.

• $$M = U \Sigma V^{T}$$
• $$U \text{ : The columns of U represent the principal axes of the transformed point set in the transformed coordinate system.}$$
• $$V \text{ : The columns of V represent the principal axes of the original point set in the original coordinate system.}$$
• $$\Sigma \text{ : the variances of the transformed points along these principal axes.}$$

• 따라서 $M = U \Sigma V^{T}$ 는 ① $V^{T}$ 를 통하여 original coordinate system의 principal axes 성분을 제거하여 normalized space로 principal axes를 변경하고 ② normalized space 에서 $\Sigma$ 만큼 scale을 조정한 뒤 ③ 최종적으로 변환하고자 하는 transformed coordinate system으로 principal axes를 변환하는 과정입니다.
• 이 때, 필요한 정보는 scale이 제거된 순수한 rotation 정보인 $UV^{T}$ 고 이는 다음과 같은 전개로 구할 수 있음을 확인하였습니다.

• $$R = MQ^{-1/2} = (U \Sigma V^{T})(V \Sigma^{-1} V^{T}) = UV^{T}$$

• 즉, $UV^{T}$ 는 original coordinate system을 normalized coordinate systme으로 변환하고 다시 transformed coordinate system으로 변환하기 때문에 순수한 의미의 rotation 행렬이라고 볼 수 있습니다.

• 위 식에서 두 orthogonal matrix의 곱으로 $R$ 을 표현하였기 때문에, $RR^{T} = I$ 이고 determinant 또한 1임을 알 수 있습니다.

• 위 슬라이드에서는 이전 슬라이드 식 전개를 위해 $Q$ 의 고유값 분해 시 사용 방법을 기술하였습니다. 앞에서는 고유값 분해의 개선 버전인 특이값 분해를 이용하여 설명하였으므로 같은 논리로 생각하셔도 됩니다.

• 추가적으로 위 슬라이드의 고유값 분해 성질을 이용하여서도 앞에서 구한 $R$ 이 rotation 행렬의 요소인 $R^{T}R = I$ 인 것과 $\text{det}(R) = 1$ 임을 보일 수 있습니다.

$RR^{T} = I$

• $$R^T R = (M Q^{(-1/2)})^T (M Q^{(-1/2)}) = (Q^{(-1/2)})^T M^T M Q^{(-1/2)} = (Q^{(-1/2)})^T Q Q^{(-1/2)} = (Q^{(-1/2)})^T Q^{(1/2)} Q^{(1/2)} Q^{(-1/2)}$$

• 다음 성질들을 이용하여 식을 전개해 보도록 하겠습니다.

• $$Q^{(-1/2)} = V \Lambda^{(-1/2)} V^T, \text{where } \Lambda^{(-1/2)} \text{ is a diagonal matrix with the square roots of the eigenvalues.}$$
• $$Q^{(1/2)} = V \Lambda^{(1/2)} V^T, \text{where } \Lambda^{(1/2)} \text{ is a diagonal matrix with the square roots of the eigenvalues.}$$
• $$\Lambda^{(-1/2)} ,\Lambda^{(1/2)} \text{ are reciprocals of each other.}$$
• $$V^T V = V V^T = I$$

• $$\therefore \begin{align} (Q^{(-1/2)})^T Q^{(1/2)} Q^{(1/2)} Q^{(-1/2)} &= (V \Lambda^{(-1/2)} V^T)^T (V \Lambda^{(1/2)} V^T) (V \Lambda^{(1/2)} V^T) (V \Lambda^{(-1/2)} V^T) \\ &= V \Lambda^{(-1/2)} V^T V \Lambda^{(1/2)} V^T V \Lambda^{(1/2)} V^T V \Lambda^{(-1/2)} V^T \\ &= VV^{T} = I \end{align}$$

$\text{det}(R) = 1$

• $$\text{det}(R) = \text{det}(M Q^{(-1/2)}) = \text{det}(M) \text{det}(Q^{(-1/2)}) = \text{det}(M) \text{det}(V \Lambda^{(-1/2)} V^T) = \text{det}(M) \text{det}(V) \text{det}(\Lambda^{(-1/2)}) \text{det}(V^T) = \text{det}(M)\text{det}(\Lambda^{(-1/2)})$$

• 식의 전개를 위해 $\Lambda^{(-1/2)}$ 를 살펴보겠습니다.

• $$\Lambda^{(-1/2)} = \text{diag}(1/\text{sqrt}(\lambda_{1}), 1/\text{sqrt}(\lambda_{2}), \cdots , 1/\text{sqrt}(\lambda_{1n}))$$
• $$\begin{align} \text{det}(\Lambda^{(-1/2)}) &= 1/\text{sqrt}(\lambda_{1}) * 1/\text{sqrt}(\lambda_{2}) * \cdots * 1/\text{sqrt}(\lambda_{1n}) \\ &= 1/\text{sqrt}(\lambda_{1} * \lambda_{2} * \cdots * \lambda_{n}) \\ &= 1/\text{sqrt}(\text{det}(\Lambda)) \\ &= 1/\text{sqrt}(\text{det}(Q)) \end{align}$$

• 따라서 앞의 식을 다음과 같이 전개할 수 있습니다.

• $$\begin{align} \text{det}(R) &= \cdots \\ &= \text{det}(M)\text{det}(\Lambda^{(-1/2)}) \\ &= \text{det}(M) / \text{sqrt}(\text{det}(Q)) \\ &= \text{det}(M) / \text{sqrt}(\text{det}(M^{T})\text{det}(M)) \\ &= \text{det}(M)/\text{det}(M) = 1 \end{align}$$

• 따라서 $\text{det}(R) = 1$ 임을 확인할 수 있습니다.

Multiple View Geometry 글 목차