Segmentation의 Entropy 표현 방법

Segmentation의 Entropy 표현 방법

2021, Dec 01    


segmentation 관련 글 목차


목차



Entropy map의 의미


  • segmentation 관련 논문 또는 uncertainty 관련 논문을 읽다 보면 entropy map과 관련된 이미지를 볼 수 있습니다.


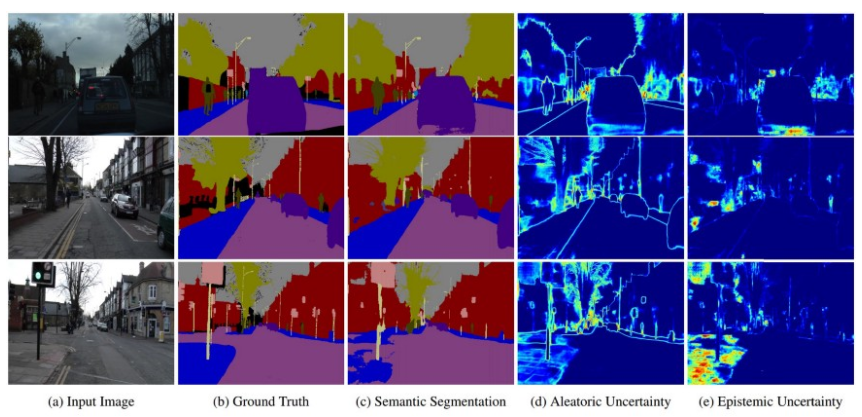
Drawing


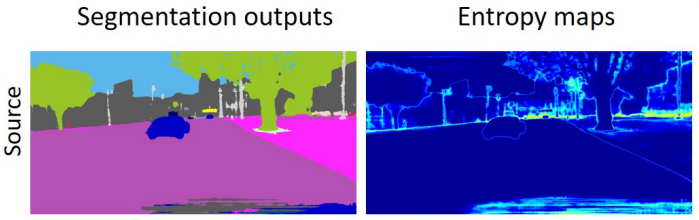
  • 위 그림에서 파란색 바탕에 밝은 엣지들로 표현된 것들이 entropy map이며 파란색에 가까울수록 entropy 값이 작고 빨간색에 가까울수록 entropy 값이 큰 것을 의미합니다.
  • entropy의 정확한 의미는 기초 정보 이론 (Entropy, Cross Entropy, KL divergence 등) 내용을 참조해 주시면 됩니다.
  • 간략하게 설명하면 entropy가 클수록 사용자가 얻을 정보가 작다고 보면 됩니다. 즉, 부정적인 값입니다. 흔히 말하는 불확실성에 대응합니다.
  • entropy 값이 크다는 것은 불확실하다는 것이고 그만큼 정보의 양이 작다는 것을 의미합니다. 반대로 entropy 값이 작다는 것은 확실하다는 것이고 그만큼 정보의 양도 많다는 것을 의미합니다. 예를 들어 내일 비올 확률이 50% 라고 하면 불확실 하다는 것이고 우산을 챙겨야 할지 아닐 지 고민스러워 집니다. 이 경우 정보의 양이 작습니다. 반면 내일 비올 확률이 100%라고 하면 확실하다는 것이고 내일 우산을 챙겨야 한다는 결정을 할 수 있으므로 정보의 양이 크다고 말할 수 있습니다.


  • 위 entropy map에서 파란색에 가까울수록 entropy 값이 적고 빨간색에 가까울수록 entropy 값이 크다고 설명하였습니다. 즉 파란색에 가까울수록 불확실성이 작다는 뜻이고 출력의 확률이 한 클래스에 높게 배정되었다는 뜻이됩니다. 반면 빨간색에 가까운 entropy 값은 불확실하다는 뜻이고 출력의 확률이 여러 클래스에 고르게 배정되어 있다는 뜻입니다. 앞의 예시에서 비가 올 확률이 50% 라는 것과 유사한 상태입니다.
  • 만약 모든 픽셀에서 불확실성 없이 출력을 한다면 entropy map은 모두 파란색일 것이고 모둔 픽셀이 불확실하다면 entropy map은 모두 빨간색일 것입니다.
  • 일반적으로 segmentation에서 클래스가 나뉘는 경계 부근에서 entropy가 커지는 경향이 있습니다.
  • 그러면 Entropy map을 어떻게 구하는 지 살펴보도록 하겠습니다.


Entropy map을 구하는 방법


  • segmentation의 출력은 Pytorch의 표현 방법을 기준으로 (Channel, Height, Width)의 모양을 가집니다.


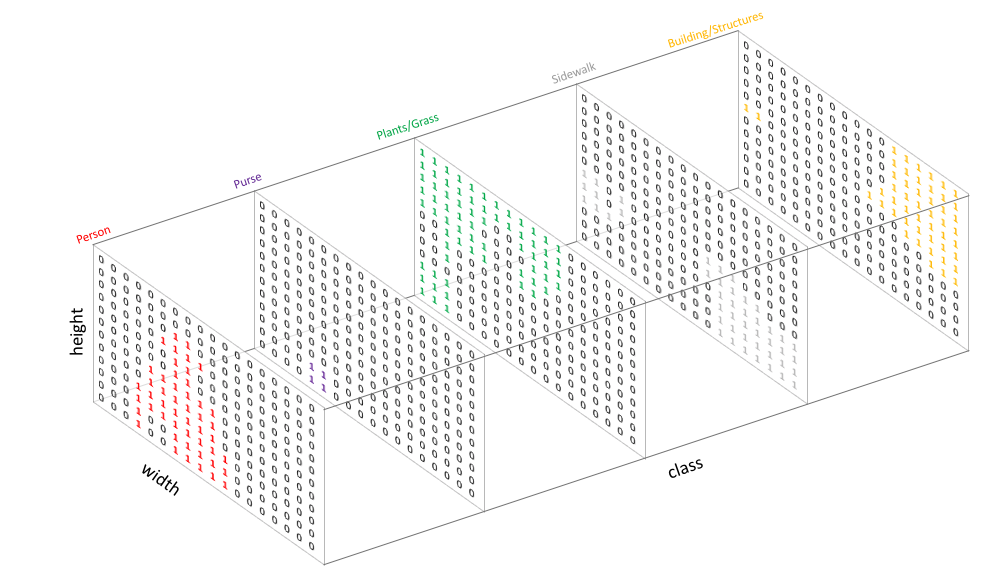
Drawing


  • 위 그림을 참조하면 Channel 방향으로 Height, Width의 크기만큼의 출력을 가짐을 알 수 있습니다.
  • Entropy를 구하는 식은 다음과 같습니다.


  • \[\text{Entropy} = p \log{p} \tag{1}\]


  • 식 (1)에서 \(p\) 는 확률을 의미합니다. 즉 Entropy를 구하기 위해서는 확률 값을 필요로 하며 각 픽셀 별로 Entropy를 구하기 위해서는 각 픽셀 별로 확률 값을 필요로 합니다.


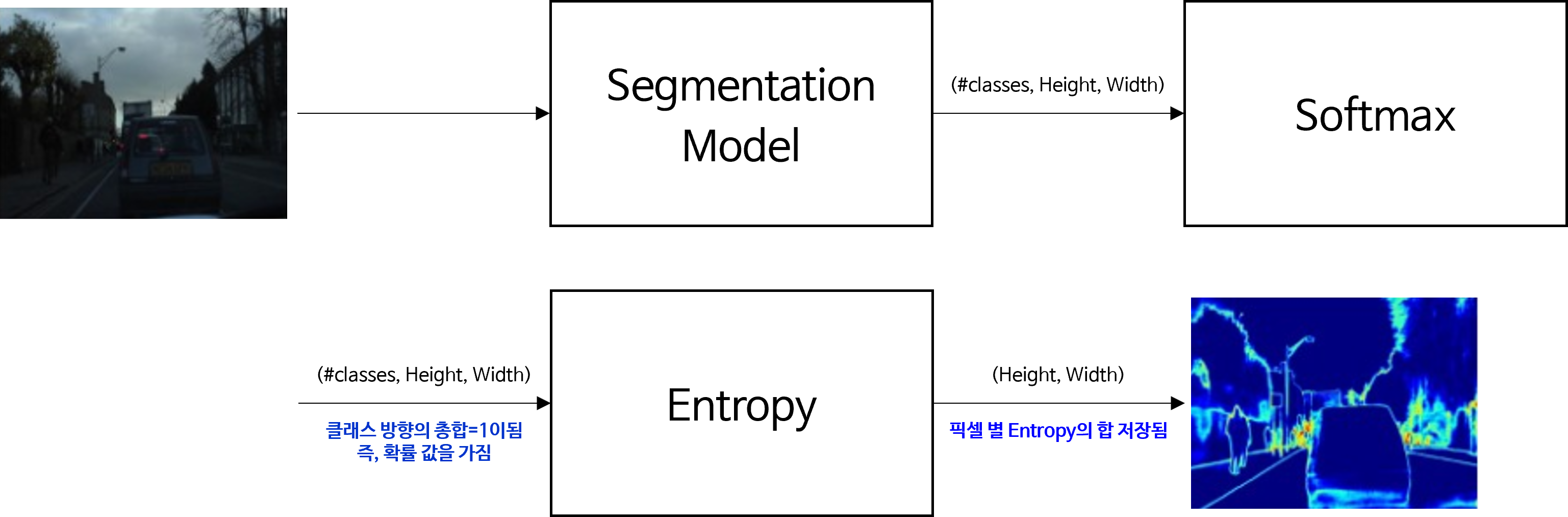
Drawing


  • 위 프로세스와 같이 입력된 이미지를 segmentation 모델을 통하여 (클래스의 갯수, height, width)의 크기로 출력을 하고 클래스 dimension 방향으로 softmax를 적용하여 클래스 별 선택될 확률을 구할 수 있도록 설정합니다.
  • 그러면 픽셀 단위로 확률을 구할 수 있으므로 Entropy를 구할 준비가 완료 됩니다.


  • \[E_{x_{t}}^{(h, w)} = -\frac{1}{\log{(C)}} \sum_{c=1}^{C} P_{x_{t}}^{(c, h, w)} \log{(P_{x_{t}}^{(c, h, w)})} \tag{2}\]


  • 위 식과 같이 각 픽셀 별 Entropy를 구할 수 있고 우변의 식에서 \(\log{(C)}\) 로 나누어 주는 term은 생략하기도 합니다.
  • 만약 이미지를 대표하는 Entropy 값을 하나 구하고 싶으면 다음과 같이 합을 하여 구할 수 있습니다.


  • \[\mathcal{L}_{\text{ent}}(x_{t}) = \sum_{h, w} E_{x_{t}}^{(h, w)} \tag{3}\]


  • 그러면 위 Entropy 식을 실제 Pytorch의 TorchVision에서 제공하는 DeepLab V3 모델로 한번 구해보도록 하겠습니다.


Torchvision 모델로 Entropy map 구하기


  • 예제에서 사용할 TorchVision의 DeepLab v3는 Pascal VOC 데이터셋을 이용하여 pre-train 되었습니다.


import torch
import torchvision.transforms as T
from torchvision import models
import matplotlib.pyplot as plt
import numpy as np
from PIL import Image

# Define the helper function
def decode_segmap(image, nc=21):
  
    label_colors = np.array([(0, 0, 0),  # 0=background
               # 1=aeroplane, 2=bicycle, 3=bird, 4=boat, 5=bottle
               (128, 0, 0), (0, 128, 0), (128, 128, 0), (0, 0, 128), (128, 0, 128),
               # 6=bus, 7=car, 8=cat, 9=chair, 10=cow
               (0, 128, 128), (128, 128, 128), (64, 0, 0), (192, 0, 0), (64, 128, 0),
               # 11=dining table, 12=dog, 13=horse, 14=motorbike, 15=person
               (192, 128, 0), (64, 0, 128), (192, 0, 128), (64, 128, 128), (192, 128, 128),
               # 16=potted plant, 17=sheep, 18=sofa, 19=train, 20=tv/monitor
               (0, 64, 0), (128, 64, 0), (0, 192, 0), (128, 192, 0), (0, 64, 128)])

    r = np.zeros_like(image).astype(np.uint8)
    g = np.zeros_like(image).astype(np.uint8)
    b = np.zeros_like(image).astype(np.uint8)

    for l in range(0, nc):
        idx = image == l
        r[idx] = label_colors[l, 0]
        g[idx] = label_colors[l, 1]
        b[idx] = label_colors[l, 2]

    rgb = np.stack([r, g, b], axis=2)
    return rgb

def segment_and_entropy(net, path, show_orig=True, classes=-1, dev='cuda'):
    img = Image.open(path)
    if show_orig: plt.imshow(img); plt.axis('off'); plt.show()
    # Comment the Resize and CenterCrop for better inference results
    trf = T.Compose([T.Resize(640), 
                   #T.CenterCrop(224), 
                   T.ToTensor(), 
                   T.Normalize(mean = [0.485, 0.456, 0.406], 
                               std = [0.229, 0.224, 0.225])])
    inp = trf(img).unsqueeze(0).to(dev)
    out = net.to(dev)(inp)['out']
    om = torch.argmax(out.squeeze(), dim=0).detach().cpu().numpy()
    rgb = decode_segmap(om)
    plt.imshow(rgb); plt.axis('off'); plt.show()
    
    out_soft = torch.softmax(out, dim=1)    
    entropy_map = -out_soft * torch.log(out_soft + 1e-6)
        
    if classes == -1:
        entropy_map = torch.sum(entropy_map, dim=1)
    else:
        indices = torch.tensor(classes)
        entropy_map = torch.index_select(entropy_map, 1, indices)
        entropy_map = torch.sum(entropy_map, dim=1)
    
    ## opencv version of jetmap entropy
    # entropy_map = entropy_map.squeeze(0)
    # entropy_map = entropy_map.detach().numpy()
    # entropy_map = entropy_map / np.max(entropy_map) * 255
    # entropy_map = entropy_map.astype(np.uint8)
    # entropy_map = cv2.applyColorMap(entropy_map, cv2.COLORMAP_JET)
    
    plt.imshow(entropy_map, cmap=plt.cm.jet); plt.axis('off'); plt.show()
    entropy = np.sum(entropy_map)
    
    return entropy

dlab = models.segmentation.deeplabv3_resnet101(pretrained=1).eval()
path = "" # 이미지 경로

# 전체 클래스에 대한 entropy 계산
entropy = segment_and_entropy(dlab, path, classes=-1)
# 특정 클래스에 대한 entropy 계산
# entropy = segment_and_entropy(dlab, path, classes=[0, 3, 5])

print(entropy)


  • 위 코드를 통하여 원본 이미지, segmentation, entropy 3가지를 출력할 수 있습니다.


Drawing


  • 위 그림을 살펴보면 상대적으로 Entropy가 낮은 가장 왼쪽의 오토바이 이미지에서 Entropy의 총합이 낮은 것을 확인할 수 있고 가운데와 오른쪽 이미지에서는 Entropy가 높은 것을 확인할 수 있습니다.


  • 아래는 인터넷에서 임의의 말 사진을 받아서 출력을 해본 예제입니다. 말의 클래스 번호는 13이므로 다음 코드를 실행하였습니다.
  • entropy = segment_and_entropy(dlab, path, classes=13, dev='cpu')


Drawing


  • 임의의 말 사진에 대해서도 일반적인 성능이 나오는 것을 확인할 수 있습니다. 파란색 영역은 Entropy가 작은 영역으로 예측의 불확실성이 작은 반면 빨간색 영역은 Entropy가 큰 영역으로 argmax를 통해 출력을 구할 때, 불확실성이 큰 것을 알 수 있습니다. 말의 갈기나 꼬리 등의 털 등에서 불확실성이 큰 것을 확인할 수 있으며 직관적으로 수긍할 수 있는 불확실성 입니다.



segmentation 관련 글 목차


Twitter Facebook Google+
# deep learning # segmentation # entropy