pytorch 기본 문법 및 코드, 팁 snippets

pytorch 기본 문법 및 코드, 팁 snippets

2019, Mar 01    


  • 이 글은 pytorch 사용 시 참조할 수 있는 코드 또는 팁들을 모아 놓았습니다.
  • 이 글에서는 기본 문법 및 연산 관련, 셋팅 및 문법 관련 내용, 자주 사용하는 함수 그리고 자주 사용하는 코드 분류로 정리하였습니다.


목차








Pytorch 란?


  • 출처 : http://www.itworld.co.kr/news/129659


Drawing



PyTorch 패키지의 구성 요소


  • torch
    • main namespace로 tensor등의 다양한 수학 함수가 패키지에 포함되어 있습니다.
    • NumPy와 같은 구조를 가지고 있어서 numpy와 상당히 비슷한 문법 구조를 가지고 있습니다.
  • torch.autograd
    • 자동 미분을 위한 함수가 포함되어 있습니다.
    • 자동 미분의 on, off를 제어하는 enable_grad 또는 no_grad나 자체 미분 가능 함수를 정의할 때 사용하는 기반 클래스인 Function등이 포함됩니다.
  • torch.nn
    • 신경망을 구축하기 위한 다양한 데이터 구조나 레이어가 정의되어 있습니다.
    • CNN, LSTM, 활성화 함수(ReLu), loss 등이 정의되어 있습니다.
  • torch.optim
    • SGD 등의 파라미터 최적화 알고리즘 등이 구현되어 있습니다.
  • torch.utils.data
    • Gradient Descent 계열의 반복 연산을 할 때, 사용하는 미니 배치용 유틸리티 함수가 포함되어 있습니다.
  • torch.onnx
    • ONNX(Open Neural Network eXchange) 포맷으로 모델을 export 할 때 사용합니다.
    • ONNX는 서로 다른 딥러닝 프레임워크 간에 모델을 공유할 때 사용하는 새로운 포맷입니다.


PyTorch 기초 사용법


nums = torch.arange(9)
# : tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])


  • 먼저 위와 같이 pytorch의 torch라는 것을 통하여 생성할 수 있습니다. 여기서 보면 앞에서 언급한 바와 같이 numpy와 상당히 비슷한 것을 느낄 수 있습니다.


nums.shape
# torch.Size([9])



type(nums)
# torch.Tensor


  • 여기 까지 보면 뭔가 상당히 numpy 스러운 문법 구조를 가지고 있음을 아실 수 있을 것입니다.


# tensor를 numpy로 타입 변환
nums.numpy()
# array([0, 1, 2, 3, 4, 5, 6, 7, 8], dtype = int64)

nums.reshape(3, 3)
# tensor([ [0, 1, 2],
#           [3, 4, 5],
#           [6, 7, 8] ]])

nums = torch.arange(9).reshape(3, 3)
nums
# tensor([[0, 1, 2],
#         [3, 4, 5],
#         [6, 7, 8]])
nums + nums
# tensor([[ 0,  2,  4],
#         [ 6,  8, 10],
#         [12, 14, 16]])


  • 그 다음으로는 Tensor를 직접 생성하고 조작하는 방법들에 대하여 다루어 보도록 하겠습니다.


텐서의 생성과 변환


  • 텐서는 pytorch의 가장 기본이 되는 데이터 구조와 기능을 제공하는 다차원 배열을 처리하기 위한 데이터 구조입니다.
  • API 형태는 Numpy의 ndarray와 비슷하며 GPU를 사용하는 계산도 지원합니다.
  • 텐서는 각 데이터 형태별로 정의되어 있습니다.
    • torch.FloatTensor : 32bit float point
    • torch.LongTensor : 64bit signed integer
  • GPU 상에서 계산할 때에는 torch.cuda.FloatTensor를 사용합니다. 일반적으로 Tensor는 FloatTensor라고 생각하면 됩니다.
  • 어떤 형태의 텐서이건 torch.tensor라는 함수로 작성할 수 있습니다.
import torch
import numpy as np

# 2차원 형태릐 list를 이용하여 텐서를 생성할 수 있습니다.
torch.tensor([[1,2],[3,4.]])
# : tensor([[1., 2.],
#         [3., 4.]])
        
# device를 지정하면 GPU에 텐서를 만들 수 있습니다.
torch.tensor([[1,2],[3,4.]], device="cuda:0")
# : tensor([[1., 2.],
#         [3., 4.]], device='cuda:0')
        
# dtype을 이용하여 텐서의 데이터 형태를 지정할 수도 있습니다.
torch.tensor([[1,2],[3,4.]], dtype=torch.float64)
# : tensor([[1., 2.],
#         [3., 4.]], dtype=torch.float64)
        
# arange를 이용한 1차원 텐서
torch.arange(0, 10)
# : tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# 모든 값이 0인 3 x 5의 텐서를 작성하여 to 메소드로 GPU에 전송
torch.zeros(3, 5).to("cuda:0")
# :tensor([[0., 0., 0., 0., 0.],
#         [0., 0., 0., 0., 0.],
#         [0., 0., 0., 0., 0.]], device='cuda:0')
        
# normal distribution으로 3 x 5 텐서를 작성
torch.randn(3, 5)
# : tensor([[-0.4615, -0.4247,  0.1998, -0.5937, -0.4767],
#         [ 0.7864,  0.3831, -0.7198, -0.0181, -1.1796],
#         [-0.4504, -1.3181,  0.2657,  0.6829, -1.1690]])
        
# 텐서의 shape은 size 메서드로 확인
t = torch.randn(3, 5)
t.size()
# : torch.Size([3, 5])


  • 텐서는 Numpy의 ndarray로 쉽게 변환할 수 있습니다.
  • 단, GPU상의 텐서는 그대로 변환할 수 없으며, CPU로 이동 후에 변환해야 합니다.
# numpy를 사용하여 ndarray로 변환
t = torch.tensor([[1,2],[3,4.]])
x = t.numpy()

# GPU 상의 텐서는 to 메서드로 CPU의 텐서로 변환 후 ndarray로 변환해야 합니다.
t = torch.tensor([[1,2],[3,4.]], device="cuda:0")
x = t.to("cpu").numpy()


  • torch.linspace(시작, 끝, step)
    • 시작과 끝을 포함하고 step의 갯수만큼 원소를 가진 등차 수열을 만듭니다.
    • 예를 들어 torch.linspace(0, 10, 5) 라고 하면
    • tensor([0.0, 2.5, 5.0, 7.5, 10.0])의 값을 가집니다.
  • torch에서 바로 이런 값들을 만들면 torch 내부적으로도 사용할 수 있지만 numpy와 호환되는 라이브러리에도 사용 가능합니다.
    • 왜냐하면 torch를 numpy로 바꿀 수 있기 때문입니다.
x = torch.linspace(0, 10, 5)
y = torch.exp(x)

plt.plot(x.numpy(), y.numpy())


텐서의 인덱스 조작


  • 텐서의 인덱스를 조작하는 방법은 여러가지가 있습니다.
  • 텐서는 Numpy의 ndarray와 같이 조작하는 것이 가능합니다. 배열처럼 인덱스를 바로지정 가능하고 슬라이스, 마스크 배열을 사용할 수 있습니다.
t = torch.tensor([
    [1,2,3],[4,5,6.]
])

# 인덱스 접근
t[0, 2]
: tensor(3.)

# 슬라이스로 접근
t[:, :2]
: tensor([[1., 2.],
        [4., 5.]])
        
# 마스크 배열을 이용하여 True 값만 추출
t[t > 3]
: tensor([4., 5., 6.])

# 슬라이스를 이용하여 일괄 대입
t[:, 1] = 10

# 마스크 배열을 사용하여 일괄 대입
t[t > 5] = 20


텐서 연산


  • 텐서는 Numpy의 ndarray와 같이 다양한 수학 연산이 가능하며 GPU를 사용할 시에는 더 빠른 연산이 가능합니다.
  • 텐서에서의 사칙연산은 같은 타입의 텐서 간 또는 텐서와 파이썬의 스칼라 값 사이에서만 가능합니다.
    • 텐서간이라도 타입이 다르면 연산이 되지 않습니다. FloatTensor와 DoubleTensor간의 사칙연산은 오류가 발생합니다.
  • 스칼라 값을 연산할 때에는 기본적으로 broadcasting이 지원됩니다.
# 길이 3인 벡터
v = torch.tensor([1,2,3.])
w = torch.tensor([0, 10, 20])

# 2 x 3의 행렬
m = torch.tensor([
    [0, 1, 2], [100, 200, 300.]
])

# 벡터와 스칼라의 덧셈
v2 = v + 10

# 제곱
v2 = v ** 2

# 동일 길이의 벡터간 덧셈 연산
z =  v - w

# 여러 가지 조합
u = 2 * v - w / 10 + 6.0

# 행렬과 스칼라 곱
m2 = m * 2.0

# (2, 3)인 행렬과 (3,)인 벡터간의 덧셈이므로 브로드캐스팅 발생
m + v

:tensor([[  1.,   3.,   5.],
        [101., 202., 303.]])
        
# 행렬 간 처리
m + m

:tensor([[  0.,   2.,   4.],
        [200., 400., 600.]])


텐서의 차원 조작


  • 텐서의 차원을 변경하는 view나 텐서를 결합하는 stack, cat, 차원을 교환하는 t, transpose도 사용됩니다.
  • view는 numpy의 reshape와 유사합니다. 물론 pytorch에도 reshape 기능이 있으므로 view를 사용하던지 reshape을 사용하던지 사용방법은 같으므로 선택해서 사용하면 됩니다. (reshape를 사용하길 권장합니다.)
  • cat은 다른 길이의 텐서를 하나로 묶을 때 사용합니다.
  • transpose는 행렬의 전치 외에도 차원의 순서를 변경할 때에도 사용됩니다.
x1 = torch.tensor([
    [1, 2], [3, 4.]
])

x2 = torch.tensor([
    [10, 20, 30], [40, 50, 60.]
])

# 2 x 2 행렬을 4 x 1로 변형합니다.
x1.view(4,1)
# tensor([[1.],
#         [2.],
#         [3.],
#         [4.]])

x1.reshape(4,1)
# tensor([[1.],
#         [2.],
#         [3.],
#         [4.]])

# 2 x 2 행렬을 1차원 벡터로 변형합니다.
x1.view(-1)
# tensor([1,2,3,4])

x1.reshape(-1)
# tensor([1,2,3,4])
        
# -1을 사용하면 shape에서 자동 계산 가능한 부분에 한해서 자동으로 입력 됩니다.
# 계산이 불가능 하면 오류가 발생합니다.
x1.view(1, -1)
# tensor([[1.],
#         [2.],
#         [3.],
#         [4.]])

x1.reshape(1, -1)
# tensor([[1.],
#         [2.],
#         [3.],
#         [4.]])

# 2 x 3 행렬을 전치해서 3 x 2 행렬을 만듭니다.
x2.t()
# tensor([[10., 40.],
#         [20., 50.],
#         [30., 60.]])
        
# dim = 1 로 결합하면 2 x 5의 행렬로 묶을 수 있습니다.
torch.cat([x1, x2], dim=1)
# tensor([[ 1.,  2., 10., 20., 30.],
#         [ 3.,  4., 40., 50., 60.]])
        
# transpose(dim0, dim1)을 사용하면 dim0의 차원과 dim1의 차원을 교환합니다.
# transpose(0, 3) 이라고 하면 0차원과 3차원을 교환하게 됩니다.
# 아래 예제는 HWC(높이, 너비, 컬러) 차원을 CHW(컬러, 높이, 너비)로 변형하는 예제입니다.
hwc_img_data = torch.rand(100, 64, 32, 3)
chw_img_data = hwc_img_data.transpose(1,2).transpose(1,3)
chw_img_data.size()
# torch.Size([100, 3, 64, 32])


Tensor 생성


  • Tensor를 생성할 때 대표적으로 사용하는 함수가 rand, zeros, ones 입니다. 이 때, 첫 인자는 dimension 입니다.
  • 각 dimension은 tuple 형태로 묶어서 지정해 주어도 되고 콤마 형태로 풀어서 지정해 주어도 됩니다.
  • 예를 들어 torch.rand((2, 3))와 torch.rand(2, 3) 모두 같은 shape인 (2, 3)을 가집니다.
  • 먼저 랜덤 넘버 생성에 대하여 다루어 보겠습니다.
import torch
x = torch.rand(2,3)
print(x)

 0.1330  0.3113  0.9652
 0.1237  0.4056  0.8464
[torch.FloatTensor of size 2x3]


  • 다음과 같이 순열을 생성할 수도 있습니다.


torch.torch.randperm(5)

2
3
4
0
1
[torch.LongTensor of size 5]


  • 다음은 모든 값이 0인 zeros tensor를 생성해 보도록 하겠습니다.


zeros = torch.zeros(2,3)

: tensor([[0., 0., 0.],
        [0., 0., 0.]])

torch.zeros_like(zeros)


  • 다음은 모든 값이 1인 ones Tensor 생성해 보도록 하겠습니다.


torch.ones(2,3)

: tensor([[1., 1., 1.],
        [1., 1., 1.]])


  • arange를 이용한 Tensor 생성
  • torch.arange(시작, 끝, step)을 인자로 사용하며 시작은 이상, 끝은 미만의 범위를 가지고 step만큼 간격을 두며 Tensor를 생성합니다.
# torch.arange(start,end,step=1) -> [start,end) with step
torch.arange(0,3,step=0.5)

: tensor([0.0000, 0.5000, 1.0000, 1.5000, 2.0000, 2.5000])


Tensor 데이터 타입


  • Float 타입의 m행 n열 Tensor 생성하기
# 2행 3열의 Float 타입의 Tensor 생성
torch.cuda.FloatTensor(2,3)

: tensor([[2.0000e+00, 3.0000e+00, 1.4013e-45],
        [0.0000e+00, 0.0000e+00, 0.0000e+00]], device='cuda:0')


  • 리스트를 입력하여 특정 리스트를 Tensor로 변환하기
torch.cuda.FloatTensor([2,3])

: tensor([2., 3.], device='cuda:0')


  • Float 타입을 Int 타입으로 형변환
x = torch.cuda.FloatTensor([2,3])
x.type_as(torch.cuda.IntTensor())

: tensor([2, 3], device='cuda:0', dtype=torch.int32)


Numpy to Tensor 또는 Tensor to Numpy


  • Numpy를 생성한 후 Tensor로 변환한 후 다시 Numpy로 변환해 보고 추가적으로 변환하는 방법도 알아보겠습니다.


import numpy as np
x1 = np.ndarray(shape=(2,3), dtype=int,buffer=np.array([1,2,3,4,5,6]))
# array([[1, 2, 3],
#        [4, 5, 6]])

torch.from_numpy(x1)
# tensor([[1, 2, 3],
#         [4, 5, 6]], dtype=torch.int32)
        
x2 = torch.from_numpy(x1)
x2.numpy()
# array([[1, 2, 3],
#        [4, 5, 6]])

x2.float()
# tensor([[1., 2., 3.],
#         [4., 5., 6.]])


CPU 타입과 GPU 타입의 Tensor


  • 딥러닝 프레임워크에서는 CPU와 GPU 두 타입에 대한 Tensor 생성이 가능합니다.
  • PyTorch에서는 어떻게 사용할 수 있는지 알아보겠습니다.


x = torch.FloatTensor([[1,2,3],[4,5,6]])
x_gpu = x.cuda()
# 1  2  3
# 4  5  6
# [torch.cuda.FloatTensor of size 2x3 (GPU 0)]

x_cpu = x_gpu.cpu()
x_cpu
# 1  2  3
# 4  5  6
# [torch.FloatTensor of size 2x3]


Tensor 사이즈 확인하기


  • Tensor 사이즈를 확인하려면 .size()를 이용하여 확인하면 됩니다.
x = torch.cuda.FloatTensor(10, 12, 3, 3)
x.size()
# torch.Size([10, 12, 3, 3])


Index (slicing) 기능 사용방법


  • Index 또는 slicing 기법은 Tensor에서 특정 값만 조회하는 것을 말합니다.
  • 배열, 행렬에서도 인덱스 기능을 통하여 특정 값들을 조회하는 것 처럼 Tensor에서도 조회할 수 있습니다.
  • 먼저 torch.index_select함수를 이용해 보겠습니다. 파라미터는 input, dim, index가 차례로 입력됩니다. 이 함수는 torch에서 제공하는 인덱싱 방법입니다.
# torch.index_select(input, dim, index)
x = torch.rand(4,3)
# tensor([[0.4898, 0.2505, 0.6500],
#         [0.0976, 0.4117, 0.9705],
#         [0.7069, 0.0546, 0.7824],
#         [0.4921, 0.9863, 0.3936]])
    
# 3번째 인자에는 torch.LongTensor를 이용하여 인덱스를 입력해 줍니다.
torch.index_select(x,0,torch.LongTensor([0,2]))
# tensor([[0.4898, 0.2505, 0.6500],
#         [0.7069, 0.0546, 0.7824]])


  • 하지만 위 처럼 인덱식 하는 방법은 뭔가 python이나 numpy와는 조금 이질적인 감이 있습니다.
  • 이번에는 좀더 파이썬스럽게 인덱싱을 해보겠습니다. 아래 방법이 좀더 파이썬 유저에게 친숙한 방법입니다.


print(x)
# tensor([[0.4898, 0.2505, 0.6500],
#         [0.0976, 0.4117, 0.9705],
#         [0.7069, 0.0546, 0.7824],
#         [0.4921, 0.9863, 0.3936]])

x[:, 0]
# tensor([0.4898, 0.0976, 0.7069, 0.4921])

x[0, :]
# tensor([0.4898, 0.2505, 0.6500])

x[0:2, 0:2]
# tensor([[0.4898, 0.2505],
#         [0.0976, 0.4117]])


  • 이번에는 mask 기능을 통하여 인덱싱 하는 방법에 대하여 알아보겠습니다.
  • torch.masked_select(input, mask) 함수를 이용하여 선택할 영역에는 1을 미선택할 영역은 0을 입력 합니다.
  • 인풋 영역과 마스크할 영역의 크기는 같아야 오류 없이 핸들링 할 수 있습니다.


x = torch.randn(2,3)
# tensor([[ 0.6122, -0.7963, -0.3964],
#         [ 0.6030,  0.1522, -1.0622]])

# mask는 0,1 값을 가지고 ByteTensor를 이용하여 생성합니다.
# (0,3)과 (1,1) 데이터 인덱싱
mask = torch.ByteTensor([[0,0,1],[0,1,0]])
torch.masked_select(x,mask)
# tensor([-0.3964,  0.1522])


Join(cat, stack) 기능 사용 방법


  • PyTorch에서 torch.cat(seq, dim)을 이용하여 concaternate 연산을 할 수 있습니다.
  • dim은 concaternate할 방향을 정합니다.


x = torch.cuda.FloatTensor([[1, 2, 3], [4, 5, 6]])
y = torch.cuda.FloatTensor([[-1, -2, -3], [-4, -5, -6]])
z1 = torch.cat([x, y], dim=0)
# tensor([[ 1.,  2.,  3.],
#         [ 4.,  5.,  6.],
#         [-1., -2., -3.],
#         [-4., -5., -6.]], device='cuda:0')

z2 = torch.cat([x, y], dim=1)
# tensor([[ 1.,  2.,  3., -1., -2., -3.],
#         [ 4.,  5.,  6., -4., -5., -6.]], device='cuda:0')


  • torch.stack 을 이용하여도 concaternate를 할 수 있습니다.


# torch.stack(sequence,dim=0) -> stack along new dim

x = torch.FloatTensor([[1,2,3],[4,5,6]])
x_stack = torch.stack([x,x,x,x],dim=0)
# tensor([[[1., 2., 3.],
#          [4., 5., 6.]],

#         [[1., 2., 3.],
#          [4., 5., 6.]],

#         [[1., 2., 3.],
#          [4., 5., 6.]],

#         [[1., 2., 3.],
#          [4., 5., 6.]]])


slicing 기능 사용 방법


  • slicing 기능은 Tensor를 몇개의 부분으로 나뉘는 기능입니다.
  • torch.chunk(tensor, chunks, dim=0) 또는 torch.split(tensor,split_size,dim=0)함수를 이용하여 Tensor를 나뉠 수 있습니다.


# torch.chunk(tensor, chunks, dim=0) -> tensor into num chunks

x_1, x_2 = torch.chunk(z1,2,dim=0)
y_1, y_2, y_3 = torch.chunk(z1,3,dim=1)

print(z1)
#   1  2  3
#   4  5  6
#  -1 -2 -3
#  -4 -5 -6
#  [torch.FloatTensor of size 4x3]
 
 print(x1)
#   1  2  3
#   4  5  6
#  [torch.FloatTensor of size 2x3], 
 
 print(x2)
#  -1 -2 -3
#  -4 -5 -6
#  [torch.FloatTensor of size 2x3]
 
 print(y1)
#   1
#   4
#  -1
#  -4
#  [torch.FloatTensor of size 4x1], 
 
 print(y2)
#   2
#   5
#  -2
#  -5
#  [torch.FloatTensor of size 4x1]
 
 print(y3)
#   3
#   6
#  -3
#  -6
#  [torch.FloatTensor of size 4x1]


squeezing 기능 사용 방법


  • squeeze 함수를 사용하면 dimension 중에 1로 되어 있는 것을 압축할 수 있습니다.
  • dimension이 1이면 사실 불필요한 차원일 수 있기 때문에 squeeze를 이용하여 압축 시키는 것이 때론 필요할 수 있는데, 그 때 사용하는 함수 입니다.
  • torch.squeeze(input, dim)으로 사용할 수 있고, dim을 지정하지 않으면 dimeion이 1인 모든 차원을 압축하고 dim을 지정하면 지정한 dimension만 압축합니다.
>>> x = torch.zeros(2, 1, 2, 1, 2)
>>> x.size()
# torch.Size([2, 1, 2, 1, 2])
>>> y = torch.squeeze(x)
>>> y.size()
# torch.Size([2, 2, 2])
>>> y = torch.squeeze(x, 0)
>>> y.size()
# torch.Size([2, 1, 2, 1, 2])
>>> y = torch.squeeze(x, 1)
>>> y.size()
# torch.Size([2, 2, 1, 2])


  • 반면 unsqueeze 함수를 사용하면 dimension을 추가할 수 있습니다. squeeze와 정확히 반대라고 보시면 됩니다.
  • unsqueeze 함수는 dimension을 반드시 입력 받게 되어 있습니다.
>>> x = torch.zeros(2,3,4)
>>> torch.unsqueeze(x, 0)
# torch.Size([1, 2, 3, 4])

>>> x = torch.tensor([1, 2, 3, 4])
>>> torch.unsqueeze(x, 0)
# tensor([[ 1,  2,  3,  4]])
>>> torch.unsqueeze(x, 1)
# tensor([[ 1],
#         [ 2],
#         [ 3],
#         [ 4]])


Initialization, 초기화 방법


  • init.uniform함수를 사용하면 uniform 또는 normal 분포의 초기화 Tensor를 만들 수 있습니다.
  • 또는 상수 형태를 바로 만들 수도 있습니다. 예제는 아래와 같습니다.
import torch.nn.init as init

x1 = init.uniform(torch.FloatTensor(3,4),a=0,b=9) 
>>> print(x1)

# 3.4121  0.9464  5.3126  4.3104
#   7.3428  8.3997  7.2747  7.9227
#   4.2563  0.1993  6.2227  5.7939
#  [torch.FloatTensor of size 3x4]
 
x2 = init.normal(torch.FloatTensor(3,4),std=0.2)
>>> print(x2)

# -0.1121  0.3684  0.0316  0.1426
#   0.1499 -0.2384  0.0183  0.0429
#   0.2808  0.1389  0.1057  0.1746
#  [torch.FloatTensor of size 3x4]
 
x3 = init.constant(torch.FloatTensor(3,4),3.1415)
>>> print(x3)

# 3.1415  3.1415  3.1415  3.1415
#   3.1415  3.1415  3.1415  3.1415
#   3.1415  3.1415  3.1415  3.1415
#  [torch.FloatTensor of size 3x4]


Math Operation


  • dot : 벡터 내적
  • mv : 행렬과 벡터의 곱
  • mm : 행렬과 행렬의 곱
  • matmul : 인수의 종류에 따라서 자동으로 dot, mv, mm을 선택
a = torch.tensor([1,2,3,4,5,6]).view(3,2)
b = torch.tensor([9,8,7,6,5,4]).view(2,3)
ab = torch.matmul(a,b)
ab = a@b # @ 연산자를 이용하여 간단하게 행렬곱을 표현할 수 있음


  • Tensor의 산술 연산 방법에 대하여 알아보겠습니다.
  • +연산자 또는 torch.add()
x1 = torch.FloatTensor([[1,2,3],[4,5,6]])
x2 = torch.FloatTensor([[1,2,3],[4,5,6]])
add = x1 + x2
# add = torch.add(x1,x2) 또한 가능합니다.
>>> print(add)
#  2   4   6
#  8  10  12
#  [torch.FloatTensor of size 2x3]


  • +연산자를 이용한 broadcasting 또는 torch.add() with broadcasting
x1 = torch.FloatTensor([[1,2,3],[4,5,6]])
>>> x1 + 10 # torch.add(x1, 10) 또한 가능합니다.
# 11  12  13
# 14  15  16
# [torch.FloatTensor of size 2x3]


  • *연산자 또는 torch.mul()
x1 = torch.FloatTensor([[1,2,3],[4,5,6]])
x2 = torch.FloatTensor([[1,2,3],[4,5,6]])
>>> x1*x2 # torch.mul(x1,x2)
# 1   4   9
# 16  25  36
# [torch.FloatTensor of size 2x3]


  • *연산자를 이용한 broadcasting 또는 torch.mul() with broadcasting
x1 = torch.FloatTensor([[1,2,3],[4,5,6]])
>>> x1 * 10
# 10  20  30
# 40  50  60
# [torch.FloatTensor of size 2x3]


  • /연산자 또는 torch.div()
x1 = torch.FloatTensor([[1,2,3],[4,5,6]])
x2 = torch.FloatTensor([[1,2,3],[4,5,6]])
>>> x1/x2 # torch.div(x1, x2)
#  1  1  1
#  1  1  1
# [torch.FloatTensor of size 2x3]


  • /연산자를 이용한 broadcsting 또는 torch.div() with broadcasting
x1 = torch.FloatTensor([[1,2,3],[4,5,6]])
>>> x1 / 5
#  0.2000  0.4000  0.6000
#  0.8000  1.0000  1.2000
# [torch.FloatTensor of size 2x3]


  • power 연산 : torch.pow(input,exponent)
x1 = torch.FloatTensor([ [1,2,3], [4,5,6] ])
>>> x1**2 # torch.pow(x1,2)
# tensor([[ 1.,  4.,  9.],
#         [16., 25., 36.]])


  • exponential 연산 : torch.exp(tensor,out=None)
x1 = torch.FloatTensor([ [1,2,3], [4,5,6] ])
>>> torch.exp(x1)
# tensor([[  2.7183,   7.3891,  20.0855],
#         [ 54.5981, 148.4132, 403.4288]])


  • torch.log(input, out=None) -> natural logarithm
x1 = torch.FloatTensor([ [1,2,3], [4,5,6] ])
>>> torch.log(x1)
# tensor([[0.0000, 0.6931, 1.0986],
#         [1.3863, 1.6094, 1.7918]])


  • torch.mm(mat1, mat2) -> matrix multiplication
  • Tensor(행렬)의 곱을 연산하므로 shape이 잘 맞아야 연산이 가능합니다.
x1 = torch.FloatTensor(3,4)
x2 = torch.FloatTensor(4,5)
torch.mm(x1,x2).size()


  • torch.bmm(batch1, batch2) -> batch matrix multiplication
  • Tensor(행렬)의 곱을 batch 단위로 처리합니다. torch.mm에서는 단일 Tensor(행렬)로 계산을 한 반면에 batch 단위로 한번에 처리하므로 좀 더 효율적입니다.
x1 = torch.FloatTensor(10,3,4)
x2 = torch.FloatTensor(10,4,5)
torch.bmm(x1,x2).size()


  • torch.dot(tensor1,tensor2)는 두 tensor의 dot product 연산을 수행합니다.
>>> torch.dot(torch.tensor([2, 3]), torch.tensor([2, 1]))
# tensor(7)


  • torch.t()를 이용하면 transposed tensor를 구할 수 있습니다.
x1 = torch.FloatTensor(2,3)
x2 = x1.t()
>>> print(x1.size())
# torch.Size([2, 3])

>>> print(x2.size())
# torch.Size([3, 2])


  • 반면 torch.transpose()를 이용하여 특정 dimension을 변경할 수 있습니다.
x1 = torch.FloatTensor(10,3,4,5)
>>> x1.size()
# torch.Size([10, 3, 4, 5])

>>> torch.transpose(x1,1,2).size()
# torch.Size([10, 4, 3, 5])

>>> torch.transpose(x1,2,3).size()
# torch.Size([10, 3, 5, 4])


  • eigenvalue와 eigenvector를 구하는 방법은 아래와 같습니다.
  • 출력은 각각 eigenvalue와 eigenvector입니다.
x1 = torch.FloatTensor(4,4)
>>> torch.eig(x1,eigenvectors=True)

# 1.00000e-12 *
#    -0.0000  0.0000
#     0.0000  0.0000
#     4.7685  0.0000
#     0.0000  0.0000
#   [torch.FloatTensor of size 4x2], 
  
#   -6.7660e-13  6.6392e-13 -3.0669e-15  1.7105e-20
#    7.0711e-01  7.0711e-01  1.0000e+00 -1.0000e+00
#    2.1701e-39 -2.1294e-39 -2.8813e-10  1.8367e-35
#    7.0711e-01  7.0711e-01  7.3000e-07  3.2207e-10
#   [torch.FloatTensor of size 4x4]))


Gradient를 구하는 방법


  • Pytorch를 이용하여 Gradient를 구하는 방법에 대하여는 제 블로그의 다른 글에서 자세하게 다루었습니다.
    • 링크 : https://gaussian37.github.io/dl-pytorch-gradient/


벡터와 텐서의 element-wise multiplication


  • 딥러닝에서 연산을 하다보면 다음과 같은 그림의 연산을 하는 경우가 종종 발생합니다.


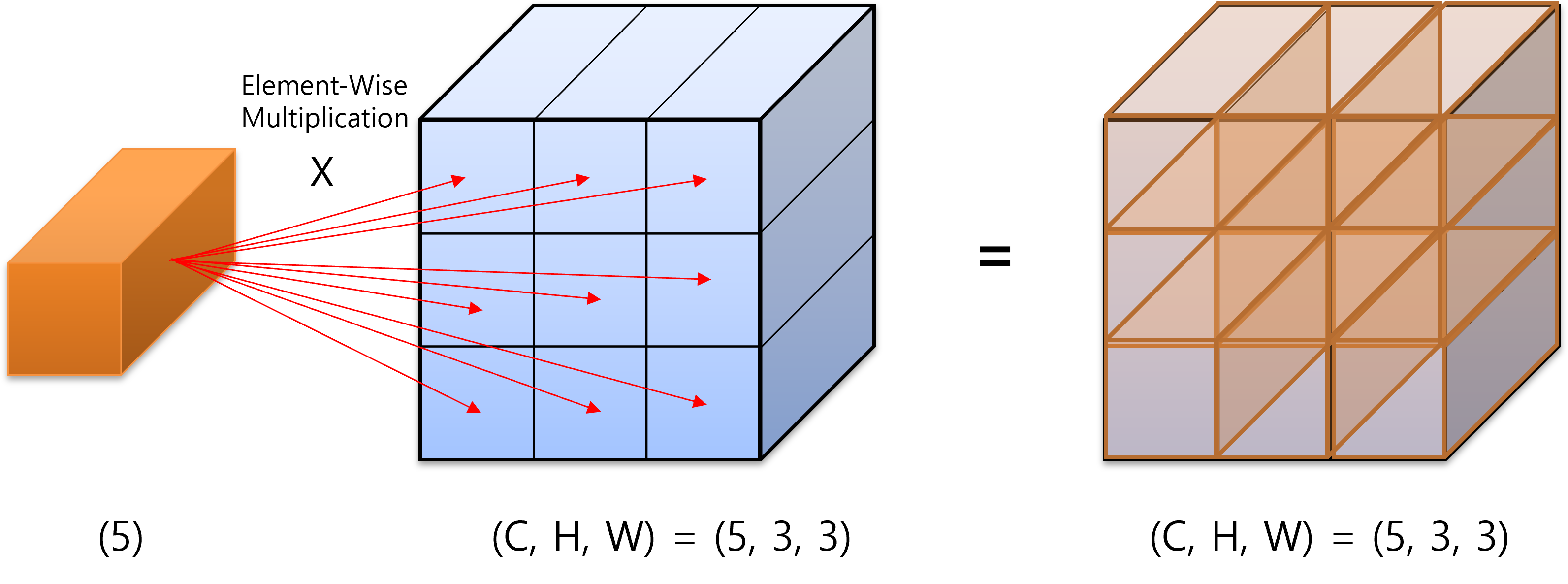
Drawing


  • 위 연산은 element를 5개 가지는 주황색의 벡터와 (C, H, W) = (5, 3, 3)를 element-wise multiplication 하는 연산입니다. multiplication의 방향은 C=Channel 방향으로 곱해집니다.
  • 다음 코드를 통해 channel 크기가 같은 벡터와 텐서를 생성해 보겠습니다.


A = torch.ones(5, 3, 3)
# tensor([[[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]],

#         [[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]],

#         [[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]],

#         [[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]],

#         [[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]]])

v = torch.arange(1, 5)
# tensor([1, 2, 3, 4, 5])


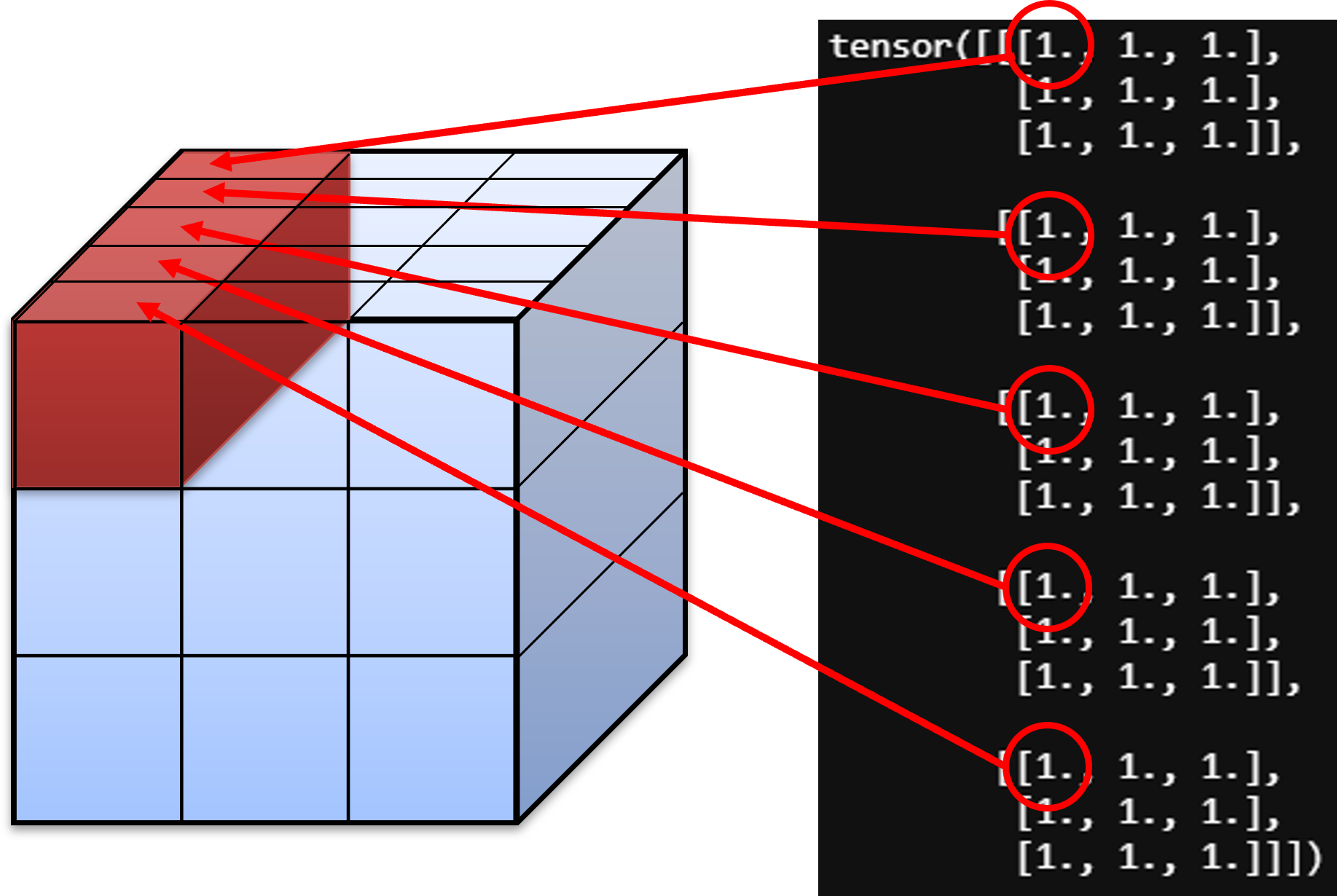
Drawing


  • 파란색의 Tensor 값은 모두 1을 가진다고 가정해 보겠습니다.


Drawing


  • 반면 주황색의 벡터는 1, 2, 3, 4, 5를 차례대로 가진다고 가정해 보겠습니다.
  • 이 때, channel 방향으로 element-wise multiplication을 하면 Tensor는 channel 방향으로 1, 2, 3, 4, 5를 가지게 됩니다.


  • 이와 같은 연산을 하기 위해서는 다음 절차를 따르는 방법을 많이 사용합니다.
  • ① view를 사용하여 벡터를 텐서와 같은 shape으로 맞추어서 텐서로 만듭니다.
  • ② 두 텐서를 곱합니다.


A = torch.ones(5, 3, 3)
print("A.shape : ", A.shape)
# A.shape :  torch.Size([5, 3, 3])
print(A)
# tensor([[[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]],

#         [[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]],

#         [[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]],

#         [[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]],

#         [[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]]])

v = torch.arange(0, 5)
print("v.shape : ", v.shape)
# v.shape :  torch.Size([5])
print(v)
# tensor([0, 1, 2, 3, 4])

v_tensor = v.view(v.size()[0], 1, 1)
print("v_tensor.shape : ", v_tensor.shape)
# v_tensor.shape :  torch.Size([5, 1, 1])
print(v_tensor)
# tensor([[[0]],

#         [[1]],

#         [[2]],

#         [[3]],

#         [[4]]])

result = v_tensor * A
print("result.shape : ", result.shape)
# result.shape :  torch.Size([5, 3, 3])
print(result)
# tensor([[[0., 0., 0.],
#          [0., 0., 0.],
#          [0., 0., 0.]],

#         [[1., 1., 1.],
#          [1., 1., 1.],
#          [1., 1., 1.]],

#         [[2., 2., 2.],
#          [2., 2., 2.],
#          [2., 2., 2.]],

#         [[3., 3., 3.],
#          [3., 3., 3.],
#          [3., 3., 3.]],

#         [[4., 4., 4.],
#          [4., 4., 4.],
#          [4., 4., 4.]]])


gather 기능 사용 방법


  • torch.gather 함수는 tensor에서 인덱스를 기준으로 특정 값들을 추출하기 위해 사용됩니다. 파이썬에서 사용하는 인덱싱 기능과 유사한 기능이라고 생각하면 됩니다. 다만, onnx 등과의 호환성을 위해 torch의 함수를 사용한다거나 또는 최적화를 위해 가능한한 torch 함수를 이용해야 한다면 인덱싱 대신 torch.gather 함수를 사용하는 것을 권장합니다.
  • gather 함수를 사용할 때, 첫번째 인자는 tensor가 입력이 되고 두번째 인자는 조회할 차원(0, 1, 2, …)을 입력하면 되며 입력할 tensor의 차원을 입력한다고 생각하면 됩니다. 세번째 인자는 index가 tensor 타입으로 입력하면 됩니다.


A = torch.arange(1, 10)
indices = torch.tensor([0, 3, 5, 6])
print(torch.gather(A, 0, indices))
# tensor([1, 4, 6, 7])


  • 위 코드를 살펴보면 indices에 해당하는 인덱스를 조회하는 것을 알 수 있습니다.


A = torch.arange(25).reshape(5, 5)
# tensor([[ 0,  1,  2,  3,  4],
#         [ 5,  6,  7,  8,  9],
#         [10, 11, 12, 13, 14],
#         [15, 16, 17, 18, 19],
#         [20, 21, 22, 23, 24]])
indices = torch.tensor([
    [0, 1, 2],
    [1, 2, 3],
    [2, 3, 3],
    [3, 4, 1],
    [0, 0, 0]
])

print(torch.gather(A, 1, indices))
# tensor([[ 0,  1,  2],
#         [ 6,  7,  8],
#         [12, 13, 13],
#         [18, 19, 16],
#         [20, 20, 20]])


  • indeces를 살펴보면 A tensor의 같은 크기이며 인덱스의 정보가 저장되어 있습니다. 예를 들어 indices의 0번째 행을 보면 0, 1, 2 인덱스가 있고 A의 0번째 행의 0, 1, 2 열의 값을 가져오면 0, 1, 2가 되는 것을 확인할 수 있습니다. 또한 indices의 마지막 행을 보면 0, 0, 0 인덱스가 있고 A의 마지막 행의 0, 0, 0 열을 가져오면 20, 20, 20이 되는 것을 확인할 수 있습니다.
  • 아래는 3차원의 예제이며 차원이 늘어나면 그 늘어난 차원에 대응하여 인덱싱을 하면 됩니다.


A = torch.arange(27).rehspae(3, 3, 3)
# tensor([[[ 0,  1,  2],
#          [ 3,  4,  5],
#          [ 6,  7,  8]],

#         [[ 9, 10, 11],
#          [12, 13, 14],
#          [15, 16, 17]],

#         [[18, 19, 20],
#          [21, 22, 23],
#          [24, 25, 26]]])

indices = torch.tensor([
    [[0,0,0],[1,1,1],[2,2,2]],
    [[1,1,1],[2,2,2,],[0,0,0]],
    [[0,1,2],[0,1,2],[0,1,2]]])
    
torch.gather(A, 2, indices)
# tensor([[[ 0,  1,  2],
#          [ 3,  4,  5],
#          [ 6,  7,  8]],

#         [[ 9, 10, 11],
#          [12, 13, 14],
#          [15, 16, 17]],

#         [[18, 19, 20],
#          [21, 22, 23],
#          [24, 25, 26]]])


expand와 repeat 기능 사용 방법


  • expand와 repeat은 torch에서 값을 반복시키는 대표적인 연산입니다.
  • 먼저 expand는 특정 텐서를 반복하여 생성하며 개수가 1인 차원에만 적용하여 반복할 수 있습니다.


x = torch.tensor([[1], [2], [3]])
x.size()
#  torch.Size([3, 1])

x.expand(3, 4)
# tensor([[1, 1, 1, 1],
#         [2, 2, 2, 2],
#         [3, 3, 3, 3]])

x.expand(-1, 4)
# tensor([[1, 1, 1, 1],
#         [2, 2, 2, 2],
#         [3, 3, 3, 3]])


  • 위 코드를 살펴보면 (3, 1) 크기에서 1에 해당하는 차원을 4의 크기로 확대하면 기존에 가지고 있던 값이 복사되게 됩니다.
  • 앞에서 설명한 바와 같이 차원이 1인 곳에만 적용 가능하므로 크기를 늘릴 차원에만 그 크기만큼 숫자를 입력하고 변함이 없는 차원은 -1로 입력하는 것이 쉽게 사용할 수 있는 방법입니다.
  • 아래와 같이 사용하면 여러 차원에도 적용할 수 있습니다.


y = torch.rand(3, 1, 1)
# tensor([[[0.4637]],

#         [[0.5258]],

#         [[0.2620]]])

y.expand(-1, 3, 4)
# tensor([[[0.4637, 0.4637, 0.4637, 0.4637],
#          [0.4637, 0.4637, 0.4637, 0.4637],
#          [0.4637, 0.4637, 0.4637, 0.4637]],

#         [[0.5258, 0.5258, 0.5258, 0.5258],
#          [0.5258, 0.5258, 0.5258, 0.5258],
#          [0.5258, 0.5258, 0.5258, 0.5258]],

#         [[0.2620, 0.2620, 0.2620, 0.2620],
#          [0.2620, 0.2620, 0.2620, 0.2620],
#          [0.2620, 0.2620, 0.2620, 0.2620]]])


  • expand 연산은 차원이 1인 어떤 차원의 값을 원하는 사이즈 만큼 같은 값으로 채우는 반면 repeat 연산은 어떤 tensor를 완전히 반복하여 값을 채웁니다.


x = torch.rand(2, 3) 
# tensor([[0.3420, 0.6117, 0.8471],
#         [0.0250, 0.7804, 0.5909]])

x.repeat(3, 2, 2)
# tensor([[[0.3420, 0.6117, 0.8471, 0.3420, 0.6117, 0.8471],
#          [0.0250, 0.7804, 0.5909, 0.0250, 0.7804, 0.5909],
#          [0.3420, 0.6117, 0.8471, 0.3420, 0.6117, 0.8471],
#          [0.0250, 0.7804, 0.5909, 0.0250, 0.7804, 0.5909]],

#         [[0.3420, 0.6117, 0.8471, 0.3420, 0.6117, 0.8471],
#          [0.0250, 0.7804, 0.5909, 0.0250, 0.7804, 0.5909],
#          [0.3420, 0.6117, 0.8471, 0.3420, 0.6117, 0.8471],
#          [0.0250, 0.7804, 0.5909, 0.0250, 0.7804, 0.5909]],

#         [[0.3420, 0.6117, 0.8471, 0.3420, 0.6117, 0.8471],
#          [0.0250, 0.7804, 0.5909, 0.0250, 0.7804, 0.5909],
#          [0.3420, 0.6117, 0.8471, 0.3420, 0.6117, 0.8471],
#          [0.0250, 0.7804, 0.5909, 0.0250, 0.7804, 0.5909]]])

x.repeat(3, 2, 2).shape
# torch.Size([3, 4, 6])


  • 위 코드를 살펴보면 x의 값이 repeat한 크기 만큼 반복되는 것을 알 수 있습니다.
  • 크기를 살펴보면 x : (2, 3) 크기에 (3, 2, 2)로 반복을 하면 (3, 2 X 2, 3 X 2) = (3, 4, 6)이 됨을 알 수 있습니다.


 y = torch.rand(2, 3, 2)

 y.repeat(3, 4, 5, 6).shape
#  torch.Size([3, 8, 15, 12])


  • 차원을 더 크게 살펴보면 y : (2, 3, 2)를 (3, 4, 5, 6) 으로 repeat 하면 (3, 2 X 4, 3 X 5, 2 X 6) = (3, 8, 15, 12)가 됨을 알 수 있습니다.


  • expand와 repeat은 기존의 tensor를 이용하여 더 큰 크기의 tensor를 만든다는 점에서 같지만 내부적인 동작 방식에 의한 큰 차이가 있습니다.
  • expand의 경우 원본 tensor를 참조하여 만들기 때문에 원본 tensor의 값이 변경이 되면 expand의 값 또한 변경됩니다. 반면 repeat은 깊은 복사로 만들어지기 때문에 원본 tensor가 변경되더라도 값 변경이 발생하지 않습니다. 아래 코드를 참조하시기 바랍니다.


a = torch.rand(1, 1, 3)
# tensor([[[0.5504, 0.9687, 0.1062]]])
b = a.expand(4, -1, -1)
c = a.repeat(4, 1, 1)

print(b.shape)
# torch.Size([4, 1, 3])
print(c.shape)
# torch.Size([4, 1, 3])

a[0, 0, 0] = 0
print(a)
# tensor([[[0.0000, 0.9687, 0.1062]]])

print(b)
# tensor([[[0.0000, 0.9687, 0.1062]],

#         [[0.0000, 0.9687, 0.1062]],

#         [[0.0000, 0.9687, 0.1062]],

#         [[0.0000, 0.9687, 0.1062]]])

print(c)
# tensor([[[0.5504, 0.9687, 0.1062]],

#         [[0.5504, 0.9687, 0.1062]],

#         [[0.5504, 0.9687, 0.1062]],

#         [[0.5504, 0.9687, 0.1062]]])


  • 위 코드를 살펴보면 a.expand()를 통해 생성된 b의 값이 원본 tensor인 a의 변경에 따라 같이 변경된 것을 확인할 수 있습니다.


topk 기능 사용 방법


  • topk는 tensor에서 값이 가장 큰 k 개를 추출하는 연산을 의미합니다. 이 연산을 이용하여 feature에서 의미가 가장 큰 k를 추출하는 post processing에서 유용하게 사용할 수 있습니다.


 x = torch.arange(1., 6.)
# tensor([ 1.,  2.,  3.,  4.,  5.])
values, indices = torch.topk(x, 3)
print(values)
# tensor([5., 4., 3.])  
print(indices)
# tensor([4, 3, 2])


  • 위 코드의 의미는 topk 함수에서 첫번째 파라미터로 입력받은 텐서 x의 dimension 별 가장 큰 3개의 값과 그 위치를 추출하는 것입니다. dimension은 3번째 인자이고 따로 입력하지 않은 경우 마지막 dimension을 사용하게 됩니다.
  • 가장 큰 값이 5, 4, 3 순서로 추출되었고 그 위치 인덱스는 4, 3, 2 인것을 확인할 수 있습니다.


x = torch.rand(2, 4, 3) 
# tensor([[[0.6340, 0.6071, 0.1662],
#          [0.0580, 0.5568, 0.9077],
#          [0.8181, 0.6997, 0.7513],
#          [0.3967, 0.7240, 0.3160]],

#         [[0.2583, 0.7943, 0.3591],
#          [0.0139, 0.3078, 0.6734],
#          [0.9162, 0.2517, 0.7321],
#          [0.0617, 0.8910, 0.8623]]])

values, indices = torch.topk(x, 2)
print(values)
# tensor([[[0.6340, 0.6071],
#          [0.9077, 0.5568],
#          [0.8181, 0.7513],
#          [0.7240, 0.3967]],

#         [[0.7943, 0.3591],
#          [0.6734, 0.3078],
#          [0.9162, 0.7321],
#          [0.8910, 0.8623]]])
print(indices)
# tensor([[[0, 1],
#          [2, 1],
#          [0, 2],
#          [1, 0]],

#         [[1, 2],
#          [2, 1],
#          [0, 2],
#          [1, 2]]])


  • 차원을 확장해서 출력을 해보았습니다. 이 때, values의 값은 마지막 차원을 기준으로 top 2의 값을 저장하고 있고 indices는 그 위치를 저장하고 있습니다.
  • indices의 의미를 살펴보면 가장 첫번째 2개의 값인 0, 1은 x의 가장 첫번째 값인 0.6340, 0.6071, 0.1662 중 0번째, 1번째 값이라는 의미 입니다.
  • 이 indices 값을 어떻게 쓰면 편리하게 쓸 수 있을까요? torch.gather 함수를 이용하면 쉽게 사용할 수 있습니다. 


torch.gather(x, -1, indices) == values

# tensor([[[True, True],
#          [True, True],
#          [True, True],
#          [True, True]],

#         [[True, True],
#          [True, True],
#          [True, True],
#          [True, True]]])


  • torch.gather는 해당 인덱스에 대응되는 값을 추출하는 역할을 합니다. 따라서 위 코드와 같이 사용할 수 있습니다.


  • 어떤 차원에서도 topk를 이용하여 특정 차원을 기준으로 topk 개의 값을 추출할 수 있습니다.


values, indices = torch.topk(x, 2, dim=1)
print(values)
# tensor([[[0.8181, 0.7240, 0.9077],
#          [0.6340, 0.6997, 0.7513]],

#         [[0.9162, 0.8910, 0.8623],
#          [0.2583, 0.7943, 0.7321]]])

print(indices)
# tensor([[[2, 3, 1],
#          [0, 2, 2]],

#         [[2, 3, 3],
#          [0, 0, 2]]])


torch.gather(x, 1, indices) == values
# tensor([[[True, True, True],
#          [True, True, True]],

#         [[True, True, True],
#          [True, True, True]]])


  • 지금까지 topk의 사용방법과 torch.gather를 이용하여 indices를 어떻게 사용하는 지 살펴보았습니다. 실제 많이 사용하는 사례는 다음과 같습니다.
  • x, y의 shape이 같고 x의 최댓값의 위치에 해당하는 y의 값을 찾고자 합니다 이 떄 아래와 같이 사용할 수 있습니다.


x = torch.rand(3, 4, 5)
y = torch.rand(3, 4, 5)

# x의 2번째 차원을 기준으로 가장 큰 값을 하나 뽑습니다.
values, indices = torch.topk(x, 1, dim=2)
# x에서 추출된 값과 똑같은 위치에서 y의 값을 하나 뽑습니다.
torch.gather(y, 2, indices)


pytorch import 모음


import torch
import torchvision
import torch.nn as nn # neural network 모음. (e.g. nn.Linear, nn.Conv2d, BatchNorm, Loss functions 등등)
import torch.optim as optim # Optimization algorithm 모음, (e.g. SGD, Adam, 등등)
import torch.nn.functional as F # 파라미터가 필요없는 Function 모음
from torch.utils.data import DataLoader # 데이터 세트 관리 및 미니 배치 생성을 위한 함수 모음
import torchvision.datasets as datasets # 표준 데이터 세트 모음
import torchvision.transforms as transforms # 데이터 세트에 적용 할 수있는 변환 관련 함수 모음
from torch.utils.tensorboard import SummaryWriter # tensorboard에 출력하기 위한 함수 모음
import torch.backends.cudnn as cudnn # cudnn을 다루기 위한 값 모음

from torchsummary import summary # summary를 통한 model의 현황을 확인 하기 위함
import torch.onnx # model을 onnx 로 변환하기 위함


pytorch 셋팅 관련 코드


# pytorch 내부적으로 사용하는 seed 값 설정
torch.manual_seed(seed)

# cuda를 사용할 경우 pytorch 내부적으로 사용하는 seed 값 설정
torch.cuda.manual_seed(seed)


GPU 셋팅 관련 코드


# cuda가 사용 가능한 지 확인
torch.cuda.is_available()

# cuda가 사용 가능하면 device에 "cuda"를 저장하고 사용 가능하지 않으면 "cpu"를 저장한다.
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

# 멀티 GPU 사용 시 사용 가능한 GPU 셋팅 관련
# 아래 코드의 "0,1,2"는 GPU가 3개 있고 그 번호가 0, 1, 2 인 상황의 예제입니다.
# 만약 GPU가 5개이고 사용 가능한 것이 0, 3, 4 라면 "0,3,4" 라고 적으면 됩니다.
os.environ["CUDA_VISIBLE_DEVICES"] = "0,1,2"

# 현재 PC의 사용가능한 GPU 사용 갯수 확인
torch.cuda.device_count()

# 사용 가능한 device 갯수에 맞춰서 0번 부터 GPU 할당
os.environ["CUDA_VISIBLE_DEVICES"] = ",".join(list(map(str, list(range(torch.cuda.device_count())))))

# 실제 사용할 GPU만 선택하려면 아래와 같이 입력하면 됩니다. (예시)
os.environ["CUDA_VISIBLE_DEVICES"] = "1, 4, 6"

# cudnn을 사용하도록 설정. GPU를 사용하고 있으면 기본값은 True 입니다.
import torch.backends.cudnn as cudnn
cudnn.enabled = True

# inbuilt cudnn auto-tuner가 사용 중인 hardware에 가장 적합한 알고리즘을 선택하도록 허용합니다.
cudnn.benchmark = True


  • 위 코드와 같이 device의 유형을 선택하면 GPU가 존재하면 cuda:0에 할당되고 GPU가 없으면 cpu에 할당 되도록 할 수 있습니다.


  • GPU device의 사용 가능한 메모리를 코드 상에서 확인하려면 아래 함수를 사용합니다.


# unit : byte
torch.cuda.get_device_properties("cuda:0").total_memory

# unit : mega byte
torch.cuda.get_device_properties("cuda:0").total_memory // 1e6

# unit : giga byte
torch.cuda.get_device_properties("cuda:0").total_memory // 1e9


  • 멀티 GPU 사용 시 사용 시 아래 코드를 사용하여 전체 사용 가능한 GPU 메모리를 확인할 수 있습니다.


gpu_ids = list(map(str, list(range(torch.cuda.device_count()))))
total_gpu_memory = 0
for gpu_id in gpu_ids:
    total_gpu_memory += torch.cuda.get_device_properties("cuda:" + gpu_id).total_memory


GPU 메모리 해제 방법


  • CUDA 할당 된 Tensor를 GPU에서 완전히 메모리 해제를 하려면 ① 변수를 제거하고 ② cache를 비워야 실제 메모리에서 해제됩니다.
  • 변수가 제거되어도 cache를 남겨두는 이유는 동일한 목적으로 변수가 생성될 때, 빠르게 생성하기 위하여 메모리를 잡고 있습니다. 왜냐하면 실제 Tensor를 사용할 때, 반복적으로 Tensor를 생성하기 때문입니다.
  • 만약 임시로 Tensor를 만들었다가 제거해야 한다면 아래와 같이 변수 제거 후 cache를 비우면 메모리에서 완전 제거됩니다.
  • 변수 제거는 del 변수명을 사용하고 cache를 비울 때에는 torch.cuda.empty_cache()를 사용합니다.


import torch

print(torch.cuda.memory_allocated())
# 0
print(torch.cuda.memory_reserved())
# 0

A = torch.rand(1000000000).cuda()
print(torch.cuda.memory_allocated())
# 4000000000 
print(torch.cuda.memory_reserved())
# 4001366016

del A
print(torch.cuda.memory_allocated())
# 0 
print(torch.cuda.memory_reserved())
# 4001366016

torch.cuda.empty_cache()
print(torch.cuda.memory_allocated())
# 0
print(torch.cuda.memory_reserved())
# 0


offline에서 torchvision.models 사용


  • torchvision.models에서 제공되는 pretrained 모델을 offline에서 사용해야 하는 경우 online이 가능한 환경에서 아래와 같은 코드로 모델을 받습니다. 아래 코드는 resnet 예시이며 다양한 모델 리스트는 아래 링크에서 참조 가능합니다.
  • torchvision.models : https://pytorch.org/serve/model_zoo.html


import torchvision.models as models
models.resnet34(pretrained=True)


  • 위 코드에서 models.resnet34(pretrained=True)을 실행할 때, 모델을 어느 경로에 다운 받는 지 확인할 수 있습니다. 그 경로는 보통 .cache/torch/hub/checkpoints에 있습니다.
  • 윈도우의 경우 C 드라이버를 주요 저장 공간으로 쓴다면 C:\Users\사용자명\.cache\torch\hub\checkpoints\으로 되어 있을 것이고 리눅스의 경우 ~/.cache\torch\hub\checkpoints 경로를 사용합니다.
  • 이 때, 이 경로에 있는 resnet34-333f7ec4.pth와 같은 파일을 offline 환경에 위치시키면 됩니다. 예를 들어서 인터넷이 되는 윈도우 PC에서 model을 다운 받고 C:\Users\사용자명\.cache\torch\hub\checkpoints\에서 resnet34-333f7ec4.pth 파일을 복사한 뒤 인터넷이 안되는 리눅스 PC의 ~/.cache/torch/hub/checkpoints 에 복사한 파일을 붙여 넣고 사용하면 됩니다.
  • 단 pytorch의 버전에 따라서 모델의 - 뒤에 숫자와 영어로 되어 있는 부분이 다를 수 있으므로 실제 사용하는 offline 환경에서 필요로 하는 버전명으로 교체해서 사용하면 됩니다. offline에서 사용하는 버전명은 그 환경에서 동일하게 models.resnet34(pretrained=True)와 같이 입력하면 알 수 있습니다.


dataloader의 num_workers 지정


  • 참조 : https://discuss.pytorch.org/t/guidelines-for-assigning-num-workers-to-dataloader/813
  • pytorch를 이용하여 학습을 할 때, 데이터를 불러오는 방법으로 DataLoder(from torch.utils.data import DataLoader)를 사용합니다.
  • Dataloader의 num_workers는 CPU → GPU로 데이터를 로드할 때 사용하는 프로세스의 갯수를 뜻합니다.
  • 컴퓨터에서 병목 현상이 발생하는 대표적인 구간이 바로 I/O(Input/Output) 연산입니다. 따라서 I/O 연산에 최대 사용할 수 있는 코어를 적당하게 나누어 주어서 병목 현상을 제거하는 것이 전체 학습 시간을 줄일 수 있는 데 도움이 됩니다.
  • num_workers = 0이 기본값으로 사용됩니다. 이 옵션의 의미는 data loading이 오직 main process에서만 발생하도록 하는 synchronous 방법을 의미합니다.
  • 따라서 num_workers > 0 조건이 되도록 설정하여 asynchronous 하게 data loading이 가능해 지기 때문에, GPU 연산과 병렬적으로 data lodaing이 가능해지게 되어 병목 문제를 개선할 수 있습니다.
  • 여기서 적당하게라는 것이 상당히 휴리스틱하여 파이토치 디스커션에도 많은 의견이 있었습니다. (위 링크를 참조하시기 바랍니다.)
  • 참조 링크 중 실험적으로 접근해 본 한 사람의 의견으로는 num_workers = 4 x num_GPU가 사용하기 좋았다라는 의견이 있었습니다. 예를 들어 GPU 2개를 사용하면 num_workers = 8을 사용하는 것입니다.
  • 이 관계식을 참조하여 저 또한 실험을 해보았고 위 관계식 처럼 사용해 보니 나쁘지 않았습니다. 휴리스틱하게 접근한 방법이므로 최적은 아니지만 저는 위 관계식 대로 사용하여 num_workers = torch.cuda.device_count() * 4로 적용하여 사용합니다.


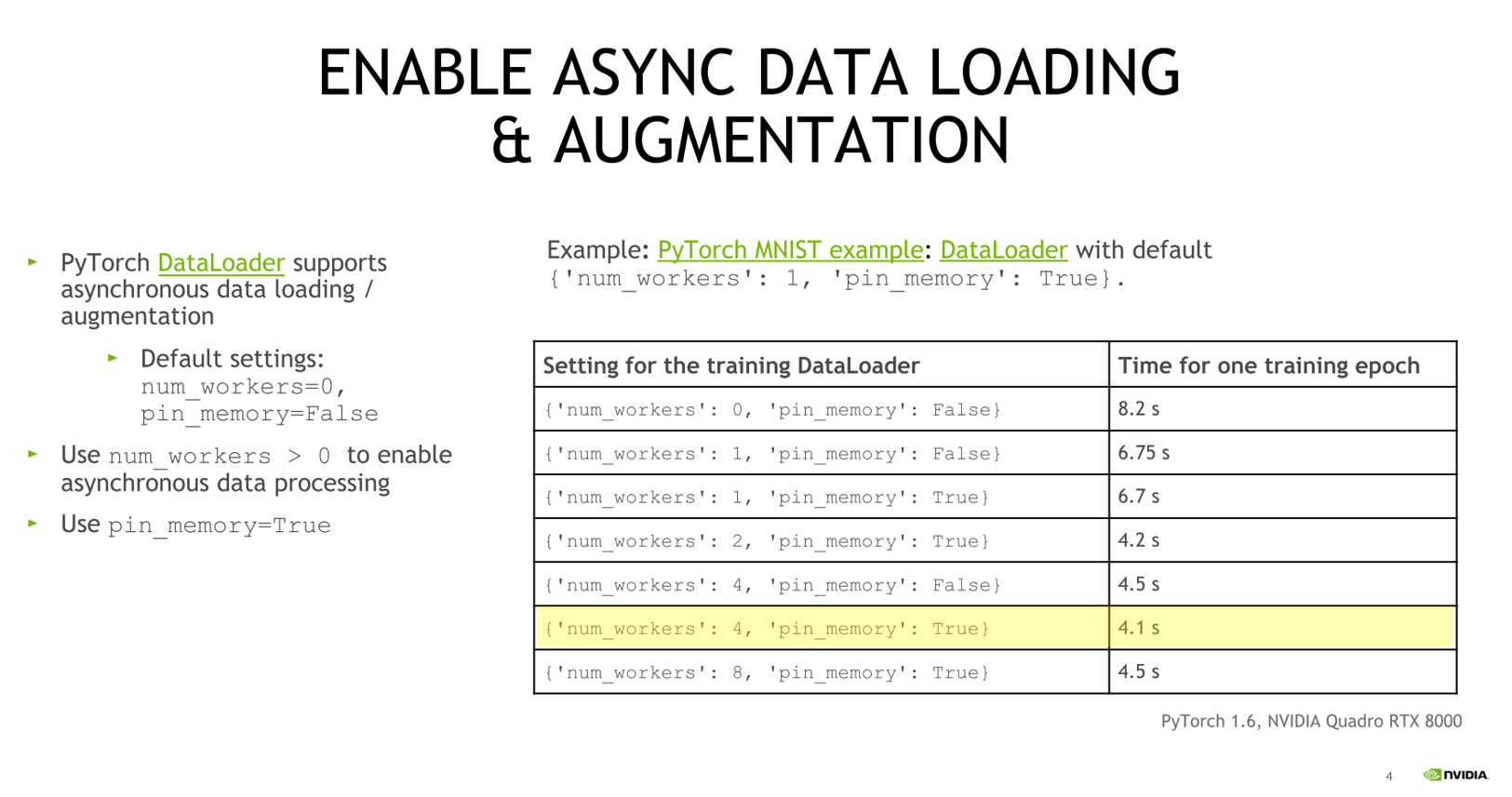
Drawing


  • 위 내용은 NVIDIA의 conference의 내용이며 기본 값인 num_workers=0, pin_memory=False를 num_workers > 0과 pin_memory=True로 변경하면서 실험 하였을 때, 성능 변화를 나타낸 것입니다. NVIDIA에서도 num_workers > 0과 pin_memory=True를 사용하기를 추천하며 특히 CPU와 RAM의 자원이 충분하다면 더 좋은 효과를 볼 수 있습니다.


dataloader의 pin_memory


  • torch.utils.data.DataLoader()를 사용할 때, 옵션으로 pin_memory = True 라는 것이 있습니다. 이 옵션의 의미에 대하여 알아보도록 하겠습니다. (pin memory : 고정된 메모리)
  • 먼저 pin_memory = False가 기본값으로 사용됩니다. 이 옵션의 의미는 CPU → GPU로의 메모리 복사 시 오직 main process에서만 복사가 발생하도록 하는 synchronous 방법을 의미합니다. 하드웨어 자원이 많을 때, 궂이 하나의 프로세스에서만 작업하는 것은 비효율적입니다.
  • pin_memory = True로 설정하면 학습 중에 CPU가 데이터를 GPU로 전달하는 속도를 향상시킵니다. 따라서 이 옵션은 GPU를 사용하여 학습할 때에는 항상 사용한다고 보셔도 됩니다.
  • pin_memory 관련 내용은 NVIDIA의 CUDA와 연관되어 있습니다. 전체 내용은 아래 링크를 통해 확인하면 되고 링크의 내용에서도 pinned memory 방식으로 사용하면 GPU 학습 시 더 큰 bandwidth를 사용할 수 있다고 설명합니다.
  • 링크 : https://developer.nvidia.com/blog/how-optimize-data-transfers-cuda-cc/


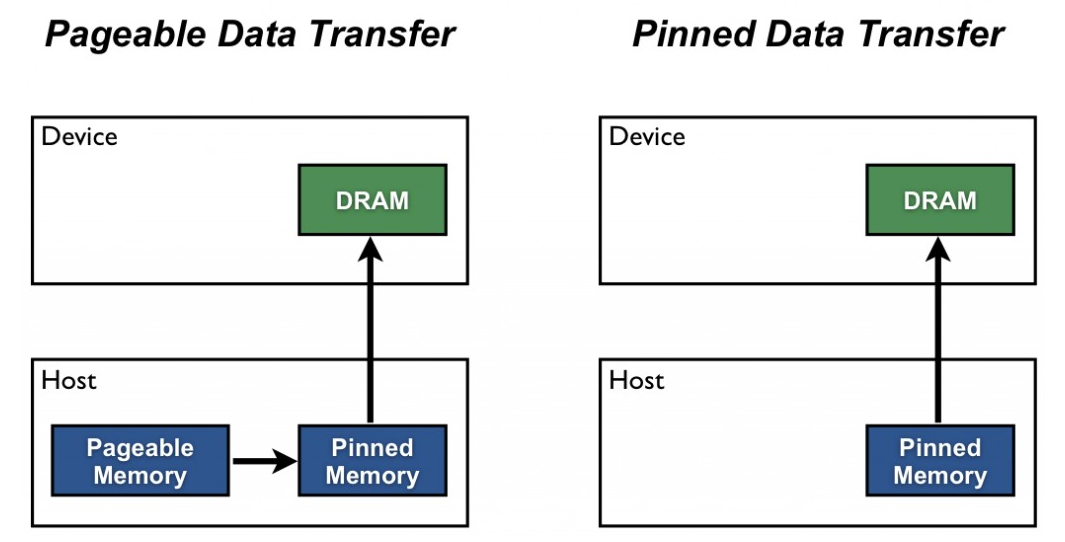
Drawing


  • 위 그림에서 Host는 CPU이고 Device는 GPU입니다. 즉, 데이터 torch.utils.data.DataLoader를 통하여 Host에서 Device로 데이터를 불러옵니다. 일반적인 방식은 CPU에서 페이징기법을 통해 pageable memory를 관리하는데 이는 가상 메모리를 관리하는 블록입니다. 이 가상 메모리는 실제 메모리 블록에 대응이 되도록 되어 있습니다.
  • 따라서 CPU → GPU로 데이터를 전달하기 위해서는 ① pageable memory에서 전달할 데이터들의 위치를 읽고, ② 전달할 데이터를 pinned memory에 모아서 복사한 다음에 ③ pinned moemry 영역에 있는 데이터를 GPU로 전달합니다.
  • pin_memory = True 옵션은 ① → ②의 과정을 줄여서 GPU 학습 시 효율적으로 CPU → GPU로 데이터를 전달합니다. 즉, pageable memory에서 전달할 데이터들을 확인한 다음 pinned memory 영역에 옮기지 않고 CPU 메모리 영역에 GPU로 옮길 데이터들을 바로 저장하는 방식입니다. 따라서 DataLoader는 추가 연산 없이 이 영역에 있는 데이터들을 GPU로 바로 옮길 수 있습니다.
  • 이런 연산 과정 때문에 pin_memory를 사용하는 것을 page-locked memory 라고도 합니다.
  • 이 연산 과정을 이해한다면 CPU만을 이용하여 학습을 하는 경우 이 옵션을 사용할 필요가 없다는 것을 아실 수 있습니다.
  • 다시 정리하면 GPU를 이용할 때에는 torch.utils.data.DataLodaer(pin_memory = True)를 사용하면 됩니다.


GPU 사용 시 data.cuda(non_blocking=True) 사용


  • 참조 : https://developer.nvidia.com/blog/how-overlap-data-transfers-cuda-cc/
  • GPU를 이용하여 학습할 때, 바로 앞의 dataloader의 pin_memory 사용과 더불어 data의 .cuda(non_blocking=True)는 일반적으로 반드시 사용하는 옵션입니다. 사용 방법은 아래와 같습니다.


for i, (images, target) in enumerate(train_loader):
    # measure data loading time
    data_time.update(time.time() - end)

    if args.gpu is not None:
        images = images.cuda(args.gpu, non_blocking=True)
    if torch.cuda.is_available():
        target = target.cuda(args.gpu, non_blocking=True)

    # compute output
    output = model(images)
    loss = criterion(output, target)


  • 위 코드를 보면 images = images.cuda(args.gpu, non_blocking=True)와 같이 데이터를 .cuda()로 변환하면서 GPU 연산을 지원하도록 하는데 이 때, non_blocking=True를 옵션으로 지정해 줍니다.
  • 이 옵션은 CPU → GPU로 데이터를 전달하는 메커니즘과 연관된 옵션입니다. .cuda(non_blocking=True)를 앞의 pin_memory와 연관하여 설명해보겠습니다.
  • Host(CPU) → GPU 복사는 pin(page-lock)memory에서 생성 될 때 훨씬 빠릅니다. 따라서 CPU 텐서 및 스토리지는 pinned region에 데이터를 넣은 상태로 객체의 복사본을 전달하는 pin_memory 메서드를 사용합니다.
  • 또한 텐서 및 스토리지를 고정하면 비동기(asynchronous) GPU 복사본을 사용할 수 있습니다. 비동기식으로 GPU에 데이터 전달 기능을 추가하려면 non_blocking = True 인수를 to() 또는 cuda() 호출 시 argument로 전달하면 됩니다.


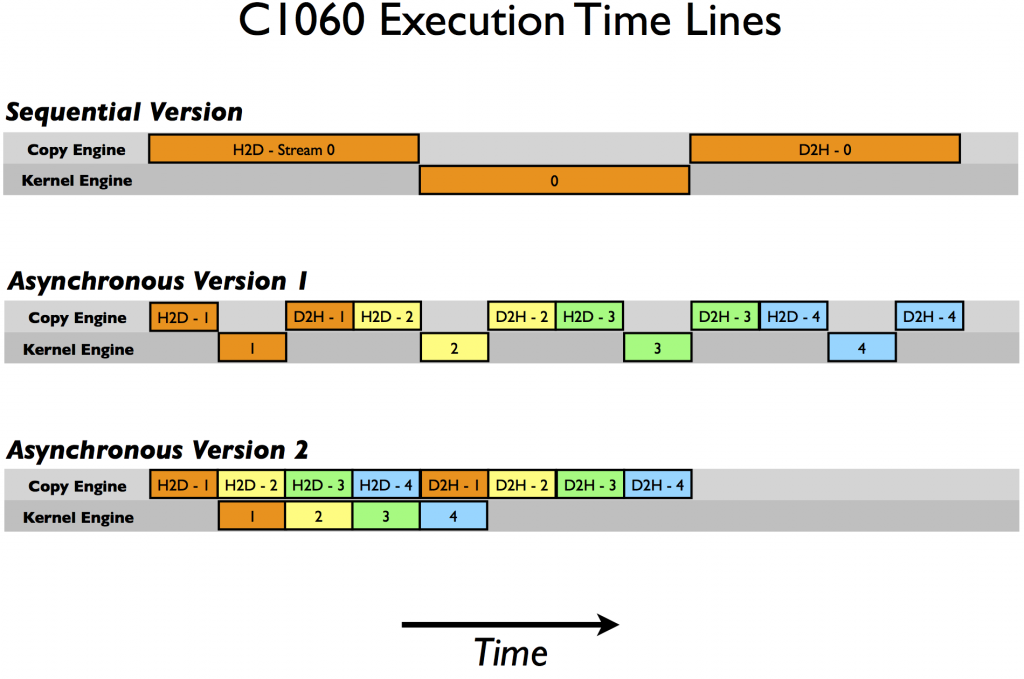
Drawing


  • 위 그림의 첫번째가 동기식(synchronous) 방식이고 두번째, 세번째가 비동기식(asynchronous)방식입니다. 동기식 방식의 경우 CPU → GPU로 데이터 전달이 끝이나야 그 다음 연산이 진행되는 반면에 비동기식 방식에서는 데이터 전송과 GPU 연산이 동시에 발생할 수 있습니다.
  • 이와 같은 방법을 통하여 데이터 전송과 계산을 겹쳐서 (비동기식)으로 할 수 있으므로 연산 속도 향상에 도움을 줍니다.


optimizer.zero_grad(), loss.backward(), optimizer.step()


  • optimizer.zero_grad() : 이전 step에서 각 layer 별로 계산된 gradient 값을 모두 0으로 초기화 시키는 작업입니다. 0으로 초기화 하지 않으면 이전 step의 결과에 현재 step의 gradient가 누적으로 합해져서 계산되어 집니다.
  • loss.backward() : 각 layer의 파라미터에 대하여 back-propagation을 통해 gradient를 계산합니다.
  • optimizer.step() : 각 layer의 파라미터와 같이 저장된 gradient 값을 이용하여 파라미터를 업데이트 합니다. 이 명령어를 통해 파라미터가 업데이트되어 모델의 성능이 개선됩니다.


optimizer.step()을 통한 파라미터 업데이트와 loss.backward()와의 관계


  • pytorch에서 학습 시, weight를 업데이트 하는 시점은 optimizer.step()이 실행되는 시점입니다. (참조)
  • optimizer.step()을 사용하는 순서를 확인해 보면 뉴럴네트워크의 출력값과 라벨 값을 loss 함수를 이용하여 계산을 하고 그 loss 함수의 .backward() 연산을 한 뒤에 optimizer.step()을 통해 weight를 업데이트 합니다.
  • 보통 loss function은 다음과 같이 선언합니다.


criterion = nn.CrossEntropyLoss()
out = model(input)
loss = criterion(out, target)
loss.backward()


  • optimizer의 선언 및 사용은 다음과 같습니다.


optimizer = optim.Adam(model.parameters(), lr=lr)
optimizer.step()


  • 프레임워크의 순서 상 ① loss 계산, ② loss.backward()로 gradient 계산, ③ optimizer.step()으로 weight 업데이트 순서가 되어야 합니다.
  • 이 떄, loss와 optimizer는 어떤 관계로 연결되어서 loss를 통해 계산한 gradient를 optimizer로 weight 업데이트 할 수 있을까요?
  • 위 예제에서 loss와 optimizer의 연결 포인트는 딥러닝 네트워크가 선언된 객체인 model의 각각이 가지고 있는 weight의 gradient 값입니다.
  • 예를 들어 model의 convolution 레이어 중 하나의 이름이 conv1 이라면 model.conv1.weight.grad에 loss에 따라 계산된 gradient가 저장되어 있습니다.
  • .layer.weight.grad에 gradient가 저장되는 시점은 loss.backward()가 실행되는 시점이고 이 때, gradient가 계산되어 .layer.weight.grad에 저장됩니다. 따라서 .backward() 이후에 grad 값을 출력하면 그 layer의 gradient 값을 볼 수 있습니다.
  • optimizer 객체는 model.parameters()를 통해 생성되었기 때문에 loss.backward()를 통해 .layer.weight.grad에 저장된 각 layer의 gradient는 optimizer에서 바로 접근하여 사용가능해집니다.
  • 따라서 앞에서 설명한 바와 같이 optimizer와 loss.backward()는 같은 model 객체를 사용하고 loss.backward()의 출력값이 각 model 객체 layer들의 grad 멤버 변수에 저장되고 이 값을 optimizer의 입력값으로 다시 사용함으로써 두 연산이 연결되어집니다.


gradient를 직접 zero로 셋팅하는 이유와 활용 방법


  • pytorch에서는 학습 시, weight에 계산된 gradient를 0으로 셋팅하는 함수가 있습니다. 이 함수를 사용하는 이유는 기본적으로 어떤 weight의 gradient를 계산하였을 때, 그 값이 기존 gradient를 계산한 값에 누적되기 때문입니다.
  • 먼저 다음 코드를 통하여 gradient가 누적되는 것을 살펴보겠습니다. 다음 코드는 sin을 미분하였을 때, cos이 되고 cos(0)은 1임을 이용하여 x의 grad값이 어떻게 변화하는 지 살펴보는 코드입니다.


import torch
from torch.autograd import Variable

x = Variable(torch.Tensor([[0]]), requires_grad=True)

for t in range(5):
    y = x.sin() 
    y.backward()
    print(x.grad)


  • 위 코드를 실행하면 x.grad값은 1, 2, 3, 4, 5로 계속 1씩 누적되어 증가하는 것을 확인할 수 있습니다.
  • 반면 다음 코드를 살펴보도록 하겠습니다.


x = Variable(torch.Tensor([[0]]), requires_grad=True) 

for t in range(5):
    if x.grad is not None:
        x.grad.data.zero_()
    y = x.sin() 
    y.backward()
    print(x.grad) # shows 1


  • 위 코드의 경우 x.grad를 0으로 초기화 하기 때문에 계산된 gradient가 누적되지 않습니다.


  • gradient를 초기화 하는 방법은 대표적으로 ① optimizer.zero_grad()를 이용하여 optimizer에 연결된 weight들의 gradient를 모두 0으로 만드는 방법이 있고 ② 위 코드와 같이 각 weight 별 접근하여 weight.grad.data.zero_()와 같이 weight 별 gradient를 0으로 초기화하는 방법이 있습니다.
  • 일반적으로 ① 방법을 사용하여 한번에 모든 weight의 계산된 gradient를 초기화 합니다. 딥러닝에서는 weight의 수가 너무 많기 떄문에 ②와 같은 방법을 통해서 초기화 하기에는 불편하기 때문입니다. ②와 같은 방법은 보통 몇몇 케이스를 테스트 할 때 종종 사용하곤 합니다.
  • 그러면 optimizer.zero_grad()를 이용하여 gradient를 언제 초기화 하는 지 살펴보겠습니다.


  • 보통 학습을 할 때에는 GPU 메모리의 한계로 인하여 한번에 GPU를 통해 연산되는 데이터 양이 제한적입니다. 예를 들어 데이터가 총 100개가 있으면 20개씩 데이터를 분할하여 5번 나눠서 학습을 하곤 합니다. 이 때, 20개라는 데이터의 크기를 batch size라고 합니다. 그리고 5번 이라는 나눠서 학습하는 횟수를 iteration이라고 합니다. 따라서 batch size * iteration을 하면 현재 가지고 있는 데이터 전체를 대상으로 학습을 하게 됩니다. 전체 데이터를 학습한 단위를 epoch이라고 합니다. 10 epoch을 학습하였다는 뜻은 100개의 데이터를 10번 반복학습 하였다는 뜻입니다.
  • batch size, iteration, epoch의 정의를 이해하시고 계속 글을 읽으시기 바랍니다.


  • 계산된 gradient가 실제 weight에 update되는 순간은 optimizer.step()입니다. 이 내용은 앞의 글 optimizer.step()을 통한 파라미터 업데이트와 loss.backward()와의 관계을 참조하시기 바랍니다.
  • 위 예제를 기준으로 한 epoch에서 각 iteration 마다 20개의 batch를 학습하면 총 5번의 gradient가 계산되어야 합니다. 이 때, pytorch에서는 기본적으로 이 gradient를 누적 하여 합하게 됩니다. 따라서 다음과 같은 2가지 전략을 세울 수 있습니다.


  • ① iteration 마다 weight를 update 하는 방법 : gradient가 누적되지 않게 iteration 시작 시 이전 iteration에서 계산된 gradient를 0으로 초기화합니다. 아래 코드를 살펴보겠습니다.


########### iteration 마다 weight를 update 하는 방법 ##############

# epochs 만큼 반복 학습한다. 위 예시에서 10번 반복학습에 해당함.
for epoch in range(epochs):
    # 위 예시에서 batches는 총 5개의 batch를 가지고 있으며,
    # 각 train_data는 20개의 데이터를 가지고 있음
    for num_train, (trarin_data, target_data) in enumerate(batches):
        # ★★★ gradient를 0으로 셋팅함 ★★★
        optimizer.zero_grad()
        # ★★★★★★★★★★★★★★★★★★
        out = nn_model(trarin_data)
        loss = loss_function(out, target_data)
        loss.backward()
        loss_sum += loss.item()
        # iteration 마다 계산된 gradient를 weight에 반영
        optimizer.step()
    loss_list.append(loss_sum / (num_train + 1))


  • ② epoch 마다 weight를 update 하는 방법 : 모든 iteration에서 계산된 gradient를 누적하여 한번에 weight update를 합니다. 따라서 epoch이 시작 시 계산된 gradient를 0으로 초기화 합니다. 아래 코드를 살펴보겠습니다.


########### epoch 마다 weight를 update 하는 방법 ##############

# epochs 만큼 반복 학습한다. 위 예시에서 10번 반복학습에 해당함.
for epoch in range(epochs):
    # ★★★ gradient를 0으로 셋팅함 ★★★
    optimizer.zero_grad()
    # ★★★★★★★★★★★★★★★★★★

    # 위 예시에서 batches는 총 5개의 batch를 가지고 있으며,
    # 각 train_data는 20개의 데이터를 가지고 있음
    for num_train, (trarin_data, target_data) in enumerate(batches):
        out = nn_model(trarin_data)
        loss = loss_function(out, target_data)
        loss.backward()
        loss_sum += loss.item()
    # epoch 마다 계산된 gradient를 weight에 반영
    optimizer.step()
    loss_list.append(loss_sum / (num_train + 1))


  • 위 두 가지 경우의 코드와 같은 방법으로 weight를 update를 할 수 있으며 방법에 따라 optimizer.zero_grad()를 실행하는 시점이 달라집니다.
  • 일반적으로 ① 방법인 iteration 마다 weight를 업데이트 하는 방법을 많이 사용하고 저 또한 이 방법을 사용하여 학습합니다.


validation의 Loss 계산 시 detach 사용 관련



  • 학습 중 일부 epoch을 진행한 다음에 CUDA error: out of memory 에러가 발생하는 경우가 있습니다.
  • 이번에 다룰 내용은 loss 계산 중에 이러한 에러가 발생하는 경우에 대하여 다루도록 하겠습니다.
  • 학습 단계에서 가장 기본적으로 Train 데이터 셋과 Validation 데이터 셋에 대하여 Loss를 구합니다.
  • Train 데이터 셋을 사용하는 경우 ① Loss를 구하고 ② Loss의 .backward()를 이용하여 backpropagation을 적용합니다.
  • 반면 Validation 데이터 셋을 사용하는 경우 Loss만 구하고 backpropagation은 적용하지 않습니다.
  • 이러한 차이점으로 인하여 의도치 않게 Pytorch를 사용할 떄, CUDA error: out of memory 문제가 발생하곤 합니다.
  • Pytorch 사용 시, ① model → ② optimizer → ③ loss 순서로 연결이 되어 있습니다. 예를 들어 다음 코드와 같습니다.
out = model(input)
criterion = nn.CrossEntropyLoss()
loss = criterion(out, target)
loss.backward()


  • 이 때, loss를 backward() 하지 않으면 backpropagation을 하기 위한 그래프의 히스토리가 loss에 계속 쌓이게 됩니다. 각 epoch의 loss를 구하기 위하여 각 batch에서 계산된 loss를 모두 더한 뒤 평균을 내는 방법을 많이 사용합니다. loss의 backward() 연산을 하면 연결된 그래프에 backpropagation 계산을 하게 되므로 히스토리가 쌓이지 않지만 backward()를 하지 않고 사용하면 히스토리가 계속 쌓이게 되고 GPU 연산에도 영향을 끼쳐서 CUDA error: out of memory 문제가 발생하곤 합니다.
  • 이 경우 loss에 .detach() 함수를 사용하여 그래프의 히스토리를 의도적으로 끊는 방법을 사용하여 메모리 문제를 피할 수 있습니다.


out = model(input)
criterion = nn.CrossEntropyLoss()
loss = criterion(out, target).detach()


  • 이 경우 loss의 그래프가 끊어졌기 떄문에 backward()를 사용할 수 없습니다. 따라서 이 경우는 backward()를 사용하지 않는 validation 데이터 셋 연산 시 위 코드와 같이 loss의 .detach()를 사용할 수 있습니다.


  • 정리하면 다음과 같습니다.
  • Train 데이터 셋 : Train 시 loss.backward()를 사용하고 loss.backward() 시, loss의 그래프 히스토리가 초기화되므로 epoch이 진행 됨에 따라 그래프가 계속 누적되어 메모리 문제가 발생하지 않음
  • Validation(Test) 데이터 셋 : Validation(Test) 시 loss.backward()를 사용하지 않으므로 loss의 그래프 히스토리가 계속 누적되어 epoch이 진행됨에 따라 메모리 문제가 발생하게 됨. 따라서 loss.detach()를 이용하여 loss의 그래프가 누적되지 않도록 의도적으로 끊어주어 메모리 문제를 개선할 수 있음


model.eval()와 torch.no_grad() 비교


  • model.eval() : .eval()모드를 사용하면 모델 내부의 모든 layer가 evaluation 모드가 됩니다. evaluation 모드에서는 batchnorm, dropout과 같은 기능들이 사용되지 않습니다.
  • torch.no_grad() : 어떤 Tensor가 .no_grad()로 지정이 되면 autograd 엔진에게 이 정보를 알려주고 학습에서 제외됩니다. 학습에서 제외되기 때문에 Backprop에 필요한 메모리 등을 절약할 수 있으므로 이 Tensor를 사용하여 계산 시 연산 속도가 빨라집니다. 하지만 Backprop을 할 수 없으므로 학습은 불가능 합니다.


  • 처음에 사용할 때에는 헷갈릴 수 있지만 기능이 구현된 목적에 맞게 사용하면 헷갈림 없이 사용할 수 있습니다.
  • model.eval()은 실제 inference를 하기 전에 model의 모든 layer를 evaluation 모드로 변경하기 위해 사용하면 됩니다. 특히 dropout과 batchnorm이 model에 포함되어 있다면 반드시 사용해야 합니다.
  • 반면 torch.no_grad()는 특정 레이어에서 backprop을 적용시키지 않기 위하여 사용됩니다. 따라서 학습에서 제외할 layer가 있다면 그 layer를 위해 사용하면 됩니다.


import torch

drop = torch.nn.Dropout(p=0.3)
x = torch.ones(1, 10)

# Train mode (default after construction)
drop.train()
print(drop(x))
# tensor([[1.4286, 1.4286, 0.0000, 1.4286, 0.0000, 1.4286, 1.4286, 0.0000, 1.4286, 1.4286]])

# Eval mode
drop.eval()
print(drop(x))
# tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])


  • 위 예제를 살펴보면 .train(), .eval() 모드에 따라서 dropout을 적용한 결과가 달라집니다.
  • eval 모드에서는 dropout이 비활성화가 되고 input을 그대로 pass해주는 역할만 합니다.
  • 반면 train 모드에서는 torch.nn.Dropout(p)에 사용되는 확률값 p를 받아서 사용됩니다.


  • 추가적으로 torch.no_grad()의 사용 케이스에 대하여 간략하게 소개하면서 마무리 하겠습니다.


x = torch.tensor([1], requires_grad=True)

# with 구문을 이용하여 Tensor의 성분을 no_grad로 변경
with torch.no_grad():
  y = x * 2
y.requires_grad
# False

# decorator를 이용하여 Tensor의 성분을 no_grad로 변경
@torch.no_grad()
def doubler(x):
    return x * 2
z = doubler(x)
z.requires_grad
# False


Dropout 적용 시 Tensor 값 변경 메커니즘


  • Tensor의 Train 모드에서는 dropout이 적용된 Tensor는 값 일부가 0으로 바뀌게 됩니다.
  • 이 떄, Dropout이 적용된 Tensor가 어떻게 바뀌는 지 간단하게 살펴보도록 하겠습니다.


import torch

drop = torch.nn.Dropout(p=0.3)
x = torch.ones(1, 10)

# Train mode (default after construction)
drop.train()
print(drop(x))
# tensor([[1.4286, 1.4286, 0.0000, 1.4286, 0.0000, 1.4286, 1.4286, 0.0000, 1.4286, 1.4286]])

# Eval mode
drop.eval()
print(drop(x))
# tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]])


  • 위 예제를 보면 Dropout을 적용하기 이전의 값은 모두 1을 가지고 있습니다.
  • 반면 dropout이 적용되면 일부 값은 0을 가지고 0이 되지 않은 값은 기존의 값 1보다 더 커진것을 알 수 있습니다.
  • 이와 같이 값이 변경 되는 것은 처음에 Dropout을 선언할 때, 입력한 파라미터 p와 (torch.nn.Dropout(p)) 연관되어 있습니다.
  • 위 예제에서 p = 0.3이라는 뜻은 전체 값 중 0.3의 확률로 0이 된다는 것을 뜻합니다.
  • 이 때 0이 되지 않은 0.7에 해당하는 값은 (1/0.7) 만큼 scale이 됩니다. 따라서 (1/0.7 = 1.4286…)이 됩니다.
  • 정리하면 Dropout에 적용된 p 만큼의 비율로 Tensor의 값이 0이되고 0이되지 않은 값들은 기존값에 (1/(1-p)) 만큼 곱해져서 값이 커집니다.


재현을 위한 랜덤 seed값 고정


  • Pytorch에서 코드를 재현하기 위해서는 랜덤 Seed 값을 고정을 해주어야 합니다. 먼저 파이썬, Numpy, Pytorch의 Seed을 수동으로 설정해주어야 하고 추가적으로 cudnn에 대한 설정이 필요합니다.
  • 먼저 torch.backends.cudnn.benchmark = False가 되어야 합니다. 아래 참조 1의 설명에 따르면 (This flag allows you to enable the inbuilt cudnn auto-tuner to find the best algorithm to use for your hardware.) 이 옵션을 통해서 cudnn이 하드웨어에 따라 최적화된 알고리즘을 사용한다고 되어 있습니다. 반대로 말하면 하드웨어의 상태에 따라서 사용되는 알고리즘이 다르다는 것을 뜻하므로 재현을 위해서는 옵션을 꺼줍니다.
  • 추가적으로 torch.backends.cudnn.deterministic = True 옵션을 사용하면 cudnn에서 같은 input에 대하여 재현 가능하도록 만들어 줍니다. 아래 참조 2 링크를 참조하시기 바랍니다.
  • 따라서 cudnn에 관한 2가지 옵션을 동시에 사용하시면 됩니다.
  • 매뉴얼 랜덤 Seed와 cudnn 옵션의 조합은 아래와 같이 사용하시면 됩니다.


seed=1
torch.manual_seed(seed)
np.random.seed(seed)
random.seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True


contiguous()의 의미


  • 참조 : https://stackoverflow.com/questions/48915810/pytorch-what-does-contiguous-do
  • pytorch 코드를 살펴볼 때, .contiguous() 라는 코드를 종종 볼 수 있습니다. 이 코드의 의미는 무엇일까요?
  • 결론적으로 사용자 입장에서는 큰 차이가 없을 수 있으며 이와 관련된 에러가 발생 시 .contiguous() 를 실행하여 에러를 회피하도록 하면 됩니다.
  • 다만 이 값이 가지는 의미를 살펴보기 위해 torch의 tensor가 동작하는 방식을 살펴보면 다음과 같습니다.
    • ① tensor에 해당하는 값을 실제 메모리에 할당합니다.
    • ② 사용할 떄에는 meta 정보에 따라 사용자에게 값이 보여집니다.
  • 이와 같은 방식을 사용하는 이유는 tensor를 사용할 때, 같은 값의 형 변환이 자주 발생하게 되는데 이 때마다 메모리 할당이 다시 일어나게 되면 비효율적이기 때문에 메모리에 저장된 값은 유지할 체 사용자에게는 shape 등의 형이 변경된 것 처럼 보여줍니다. 이 때, 사용자가 원하는 형으로 보여주기 위하여 meta 정보를 사용합니다.


  • 예를 들어 0, 1, 2, 3, 4의 값을 가지는 tensor가 있다고 가정해 보겠습니다.


Drawing


  • 먼저 어떤 tensor의 값이 실제 메모리에 위 그림과 같이 연속적으로 저장되어 있고 사용자도 이와 같은 순서의 데이터를 사용한다고 하면 contiguous 하다고 말합니다.


Drawing


  • 반면 어떤 tensor가 위 그림과 같이 메모리에 저장되어 있으나 사용자는 0, 1, 2, 3, 4 순서로 연속해서 사용할 수 있다고 하면 이러한 tensor는 non contiguous 하다고 말할 수 있습니다.


A = torch.tensor([[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11]]) 
# tensor([[ 0,  1,  2,  3],
#         [ 4,  5,  6,  7],
#         [ 8,  9, 10, 11]])

A.is_contiguous()
# True

A_t = A.T
# tensor([[ 0,  4,  8],
#         [ 1,  5,  9],
#         [ 2,  6, 10],            
#         [ 3,  7, 11]])   


A_t.is_contiguous()
# False

A_t_contiguous = A_t.contiguous()
# tensor([[ 0,  4,  8],
#         [ 1,  5,  9],
#         [ 2,  6, 10],            
#         [ 3,  7, 11]])   

A_t_contiguous.is_contiguous()
# True


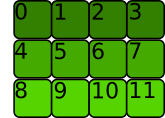
  • 먼저 A가 사용자에게 보여지는 방식은 아래와 같이 행렬려 보여지게 됩니다.


Drawing


  • 그리고 A는 처음 저장될 때, 아래와 같은 순서로 메모리에 저장됩니다.


Drawing


  • tensor를 처음 생성하였을 때에는 실제 메모리에 저장된 순서와 meta 정보가 같습니다. 따라서 A.is_contiguous()는 True 값을 가집니다.
  • 그러면 A를 Transpose한 A.T를 살펴보겠습니다.


Drawing


  • 먼저 A.T는 위 행렬과 같은 형태로 사용자가 사용하게 됩니다.


Drawing


  • 하지만 앞에서 설명한 바와 같이 실제 메모리에 저장된 순서가 바뀐게 아니라 사용자에게 보여주는 meta 정보가 바뀐 것이므로 메모리에 저장된 값은 A와 동일하며 위 그림과 같습니다.
  • 이 경우에 A_t.is_contiguous()는 False를 가집니다.
  • 의도적으로 메모리에 저장된 순서를 현재 meta 정보와 같이 변경하려고 하면 .contiguou()를 통해 변경할 수 있습니다. A_t_contiguous = A_t.contiguous() 를 통해 meta 정보와 같은 방향으로 메모리 업데이트를 하면 다음과 같이 변경됩니다.


Drawing



Drawing


  • A_t_contiguous는 실제 메모리에 저장된 값의 순서와 사용자가 사용하는 값의 순서가 같습니다. 따라서 A_t_contiguous.is_contiguous()는 True 값을 가지게 됩니다.


opencv로 이미지를 읽어서 tensor로 변환


  • opencv로 이미지를 읽은 후 tensor로 변환하는 과정은 다음과 같습니다.
  • 먼저 opencv와 같은 라이브러리로 이미지를 읽으면 (H, W, C)와 같은 형태로 읽게 되어 있으며 pytorch에서 다루는 tensor는 (B, C, H, W) 형태로 사용하게 됩니다. 그리고 학습 시 사용하는 tensor 값의 범위는 0 ~ 1로 스케일이 변경되도록 많이 사용합니다.
  • 아래 코드의 load_image를 사용하면 이미지를 opencv로 읽어서 BGR을 RGB로 바꾼 뒤, 원하는 사이즈로 resize까지 적용합니다.
  • 그리고 tensorify를 사용하면 (H, W, C) 형태의 numpy 데이터를 (B, C, H, W)의 tensor로 변경해 줍니다. 이 때 tensor의 크기는 (1, C, H, W)가 되며 값의 범위도 0 ~ 1 로 변경됩니다.


load_images = lambda path, h, w: cv2.resize(cv2.cvtColor(cv2.imread(path, cv2.IMREAD_UNCHANGED), cv2.COLOR_BGR2RGB), ((w, h)))
tensorify = lambda x: torch.Tensor(x.transpose((2, 0, 1))).unsqueeze(0).float().div(255.0)

img_tensor = tensorify(load_images("img.png", 400, 300))
print(img_tensor.shape)
# torch.Size([1, 3, 400, 300])


torch.argmax(input, dim, keepdim)


  • 딥러닝 각 framework마다 존재하는 argmax 함수에 대하여 다루어 보겠습니다. keras, tensorflow와 사용법이 유사하니 참조하시면 됩니다. 아래 링크는 pytorch의 링크입니다.
    • pytorch 링크 : https://pytorch.org/docs/stable/torch.html
  • argmax 함수가 받는 argument는 차례대로 input, dim, keepdim 입니다. input은 Tensor를 나타내고 dim은 몇번 째 축을 기준으로 argmax 연산을 할 지 결정합니다. 마지막으로 keepdim은 argmax 연산을 한 축을 생략할 지 그대로 둘 지에 대한 기준이 됩니다. argmax를 하면 각 축마다 값이 1개만 남게 되므로 필요 여부에 따라 남길 수도 있고 삭제 할 수도 있습니다.


  • pytorch를 이용하여 이미지 처리를 할 때, 주로 사용하는 방법은 다음과 같습니다.


# 1. input이 (channel, height, widht) 인 경우
torch.argmax(input, dim = 0, keepdim = True)

# 2. input이 (batch, channel, height, width) 인 경우
torch.argmax(input, dim = 1, keepdim = True)


  • 일반적으로 이미지 처리를 할 때, 출력의 channel의 갯수 만큼 클래스 label을 가지고 있는 경우가 많습니다. 이 때, 가장 큰 값을 argmax 함으로써 가장 큰 인덱스를 구할 수 있습니다.
  • 예를 들어 segmentation을 하는 경우 위의 코드와 같은 형태가 그대로 사용될 수 있습니다. 1번 케이스의 경우 batch가 고려되지 않은 것이고 2번 케이스의 경우 batch가 고려된 것입니다. segmentation의 경우 이미지의 height, width의 크기에 channel의 갯수가 label의 갯수와 동일하게 되어 있습니다. 그 중 가장 큰 값을 가지는 channel이 그 픽셀의 label이 되게 됩니다.
  • 따라서 argmax를 취하면 channel은 1로 되고 height와 width의 크기는 유지됩니다.


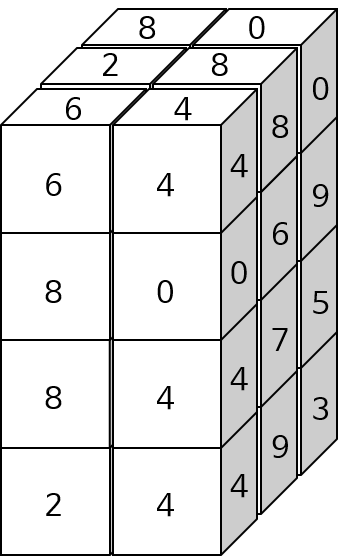
Drawing


  • 위 그림을 예제로 이용하여 각 축에 대하여 argmax한 결과를 알아보도록 하겠습니다.
  • 아래 예제 코드에서는 0번째 (channel), 1번째 (height), 2번째 (width) 방향으로 각각 argmarx를 한 것입니다. 또한 keepdim을 기본값인 False로 둘 경우와 True로 둘 경우를 구분하여 어떻게 shape이 변화하는 지 살펴보았습니다.



# channel : 3, height : 4, width : 2로 가정합니다.
>> A = torch.randint(10, (3, 4, 2))
>> print(A)

tensor([[[6, 4],
         [8, 0],
         [8, 4],
         [2, 4]],

        [[2, 8],
         [3, 6],
         [4, 7],
         [0, 9]],

        [[8, 0],
         [3, 9],
         [0, 5],
         [7, 3]]])

# 0번째 축(channel) 기준 argmax w/o Keepdim
 >> torch.argmax(A, dim=0)
tensor([[2, 1],
        [0, 2],
        [0, 1],
        [2, 1]])

>> torch.argmax(A, dim=0).shape
torch.Size([4, 2])

# 0번째 축(channel) 기준 argmax w/ Keepdim
>> torch.argmax(A, dim=0, keepdim = True)
tensor([[[2, 1],
         [0, 2],
         [0, 1],
         [2, 1]]])

 >> torch.argmax(A, dim=0, keepdim = True).shape
 torch.Size([1, 4, 2])

# 1번째 축(height) 기준 argmax w/o Keepdim
>> torch.argmax(A, dim=1)
tensor([[2, 3],
        [2, 3],
        [0, 1]])
 
 >> torch.argmax(A, dim=1).shape
torch.Size([3, 2])


# 1번째 축(height) 기준 argmax w/ Keepdim
>> torch.argmax(A, dim=1, keepdim = True)
tensor([[[2, 3]],

        [[2, 3]],

        [[0, 1]]])

>> torch.argmax(A, dim=1, keepdim = True).shape
torch.Size([3, 1, 2])


# 2번째 축(width) 기준 argmax w/o Keepdim
>> torch.argmax(A, dim=2)
tensor([[0, 0, 0, 1],
        [1, 1, 1, 1],
        [0, 1, 1, 0]])

>> torch.argmax(A, dim=2).shape
torch.Size([3, 4])

# 2번째 축(width) 기준 argmax w/ Keepdim
>> torch.argmax(A, dim=2, keepdim=True)
tensor([[[0],
         [0],
         [0],
         [1]],

        [[1],
         [1],
         [1],
         [1]],

        [[0],
         [1],
         [1],
         [0]]])


>> torch.argmax(A, dim=2, keepdim=True).shape
torch.Size([3, 4, 1])


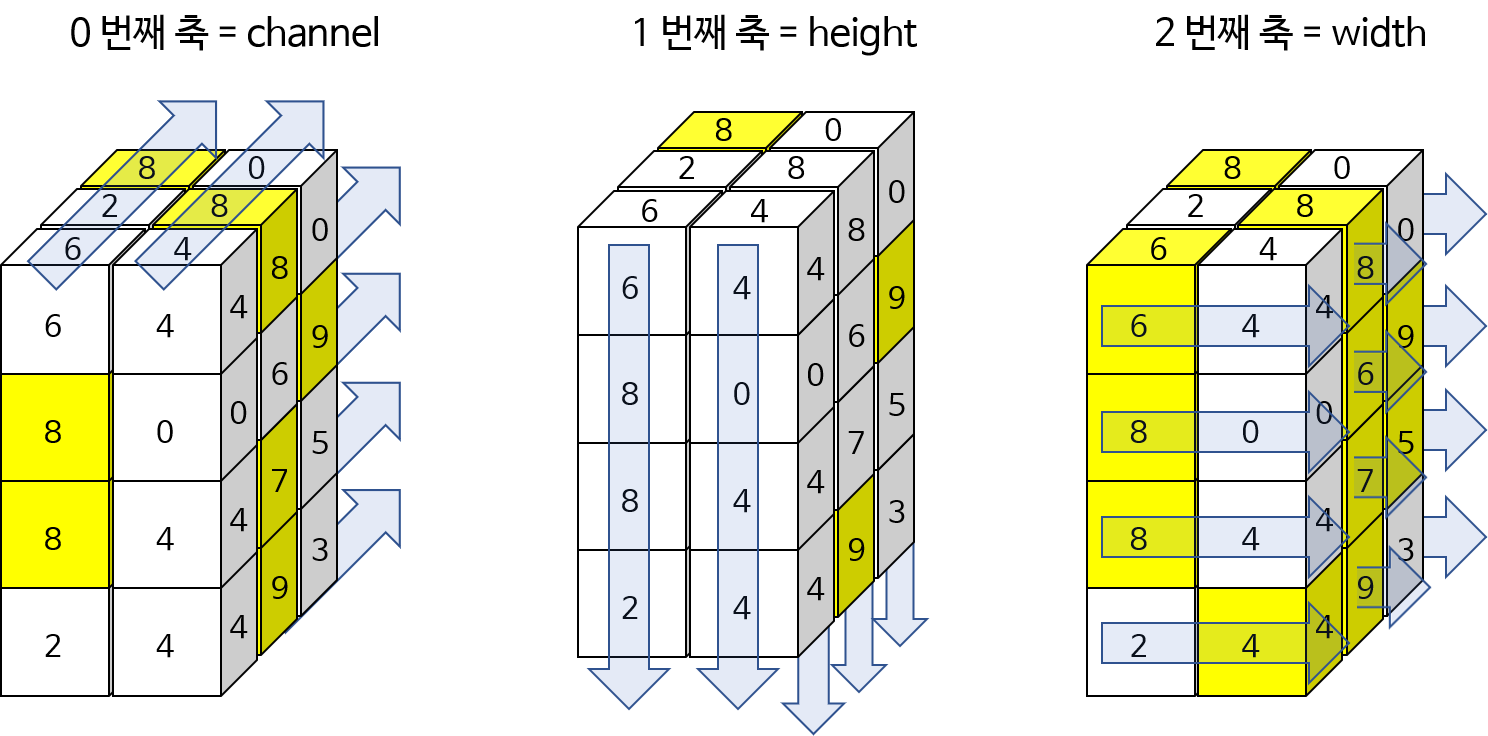
Drawing


  • 위 그림을 보면 왼쪽 부터 0번째 축, 1번째 축, 2번째 축 방향을 기준으로 argmax하였을 때 선택된 결과를 노란색 음영으로 표시하였습니다. 위 코드 결과를 그대로 표현한 것으로 이해하는 데 참조하시기 바랍니다.


  • 이번에는 간단하게 height와 width만 고려하여 다루어 보겠습니다.


# 간단하게 height, width의 크기만을 이용하여 다루어 보겠습니다.
>> B = torch.rand(3, 2)

tensor([[0.8425, 0.3970],
        [0.5268, 0.7384],
        [0.5639, 0.3080]])

# 1번 예제. 아래 첫번째 그림 참조
>> torch.argmax(B, dim=0)
tensor([0, 1])

>> torch.argmax(B, dim=0, keepdim=True)
tensor([[0, 1]])

# 2번 예제. 아래 두번째 그림 참조
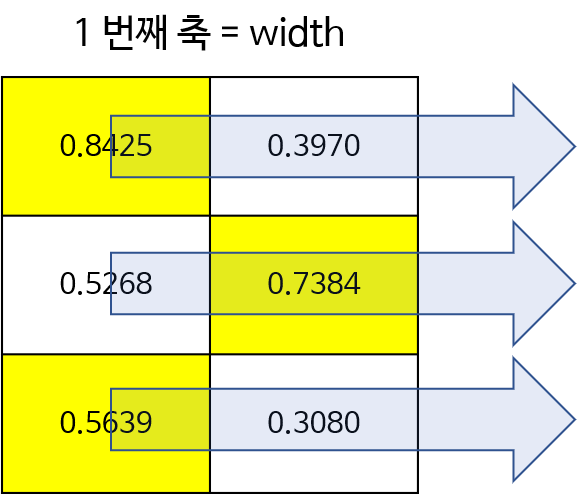
>> torch.argmax(B, dim=1)
tensor([0, 1, 0])

>> torch.argmax(B, dim=1, keepdim=True)
tensor([[0],
        [1],
        [0]])


  • 위의 1번 예제에 해당하는 그림입니다. 매트릭스에서 0번째 축은 세로(height)축입니다. 따라서 각 열에서 세로 방향으로 최대값이 선택됩니다.


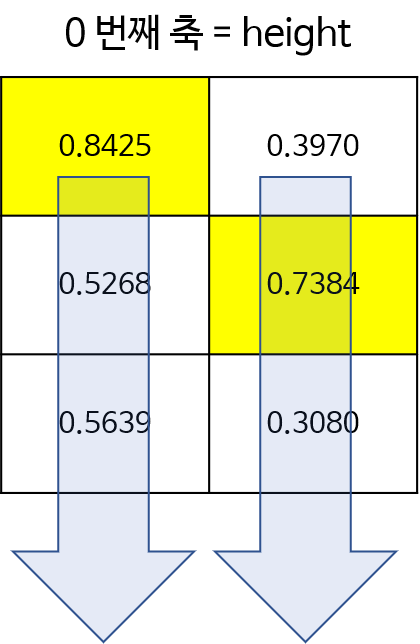
Drawing


  • 다음으로 2번 예제에 해당하는 그림입니다. 매트릭스에서 1번째 축은 가로(width)축입니다. 따라서 각 행에서 가로 방향으로 최댁밧이 선택됩니다.


Drawing


Numpy → Tensor : torch.from_numpy(numpy.ndarray)


  • torch에서 numpy를 이용해 선언한 데이터를 Tensor 타입으로 변환하려면 아래와 같이 사용할 수 있습니다.


A = np.random.rand(3, 100, 100)
torch.from_numpy(A)


Tensor → Numpy


  • 이번에는 위 내용과 반대로 Tensor를 Numpy로 변경하는 방법에 대하여 알아보도록 하겠습니다. 정확히는 깊은 복사 후 Numpy로 형 변환하는 작업입니다.
  • ① Tensor가 backprop 시 연산이 되지 않도록 .detach()를 하여 그래프에서 분리시킵니다.
  • ② 일반적으로 numpy는 CPU 기반의 연산을 사용합니다. 즉, GPU 연산을 사용하지 않으므로 .cpu()를 통해 CPU 모드로 변환합니다.
  • ③ 마지막으로 numpy()로 변환해 줍니다.
  • 이 과정을 통해 어떤 Tensor A가 있다면 A_np = A.detach().cpu().numpy()를 통해 numpy로 변환이 가능합니다. 이 때, 기본적으로 float32 타입으로 변환됩니다.


torch.Tensor().numpy()
torch.Tensor().cpu().data.numpy()
torch.Tensor().cpu().detach().numpy()


  • GPU에 사용되거나 학습에 사용된 경우에 따라서 tensor를 numpy로 바꾸려면 위 3가지 방법 중 하나를 따르게 되어 있습니다. 상황에 맞게 사용하면 됩니다.


torch.unsqueeze(input, dim)


  • 이번에는 바로 앞의 squeeze 예제를 이어 Tensor의 dimension을 늘려보도록 하겠습니다.
  • torch.unsqueeze(input, dim)은 squeeze와는 반대로 diemnsion을 늘려주고 그 값은 1로 만듭니다.
  • 이 때 선택할 수 있는 dimension은 0 부터 마지막 dimension 까지 입니다. 예를 들어 원래 input의 dimension이 2이면 0 (맨 앞), 1 (가운데), 2 (맨 끝)에 dimension을 늘려줄 수 있습니다.


import torch

tensor = torch.rand(5, 5)
print(tensor.shape)
# torch.Size([5, 5])

tensor = torch.unsqueeze(tensor, 0)
print(tensor.shape)
# torch.Size([1, 5, 5])

tensor = torch.rand(5, 5)
tensor = torch.unsqueeze(tensor, 1)
print(tensor.shape)
# torch.Size([5, 1, 5])

tensor = torch.rand(5, 5)
tensor = torch.unsqueeze(tensor, 2)
print(tensor.shape)
# torch.Size([5, 5, 1])


torch.squeeze(input, dim)


  • Tensor의 dimension을 맞추기 위해서 dimension을 변경해야 할 경우가 있습니다. 특히 이번에 알아볼 경우는 dimension을 축소하는 경우입니다.
  • dimension 축소를 위해서는 tensor.squeeze() 함수를 이용하고 아래와 같이 응용할 수 있습니다.
  • torch.squeeze() 함수는 어떤 dimension의 값이 1일 때, 그 dimension을 제거해 줍니다.


import torch

tensor = torch.rand(1, 5, 5)
print(tensor.shape)
# torch.Size([1, 5, 5])

tensor = torch.squeeze(tensor, 0)
print(tensor.shape)
# torch.Size([5, 5])

tensor = torch.rand(1, 5, 5)
tensor = torch.squeeze(tensor, 1)
print(tensor.shape)
# torch.Size([1, 5, 5])


  • 위 예제와 같이 torch.squeeze(tensor, 1)에서는 dimension의 값이 1이 아니므로 dimension이 제거 되지 않았습니다.


Variable(data)


  • Variable은 from torch.autograd import Variable을 통해 import 할 수 있습니다.
  • Variable은 tensor에 데이터를 집어 넣을 때, Variable 타입으로 기존의 데이터를 변경하여 사용하곤 합니다.
  • Variable을 생성할 때 가장 많이 사용하는 옵션 중 하나는 Variable이 학습이 필요한 weight 인 지 아닌 지 지정해 주는 옵션입니다. 다음과 같이 사용할 수 있습니다.


import torch
from torch.autograd import Variable

v1 = Variable(torch.rand(3), requires_grad = True)
print(v1)
# tensor([0.8407, 0.9296, 0.6941], requires_grad=True)

with torch.no_grad():
    v2 = Variable(torch.rand(3))
print(v2)
# tensor([0.3445, 0.2108, 0.4271])


  • 위 처럼 with torch.no_grad(): 로 감싸준 경우 명확하기 학습이 필요 없음을 명시하므로 가독성에 좋습니다. 즉, inference 용도로만 사용한다는 뜻입니다.
  • 이전에는 이를 volatile 옵션을 사용하기도 하였습니다. 예를 들어 volatile = True의 경우 inference 용도로만 사용한 경우로 위의 no_grad()와 동일한 목적의 Variable로 해석할 수 있습니다. 가끔씩 보이는 legacy 코드에서 volatile 파라미터가 있다면 True 인 경우 inference 용도인 것으로 해석하시면 됩니다.


F.interpolate()와 nn.Upsample()


  • 참조 : https://pytorch.org/docs/stable/nn.functional.html
  • 참조 : https://pytorch.org/docs/master/generated/torch.nn.Upsample.html


  • 딥러닝에서 interpolation은 작은 feature의 크기를 크게 변경시킬 대 사용됩니다.
  • 사용할 수 있는 대표적인 방법으로는 F.interpolate()와 nn.Upsample() 방법이 있습니다.
  • 먼저, pytorch에서 제공하는 torch.nn.functional의 interpolate가 어떻게 사용되는 지 알아보도록 하겠습니다.


torch.nn.functional.interpolate(
    input, # input tensor
    size=None, # output spatial size로 int나 int 형 tuple이 입력으로 들어옵니다. (height, width)
    scale_factor=None, # spatial size에 곱해지는 scale 값
    mode='nearest', # 어떤 방법으로 upsampling할 것인지 정하게 됩니다. 'nearest', 'linear', 'bilinear', 'bicubic', 'trilinear', 'area'
    align_corners=False, # interpolate 할 때, 가장자리를 어떻게 처리할 지 방법으로 아래 그림 참조.
)


  • functional.interpolate 함수에서 필수적으로 사용하는 것은 input, size, mode이고 추가적으로 align_corners를 사용합니다.
  • input은 입력 Tensor입니다.
  • size는 interpolate 할 목표 사이즈 입니다. 이 때, 입력해야 할 사이즈는 batch와 channel을 뺀 사이즈이어야 합니다. 예를 들어 이미지의 경우 height와 width만 있기 때문에 (new_height, new_width) 형태이어야 합니다. Tensor의 크기와 대응되도록 height, width 순서로 입력해야 합니다. (size 와 scale_factor 중 하나만 입력 해야 합니다.)
  • scale_factor 또한 intperpolate 할 목표 사이즈가 됩니다. (size 와 scale_factor 중 하나만 입력 해야 합니다.)
  • mode는 upsampling 하는 방법으로 nearest 또는 bilinear를 대표적으로 사용할 수 있습니다.
    • nearest 같은 경우 주변 값을 실제 사용하는 것으로 현재 존재하는 실제 픽셀 값을 사용해야 하는 경우 nearest를 사용할 수 있습니다. 예를 들어 input의 feature 값이 정수 인데 interpolate 한 output의 값들도 정수가 되어야 한다면 nearest를 사용하여 소수값이 생기지 않도록 할 수 있습니다.
    • bilinear는 bilinear interpolation 방법을 이용한 것으로 이미지와 같은 height, width의 속성을 가지는 데이터에 적합한 interpolation 방법입니다. height, width로 구성된 2차원 평면이므로 interpolation 할 때 사용되는 변수도 2개입니다. 이 방법은 단 방향의, 1개의 변수를 이용하여 interpolation 하는 linear 보다 좀 더 나은 방법입니다.


import torch
import torch.nn as nn
import torch.nn.functional as F

input = torch.arange(0, 16, dtype=torch.float32).reshape(1, 1, 4, 4)
# size : torch.Size([1, 1, 4, 4])
# value : tensor([[[[ 0.,  1.,  2.,  3.],
#                   [ 4.,  5.,  6.,  7.],
#                   [ 8.,  9., 10., 11.],
#                   [12., 13., 14., 15.]]]])

F.interpolate(input, scale_factor=2, mode='nearest')
# tensor([[[[ 0.,  0.,  1.,  1.,  2.,  2.,  3.,  3.],
#           [ 0.,  0.,  1.,  1.,  2.,  2.,  3.,  3.],
#           [ 4.,  4.,  5.,  5.,  6.,  6.,  7.,  7.],
#           [ 4.,  4.,  5.,  5.,  6.,  6.,  7.,  7.],
#           [ 8.,  8.,  9.,  9., 10., 10., 11., 11.],
#           [ 8.,  8.,  9.,  9., 10., 10., 11., 11.],
#           [12., 12., 13., 13., 14., 14., 15., 15.],
#           [12., 12., 13., 13., 14., 14., 15., 15.]]]])

F.interpolate(input, scale_factor=0.8, mode='nearest')
# tensor([[[[ 0.,  1.,  2.],
#           [ 4.,  5.,  6.],
#           [ 8.,  9., 10.]]]])

F.interpolate(input, size=(5, 3), mode='bilinear')
# tensor([[[[ 0.1667,  1.5000,  2.8333],
#           [ 2.9667,  4.3000,  5.6333],
#           [ 6.1667,  7.5000,  8.8333],
#           [ 9.3667, 10.7000, 12.0333],
#           [12.1667, 13.5000, 14.8333]]]])


  • align_corners 내용은 다음 그림을 참조해 보겠습니다.


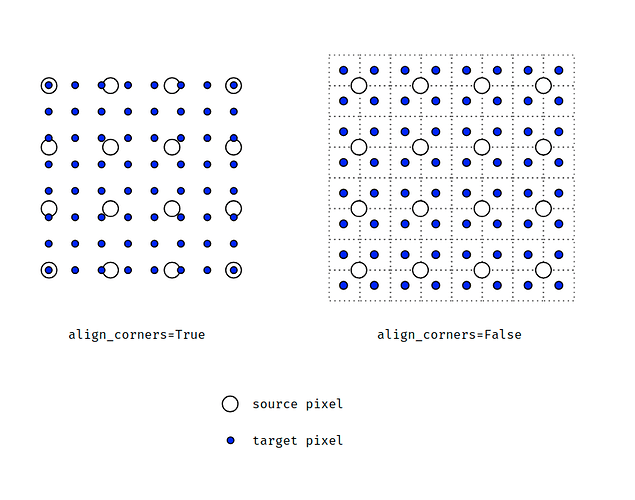
Drawing


  • 위 그림은 source가 (4, 4) 크기일 때, target은 (8, 8)로 2배 upsampling 하는 예제입니다.
  • align_corners기준으로 왼쪽 그림이 align_corners = True인 상태이고 오른쪽 그림이 False인 상태입니다.
  • 픽셀 영역으로 grid를 만들 었을 때, source는 grid의 교차점에 위치한 것을 전제로 합니다. align_corners=False의 그림을 참조하시면 됩니다. 이 때, align_corners=True이면 target 또한 source와 같이 grid의 교차점에 값을 위치시키려고 하나 align_corners=False이면 target은 한 픽셀 영역을 가지려고 합니다. 위의 그림을 참조하시기 바랍니다.
  • 따라서 align_corners=True인 상태라면 source의 끝점과 target의 끝점이 일치한 상태에서 interpolation이 됩니다. 말 그대로 corner 기준으로 정렬이 맞춰진 것입니다.
  • 반면 align_corners=False가 되면 target은 하나의 픽셀 영역이 되고 source의 픽셀들이 target의 픽셀의 grid points가 되도록 구성합니다.
  • segmentation을 할 때, align_corners = True로 두면 좀 더 성능이 좋다고 알려져 있습니다. 따라서 이 값은 True로 두는 것을 권장합니다. 다만 ONNX로 변환해야 하는 경우 버전에 따라서 반드시 align_corners = False로 두어야 하는 경우가 있으므로 이 점은 유의하여 사용하시길 바랍니다.
  • 그러면 예제를 살펴보도록 하겠습니다.



import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np

input = torch.arange(0, 16, dtype=torch.float32).reshape(1, 1, 4, 4)
# size : torch.Size([1, 1, 4, 4])
# value : tensor([[[[ 0.,  1.,  2.,  3.],
#                   [ 4.,  5.,  6.,  7.],
#                   [ 8.,  9., 10., 11.],
#                   [12., 13., 14., 15.]]]])

# align_corners가 True일 때와 False일 때의 값 차이 확인
F.interpolate(input, scale_factor=2, mode='bilinear', align_corners=False)
# tensor([[[[ 0.0000,  0.2500,  0.7500,  1.2500,  1.7500,  2.2500,  2.7500,  3.0000],
#           [ 1.0000,  1.2500,  1.7500,  2.2500,  2.7500,  3.2500,  3.7500,  4.0000],
#           [ 3.0000,  3.2500,  3.7500,  4.2500,  4.7500,  5.2500,  5.7500,  6.0000],
#           [ 5.0000,  5.2500,  5.7500,  6.2500,  6.7500,  7.2500,  7.7500,  8.0000],
#           [ 7.0000,  7.2500,  7.7500,  8.2500,  8.7500,  9.2500,  9.7500, 10.0000],
#           [ 9.0000,  9.2500,  9.7500, 10.2500, 10.7500, 11.2500, 11.7500, 12.0000],
#           [11.0000, 11.2500, 11.7500, 12.2500, 12.7500, 13.2500, 13.7500, 14.0000],
#           [12.0000, 12.2500, 12.7500, 13.2500, 13.7500, 14.2500, 14.7500, 15.0000]]]])

F.interpolate(input, scale_factor=2, mode='bilinear', align_corners=True)
# tensor([[[[ 0.0000,  0.4286,  0.8571,  1.2857,  1.7143,  2.1429,  2.5714,  3.0000],
#           [ 1.7143,  2.1429,  2.5714,  3.0000,  3.4286,  3.8571,  4.2857,  4.7143],
#           [ 3.4286,  3.8571,  4.2857,  4.7143,  5.1429,  5.5714,  6.0000,  6.4286],
#           [ 5.1429,  5.5714,  6.0000,  6.4286,  6.8571,  7.2857,  7.7143,  8.1429],
#           [ 6.8571,  7.2857,  7.7143,  8.1429,  8.5714,  9.0000,  9.4286,  9.8571],
#           [ 8.5714,  9.0000,  9.4286,  9.8571, 10.2857, 10.7143, 11.1429,  11.5714],
#           [10.2857, 10.7143, 11.1429, 11.5714, 12.0000, 12.4286, 12.8571,  13.2857],
#           [12.0000, 12.4286, 12.8571, 13.2857, 13.7143, 14.1429, 14.5714,  15.0000]]]])


  • 그 다음으로 nn.Upsample() 을 다루는 방법에 대하여 다루어 보도록 하겠습니다. 이 방법 또한 앞에서 다룬 F.interpolate()와 거의 같습니다.
  • F.interpolate()가 upsampling / downsampling을 모두 할 수 있듯이 nn.Upsample() 또한 upsampling / downsampling을 할 수 있지만 의미론 상 Upsample의 목적으로만 사용하는 것이 좋습니다.
  • 먼저 Upsample의 형태에 대하여 알아보도록 하겠습니다.


torch.nn.Upsample(
    size: Optional[Union[T, Tuple[T, ...]]] = None, 
    scale_factor: Optional[Union[T, Tuple[T, ...]]] = None, 
    mode: str = 'nearest', 
    align_corners: Optional[bool] = None
)


  • Upsample 함수는 1D, 2D, 3D 데이터를 모두 입력으로 받을 수 있습니다. 여기서 Dimension은 Batch 사이즈를 제외한 크기입니다. 따라서 입력은 batch_size x channels x height x width의 크기를 가집니다. 예를 들어 이미지 데이터의 경우 입력이 4차원이 되는데 그 이유는 앞의 예시와 같습니다. 예를 들어 32 batch의 (224, 224) 크기의 컬러 이미지이면 (32, 3, 224, 224)가 됩니다.
  • 중요한 것은 Upsample에 어떤 방식으로 Output의 크기를 명시할 것인가 입니다. 이것에 해당하는 것이 위 코드에서 size 또는 scale_factor에 해당합니다. size는 특정 size로 Upsampling 하는 방법입니다. 즉, 정확한 사이즈를 정해주는 방법입니다. 반면 scale_factor는 현재 input 대비 몇 배를 해줄 지 정해주는 scale 값에 해당합니다.
  • size와 scale_factor 중 어떤 것을 사용해도 상관없지만 중요한 것은 모호성을 줄이기 위해 둘 중 하나만을 사용하는 것입니다. 따라서 모델에 따라서 필요한 것을 사용하시길 바랍니다.
  • 앞의 interpolate와 동일하게 feature를 크게 만들기 위한 방법으로 nearest, linear, bilinear, bicubic, trilinear가 있고 기본값은 nearest 입니다.
  • 이미지를 다룰 때에는 주로 사용하는 방법이 nearest와 bileanear 방법인데 앞에서 설명한 바와 같이 필요에 따라 옵션을 사용하시면 됩니다.
  • Upsample을 이용한 예제를 다음과 같이 사용해 보도록 하겠습니다. 사용 결과는 F.interpolate()와 같으므로 결과 값은 빼겠습니다.


import torch
import torch.nn as nn
import torch.nn.functional as F

input = torch.arange(0, 16, dtype=torch.float32).reshape(1, 1, 4, 4)

# F.interpolate(input, scale_factor=2, mode='nearest')
m = nn.Upsample(scale_factor=2, mode = 'nearest')
m(input)

# F.interpolate(input, scale_factor=0.8, mode='nearest')
m = nn.Upsample(scale_factor=0.8, mode='nearest')
m(input)

# F.interpolate(input, scale_factor=2, mode='bilinear', align_corners=False)
m = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False)
m(input)

F.interpolate(input, size=(5, 3), mode='bilinear', align_corners=False)
m = nn.Upsample(size=(5, 3), mode='bilinear', align_corners=False)
m(input)


block을 쌓기 위한 Module, Sequential, ModuleList, ModuleDict


  • 출처 :https://towardsdatascience.com/pytorch-how-and-when-to-use-module-sequential-modulelist-and-moduledict-7a54597b5f17
  • torch.nn에 있는 Module, Sequential, ModuleList, ModuleDict는 모두 Network block을 쌓기 위하여 사용되는 클래스입니다. 즉, 다음과 같이 사용할 수 있습니다.


import torch.nn as nn

# nn.Module
# nn.Sequential
# nn.ModuleList
# nn.ModuleDict


  • 먼저 각 기능들을 언제 사용할 지 정리해 본 후 차례대로 설명하겠습니다.


  • Module : 여러 개의 작은 블록으로 구성된 큰 블록이 있을 때
  • Sequential : 레이어에서 작은 블록을 만들고 싶을 때
  • ModuleList : 일부 레이어 또는 빌딩 블록을 반복하면서 어떤 작업을 해야 할 때
  • ModuleDict : 모델의 일부 블록을 매개 변수화 해야하는 경우 (예 : activation 기능)


Module : The main building block

  • 먼저 Module에 대하여 알아보도록 하겠습니다. Module은 가장 기본이 되는 block 단위입니다.
  • 따라서 모든 pytorch의 기본 block들은 Module에서 부터 상속 받아서 사용되므로 Netowkr를 만들 때 반드시 사용됩니다.
  • 그러면 Sequential 또는 ModuleList 없이 단순히 Module만 사용한 아래 예제를 살펴보도록 하겠습니다.



import torch.nn.functional as F

class CNNClassifier(nn.Module):
    def __init__(self, in_c, n_classes):
        super().__init__()
        self.conv1 = nn.Conv2d(in_c, 32, kernel_size=3, stride=1, padding=1)
        self.bn1 = nn.BatchNorm2d(32)
        
        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1)
        self.bn2 = nn.BatchNorm2d(32)

        self.fc1 = nn.Linear(32 * 28 * 28, 1024)
        self.fc2 = nn.Linear(1024, n_classes)
        
    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = F.relu(x)
        
        x = self.conv2(x)
        x = self.bn2(x)
        x = F.relu(x)

        x = x.view(x.size(0), -1) # flat
        
        x = self.fc1(x)
        x = F.sigmoid(x)
        x = self.fc2(x)
        
        return x


  • 상당히 단순한 모델입니다. forward를 보면 Convolution → BatchNorm → ReLu로 이어지는 블록을 차례대로 이은 구조입니다.
  • __init__에서 선언된 각 객체들이 Module block 입니다. (nn.Conv2d, nn.BatchNor2d 등)
  • 위 코드를 보면 Convolution → BatchNorm → ReLu 블록이 이어져서 사용됨에도 불구하고 함수 처럼 사용하지 못하는 것은 다소 비효율적으로 보입니다. 이것을 개선하기 위하여 Sequential과 ModuleList를 사용할 수 있습니다.


Sequential: stack and merge layers


  • 그 다음으로는 Sequential 입니다. Sequential은 마치 컨태이너 처럼 Module을 담는 역할을 합니다. Sequential에 쌓은 순서대로 Module은 실행되고 같은 Sequential에 쌓인 Module 들은 한 단위처럼 실행됩니다.
  • 따라서 Module 중에서 동시에 쓰이는 것을 Sequential로 묶어서 사용하면 코드가 간단해집니다.
  • 예를 들어 위 예제에서 Convolution → BatchNorm → ReLu는 3개의 Module이 연달아 사용되기 때문에 마치 하나의 단위처럼 생각할 수 있습니다. 따라서 이 3개의 Module을 Sequential로 만들어 보겠습니다.


class CNNClassifier(nn.Module):
    def __init__(self, in_c, n_classes):
        super().__init__()
        self.conv_block1 = nn.Sequential(
            nn.Conv2d(in_c, 32, kernel_size=3, stride=1, padding=1),
            nn.BatchNorm2d(32),
            nn.ReLU()
        )
        
        self.conv_block2 = nn.Sequential(
            nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1),
            nn.BatchNorm2d(64),
            nn.ReLU()
        )
        
        self.decoder = nn.Sequential(
            nn.Linear(32 * 28 * 28, 1024),
            nn.Sigmoid(),
            nn.Linear(1024, n_classes)
        )

        
    def forward(self, x):
        x = self.conv_block1(x)
        x = self.conv_block2(x)

        x = x.view(x.size(0), -1) # flat
        
        x = self.decoder(x)
        
        return x


  • 위 코드를 보면 __init__에서도 단위 별로 묶어서 표현할 수 있고 forward에서는 코드가 훨씬 간결해 진것을 확인할 수 있습니다.
  • 위 코드에서 conv_block1과 conv_block2 또한 코드가 중복되었습니다. 중복되는 코드를 함수로 빼면 더 간결하게 쓸 수 있습니다.



def conv_block(in_f, out_f, *args, **kwargs):
    return nn.Sequential(
        nn.Conv2d(in_f, out_f, *args, **kwargs),
        nn.BatchNorm2d(out_f),
        nn.ReLU()
    )

class CNNClassifier(nn.Module):
    def __init__(self, in_c, n_classes):
        super().__init__()
        self.conv_block1 = conv_block(in_c, 32, kernel_size=3, padding=1)
        
        self.conv_block2 = conv_block(32, 64, kernel_size=3, padding=1)

        
        self.decoder = nn.Sequential(
            nn.Linear(32 * 28 * 28, 1024),
            nn.Sigmoid(),
            nn.Linear(1024, n_classes)
        )

        
    def forward(self, x):
        x = self.conv_block1(x)
        x = self.conv_block2(x)

        x = x.view(x.size(0), -1) # flat
        
        x = self.decoder(x)
        
        return x


  • 위 코드도 충분히 깔끔하지만 더 큰 네트워크를 쌓기 위해서 위 코드를 더 깔끔하게 만들어 보겠습니다. 다음부터 쓰이는 기법들은 큰 네트워크를 쌓을 때 상당히 도움이 됩니다.



def conv_block(in_f, out_f, *args, **kwargs):
    return nn.Sequential(
        nn.Conv2d(in_f, out_f, *args, **kwargs),
        nn.BatchNorm2d(out_f),
        nn.ReLU()
    )

class CNNClassifier(nn.Module):
    def __init__(self, in_c, n_classes):
        super().__init__()
        self.encoder = nn.Sequential(
            conv_block(in_c, 32, kernel_size=3, padding=1),
            conv_block(32, 64, kernel_size=3, padding=1)
        )

        self.decoder = nn.Sequential(
            nn.Linear(32 * 28 * 28, 1024),
            nn.Sigmoid(),
            nn.Linear(1024, n_classes)
        )

        
    def forward(self, x):
        x = self.encoder(x)
        x = x.view(x.size(0), -1) # flat
        x = self.decoder(x)
        return x


  • 만약 위 코드에서 사용된 self.encoder 부분이 계속 늘어난다면 단순히 코드를 나열하는 것은 좋은 방법이 아닙니다. 예를 들어 다음 예는 별로 좋지 않습니다.


self.encoder = nn.Sequential(
            conv_block(in_c, 32, kernel_size=3, padding=1),
            conv_block(32, 64, kernel_size=3, padding=1),
            conv_block(64, 128, kernel_size=3, padding=1),
            conv_block(128, 256, kernel_size=3, padding=1),

        )


  • 이런 경우 당연히 반복문을 이용하여 코드를 간결하게 작성할 수 있습니다. 이 때 반복문을 진행하면서 변경해주어야 할 것은 input과 output의 channel 수 입니다.
  • input과 output의 channel 수는 list를 이용하여 정의해 두는 방법을 많이 사용합니다. 간단하기 때문입니다. 핵심은 반복문을 사용하되 channel의 크기는 미리 저장해 두고 사용하면 된다는 것입니다.


class CNNClassifier(nn.Module):
    def __init__(self, in_c, n_classes):
        super().__init__()
        self.enc_sizes = [in_c, 32, 64]
        conv_blocks = [conv_block(in_f, out_f, kernel_size=3, padding=1) 
                       for in_f, out_f in zip(self.enc_sizes, self.enc_sizes[1:])]
        self.encoder = nn.Sequential(*conv_blocks)
        
        self.decoder = nn.Sequential(
            nn.Linear(32 * 28 * 28, 1024),
            nn.Sigmoid(),
            nn.Linear(1024, n_classes)
        )
        
    def forward(self, x):
        x = self.encoder(x)
        x = x.view(x.size(0), -1) # flat
        x = self.decoder(x)
        
        return x


  • 위 코드를 보면 conv_blocks에서 블록을 convolution 블록을 생성합니다. 이 때 self.enc_sizes 리스트를 이용하여 input channel과 output의 channel을 정의해 줍니다. 당연히 n번째 block의 output channel 수가 n+1 번째 block의 input channel 수가 되므로 이를 이용하여 리스트를 교차해서 접근하면 됩니다. (위 코드에서도 이 방법을 사용하였습니다.)
  • * 연산자를 리스트와 같이 사용하면 아래와 같이 편하게 사용할 수 있습니다. 상세내용은 다음 링크를 참조하시기 바랍니다. -링크 : https://gaussian37.github.io/python-basic-asterisk/


a = [1, 2, 3, 4, 5]
b = [10, *a]
print(b)
# [10, 1, 2, 3, 4, 5]


  • 최종적으로 Encoder와 Decoder를 분리하고 *를 이용하여 코드를 간결하게 하면 다음과 같이 정리할 수 있습니다.



def conv_block(in_f, out_f, *args, **kwargs):
    return nn.Sequential(
        nn.Conv2d(in_f, out_f, *args, **kwargs),
        nn.BatchNorm2d(out_f),
        nn.ReLU()
    )

def dec_block(in_f, out_f):
    return nn.Sequential(
        nn.Linear(in_f, out_f),
        nn.Sigmoid()
    )

class CNNClassifier(nn.Module):
    def __init__(self, in_c, enc_sizes, dec_sizes,  n_classes):
        super().__init__()
        self.enc_sizes = [in_c, *enc_sizes]
        self.dec_sizes = [32 * 28 * 28, *dec_sizes]

        conv_blokcs = [conv_block(in_f, out_f, kernel_size=3, padding=1) 
                       for in_f, out_f in zip(self.enc_sizes, self.enc_sizes[1:])]
        self.encoder = nn.Sequential(*conv_blokcs)
        
        dec_blocks = [dec_block(in_f, out_f) 
                       for in_f, out_f in zip(self.dec_sizes, self.dec_sizes[1:])]
        self.decoder = nn.Sequential(*dec_blocks)
        
        self.last = nn.Linear(self.dec_sizes[-1], n_classes)
        
    def forward(self, x):
        x = self.encoder(x)
        x = x.view(x.size(0), -1) # flat
        x = self.decoder(x)
        return x


ModuleList : when we need to iterate


  • ModuleList는 Module을 리스트 형태로 담을 때 사용합니다. 앞에서 사용한 Sequential과 동일하게 저장한 Module을 차례대로 접근하면서 실행할 때 사용할 수 있습니다.
  • ModuleList와 Sequential의 차이점은 내부적으로 forward 연산의 발생 유무 차이입니다.
  • Sequential의 경우 Sequential로 묶은 단위에서는 자동적으로 forward 연산이 발생하기 때문에 완전한 한 단위로 움직입니다. 즉, Sequential 내부의 각 Module을 접근하여 어떤 작업을 하는 것에는 어려움이 있습니다. 앞의 Sequential 예시들을 보면 Sequential 단위로 함수를 만든 다음에 Sequential 단위 만큼 한번에 사용하였지 Sequential 내부 Module을 접근하여 사용하지는 않았습니다.
  • 반면 ModuleList는 리스트 형태로 각 Module을 접근하여 사용할 수 있습니다. 따라서 forward 함수에서 for 문을 통하여 iterate 하면서 Module들을 실행합니다. 다음 코드를 살펴보겠습니다.


import torch

class MyModule(nn.Module):
    def __init__(self, sizes):
        super().__init__()
        self.layers = nn.ModuleList([nn.Linear(in_f, out_f) for in_f, out_f in zip(sizes, sizes[1:])])
        self.trace = []
        
    def forward(self,x):
        # ModuleList 에서는 각 Module을 하나 하나 접근할 수 있습니다.
        for layer in self.layers:
            x = layer(x)
            self.trace.append(x)
        return x

model = MyModule([1, 16, 32])
model(torch.rand((4,1)))
[print(trace.shape) for trace in model.trace]
# torch.Size([4, 16]) torch.Size([4, 32]) [None, None]


ModuleDict: when we need to choose


  • ModuleDict을 이용하면 Module을 Dictionary 형태로 사용할 수 있습니다. 아주 간단하므로 아래 예제를 통하여 살펴보도록 하겠습니다.


def conv_block(in_f, out_f, activation='relu', *args, **kwargs):
    
    activations = nn.ModuleDict([
                ['lrelu', nn.LeakyReLU()],
                ['relu', nn.ReLU()]
    ])
    
    return nn.Sequential(
        nn.Conv2d(in_f, out_f, *args, **kwargs),
        nn.BatchNorm2d(out_f),
        activations[activation]
    )

print(conv_block(1, 32,'lrelu', kernel_size=3, padding=1))
print(conv_block(1, 32,'relu', kernel_size=3, padding=1))


shape 변경을 위한 transpose


  • pytorch에서는 이미지 데이터를 (channel, height, width) 순으로 다룹니다. 이 순서는 opencv와 같은 다른 이미지 처리 라이브러리와 순서가 다릅니다. opencv를 이용하여 이미지를 읽으면 (height, width, channel)의 순서로 데이터가 변수에 저장됩니다.
  • 다음은 numpy를 이용하여 채널의 순서를 바꾸는 방법과 torch를 이용하여 채널의 순서를 바꾸는 방법에 대하여 정리해 보겠습니다.


import cv2
import torch

A = np.ones((100, 120, 3))
# numpy를 이용하여 image의 채널 순서를 변경합니다.
A_transposed = np.transpose(A, (2, 0, 1))
print(A_transposed.shape)
# (3, 100, 120)

B = torch.Tensor(A)
B_transposed = torch.transpose(B, 1, 2)
print(B_transposed.shape)
# torch.Size([100, 3, 120])

B_transposed2 = torch.transpose(B_transposed, 0, 1)
print(B_transposed2.shape)
# torch.Size([3, 100, 120])


  • 위 코드를 참조하면 numpy는 np.transpose의 인자를 튜플 또는 리스트로 받아서 한번에 채널의 순서를 바꿀 수 있어서 간편한 반면 torch.transpose는 두 채널을 교환하는 것이 가능하므로 다소 불편합니다. 가능하면 numpy 단계에서 한번에 변경하는 것을 추천드립니다.


permute를 이용한 shape 변경


  • 앞에서 설명한 torch.transpose를 이용하여 shape을 변경하는 방법을 살펴보았습니다. torch.transpose의 경우 교환하고 싶은 2개의 각 dimension을 1:1 교환하는 방법이었습니다.
  • 반면 .permute()를 이용하면 채널 방향의 순서를 한번에 쉽게 바꿀 수 있습니다. 사용 방법은 다음과 같습니다.


A = torch.ones(1, 3, 10, 20)
print(A.shape)
#torch.Size([1, 3, 10, 20]) 

A = A.permute(1, 3, 0, 2)
print(A.shape)
#torch.Size([3, 20, 1, 10])


  • 위 예시와 같이 .permute()를 사용하면 기존의 dimension의 인덱스 0, 1, 2, 3, … 을 기준으로 이동하였으면 하는 위치에 기존의 인덱스를 적으면 됩니다. 위 예제에서의 이동 방향은 다음과 같습니다.
    • 기존 : 1번 차원 → 0번 차원
    • 기존 : 3번 차원 → 1번 차원
    • 기존 : 0번 차원 → 2번 차원
    • 기존 : 2번 차원 → 3번 차원
  • 만약에 A.permute(0, 1, 2, 3)으로 입력하면 변경이 전혀 없고 A.permute(3, 2, 1, 0)으로 입력하면 차원이 완전히 반대로 변경 됩니다.


nn.Dropout vs. F.dropout


  • 참조 : https://stackoverflow.com/questions/53419474/using-dropout-in-pytorch-nn-dropout-vs-f-dropout
  • 파이토치를 사용하다 보면 nn 모듈에 있는 기능과 F 즉, nn.functional 모듈에 있는 기능이 있습니다. 이름도 중복되어 있어서 무슨 차이점이 있을 지 궁금한 경우가 있습니다.
  • 간단히 말하면 nn 모듈의 기능들은 nn.functional 모듈에 있는 함수들을 사용하여 더 편하게 만든 high level API입니다.
  • 이 글에서 다루는 Dropout의 경우 nn.Dropout()과 nn.functional.dropout() 2가지가 있습니다. nn.Dropout()이 high level API 이므로 사용하기는 더 쉽습니다.
  • 가장 편리한 점 2가지는 ① model이 training 모드일 때 Dropout이 사용되도록 하고 eval 모드일 때에는 자동적으로 사용되지 않도록 하는 것 입니다. ② Dropout에 사용된 내역에 전체 모델 이력에 저장되어 추적이 가능합니다.
  • 다음 코드를 살펴보도록 하겠습니다.


import torch
import torch.nn as nn

class Model1(nn.Module):
    # Model 1 using functional dropout
    def __init__(self, p=0.0):
        super().__init__()
        self.p = p

    def forward(self, inputs):
        return nn.functional.dropout(inputs, p=self.p, training=True)

class Model2(nn.Module):
    # Model 2 using dropout module
    def __init__(self, p=0.0):
        super().__init__()
        self.drop_layer = nn.Dropout(p=p)

    def forward(self, inputs):
        return self.drop_layer(inputs)
model1 = Model1(p=0.5) # functional dropout 
model2 = Model2(p=0.5) # dropout module

# creating inputs
inputs = torch.rand(10)
# forwarding inputs in train mode
print('Normal (train) model:')
print('Model 1', model1(inputs))
# Model 1 tensor([ 1.5040,  0.0000,  0.0000,  0.8563,  0.0000,  0.0000,  1.5951,
#          0.0000,  0.0000,  0.0946])
print('Model 2', model2(inputs))
# Model 2 tensor([ 0.0000,  0.3713,  1.9303,  0.0000,  0.0000,  0.3574,  0.0000,
#          1.1273,  1.5818,  0.0946])
print()

# switching to eval mode
model1.eval()
model2.eval()

# forwarding inputs in evaluation mode
print('Evaluation mode:')
print('Model 1', model1(inputs))
# Model 1 tensor([ 0.0000,  0.3713,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,
#          0.0000,  0.0000,  0.0000])
print('Model 2', model2(inputs))
# Model 2 tensor([ 0.7520,  0.1857,  0.9651,  0.4281,  0.7883,  0.1787,  0.7975,
#          0.5636,  0.7909,  0.0473])

# show model summary
print(model1)
# Model1()
print(model2)
# Model2(
#   (drop_layer): Dropout(p=0.5)
# )


  • 위 코드를 보면 model1의 경우 간단하게 nn.Dropout()에 drop rate 파라미터값 하나만 사용하였습니다. 또한 model을 print 하였을 때 그 이력까지 남아있어서 편리함이 있습니다.
  • 정리하면 둘 다 드롭 아웃 적용 측면에서 완전히 동일하며 사용법의 차이가 크지 않더라도 nn.Dropout을 nn.functional.dropout보다 선호하는 몇 가지 이유가 있습니다.
  • 드롭 아웃은 훈련 중에만 적용되도록 설계되었으므로 모델의 예측 또는 평가를 수행 할 때 드롭 아웃을 해제해야 합니다.
  • 드롭 아웃 모듈 nn.Dropout은 이 기능을 편리하게 처리하고 모델이 평가 모드로 들어가자마자 드롭 아웃을 종료하는 반면 nn.functional.dropout은 평가 / 예측 모드를 신경 쓰지 않습니다.
  • nn.functional.dropout을 training = False로 설정하여 끌 수는 있지만 nn.Dropout과 같은 편리한 방법은 아닙니다.
  • 또한 드롭률는 모듈에 저장되므로 추가 변수에 저장할 필요가 없습니다. 더 큰 네트워크에서는 다른 드롭률로 다른 드롭 아웃 레이어를 만들려고 할 수 있습니다. 여기서 nn.Dropout은 가독성을 높이고 레이어를 여러 번 사용할 때 편리하게 사용할 수 있도록 합니다.
  • 마지막으로, 모델에 할당 된 모든 모듈이 모델에 등록됩니다. 따라서 클래스를 추적하여 모델을 추적하므로 eval()을 호출하여 드롭 아웃 모듈을 끌 수 있습니다. nn.functional.dropout을 사용할 때에는 모델이 인식하지 못하므로 summary에 표시되지 않습니다.


nn.AvgPool2d vs. nn.AdaptiveAvgPool2d


  • nn.AvgPool2d와 nn.AdaptiveAvgPool2d 모두 pooling을 하기 위해 사용됩니다. 차이점은 어떻게 사용하는 지 방식이 조금 다릅니다.
  • 차이점에 대하여 간략하게 설명하면 AvgPool2d에서는 pooling 작업에 대한 kernel 및 stride 크기를 정의해야 동작합니다. 예를 들어 kernel=3, stride=2, padding=0을 사용하는 avg_pool2d는 5x5 텐서를 3x3 텐서로, 7x7 텐서는 4x4 텐서로 줄입니다.
  • 반면 AdaptiveAvgPool2d에서는 pooling 작업이 끝날 때 필요한 출력 크기를 정의하며, 이를 위해 사용할 풀링 매개 변수를 입력합니다. 예를 들어 출력 크기=(3,3)를 사용하는 AdaptiveAvgPool2d는 5x5 및 7x7 텐서 모두를 3x3 텐서로 줄입니다. 이 기능은 입력 크기에 변동이 있고 CNN 상단에서 FC Layer를 사용하는 경우에 특히 유용합니다.


  • 그러면 AvgPool2d 부터 방법을 설명드리겠습니다.
  • AvgPool2d의 공식 문서를 읽어보면 상당히 내용이 길지만 일반적으로 사용하는 파라미터 기준으로 설명하면 처음 2개의 파라미터인 kernel_size와 stride를 입력하여 Average Pooling을 하여 \((N, C, H_{in}, W_{in})\) 크기의 입력을 \((N, C, H_{out}, W_{out})\) 크기로 변경하는 역할을 합니다.


  • \[H_{out} = \Bigl\lfloor \frac{H_{in} + 2 \times \text{padding[0]} - \text{kernel_size[0]}}{\text{stride[0]}} + 1 \Bigr\rfloor\]
  • \[W_{out} = \Bigl\lfloor \frac{W_{in} + 2 \times \text{padding[1]} - \text{kernel_size[1]}}{\text{stride[1]}} + 1 \Bigr\rfloor\]


  • 여기서 핵심이 되는 kernel_size와 stride 크기는 직접 입력해 주어야 합니다. padding은 기본값이 0이기 때문에 입력하지 않으면 0이 됩니다.
  • 코드는 다음과 같이 사용할 수 있습니다.


# pool of square window of size=3, stride=2
m = nn.AvgPool2d(3, stride=2)
# pool of non-square window
m = nn.AvgPool2d((3, 2), stride=(2, 1))
input = torch.randn(20, 16, 50, 32)
output = m(input)


  • 반면 nn.AdaptiveAvgPool2d는 kernel_size, stride, padding을 입력하는 대신에 output의 사이즈를 입력해 줍니다.
  • 그러면 위의 식에 따라서 자동으로 kernel_size, stride, padding이 결정되어 pooling을 할 수 있습니다. 즉, Average Pooling을 할 때, 출력 크기 조절하기가 상당히 쉬워집니다. 사용 방법은 다음과 같습니다.


# target output size of 5x7
m = nn.AdaptiveAvgPool2d((5,7))
input = torch.randn(1, 64, 8, 9)
output = m(input)
# torch.Size([1, 64, 5, 7])

# target output size of 7x7 (square)
m = nn.AdaptiveAvgPool2d(7)
input = torch.randn(1, 64, 10, 9)
output = m(input)
# torch.Size([1, 64, 7, 7])

# target output size of 10x7
m = nn.AdaptiveMaxPool2d((None, 7))
input = torch.randn(1, 64, 10, 9)
output = m(input)
# torch.Size([1, 64, 10, 7])


  • AdaptiveAvgPool2d가 동작되는 원리를 잠시 살펴보면 다음과 같습니다. 다음과 같은 입력 텐서와 AdaptiveAvgPool2d가 있다고 가정해 보겠습니다.


input = torch.tensor([[[[1,2.,3], [4,5,6], [7,8,9]]]], dtype = torch.float)

# torch.Size([1, 1, 3, 3])
# tensor([[[[1., 2., 3.],
#           [4., 5., 6.],
#           [7., 8., 9.]]]])

output = nn.AdaptiveAvgPool2d((2,2))(input)
# tensor([[[[3., 4.],
#           [6., 7.]]]])


  • 이 경우 출력의 사이즈가 (3, 3) → (2, 2)로 고정되므로 kernel의 크기는 (2, 2)로 자동적으로 정해집니다. 따라서 다음과 같이 계산 됩니다.


tensor([[[[(1+2+4+5)/4., (2+3+5+6)/4.],     = tensor([[[[3., 4.],
          [(4+5+7+8)/4., (5+6+8+9)/4.]]]])              [6., 7.]]]])


optimizer.state_dict() 저장 결과


  • 이번 글에서는 pytorch에서 학습 과정을 저장할 때, model과 함께 더불어 저장하는 optimizer에 대하여 다루어 보겠습니다.
  • checkpoint에 optimizer 를 저장할 때, optimizer.state_dict()를 이용하여 저장합니다. 이 때, 사용되는 optimizer.state_dict()를 이해하면 저장된 checkpoint의 optimizer를 이해할 수 있습니다.
  • 앞에서 설명한 바와 같이 optimizer.state_dict()를 이용하면 현재 사용하고 있는 optimizer의 상태 및 하이퍼파라미터를 저장할 수 있습니다.
  • optimizer.state_dict()의 출력 결과는 dictionary 형태의 state와 list 형태의 param_groups가 있습니다.
  • 예를 들어 현재 optimizer 상태를 저장하기 위해 optimizer_checkpoint = optimizer.state_dict()로 할당 받은 상태라고 가정하겠습니다.
  • 아래 예제 코드는 현재 가장 많이 사용하는 optimizer인 Adam을 이용한 것입니다


# optimizer = torch.optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)
# 위와 같이 선언된 optimizer를 checkpoint['optimizer']에 저장하였다고 가정한다. (관습적으로 이 형식으로 저장한다.)

optimizer_checkpoint = checkpoint['optimizer'] 
print(optimizer_checkpoint.keys())
# dict_keys(['state', 'param_groups'])

optimizer_checkpoint_states = optimizer_checkpoint['state']
print(optimizer_checkpoint_state.keys())
# dict_keys([140610494128064, 140610158587976, 140610158588048, ... , ])

a_key = list(optimizer_checkpoint_states.keys())[0]
optimizer_checkpoint_state = optimizer_checkpoint_states[a_key]
print(optimizer_checkpoint_state.keys())
# dict_keys(['step', 'exp_avg', 'exp_avg_sq'])

optimizer_checkpoint_param_groups = optimizer_checkpoint['param_groups'] # list
# optimizer_checkpoint_param_groups는 사용된 optimizer의 갯수 만큼 저장 됩니다.
# 만약 1개의 optimizer를 사용하였다면 list의 원소 갯수는 1개 입니다.
optimizer_checkpoint_param_group = optimizer_checkpoint_param_groups[0] 
print(optimizer_checkpoint_param_group .keys())
#  dict_keys(['lr', 'betas', 'eps', 'weight_decay', 'amsgrad', 'initial_lr', 'params'])


  • Adam을 이용한 optimizer.state_dict()의 계층 구조를 정리하면 다음과 같습니다.
  • optimizer
    • state (dictionary) : 현재 optimization state를 저장하고 있습니다.
      • step (int)
      • exp_avg (torch.Tensor) : exponential moving average of gradient values로 Adam 에서 사용됩니다
      • exp_avg_sq (torch.Tensor) : exponential moving average of squared gradient values로 Adam 에서 사용됩니다.
    • param_groups (list) : 모든 parameter_group을 저장하고 있으며 각 parameter_group은 최적화해야 하는 텐서를 지정합니다. 각 parameter_group의 내용은 Adam과 관련되어 있습니다.
      • parameters0 (dictionary)
        • lr (float)
        • betas (tuple)
        • eps (float)
        • weight_decay (float)
        • amsgrad (bool)
        • initial_lr (float)
        • params (list) : 모델에서 사용된 layer의 id를 나타냅니다.
          • id1 (int)
          • id2 (int)
          • …
      • parameters1 (dictionary)
      • …


  • 사전에 pre-traiend된 weight를 이용하여 학습을 재개할 때, model의 파라미터와 더불어 optimizer에 사용된 하이퍼 파라미터와 각 optimizer 알고리즘에서 사용하는 값들을 불러와서 학습이 중단된 위치에서 그대로 학습이 가능해 지도록 합니다.


torch.einsum 함수 사용 예제


  • einsum에 관한 자세한 내용은 아래 링크를 참조해 보시기 바랍니다. 아래 링크의 글은 numpy를 기준으로 einsum이 어떻게 동작하는 지 정리하였습니다.
    • einsum 작동 방법 : https://gaussian37.github.io/python-basic-numpy-snippets/#npeinsum-1
  • 이 글에서는 torch에서 어떻게 einsum을 사용할 수 있는 지 살펴보겠습니다. 다행스럽게도 numpy와 torch 모두 같은 einsum 문법을 가지므로 링크의 글을 이해시면 바로 아래 예제들이 이해되실 것이라 확신합니다.


import torch

x = torch.rand((2, 3))
# tensor([[0.4532, 0.9428, 0.2407],
#         [0.8347, 0.9062, 0.6289]])

# permutation of tensor
torch.einsum("ij->ji", x)
# tensor([[0.4532, 0.8347],
#         [0.9428, 0.9062],
#         [0.2407, 0.6289]])

# summation
torch.einsum("ij->", x)
# tensor(4.0065)

# column sum
torch.einsum("ij->j", x)
# tensor([1.2879, 1.8490, 0.8696])

# row sum
torch.einsum("ij->i", x)
# tensor([1.6367, 2.3698])

# matrix vector maultiplication
x = torch.rand((2, 3)) # matrix
v = torch.rand((1, 3)) # row vector
torch.einsum("ij,kj->ik",x, v)
# tensor([[0.4350],
#         [0.4490]])

# matrix multiplication
torch.einsum("ij,kj -> ik", x, x) # (2, 3) x (3, 2) = (2, 2)
# tensor([[1.4515, 1.3514],
#         [1.3514, 1.6305]])

# Dot product first row with first row of matrix
torch.einsum("i,i->", x[0], x[0])
# tensor(1.4515)

# Dot product with matrix
torch.einsum("ij, ij ->", x, x)
# tensor(3.0820)

# Elementi-wise multiplication
torch.einsum("ij,ij->ij", x, x)
# tensor([[0.3168, 0.2191, 0.9157],
#         [0.4442, 0.8674, 0.3189]])

# Outer product
a = torch.rand((3))
b = torch.rand((5))
torch.einsum("i,j->ij", a, b)
# tensor([[0.0063, 0.0565, 0.0257, 0.0289, 0.0305],
#         [0.0395, 0.3536, 0.1606, 0.1805, 0.1908],
#         [0.0187, 0.1673, 0.0760, 0.0854, 0.0903]])

# Batch matrix multiplication
a = torch.rand((3, 2, 5))
b = torch.rand((3, 5, 3))
torch.einsum("ijk, ikl -> ijl", a, b) # (3, 2, 3)

# tensor([[[1.2546, 0.5082, 0.6137],
#          [0.5740, 0.3331, 0.3978]],

#         [[0.4245, 1.2722, 0.6595],
#          [0.8763, 2.3071, 1.2626]],

#         [[1.1468, 1.2578, 1.0330],
#          [1.2937, 1.2770, 1.2563]]])

# Matrix diagonal
x = torch.rand((3, 3))
torch.einsum("ii->i", x)
# tensor([0.6335, 0.0308, 0.3003])

# Matrix trace
torch.einsum("ii->", x)
# tensor(0.9646)


torch.softmax 함수 사용 예제


  • softmax 함수는 출력을 확률값 형태로 나타내기 위하여 자주 사용되는 함수입니다. softmax 함수의 기본적인 사용 방법은 다음과 같습니다.
    • torch.softmax(Tensor, dim)
  • 첫번째 인자는 Tensor이고 두번째 인자는 dimension 입니다. 즉, 첫번째 인자를 어떤 dimension을 기준으로 softmax를 계산할 지 정하게 됩니다.
  • dimension으로 올 수 있는 숫자는 Tensor의 차원에 따라 달라집니다. Tensor의 차원이 3차원이면 0, 1, 2가 올 수 있고 음의 인덱스는 -1, -1, -3이 올 수 있습니다. 즉, Tensor의 차원 수 만큼 올 수 있습니다. 아래 코드를 참조하시기 바랍니다.


print(torch.softmax(torch.ones((1, 2, 3, 4)), dim=0))
# tensor([[[[1., 1., 1., 1.],
#           [1., 1., 1., 1.],
#           [1., 1., 1., 1.]],

#          [[1., 1., 1., 1.],
#           [1., 1., 1., 1.],
#           [1., 1., 1., 1.]]]])
print(torch.softmax(torch.ones((1, 2, 3, 4)), dim=1))
# tensor([[[[0.5000, 0.5000, 0.5000, 0.5000],
#           [0.5000, 0.5000, 0.5000, 0.5000],
#           [0.5000, 0.5000, 0.5000, 0.5000]],

#          [[0.5000, 0.5000, 0.5000, 0.5000],
#           [0.5000, 0.5000, 0.5000, 0.5000],
#           [0.5000, 0.5000, 0.5000, 0.5000]]]])
print(torch.softmax(torch.ones((1, 2, 3, 4)), dim=2))
# tensor([[[[0.3333, 0.3333, 0.3333, 0.3333],
#           [0.3333, 0.3333, 0.3333, 0.3333],
#           [0.3333, 0.3333, 0.3333, 0.3333]],

#          [[0.3333, 0.3333, 0.3333, 0.3333],
#           [0.3333, 0.3333, 0.3333, 0.3333],
#           [0.3333, 0.3333, 0.3333, 0.3333]]]])
print(torch.softmax(torch.ones((1, 2, 3, 4)), dim=3))
# tensor([[[[0.2500, 0.2500, 0.2500, 0.2500],
#           [0.2500, 0.2500, 0.2500, 0.2500],
#           [0.2500, 0.2500, 0.2500, 0.2500]],

#          [[0.2500, 0.2500, 0.2500, 0.2500],
#           [0.2500, 0.2500, 0.2500, 0.2500],
#           [0.2500, 0.2500, 0.2500, 0.2500]]]])
print(torch.softmax(torch.ones((1, 2, 3, 4)), dim=-1)) # same with dim=3
# tensor([[[[0.2500, 0.2500, 0.2500, 0.2500],
#           [0.2500, 0.2500, 0.2500, 0.2500],
#           [0.2500, 0.2500, 0.2500, 0.2500]],

#          [[0.2500, 0.2500, 0.2500, 0.2500],
#           [0.2500, 0.2500, 0.2500, 0.2500],
#           [0.2500, 0.2500, 0.2500, 0.2500]]]])


torch.repeat 함수 사용 예제


  • torch.repeat 함수는 Tensor의 값을 반복하여 생성하여 만드는 함수입니다. 아래 예제를 살펴 보겠습니다.


torch.ones(1)
# tensor([1.])

torch.ones(1).repeat(2, 3)
# torch.Size([2, 3])
# tensor([[1., 1., 1.],
#         [1., 1., 1.]])

torch.ones(2, 3)
# tensor([[1., 1., 1.],
#         [1., 1., 1.]])

torch.ones(2, 3).repeat(3, 4).shape
# torch.Size([6, 12])

torch.ones(2, 3).repeat(3, 4, 5).shape
# torch.Size([3, 8, 15])


  • 위 코드를 살펴보면 torch.ones(1)와 같이 1개의 스칼라 값을 가지는 경우 (2, 3)으로 repeat 하였을 때, shape은 (2, 3)이 되는 것을 확인할 수 있습니다.
  • 2차원 Tensor를 repeat 할 때에는 repeat을 최소 2차원 크기를 주어야 합니다. 기존 Tensor의 차원보다 더 작은 차원을 repeat하면 에러가 발생하게 됩니다. 어떤 크기로 repeat해야 할 지 모르는 차원이 생기기 때문입니다.
  • 위 예제에서 (2, 3)을 (3, 4) 크기로 repeat하게 되면 (2 X 3, 3 X 4) = (6, 12)의 크기로 변경되는 것을 볼 수 있습니다.
  • 반면 (2, 3)을 (3, 4, 5) 크기로 repeat하게 되면 (3, 2 X 4, 3 X 5) = (3, 8, 15)의 크기로 변경되는 것을 볼 수 있습니다. 어떻게 반복되면서 Tensor가 늘어나는 지 이해하시면 됩니다.


torch.arange(0, 4)
# tensor([0, 1, 2, 3])

torch.arange(0, 4).repeat(3, 4)
# tensor([[0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3],
#         [0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3],
#         [0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3]])


  • 위 예제를 보면 실제 어떻게 기존 Tensor가 반복되어 repeat함수를 통해 값이 채워지는 지 알 수 있습니다. 이 패턴을 이용하여 반복된 형태의 데이터를 쉽게 생성할 수 있습니다.


torch.scatter 함수 사용 예제


  • 참조 : https://pytorch.org/docs/stable/generated/torch.Tensor.scatter_.html#torch.Tensor.scatter_
  • torch.scatter는 index가 가리키는 위치에 특정 값을 대입하는 연산을 의미합니다. scatter가 흩뿌리다는 의미를 가지듯이 특정 인덱스에 특정 값을 대입하는 연산으로 값을 흩뿌린다고 생각하면 좋을 것 같습니다.
  • 연산 방식에는 torch.scatter와 torch.scatter_가 있습니다. torch.scatter는 out-of-place 버전으로 별도 메모리를 할당받아 추가로 데이터를 만드는 버전이고 torch.scatter_는 inplace 버전으로 기존의 데이터에 그대로 사용하는 방법입니다.


  • torch.scatter_ 즉, inplace 기준으로 동작되는 방법은 아래와 같습니다.


  • Tensor.scatter_(dim, index, src, reduce=None) → Tensor


self[index[i][j][k]][j][k] = src[i][j][k]  # if dim == 0
self[i][index[i][j][k]][k] = src[i][j][k]  # if dim == 1
self[i][j][index[i][j][k]] = src[i][j][k]  # if dim == 2


  • self는 inplace 동작 기준으로 기존의 tensor 그대로를 의미합니다.
  • dim 값에 따라서 어떤 dimension에 src 값이 대입되는 지 달라집니다.


  • 사용되는 파라미터는 다음과 같습니다.
  • dim (int) : 인덱스가 적용될 dimension을 입력합니다. 2차원에서 0번째는 행방향, 1번째는 열방향을 의미합니다.
  • index (LongTensor) : scatter할 값의 입력할 값인 src와 같은 차원을 가지도록 지정해야 합니다. 만약 인덱스가 비어있으면 변경되지 않습니다.
  • src (Tensor or float) : dim 방향에 index로 실제 입력할 값입니다.
  • reduce (str, optional) : 값을 넣지 않으면 src 값을 단순 대입하게 됩니다. 만약 add를 사용하면 대입 대신에 덧셈이 적용되고 multiply를 사용하면 곱셈이 적용됩니다.


src = torch.arange(1, 11).reshape((2, 5))
print(src)
# tensor([[ 1,  2,  3,  4,  5],
#         [ 6,  7,  8,  9, 10]])

index = torch.tensor([[0, 1, 2, 0, 2]])
torch.zeros(3, 5, dtype=src.dtype).scatter_(0, index, src)
# tensor([[1, 0, 0, 4, 0],
#         [0, 2, 0, 0, 0],
#         [0, 0, 3, 0, 5]])


  • 위 예제에서 scatter_의 dim=0 이므로 행 방향 (↓)으로 (3, 5) 사이즈의 zero tensor에 1, 2, 3, 4, 5가 각 인덱스 별로 대입된 것을 볼 수 있습니다. 6, 7, 8, 9 10에 해당하는 인덱스는 지정되지 않았으므로 무시됩니다.


src = torch.arange(1, 11).reshape((2, 5))
print(src)
# tensor([[ 1,  2,  3,  4,  5],
#         [ 6,  7,  8,  9, 10]])

index = torch.tensor([[0, 1, 2], [0, 1, 4]])
torch.zeros(3, 5, dtype=src.dtype).scatter_(1, index, src)

# tensor([[1, 2, 3, 0, 0],
#         [6, 7, 0, 0, 8],
#         [0, 0, 0, 0, 0]])


  • 위 예제에서는 scatter_가 dim=1 이므로 열 방향 (→)으로 (3, 5) 사이즈의 zero tensor에 연산된 것을 볼 수 있습니다.
  • 이와 같은 연산은 one hot을 만들 때 유용하게 사용할 수 있으며 다음 링크에서 참조할 수 있습니다.


torch.split 함수 사용 예제


  • torch.split는 tensor를 쪼개는 역할을 합니다. 텐서를 쪼갤 때 등분해야 할 크기 또는 비율 등을 입력하여 쪼갭니다 아래 예시를 살펴보면 간단히 이해할 수 있습니다.
  • 함수의 사용 방법은 torch.split(tensor, size or ratio, dim) 입니다.


a = torch.arange(10).reshape(5,2)
# tensor([[0, 1],
#         [2, 3],
#         [4, 5],
#         [6, 7],
#         [8, 9]])

 torch.split(a, 2)
#  (tensor([[0, 1],
#          [2, 3]]),
#  tensor([[4, 5],
#          [6, 7]]),
#  tensor([[8, 9]]))

torch.split(a, [1,4])
# (tensor([[0, 1]]),
#  tensor([[2, 3],
#          [4, 5],
#          [6, 7],
#          [8, 9]]))


torch.nan_to_num 함수 사용 예제


  • 파이썬, pytorch를 이용하여 계산을 다룰 때, 유념해야 할 2가지 숫자가 있습니다. 바로 nan과 inf 입니다. 계산 과정 중 nan이나 inf가 발생하게 되면 원하는대로 계산이 안되거나 오류가 발생하기 떄문입니다.
  • 이 2가지 값을 피하는 가장 좋은 방법은 왜 이 값이 도출되었는 지 확인하는 것입니다.
  • 경우에 따라서 만약 이 값이 도출이 된다면 강제로 변환 시킬 수 있는 함수가 pytorch에 구현되어 있는데 torch.nan_to_num을 사용하면 됩니다.


import torch

x = torch.tensor([float('nan'), float('inf'), -float('inf'), 3.14])
torch.nan_to_num(x)
# tensor([ 0.0000e+00,  3.4028e+38, -3.4028e+38,  3.1400e+00])
torch.nan_to_num(x, nan = 0.0, posinf=1e10, neginf=-1e10)
# tensor([ 0.0000e+00,  1.0000e+10, -1.0000e+10,  3.1400e+00])


  • nan, posinf, neginf에 해당하는 값이 있을 때, 기본값으로 변환해주는 역할을 하며 변경되는 값은 함수 호출 시 파라미터를 통해 변경할 수 있습니다.


F.grid_sample 함수 사용 예제


  • 참조 : https://pytorch.org/docs/stable/generated/torch.nn.functional.grid_sample.html
  • 참조 : https://programmersought.com/article/95846904929/


  • grid_sample은 torch.nn.functional.grid_sample(input, grid, mode='bilinear', padding_mode='zeros', align_corners=None) 와 같은 형태로 쓰이는 sampling 방법이며 torch에서 제공하는 bilinear interpolation과 유사한 역할을 하지만 좀 더 유연하게 sampling 할 수 있는 방법을 제공합니다.
  • pytorch의 document에서 제공하는 용어로 grid를 flow-field 라고도 하며 input과 grid가 주어졌을 때, grid의 입력 값과 픽셀 위치를 사용하여 output을 계산하는 것으로 설명합니다.
  • input은 4D 또는 5D 의 차원으로 입력 받습니다. 이미지의 경우 4D가 되는데 각 인자의 크기 형태는 다음과 같습니다.
    • input : \((N, C, H_{\text{in}}, W_{\text{in}})\)
    • grid : \((N, H_{\text{out}}, W_{\text{out}}, 2)\)
    • output : \((N, C, H_{\text{out}}, W_{\text{out}})\)


Drawing


  • 위 그림과 같이 input의 어떤 픽셀을 이용하여 grid에서 정의한 (x, y) 좌표에 대응하는 값이 output에 대응되게 됩니다.
  • grid의 값은 -1 ~ 1의 사이의 소수점 값을 가지게 되고 input의 전체 영역을 -1 ~ 1이라고 보았을 때, 이산적인 input의 픽셀 값의 위치를 -1 ~ 1 사이의 연속적인 값으로 간주하고 sampling하여 output으로 출력하게 됩니다. 따라서 grid의 값은 -1 ~ 1 사이로 normalization을 해주어야 하며 방법은 다음과 같습니다.


# normalize scale (0, HEIGHT_SIZE-1/WIDTH_SIZE-1) → (0, 1)
xs /= WIDTH_SIZE - 1 
ys /= HEIGHT_SIZE - 1
# shift and resize (0, 1) → (-0.5, 0.5) → (-1, 1)
xs = (xs - 0.5) * 2
ys = (ys - 0.5) * 2


  • 위 방법을 통하면 좌표의 범위를 -1 ~ 1 사이로 normalization 할 수 있습니다.
  • normalized된 grid의 좌표를 이용하여 sampling은 다음과 같이 사용할 수 있습니다. 예를 들어 input의 사이즈가 height = 10, width = 20 이라고 하면 sampling 할 때 grid의 좌표가 (-1, -1)이면 input의 (0, 0)의 RGB를 가져오게 되고 grid의 좌표가 (1, 1)이라면 input의 (9, 19)의 RGB 를 가져오게 됩니다. grid의 좌표가 (0, 0)이면 input의 (4.5, 9.5)의 픽셀을 가져오게 됩니다. 하지만 소수점의 픽셀은 없기 때문에 interpolation을 하여 input에서 grid의 좌표에 맞는 RGB 값을 가져옵니다. 이와 같은 방법으로 sampling 하는 것을 grid sampling이라고 합니다.


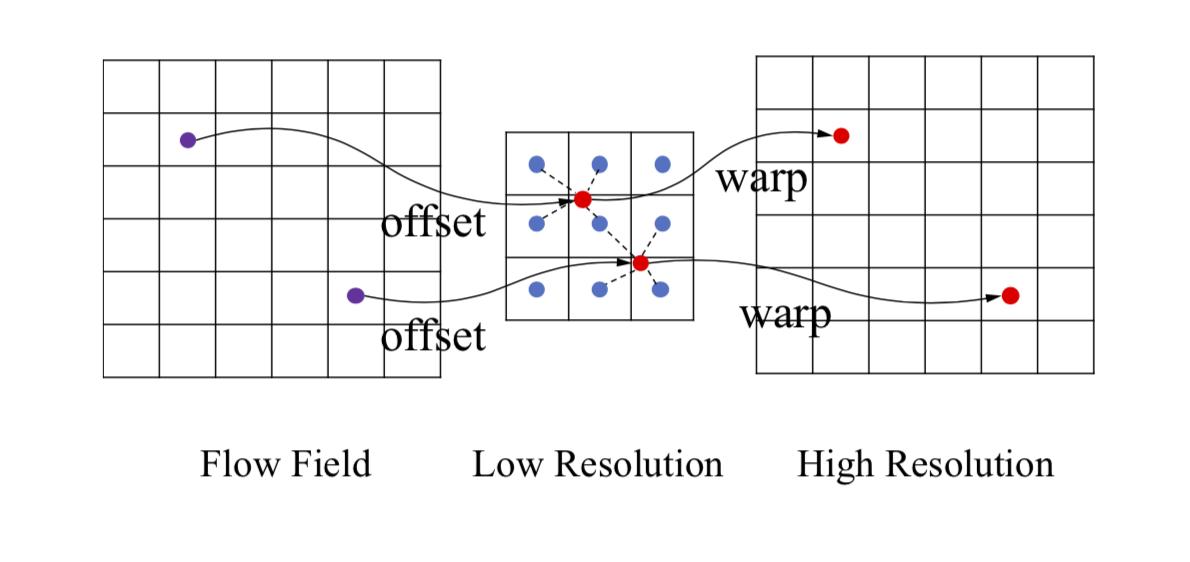
Drawing


  • 그림으로 나타내면 위와 같습니다. 위 그림의 Low Resolution이 Input이고 Flow Field가 Grid 좌표가 됩니다. 이와 같이 Flow Field라고 나타내는 이유는 Optical Flow에서 이와 같은 형태로 sampling 하여 사용하기 때문에 이와 같은 용어를 차용하였습니다.


  • grid_sample을 사용할 때, grid를 정의하는 것이 약간 헷갈릴 수 있습니다. 간단하게 설명하면 grid를 정의하는 각 좌표가 \(x, y, z\) 순으로 정의되어야 한다는 것입니다. 보통 이미지에서는 \(x, y\) 좌표만 사용하니 이 예시로 설명해 보도록 하겠습니다.


in_data = torch.arange(4*4).view(1, 1, 4, 4).float()
print(in_data)
# tensor([[[[ 0.,  1.,  2.,  3.],
#           [ 4.,  5.,  6.,  7.],
#           [ 8.,  9., 10., 11.],
#           [12., 13., 14., 15.]]]])

d = torch.linspace(-1, 1, 8)
grid_1, grid_2 = torch.meshgrid((d, d))

grid_1
# tensor([[-1.0000, -1.0000, -1.0000, -1.0000, -1.0000, -1.0000, -1.0000, -1.0000],
#         [-0.7143, -0.7143, -0.7143, -0.7143, -0.7143, -0.7143, -0.7143, -0.7143],
#         [-0.4286, -0.4286, -0.4286, -0.4286, -0.4286, -0.4286, -0.4286, -0.4286],
#         [-0.1429, -0.1429, -0.1429, -0.1429, -0.1429, -0.1429, -0.1429, -0.1429],
#         [ 0.1429,  0.1429,  0.1429,  0.1429,  0.1429,  0.1429,  0.1429,  0.1429],
#         [ 0.4286,  0.4286,  0.4286,  0.4286,  0.4286,  0.4286,  0.4286,  0.4286],
#         [ 0.7143,  0.7143,  0.7143,  0.7143,  0.7143,  0.7143,  0.7143,  0.7143],
#         [ 1.0000,  1.0000,  1.0000,  1.0000,  1.0000,  1.0000,  1.0000,  1.0000]])

grid_2
# tensor([[-1.0000, -0.7143, -0.4286, -0.1429,  0.1429,  0.4286,  0.7143,  1.0000],
#         [-1.0000, -0.7143, -0.4286, -0.1429,  0.1429,  0.4286,  0.7143,  1.0000],
#         [-1.0000, -0.7143, -0.4286, -0.1429,  0.1429,  0.4286,  0.7143,  1.0000],
#         [-1.0000, -0.7143, -0.4286, -0.1429,  0.1429,  0.4286,  0.7143,  1.0000],
#         [-1.0000, -0.7143, -0.4286, -0.1429,  0.1429,  0.4286,  0.7143,  1.0000],
#         [-1.0000, -0.7143, -0.4286, -0.1429,  0.1429,  0.4286,  0.7143,  1.0000],
#         [-1.0000, -0.7143, -0.4286, -0.1429,  0.1429,  0.4286,  0.7143,  1.0000],
#         [-1.0000, -0.7143, -0.4286, -0.1429,  0.1429,  0.4286,  0.7143,  1.0000]])


  • 위 예시를 살펴보면 grid_1은 세로 방향인 \(y\) 좌표 값이 변경됩니다. 즉, \(y\) 좌표값을 의미하는 반면 grid_2는 가로 방향인 \(x\) 좌표 값이 변경되는 것을 통해 \(x\) 좌표값을 의미함을 알 수 있습니다.
  • 이미지를 다룰 때, grid_sample에 입력되는 인자인 grid의 크기는 (B, H, W, 2)이며 마지막 차원인 2는 \(x, y\) 좌표를 의미합니다. 따라서 \(x, y\) 좌표 순서로 입력되기 위하여 다음과 같이 grid가 정의 됩니다.


grid = torch.stack((grid_2, grid_1), 2)
grid = grid.unsqueeze(0)

print(grid.shape)
# torch.Size([1, 8, 8, 2])
print(grid)
# tensor([[[[-1.0000, -1.0000],
#           [-0.7143, -1.0000],
#           [-0.4286, -1.0000],
#           [-0.1429, -1.0000],
#           [ 0.1429, -1.0000],
#           [ 0.4286, -1.0000],
#           [ 0.7143, -1.0000],
#           [ 1.0000, -1.0000]],

#          [[-1.0000, -0.7143],
#           [-0.7143, -0.7143],
#           [-0.4286, -0.7143],
#           [-0.1429, -0.7143],
#           [ 0.1429, -0.7143],
#           [ 0.4286, -0.7143],
#           [ 0.7143, -0.7143],
#           [ 1.0000, -0.7143]],

#          [[-1.0000, -0.4286],
#           [-0.7143, -0.4286],
#           [-0.4286, -0.4286],
#           [-0.1429, -0.4286],
#           [ 0.1429, -0.4286],
#           [ 0.4286, -0.4286],
#           [ 0.7143, -0.4286],
#           [ 1.0000, -0.4286]],

#          [[-1.0000, -0.1429],
#           [-0.7143, -0.1429],
#           [-0.4286, -0.1429],
#           [-0.1429, -0.1429],
#           [ 0.1429, -0.1429],
#           [ 0.4286, -0.1429],
#           [ 0.7143, -0.1429],
#           [ 1.0000, -0.1429]],

#          [[-1.0000,  0.1429],
#           [-0.7143,  0.1429],
#           [-0.4286,  0.1429],
#           [-0.1429,  0.1429],
#           [ 0.1429,  0.1429],
#           [ 0.4286,  0.1429],
#           [ 0.7143,  0.1429],
#           [ 1.0000,  0.1429]],

#          [[-1.0000,  0.4286],
#           [-0.7143,  0.4286],
#           [-0.4286,  0.4286],
#           [-0.1429,  0.4286],
#           [ 0.1429,  0.4286],
#           [ 0.4286,  0.4286],
#           [ 0.7143,  0.4286],
#           [ 1.0000,  0.4286]],

#          [[-1.0000,  0.7143],
#           [-0.7143,  0.7143],
#           [-0.4286,  0.7143],
#           [-0.1429,  0.7143],
#           [ 0.1429,  0.7143],
#           [ 0.4286,  0.7143],
#           [ 0.7143,  0.7143],
#           [ 1.0000,  0.7143]],

#          [[-1.0000,  1.0000],
#           [-0.7143,  1.0000],
#           [-0.4286,  1.0000],
#           [-0.1429,  1.0000],
#           [ 0.1429,  1.0000],
#           [ 0.4286,  1.0000],
#           [ 0.7143,  1.0000],
#           [ 1.0000,  1.0000]]]])


  • 위 정의된 grid를 살펴보면 \(x, y\) 순서로 sampling할 좌표값을 정의한 것으로 이해하시면 됩니다. 즉, \((x=0, y=0)\) 의 좌표는 \((-1, -1)\) 에서 샘플링 하는 것이고 \((x=1, y=0)\) 의 좌표는 \((-0.7143, -1)\) 에서 샘플링 하는 것입니다.
  • 정의된 grid를 이용하여 grid_sample을 사용하면 다음과 같습니다.


output_align_corner_true = torch.nn.functional.grid_sample(in_data, grid, align_corners=True)
print(output_align_corner_true)
# tensor([[[[ 0.0000,  0.4286,  0.8571,  1.2857,  1.7143,  2.1429,  2.5714,  3.0000],
#           [ 1.7143,  2.1429,  2.5714,  3.0000,  3.4286,  3.8571,  4.2857,  4.7143],
#           [ 3.4286,  3.8571,  4.2857,  4.7143,  5.1429,  5.5714,  6.0000,  6.4286],
#           [ 5.1429,  5.5714,  6.0000,  6.4286,  6.8571,  7.2857,  7.7143,  8.1429],
#           [ 6.8571,  7.2857,  7.7143,  8.1429,  8.5714,  9.0000,  9.4286,  9.8571],
#           [ 8.5714,  9.0000,  9.4286,  9.8571, 10.2857, 10.7143, 11.1429, 11.5714],
#           [10.2857, 10.7143, 11.1429, 11.5714, 12.0000, 12.4286, 12.8571, 13.2857],
#           [12.0000, 12.4286, 12.8571, 13.2857, 13.7143, 14.1429, 14.5714, 15.0000]]]])

output_align_corner_false = torch.nn.functional.grid_sample(in_data, grid)
print(output_align_corner_false)
# tensor([[[[ 0.0000,  0.0357,  0.3214,  0.6071,  0.8929,  1.1786,  1.4643,  0.7500],
#           [ 0.1429,  0.3571,  0.9286,  1.5000,  2.0714,  2.6429,  3.2143,  1.6429],
#           [ 1.2857,  2.6429,  3.2143,  3.7857,  4.3571,  4.9286,  5.5000,  2.7857],
#           [ 2.4286,  4.9286,  5.5000,  6.0714,  6.6429,  7.2143,  7.7857,  3.9286],
#           [ 3.5714,  7.2143,  7.7857,  8.3571,  8.9286,  9.5000, 10.0714,  5.0714],
#           [ 4.7143,  9.5000, 10.0714, 10.6429, 11.2143, 11.7857, 12.3571,  6.2143],
#           [ 5.8571, 11.7857, 12.3571, 12.9286, 13.5000, 14.0714, 14.6429,  7.3571],
#           [ 3.0000,  6.0357,  6.3214,  6.6071,  6.8929,  7.1786,  7.4643,  3.7500]]]])


  • align_corners가 True인 경우에는 input의 크기에 딱 맞게 sampling이 되는 것을 볼 수 있습니다. 반면 align_corners가 False인 경우에는 약간 값이 이상하게 sampling이 되는데 그 이유에 대하여 살펴보겠습니다.


  • 먼저 align_corners = True인 경우 부터 살펴보도록 하겠습니다. align_corner가 의미하는 것은 앞에서 정의한 좌표값의 위치를 코너에 맞출 지, 아닐 지 결정하는 것에 해당합니다.
  • 아래 예제는 위 코드를 통해 실행한 예제에서 in_data에서 (-0.7143, -0.7143)에 해당하는 값을 샘플링 하였을 때 (grid는 \(x, y\) 각각의 범위가 -1 ~ 1이었음) 어떤 값이 샘플링 되는 지 살펴보는 내용입니다. 위 예제에서는 align_corners = True에서 샘플링 위치가 (-0.7143, -0.7143)일 때, 2.1429가 얻어졌음을 알 수 있습니다.
  • 먼저 align_corners = True일 때, 동작 방식에 대하여 살펴보도록 하겠습니다.
  • 아래 그림의 좌표와 색 영역을 나타낸 그림은 위키피디아의 bilinear interpolation 개념 설명에 해당하는 것이며 아래 링크에서 참조할 수 있습니다.
    • https://en.wikipedia.org/wiki/Bilinear_interpolation


Drawing


  • 위 그림과 같이 align_corners = True의 경우 샘플링할 in_data를 corner에 붙혀서 bilinear interpolation 연산을 하게 됩니다.


Drawing


  • 위 식과 같이 bilinear interpolation 연산 시에는 연산할 영역에서 면적의 상대적인 크기가 weight로 사용됩니다. 따라서 각 점의 좌표와 면적의 비율을 이용하면 bilinear interpolation 계산을 할 수 있습니다. 점과 면적의 비율이 곱해지는 것의 관계를 살펴보면 됩니다.


Drawing


  • pytorch에서 얻은 값과 약간의 차이는 있지만 거의 같은 값을 구할 수 있었습니다. (biliear interpolation에서의 약간의 차이가 있는 것으로 추정됩니다.) 위 계산된 엑셀표는 다음 링크에서 참조할 수 있습니다.


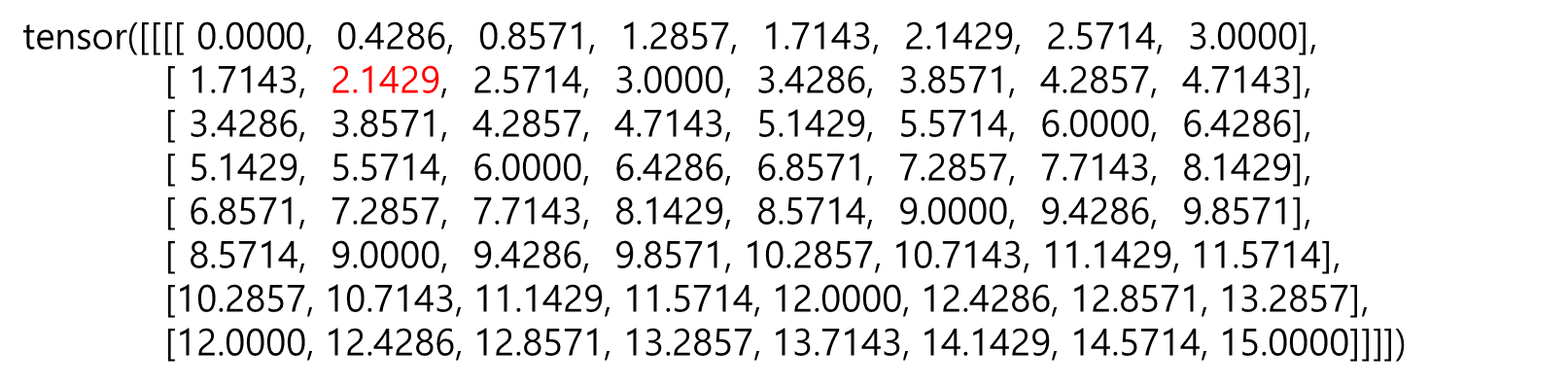
Drawing


  • 이와 같은 방법으로 align_corners=True일 때의 동작 방식을 이해할 수 있습니다.


  • 이번에는 align_corners=False일 때의 동작 방식에 대하여 알아보도록 하겠습니다. align_corners=False 일 때에는 in_data의 값이 corner에 정렬되는 것이 아니라 아래 그림과 같이 grid의 중앙에 위치하게 됩니다.


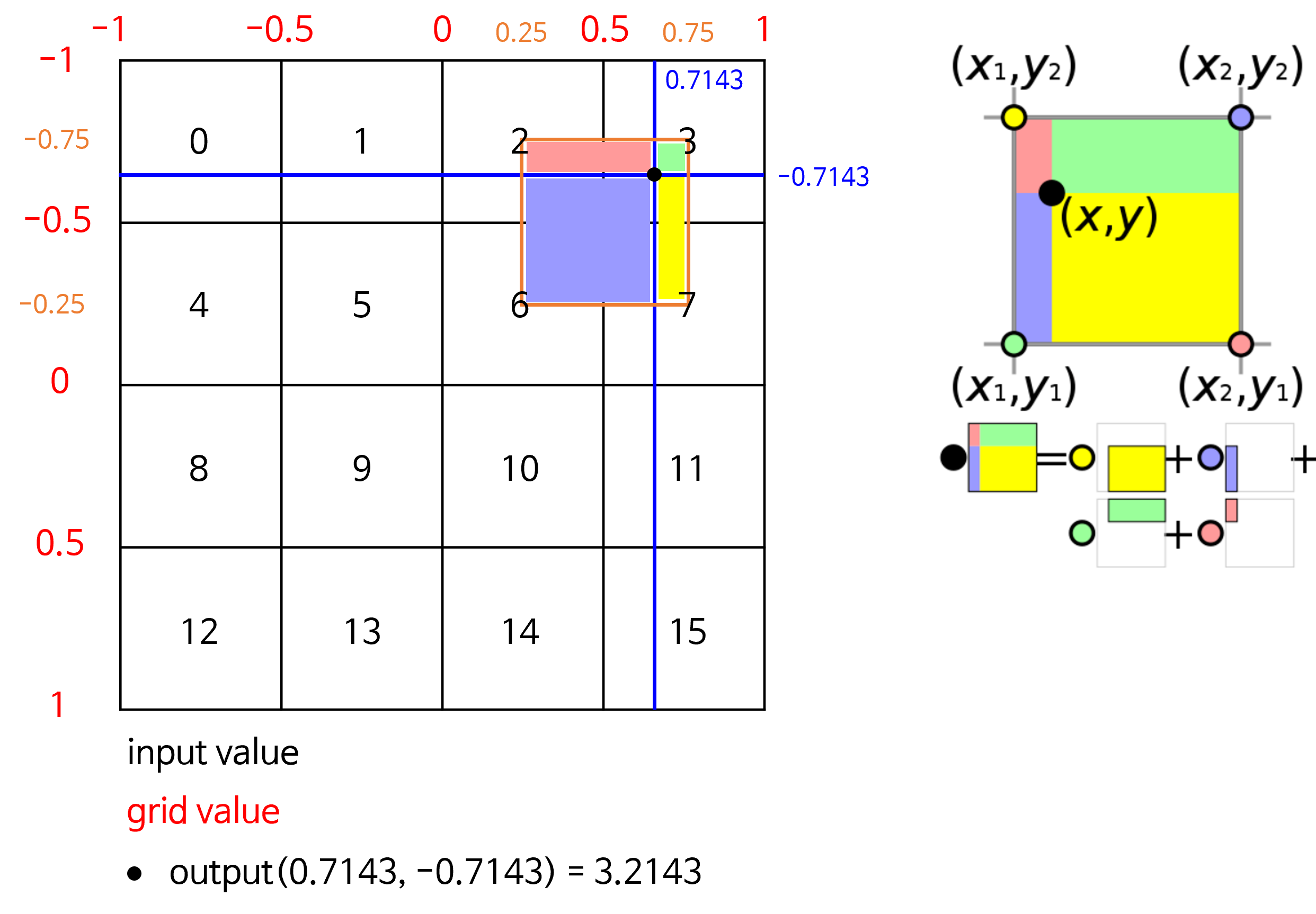
Drawing


  • 따라서 위 그림과 같이 bilinear interpolation 시 샘플링 되는 값과 위치가 바뀌게 되는 것을 알 수 있습니다. 앞의 align_corners=True인 경우와 비교하였을 때, 면적이 생성되는 위치가 다름을 알 수 있습니다. 그러면 위 예제의 output(0.7143, -0.7143) = 3.2143이 어떻게 계산되는 지 살펴보도록 하겠습니다.


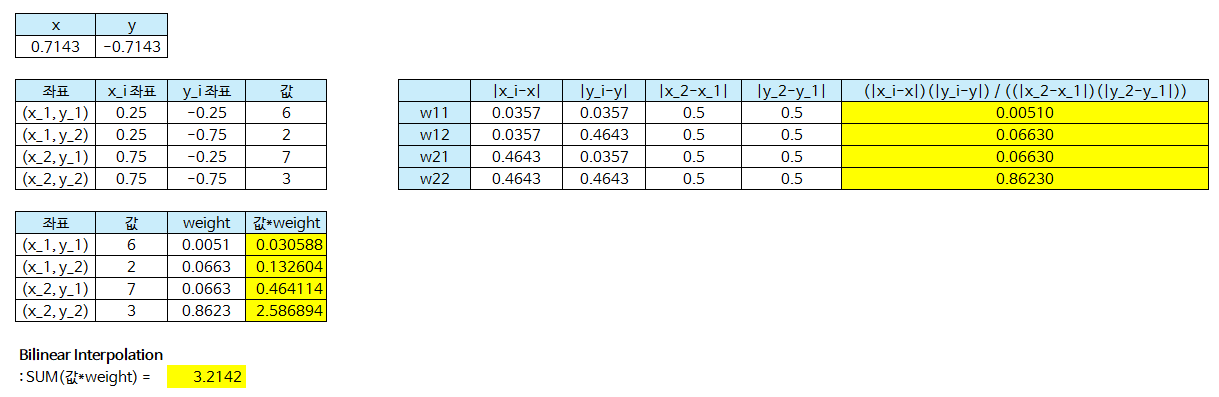
Drawing



Drawing


  • 따라서 위 계산과 같이 align_corners=False인 경우의 동작 방식과 계산 결과를 확인할 수 있습니다.


  • 정리하면 grid_sample을 사용할 때, 인풋을 다음과 같이 정의하여 사용하면 됩니다.
    • input : \((N, C, H_{\text{in}}, W_{\text{in}})\)
    • grid : \((N, H_{\text{out}}, W_{\text{out}}, 2)\)
      • grid 범위 : \([-1, -1] \sim [1, 1]\) 이며 \([-1, -1]\) 은 upper-left corner를 의미하고 \([1, 1]\) 은 bottom-right corner를 의미합니다.
      • grid 의 채널(C)의 좌표 순서 : \(x, y (,z)\)
    • output : \((N, C, H_{\text{out}}, W_{\text{out}})\)


  • grid_sample은 이미지 복원을 할 때, 종종 사용되기도 하며 특히 opencv의 cv2.remap 함수와 같은 용도로 pytorch에서 사용할 수 있습니다.
  • 카메라의 렌즈 왜곡과 같은 문제를 효율적으로 접근하기 위하여 cv2.remap 함수를 사용하는데 이 역할이 학습에 추가된다면 F.grid_sample을 사용할 수 있습니다.
  • 렌즈 왜곡 문제를 다루기 위하여 F.grid_sample 사용방법은 아래 링크를 참조하시기 바랍니다.


파이썬 파일을 읽어서 네트워크 객체 생성


  • pytorch에서 모델을 불러올 때, 모델에 해당하는 model.py 코드를 직접 접근하여 import가 필요할 때가 있습니다. 예를 들면 argument로 모델을 입력하면 직접 파일을 접근하여 모델을 불러와야 하는 경우에 해당합니다.
  • 다음 코드는 ① 모델 코드가 있는 위치를 읽을 수 있도록 path를 추가한 뒤 ② 모델을 import하여 객체를 생성하는 코드입니다. (모델의 클래스 명은 Net인 것으로 가정하겠습니다.)


import os
import sys
import importlib

def get_model(path):
    # 시스템에 모델의 path를 추가합니다.
    sys.path.append(os.path.dirname(path))
    
    # model을 import 합니다.
    net = importlib.import_module(os.path.basename(path).split('.')[0])
    model = net.Net()
    return model


weight 초기화 방법


  • 이번 글에서는 딥러닝 네트워크 모델에서 각 layer 및 연산에 접근하여 weight를 초기화 하는 방법에 대하여 다루어 보도록 하겠습니다.
  • 아래 코드에서 예제로 사용하는 He initialization은 링크를 참조하시기 바랍니다.


# 모든 neural network module, nn.Linear, nn.Conv2d, BatchNorm, Loss function 등.
import torch.nn as nn 
# 파라미터가 없는 함수들 모음
import torch.nn.functional as F 

class CNN(nn.Module):
    def __init__(self, in_channels, num_classes):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(
                in_channels=in_channels,
                out_channels=6,
                kernel_size=(3,3),
                stride=(1,1),
                padding=(1,1)
        )
        self.pool = nn.MaxPool2d(kernel_size=(2,2), stride = (2,2))
        self.conv2 = nn.Conv2d(
                in_channels=6,
                out_channels=16,
                kernel_size=(3,3),
                stride=(1,1),
                padding=(1,1)
        )
        self.fc1 = nn.Linear(16*7*7, num_classes)
        # 예제의 핵심인 initialize_weights()로 __init__()이 호출될 때 실행됩니다.
        self.initialize_weights()

    def forward(self, x):
        x = F.relu(self.conv1(x))
        x = self.pool(x)
        x = F.relu(self.conv2(x))
        x = self.pool(x)
        x = x.reshape(x.shape[0], -1)
        x = self.fc1(x)
        
        return x
    
    # 각 지정된 연산(Conv2d, BatchNorm2d, Linear)에 따라 각기 다른 초기화를 줄 수 있습니다.
    def initialize_weights(self):
        for m in self.modules():
            # convolution kernel의 weight를 He initialization을 적용한다.
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_uniform_(m.weight)
                
                # bias는 상수 0으로 초기화 한다.
                if m.bias is not None:
                    nn.init.constant_(m.bias, 0)
            
            elif isinstance(m, nn.BatchNorm2d):
                nn.init.constant_(m.weight, 1)
                nn.init.constant_(m.bias, 0)
        
            elif isinstance(m, nn.Linear):
                nn.init.kaiming_uniform_(m.weight)
                nn.init.constant_(m.bias, 0)

        
if __name__ == '__main__':
    model = CNN(in_channels=3,num_classes=10)
    
    # He initialization과 Constant로 초기화 한것을 확인할 수 있습니다.
    for param in model.parameters():
        print(param)


load와 save 방법


  • pytorch에서 학습한 결과를 저장하고 불러오는 방법에 대하여 간략하게 다루어 보겠습니다.
  • 아래 코드에서 핵심 함수인 save_checkpoint와 load_checkpoint를 자세히 살펴보면 어떻게 저장하고 불러오는 지 알 수 있습니다.
  • 이 부분의 구조를 알기 위해서는 state_dict에 대하여 이해해야 합니다. 먼저 state_dict는 dictionary 입니다. 따라서 이 형태에 맞게 데이터를 쉽게 저장하거나 불러올 수 있습니다.
  • state_dict에는 각 계층을 매개변수 Tensor로 매핑합니다.(dictionary 이므로 mapping에 용이합니다.) 이 때, 학습 가능한 매개변수를 갖는 계층(convolution layer, linear layer 등)등이 모델의 state_dict 에 항목을 가지게 됩니다.
  • 옵티마이저 객체(torch.optim) 또한 옵티마이저의 상태 뿐만 아니라 사용된 Hyperparameter 정보가 포함된 state_dict를 갖습니다.
  • inference를 위해 모델을 저장할 때는 학습된 모델의 학습된 매개변수만 저장하며 방법은 torch.save() 함수를 이용합니다.
  • PyTorch에서는 모델을 저장할 때 .pt 또는 .pth 확장자를 사용하는 것이 일반적인 규칙이며 아래 코드와 같이 tar를 통한 압축 형태로 *.pth.tar와 같이 많이 사용합니다.
  • 이 이후에 inference 용도로 사용하려면 반드시 model.eval()을 실행하여 dropout 및 batch normalization이 evaluation 모드로 설정되도록 해야 합니다.


# Imports
import torch
import torchvision
# neural network modules
import torch.nn as nn 
# Optimization algorithms, SGD, Adam, etc.
import torch.optim as optim 
# parameter가 필요 없는 함수들
import torch.nn.functional as F
# dataset 관리와 mini batch 생성 관련
from torch.utils.data import DataLoader
# standard dataset 접근
import torchvision.datasets as datasets
# dataset transformation을 통한 augmentation
import torchvision.transforms as transforms 

def save_checkpoint(state, filename="my_checkpoint.pth.tar"):
    print("=> Saving checkpoint")
    torch.save(state, filename)
    

def load_checkpoint(checkpoint, model, optimizer):
    print("=> Loading checkpoint")
    model.load_state_dict(checkpoint['state_dict'])
    optimizer.load_state_dict(checkpoint['optimizer'])

def main():
    # Initialize network
    model = torchvision.models.vgg16(pretrained=False)
    optimizer = optim.Adam(model.parameters())
    
    checkpoint = {
        'state_dict' : model.state_dict(), 
        'optimizer': optimizer.state_dict(),
        # 'epoch' : epoch,
        # 'scheduler' : scheduler.state_dict(),
        # 'lr' : lr,
        # 'best_val', best_val
    }
    # Try save checkpoint
    save_checkpoint(checkpoint)
    
    # Try load checkpoint
    load_checkpoint(torch.load("my_checkpoint.pth.tar"), model, optimizer)
    # model.eval()

if __name__ == '__main__':
    main()


Dataloader 사용 방법


  • pytorch 에서는 DataLoader를 이용하여 model에 데이터를 넣습니다.
  • 아래 예제는 대표적인 DataLoader를 사용하는 방법이며 torchvision을 통하여 import 한 datasets에는 사용할 수 있는 대부분의 데이터 셋이 있기 때문에 매우 유용합니다.
  • 아래 예제에서는 간단하게 MNIST를 추가해 보겠습니다. 사용하는 mean과 std도 모두 예제로 사용한 것이므로 상황에 맞추어 사용하시기 바랍니다.


import torch
from torchvision import datasets, transforms

batch_size = 32
test_batch_size = 32

# train 데이터를 사용하기 위한 train_loader 생성
train_loader = torch.utils.data.DataLoader(
    datasets.MNIST(
        root = "datasets/", # 현재 경로에 datasets/MNIST/ 를 생성 후 데이터를 저장한다.
        train = True, # train 용도의 data 셋을 저장한다.
        download = True,
        transform = transforms.Compose([
            transforms.ToTensor(), # tensor 타입으로 데이터 변경
            transforms.Normalize(mean = (0.5,), std = (0.5,)) # data를 normalize 하기 위한 mean과 std 입력
        ])
    ),
    batch_size=batch_size, 
    shuffle=True
)

# test 데이터를 사용하기 위한 test_loader 생성
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST(
        root = "datasets/", # 현재 경로에 datasets/MNIST/ 를 생성 후 데이터를 저장한다.
        train = False, # test 용도의 data 셋을 저장한다.
        download = True,
        transform = transforms.Compose([
            transforms.ToTensor(), # tensor 타입으로 데이터 변경
            transforms.Normalize(mean = (0.5,), std = (0.5,)) # train과 동일한 조건으로 normalize 한다.            
        ])
    ),
    batch_size = test_batch_size,
    shuffle = True
)


  • train_loader와 test_loader는 generator와 같이 동작하므로 next 를 통하여 샘플을 생성할 수 있습니다.


image, label = next(iter(train_loader))

print(image.shape)
# torch.Size([32, 1, 28, 28])

print(label.shape)
# torch.Size([32])


pre-trained model 사용 방법


  • 앞에서 모델을 save, load 하는 방법을 알아보았습니다. 저장한 pre-trained model을 읽을 때, 아래와 같은 정보로 모델이 저장되어 있다고 가정하겠습니다.


checkpoint = {
    'state_dict' : model.state_dict(), 
    'optimizer': optimizer.state_dict(),
    'epoch' : epoch,
    'scheduler' : scheduler.state_dict(),
    'lr' : lr,
    'best_val', best_val
}


  • 위 6가지 정도의 정보는 모델의 학습을 계속 이어 나갈 때 꼭 필요한 정보입니다. 최소한의 정보이므로 모델을 저장할 때 꼭 저장하길 추천드립니다.
  • 위 6가지 정보를 저장하였을 때, 불러와서 사용하는 방법은 다음과 같습니다.


resume_file_path = "../path/to/the/.../pre_trained.pth"
checkpoint = torch.load(resume_file_path)

model.load_state_dict(checkpoint['state_dict'])
start_epoch = checkpoint['epoch']
optimizer.load_state_dict(checkpoint['optimizer'])
scheduler.load_state_dict(checkpoint['scheduler'])
best_val = checkpoint['best_val']


pre-trained model 수정 방법


  • 상황에 따라서 딥러닝 모델을 그대로를 사용하기 보다는 일부 layer를 수정해야 하는 경우가 종종 있습니다.
  • 이 때, 기존의 딥러닝 모델을 통해 학습을 완료한 pre-trained weight가 있다면 일부 layer 수정에 따라서 pre-trained weight도 수정을 해야합니다.
  • 이 경우 pre-trained weight를 불러와서 필요없는 layer를 제거하는 방법에 대하여 간략하게 정리하도록 하겠습니다.
  • 먼저 *.pth 형태의 pre-trained weight를 불러오겠습니다. weight_path는 pre-trained weight 파일이 저장된 경로입니다.


# pre-trained weight를 불러옵니다.
pretrained_weight= torch.load(weight_path)


  • 위 코드를 실행하면 pretrained_weight에 collections.OrderedDict 타입으로 정보들이 저장됩니다.
  • pretrained_weight의 key는 layer의 이름이고 value는 layer의 weight 값입니다.
  • 먼저 다음과 같이 key 값을 탐색하여 필요 없는 layer를 찾습니다.


for i, key in enumerate(pretrained_weight.keys()):
    print("%d th, layer : %s" %(i, key))


  • 1) 필요 없는 layer를 직접 제거하는 방법
  • 위의 출력문을 통하여 필요 없는 layer의 목록을 직접 리스트에 저장한 후 pretrained_weight에서 key값(layer)을 제거합니다.


delete_layers = []
delete_layers.append("key value (layer name)")

for delete_layer in delete_layers:
    del pretrained_weight[delete_layer]


  • 2) 필요 없는 layer의 시작 번호(0번 부터 시작)를 입력하면 그 이후의 모든 layer를 제거하는 방법입니다.
  • 이 방법이 유용한 이유는 일반적으로 어떤 layer를 삭제해야 한다면 그 layer 이후의 layer 또한 삭제가 필요한 경우가 많기 때문입니다. 즉, 삭제할 layer가 듬성 등성 존재하는 경우는 거의 없으며 어떤 layer 부터 출력단 끝까지 덜어내야 하는 경우가 대다수입니다.
  • 그러면 앞의 출력문을 통하여 제거해야 할 시작점의 인덱스를 이용하여 아래와 같이 삭제해 보겠습니다.


# [0, delete_start_number) 범위의 layer만 남기고 나머지는 삭제합니다.
delete_start_number = 100
delete_layers = [key for i, key in enumerate(pretrained_weight.keys()) if i >= delete_start_number]
for delete_layer in delete_layers:
    del pretrained_weight[delete_layer]


pre-trained model fine tuning 방법


  • pre-trained 모델을 이용하여 fine turing을 하기 위해서는 선언된 모델의 requires_grad를 False로 입력하면 됩니다.
  • 아래 코드는 임의의 뉴럴 네트워크를 이용하여 특정 layer는 학습을 하도록 하고 특정 layer는 학습하지 않도록 하는 코드입니다.


import torch
import torch.nn as nn

class CustomModel(nn.Module):   
    def __init__(self):
        super(CustomModel, self).__init__()

        self.freeze_layers = nn.Sequential(
            # Defining a 2D convolution layer
            nn.Conv2d(1, 4, kernel_size=3, stride=1, padding=1),
            nn.BatchNorm2d(4),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=2, stride=2),
            # Defining another 2D convolution layer
            nn.Conv2d(4, 4, kernel_size=3, stride=1, padding=1),
            nn.BatchNorm2d(4),
            nn.ReLU(inplace=True),
            nn.MaxPool2d(kernel_size=2, stride=2),
        )

        self.non_freeze_layers = nn.Linear(4 * 7 * 7, 10)

    # Defining the forward pass    
    def forward(self, x):
        x = self.freeze_layers(x)
        x = x.view(x.size(0), -1)
        x = self.linear_layers(x)
        return x

custom_model = CustomModel()


  • 위 코드와 같이 모델을 선언하면 freeze_layers와 non_freeze_layers를 prefix로 각 layer를 접근할 수 있습니다. 각 layer를 살펴보는 방법은 다음과 같습니다.


for name, param in custom_model.named_parameters():
    print("name : ", name)
    print("requires_grad : ", param.requires_grad)
    print()

# name :  freeze_layers.0.weight
# requires_grad :  True

# name :  freeze_layers.0.bias
# requires_grad :  True

# name :  freeze_layers.1.weight
# requires_grad :  True

# name :  freeze_layers.1.bias
# requires_grad :  True

# name :  freeze_layers.4.weight
# requires_grad :  True

# name :  freeze_layers.4.bias
# requires_grad :  True

# name :  freeze_layers.5.weight
# requires_grad :  True

# name :  freeze_layers.5.bias
# requires_grad :  True

# name :  non_freeze_layers.weight
# requires_grad :  True

# name :  non_freeze_layers.bias
# requires_grad :  True


  • 위 코드의 출력 결과에서 살펴볼 점은 2가지입니다. 첫번째로 각 parameter의 name과 requires_grad값입니다.
  • 첫번째로 각 parameter의 name은 실제 모델에서 layer를 선언할 때 사용한 변수명을 따릅니다. 따라서 fine tuning 시 freeze / non_freeze 대상을 구별하여 변수명을 선언하면 구현하는 데 도움이 됩니다.
  • 두번째 내용인 requires_grad을 살펴보면 기본적으로 모델의 각 layer를 선언할 때, requires_grad=True로 설정되기 때문에 위 결과와 같이 모든 layer는 requires_grad : True가 되는 것을 확인할 수 있습니다.
  • 이 2가지 내용을 이용하여 freeze_layers로 시작하는 layer는 학습하지 않도록 requires_grad=False로 셋팅해보면 다음과 같습니다.


non_freeze_prefix = "non_freeze"
for name, param in custom_model.named_parameters():
    if name.startswith(non_freeze_prefix) == False:
        param.requires_grad = False 

for name, param in custom_model.named_parameters():
    print("name : ", name)
    print("requires_grad : ", param.requires_grad)
    print()

# name :  freeze_layers.0.weight
# requires_grad :  False

# name :  freeze_layers.0.bias
# requires_grad :  False

# name :  freeze_layers.1.weight
# requires_grad :  False

# name :  freeze_layers.1.bias
# requires_grad :  False

# name :  freeze_layers.4.weight
# requires_grad :  False

# name :  freeze_layers.4.bias
# requires_grad :  False

# name :  freeze_layers.5.weight
# requires_grad :  False

# name :  freeze_layers.5.bias
# requires_grad :  False

# name :  non_freeze_layers.weight
# requires_grad :  True

# name :  non_freeze_layers.bias
# requires_grad :  True


  • 위 코드의 결과를 살펴보면 마지막 2개의 non_freeze_layer에 해당하는 weight, bias를 제외하고 모두 requires_grad = False로 되어있음을 알 수 있습니다.


checkpoint 값 변경 후 저장


  • checkpoint의 값을 변경 후 저장하는 방법에 대하여 알아보도록 하겠습니다. checkpoint는 아래와 같은 구조로 저장되어 있다고 가정하겠습니다.


checkpoint = {
    'state_dict' : model.state_dict(), 
    'optimizer': optimizer.state_dict(),
    'epoch' : epoch,
    'scheduler' : scheduler.state_dict(),
    'lr' : lr,
    'best_val', best_val
}


  • 이 때, checkpoint의 값을 변경 후 다시 저장하려면 아래와 같은 예시로 저장하면 됩니다.


resume_file_path1 = "../path/to/the/.../pre_trained1.pth"
resume_file_path2 = "../path/to/the/.../pre_trained2.pth"
checkpoint1 = torch.load(resume_file_path1)
checkpoint2 = torch.load(resume_file_path2)

checkpoint1['state_dict'] = checkpoint2['state_dict']
torch.save(state, filename)


Learning Rate Scheduler 사용 방법


  • Pytorch에서 Learning rate와 관련된 자세한 설명을 확인하고 싶으면 아래 링크를 참조하시기 바랍니다.
    • 참조 : https://gaussian37.github.io/dl-pytorch-lr_scheduler/
  • 참조 : https://pytorch.org/docs/stable/optim.html#torch.optim.lr_scheduler.ReduceLROnPlateau
  • 아래 예제는 대표적인 learning rate scheduler 중 하나인 ReduceLROnPlateau를 사용한 예제이며 위 링크의 다른 스케줄러를 상황에 맞추어 사용해도 됩니다.
  • 대부분의 scheduler는 아래 프로세스를 따르므로 아래 코드를 참조하여 사용하시길 바랍니다.


# model → optimizer → scheduler
model = Net().to(device)

learning_rate = 0.01
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

from torch.optim.lr_scheduler import ReduceLROnPlateau
scheduler = ReduceLROnPlateau(optimizer, mode = 'max', factor = 0.1, paience = 5, verbose = True)

for epoch in range(10):
    train(...)
    val_loss = validate(...)
    # Note that step should be called after validate()
    scheduler.step(val_loss)


  • 위 코드를 보면 ① 먼저 model을 선언한 다음 ② 그 모델을 optimizer에 할당합니다. 그 다음 ③ 스케쥴러에 optimizer를 할당합니다.
  • 위 순서에 따라 model, optimizer, scheduler가 모두 엮이게 됩니다.
  • 스케쥴러 업데이트는 보통 validation 과정을 거친 후 사용합니다. 위 코드와 같이 validation loss를 scheduler.step()의 입력으로 주면 그 loss값과 scheduler 선언 시 사용한 옵션들을 이용하여 learning_rate를 dynamic하게 조절할 수 있습니다.


model의 parameter 확인 방법


  • 모델의 파라미터를 확인 하는 방법은 model.parameters()를 통해 가능합니다. 단, model.parameters()는 generator 타입이므로 for문과 같이 순회하면서 또는 next를 이용하여 값을 접근할 수 있습니다. 다음 코드를 참조하시기 바랍니다.


next(model.parameters())
# 바로 다음 값 1개 확인

for param in model.parameters():
    print(param)


Tensor 깊은 복사


  • Tensor를 깊은 복사하려면 .clone()을 이용하여 복제한 다음, .detach()를 통하여 연결성을 끊어야 합니다.


A = torch.randn(10)
B = A.clone().detach()


일부 weight만 업데이트 하는 방법


  • 일반적으로 학습할 때를 제외하고는 모델의 weight를 pre-trained weight로 사용합니다.
  • 모델에 pre-trained weight를 적용하기 위해서는 다음 과정을 거칩니다.
    • ① 모델 클래스를 이용하여 model 객체를 생성합니다. 객체명을 model이라고 하겠습니다.
    • ② pre-trained weight인 pickle 파일(p, pt, pth 확장자)을 불러옵니다. 불러온 데이터는 layer의 이름을 key값으로 하고 layer의 weight를 value값으로 하는 dictionary 형태이며 일반적으로 OrderedDict 타입입니다. (from collections import OrderedDict) 이 데이터를 pretrained_dict 라고 하겠습니다.
    • ③ pretrained_dict를 model의 각 layer에 적용하려면 model.load_state_dict(pretrained_dict)을 사용하면 됩니다. 그러면 각 layer에 pretrained_dict에 저장된 값이 덮어써지게 됩니다.


  • 만약 모든 weight가 아닌 weight 일부를 변경하고 싶으면 어떻게 해야 할까요? 위 방법을 조금 응용하면 됩니다.
  • 위 과정 중 ② 를 통하여 모든 layer 별 이름이 key 값으로 정해지고 그 layer의 weight값이 value 값이 되는 것을 확인할 수 있었습니다.
  • 그리고 ③의 model.load_state_dict(pretrained_dict)를 실행하려면 model의 모든 layer와 pre-train 데이터의 모든 key에 해당하는 layer가 1대1 대응이 되어야 성공적으로 수행됩니다.
  • 따라서 적용해야 할 model의 전체 layer의 key(이름), value(weight)를 저장한 dictionary와 업데이트 할 layer에 해당하는 key, value만 저장한 dictionary를 2개 준비합니다.
    • 전체 layer : model_dict = model.state_dict()을 통해 확인 가능합니다.
    • 업데이트 할 layer : 업데이트 할 layer만 key, value 값을 준비해야 하며 key는 실제 model에서 사용하는 layer의 key(이름)과 같아야합니다. 이 값을 update_dict 라고 하겠습니다.
  • model_dict.update(update_dict)를 통하여 전체 dictionary 중 weight를 업데이트 할 update_dict의 값만 model_dict에 덮어쓰기가 됩니다.
  • 이 방법을 통하여 부분적으로 weight 업데이트를 할 수 있습니다. 아래는 ResNet-50을 이용하여 weight를 부분적으로 업데이트 한 예제입니다.


import torch
model = torch.hub.load('pytorch/vision:v0.6.0', 'resnet50', pretrained=True)
model_dict = model.state_dict()

update_dict # update_dict is subset of model_dict

# 1. filter out unnecessary keys
filtered_update_dict = {k: v for k, v in update_dict.items() if k in model_dict}
# 2. overwrite entries in the existing state dict
model_dict.update(filtered_update_dict) 
# 3. load the new state dict
model.load_state_dict(model_dict)


OpenCV로 입력 받은 이미지 torch 형태로 변경


  • OpenCV를 이용하여 이미지 데이터를 입력 받고 입력 받은 데이터를 torch 타입 및 (Batch, Channel, Height, Width) 형태로 바꾸는 예시를 살펴보겠습니다. 아래는 하나의 컬러 이미지를 이용하므로 (1, 3, height, width) 형태를 사용한 예시입니다. 순서는 다음과 같습니다.
  • ① OpenCV를 이용하여 이미지 데이터 읽기
  • ② (Optional) BGR → RGB
  • ③ Numpy → Tensor
  • ④ Dimension 변경
  • ⑤ (Channel, Height, Width) → (Batch, Channel, Height, Width)


# ① OpenCV를 이용하여 이미지 데이터 읽기 
img = cv2.imread("image.png")
# ② (Optional) BGR → RGB
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# ③ Numpy → Tensor
img = torch.Tensor(img)
# ④ Dimension 변경
img = img.permute(2, 0, 1)
# ⑤ (Channel, Height, Width) → (Batch, Channel, Height, Width)
img = torch.unsqueeze(img, 0)



convolution - batchnorm 사용 시, convolution bias 사용 하지 않음


  • 참조 : https://d2l.ai/chapter_convolutional-modern/batch-norm.html
  • 참조 : https://learnml.today/speeding-up-model-with-fusing-batch-normalization-and-convolution-3
  • 참조 : https://stackoverflow.com/questions/46256747/can-not-use-both-bias-and-batch-normalization-in-convolution-layers
  • 참조 : https://stackoverflow.com/questions/56544217/why-we-dont-need-bias-in-convolution-layer-after-batchnorm-and-activation/56704082
  • 참조 : https://stats.stackexchange.com/questions/482305/batch-normalization-and-the-need-for-bias-in-neural-networks


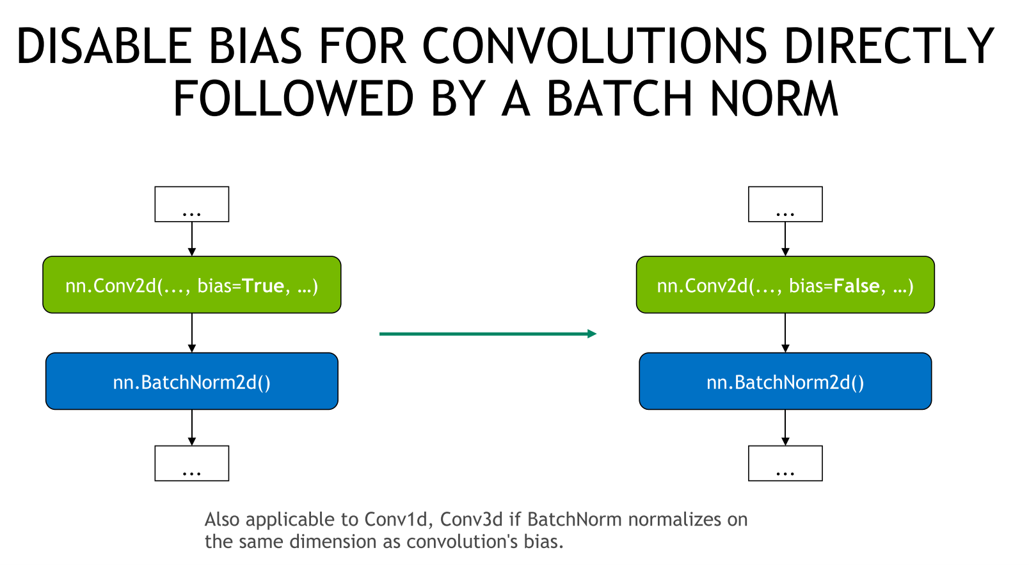
Drawing


  • Convolution과 Batch Normalization이 연속적으로
Twitter Facebook Google+
# pytorch # snippets # import # pytorch setting # pytorch GPU # argmax # squeeze # unsqueeze # interpolate # upsample # module # Sequential # ModuleList # weight initialize # load # save # dataloader # pretraiend