카메라 모델과 렌즈 왜곡 (lens distortion)

Vision 관련 글 목차

• 사전 지식 : 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습

• 참조 : https://kr.mathworks.com/help/vision/ug/camera-calibration.html
• 참조 : http://jinyongjeong.github.io/2020/06/19/SLAM-Opencv-Camera-model-%EC%A0%95%EB%A6%AC/
• 참조 : http://jinyongjeong.github.io/2020/06/15/Camera_and_distortion_model/
• 참조 : https://docs.nvidia.com/vpi/algo_ldc.html
• 참조 : http://www.gisdeveloper.co.kr/?p=6868
• 참조 : https://ori.codes/artificial-intelligence/camera-calibration/camera-distortions/
• 참조 : http://www.close-range.com/docs/Decentering_Distortion_of_Lenses_Brown_1966_may_444-462.pdf

• 이번 글에서는 카메라 모델의 특성, 카메라 렌즈 왜곡 모델 그리고 렌즈 왜곡을 제거하는 방법 등에 대하여 알아보도록 하겠습니다.
• 특히 가장 많이 사용되는 카메라 모델인 Generic Camera Model을 기준으로 살펴볼 예정이며 전체 내용을 이해하기 위해서는 사전 지식의 카메라 캘리브레이션 및 카메라 파라미터 내용을 먼저 이해하기를 권장 드립니다.

목차

• 화각에 따른 카메라의 종류

• Radial Distotion과 Tangential Distortion

• Generic 카메라 모델과 Brown 카메라 모델

• Generic 카메라 모델의 3D → 2D

• Generic 카메라 모델의 2D → 3D

• Generic 카메라 모델 3D → 2D 및 2D → 3D python 실습

• 왜곡된 영상의 왜곡 보정의 필요성과 단점

• 왜곡 보정 방법

• Generic 카메라 모델 왜곡 보정을 위한 mapping 함수 구하기

• Generic 카메라 모델 remap을 이용한 왜곡 영상 → 왜곡 보정 영상

• Generic 카메라 모델 Pytorch를 이용한 왜곡 영상 → 왜곡 보정 영상

• Generic 카메라 모델의 왜곡 보정 시 변환 좌표 구하기

• World-to-Image 방법

• Image-to-World 방법

화각에 따른 카메라의 종류

• 카메라에서 가장 중요한 부분 중 하나가 렌즈입니다. 핀홀 모델 카메라는 이론적으로 빛의 직진성을 이용하여 만든 이상적이면서 간단한 카메라 모델이지만 빛의 유입량이 적어 정상적인 이미지를 만들어낼 수 없습니다.
• 따라서 렌즈를 이용하여 카메라에 다양한 영역의 빛이 많이 유입될 수 있도록 (사람의 수정체와 같습니다.) 조절할 수 있습니다. 렌즈의 형태에 따라 카메라가 빛을 유입할 수 있는 영역이 달라지기 때문에 아래 그림과 같이 렌즈에 따른 화각이 결정됩니다.

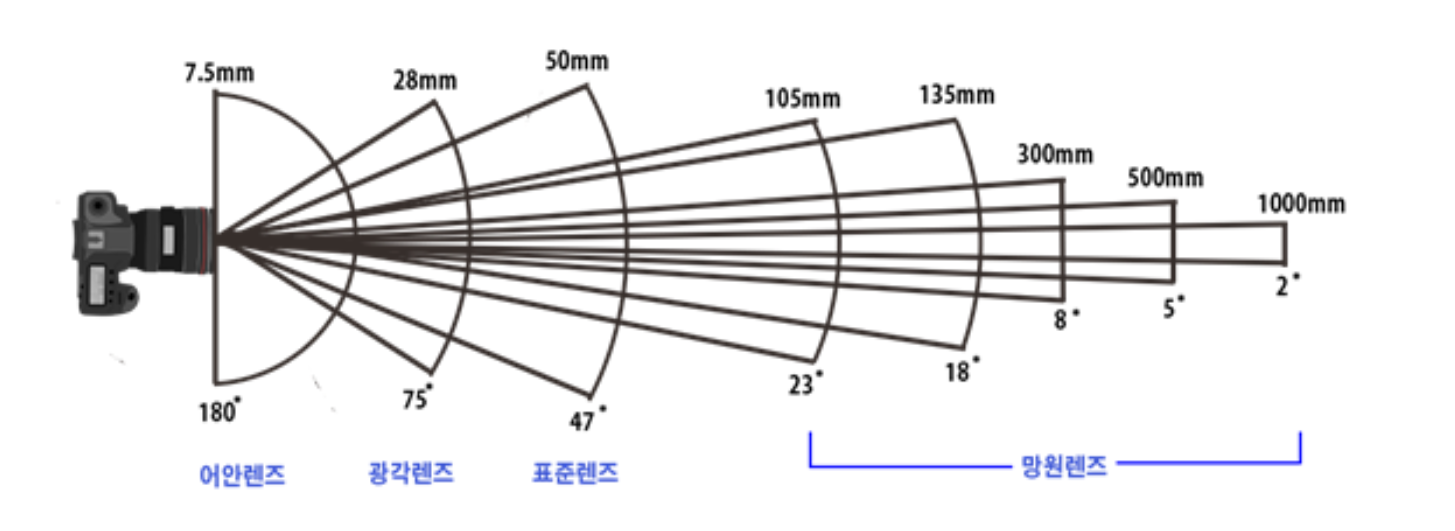
• 위 그림의 화각과 초점 거리 (focal length)는 설명을 위한 예시이며 절대적인 기준은 아닙니다.
• 이번 글에서는 표준 렌즈를 사용하는 표준 카메라와 어안 렌즈를 사용하는 어안 카메라에서 렌즈로 인한 물체의 휘어지는 Distortion이 발생하였을 때 처리하는 방법에 대하여 살펴볼 예정입니다.
• 다양한 카메라 렌즈를 수학적으로 모델링 하기 위하여 수학적으로 정의한 카메라 모델을 사용할 것입니다. 본 글에서는 크게 2가지의 카메라 모델을 사용할 예정이며 각 카메라 모델의 이름은 Generic Camera Model과 Brown Camera Model이며 이 모델의 간략한 내용은 글 아래에서 설명하겠습니다.
• 카메라 모델은 카메라 렌즈를 수학적으로 정확히 모방하기 보다는 카메라 렌즈에 의한 왜곡을 임의의 수학적 모델링 식으로 표현할 수 있도록 문제를 정의한 후 최적화하여 왜곡을 가장 잘 표현할 수 있는 수식을 찾는 방법을 이용합니다.
• 이 때, 발생하는 왜곡은 대표적으로 Radial Distortion과 Tangential Distortion이 있습니다.
• 본 글에서 살펴볼 Generic Camera Model은 Radial Distortion만을 고려하여 다항식(polynomial)으로 왜곡을 표현합니다. Radial Distortion의 왜곡이 상대적으로 더 크기 때문에 그 부분을 잘 모델링 하는 것이 중요하기 때문입니다.
• 반면 Brown Camera Model이라는 모델은 Radial Distortion과 Tangential Distortion을 모두 고려하여 다항식(polynomial)으로 모델링 합니다. 하지만 이 모델의 경우 작은 Raidal Distortion만을 고려하기 때문에 일반적으로 사용하는 데 한계가 있습니다.
• 경험적으로 Brown Camera Model을 사용하여도 되는 영상에서는 Generic Camera Model을 사용할 수 있지만 렌즈 왜곡이 커서 Generic Camera Model을 사용해야 하는 경우에는 Brown Camera Model이 정상 동작 하지 않는 경우가 발생하기 때문에 가능한 Generic Camera Model을 사용하길 권장합니다.
• 최신의 연구 동향을 위하여 Unified Camera Model, Double Sphere Camera Model 등을 살펴보는 것도 도움이 될 수 있으며 아래 링크를 참조해 보시기 바랍니다.
  • 링크 : Double Sphere 카메라 모델 및 다양한 카메라 모델의 종류 (Pinhole, UCM, EUCM, Kannala-Brandt Camera Model 등)
• 그러면 먼저 Radial Distortion과 Tangential Distortion에 대하여 살펴보도록 하겠습니다.

Radial Distotion과 Tangential Distortion

• 카메라 렌즈로 인하여 발생하는 왜곡은 크게 Radial Distotion과 Tangential Distortion가 있습니다. 먼저 Radial Distortion 부터 살펴보도록 하겠습니다.

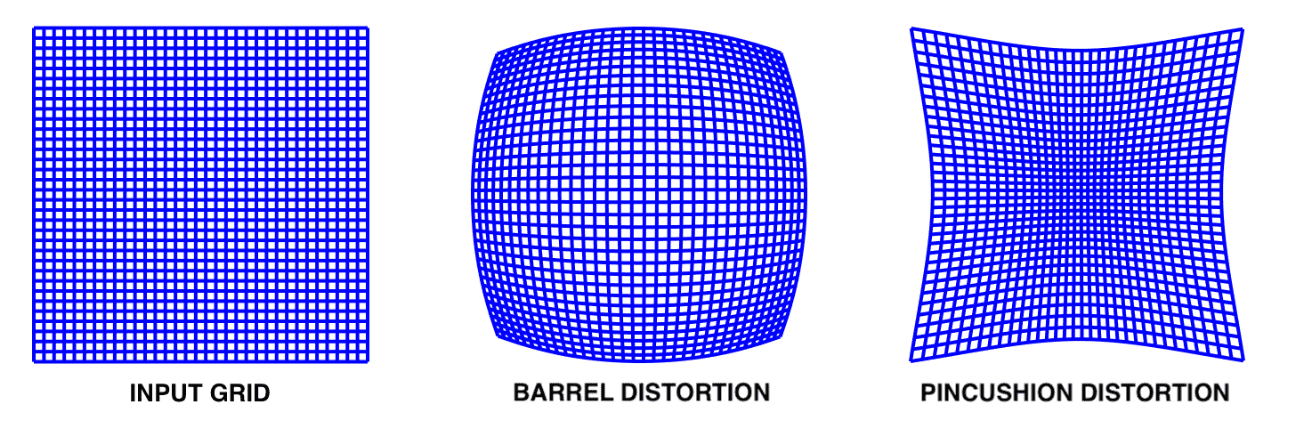
• 위 그림은 Radial Distortion을 나타냅니다. Radial Distortion은 빛이 렌즈로 입사할 때, 균등하게 들어오지 않고 영역 별로 불균등하게 들어오기 때문에 발생합니다. 이와 같은 이유는 카메라 렌즈를 의도적으로 설계하여 특정 영역을 더 많이 볼 수 있도록 만들기 때문입니다.
• 예를 들어 넓은 영역을 보고 싶으면 렌즈 가장자리에 더 많은 빛을 모을 수 있어야 더 많은 빛이 들어와서 이미지 센서에 투영되어 상이 맺힐 수 있습니다.
• 따라서 실세계에서 빛은 직진하지만 카메라 렌즈로 인하여 굽어져서 들어오게 되어 영역 별로 빛이 많이 모이기도 하고 작게 모이기도 합니다. 이러한 이유로 이미지 안에서 물체가 굽어져 보이는 현상이 발생합니다.
• 카메라 렌즈 설계 방법에 따라 어떤 영역에 빛을 더 많이 모이게 할 지를 정할 수 있으며 방법에 따라서 Radial Distortion이 Barrel Distortion이 되거나 Pincusion Distortion이 됩니다.
• Barrel Distortion은 빛이 렌즈를 투과하였을 때, 바깥쪽으로 꺽이도록 설계되어 있습니다. 즉, 빛이 바깥 영역으로 점점 쏠리게 되어 더 넓은 영역을 볼 수 있도록 만듭니다. 이러한 이유로 넓은 영역을 봐야 하는 광각 카메라나 어안 카메라에서 이와 같은 왜곡이 발생합니다.
• 반대로 Pincusion Distortion은 빛이 렌즈를 투과하였을 떄, 안쪽으로 꺽이도록 설계되어 있습니다. 즉, 렌즈 가운데 영역으로 점점 쏠리게 되어 더 좁은 영역을 볼 수 밖에 없지만 더 멀리서 투영된 빛도 맺힐 수 있도록 만듭니다. 따라서 더 멀리 있는 영역을 봐야하는 원거리용 카메라에서 이와 같은 왜곡이 발생합니다.
• 이와 같은 Radial Distortion은 앞으로 다룰 카메라 모델에서 Distortion Center (Image Center)로 부터 계산된 Radial Distance를 다항 함수를 통하여 모델링 합니다. 이 내용은 아래 글에서 다루도록 하겠습니다.

• Tangential Distortion는 카메라 렌즈와 이미지 센서가 평행하게 장착되어 생산되지 못하였을 때 발생하는 왜곡입니다. Tangential Distortion이 발생하면 이미지는 비스듬히 기울어져 있습니다. 이러한 이유로 직선이 약간 굽어보이게 됩니다.

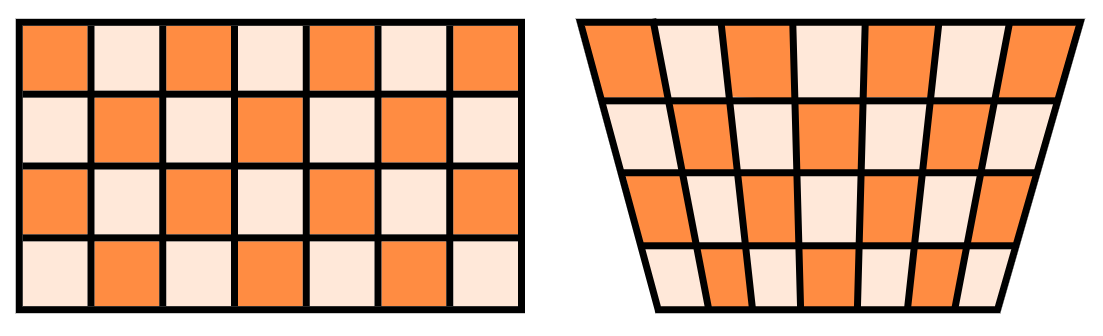
• 카메라 렌즈와 이미지 센서가 평행하지 않으면 위 그림과 같이 기울어지게 되며 왜곡이 발생하게 됩니다.

Generic 카메라 모델과 Brown 카메라 모델

• Generic Camera Model은 이름 그대로 어안 렌즈부터 망원 렌즈 까지 모두 사용 가능한 범용적인 카메라 모델이며 특히 화각이 120도 이상의 광각 렌즈에서 효과를 발휘합니다. 결론적으로는 Generic Camera Model 하나만 잘 활용해도 180도 이하 화각의 카메라에서는 충분히 잘 사용할 수 있습니다.
• Brown Camera Model은 보통 화각이 100도 이하인 카메라 환경에서 주로 사용합니다. Generic Camera Model에 비해 계산도 간단한 장점도 있습니다. 다만 Generic Camera Model과 같이 넓은 화각에서는 이 카메라 모델을 사용할 수 없습니다. 사용 시, 정확성이 많이 떨어지게 됩니다. Brown Camera Model은 간단히 원거리 용도의 카메라에 주로 사용한다고 생각하면 되며 Pinhole Camera Model 모델링에 가깝습니다.

• 앞으로 살펴볼 식을 보면 Generic Camera Model은 Tangential Distortion의 영향 보다 Radial Distortion에 집중하여 다항식으로 모델링 한 것을 살펴볼 수 있습니다. 반면 Brown Camera Model은 적당한 다항식 차수의 다항식으로 Radial Distortion을 모델링하고 2차 다항식으로 Tangential Distortion을 모델링합니다. Generic Camera Model에서 이와 같은 방식을 취하는 이유는 화각이 넓은 카메라에서는 Radial Distortion의 영향이 크기 때문에 Tangential Distortion을 무시할 수 있으며 생산 기술의 발전으로 카메라 렌즈와 이미지 센서가 평행에 가깝게 생산될 수 있어 Tangential Distortion를 실질적으로 무시할 정도가 되기 때문입니다. 따라서 Brown Camera Model에서도 Tangential Distortion을 무시하기도 하며 이와 같은 경우에는 Generic Camera Model과 유사해 집니다.
• 어떤 카메라 모델을 사용해야 할 지 고민이 된다면 Generic Camera Model을 고민없이 사용하는 것이 좋은 방법일 수 있습니다.

Generic 카메라 모델

• Generic 카메라 모델은 A Generic Camera Model and Calibration Method for Conventional, Wide-Angle, and Fish-Eye Lenses 논문에서 제안한 카메라 모델입니다. 본 글에서는 이 글에서 다루는 핵심적인 방법론만 다루도록 하겠습니다. 논문의 자세한 리뷰는 아래 링크에서 확인하시면 됩니다.
  • A Generic Camera Model and Calibration Method for Conventional, Wide-Angle, and Fish-Eye Lenses 리뷰
• 본 글에서 사용되는 intrinsic 파라미터 \(f_{x}, \alpha, c_{x}, f_{y}, c_{y}\) 그리고 Radial Distortion을 모델링 하기 위한 방정식의 \(k_{0}, k_{1}, k_{2}, k_{3}, k_{4}\) 인 coefficient는 Zhang's Method를 이용한 카메라 캘리브레이션 방법을 통하여 찾을 수 있습니다.
• 이 값의 정확한 의미와 파라미터 추정 방법은 아래 글에서 참조하시기 바랍니다.
  • 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습

Generic 카메라 모델의 3D → 2D

• 지금부터 살펴볼 내용은 Generic 카메라 모델을 이용하여 임의의 3D 포인트를 2D 이미지에 투영하는 방법입니다.

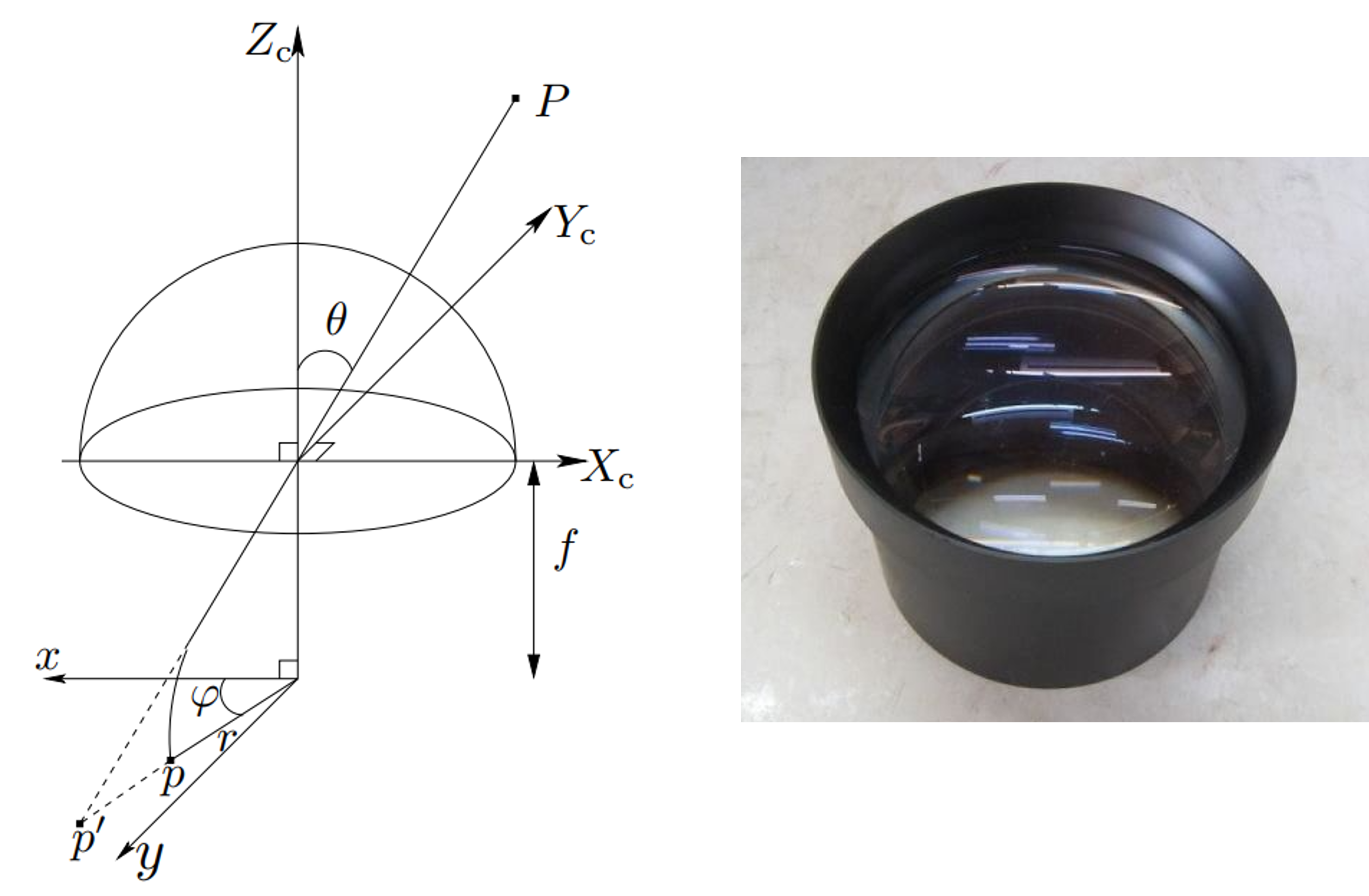
• 왼쪽 그림은 Generic 카메라 모델 논문에서 발췌한 이미지이며 반원 형태는 카메라 렌즈를 나타냅니다. 따라서 오른쪽 그림과 같이 카메라 렌즈가 위를 향하는 형태로 생각하시면 됩니다. 그러면 설명의 편의를 위하여 다음과 같이 그림을 일부 다시 표현하겠습니다.

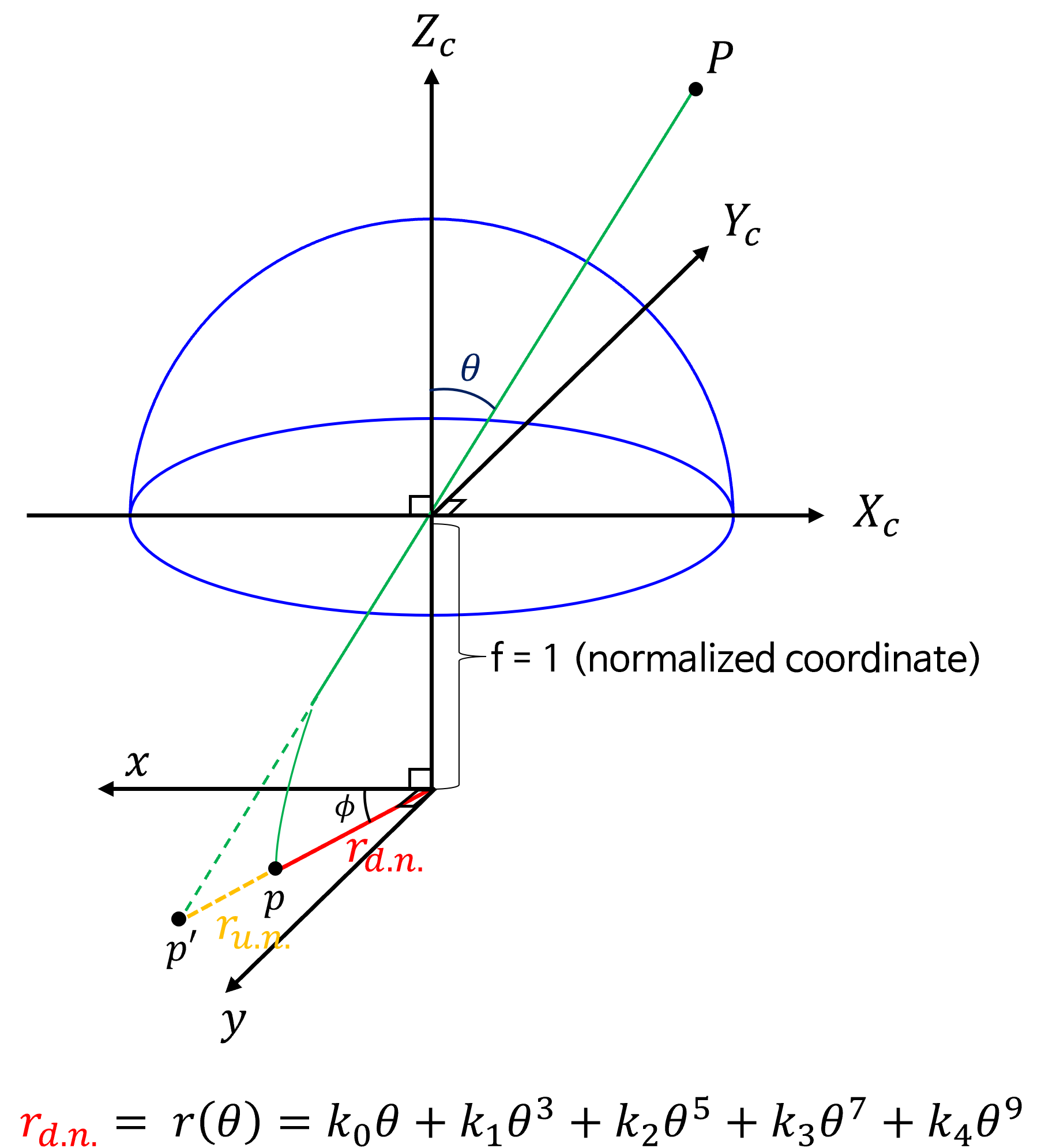
• 위 그림에서 \(X_{c}, Y_{c}, Z_{c}\) 는 카메라 좌표계의 좌표축을 의미 합니다. 즉 원점이 카메라의 원점에 해당합니다. 따라서 3차원 공간의 점 \(P\) 는 카메라 좌표계에서의 임의의 점을 의미합니다.
• 만약 카메라 렌즈 왜곡인 없는 Pinhole 카메라 모델에서는 점 \(P\) 가 초록색 선을 따라서 카메라 원점에 직선으로 입사하고 \(p'\) 의 normalized coordinate로 투영됩니다. (관련 내용은 사전 지식 링크를 참조하시면 됩니다.)
• 하지만 카메라 렌즈의 radial distortion으로 인하여 직선 형태로 입사하여 \(p'\) 에 맺히지 못하고 휘어져서 \(p\) 에 입사하게 됩니다.
• 이 때, 3D 공간 상의 점 \(P\) 가 입사하는 입사각을 \(\theta\) 라고 합니다.

• 여기서 알고 싶은 점은 \(\theta\) 를 이용하여 어떻게 \(r_{\text{d.n.}}\) 를 계산할 수 있을까? 입니다. 이것을 모델링 하는 것이 Generic 카메라 모델의 역할이 됩니다. (\(\text{d.n.}\) 는 distorted normalied 입니다.)
• 본 글에서 살펴보는 카메라 모델은 undistorted normalized 좌표계와 distorted normalized 좌표계는 카메라 렌즈에 의한 왜곡 여부가 반영된 normalized 좌표계인 지를 나타냅니다. undistorted normalized 좌표계는 pinhole 카메라 모델과 같이 왜곡이 없는 normalized 좌표계이고 distorted normalized 좌표계는 위 그림과 같이 카메라 렌즈에 의한 왜곡이 발생한 normalized 좌표계 입니다.

• 따라서 3D → 2D 변환의 전체 순서는 다음과 같습니다.
• ① 카메라 좌표계 → undistorted normalized 좌표계로 변환
• ② undistorted normalized 좌표계 → distorted normalized 좌표계로 변환
• ③ distorted normalized 좌표계 → 이미지 좌표계로 변환
• 즉, 3D 포인트를 먼저 undistorted normalized 좌표계로 변환한 후 렌즈 왜곡을 반영하여 distorted normalized 좌표계로 변환 후 최종적으로 이미지에 투영시키는 순서를 가집니다.
• 따라서 위 그림으로 표현하면 한번에 \(P\) 에서 \(p\) 로 가는 것이 아니라 \(P \to p' \to p\) 로 변환하는 과정을 거치게 됩니다.

① 카메라 좌표계 → undistorted normalized 좌표계로 변환

• 임의의 점 \(P\) 의 좌표가 \(X_{c}, Y_{c}, Z_{c}\) 라고 가정하겠습니다. 그러면 undistorted normalized 좌표계로의 변환은 pinhole 카메라 모델로 가정하여 단순히 \(Z_{c}\) 로 나누어 \(Z_{c}\) 가 \(1\) 인 normalized 좌표계로 변환하면 됩니다. 따라서 식은 다음과 같습니다.

• \[x_{\text{u.n.}} = X_{c} / Z_{c} \tag{1}\]
• \[y_{\text{u.n.}} = Y_{c} / Z_{c} \tag{2}\]
• \[z_{\text{u.n.}} = Z_{c} / Z_{c} = 1 \tag{3}\]

② undistorted normalized 좌표계 → distorted normalized 좌표계로 변환

• 이번에는 undistorted normalized 좌표계에서 distorted normalized 좌표계로 변환하는 작업을 해보겠습니다. 설명의 편의 상 그림의 표기를 조금 변경하여 나타내었습니다.

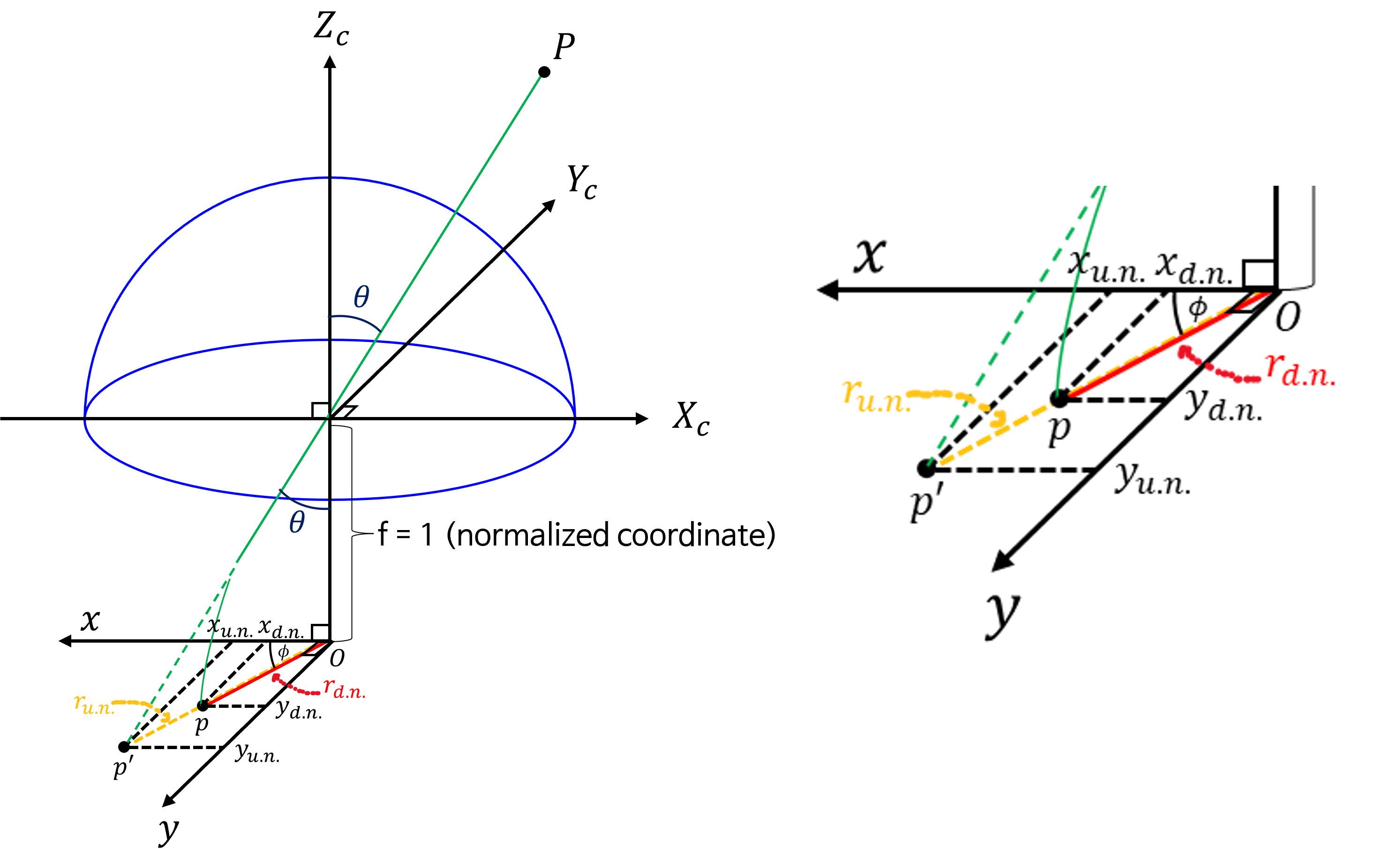
• 변환의 전체 과정은 \(p'\) 를 이용하여 입사각 \(\theta\) 를 알아내고 \(\theta\) 를 통하여 \(r_{\text{d.n.}}\) 를 추정 후 최종적으로 distorted normalized 좌표계로 변환하는 것입니다.

• 먼저 \(\theta\) 를 계산하는 방식은 다음과 같습니다. 삼각 함수를 이용하여 계산합니다.
• 위 그림에서 \(r_{\text{u.n.}}\) 는 원점과 \(p'\) 의 거리이므로 다음과 같이 \(x_{\text{u.n.}}\) 과 \(y_{\text{u.n.}}\) 을 이용합니다.

• \[r_{\text{u.n.}}^{2} = x_{\text{u.n.}}^{2} + y_{\text{u.n.}}^{2} \tag{4}\]
• \[r_{\text{u.n.}} = \sqrt{x_{\text{u.n.}} ^{2} + y_{\text{u.n.}}^{2}} \tag{5}\]
• \[\theta = \tan^{-1}{(r_{\text{u.n.}})} \tag{6}\]

• 이와 같은 방법으로 \(\theta\) 를 계산하면 다음 식 (7)을 이용하여 \(r_{\text{d.n.}}\) 를 추정합니다.

• \[r_{\text{d.n.}} = r(\theta) = k_{0}\theta + k_{1}\theta^{3} + k_{2}\theta^{5} + k_{3}\theta^{7} + k_{4}\theta^{9} \tag{7}\]

• 위 식을 통하여 \(r_{\text{d.n.}}\) 를 추정하는 모델링의 전제는 점 \(p'\) 와 \(p\) 가 축과 이루는 각도가 \(\phi\) 로써 동일하다는 가정입니다. 즉, 방사형에서 같은 방위각에 존재하되 같은 방위각에서의 위치가 변경된다는 것을 가정으로 모델링 합니다.
• 따라서 식 (7) 에서 구한 \(r_{\text{d.n.}}\) 은 \(r_{\text{u.n.}}\) 과 겹치는 선이 됩니다. 따라서 같은 방위각을 가짐을 이용하면 삼각함수를 통해 \(x_{\text{d.n.}}, y_{\text{d.n.}}\) 을 구할 수 있습니다.
• 식 (7)의 다항식 구성을 보면 홀수 차수의 항으로만 이루어 진 것을 알 수 있습니다. 이와 같이 짝수 차수의 항을 배제한 것은 우함수 (even function)의 특성상 \(r(\theta) = r(-\theta)\) 가 만족되면 부호가 다른 \(\theta\) 의 점이 한 곳으로 투영되는 문제가 발생할 수 있기 때문입니다. 따라서 기함수 (odd function)만 포함하여 다항식을 구성합니다.

• \[x_{\text{d.n.}} = r_{\text{d.n.}} \cos{\phi} = r_{\text{d.n.}} \frac{x_{\text{u.n.}}}{r_{\text{u.n.}}} \tag{8}\]
• \[y_{\text{d.n.}} = r_{\text{d.n.}} \sin{\phi} = r_{\text{d.n.}} \frac{y_{\text{u.n.}}}{r_{\text{u.n.}}} \tag{9}\]

③ distorted normalized 좌표계 → 이미지 좌표계로 변환

• 앞의 방식으로 \(x_{\text{d.n.}}, y_{\text{d.n.}}\) 를 구하면 최종적으로 카메라 intrinsic을 이용하여 다음과 같이 \(u, v\) 좌표로 변환할 수 있습니다.
• 앞에서 구한 \(x_{\text{d.n.}}, y_{\text{d.n.}}\) 는 \(z = 1\) 인 distorted normalzied 좌표계에서 값을 구한 결과 이므로 아래 식의 파라미터 정보를 이용하여 식 (10), (11)과 같이 \(u, v\) 를 구할 수 있습니다.

• \[\text{camera intrinsic : } = \begin{bmatrix} f_{x} & \alpha & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{bmatrix}\]

• \[u = f_{x} \cdot x_{\text{d.n.}} + \alpha \cdot y_{\text{d.n.}} + c_{x} \tag{10}\]
• \[v = f_{y} \cdot y_{\text{d.n.}} + c_{y} \tag{11}\]

• 따라서 Generic 카메라 모델의 3D → 2D로 변환하는 과정의 핵심은 \(\theta \to r_{\text{d.n.}}\) 으로 추정하는 것임을 알 수 있었습니다.

• 지금까지 내용을 코드로 나타내면 다음과 같습니다.

X_c, Y_c, Z_c # given data

#################### undistorted normalized coordinate ######################
x_un = X_c / Z_c
y_un = Y_c / Z_c

#################### distorted normalized coordinate ########################
r_un = np.sqrt(x_un**2 + y_un**2)
theta = np.arctan(r_un)
r_dn = 1*theta + k1*theta**3 + k2*theta**5 + k3*theta**7 + k4*theta**9

x_dn = r_dn * (x_un/r_un)
y_dn = r_dn * (y_un/r_un)

################################ image plane ###############################
u = np.round(fx*x_dn + skew*y_dn + cx)
v = np.round(fy*y_dn + cy)

Generic 카메라 모델의 2D → 3D

• 이번에는 2D 이미지의 픽셀 좌표를 어떻게 3D로 변환하는 지 살펴보도록 하겠습니다. 방법은 앞에서 다룬 3D → 2D 로 변환하는 방법을 역으로 이용하면 됩니다. 따라서 다음과 같은 순서의 방법을 가집니다.

• ① 이미지 좌표계 → distorted normalized 좌표계로 변환
• ② distorted normalized 좌표계 → undistorted normalized 좌표계로 변환
• ③ undistorted normalized 좌표계로 변환 → 카메라 좌표계로 변환

① 이미지 좌표계 → distorted normalized 좌표계로 변환

• 앞에서 distorted normalized 좌표계 → 이미지 좌표계롸 변환을 할 때, 카메라 intrinsic 파라미터를 사용하여 변환하였었습니다. 이번에는 그 반대 과정을 그대로 적용하면 됩니다.
• 아래 식 (12)는 식 (10)을 \(x_{\text{d.n.}}\) 기준으로 정리한 것이고 식 (13)은 식 (11)을 \(y_{\text{d.n.}}\) 기준으로 정리한 것입니다.

• \[x_{\text{d.n.}} = \frac{u - c_{x} \alpha y_{\text{d.n.}}}{f_{x}} \tag{12}\]
• \[y_{\text{d.n.}} = \frac{v - c_{y}}{f_{y}} \tag{13}\]

② distorted normalized 좌표계 → undistorted normalized 좌표계로 변환

• 2D → 3D로 다시 역변환 하기 위한 핵심 부분은 바로 이 부분입니다. 왜냐하면 식 (7)의 역함수를 바로 찾을 수 없기 때문에 numeric한 방법으로 근사해를 구해야 하기 때문입니다.
• 먼저 구하고자 하는 값은 식 (8), (9) 의 역방향 값입니다.

• \[x_{\text{d.n.}} = r_{\text{d.n.}} \frac{x_{\text{u.n.}}}{r_{\text{u.n.}}}\]
• \[\therefore x_{\text{u.n.}} = r_{\text{u.n.}}\frac{x_{\text{d.n.}}}{r_{\text{d.n.}}} \tag{14}\]

• \[y_{\text{d.n.}} = r_{\text{d.n.}} \frac{y_{\text{u.n.}}}{r_{\text{u.n.}}}\]
• \[\therefore y_{\text{u.n.}} = r_{\text{u.n.}}\frac{y_{\text{d.n.}}}{r_{\text{d.n.}}} \tag{15}\]

• distorthed normalized 좌표계에서 식 (14), (15)의 우변의 항목 중 알 수 있는 것은 \({r_{\text{d.n.}}}, x_{\text{d.n.}}, y_{\text{d.n.}}\) 입니다.
• 반면 \(r_{\text{u.n.}}\) 은 직접적으로 알 수 없고 \(\theta\) 를 알 수 있습니다.

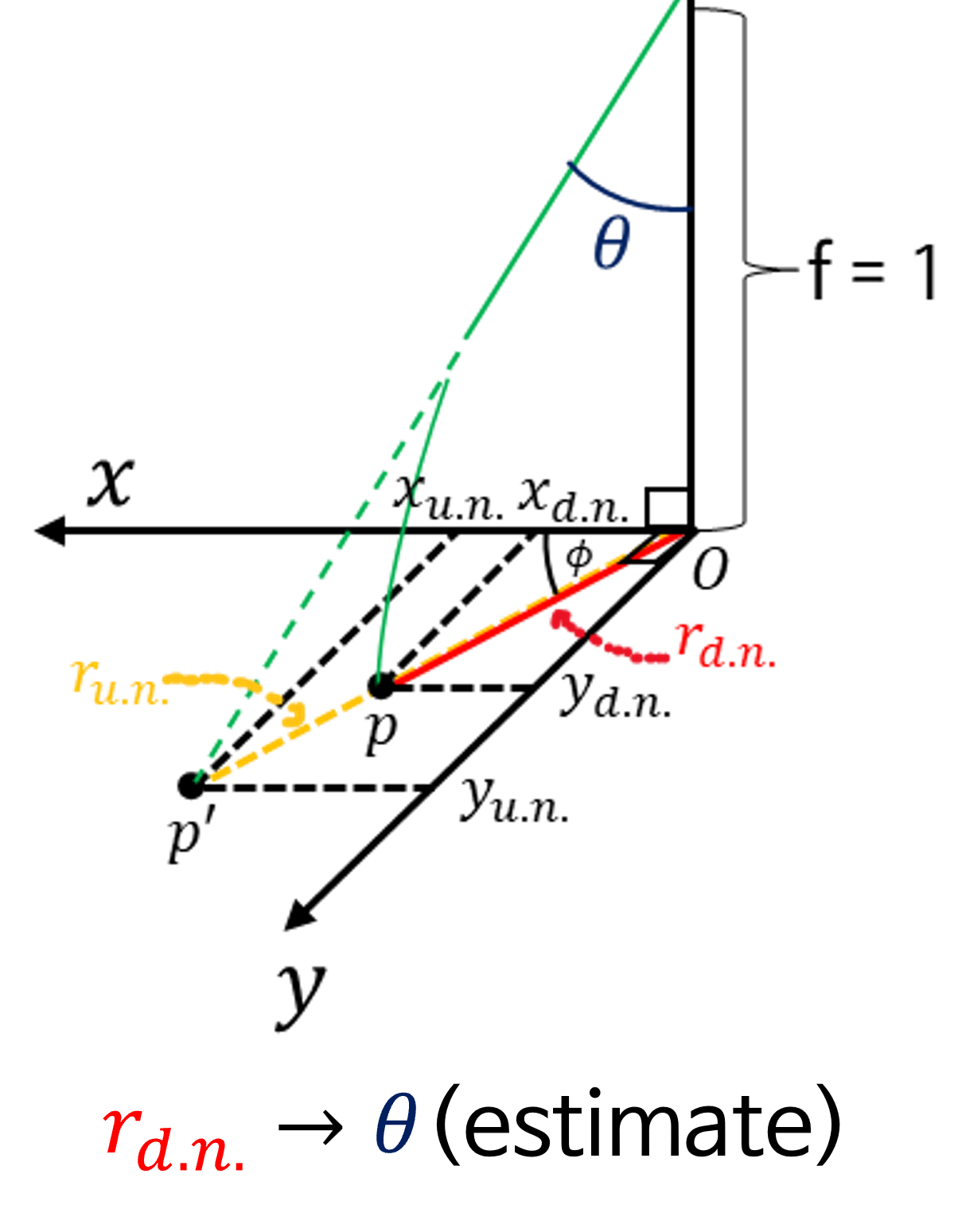
• 위 그림과 같이 \(\theta\) 를 알면 \(\tan{(\theta)} = r_{\text{u.n.}} / 1\) 를 계산할 수 있습니다.
• 즉, 식 (7)에서 \(\theta\) 를 통해 \(r(\theta)\) 를 추정한 것과 반대로 \(r(\theta)=r_{\text{d.n.}}\) 를 통해 \(\theta\) 를 추정하는 것이 문제의 핵심이 됩니다. 이 문제를 다음과 같이 나타낼 수 있습니다.

• \[r(\theta') = k_{0}\theta'^{1} + k_{1}\theta'^{3} + k_{2}\theta'^{5} + k_{3}\theta'^{7} + k_{4}\theta'^{9} = r_{\text{d.n.}} \tag{16}\]

• 식 (16) 에서 \(r(\theta') = r_{\text{d.n.}}\) 을 만족하는 \(\theta'\) 를 찾는 문제로 정의할 수 있고 closed-form 형태의 풀이법이 없기 때문에 numeric한 방식으로 \(\theta'\) 를 근사화 시켜야 합니다.
• 이러한 문제를 풀 때, 가장 흔히 사용되는 방법이 newton-raphson method 줄여서 newton-method 방법을 사용합니다. 상세 내용은 다음 링크를 참조하시기 바랍니다.
  • newton-raphson method 내용 참조
• newton-method 방법을 적용하기 위하여 식 (16)을 다음과 같이 변경합니다.

• \[f(\theta') = k_{0}\theta'^{1} + k_{1}\theta'^{3} + k_{2}\theta'^{5} + k_{3}\theta'^{7} + k_{4}\theta'^{9} - r_{\text{d.n.}} = 0 \tag{17}\]

• 식 (17)과 같이 우변을 0으로 만드는 해 \(\theta'\) 를 찾는 문제로 변환한다면 newton-method를 통하여 해를 근사화 하여 찾을 수 있습니다. newton-method 방법에 따라 \(\theta'\) 를 추정하면 다음 식과 같이 반복적인 방법으로 오차를 줄여가면서 구할 수 있습니다. 일반적으로 newton-method로 근을 추정할 때, 반복 횟수의 최대 값을 주거나 오차가 일정 임계값 보다 작아지면 반복을 멈추는 방법을 사용합니다.

• \[\theta'_{i+1} = \theta'_{i} - \frac{f(\theta'_{i})}{\partial \ f(\theta'_{i})} \tag{18}\]

• 식 (18)의 \(f(\theta'_{i})\) 는 앞에서 다룬 것과 같이 다음과 같습니다.

• \[f(\theta'_{i}) = k_{0}\theta'^{1}_{i} + k_{1}\theta'^{3}_{i} + k_{2}\theta'^{5}_{i} + k_{3}\theta'^{7}_{i} + k_{4}\theta'^{9}_{i} - r_{\text{d.n.}} = 0 \tag{19}\]

• 반면 \(\partial \ f(\theta'_{i})\) 는 \(f(\theta'_{i})\) 를 \(\theta'\) 에 대하여 1차 미분한 값을 뜻합니다. 따라서 다음과 같이 정리할 수 있습니다.

• \[\partial f(\theta'_{i}) = k_{0} + 3k_{1}\theta'^{2}_{i} + 5k_{2}\theta'^{4}_{i} + 7k_{3}\theta'^{6}_{i} + 9k_{4}\theta'^{8}_{i} \tag{20}\]

• 따라서 식 (18)을 이용하여 정리하면 다음과 같이 newton-method 방법을 적용할 수 있습니다.

• \[\begin{align} \theta'_{i+1} &= \theta'_{i} - \frac{f(\theta'_{i})}{\partial \ f(\theta'_{i})} \\ &= \theta'_{i} - \frac{k_{0}\theta'^{1} + k_{1}\theta'^{3} + k_{2}\theta'^{5} + k_{3}\theta'^{7} + k_{4}\theta'^{9} - r_{\text{d.n.}}}{k_{0} + 3k_{1}\theta'^{2}_{i} + 5k_{2}\theta'^{4}_{i} + 7k_{3}\theta'^{6}_{i} + 9k_{4}\theta'^{8}_{i}} \end{align} \tag{21}\]

• 식 (21)의 최적화를 위한 반복 종료 조건은 보통 다음 2가지 방식을 많이 사용 합니다.

• \[\vert \theta'_{i+1} - \theta'_{i} \vert \lt \text{tolerance} \tag{22}\]
• \[i \gt \text{max iterations} \tag{23}\]

• 지금 까지 살펴본 방법은 \(x_{\text{d.n.}}, y_{\text{d.n.}}\) 을 알 때, \({r_{\text{d.n.}}}\) 를 구하고 이 값을 이용하여 \(\theta'\) 를 추정하는 것이었습니다.
• 즉, 렌즈 왜곡이 반영된 어떤 이미지의 \((u, v)\) 좌표에서 \(K^{-1}\) 을 적용하면 \(x_{\text{d.n.}}, y_{\text{d.n.}}\) 을 얻을 수 있는데 이 값에 대응되는 \(r_{\text{d.n.}}\) 은 픽셀 별로 조금씩 다를 수 있기 때문에 사전에 필요한 모든 픽셀에 대하여 관계를 구해놓으면 편하게 사용할 수 있습니다.
• 예를 들어 \((u, v)\) 는 \(\theta'\) 에 대응된다. 라는 관계를 모든 유효한 \((u, v)\) 에 대하여 미리 구해 놓습니다. (0, 0) ~ (100, 100) 의 모든 \((u, v)\) 좌표에 대하여 대응되는 \(\theta'\) 값을 필요로 하면 사전에 이 좌표들에 대해서 관계를 구해 놓을 수 있습니다.
• 이와 같은 관계를 나타내는 자료 구조를 LUT (Look Up Table) 라고 하며 보통 테이블에서 \((u, v)\) 의 인덱스를 접근하면 \(\theta'\) 값을 읽어올 수 있도록 구성해 둡니다. 더 나아가 추가적인 연산 없이 식 (14), (15)의 계산을 하기 위하여 \((u, v)\) 의 인덱스를 접근하면 \(r_{\text{d.n.}}\) 과 \(\tan{(\theta')} = r_{\text{u.n.}}\) 을 얻을 수 있도록 구성해 놓을 수도 있습니다.

• 식 (21), (22), (23)의 조건을 반영한 python 코드를 살펴보면 다음과 같습니다.
• 먼저 아래는 식 (21)의 newton-method를 구현한 함수 입니다.

def f_theta_pred(theta_pred, r, k0, k1, k2, k3, k4):
    return k0*theta_pred + k1*theta_pred**3 + k2*theta_pred**5 + k3*theta_pred**7 + k4*theta_pred**9 - r

def f_theta_pred_prime(theta_pred, r, k0, k1, k2, k3, k4):
    return k0 + 3*k1*theta_pred**2 + 5*k2*theta_pred**4 + 7*k3*theta_pred**6 + 9*k4*theta_pred**8

def rdn2theta(x_dn, y_dn, k0, k1, k2, k3, k4, max_iter=300, tol=1e-10):
    r_dn = np.sqrt(x_dn**2 + y_dn**2)
    theta_init = np.arctan(r_dn)

    # newton-method
    theta_pred = theta_init
    for _ in range(max_iter):        
        prev_theta_pred = theta_pred
        
        f_theta_value = f_theta_pred(theta_pred, r_dn, 1, k1, k2, k3, k4)
        f_theta_prime_value = f_theta_pred_prime(theta_pred, r_dn, 1, k1, k2, k3, k4)
        theta_pred = theta_pred - f_theta_value/f_theta_prime_value
        if np.abs(theta_pred - prev_theta_pred) < tol:
            break
    
    r_un = np.tan(theta_pred)
    x_un = r_un * (x_dn / r_dn)
    y_un = r_un * (y_dn / r_dn)
    return x_un, y_un, r_dn, theta_pred

• 아래는 scipy를 이용하여 구한 방법입니다. scipy.optimize의 root_scalar를 이용하면 더 안정적인 방법으로 구할 수 있습니다. 일반적인 상황에서는 앞에서 구현한 함수와 아래의 root_scalar를 이용한 \(\theta'\) 추정 값은 같습니다.

from scipy.optimize import root_scalar

def f_theta_pred(theta_pred, r, k0, k1, k2, k3, k4):
    return k0*theta_pred + k1*theta_pred**3 + k2*theta_pred**5 + k3*theta_pred**7 + k4*theta_pred**9 - r

def f_theta_pred_prime(theta_pred, r, k0, k1, k2, k3, k4):
    return k0 + 3*k1*theta_pred**2 + 5*k2*theta_pred**4 + 7*k3*theta_pred**6 + 9*k4*theta_pred**8

def rdn2theta(x_dn, y_dn, k0, k1, k2, k3, k4):
    r_dn = np.sqrt(x_dn**2 + y_dn**2)
    theta_init = np.arctan(r_dn)

    # newton-method
    result = root_scalar(
        f_theta_pred, 
        args=(r_dn, k0, k1, k2, k3, k4), 
        method='newton', 
        x0=theta_init, 
        fprime=f_theta_pred_prime
    )
    
    theta_pred = result.root    
    r_un = np.tan(theta_pred)
    x_un = r_un * (x_dn / r_dn)
    y_un = r_un * (y_dn / r_dn)
    return x_un, y_un, r_dn, theta_pred

• 앞에서 언급한 LUT는 이미지 좌표계에서 \((u, v)\) 에 해당하는 \(\theta'\) 및 \(r_{\text{d.n.}}, r_{\text{u.n.}}\) 을 직접적으로 접근하기 위한 자료 구조임을 설명하였습니다.
• LUT 값을 채우기 위해서는 다음 식의 빨간색 부분의 순서대로 값을 추정해야 하며 최종적으로 \(\theta'\) 를 통하여 \((x_{\text{u.n.}}, y_{\text{u.n.}})\) 을 추정할 수 있습니다.

• \[\color{red}{(u, v) \to (x_{\text{d.n.}}, y_{\text{d.n.}}) \to r_{\text{d.n.}} \to \theta' \to r_{\text{u.n.}}} \to (x_{\text{u.n.}}, y_{\text{u.n.}}) \tag{24}\]

• 아래 예제는 식 (14), (15) 를 바로 적용하기 위하여 \(r_{\text{d.n.}}, r_{\text{u.n.}}\) 값을 LUT에 할당합니다.
• 아래 코드의 mask_valid는 vignetting 영역을 제외하기 위함이며 더 나아가 실제로 필요한 영역에 대한 mask_valid를 생성한 다음에 그 영역에서만 LUT를 구할 수도 있습니다. vignetting 영역을 제거하기 위한 mask 생성은 아래 링크를 참조하시기 바랍니다.
  • Fisheye Camera의 Vignetting 영역 인식 방법 : https://gaussian37.github.io/vision-concept-fisheye_camera/#fisheye-camera%EC%9D%98-vignetting-%EC%98%81%EC%97%AD-%EC%9D%B8%EC%8B%9D-%EB%B0%A9%EB%B2%95-1

lut = np.zeros((img.shape[0], img.shape[1], 2)).astype(np.float32)
for u in range(img.shape[1]):
    for v in range(img.shape[0]):
        # check (u, v) is valid image area (ex. checking vignetting area)
        if mask_valid[v][u]:
            y_dn = (v - cy)/fy
            x_dn = (u - skew*y_dn - cx)/fx
            _, _, r_dn, theta_pred = rdn2theta_scipy(x_dn, y_dn, 1, k1, k2, k3, k4)
            
            # r_dn
            lut[v][u][0] = r_dn
            # r_un
            lut[v][u][1] = np.tan(theta_pred)
            # theta_pred
            lut[v][u][2] = theta_pred

• 위 방법을 통하여 LUT를 마련하면 다음과 같이 \((u, v) \to (x_{\text{u.n.}}, y_{\text{u.n.}})\) 로 변환할 수 있습니다.
• 아래 예시는 앞의 코드에서 생성한 LUT를 통하여 임의의 \((u, v) = (100, 50)\) 에서의 \((x_{\text{u.n.}}, y_{\text{u.n.}})\) 값을 추정한 결과입니다.

u = 100
v = 50

r_dn = lut[v][u][0]
r_un = lut[v][u][1]

y_dn = (v - cy)/fy
x_dn = (u - skew*y_dn - cx)/fx

x_un = r_un * x_dn/r_dn
y_un = r_un * y_dn/r_dn

• 이와 같은 LUT 방식의 사용은 한번만 연산을 하면 별도 연산 없이 테이블만 접근하여 사용하면 되기 때문에 상당히 효율적입니다. 하지만 필요한 LUT의 사이즈가 커지게 된다면 이미지 별 LUT를 모두 가지고 있는 것은 메모리 차원에서 문제가 될 수도 있습니다.
• 따라서 아래 방법과 같이 LUT의 값들을 다항식으로 표현한 후 polynomial curve fitting을 통하여 계수를 찾으면 정확도를 조금 낮추더라도 LUT를 항상 가지고 있어야 하는 점에서 자유로워 질 수 있습니다.
• polynomial curve fitting을 통하여 LUT를 대체하려는 이유는 다음과 같습니다. generic camera model에서 식 (7)을 통하여 \(\theta \to r_{\text{d.n.}}\) 을 구하였는데, 이 때 기함수로 구성된 9차 방정식을 사용하였습니다. 이 함수의 역함수인 \(r_{\text{d.n.}} \to \theta\) 의 관계식을 찾는 것이 목적이 되겠으나 다차 방정식의 역함수를 바로 찾을 수 없기 때문에 polynomial curve fitting을 통해서 찾는 것입니다.
• 간단한 예를 들면 \(\theta \to r_{\text{d.n.}}\) 의 과정이 \(y = 2x\) 라면 \(r_{\text{d.n.}} \to \theta\) 의 과정은 \(y = \frac{1}{2}x\) 인데, 이 과정을 polynomial curve fitting을 통해 근사화 한다는 것이 살펴볼 방법 입니다.

• polynomial curve fitting을 하기 위해서는 아래 식을 최적화 하기 위한 src와 target 데이터가 필요합니다.

• \[\theta' = l_{0}r_{\text{d.n.}} + l_{1}r_{\text{d.n.}}^{3} + l_{2}r_{\text{d.n.}}^{5} + l_{3}r_{\text{d.n.}}^{7} + l_{4}r_{\text{d.n.}}^{9} \tag{25}\]

• 식 (25)의 src는 \(r_{\text{d.n.}}\) 이고 target은 \(\theta'\) 가 됩니다. 이 값은 LUT의 각 \((u, v)\) 의 성분을 구하면서 확인할 수 있던 것으로 아래 코드를 통해 구할 수 있습니다.

src_r_dn = []
target_theta_pred = []
for u in range(img.shape[1]):
    for v in range(img.shape[0]):
        # check (u, v) is valid image area (ex. checking vignetting area)
        if mask_valid[v][u]:
            y_dn = (v - cy)/fy
            x_dn = (u - skew*y_dn - cx)/fx
            _, _, r_dn, theta_pred = rdn2theta_scipy(x_dn, y_dn, 1, k1, k2, k3, k4)
            src_r_dn.append(r_dn)
            target_theta_pred.append(theta_pred)

src_r_dn = np.array(src_r_dn)
target_theta_pred = np.array(target_theta_pred)

from scipy.optimize import curve_fit

def polyfit_func(x, l0, l1, l2, l3, l4):
    return l0*x + l1*x**3 + l2*x**5 + l3*x**7 + l4*x**9

coeffs, _ = curve_fit(polyfit_func, src_r_dn, target_theta_pred.reshape(-1))

• 위 코드에서 coeffs가 식 (25)의 \(l_{0}, l_{1}, l_{2}, l_{3}, l_{4}\) 를 나타내고 아래 함수를 통하여 \(r_{\text{d.n.}} \to \theta\) 을 추정할 수 있습니다.

def get_polyfit_theta_pred(r_dn, l0, l1, l2, l3, l4):
    return l0*r_dn + l1*r_dn**3 + l2*r_dn**5 + l3*r_dn**7 + l4*r_dn**9

• 이와 같은 polynomial curve fitting을 통하여 \((u, v) \to (x_{\text{d.n.}}, y_{\text{d.n.}}) \to r_{\text{d.n.}} \to \theta' \to (x_{\text{u.n.}}, y_{\text{u.n.}})\) 을 구하면 다음과 같습니다.

u = 100
v = 50 

y_dn = (v - cy)/fy
x_dn = (u - skew*y_dn - cx)/fx

r_dn = np.sqrt(x_dn**2 + y_dn**2)
theta_pred = get_polyfit_theta_pred(r_dn, coeffs[0], coeffs[1], coeffs[2], coeffs[3], coeffs[4])
r_un = np.tan(theta_pred)

x_un = r_un * x_dn/r_dn
y_un = r_un * y_dn/r_dn

• 이와 같은 방법으로 polynomial curve fitting을 하면 \((u, v)\) 의 \((x_{\text{u.n.}}, y_{\text{u.n.}})\) 을 알 수 있습니다.

③ undistorted normalized 좌표계로 변환 → 카메라 좌표계로 변환

• 지금까지 undistorted normalized 좌표계로 좌표값을 옮기는 방법에 대하여 설명하였습니다. 이 좌표값을 카메라 좌표계로 옮기기 위해서는 \(Z_{c}\) 값을 필요로 합니다.
• 일반적으로 \(Z_{c}\) 값은 알 수 없으나, Depth Estimation을 통해 \(Z_{c}\) 를 구하거나 이미 알고 있는 값이라면 다음과 같이 사용할 수 있습니다.

• \[(X_{c}, Y_{c}, Z_{c}) = (x_{\text{u.n.}} \cdot Z_{c}, y_{\text{u.n.}} \cdot Z_{c}, Z_{c}) \tag{26}\]

• 지금까지 사용한 방법을 통하여 generic camera 모델을 사용 시, 어떻게 3D → 2D, 2D → 3D 로 변환하는 지 살펴보았습니다.
• 지금부터는 앞에서 사용한 내용 및 코드를 활용하여 실제 Fisheye Camera 이미지를 통해 어떻게 적용하는 지 살펴보도록 하겠습니다.

Generic 카메라 모델 3D → 2D 및 2D → 3D python 실습

• 앞에서 배운 내용을 실제 데이터를 통해서 확인하기 위하여 다음 이미지와 카메라 파라미터를 사용하도록 하겠습니다. 카메라 파라미터는 Zhang's method를 통하여 사전에 구한 값입니다.
• 이미지 링크 : https://drive.google.com/file/d/1pz0sMqCEXqVv_cL5eoYNLgJPJBcFwzoJ/view?usp=drive_link
• intrinsic과 distortion coefficient

print(K) # intrinsic
fx = K[0][0]
skew = K[0][1]
cx = K[0][2]
fy = K[1][1]
cy = K[1][2]
# [[567.85821196   0.         960.58762478]
#  [  0.         567.33818371 516.27957345]
#  [  0.           0.           1.        ]]

print(D) # distortion coefficient
k1, k2, k3, k4 = D[0], D[1], D[2], D[3]
# [[-0.07908567]
#  [ 0.03639387]
#  [-0.04227248]
#  [ 0.01444498]]

• 위 이미지를 보면 가운데 있는 체커보드 판은 가로 세로 크기가 10cm (0.1m) 이며 카메라 좌표계 기준으로 좌표를 기록하였습니다.
• 매뉴얼한 방식으로 좌표를 측정한 것이라 오차가 발생합니다. 실습 용도로 사용하는 것으로 기본적인 오차는 감수하고 보시면 될 것 같습니다.
• 카메라 좌표계 기준으로 체커 보드 좌상단에 적힌 값은 \((X_{c}, Y_{c})\) 좌표값을 의미하며 \(Z_{c}\) 는 0.8m입니다. 그러면 앞에서 배운 방법을 통하여 좌 상단의 4개의 점에 대하여 3D → 2D, 2D → 3D로 복원하는 실습을 해보도록 하겠습니다. 좌 상단 점의 3D 좌표 정보와 2D 좌표 정보는 다음과 같습니다.

① (X_c, Y_c, Z_c) = (-0.56, -0.37, 0.8), (u, v) = (640,  309)
② (X_c, Y_c, Z_c) = (-0.46, -0.37, 0.8), (u, v) = (690,  303)
③ (X_c, Y_c, Z_c) = (-0.56, -0.27, 0.8), (u, v) = (631,  365)
④ (X_c, Y_c, Z_c) = (-0.46, -0.27, 0.8), (u, v) = (682,  360)

• ②, ③, ④는 개인적으로 실습해보시길 바랍니다. 이번 글에서는 ①을 기준으로 실습을 하겠습니다.

X_c = -0.56 
Y_c = -0.37
Z_c = 0.8

#################### undistorted normalized coordinate ######################
x_un = X_c / Z_c
y_un = Y_c / Z_c
print(x_un, y_un)
# -0.7000000000000001 -0.46249999999999997

#################### distorted normalized coordinate ########################
r_un = np.sqrt(x_un**2 + y_un**2)
theta = np.arctan(r_un)
r_dn = 1*theta + k1*theta**3 + k2*theta**5 + k3*theta**7 + k4*theta**9

x_dn = r_dn * (x_un/r_un)
y_dn = r_dn * (y_un/r_un)
print(x_dn, y_dn)
# [-0.56263603] [-0.37174167]

################################ image plane ###############################
u = np.round(fx*x_dn + skew*y_dn + cx)
v = np.round(fy*y_dn + cy)

print(u, v)
# [641.] [305.]

• checkerboard에서 추정한 값은 (640, 309)인 반면 3D → 2D 로 투영하였을 때, 값은 (641, 305)가 됩니다. 차이는 존재하지만 유사하게 추정된 것을 확인할 수 있습니다.

• 앞에서 설명한 코드를 사용하여 2D → 3D 로 변환하는 내용을 확인해 보도록 하겠습니다.
• 먼저 LUT를 사용하여 3D 포인트를 복원하는 방법입니다. LUT는 앞에서 설명한 코드에서 구한 것으로 가정하겠습니다.

u = 641
v = 305
r_dn = lut[v][u][0]
r_un = lut[v][u][1]

y_dn = (v - cy)/fy
x_dn = (u - skew*y_dn - cx)/fx

x_un = r_un * x_dn/r_dn
y_un = r_un * y_dn/r_dn

print(x_un * 0.8, y_un * 0.8, 0.8)
# -0.5603736513270253 -0.37080293297387945 0.8

• 원래 \((X_{c}, Y_{c}, Z_{c}) = (-0.56, -0.37, 0.8)\) 인 것과 비교하면 유사하게 복원된 것을 확인할 수 있습니다.
• 다음으로 polynomial curve fitting을 사용하여 3D 포인트를 복원하는 방법입니다. polyfit은 앞에서 설명한 코드로 fitting 한 것으로 가정하겠습니다.

u = 641
v = 305

y_dn = (v - cy)/fy
x_dn = (u - skew*y_dn - cx)/fx

r_dn = np.sqrt(x_dn**2 + y_dn**2)
theta_pred = get_polyfit_theta_pred(r_dn, coeffs[0], coeffs[1], coeffs[2], coeffs[3], coeffs[4])
r_un = np.tan(theta_pred)

x_un = r_un * x_dn/r_dn
y_un = r_un * y_dn/r_dn
print(x_un * 0.8, y_un* 0.8, 0.8)
# -0.5598187209024351 -0.3704357318598599 0.8

• 이 값 또한 \((X_{c}, Y_{c}, Z_{c}) = (-0.56, -0.37, 0.8)\) 와 유사한 것을 확인할 수 있습니다.

• 지금 까지 확인한 방법을 통하여 Fisheye Camera와 같은 렌즈 왜곡이 큰 영상에서도 Generic Camera Model을 이용하여 3D → 2D Projection과 2D → 3D Unprojection 사용이 가능함을 확인하였습니다.
• 다음에 확인할 내용은 intrinsic과 distortion coefficient를 이용하여 카메라 렌즈 왜곡을 보정하여 perspective view 영상을 만드는 방법에 대하여 알아보도록 하겠습니다.

왜곡된 영상의 왜곡 보정의 필요성과 단점

• 왜곡 보정은 카메라 렌즈 왜곡으로 앞에서 다룬 Barrel Distortion 이나 Pincushion Distortion과 같은 카메라 왜곡이 발생하여 생기는 영상 내 비선형성을 제거하거자 하는 목적으로 사용됩니다. 즉, 실제 직선 성분을 영상에서도 직선 성분으로 만들어 Perspective View 형태의 영상으로 만드는 작업을 의미합니다.
• 핀홀 카메라 모델에서는 창문, 차선, 도로 경계, 건물 끝 부분과 같이 실제 직선 성분은 영상에서 또한 직선으로 표현됩니다. 반면 렌즈 왜곡이 발생한 이미지에서는 직선이 휘어져서 보이게 됩니다.
• 이와 같은 왜곡이 발생하게 되면 컴퓨터 비전에서 사용하는 다양한 알고리즘이나 가정들을 사용할 수 없게 됩니다. 왜냐하면 선형 변환의 가정을 사용하기 어렵기 때문입니다. 특히 Multiple View Geometry와 같이 여러 카메라 간의 관계를 정의할 때, 선형 변환의 관계를 이용하는 데, 카메라 렌즈 왜곡이 발생하면 이 때 사용하는 알고리즘을 사용할 수 없습니다.
• 뿐만 아니라 다양한 연구들 또한 렌즈 왜곡이 없는 영상에서 이루어지기 때문에 연구 결과를 이용하는 것에도 어려움이 발생합니다. (다양한 연구들 또한 이러한 왜곡을 없애기 위해 사전에 왜곡 보정 작업을 진행합니다.) 렌즈 왜곡이 없는 상황에서 연구가 진행되어야 알고리즘의 성능 평가가 용이해 지기 때문입니다.

• 정리하면 왜곡 보정을 하였을 때 얻을 수 있는 대표적인 장점은 다음과 같습니다.
• ① 영상을 핀홀 카메라 모델의 perspective view 처럼 만들어서 선형 변환의 성질을 이용할 수 있습니다.
• ② perspective view 기반에서는 렌즈 왜곡이 없다고 가정하기 때문에 사용하고자 하는 알고리즘이 간단해 질 수 있습니다.
• ③ perspective view를 기반으로 개발된 다양한 알고리즘과 최신 연구들을 이용할 수 있습니다.

• 반면 렌즈 왜곡을 하면 대표적으로 다음 3가지 문제가 발생할 수 있습니다.
• ① 렌즈 왜곡에 필요한 카메라 intrinsic, distortion coefficient에 따라 왜곡 보정의 결과가 달라질 수 있습니다. 따라서 카메라 캘리브레이션 결과에 민감합니다.
• ② 왜곡 보정을 하기 위한 추가적인 연산이 필요합니다. 실시간으로 동작해야 하는 기능에서는 이 부분이 고려되어야 합니다.
• ③ 영상에서 정보가 손실되는 영역이 발생합니다. 손실 영역이라고 하면 크게 2종류가 발생합니다. 첫번째는 잘려가나가 하는 영역이 발생하는 것이고 두번째는 픽셀 해상도가 줄어드는 점입니다.

• 위 단점 중 ① 캘리브레이션 관련 문제와 ② 연산 문제는 현재 큰 문제가 되지 않습니다. 캘리브레이션 관련 문제 또한 많은 연구 및 개선이 되어 안정적으로 왜곡 보정을 적용할 수 있고 연산 문제는 하드웨어의 발전으로 실시간으로 처리하는 데 문제가 없습니다.
• 하지만 ③ 정보 손실 문제는 왜곡 보정을 해야 하는 지 결정해야 할 만큼 중요한 문제로 남아있습니다. 앞에서 언급한 2가지 문제인 영역 손실 문제와 해상도 손실 문제에 대하여 살펴 보도록 하겠습니다.

왜곡 보정 방법

• 영상 왜곡 보정 방법은 intrinsic 파라미터와 Distortion Coefficient의 역할 및 카메라 모델의 동작 방식을 이해하면 손쉽게 구할 수 있습니다.
• 이번에는 왜곡 보정의 방법에 대하여 간단하게 살펴보고 실습해 보도록 하겠습니다. 이 글의 뒷부분에서 다루는 내용은 왜곡 보정의 원리를 이해한 뒤 opencv 함수를 이용하여 사용하는 내용입니다. opencv에서도 잘 최적화된 방식으로 구현되어 있기 때문에 원리만 이해하고 실제 사용은 opencv 함수를 사용하시면 됩니다.

• 왜곡 보정영상은 다음 그림과 같이 Barrel Distortion이나 Pincushion Distortion에서 나타나는 왜곡을 보정하여 직선이 영상에서도 그대로 직선으로 보일 수 있도록 합니다.

• 왜곡 보정하는 방법은 앞의 글을 이해하면 굉장히 간단합니다. 다음 절차를 통해 왜곡 보정을 진행할 수 있습니다.
• ① 왜곡 보정 영상의 사이즈 \((W, H)\) 를 임의로 정의합니다. \((W, H)\) 사이즈의 이미지에서 왜곡 보정 영상의 좌표를 \((u_{\text{undist}}, v_{\text{undist}})\) 로 가정하겠습니다.
• ② \((u_{\text{undist}}, v_{\text{undist}})\) 의 좌표를 intrinsic을 이용 (\(K^{-1}\))하여 \((x_{\text{undist norm}}, y_{\text{undist norm}})\) 으로 변환합니다.
• ③ \((x_{\text{undist norm}}, y_{\text{undist norm}})\) 을 Distortion Coefficient를 이용하여 \((x_{\text{dist norm}}, y_{\text{dist norm}})\) 으로 변환합니다.
• ④ \((x_{\text{dist norm}}, y_{\text{dist norm}})\) 에 intrinsic을 반영하여 \((u_{\text{dist}}, v_{\text{dist}})\) 를 구합니다. \((u_{\text{dist}}, v_{\text{dist}})\) 는 왜곡된 영상의 좌표이므로 이 좌표의 RGB값을 접근합니다.
• ⑤ \((u_{\text{dist}}, v_{\text{dist}})\) 의 RGB 값을 왜곡 보정 영상의 \((u_{\text{undist}}, v_{\text{undist}})\) 좌표의 RGB로 대응하면 왜곡 보정된 영상을 구할 수 있습니다.

• 왜곡 보정의 방법은 위 5가지 스텝으로 나눌 수 있습니다. 왜곡 보정의 결과 가장 큰 특이점은 실제 공간 상의 직선이 영상에서도 직선으로 보인다는 점입니다.
• 아래 영상을 살펴보면 왼쪽의 왜곡이 적용된 영상과 위 5가지 스텝으로 왜곡 보정한 영상의 예시를 살펴볼 수 있습니다.

• 앞의 ① ~ ⑤ 순서에 맞게 왜곡 보정을 하는 방법을 코드를 통하여 살펴보도록 하겠습니다.

Generic 카메라 모델 왜곡 보정을 위한 mapping 함수 구하기

• 실습에 사용한 데이터는 아래 링크에서 받을 수 있습니다.
• Fisheye Camera : https://drive.google.com/drive/folders/1z7sp5Us95L_g7hVvcAvJ6Gn5V6bUOG12?usp=drive_link
• Standard Camera : https://drive.google.com/drive/folders/1_mvJNmO_6ZaA2dyRedgt8uwcRonDG89Z?usp=drive_link

• 앞에서 다룬 영상의 왜곡 보정 방법을 구현하면 다음과 같습니다. 앞의 설명과 같이 왜곡 보정이 된 좌표가 왜곡된 영상의 어떤 좌표와 대응되는 지 확인한 다음 그 좌표의 컬러 값을 가져와서 할당하면 왜곡 보정된 영상을 만들 수 있습니다.
• 아래 코드의 map_x와 map_y는 왜곡 보정된 영상의 특정 좌표 \((u_{\text{undist}}, v_{\text{undist}})\) 가 왜곡된 영상의 어떤 좌표값을 사용해야 하는 지, 대응시켜 놓은 LUT(Look Up Table)입니다. 예를 들어 map_x[u_undist][v_undist]는 왜곡 영상에서의 대응되는 \(u_{\text{dist}}\) 좌표를 의미하고 map_y[u_undist][v_undist]는 왜곡 영상에서의 대응되는 \(v_{\text{dist}}\) 좌표를 의미합니다. 따라서 (u_dist, v_dist) = (map_x[u_undist][v_undist], map_y[u_undist][v_undist])가 됩니다.

import cv2
import numpy as np

def get_map_xy(I_d, fx, fy, cx, cy, skew, k1, k2, k3, k4, k5):   
    
    h, w = I_d.shape[:2]
    I_u = np.zeros_like(I_d)
    map_x = np.zeros((h, w), dtype=np.float32)
    map_y = np.zeros((h, w), dtype=np.float32)
    
    for v_u in range(h):
        for u_u in range(w):
            # ① 왜곡 보정 영상의 좌표인 (u_u, v_u)를 정의 합니다.

            # ② (u_u, v_u)의 좌표를 intrinsic을 이용하여 (x_un, y_un)으로 변환합니다.
            y_un = (v_u - cy)/fy
            x_un = (u_u - skew*y_un - cx)/fx 
            
            # ③ (x_un, y_un)의 좌표를 Distortion Coefficient를 이용하여 (x_dn, y_dn)으로 변환합니다.
            r_un = np.sqrt(x_un**2 + y_un**2)
            theta = np.arctan(r_un)
            r_dn = k1*theta + k2*theta**3 + k3*theta**5 + k4*theta**7 + k5*theta**9
            
            x_dn = r_dn * (x_un/r_un)
            y_dn = r_dn * (y_un/r_un)
            
            # ④ (x_dn, y_dn)에 intrinsic을 반영하여 (u_d, v_d)를 구합니다.
            u_d = np.round(fx*x_dn + skew*y_dn + cx)
            v_d = np.round(fy*y_dn + cy)
            
            # ⑤ (u_d, v_d)의 RGB 값을 왜곡 보정 영상의 좌표 (u_ud, v_ud) 좌표의 RGB로 대응하면 왜곡 보정된 영상 I_u를 구할 수 있습니다.
            if 0 <= u_d < w and 0 <= v_d < h:
                I_u[int(v_u), int(u_u), :] = I_d[int(v_d), int(u_d), :]
            
            # ※ (u_u, v_u) 좌표를 이용하여 (u_d, u_v) 좌표를 구하고 싶을 때, Look Up Table인 map_x, map_y를 구하는 과정입니다.
            map_x[v_u, u_u] = u_d
            map_y[v_u, u_u] = v_d
            
    return I_u, map_x, map_y

# Sample Code to Test the Function
I_d = cv2.cvtColor(cv2.imread('./fisheye_camera_checkboard_10cm/fisheye_camera_calibration_test_10cm_01.png'), cv2.COLOR_BGR2RGB)

fx = K[0][0]
skew = K[0][1]
cx = K[0][2]

fy = K[1][1]
cy = K[1][2]

k1, k2, k3, k4, k5 = 1, D[0], D[1], D[2], D[3]
I_u, map_x, map_y = get_map_xy(I_d, fx, fy, cx, cy, skew, k1, k2, k3, k4, k5)

• 다음으로 앞의 코드에서 다룬 map_x, map_y 값을 opencv를 이용하여 구하는 방법에 대하여 알아보도록 하겠습니다. opencv 라이브러리의 fisheye 패키지(cv2.fisheye)를 이용하면 앞에서 다룬 generic camera model을 이용할 수 있습니다.
• 먼저 아래와 같이 estimateNewCameraMatrixForUndistortRectify 함수를 통해 현재 K, D, DIM 조건에서 balance 옵션에 따라 왜곡 보정을 하였을 때 대응되는 intrinsic matrix인 new_K를 추정할 수 있습니다. new_K는 궁극적으로 구하고자 하는 map_x, map_y를 구하기 위해 필요한 값이므로 먼저 이 값을 구해야 합니다.

DIM = (width, height)
new_K = cv2.fisheye.estimateNewCameraMatrixForUndistortRectify(K, D, DIM, np.eye(3), balance=0.0)

• 위 식에서 K와 D는 실제 캘리브레이션을 통해 얻은 값이며 DIM은 입력 이미지의 해상도를 의미합니다. 따라서 K, D, DIM은 주어진 값을 그대로 사용한다고 생각하면 됩니다.
• np.eye(3)은 영상을 생성할 때, Rotation에 해당하며 위 코드와 같이 Identity를 입력하면 Rotation을 고려하지 않습니다. Rotation을 사용하는 이유는 카메라의 방향(orientation)을 고려하여 왜곡 보정을 할 수 있기 때문입니다. 예를 들면 카메라의 방향이 바닥으로 치우쳐 있고 카메라의 방향이 지면과 비교하였을 때, 얼만큼 치우쳐(회전되어) 있는 지 알 수 있으면 그 만큼 Rotation을 반영하여 카메라의 방향 또한 보정된 왜곡 보정 영상을 얻을 수 있기 때문입니다. 즉, 일관된 카메라 방향의 왜곡 보정된 영상을 얻기 위함입니다. 이 값을 적용하기 위해서는 extrinsic parameter가 필요하므로 본 글에서는 무시하고 Identity를 사용하도록 하겠습니다.
• 마지막으로 balance는 영상의 왜곡 보정 정도를 결정하는 역할을 하며 범위는 0 ~ 1의 값을 가집니다. 만약 balance가 0이면 왜곡 보정 시 발생하는 불필요한 영역을 모두 제거할 수 있도록 유효한 영역만 확대하여 왜곡 보정된 영상을 가질 수 있도록 합니다. 반면 balance가 1이면 왜곡 보정 이전의 모든 픽셀을 유지한 형태로 왜곡 보정을 하게 됩니다. 그 결과 유효하지 않은 영역 또한 모두 포함되도록 왜곡 보정된 영상을 얻게 됩니다.

• balance = 0.0인 왜곡 보정 영상은 영상의 왜곡 보정된 부분만 확대되어 표시되며 영상에 불필요한 영역은 없습니다. 다만, 필요 이상으로 영역이 제거된 것은 볼 수 있습니다.
• balance = 1.0인 왜곡 보정 영상은 원본 Fisheye Camera 영상의 모든 픽셀을 유지한 상태로 왜곡 보정이 된 것을 볼 수 있습니다. 그 결과 왜곡 보정 중 발생한 유효하지 않은 영역도 모두 포함된 것을 확인할 수 있습니다.
• balance = 0.5인 경우 유효하지 않은 영역을 조금 포함하면서 적당한 이미지 영역을 포함한 것을 볼 수 있습니다.
• 실제로 balance = 0.0인 경우는 balance = 1.0인 경우에서 필요한 영역만 crop한 후 resize하여 확대한 것과 동일합니다. 예를 들면 다음과 같습니다. (이미지가 약간 흐린 것은 이미지 편집 중 발생한 것일 뿐입니다.)

• 즉, balance는 내가 어떤 영역을 사용할 지에 대한 옵션이며 balance가 큰 값을 사용한 상태에서 유효한 영역만 crop한 후 resize 하면 balance가 작은 값을 생성해 낼 수 있습니다.
• balance가 작은 값을 사용하였을 때, 유효 영역만 확대하여 보여주는 것이므로 new_K인 intrinsic matrix는 balance가 작을 때 더 큰 fx, fy 값을 가지게 됩니다. 다음 예시를 참조해 보면 됩니다.

# K (origin intrinsic)
[[567.85821196   0.         960.58762478]
 [  0.         567.33818371 516.27957345]
 [  0.           0.           1.        ]]

# new K (balance = 0.0)
[[406.80006567   0.         957.83223697]
 [  0.         406.42752985 600.24992824]
 [  0.           0.           1.        ]]

# new K (balance = 1.0)
[[ 47.0625702    0.         959.74921218]
 [  0.          47.01947165 546.97029503]
 [  0.           0.           1.        ]]

• 위에서 구한 new_K는 왜곡 보정을 위한 초깃값 정도로 생각하시면 됩니다. 이 값을 기준으로 원하는 크기, 영역을 추가적으로 구할 수 있기 때문입니다.
• 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습에서 소개한 바와 같이 intrinsic matrix는 마치 창 (window)과 같습니다. 창 밖에 실제 존재하는 값들이 존재하고 어떤 영역에 창을 만들어서 존재하는 값들을 이미지로 형상화 하여 볼 지 결정만 하면 되기 때문입니다. 즉, balance = 0.0으로 설정하여 유효한 영역 및 특정 크기의 창이 생성되도록 new_K가 도출되었다 하더라도 new_K 값을 임의로 조정하면 원하는 영역 또는 원하는 크기의 왜곡 보정 영상을 생성하여 볼 수 있습니다. 즉, 최종적으로 opencv함수를 이용하여 map_x, map_y를 구할 때, new_K 값을 조절하여 원하는 크기의 이미지를 원하는 영역 만큼만 구체적으로 정하여 왜곡 보정을 할 수 있습니다.

• 따라서 cv2.fisheye.estimateNewCameraMatrixForUndistortRectify 함수를 사용할 때에는 다음과 같은 옵션 조건을 기본값으로 사용하고 추가적으로 원하는 크기와 ROI를 조정하는 방식을 사용하면

K # 카메라 calibration을 통해 구한 intrinsic
D # 카메라 calibration을 통해 구한 distortion
DIM # 원본 이미지의 해상도
balance = 0.0

DIM = (width, height)
new_K = cv2.fisheye.estimateNewCameraMatrixForUndistortRectify(K, D, DIM, np.eye(3), balance=0.0)

• 그러면 원하는 크기와 ROI를 고려하여 map_x, map_y를 만드는 방법을 살펴보도록 하겠습니다. 살펴볼 순서는 다음과 같습니다.
• ① resize ratio : resize ratio를 이용하면 왜곡 보정된 영상의 크기를 조정할 수 있습니다. 기본값으로 원본과 동일한 크기의 영상을 만드는 new_K를 생성하였기 때문에 영상의 가로/세로 각각의 크기를 원본과 다르게 만들고 싶으면 resize ratio를 통하여 조정할 수 있습니다. 앞의 비유를 이용하면 resize ratio를 통하여 창문의 크기를 정한것이라고 볼 수 있습니다.

• ② x/y translation : 영상의 좌상단인 원점의 위치를 조정할 수 있습니다. 영상의 크기는 정해져 있기 때문에 영상의 좌상단의 위치를 정하면 그 위치부터 원하는 영역을 볼 수 있습니다. 비유를 하면 창문의 시작 위치를 정한다는 것으로 볼 수 있습니다.

• ③ bottom/right crop : 영상의 좌상단 부분은 원하는 위치를 정한 상태입니다. 반면 영상의 하단과 우측 부분에서 불필요한 영역이 있다면 제거를 해야 합니다. 비유를 하면 창문의 하단 부분과 우측 끝 부분 중 필요 없다고 판단되는 부분을 자르는 것입니다.

• 위 비유를 통하여 new_K를 조작하는 방법에 대하여 살펴보도록 하겠습니다.

① resize ratio

• 앞의 함수를 통해 구한 new_K 값은 다음과 같습니다.

[[406.80006567   0.         957.83223697]
 [  0.         406.42752985 600.24992824]
 [  0.           0.           1.        ]]

• 1행에 resize_ratio만큼 곱하면 이미지의 가로 길이가 조정되고 2행에 resize_ratio만큼 곱하면 이미지의 세로 길이가 조정 됩니다. 이와 관련된 내용은 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습에서 확인할 수 있습니다. 방법은 다음과 같습니다.

resize_ratio = 0.5

# resize window size
new_K[0, :] *= resize_ratio
new_K[1, :] *= resize_ratio

# [[203.40003283   0.         478.91611849]
#  [  0.         203.21376492 300.12496412]
#  [  0.           0.           1.        ]]

• 위 그림의 결과와 같이 왜곡 보정 결과는 같지만 해상도가 다른 두 이미지를 얻을 수 있습니다. 즉 가로, 세로 이미지의 크기를 조절하여 new_K에 적용하면 원하는 크기의 왜곡 보정 영상을 얻을 수 있습니다.

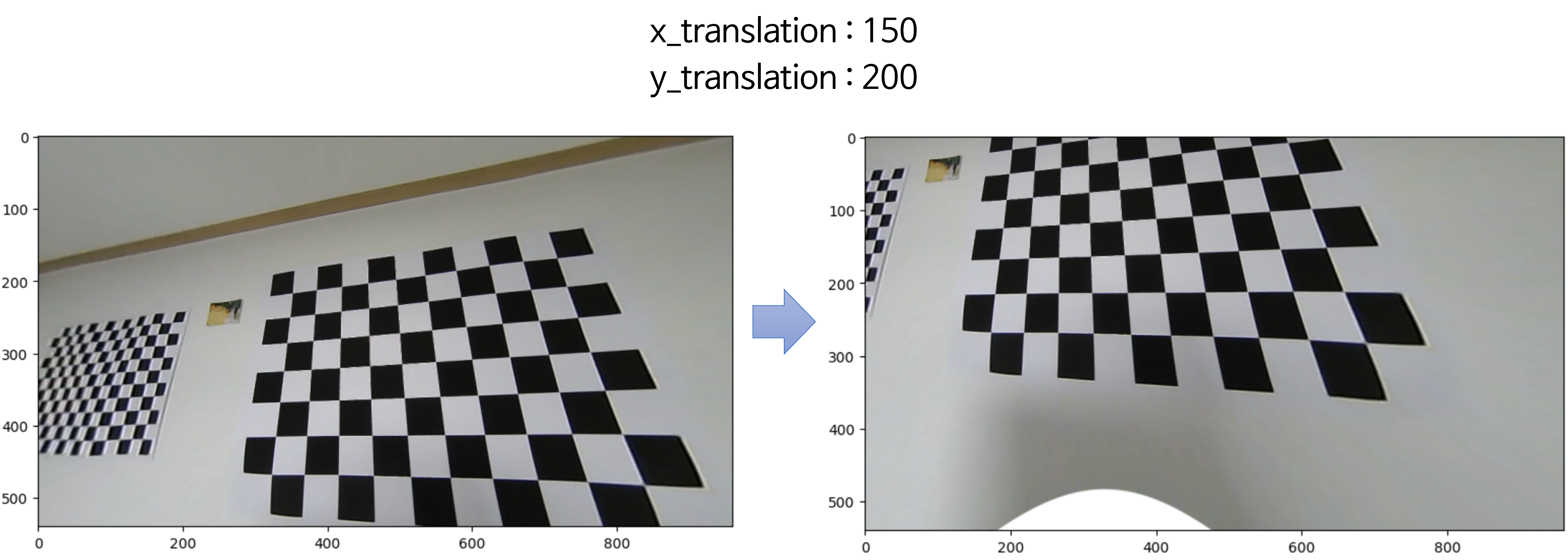
② x/y translation

• 이번에는 x/y translation을 적용해 보도록 하겠습니다.

# translation with resized window
x_translation = 150
y_translation = 200

new_K[0][2] -= x_translation
new_K[1][2] -= y_translation

# [[203.40003283   0.         328.91611849]
#  [  0.         203.21376492 100.12496412]
#  [  0.           0.           1.        ]]

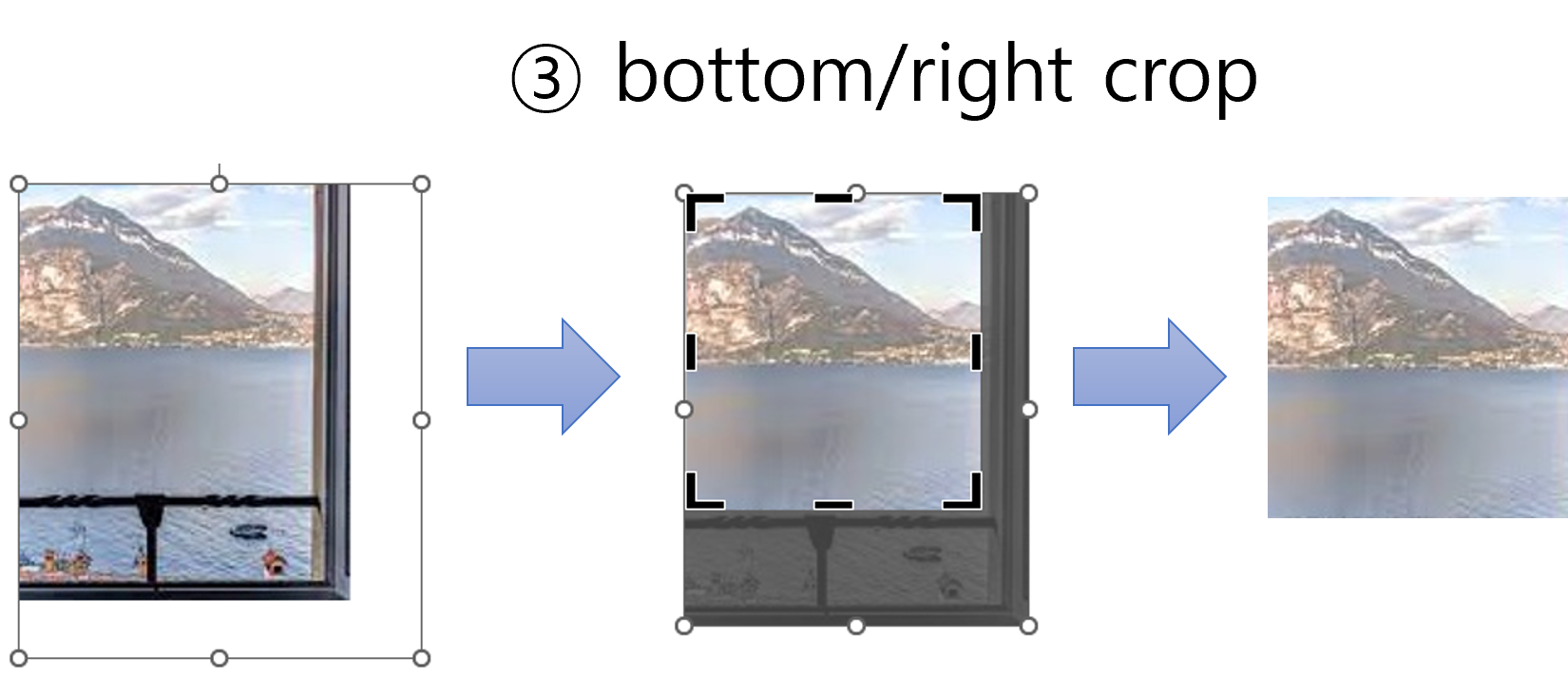
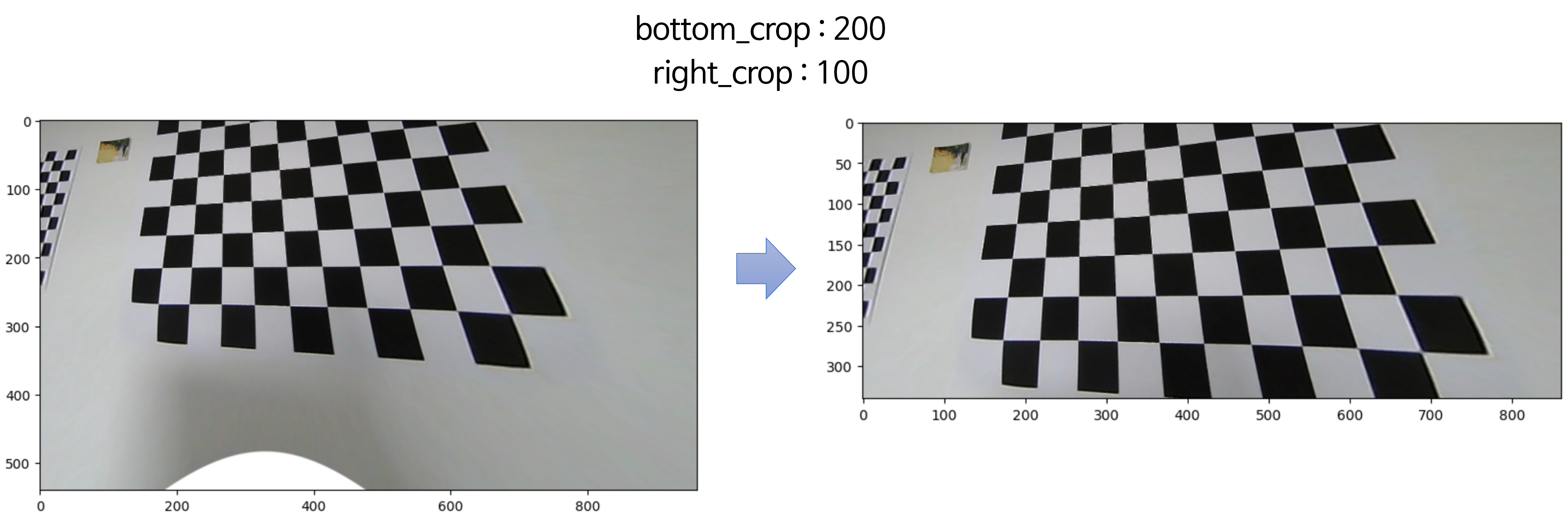
③ bottom/right crop

• 마지막으로 우측과 하단에 불필요한 영역을 제거해 보도록 하겠습니다. 아래와 같이 최종 DIM 크기를 정해주면 됩니다.

bottom_crop = 200 # ③ crop bottom area in resized image
right_crop = 100 # ③ crop right area in resize image

# crop bottom & right in resized window
new_DIM = (int(width*resize_ratio)-right_crop, int(height*resize_ratio)-bottom_crop)

• 지금까지 살펴본 내용을 통하여 new_K와 new_DIM을 정의하였고 다음 함수식을 통하여 map_x, map_y를 생성할 수 있습니다.

map_x, map_y = cv2.fisheye.initUndistortRectifyMap(K, D, np.eye(3), new_K, new_DIM, cv2.CV_32FC1)
# map_x.shape : (result_height, result_width)
# map_y.shape : (result_height, result_width)

• 지금까지 살펴본 내용을 모두 집합해 보도록 하겠습니다. 최종적으로 아래 코드를 이용하여 원하는 이미지의 해상도와 영역을 설정하여 왜곡 보정할 수 있습니다.
• 앞의 설명과 같이 ① resize_ratio 를 이용하여 왜곡 보정된 이미지의 사이즈를 결정하고 ② x_translation, y_translation을 이용하여 리사이즈된 이미지의 좌상단 원점의 시작점을 결정 후 ③ 최종적으로 필요없다고 판단되는 아랫 부분과 우측 부분 영역을 bottom_crop과 right_crop 만큼 잘라내어 원하는 크기와 영역의 왜곡 보정 영상을 얻을 수 있습니다.

img = cv2.cvtColor(cv2.imread('./fisheye_camera_checkboard_10cm/fisheye_camera_calibration_test_10cm_01.png'), cv2.COLOR_BGR2RGB)
height, width = img.shape[:2]
DIM = (width, height)
new_K = cv2.fisheye.estimateNewCameraMatrixForUndistortRectify(K, D, DIM, np.eye(3), balance=0.0)

# ① set image resolution ratio
# ② set window starting point
# ③ crop unnecessary areas

resize_ratio = 1.0 # ① height/width resize ratio
x_translation = 0 # ② select top position in resized image
y_translation = 0 # ② select left start position in resized image
bottom_crop = 0 # ③ crop bottom area in resized image
right_crop = 0 # ③ crop right area in resize image

# resize window size
new_K[0, :] *= resize_ratio
new_K[1, :] *= resize_ratio

# translation with resized window
new_K[0][2] -= x_translation    
new_K[1][2] -= y_translation    

# crop bottom & right in resized window
new_DIM = (int(width*resize_ratio)-right_crop, int(height*resize_ratio)-bottom_crop)
map_x, map_y = cv2.fisheye.initUndistortRectifyMap(K, D, np.eye(3), new_K, new_DIM, cv2.CV_16SC2)

# remap 함수는 아래 글에서 설명 예정
undistorted_img = cv2.remap(img, map_x, map_y, interpolation=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=(255, 255, 255))

Generic 카메라 모델 remap을 이용한 왜곡 영상 → 왜곡 보정 영상

• 앞에서 살펴본 바와 같이 map_x, map_y는 왜곡 보정된 영상의 특정 좌표 \((u_{\text{undist}}, v_{\text{undist}})\) 가 왜곡된 영상의 어떤 좌표값을 사용해야 하는 지, 대응시켜 놓은 LUT(Look Up Table)입니다.
• map_x, map_y를 opencv의 remap 함수와 같이 사용하면 mapping을 쉽게 할 수 있으므로 왜곡 보정 영상을 생성할 수 있습니다.
  • OpenCV remap 함수 사용 방법

undistorted_img = cv2.remap(img, map_x, map_y, interpolation=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=(255, 255, 255))

• 위 코드에서 interpolation을 사용하는 이유는 mapping 되지 않는 픽셀을 근처 값들을 이용하여 채우기 위함입니다. 일반적으로 bilinear interpolation을 사용합니다. 생성되는 영상의 품질도 나쁘지 않으면서 연산 효율이 좋기 때문입니다.
• borderMode와 borderValue는 왜곡 보정 이후 값이 완전히 없는 영역은 특정 상수 값으로 채우거나 다른 특수한 방식으로 채우기 위함입니다. 일반적으로 상수값을 넣어서 왜곡 보정 시 생성될 수 없는 영역임을 명시적으로 표현합니다.

• 만약 opencv의 remap 함수를 사용하지 않고 별도 구현해서 사용하려면 아래 코드를 이용할 수 있습니다.
• 실제 opencv의 remap과는 결과가 완전 동일하지 않습니다. 하지만 biliear interpolation의 개념에 맞게 구현한 것으로 시각적인 차이는 없음을 확인하였습니다.

def bilinear_sampler(imgs, pix_coords):
    """
    Construct a new image by bilinear sampling from the input image.
    Args:
        imgs:                   [H, W, C]
        pix_coords:             [h, w, 2]
    :return:
        sampled image           [h, w, c]
    """
    img_h, img_w, img_c = imgs.shape
    pix_h, pix_w, pix_c = pix_coords.shape
    out_shape = (pix_h, pix_w, img_c)

    pix_x, pix_y = np.split(pix_coords, [1], axis=-1)  # [pix_h, pix_w, 1]
    pix_x = pix_x.astype(np.float32)
    pix_y = pix_y.astype(np.float32)

    # Rounding
    pix_x0 = np.floor(pix_x)
    pix_x1 = pix_x0 + 1
    pix_y0 = np.floor(pix_y)
    pix_y1 = pix_y0 + 1

    # Clip within image boundary
    y_max = (img_h - 1)
    x_max = (img_w - 1)
    zero = np.zeros([1])

    pix_x0 = np.clip(pix_x0, zero, x_max)
    pix_y0 = np.clip(pix_y0, zero, y_max)
    pix_x1 = np.clip(pix_x1, zero, x_max)
    pix_y1 = np.clip(pix_y1, zero, y_max)

    # Weights [pix_h, pix_w, 1]
    wt_x0 = pix_x1 - pix_x
    wt_x1 = pix_x - pix_x0
    wt_y0 = pix_y1 - pix_y
    wt_y1 = pix_y - pix_y0

    # indices in the image to sample from
    dim = img_w

    # Apply the lower and upper bound pix coord
    base_y0 = pix_y0 * dim
    base_y1 = pix_y1 * dim

    # 4 corner vertices
    idx00 = (pix_x0 + base_y0).flatten().astype(np.int32)
    idx01 = (pix_x0 + base_y1).astype(np.int32)
    idx10 = (pix_x1 + base_y0).astype(np.int32)
    idx11 = (pix_x1 + base_y1).astype(np.int32)

    # Gather pixels from image using vertices
    imgs_flat = imgs.reshape([-1, img_c]).astype(np.float32)
    im00 = imgs_flat[idx00].reshape(out_shape)
    im01 = imgs_flat[idx01].reshape(out_shape)
    im10 = imgs_flat[idx10].reshape(out_shape)
    im11 = imgs_flat[idx11].reshape(out_shape)

    # Apply weights [pix_h, pix_w, 1]
    w00 = wt_x0 * wt_y0
    w01 = wt_x0 * wt_y1
    w10 = wt_x1 * wt_y0
    w11 = wt_x1 * wt_y1
    output = w00 * im00 + w01 * im01 + w10 * im10 + w11 * im11
    return output

def remap_bilinear(image, map_x, map_y):
    pix_coords = np.concatenate([np.expand_dims(map_x, -1), np.expand_dims(map_y, -1)], axis=-1)
    bilinear_output = bilinear_sampler(image, pix_coords)
    output = np.round(bilinear_output).astype(np.int32)
    return output   

• 이와 같은 방법을 통하여 사전에 필요한 영역의 왜곡 보정 영상을 구하기 위한 map_x, map_y를 구한 후 remap을 이용하여 실시간으로 왜곡 보정된 영상을 구할 수 있습니다. 연산 관점에서 map_x, map_y를 구하는 과정에서 연산이 소요될 뿐 remap은 빠르게 연산할 수 있기 때문입니다.

Generic 카메라 모델 Pytorch를 이용한 왜곡 영상 → 왜곡 보정 영상

• 딥러닝 모델 학습에 카메라 왜곡 보정의 개념이 사용되어야 한다면 pytorch를 이용하여 카메라 왜곡 보정을 해야 합니다. 이와 같은 경우에는 map_x, map_y는 opencv 함수를 이용하여 사전에 구하고 pytorch에서는 remap함수의 역할을 하는 grid_sample을 이용하여 왜곡 보정 영상을 구할 수 있습니다.
  • F.grid_sample 사용 방법 참조

• 앞의 링크를 통해 grid_sample의 동작 방식을 이해하면 다음과 같이 코드를 사용해야 함을 이해할 수 있습니다.

import torch
import torch.nn.functional as F

print(img.shape)
# (1080, 1920, 3)
img_tensor = torch.from_numpy(img).to(dtype=torch.float32)
img_tensor = img_tensor.permute(2, 0, 1)
img_tensor = img_tensor.unsqueeze(0)
print(img_tensor.shape)
# torch.Size([1, 3, 1080, 1920])

map_x_tensor = torch.from_numpy(map_x) # (H, W)
map_y_tensor = torch.from_numpy(map_y) # (H, W)

print(map_x_tensor.max(), map_y_tensor.max())
# (tensor(1573.9301), tensor(981.9427))

grid = torch.stack((map_x_tensor, map_y_tensor), 2) # (H, W, 2)
grid = grid.unsqueeze(0) # (B=1, H, W, 2)
grid[:, :, :, 0] *= 2/(width-1)
grid[:, :, :, 0] -= 1
grid[:, :, :, 1] *= 2/(height-1)
grid[:, :, :, 1] -= 1

undist_img_tensor = F.grid_sample(img_tensor, grid, mode='bilinear', padding_mode='zeros', align_corners=True)
# (B=1, C, H, W) -> (C, H, W) -> (H, W, C)
undist_img_tensor = undist_img_tensor.squeeze().permute(1, 2, 0)
undist_img = undist_img_tensor.detach().cpu().numpy().astype(np.uint8)

• 위 코드에서 grid = torch.stack((map_x_tensor, map_y_tensor), 2)와 같이 grid를 구성한 이유는 링크의 설명과 같이 map_x_tensor가 \(x\) 좌표를 의미하고 map_y_tensor가 \(y\) 좌표를 의미하기 때문입니다. 따라서 샘플링할 좌표의 순서를 \(x, y\) 순서로 구성한 다음 F.grid_sample을 사용하면 되므로 위 코드와 같이 사용할 수 있습니다.

Generic 카메라 모델의 왜곡 보정 시 변환 좌표 구하기

• 만약 왜곡 영상에서의 임의의 좌표 \((u_{\text{dist}}, v_{\text{dist}})\) 를 왜곡 보정하였을 때, 어떤 점으로 변환되는 지 알고 싶다면 어떻게 할 수 있을까요? 이 방법에 대하여 살펴보도록 하겠습니다.
• 앞에서 살펴본 방식은 왜곡 보정된 영상의 공간을 마련해 놓고 왜곡 영상의 좌표를 끌어와서 채우는 방법을 사용하였습니다. 이와 같은 방식으로 왜곡 보정 영상을 만들면 구멍이 생기지 않도록 깔끔하게 왜곡 보정 영상을 만들 수 있습니다.
• 관점을 전환하여 왜곡 영상의 임의의 좌표 \((u_{\text{dist}}, v_{\text{dist}})\) 가 왜곡 보정되었을 때 어느 좌표로 변환되는 지 직접적으로 알 수 있도록 LUT (Look Up Table)를 구성해 놓는다면 모든 픽셀을 왜곡 보정하지 않고 특정 원하는 픽셀들만 왜곡 보정한 위치로 옮겨서 사용할 수 있습니다. 만약 왜곡 영상에서 이미지의 feature를 추출하고 사용할 때, perspective view와 같은 선형 변환의 성질을 이용하기 위해 feature들을 왜곡 보정한 영역에 두고 사용한다면 이와 같은 방법이 적합할 수 있습니다.
• LUT를 만들기 위해 좌표 변환을 진행하는 순서는 다음과 같습니다.
  • ① \((u_{\text{dist}}, v_{\text{dist}})\)
  • ② distorted normalized coordinate
  • ③ undistorted normalized coordinate
  • ④ \((u_{\text{undist}}, v_{\text{undist}})\)
• 위 좌표에서 ① 과 ④의 관계를 대응시키는 LUT를 생성하면 좌표가 어떻게 변하는 지 한번에 알 수 있습니다. 만약 원본 이미지의 RGB값을 바로 대응시키면 왜곡 보정된 이미지를 얻을 수 있습니다.

from scipy.optimize import root_scalar

def f_theta_pred(theta_pred, r, k0, k1, k2, k3, k4):
    return k0*theta_pred + k1*theta_pred**3 + k2*theta_pred**5 + k3*theta_pred**7 + k4*theta_pred**9 - r

def f_theta_pred_prime(theta_pred, r, k0, k1, k2, k3, k4):
    return k0 + 3*k1*theta_pred**2 + 5*k2*theta_pred**4 + 7*k3*theta_pred**6 + 9*k4*theta_pred**8

def rdn2theta(x_dn, y_dn, k0, k1, k2, k3, k4):
    r_dn = np.sqrt(x_dn**2 + y_dn**2)
    theta_init = np.arctan(r_dn)

    # newton-method
    result = root_scalar(
        f_theta_pred, 
        args=(r_dn, k0, k1, k2, k3, k4), 
        method='newton', 
        x0=theta_init, 
        fprime=f_theta_pred_prime
    )
    
    theta_pred = result.root    
    r_un = np.tan(theta_pred)
    x_un = r_un * (x_dn / r_dn)
    y_un = r_un * (y_dn / r_dn)
    return x_un, y_un, r_dn, theta_pred

# ① (u_dist, v_idst)와 ④ (u_undist, v_undist) 관계를 대응시킨 LUT
lut = np.zeros((img.shape[0], img.shape[1], 2)).astype(np.float32)
for u_d in range(img.shape[1]):
    for v_d in range(img.shape[0]):
        y_dn = (v_d - cy)/fy
        x_dn = (u_d - skew*y_dn - cx)/fx
        x_un, y_un, r_dn, theta_pred = rdn2theta(x_dn, y_dn, k1, k2, k3, k4, k5)

        u_u = np.round(fx*x_un + skew*y_un + cx)
        v_u = np.round(fy*y_un + cy)

        lut[v_d][u_d][0] = u_u
        lut[v_d][u_d][1] = v_u

# LUT를 이용하여 왜곡 보정 이미지를 구하는 과정
undistorted_image = np.zeros((img.shape[0], img.shape[1], 3)).astype(np.uint8)
for u_d in range(img.shape[1]):
    for v_d in range(img.shape[0]):
        u_u = int(lut[v_d][u_d][0])
        v_u = int(lut[v_d][u_d][1])
        if (0 <= u_u) and (u_u < img.shape[1]) and (0 <= v_u) and (v_u < img.shape[0]):
            undistorted_image[v_u, u_u] = img[v_d, u_d]

• 지금부터는 World-to-Image, Image-to-World 방법에 대하여 알아보도록 하겠습니다. 아래 내용을 이해하기 위해서는 카메라 Extrinsic 캘리브레이션에 대한 개념을 명확히 이해하고 있어야 합니다.
  • 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습
• 아래 내용은 카메라 외부에 원점을 정하고 이 원점 기준의 좌표계를 World 좌표계라고 정하였을 때, World 좌표계의 임의의 3차원 점을 Image에 투영하는 방법과 Image의 특정 좌표를 다시 World 좌표계의 3차원 점으로 변환하는 방법에 대하여 다룹니다. (물론 3차원 좌표를 모두 복원하는 것은 불가능하여 좌표 하나는 고정시킵니다.)
• 본 글의 앞부분에서 다룬 Generic 카메라 모델 3D → 2D 및 2D → 3D python 실습 내용은 카메라 좌표 → 이미지 좌표 또는 이미지 좌표 → 카메라 좌표로의 2D, 3D 변환인것에 반해 이번에 사용하는 World-to-Image, Image-to-World는 카메라 외부 환경과의 2D, 3D 변환인 것에 차이점이 있습니다.

World-to-Image, Image-to-World 실습 환경

• 이번 실습에 사용할 환경은 다음과 같습니다. 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습에서 다룬 실험 데이터 입니다. 자세한 내용은 링크를 참조해 보시면 됩니다.

• 위 데이터에서 빨간/파란/초록색 축이 이 각각 \(X, Y, Z\) 축을 의미하며 World 좌표에서의 원점이 됩니다.
• 실제 카메라는 상자 위에 설치하였으며 카메라의 World 좌표 상 위치가 \((X, Y, Z) = (-0.25, 0, 0.53)\) 가 됩니다.

• 실습에 사용할 캘리브레이션 값은 다음 링크의 파일을 사용할 예정입니다.
  • 캘리브레이션 파일 링크
  • 캘리브레이션 파일 내용 설명

calib = {'ELP-USB16MP01-BL180-2048x1536': 
    {
        'Extrinsic': 
            {'Camera': 
                {'World': 
                    {
                        'R': [0.00463, -0.01405, 0.99989, -0.99998, -0.00391, 0.00457, 0.00385, -0.99989, -0.01407],
                        't': [-0.23687, -0.00677, 0.52937]}
                },
            'World': 
                {'Camera': 
                    {
                        'R': [0.00463, -0.99998, 0.00385, -0.01405, -0.00391, -0.99989, 0.99989, 0.00457, -0.01407],
                        't': [-0.00771, 0.52596, 0.24432]}}
            },
        'Intrinsic': 
            {
                'D': [1.0, -0.03688, -0.00783, 0.00217, -0.00079],
                'K': [631.65112, 0.0, 1042.45127, 0.0, 631.16614, 847.332, 0.0, 0.0, 1.0],
                "H": 1536,
                "W": 2048,
                'ReprojectionError': 0.08894
            },
        'Position': [-0.23687, -0.00677, 0.52937]
    }
}

# Active Rotation of World → Camera
R = np.array(calib['ELP-USB16MP01-BL180-2048x1536']['Extrinsic']['World']['Camera']['R']).reshape(3, 3)
# Active Translation of World → Camera
t = np.array(calib['ELP-USB16MP01-BL180-2048x1536']['Extrinsic']['World']['Camera']['t']).reshape(3, 1)

# Camera Intrinsic Parameter
K = np.array(calib['ELP-USB16MP01-BL180-2048x1536']['Intrinsic']['K']).reshape(3, 3)
# Distortion Coefficient of Generic Camera Model
D = np.array(calib['ELP-USB16MP01-BL180-2048x1536']['Intrinsic']['D'])

World-to-Image 방법

• World-to-Image는 World 좌표의 임의의 점을 Image에 투영하였을 때, 어떤 좌표에 투영되는 지 확인하는 방법입니다. 즉, World 좌표계에서의 어떤 점이 좌표 변환을 통하여 World 좌표계 → 카메라 좌표계 → 이미지 좌표계로 좌표를 변환하면 최종적으로 이미지 좌표계에서 좌표값을 확인할 수 있습니다.
• World 좌표계 → 카메라 좌표계로 좌표 변환을 할 때에는 Extrinsic 파라미터인 Rotation, Translation 이 사용되고 카메라 좌표계 → 이미지 좌표계로 좌표 변환을 할 때에는 앞에서 다룬 것과 같이 Intrinsic과 Distortion 계수가 사용됩니다.
• 이 때, World 좌표계 → 카메라 좌표계로 좌표 변환은 3D → 3D 좌표 변환인 반면에 카메라 좌표계 → 이미지 좌표계는 3D → 2D 좌표 변환으로 깊이 방향의 Dimension이 사라지는 것을 확인할 수 있었습니다. 이러한 이유로 아래 글에서 다룰 Image-to-World 즉, 이미지 좌표계에서 World 좌표계로 변환하는 과정에서는 1개의 Dimension의 값을 상수로 고정하는 방법을 사용합니다.

• 아래 코드를 통하여 World 좌표계의 점들을 이미지에 투영한 후 영상에 표시해 보도록 하겠습니다. 사용한 이미지는 다음과 같습니다.
  • 링크: https://drive.google.com/file/d/1vPtXlWT4mj6Qcz9QOa45-kOzMzTOKXi2/view?usp=sharing
• World 좌표계는 ISO 8855-2011에 따라 다음과 같습니다. 카메라 좌표계와 비교해서 보시기 바랍니다.

R = np.array(calib['ELP-USB16MP01-BL180-2048x1536']['Extrinsic']['World']['Camera']['R']).reshape(3, 3)
t = np.array(calib['ELP-USB16MP01-BL180-2048x1536']['Extrinsic']['World']['Camera']['t']).reshape(3, 1)

K = np.array(calib['ELP-USB16MP01-BL180-2048x1536']['Intrinsic']['K']).reshape(3, 3)
D = np.array(calib['ELP-USB16MP01-BL180-2048x1536']['Intrinsic']['D'])

fx = K[0][0]
skew = K[0][1]
cx = K[0][2]
fy = K[1][1]
cy = K[1][2]

k0, k1, k2, k3, k4 = D

image = cv2.cvtColor(cv2.imread("world2image_image2_world_sample.png", -1), cv2.COLOR_BGR2RGB)
for i in range(10):
    # world 좌표계 기준의 점 (X_w, Y_w, Z_w)
    X_w = 0.0 + (i * 0.05)
    Y_w = 0.0
    Z_w = 0.04
    
    # Camera 좌표계 기준의 점 (X_c, Y_c, Z_c)
    X_c, Y_c, Z_c = R @ np.array([X_w, Y_w, Z_w]).reshape(3, 1) + t
    #################### undistorted normalized coordinate ######################
    x_un = X_c / Z_c
    y_un = Y_c / Z_c
    
    #################### distorted normalized coordinate ########################
    r_un = np.sqrt(x_un**2 + y_un**2)
    theta = np.arctan(r_un)
    r_dn = 1*theta + k1*theta**3 + k2*theta**5 + k3*theta**7 + k4*theta**9
    
    x_dn = r_dn * (x_un/r_un)
    y_dn = r_dn * (y_un/r_un)
    
    ################################ image plane ###############################
    # Image 좌표계 기준의 점 (u, v)
    u = np.round(fx*x_dn + skew*y_dn + cx).astype(np.uint32)[0]
    v = np.round(fy*y_dn + cy).astype(np.uint32)[0]

    if i % 2 == 0:
        cv2.circle(image, (u, v), 4,  (0, 255, 0), -1);
        cv2.putText(image, f"({round(X_w, 2)}, {round(Y_w, 2)}, {round(Z_w, 2)})", (u + 10, v + 20), cv2.FONT_HERSHEY_COMPLEX_SMALL, 1.0, (0, 255, 0))
    else:
        cv2.circle(image, (u, v), 4, (255, 0, 255), -1);
        cv2.putText(image, f"({round(X_w, 2)}, {round(Y_w, 2)}, {round(Z_w, 2)})", (u - 150, v - 20), cv2.FONT_HERSHEY_COMPLEX_SMALL, 1.0, (255, 0, 255))

plt.figure(figsize=(15, 20))
plt.imshow(image)

• 위 체커보드의 간격은 0.05m이고 X_w의 좌표값을 0.05m 증가, Y_w의 좌표값을 0.05m 감소하면서 이미지에 투영해본 결과입니다.
• 카메라 캘리브레이션이 정상적으로 수행되었기 때문에, World-to-Image 가 정상적으로 진행된 것을 볼 수 있습니다.

• 체커보드 왼쪽에 높이 약 13cm 크기의 모형이 놓여있습니다. X_w, Y_w 값은 고정한 상태로 높이 값만 조절하면서 투영하였을 때에도 정상적으로 모형에 투영되는 것을 확인할 수 있습니다.

Image-to-World 방법

• Image-to-World는 Image 좌표의 임의의 점을 World에 역투영 하였을 떄, 어떤 좌표가 되는 지 확인하는 방법입니다. 앞에서 설명하였듯이 Image 좌표는 2D 좌표인 반면 Camera 좌표와 World 좌표는 3D 좌표입니다. 따라서 Image 좌표를 3D 좌표로 변환할 때에는 좌표값 하나를 고정해야 합니다.
• 이번 글에서는 World 좌표 중 Z_w를 고정하여 Image-to-World를 해보도록 하겠습니다. 반드시 Z_w를 고정할 필요는 없지만 Z_w의 값의 범위가 X_w, Y_w에 비하여 비교적 제한적이기 때문이고 Z_w를 상수값으로 고정한 후 X_w, Y_w를 이용하여 2D 좌표 평면을 그리면 Bird Eye View를 만들 수 있기 때문입니다. 이러한 이유로 Z_w를 고정하여 많이 사용합니다.
• 그러면 Z_w가 상수라는 가정하에 Image-to-World를 접근하는 방법의 수식을 살펴보도록 하겠습니다.

• \[R \cdot P_{\text{world}} + t = P_{\text{camera}}\]
• \[R \text{: Active Rotation From World to Camera.}\]
• \[t \text{: Active translation From World to Camera.}\]
• \[P_{w} = \begin{bmatrix} X_{w} & Y_{w} & Z_{w} \end{bmatrix}^{T} \text{: A Point in World Coordinate System.}\]
• \[P_{c} \begin{bmatrix} X_{c} & Y_{c} & Z_{c} \end{bmatrix}^{T} text{: A Point in Camera Coordinate System.}\]

• \[\begin{align} P_{\text{world}} = \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \end{bmatrix} &= R^{-1}(P_{\text{camera}} - t) = R^{T}(P_{\text{camera}} - t) \\ &= \begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix}^{T} \begin{bmatrix} X_{c} - t_{1} \\ Y_{c} - t_{2} \\ Z_{c} - t_{3} \end{bmatrix} \\ &= \begin{bmatrix} R_{11} & R_{21} & R_{31} \\ R_{12} & R_{22} & R_{32} \\ R_{13} & R_{23} & R_{33} \end{bmatrix} \begin{bmatrix} X_{c} - t_{1} \\ Y_{c} - t_{2} \\ Z_{c} - t_{3} \end{bmatrix} \end{align}\]
• \[\Rightarrow \begin{bmatrix} R_{13} & R_{23} & R_{33} \end{bmatrix} \begin{bmatrix} X_{c} - t_{1} \\ Y_{c} - t_{2} \\ Z_{c} - t_{3} \end{bmatrix} = Z_{w} \quad \text{(Used Thrid Row)}\]
• \[\Rightarrow R_{13}(X_{c} - t_{1}) + R_{23}(Y_{c} - t_{2}) + R_{33}(Z_{c} - t_{3}) = Z_{w}\]

• \[Z_{w} \text{: constant.}\]
• \[X_{c} = Z_{c} \cdot x_{\text{u.n.}} \quad \text{(u.n.: undistorted normalized.)}\]
• \[Y_{c} = Z_{c} \cdot y_{\text{u.n.}} \quad \text{(u.n.: undistorted normalized.)}\]

• 위 식에서 \(X_{c}, Z_{c}\) 를 구할 때, \(Z_{c}\) 는 depth 값이며 Generic 카메라 모델 3D → 2D 및 2D → 3D python 실습에서 관련 내용을 다루었습니다.

• \[\therefore R_{13}(X_{c} - t_{1}) + R_{23}(Y_{c} - t_{2}) + R_{33}(Z_{c} - t_{3}) = Z_{w}\]
• \[\Rightarrow R_{13}(Z_{c} \cdot x_{\text{u.n.}} - t_{1}) + R_{23}(Z_{c} \cdot y_{\text{u.n.}} - t_{2}) + R_{33}(Z_{c} - t_{3}) = Z_{w}\]
• \[\Rightarrow Z_{c}(R_{13} \cdot x_{\text{u.n.}} + R_{23} \cdot y_{\text{u.n.}} + R_{33}) = (Z_{w} + R_{13} \cdot t_{1} + R_{23} \cdot t_{2} + R_{33} \cdot t_{3})\]
• \[\therefore Z_{c} = \frac{Z_{w} + R_{13} \cdot t_{1} + R_{23} \cdot t_{2} + R_{33} \cdot t_{3}}{R_{13} \cdot x_{\text{u.n.}} + R_{23} \cdot y_{\text{u.n.}} + R_{33}}\]

• 위 식과 같이 \(Z_{w}\) 를 특정 상수 값으로 고정하면 \(X_{c}, Y_{c}, Z_{c}\) 는 다음과 같이 구할 수 있습니다.

• \[\begin{bmatrix} X_{c} \\ Y_{c} \\ Z_{c} \end{bmatrix} = \begin{bmatrix} Z_{c} \cdot x_{\text{u.n.}} \\ Z_{c} \cdot y_{\text{u.n.}} \\ \frac{Z_{w} + R_{13} \cdot t_{1} + R_{23} \cdot t_{2} + R_{33} \cdot t_{3}}{R_{13} \cdot x_{\text{u.n.}} + R_{23} \cdot y_{\text{u.n.}} + R_{33}} \end{bmatrix}\]

• 임의의 \((u, v)\) 좌표를 \((u, v) \to (x_{\text{d.n.}}, y_{\text{d.n.}}) \to (x_{\text{u.n.}}, y_{\text{u.n.}})\) 으로 변환하는 방법은 Generic 카메라 모델의 2D → 3D에서 다루었습니다. 이 부분에서의 핵심은 \(r_{\text{d.n}}\) 을 이용하여 \(\theta\) 을 구하는 점이었습니다.
• 아래 코드의 rdn2theta 함수를 이용하여 \(x_{\text{u.n.}}, y_{\text{u.n.}}\) 을 구하고 이 값을 통하여 Camera 좌표계의 좌표값을 구해보도록 하겠습니다.

def f_theta_pred(theta_pred, r, k0, k1, k2, k3, k4):
    return k0*theta_pred + k1*theta_pred**3 + k2*theta_pred**5 + k3*theta_pred**7 + k4*theta_pred**9 - r

def f_theta_pred_prime(theta_pred, r, k0, k1, k2, k3, k4):
    return k0 + 3*k1*theta_pred**2 + 5*k2*theta_pred**4 + 7*k3*theta_pred**6 + 9*k4*theta_pred**8

def rdn2theta(x_dn, y_dn, k0, k1, k2, k3, k4, max_iter=300, tol=1e-10):
    r_dn = np.sqrt(x_dn**2 + y_dn**2)
    theta_init = np.arctan(r_dn)

    # newton-method
    theta_pred = theta_init
    for _ in range(max_iter):        
        prev_theta_pred = theta_pred
        
        f_theta_value = f_theta_pred(theta_pred, r_dn, 1, k1, k2, k3, k4)
        f_theta_prime_value = f_theta_pred_prime(theta_pred, r_dn, 1, k1, k2, k3, k4)
        theta_pred = theta_pred - f_theta_value/f_theta_prime_value
        if np.abs(theta_pred - prev_theta_pred) < tol:
            break
    
    r_un = np.tan(theta_pred)
    x_un = r_un * (x_dn / r_dn)
    y_un = r_un * (y_dn / r_dn)
    return x_un, y_un, r_dn, theta_pred

def undist_norm2camera_coord(x_un, y_un, R, t, Z_w=0):
    Z_c = (Z_w + R[0, 2]*t[0] + R[1, 2]*t[1] + R[2, 2]*t[2]) / (R[0, 2]*x_un + R[1,2]*y_un + R[2, 2])
    X_c = Z_c * x_un
    Y_c = Z_c * y_un
    return X_c, Y_c, Z_c

Z_w = 0.04
u = 1032
v = 1507

y_dn = (v - cy)/fy
x_dn = (u - skew*y_dn - cx)/fx
x_un, y_un, r_dn, theta_pred = rdn2theta(x_dn, y_dn, 1, k1, k2, k3, k4)
X_c, Y_c, Z_c = undist_norm2camera_coord(x_un, y_un, R, t, Z_w)
P_c = np.array([X_c, Y_c, Z_c]).reshape(3, 1)
P_w = np.round(R.T@(P_c - t), 2)
print(f"X_w:{float(P_w[0])}, Y_w:{float(P_w[1])}, Z_w:{float(P_w[2])}")
# X_w:0.0, Y_w:0.0, Z_w:0.04

• 위 이미지 좌표 \((u, v) = (1032, 1507)\) 은 World 좌표계에서 \((X_{w}, Y_{w}, Z_{w}) = (0.0, 0.0, 0.04)\) 에 해당하는 위치의 이미지 좌표입니다. 이 이미지 좌표값과 \(Z_{w} = 0.04\) 라는 값을 이용하여 Image-to-World를 하면 위 코드 예시와 같이 \((X_{w}, Y_{w}, Z_{w}) = (0.0, 0.0, 0.04)\) 임을 구할 수 있습니다.
• 이와 같은 방법으로 임의의 \(Z_{w}\) 를 상수로 고정한 상태에서 원하는 \((u, v)\) 의 World 좌표계에서의 좌표값을 구할 수 있습니다.

• 지금까지 Generic 카메라 모델을 이용한 2D → 3D, 3D → 2D, 그리고 perspective view생성을 위한 왜곡 보정 방법까지 살펴보았습니다.
• 다음으로는 Brown 카메라 모델을 살펴보도록 하겠습니다. Brown 카메라 모델은 간략히 opencv를 이용한 사용 방법에 대해서만 다룰 예정입니다.

Brown 카메라 모델 왜곡 보정을 위한 mapping 함수 구하기

• 실습을 위해 사용한 데이터는 아래 링크를 사용하였습니다.
  • 링크 : https://data.caltech.edu/records/jx9cx-fdh55
• 본 글에서 사용한 이미지를 그대로 사용하시려면 아래 링크에서 다운 받으시면 됩니다.
  • 링크 : https://drive.google.com/file/d/1MaWrXvGuudMld2prhGk_KQDM4Q5qjpw9/view?usp=share_link

• opencv에서는 undistort 함수를 통하여 왜곡 보정을 하거나 initUndistortRectifyMap을 이용하여 왜곡 보정하는 방법이 있습니다.
• 본 글에서는 initUndistortRectifyMap을 이용하여 map_x, map_y를 구하고 이 값을 이용하여 remap 함수를 사용하여 이미지 전체를 왜곡 보정하거나 포인트의 매핑을 이용하여 포인트 단위로 왜곡 보정하는 방법에 대하여 살펴보도록 하겠습니다.
• remap 함수를 사용하는 방식을 소개하는 이유는 이 방법이 실제 사용하기에 현실적이며 undistort 함수는 느려서 실시간으로 사용할 수 없기 때문입니다. 시간 측정 시, 수백배의 시간 차이가 나는 것을 확인할 수 있습니다.

Brown 카메라 모델 remap을 이용한 왜곡 영상 → 왜곡 보정 영상

• remap 함수는 입력 이미지의 x, y 좌표를 출력 이미지의 x, y 좌표 어디에 대응시켜야 할 지 대응 관계를 아래 코드에서 살펴볼 map_x, map_y에 정의해 두고 그 관계를 매핑 시켜주는 함수 입니다.
• remap 함수는 입력과 출력이 비선형 관계이어서 관계식이 복잡할 때, 간단히 픽셀 별 대응을 통하여 복잡한 비선형 관계를 매핑 관계로 단순화 하기 때문에 연산도 간단하고 컨셉도 단순하여 많이 사용합니다.
  • 관련 링크 : remap 함수를 이용한 remapping
• remap 함수를 사용하기 위해서는 map_x, map_y룰 구해야 하며 opencv의 cv2.initUndistortRectifyMap를 이용하여 이 값들을 구할 수 있습니다.
• 앞에서 표준 카메라의 렌즈 왜곡

# 기존 intrinsic과 distortion을 이용하여 출력할 이미지 사이즈 크기의 왜곡 보정 영상을 생성하기 위한 방법
# 아래 함수를 통해 왜곡 보정된 이미지에서 동작하는 new_intrinsic을 구할 수 있음
new_intrinsic, roi = cv2.getOptimalNewCameraMatrix(
    intrinsic, distortion, imageSize=(width, height), alpha, newImageSize=(new_width, new_height)
)

# (new_width, new_height) 크기의 undistortion 이미지를 만들어 냅니다.
# cv2.getOptimalNewCameraMatrix()의 newImageSize와 같은 크기로 만들어야 외곽의 여백을 최소화 할 수 있습니다.
map_x, map_y = cv2.initUndistortRectifyMap(
    intrinsic, distortion, None, new_intrinsic, (new_width, new_height)
)

dst = cv2.remap(src, map_x, map_y, cv2.INTER_LINEAR)

Brown 카메라 모델 Pytorch를 이용한 왜곡 영상 → 왜곡 보정 영상

Vision 관련 글 목차