극 좌표계 (Polar Coordinate System)

2020, Aug 26    

calculus 관련 글 목차

목차

• 극 좌표계의 정의

• 극 좌표계 활용 예시

극 좌표계의 정의

• 이번 글은 간단하게 극 좌표계 (Polar Coordinate)에 관련된 내용을 다루어 보려고 합니다.

• 일반적으로 좌표계는 테카르트 좌표계 (직교 좌표계)를 사용합니다. 가로축이 $x$ 축이 되고 세로축이 $y$ 축이 되는 형태입니다.
• 하지만 물체의 이동 및 회전이 동시에 고려되어야 한다면 데카르트 좌표계에서는 회전에 따른 $x, y$ 의 변화를 매번 계산해야 하는 불편함이 발생합니다.
• 따라서 회전 동작을 편리하게 사용하기 위하여 고안된 좌표계가 본 글에서 소개하는 극 좌표계 (Polar Coordinate System) 입니다.

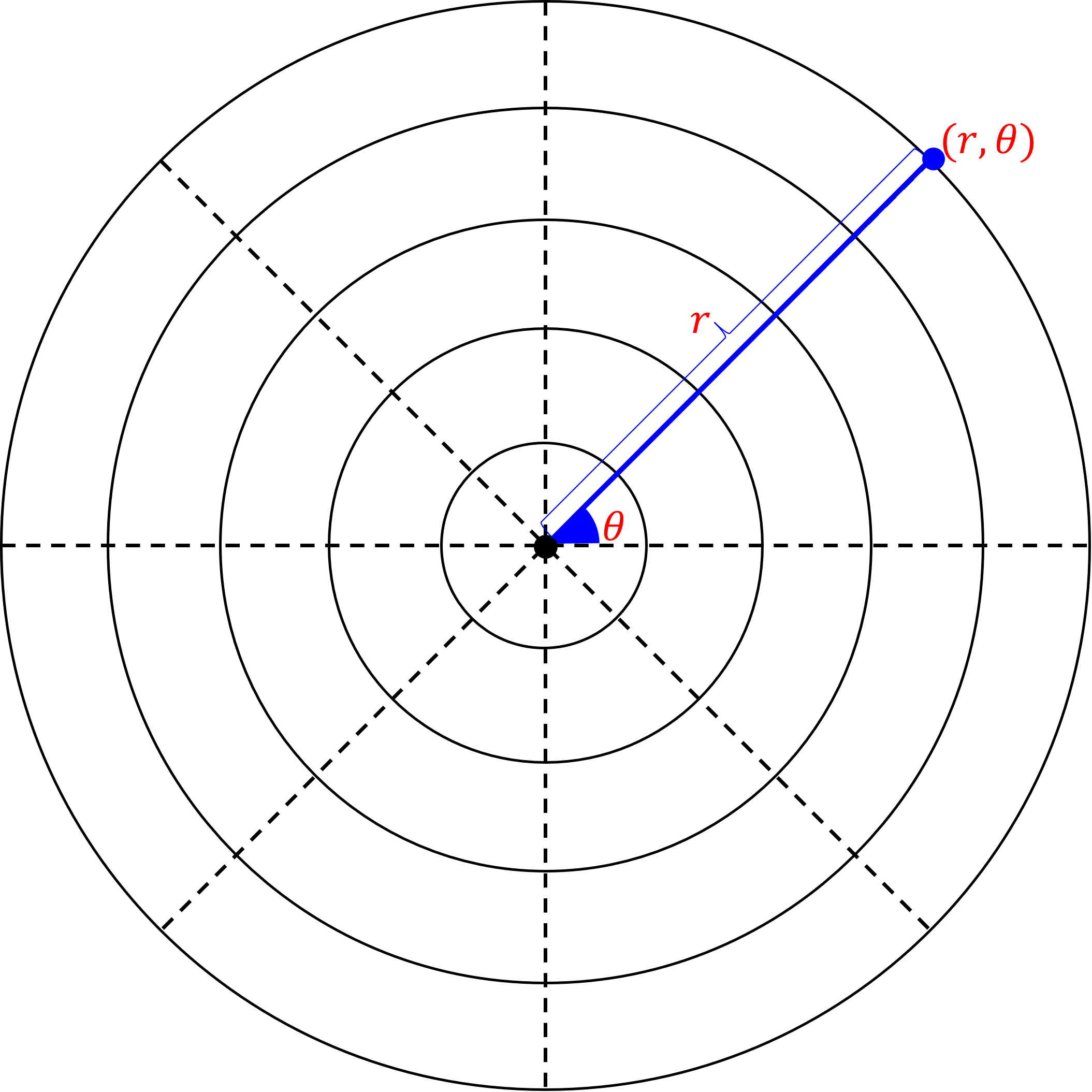
• 극 좌표계는 위 그림과 같이 원점으로부터의 거리 $r$ 과 각 $\theta$ 의 두 요소로 구성되며 극좌표계의 좌표는 $(r, \theta)$ 로 표시됩니다.
• 극 좌표계는 동심원의 형태로 평면의 모든 점을 표현할 수 있으며 주로 시간에 따른 회전의 움직임을 구현하기에 용이합니다.

• 데카르트 좌표계에서 표현된 벡터 $(x, y)$ 는 벡터의 크기와 arctan 함수를 사용하여 다음과 같이 $(r, \theta)$ 로 변환할 수 있습니다.

• $$r = \sqrt{(x^{2} + y^{2})} \tag{1}$$
• $$\theta = \text{atan2}{(y, x)} \tag{2}$$

• 참고로 $\text{atan2}{(y, x)}$ 는 1사분면에서의 $\text{atan}{(y/x)}$ 와 같습니다. 하지만 다른 사분면에서는 부호에 따라 값이 달라질 수 있습니다.
  • 참고 : atan과 atan2 비교
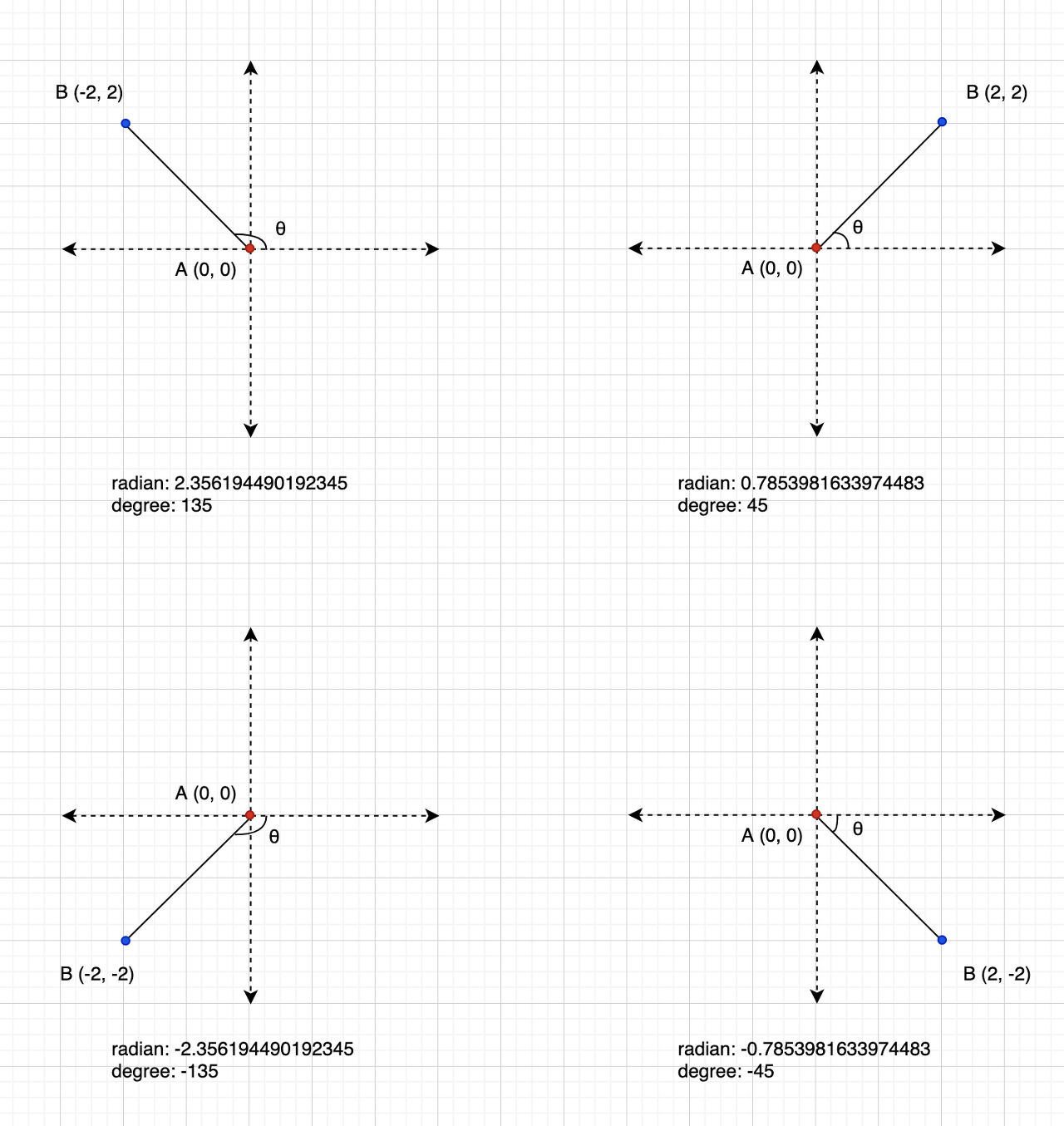
• atan은 두 점 사이의 탄젠트 값을 받아 $-\pi/2$ ~ $\pi/2$ 범위의 라디안 값 (-90도 ~ 90도)을 반환하는 반면 atan2는 두 점 사이의 상대좌표 $(x, y)$ 를 받아 $-\pi$ ~ $\pi$ 범위의 라디안 값 (-180도 ~ 180도)의 라디안 값을 반환합니다.

• • 또는 -의 부호가 표시되는 데카르트 좌표계에서는 atan2를 사용하면 좌표값을 인자로 사용하면 되기 때문에 보통 atan2를 사용합니다.

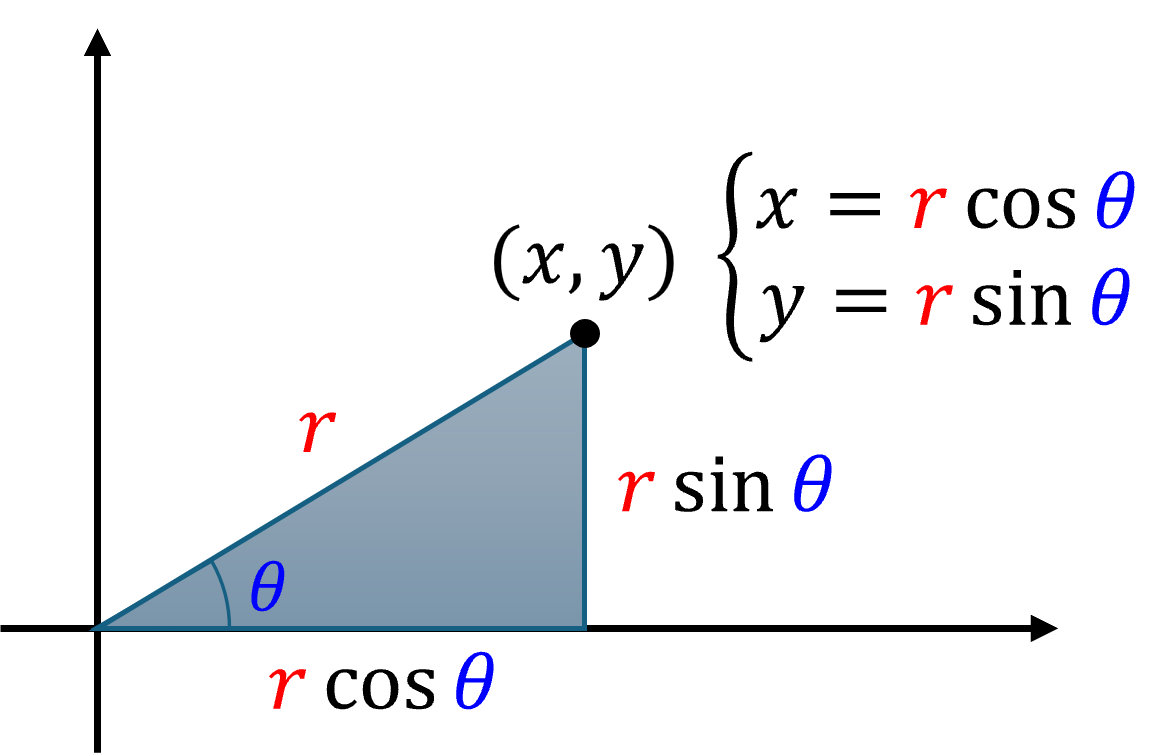
• 반대로 극 좌표계의 좌표 $(r, \theta)$ 를 데카르트 좌표계 $(x, y)$ 로 변환하는 식은 삼각함수를 사용해 구할 수 있습니다.

• $$x = r \cdot \cos{(\theta)} \tag{3}$$
• $$y = r \cdot \sin{(\theta)} \tag{4}$$
• $$r^{2} = x^{2} + y^{2} \tag{5}$$
• $$\tan{(\theta)} = \frac{y}{x} \tag{6}$$

• 위 식들을 이용하면 $(x, y)$ 와 $(r, \theta)$ 간의 변환을 자유롭게 할 수 있으며 그림으로 나타내면 다음과 같습니다.

극 좌표계 활용 예시

• 다음과 같이 직교 좌표계에서 아래와 같은 직사각형의 넓이를 구하는 것은 매우 쉽습니다.

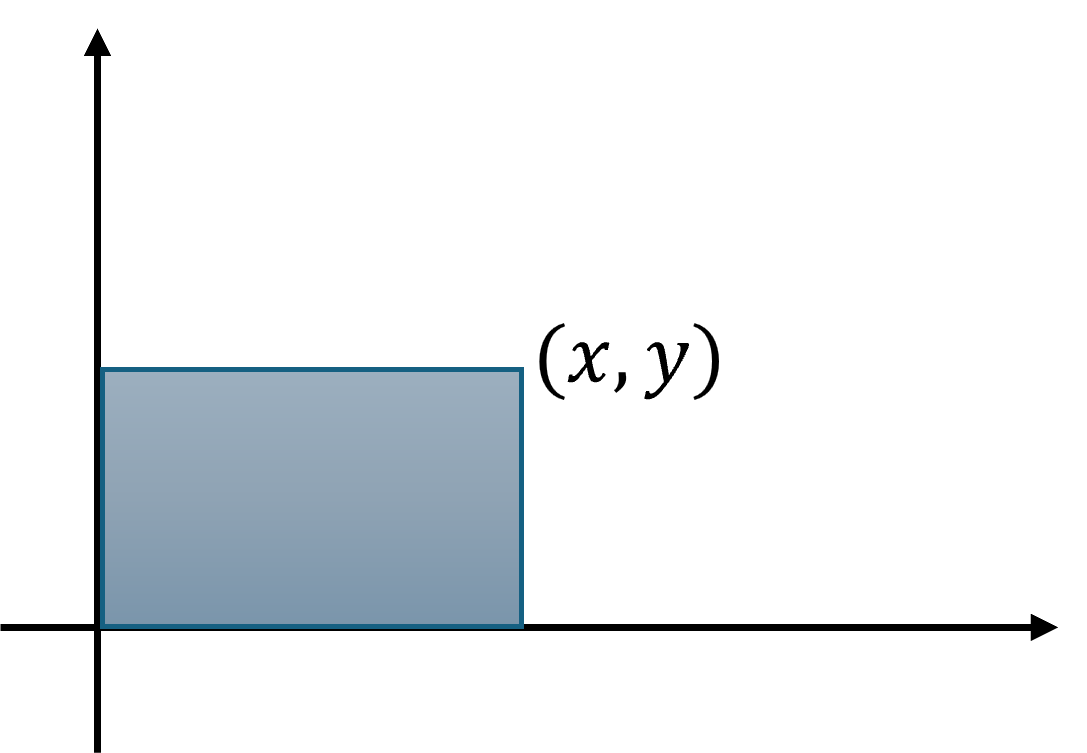
• 만약 다음과 같은 호의 넓이를 구할 때에는 극 좌표계를 사용하는 것이 좀 더 편할 수 있습니다.

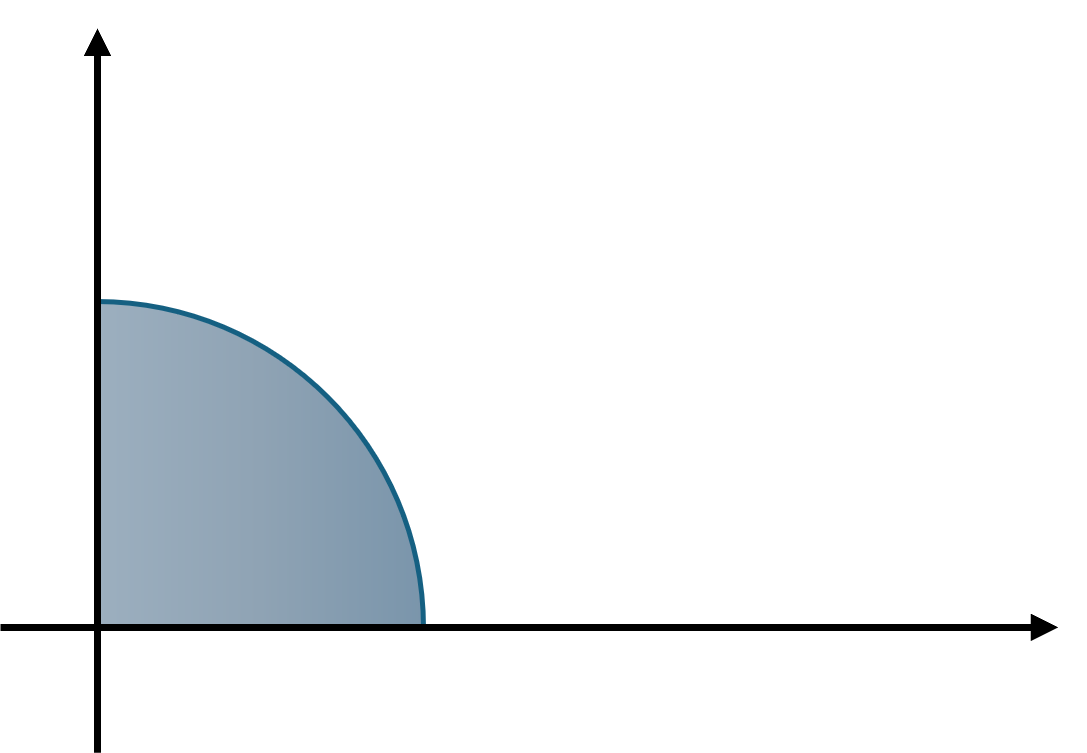
• 앞에서 극 좌표계의 사용 목적이 회전 동작을 편리하게 사용하기 위한 것으로 정의한 만큼 이와 같이 회전이 발생한 예시에서는 극 좌표계가 좀 더 효율적일 수 있습니다.

• 부채꼴의 넓이를 구하기 위하여 미소 넓이인 $ds$ 를 적분하는 방식을 사용해 보도록 하겠습니다.

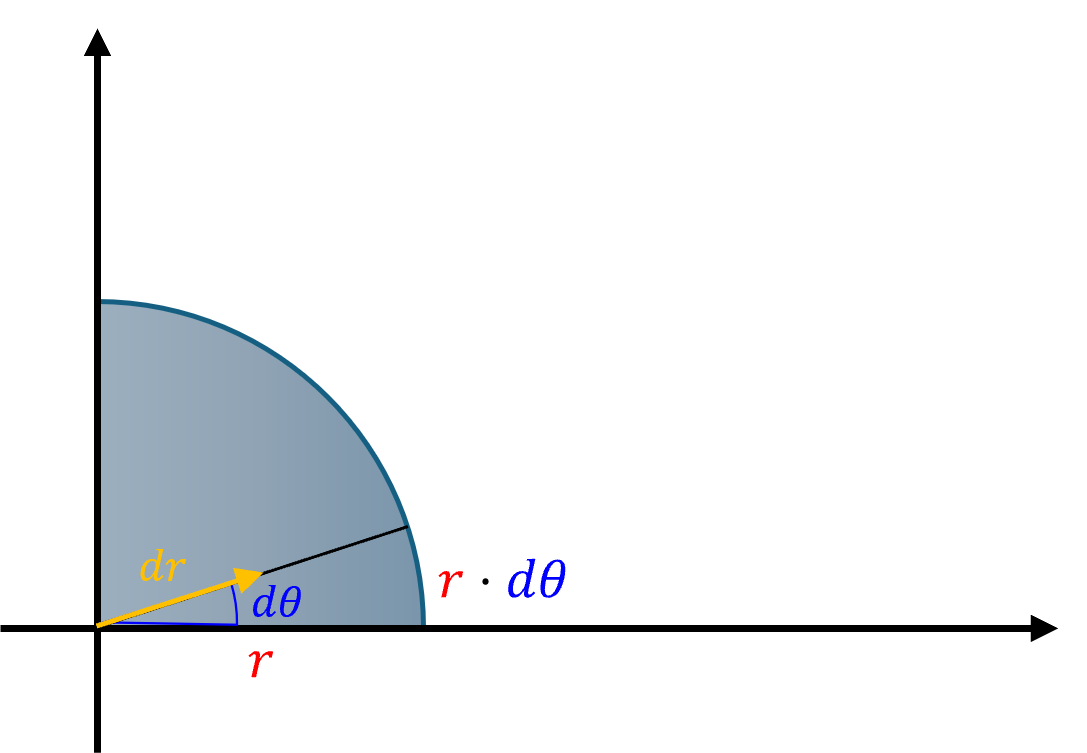
• 아래와 같이 호의 길이 변화량과 반지름의 변화량으로 면적의 변화량을 나타낼 수 있습니다.

• $$ds = dr \cdot (r \cdot d\theta) = r \cdot dr \cdot d\theta$$
• $$\text{compared to } dx \cdot dy \text{ in cartesian coordinate.}$$

• 이 성질을 이용하여 가우스 적분을 다루어 보도록 하겠습니다. 아래 링크에서도 상세한 설명을 확인할 수 있습니다.
  • 참조 : 가우스 적분 증명

• 다음과 같은 직교 좌표계에서의 적분은 사실상 사람이 직접 풀기에는 어려움이 있습니다.

• $$\int_{-\infty}^{\infty}\int_{0}^{\infty} e^{-(x^{2} + y^{2})} dxdy$$

• 위 식에서 $x$ 의 범위는 $0 \sim \infty$ 이고 $y$ 의 범위는 $-\infty \sim \infty$ 입니다. 즉, 직교좌표계에서 1, 4 사분면 전체 영역에 대하여 적분을 해주는 것을 의미합니다.
• 극 좌표계로 변환한다면 $r$ 의 범위는 $0 \sim \infty$ 가 되고 $\theta$ 의 범위는 $90^{\circ} \sim 90^{\circ}$ 가 됩니다. 따라서 다음과 같이 전개 가능합니다.

• $$\int_{-\infty}^{\infty}\int_{0}^{\infty} e^{-(x^{2} + y^{2})} dxdy = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_{0}^{\infty} e^{-r^{2}} rdrd\theta \quad (\because r^{2} = x^{2} + y^{2})$$
• $$\text{integration by substitution : } r^{2} = t \to 2rdr = dt$$
• $$\begin{align} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_{0}^{\infty} e^{-r^{2}} rdrd\theta &= \frac{1}{2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\int_{0}^{\infty} e^{-(t)} dt d\theta \\ &= \frac{\pi}{2} \int_{0}^{\infty} e^{-t} dt \\ &= -\frac{\pi}{2} \left[ e^{-t} \right]_{0}^{\infty} = \frac{\pi}{2} \end{align}$$

• 이와 같은 방식으로 극 좌표계를 이용하면 회전하는 물체에 대한 계산을 쉽게 할 수 있습니다.

calculus 관련 글 목차