NeRF, Representing Scenes as Neural Radiance Fields for View Synthesis
2022, Sep 02
- 논문 : https://arxiv.org/abs/2003.08934
- 참조 : https://youtu.be/WSfEfZ0ilw4
- 참조 : https://www.youtube.com/watch?v=JuH79E8rdKc
- 참조 : https://www.matthewtancik.com/nerf
- 참조 : https://www.youtube.com/watch?v=zkeh7Tt9tYQ
목차
-
코드 분석 - 데이터 전처리
-
코드 분석 - Ray tracing과 Positional Encoding
-
코드 분석 - NERF 모델링
-
코드 분석 - Sampling
-
코드 분석 - Volume Rendering
-
코드 분석 - Model 학습
NERF 개념 소개
NERF는 Neural Radiance Fields for View Synthesis을 의미합니다.View Synthesis에서 의미하는 바와 같이 새로은 View를 생성하게 되며 2D 이미지 여러장을 이용하여 3D 뷰를 생성해 내는 것을 의미합니다.

- 위 영상과 같이
NERF를 이용하게 되면 2D 이미지를 위 영상과 같은 깊이 정보를 가진 3D 정보 형태로 형태로 나타낼 수 있으며 기존에 가지고 있는 2D 이미지들 사이 사이의 불연속적이어서 표현할 수 없는 부분들을 매끄럽게 만들어 갈 수 있습니다. 이러한 태스크를NVS(Novel View Synthesis)또는View Interpolation이라고 부릅니다.

- 위 그림과 같이 NERF는 입력에는 없는
새로운 뷰의 이미지를 생성해 낼 수 있습니다. (물론 새로운 뷰를 생성해 내는 것이지 완전히 새로운 것을 생성해 내지는 못합니다.) 같은 공간을 카메라의 다른 각도에서 보았을 때를 가정하여NVS하는 것으로 생각하면 됩니다. 따라서 위 그림은 카메라가 움직이는 것이라고 생각하시면 됩니다.
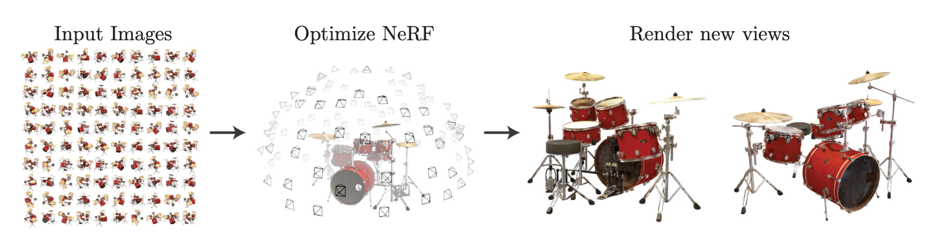
- 따라서
NERF를 구현하기 위하여 다양한 카메라 뷰에서의 입력 이미지를 이용하여 적절할 학습 방법을 통해 입력 이미지에 없는 카메라 뷰에서의 상황을 재현해 보는 것이 이번 논문의 목표라고 할 수 있습니다.

- 물론
NERF이전에도view synthesis를 위한 연구는 진행되었습니다. 하지만 360도 전체를 모두 렌덩할 때, 정면 이외의 부분에서는 부정확하게 렌더링되는 문제와 모든 부분을 저장하려고 할 때, 한 개의 상황에 대하여 너무 많은 저장 공간이 필요로 한다는 큰 단점이 있었습니다. 즉, 가능한 많은 모든 영역의 이미지가 필요로 하다는 뜻입니다. - 이러한 문제로 학습 방식으로
view synthesis를 할 때, 많은 이미지를 다 GPU를 통해 사용해야 한다는 단점도 존재하였습니다.
NERF는 이러한 문제를 개선하기 위하여 explicit feature(representation) 대신에implicit feature(representation)를 사용합니다.
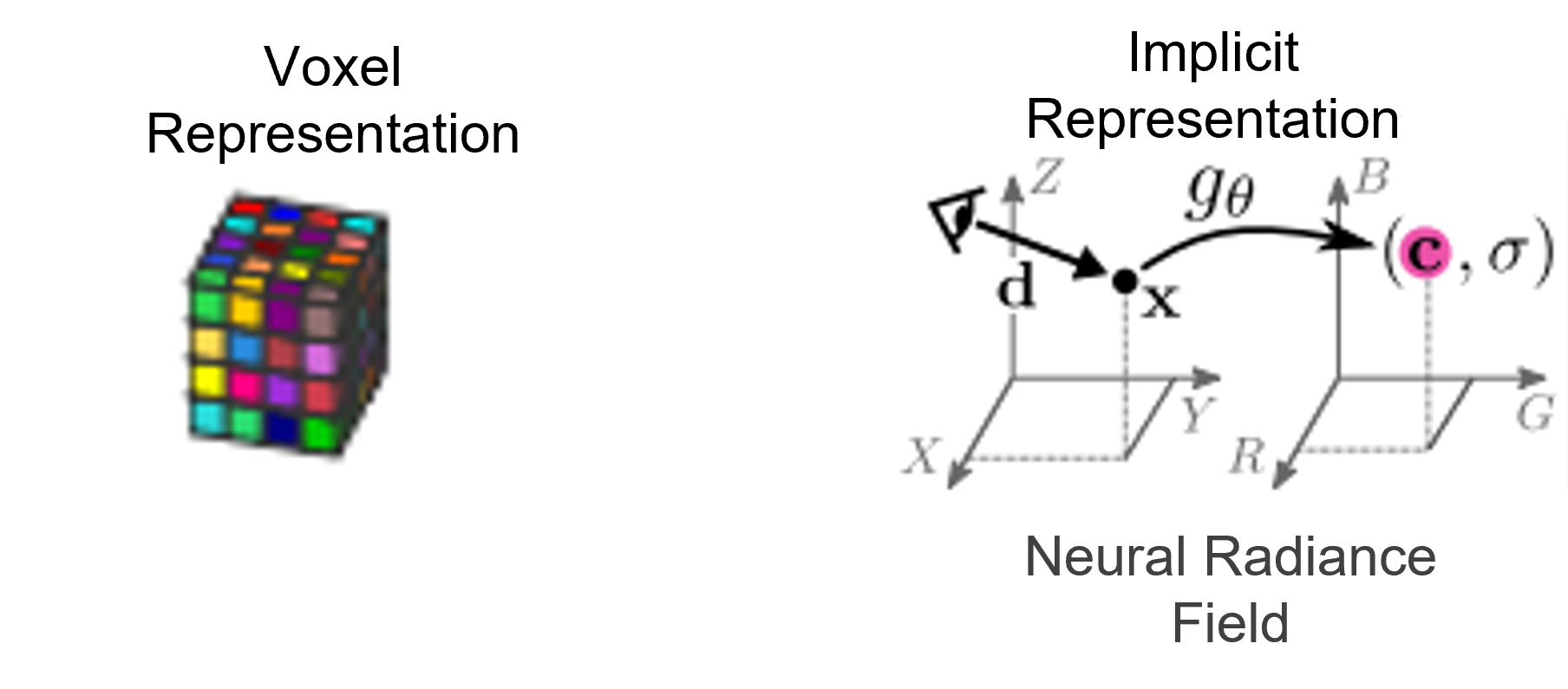
- explicit feature는 3D 공간의 정보를 Voxel Representation을 통해 나타내는 반면에
implicit feature는 뉴럴 네트워크를 통해 간접적으로 저장하는 방식을 뜻합니다. 위 그림과 같이view synthesis를 해야 할 카메라 뷰 기준에서의X, Y, Z를 네트워크의 쿼리로 입력하고 그 위치에서의 컬러값을 출력으로 뽑는 것이 방법이 될 수 있습니다. - 이와 같은 방법을 통하면 실제 필요한 것은 딥러닝 네트워크이고 무거운 Voxel Representation을 모두 저장할 필요는 없어집니다. 따라서
implicit feature를 위한 네트워크가 Voxel representation의 압축 기술이라고 말할 수도 있습니다. 추가적으로 Voxel Representation을 모두 저장할 때 발생하는 용량 문제를 해소하기 위해 해상도를 줄일 수 밖에 없던 문제 또한implicit feature를 이용하면 개선할 수 있습니다. - 또한 쿼리에 해당하는 X, Y, Z 값을 (공간 상에서) 연속적인 값으로 입력할 수 있기 때문에 출력 또한 이산적이지 않고 연속적으로 생성할 수 있어 입력에 사용되지 않은 뷰 또한 출력으로 만들 수 있습니다.
- 정리하면
implicit feature를 사용하였을 때, ① voxel representatio 보다 가벼우며 ② 공간 상에서 연속적인 출력이 가능하다는 장점이 있습니다.
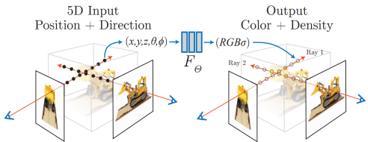
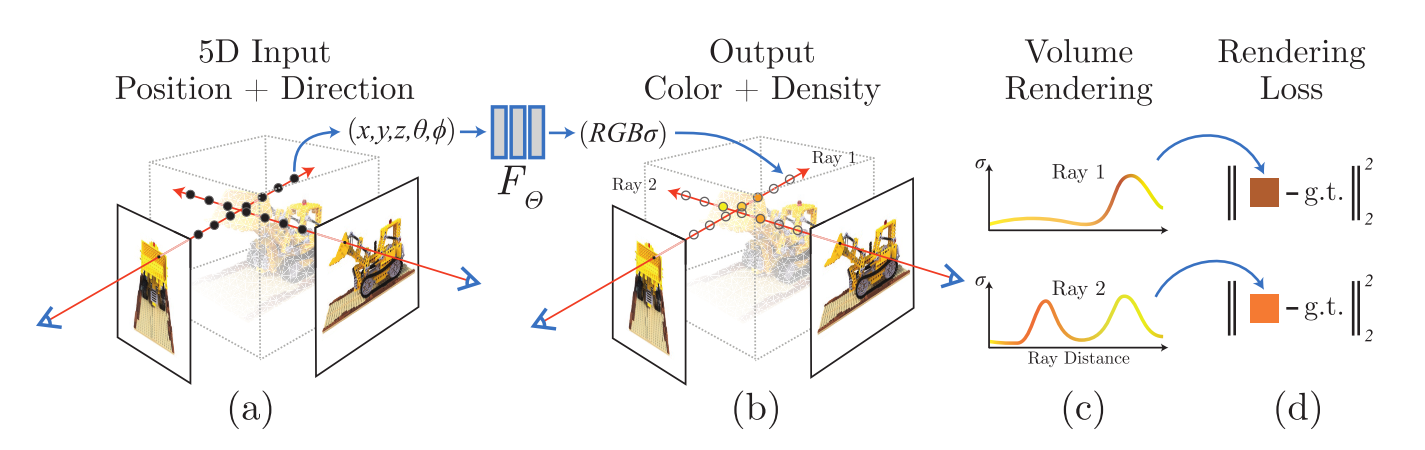
NERF는implicit feature를 이용하는 논문들 중 카메라의position과direction에 따른R, G, B,volume density를 출력하는 방식을 처음으로 사용하여 주목을 받았습니다.- 위 그림과 같이 5D Input인 \(X, Y, Z\)
Position과 \(\theta, \phi\)Direction을 입력으로 받아서 Output인 \(R, G, B\)Color와 \(\sigma\) 인Density를 출력합니다. - 이 중간 과정에 사용된 뉴럴 네트워크는 \(F_{\theta}\) 로 본 논문에서는
Fully Connected Layer즉,MLP만 사용하여 구현하였기 때문에 \(F_{\theta}\) 로 단순하게 나타냅니다.
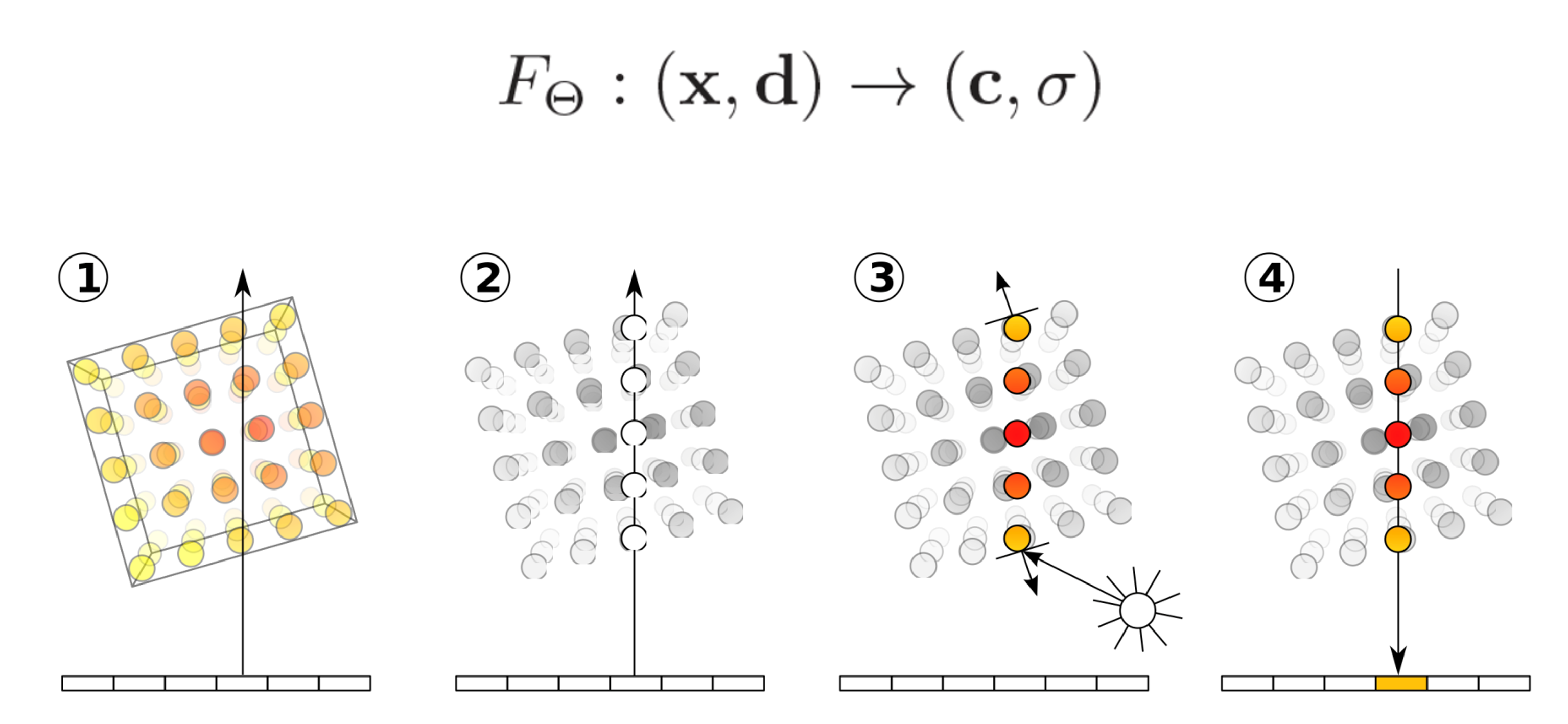
- 뉴럴 네트워크 \(F_{\theta}\) 의 역할인 \(F_{\theta} : (x, d) \to (c, \sigma)\) 를 위 그림과 같이 나타낼 수 있습니다.
- ① 하단 부분의 직사각형은 이미지를 위에서 바라본 것이며 하나의 픽셀에 해당합니다. 첫번째 그림은 각각의 픽셀에서 3D 공간 상으로 Ray가 송출되는 것을 의미합니다. 이 때, Ray가 Implicit feature로써 고려해야 할 영역을 사각형 Boundary로 표현하였습니다.
- ② Ray 상에서 실제 관심 대상으로 선정해야 할 부분을
샘플링해야 합니다. 연속적인 공간에서 Ray가 지나가는 모든 지점을 다 사용할 수 없으니 이산적으로 선택해야 할 영역을 샘플링 하는 작업이라고 생각하면 됩니다. - ③ 샘플링 한 영역에 \(F_{\theta}\) 를 이용하여 color와 density를 얻은 후 적용합니다.
- ④ 마지막으로
Volume Rendering을 통하여 역으로 픽셀의 color 값을 얻을 수 있습니다.
- 마지막 ④ 과정의
Volume Rendering과정을 통해 새로운 뷰에서의 이미지를 얻을 수 있습니다.Volume Rendering과정은미분 가능하도록 설계되며 미분 가능하기 때문에 뉴럴 네트워크의 학습 과정으로 이용될 수 있습니다. Volume Rendering의 이해를 위하여 수식을 통해 간략히 설명해 보도록 하겠습니다.
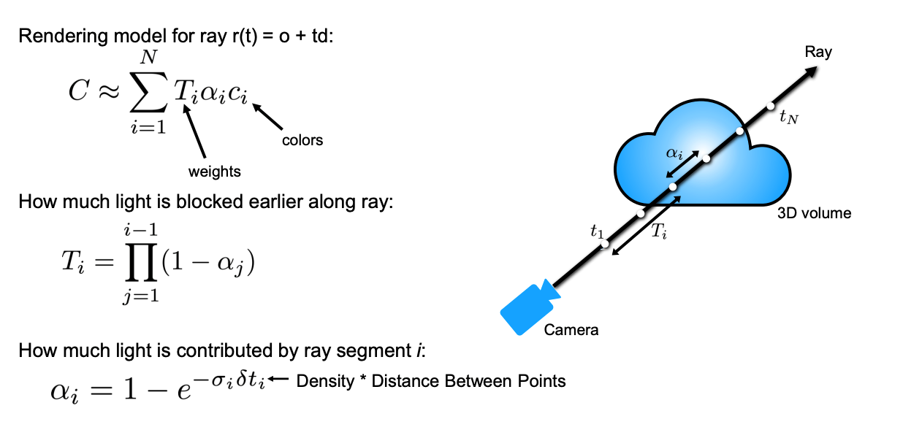
- 먼저 첫번째, 두번째 식 모두에 사용되는 \(\alpha_{i}\) 의 이해가 중요하므로 이 값의 의미를 살펴보도록 하겠습니다. 결과적으로는 \(i\) 번째 ray segment가 얼마나 의미 있는 점들이 빽빽하게 존재하는 지 정도를 의미합니다. 간단히 말하면 ray segment 지점에 물체가 존재할 가능도를 나타낸다고 볼 수 있습니다.
- \[\alpha_{i} = 1 - e^{-\sigma_{i} \delta t_{i}}\]
- 이 값은 0 ~ 1 사이의 값을 가지도록 구성되어 있으며 1에 가까울수록 \(i\) 번째 ray segment의 의미가 크다고 말합니다.
- 이 값을 결정하는 인자는 \(\sigma_{i}\) 와 \(t_{i}\) 입니다. \(\sigma_{i}\) 는 density이고 density는 0부터 무한대까지 값을 가질 수 있습니다. (물론 실제 무한대를 가지진 않습니다.) 이 값이 0에 가까워질수록 \(\alpha_{i}\) 는 0에 가까워 지고 값이 커질수록 \(\alpha_{i}\) 는 1에 가까워집니다. 즉, 어떤 segment에서 density가 클수록 ray segment의 중요도가 커진다고 말할 수 있습니다.
- 반면 \(t_{i}\) 는 샘플링된 점들 사이의 거리를 의미합니다. 거리가 멀면 멀수록 그 거리 안에 포함된 점들이 의미상으로 많아지기 때문에 ray segment의 중요도가 커집니다. 반대로 \(t_{i}\) 가 0에 가까울수록 포함된 점들의 의미가 얕아지기 때문에 ray segment의 중요도가 작아집니다.
- 종합하면 density가 높고 샘플링된 포인트 사이의 거리가 멀수록 \(\alpha_{i}\) 는 1에 가까워지고 density가 낮고 샘플링된 포인트 사이의 거리가 가까울수록 \(\alpha_{i}\) 는 0에 가까워 집니다. 따라서 ray segment가 얼마나 의미 있는 점들이 빽빽하게 존재하는 지 정도로 파악할 수 있습니다.
- 그 다음으로 \(T_{i}\) 에 대하여 이해해 보도록 하겠습니다. \(T\) 는
Transmittance를 의미하며 ray가 얼만큼 투과되는 지를 의미합니다.
- \[T_{i} = \Pi_{j=1}^{i-1} (1 - \alpha_{j})\]
- \(T_{i}\) 는 \(i\) 번째 ray segment 까지 얼만큼 ray가 가려졌는 지 정도를 측정하는 수치값입니다. 즉, \(i\) 번째 ray segment 까지 density가 많은 영역이 존재하면 가려짐 정도가 크다고 판단할 수 있습니다.
- 앞에서 살펴본 \(\alpha_{j}\) 가 클수록 density가 높다고 말할 수 있으므로 \(1 - \alpha_{j}\) 를 이용하여 density가 높을수록 \(T_{i}\) 가 작아지도록 식을 설정합니다.
- 따라서 \(1 ~ (i-1)\) 까지의 모든 \(1 - \alpha_{j}\) 값을 곱하면 \(T_{i}\)가 됩니다. 즉, \(i\) 번째 ray segment 까지의 누적된 ray의 가림 정도를 의미하며 그 가림 정도는 누적된 곱을 통하여 나타냅니다.
- 지금까지 살펴본 \(\alpha_{i}, T_{i}\) 를 이용하여 렌더링하는 방식을 살펴보겠습니다.
- \[C \approx \sum_{i=1}^{N} T_{i} \alpha_{i} c_{i}\]
- 위 식에서 \(T_{i}, \alpha{i}\) 는 앞에서 구하였고 \(c_{i}\) 는
color값입니다. - 뉴럴 네트워크를 통해 추출한 모든
color값을 단순히 더하는 것이 아니라 \(T_{i}\) 를 이용하여 각 점들에 대하여 얼만큼의 투과도를 반영하여 color 값을 반영할 지 결정합니다. 투과도가 높을수록 color값이 그대로 반영되고 투과도가 낮을수록 그 비중이 작아지게 됩니다. 마찬가지로 \(\alpha{i}\) 값을 통해 물체의 존재 여부를 반영합니다. - 따라서 각 샘플링되는 \(i\) 번째 지점에서 \(T_{i} \alpha_{i} c_{i}\) 를 계산하여 누적하는 것이 최종 컬러값을 정하는 방식이 됩니다.
- 이 때 더하는 연산은 원래 연속적인 공간에서 적분을 하는 것이지만 현실적인 계산을 위하여 이산적인 공간에서 합을 하는 방식을 이용합니다.
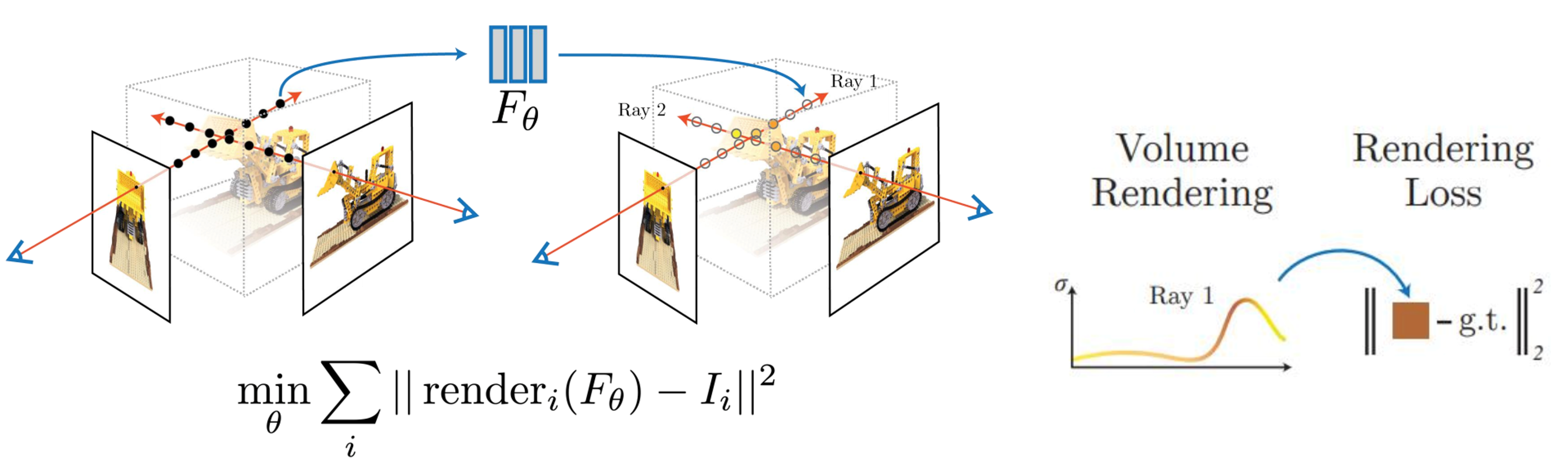
- 앞에서 사용한 방식을 이용하여 최종적인 학습을 할 때에는
rendering loss를 사용합니다. 앞에서는 임의의 픽셀에 대한 예시를 사용하였는데, 이미지에서 학습할 수 있는 영역의 픽셀에 대하여 렌더링을 한 후 학습할 수 있는 이미지를 GT로 둔 다음 L2 Loss를 최소화 하도록 학습합니다. - 따라서 어떤 하나의 Ray가 있으면 그 Ray가 Volume Rendering을 하게 되고 그 결과와 GT값의 L2 Loss를 최소화 하는 학습 방식을 통해 NERF가 학습이 됩니다.
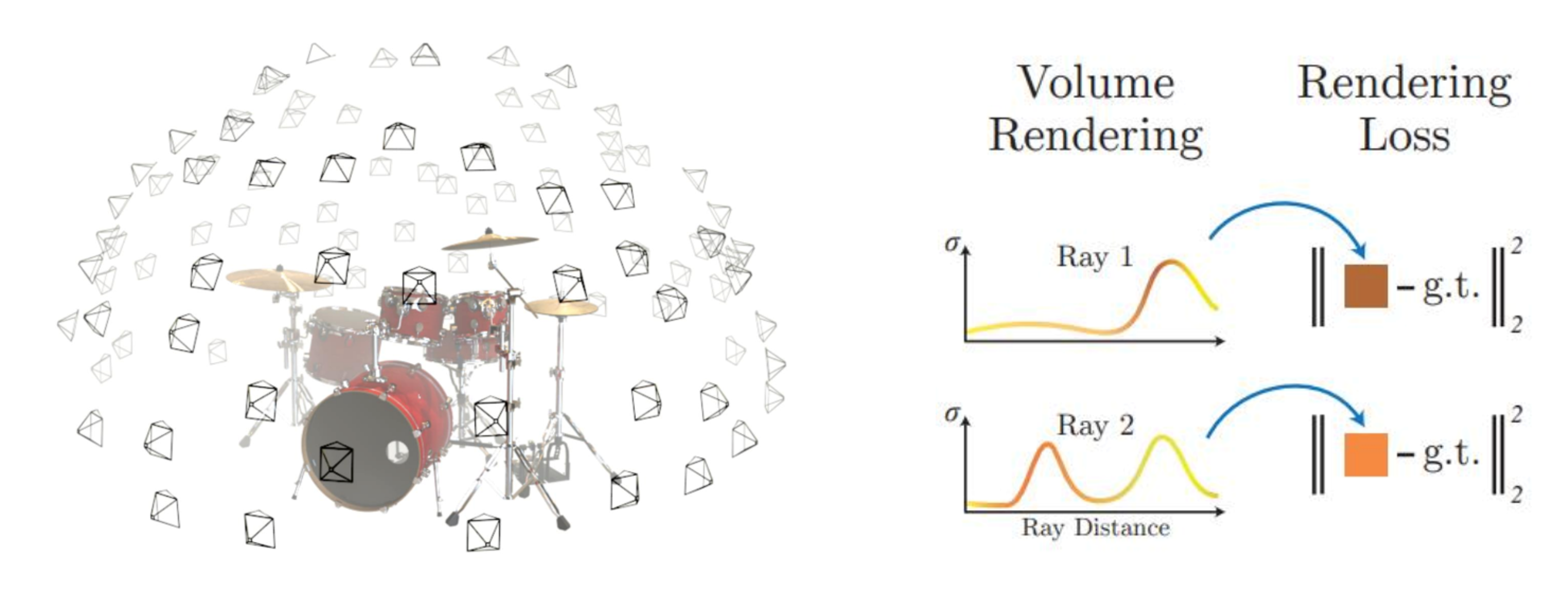
- 앞에서 사용한 방식을 하나의 이미지가 아닌 다양한 뷰의 여러개의 이미지에 대하여 학습을 하면 다양한 뷰에 대해서도
implicit feature를 가지는 뉴럴 네트워크로 학습할 수 있습니다.
- 이와 같은 방식으로 학습한 결과 카메라의 Position과 Direction에 따른 다양한 결과를 생성해 낼 수 있습니다.

- 위 그림의 왼쪽은 카메라의 Position과 Direction을 모두 움직인 결과이고 오른쪽은 카메라의 Position은 그대로 둔 채 Direction만 변경하여 결과를 낸 영상입니다.
- TV 화면을 보면 같은 물체라도 모두 색이 같은 것이 아니라 카메라의 Position 및 Direction에 따라서 어떻게 색이 변하는 지 확인할 수 있습니다.
- 또한 NERF는 3D 공간 정보를 생성해 내는 것이기 때문에 위 그림과 같이
depthmap을 생성할 수 있습니다. 이러한 depthmap을 통해 NERF가 어떻게 공간 정보를 이해하고 있는 지 이해할 수 있습니다.
카메라 intrinsic과 extrinsic의 이해
NERF의 전체 과정을 이해하려면 카메라 intrinsic과 extrinsic을 이해해야 합니다. 아래 링크를 통해 내용을 참조할 수 있으며 본 글에서는 간략히 내용을 설명하겠습니다.
- 먼저 카메라
intrinsic에 대하여 살펴보도록 하겠습니다.
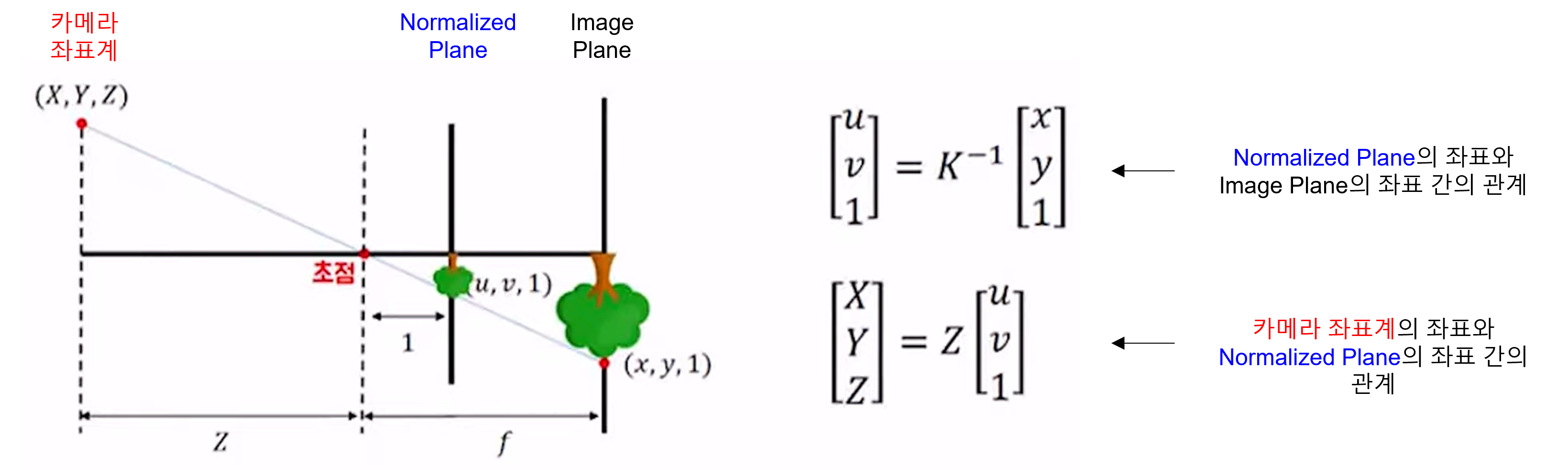
- 위 그림과 같이 카메라 좌표계의 3D 공간 상의 X, Y, Z 좌표 값이 핀홀 (초점)을 거쳐서 개념상에 존재하는 Normalized Plane으로 투영됩니다. 여기는 focal length가 1인 개념상 존재하는 공간입니다.
- Normalized Plane의 좌표를 위 그림에서는 \(u, v\) 로 표현하고 (자료마다 표기법은 다릅니다.) intrinsic 파라미터 \(K\) 를 곱하면 Image Plane의 좌표로 변환이 됩니다.
- 따라서 위 식과 같이 \(u, v\) 좌표와 \(x, y\) 좌표 간의 변환 관계를 \(K\) 로 나타낼 수 있습니다.
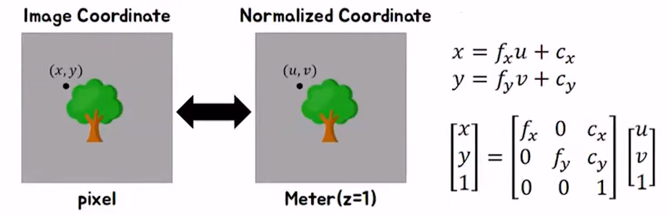
- 앞에서 정의한 intrinsic \(K\) 를 자세히 살펴보면 위 식과 같으며 \(u, v\) 좌표와 \(x, y\) 좌표 간의 변환 관계를 자세히 확인할 수 있습니다.
- 다음으로 카메라
extrinsic에 대하여 살펴보도록 하겠습니다.
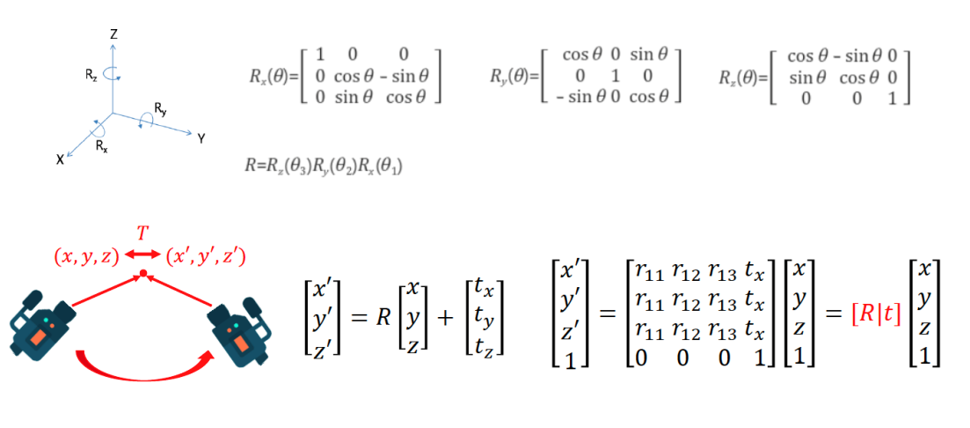
- 위 그림에서는 X, Y, Z 축 각각을 회전변환하는 방식의 회전 변환 행렬 \(R\) 과 translation을 반영하는 \(t\) 를 이용하여 회전 및 이동 변환 행렬을 만듭니다. 이와 관련된 자세한 내용은 아래 링크를 참조하시기 바랍니다.
- 링크 : 3D에서의 회전 변환
- extrinsic은 카메라의 Pose를 나타내기 위한 행렬입니다. World 좌표라는 3차원 공간 상의 기준 좌표계가 있을 때, 카메라의 위치가 바뀔 수 있습니다. 이 때, 카메라의 위치가 얼만큼 회전하고 이동하였는 지 관계를 알려면 기준 좌표계를 기준으로 회전 및 이동량을 정할 수 있습니다.
- 이 값이 \(R\) 과 \(t\) 가 되며 이 값을 위 식과 같이 정할 수 있습니다.
- 지금 까지 살펴본 카메라의
intrinsic과extrinsic은 NERF를 구현하는 데 필수적으로 사용됩니다. 따라서 의미의 이해를 하는 것이 필수적이니 살펴 보시기 바랍니다.
- 지금부터는 앞에서 살펴본 NERF를 어떻게 학습하는 지 코드를 자세히 살펴보도록 하겠습니다.