(멀티플 뷰 지오메트리) Lecture 1. 2D and 1D projective geometry

Multiple View Geometry 글 목차

참조 : https://youtu.be/LAHQ_qIzNGU?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : https://youtu.be/gQ7IUS8NKCI?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : Multiple View Geometry in Computer Vision
참조 : https://www.cuemath.com/learn/mathematics/conics-in-real-life/

이번 글에서는 2D and 1D projective geometry 내용의 강의를 듣고 정리해 보도록 하겠습니다.

위 슬라이드에서 line에 직교한 벡터 $(a, b)$ 는 다음과 같은 방식으로 도출될 수 있습니다.

$\text{line: } (a, b, c) = ax + by + c = 0$
$P = (x_{1}, y_{1}), Q = (x_{2}, y_{2}) \text{ P and Q are on the line.}$
$\text{direction vector: } d = Q - P = (x_{2} - x_{1}, y_{2} - y_{1})^{T}$
$\text{line equation 1: } ax_{1} + by_{1} + c = 0$
$\text{line equation 2: } ax_{2} + by_{2} + c = 0$

$\text{line equation 2 - line equation 1: } a(x_{2} - x_{1}) + b(y_{2} - y_{1}) = 0$
$(a, b) \cdot (x_{2} - x_{1}, y_{2} - y_{1}) = (a, b) \cdot d = 0$
$\therefore (a, b)^{T} \text{ is perpendicular to } d.$

지금 부터는 2D and 1D projective geometry 강의의 후반부로 conics, dual conics와 관련된 내용과 transform 관련 내용에 대하여 다루어 보도록 하겠습니다.

projective plane이란 3차원 공간에서 원점을 지나는 모든 직선들의 모임으로 해석할 수 있습니다. 이 관점에서 projective plane의 point는 원점을 지나는 각각의 직선 (line)이고 line은 원점을 지나는 3차원 공간 속의 2차원 평면 (plane)으로 정의할 수 있습니다.
projective plane은 일반적인 plane과 유사하지만, point at infinity라는 무한대의 점이 존재하여 모든 두 직선이 항상 교차가 되는 특성이 있습니다. 모든 point at infinity 들이 지나는 직선을 line at infinity라고 합니다.

위 슬라이드의 $C$ 는 대칭 행렬 형태를 가지며 의미는 3개의 차원이 구성하는 관계를 수치로 나타낸 것을 의미합니다.
예를 들어 (1, 1) 위치는 $x_{1}, x_{1}$ 의 관계를 수치로 나타낸 것이고 (1, 2) 는 $x_{1}, x_{2}$ 의 관계를 수치로 나타낸 것입니다. 따라서 $(i, j)$ 와 $(j, i)$ 의 관계는 같기 때문에 대칭 행렬 형태를 가지게 됩니다.

$a \cdot x_{1}^{2} + b \cdot x_{1}x_{2} + c \cdot x_{2}^{2} + d \cdot x_{1}x_{3} + e \cdot x_{2}x_{3} + f \cdot x_{3}^{2} = 0$

위 슬라이드의 $C$ 또한 3개의 차원이 구성하는 관계를 수치로 나타낸 것이며 위 식에서 $X^{T} C X = 0$ 을 만족하도록 $C$ 를 구성한 것입니다.
이와 같은 행렬 $C$ 를 homogeneouse representation of conic이라고 합니다.
homogeneouse representation of conic $C$ 는 3개 차원의 경우의 수의 관계를 수치로 나타낸 것이므로 그 관계에 따라서 다양한 기하 형태가 나타납니다. 3개 차원의 경우의 수는 다음을 의미합니다. 아래 행렬에서 $x_{d}$ 는 $x$ 차원, $y_{d}$ 는 $y$ 차원, $h_{d}$ 는 homogeneous 차원을 의미합니다. $\text{rel}(a, b)$ 는 $a, b$ 의 관계를 의미합니다.

$\begin{align} C &= \begin{bmatrix} \text{rel}(x_{d}, x_{d}) & \text{rel}(x_{d}, y_{d}) & \text{rel}(x_{d}, h_{d}) \\ \text{rel}(y_{d}, x_{d}) & \text{rel}(y_{d}, y_{d}) & \text{rel}(y_{d}, h_{d}) \\ \text{rel}(h_{d}, x_{d}) & \text{rel}(h_{d}, y_{d}) & \text{rel}(h_{d}, h_{d}) \end{bmatrix} \\ &= \begin{bmatrix} a & b/2 & d/2 \\ b/2 & c & e/2 \\ d/2 & e/2 & f \end{bmatrix} \end{align}$

그 중 $C$ 의 $\text{rank}(C) = 3$ (full rank) 인 경우 원, 타원, 포물선, 쌍곡선 형태가 나타나는 반면 $C$ 의 $\text{rank}(C) \lt 3$ 인 경우 교차선, 평행선, 단일선, 점과 같은 degenerate conic 형태가 나타나기도 합니다. 이 부분은 차례대로 설명할 예정입니다.

따라서 지금부터 다룰 conic $C$ 는 가장 작은 형태인 point를 시작하여 line, circle, ellipse, hyperbola, parabola 등을 모두 포함하는 집합이기 때문에 Multiple View Geometry에서 가장 중요하게 다루는 개념 중 하나입니다.

위 슬라이드에서 $l$ 과 $m$ 은 line을 나타내므로 각각 다음과 같습니다.

$l = \begin{bmatrix} l_{1} & l_{2} & l_{3} \end{bmatrix}^{T}$
$m = \begin{bmatrix} m_{1} & m_{2} & m_{3} \end{bmatrix}^{T}$

2개의 선 $l, m$ 의 관계 또한 3개 차원의 경우의 수인 9개로 나타내기 위해 outer product를 한 것이고 대칭 행렬로 나타내고자 $lm^{T} + ml^{T}$ 형태로 나타내어 conic $C$ 를 구성합니다.
위 식의 $C = lm^{T} + ml^{T}$ 에서 $lm^{T}$ 와 $ml^{T}$ 각각의 outer product의 rank는 1이기 때문에 outer product의 결합으로 이루어진 $lm^{T} + ml^{T}$ 은 항상 degenerate conic 임을 만족합니다.
위 슬라이드에서는 $l$ 과 $m$ 이 independent 하여 $C = lm^{T} + ml^{T}$ 의 $\text{rank}(C) = 2$ 가 만족하는 degenerate conic 상황으로 가정합니다. 따라서 위 예시와 같이 교차하는 2개의 선으로 나타낼 수 있습니다.
슬라이드의 $C = lm^{T} + ml^{T}$ 를 좀더 자세하게 풀어 쓰면 다음과 같습니다.

$l = \begin{bmatrix} l_{1} \\ l_{2} \\ l_{3} \end{bmatrix}$
$m = \begin{bmatrix} m_{1} \\ m_{2} \\ m_{3} \end{bmatrix}$
$lm^{T} = \begin{bmatrix} l_{1}m_{1} & l_{1}m_{2} & l_{1}m_{3} \\ l_{2}m_{1} & l_{2}m_{2} & l_{2}m_{3} \\ l_{3}m_{1} & l_{3}m_{2} & l_{3}m_{3}\end{bmatrix}$
$\begin{align} C = lm^{T} + ml^{T} &= \begin{bmatrix} l_{1}m_{1} & l_{1}m_{2} & l_{1}m_{3} \\ l_{2}m_{1} & l_{2}m_{2} & l_{2}m_{3} \\ l_{3}m_{1} & l_{3}m_{2} & l_{3}m_{3}\end{bmatrix} + \begin{bmatrix} m_{1}l_{1} & m_{1}l_{2} & m_{1}l_{3} \\ m_{2}l_{1} & m_{2}l_{2} & m_{2}l_{3} \\ m_{3}l_{1} & m_{3}l_{2} & m_{3}l_{3}\end{bmatrix} \\ &= \begin{bmatrix} l_{1}m_{1} + m_{1}l_{1} & l_{1}m_{2} + m_{1}l_{2} & l_{1}m_{3} + m_{1}l_{3} \\ l_{2}m_{1} + m_{2}l_{1} & l_{2}m_{2} + m_{2}l_{2} & l_{2}m_{3} + m_{2}l_{3} \\ l_{3}m_{1} + m_{3}l_{1} & l_{3}m_{2} + m_{3}l_{2} & l_{3}m_{3} + m_{3}l_{3}\end{bmatrix} \end{align}$

위 식을 살펴 보면 $C = lm^{T} + ml^{T}$ 는 대칭행렬이 됨을 알 수 있습니다.

반면 위 슬라이드에서는 $l = m$ 으로 나타내었기 때문에 한 개의 선으로 표현합니다. 따라서 $\text{rank}(C) = 1$ 인 degenerate conic 상황으로 가정합니다. 따라서 위 예시와 같이 하나의 선으로 나타낼 수 있습니다.

$x = \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix}$
$y = \begin{bmatrix} y_{1} \\ y_{2} \\ y_{3} \end{bmatrix}$
$xy^{T} = \begin{bmatrix} x_{1}y_{1} & x_{1}y_{2} & x_{1}y_{3} \\ x_{2}y_{1} & x_{2}y_{2} & x_{2}y_{3} \\ x_{3}y_{1} & x_{3}y_{2} & x_{3}y_{3}\end{bmatrix}$
$\begin{align} C^{*} = xy^{T} + yx^{T} &= \begin{bmatrix} x_{1}y_{1} & x_{1}y_{2} & x_{1}y_{3} \\ x_{2}y_{1} & x_{2}y_{2} & x_{2}y_{3} \\ x_{3}y_{1} & x_{3}y_{2} & x_{3}y_{3}\end{bmatrix} + \begin{bmatrix} y_{1}x_{1} & y_{1}x_{2} & y_{1}x_{3} \\ y_{2}x_{1} & y_{2}x_{2} & y_{2}x_{3} \\ y_{3}x_{1} & y_{3}x_{2} & y_{3}x_{3}\end{bmatrix} \\ &= \begin{bmatrix} x_{1}y_{1} + y_{1}x_{1} & x_{1}y_{2} + y_{1}x_{2} & x_{1}y_{3} + y_{1}x_{3} \\ x_{2}y_{1} + y_{2}x_{1} & x_{2}y_{2} + y_{2}x_{2} & x_{2}y_{3} + y_{2}x_{3} \\ x_{3}y_{1} + y_{3}x_{1} & x_{3}y_{2} + y_{3}x_{2} & x_{3}y_{3} + y_{3}x_{3}\end{bmatrix} \end{align}$

지금까지 배운 내용 종합하면 Point, Line, Two Lines, Circle, Ellipse, Hyperbola, Parabola을 Conic을 이용하여 표현할 수 있음을 확인하였습니다. 이번에는 각 항목을 실제 예시를 들어서 어떻게 표현하는 지 살펴보도록 하겠습니다.

① Point
- Point는 $3 \times 1$ 크기의 벡터로 표현이 가능합니다. 예를 들어 inhomogeneous coordinate의 $(2, 3)$ Point는 homogeneous coordinate에서 $(2, 3, 1)$ 로 표현됩니다. 만약 conic을 이용하여 Point를 표현하려면 degenerate dual conic 형태를 이용해야 합니다. 왜냐하면 점을 표현하려면 2개의 선 (Two Lines)이 한 점을 통과하는 형태를 나타내어야 하기 때문입니다.
- 따라서 $(2, 3, 1)$ 을 지나는 두 개의 선 $l = (1, 0, -2)^{T}$ 와 $m = (0, 1, -3)^{T}$ 를 이용하여 degenerate dual conic을 나타내면 다음과 같습니다.
- $\begin{align} C^{*} &= lm^{T} + ml^{T} \\ &= \begin{bmatrix} 1 \\ 0 \\ -2 \end{bmatrix} \begin{bmatrix} 0 & 1 & -3 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ -3 \end{bmatrix} \begin{bmatrix} 1 & 0 & -2 \end{bmatrix} \\ &= \begin{bmatrix} 0 & 1 & -3 \\ 1 & 0 & -2 \\ -3 & -2 & 12 \end{bmatrix} \end{align}$
- 위 식의 $C^{*}$ 는 두 선의 교점을 나타내므로 두 선의 교점인 Point $x = (2, 3, 1)$ 는 다음식을 만족하여 $C^{*}$ 가 Point를 나타냄을 알 수 있습니다.
- $x^{T} C^{*} x = \begin{bmatrix} 2 \\ 3 \\ 1 \end{bmatrix} \begin{bmatrix} 0 & 1 & -3 \\ 1 & 0 & -2 \\ -3 & -2 & 12 \end{bmatrix} \begin{bmatrix} 2 & 3 & 1 \end{bmatrix} = 0$
② Line
- Line은 2개의 점을 이용하여 생성할 수 있습니다. 따라서 homogeneous coordiate의 2개의 점을 이용하여 $C$ 를 구성하면 degenerate conic으로 선을 표현할 수 있습니다.
- 아래 예제는 $l = x + 2y - 3 \to (1, 2, -3)$ 이라는 식을 표현하기 위하여 2개의 점 $a = (3, 0, 1)$ 과 $b = (0, 1.5, 1)$ 을 이용해 보겠습니다. 두 점은 $l$ 상에 존재합니다.
- $\begin{align} C &= ab^{T} + ba^{T} \\ &= \begin{bmatrix} 3 \\ 0 \\ 1 \end{bmatrix} \begin{bmatrix} 0 & 1.5 & 1 \end{bmatrix} + \begin{bmatrix} 0 \\ 1.5 \\ 1 \end{bmatrix} \begin{bmatrix} 3 & 0 & 1 \end{bmatrix} \\ &= \begin{bmatrix} 0 & 4.5 & 3 \\ 4.5 & 0 & 1.5 \\ 3 & 1.5 & 2 \end{bmatrix} \end{align}$
- 위 식의 $C$ 는 Line을 나타내므로 다음과 같이 확인해 볼 수 있습니다.
- $l^{T} C l = \begin{bmatrix} 1 \\ 2 \\ -3 \end{bmatrix} \begin{bmatrix} 0 & 4.5 & 3 \\ 4.5 & 0 & 1.5 \\ 3 & 1.5 & 2 \end{bmatrix} \begin{bmatrix} 1 & 2 & -3 \end{bmatrix} = 0$
③ Two Lines
- Two Lines를 나타내는 Conic은 앞에서 Point를 나타내는 Conic을 통해 다루었습니다. $l = (1, 2, -3)$ , $m = (2, -1, 4)$ 가 있을 때, 이 두 선을 나타내는 degenerate dual conic은 다음과 같습니다.
- $\begin{align} C^{*} &= lm^{T} + ml^{T} \\ &= \begin{bmatrix} 1 \\ 2 \\ -3 \end{bmatrix} \begin{bmatrix} 2 & -1 & 4 \end{bmatrix} + \begin{bmatrix} 2 \\ -1 \\ 4 \end{bmatrix} \begin{bmatrix} 1 & 2 & -3 \end{bmatrix} \\ &= \begin{bmatrix} 4 & 3 & -2 \\ 3 & -4 & 11 \\ -2 & 11 & -24 \end{bmatrix} \end{align}$
- 선 $l$ 상의 점 $x_{1} = (-1, 2, 1)$ 과 $m$ 상의 점 $x_{2} = (-2, 0, 1)$ 모두 다음과 같이 계산하면 $C^{*}$ 이 두 선을 나타냄을 알 수 있습니다.
- $x_{1}^{T} C^{*} x_{1} = \begin{bmatrix} -1 \\ 2 \\ 1 \end{bmatrix} \begin{bmatrix} 4 & 3 & -2 \\ 3 & -4 & 11 \\ -2 & 11 & -24 \end{bmatrix} \begin{bmatrix} -1 & 2 & 1 \end{bmatrix} = 0$
- $x_{2}^{T} C^{*} x_{2} = \begin{bmatrix} -2 \\ 0 \\ 1 \end{bmatrix} \begin{bmatrix} 4 & 3 & -2 \\ 3 & -4 & 11 \\ -2 & 11 & -24 \end{bmatrix} \begin{bmatrix} -2 & 0 & 1 \end{bmatrix} = 0$
④ Circle
- 앞에서 다룬 Conic 유도식의 $a \cdot x_{1}^{2} + b \cdot x_{1}x_{2} + c \cdot x_{2}^{2} + d \cdot x_{1}x_{3} + e \cdot x_{2}x_{3} + f \cdot x_{3}^{2} = 0$ 을 통하여 $(h, k)$ 를 원의 중심으로 가지는 반지름 $r$ 인 원은 다음과 같은 형태를 가짐을 알 수 있습니다.
- $C = \begin{bmatrix} 1 & 0 & -h \\ 0 & 1 & -k \\ -h & -k & h^{2} + k^{2} -r^{2} \end{bmatrix}$
- 예를 들어 원의 중심이 $(0, 0)$ 이고 반지름이 $1$ 인 원이라면 다음과 같이 표현할 수 있습니다.
- $C = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{bmatrix}$
⑤ Ellipse
- 타원 또한 위 식을 통하여 Conic을 유도하면 타원의 중심은 $(h, k)$ 이고 장축의 길이는 $a$ , 단축의 길이는 $b$ 일 경우 다음과 같이 정의할 수 있습니다.
- $\frac{(x - h)^{2}}{a^{2}} + \frac{(y-k)^{2}}{b^{2}} = 1$
- $C = \begin{bmatrix} 1/a^{2} & 0 & -h/a^{2} \\ 0 & 1/b^{2} & -k/b^{2} \\ -h/a^{2} & -k/b^{2} & h^{2}/a^{2} + k^{2}/b^{2} - 1 \end{bmatrix}$
- 예를 들어 타원의 중심이 $(2, 3)$ 이고 장축의 길이가 $4$ , 단축의 길이가 $2$ 라면 Conic은 다음과 같이 정의 됩니다.
- $C = \begin{bmatrix} 1/16 & 0 & -1/8 \\ 0 & 1/4 & -3/4 \\ -1/8 & -3/4 & 7/16 \end{bmatrix}$
⑥ Hyperbola
- 쌍곡선도 타원의 예시와 유사하게 다음과 같이 정의할 수 있습니다.
- $\frac{(x - h)^{2}}{a^{2}} - \frac{(y-k)^{2}}{b^{2}} = 1$
- $C = \begin{bmatrix} 1/a^{2} & 0 & -h/a^{2} \\ 0 & -1/b^{2} & k/b^{2} \\ -h/a^{2} & k/b^{2} & h^{2}/a^{2} - k^{2}/b^{2} - 1 \end{bmatrix}$
⑦ Parabola
- 마지막으로 포물선의 경우 포물선의 꼭지점이 $(h, k)$ 이고 width $a$ 는 다음과 같이 정의 할 수 있습니다.
- $(y - k) = a(x - h)^{2}$
- $y - k - a(x-h)^{2} = 0$
- $$ C = $\begin{bmatrix} 0 & -a/2 & ah \ -a/2 & 1 & -k \ ah & -k & -h^{2} \end{bmatrix}$
- 예를 들어 포물선의 꼭지점이 $(2, 3)$ 이고 $a = 1$ 이라면 다음과 같이 conic을 구성할 수 있습니다.
- $C = \begin{bmatrix} 0 & -1/2 & 2 \\ -1/2 & 1 & -3 \\ 2 & -3 & -4 \end{bmatrix}$
지금까지 살펴본 방식으로 기하학에서 흔히 다루는 7 가지 경우에 대하여 모두 conic으로 나타낼 수 있음을 확인하였습니다.

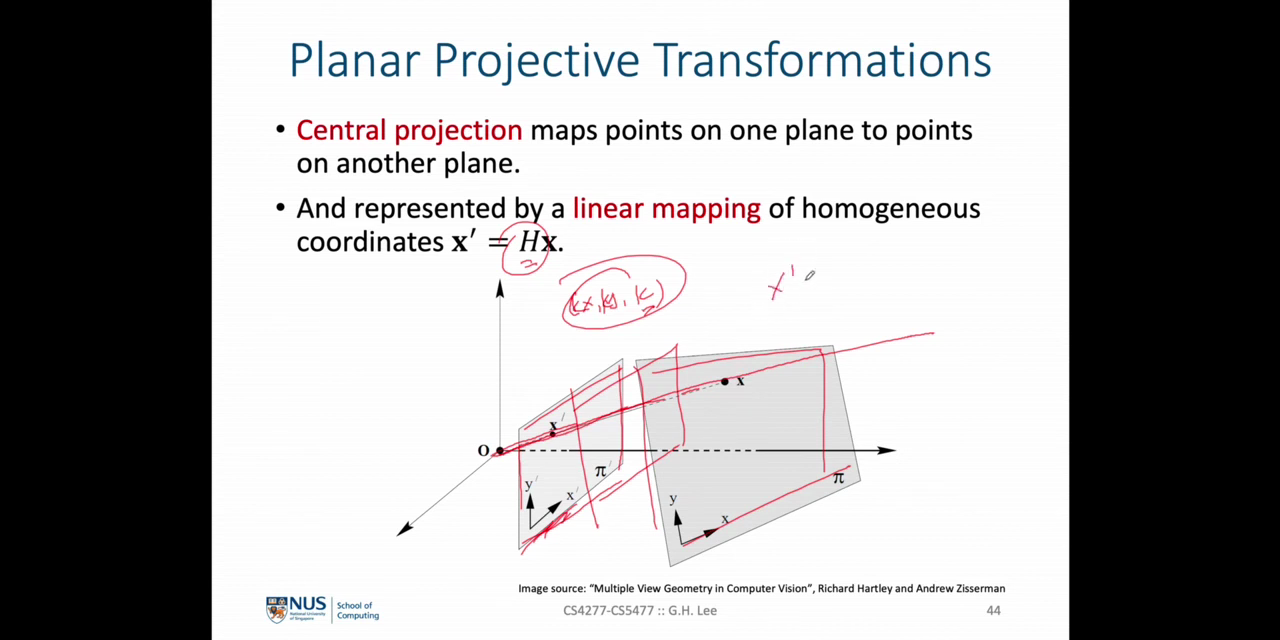
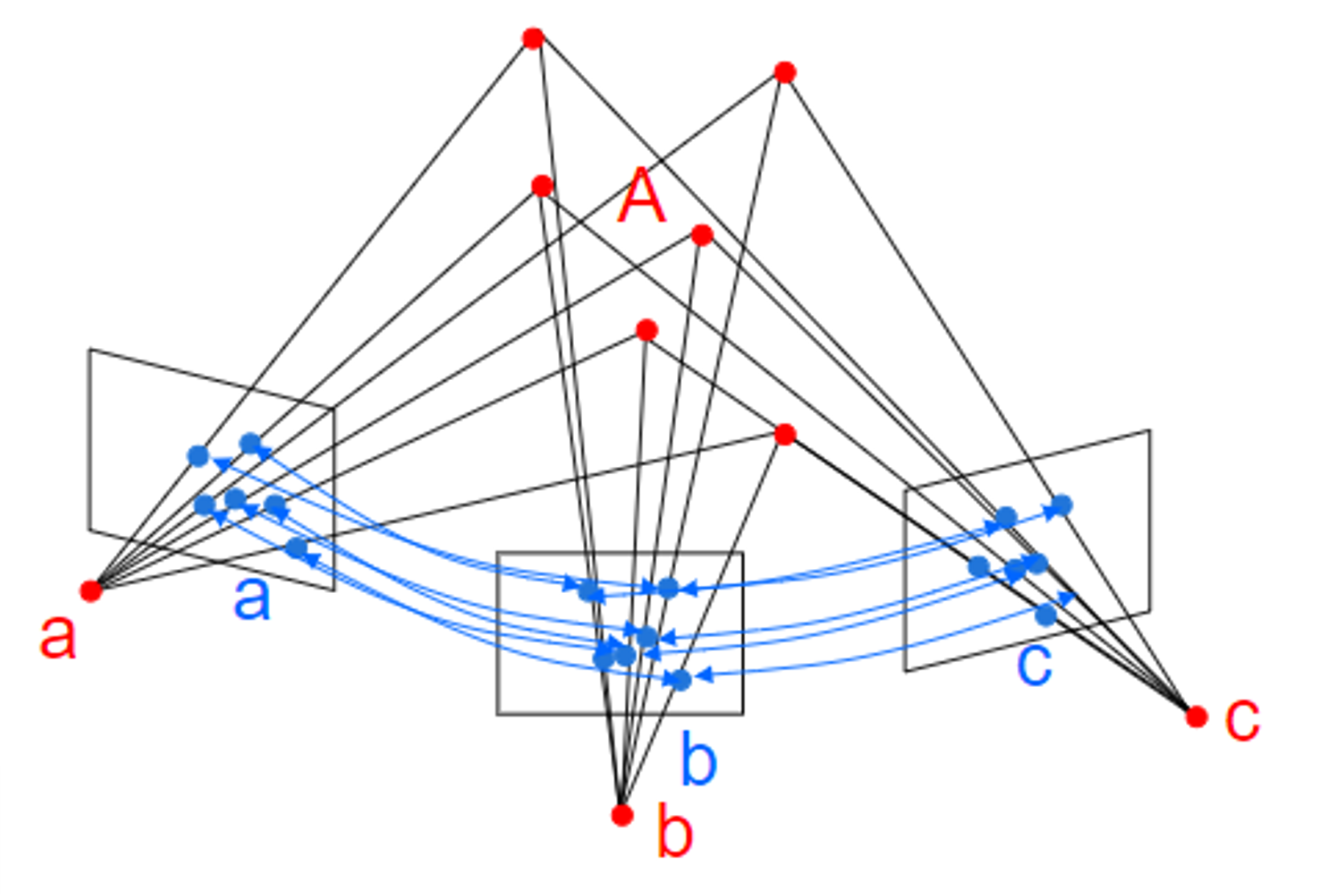
point $x_{i}$ 가 line $l$ 위에 있을 때, $l^{T} x_{i} = 0$ 으로 표현할 수 있습니다. 만약 transformed point (projective transformation) 인 $x_{i}' = H x_{i}$ 가 $l'$ 위에 있다면 ${l'}^{T} x_{i}' = 0$ 이 되고 $l$ 과 $l'$ 두 line의 관계로 나타내면 $l' = H^{-T} l$ 으로 표현할 수 있습니다. 수식 전개 과정은 아래와 같습니다.

$x_{i}' = H x_{i}$
${l'}^{T} x_{i}' = 0$
$\therefore \quad {l'}^{T} H x_{i} = 0$
${l'}^{T} H x_{i} = l^{t} x_{i}$
${l'}^{T} H = l^{t}$
$H^{T} l' = l$
$\therefore \quad l' = H^{-T} l$

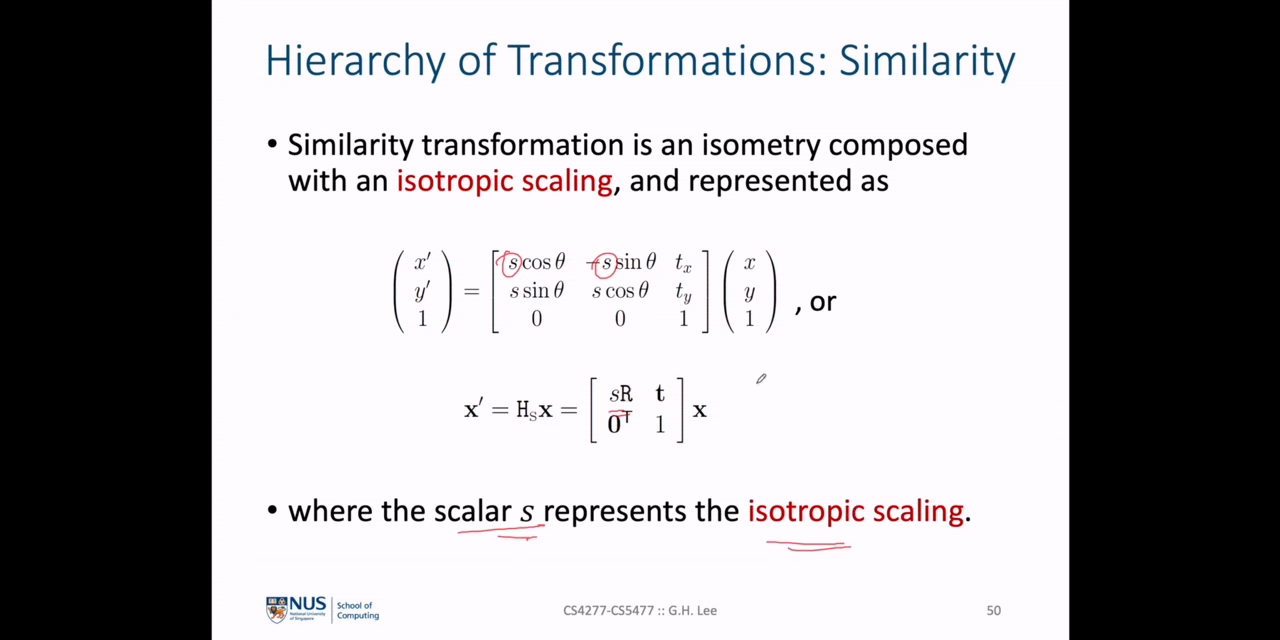
Similarity Transformation은 isotropic scaling 으로 구성되며 위 슬라이드의 식 처럼 표현됩니다.
isotropic이란 한글로 등방형이며 방향에 상관없이 일정하다는 뜻입니다. 즉, Similarity Transformation은 모든 방향에 동일한 효과를 적용합니다.
위 식에서 $s$ 는 isotropic scaling이라고 하며 Similarity Transformation 적용 시 변환의 크기를 조절합니다.

Similarity Transformation은 shape을 보존하기 때문에 equi-form transformation이라고도 합니다.
식에서 나타난 바와 같이 3개의 isometry DoF ( $\theta, t_{x}, t_{y}$ )와 isotropic scaling $s$ 를 가지므로 Similarity Transformation은 총 4 DoF를 가지며 DoF가 4개이므로 변환된 2개의 점을 알 때, 이 값들을 추정할 수 있습니다.
shape이 보존되기 때문에 Angle, ratio of two lengths, ratio of areas는 보존이되는 성질을 가집니다. 평행선은 평행선으로 유지되는 것 또한 중요한 성질입니다.

그 다음으로 Affinity에 대하여 다루어 보도록 하겠습니다.
위 슬라이드에서 설명하는 Affine Transformation 행렬은 non-singular linear transformation으로 간단히 말하면 역행렬이 존재하는 행렬이며 $A$ 부분의 2 X 2 행렬 또한 non-singular matrix로 역행렬이 존재합니다.
앞에서 살펴본 Similarity Transformation과 다르게 6 DoF로 DoF가 2개가 더 추가가 되었습니다. Similarity Transformation에서는 $\theta$ 가 정해지면 $H_{S}$ 가 정해졌으나 Affine Transformation에서는 4개의 각 성분이 모두 DoF를 가지기 때문에 DoF가 총 6개가 됩니다.
DoF가 6개이므로 기존의 3개의 점이 Affine Transformation 적용 시 어떻게 변환되는 지 관계를 알면 Affine Transformation을 구할 수 있습니다. (Similarity Transformation에서는 점 2개가 필요하였습니다.)
Affine Transformation을 적용하더라도 평행선은 그대로 유지되며 평행 선분의 길이 비율과 면적 비율은 유지됩니다. 반면 Similarity Transformation에서는 보존되었던 임의의 선의 길이 비율과 선 사이의 각도는 보존되지 않습니다. 그 이유에 대하여 Affine Transformation Matrix를 분해하여 살펴보도록 하겠습니다.

이번 슬라이드와 다음 슬라이드에서는 Affine Transformation을 SVD (Singular Value Decomposition)으로 분해하였을 때, 각 성분이 가지는 의미를 나타냅니다. 위 슬라이드에서는 먼저 어떻게 분해될 수 있는 지 설명합니다.

Affine Transformation의 의미를 기하학적으로 이해하기 위한 방법으로 rotation과 non-isotropic scaling 두 가지 선형 변환의 합성으로 생각하는 방법이 있습니다. 먼저 Affine Transformation은 아래와 같이 분해 됩니다.

$A = R(\theta) R(-\phi) D R(\phi)$
$R(\theta), R(\phi) \text{ : rotation by} \theta, \phi \text{ respectively}$
$D = \begin{bmatrix} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{bmatrix} \text{ : diagonal matrix}$

위 식과 같이 분해되는 이유는 아래와 같습니다. affine transformation matrix를 Singular Value Decomposition을 하고 SVD 결과의 $U, V$ 가 orthogonal matrix이므로 $U^{-1} = U^{T}$ , $V^임을{-1} = V^{T}$ 임을 이용하여 전개하였습니다.

$A = U D V^{T} = U (V^{-1}V) D V^{T} = U (V^{T}V) D V^{T} = (U V^{T})V D V^{T}$
$= R(\theta)(R(-\phi) D R(\phi))$

회전 행렬 관련 글에서 다룬 바와 같이 orthogonal matrix는 rotation 임을 만족하기 때문에 $U = R(\theta)$ , $V = R(-\phi)$ , $V^{T} = R(\phi)$ 로 표현할 수 있어서 위 식과 같이 전개됩니다.

따라서 식을 위 슬라이드와 같이 시각적으로 나타낼 수 있습니다. 위 슬라이드는 affine transformation인 $A$ 를 바로 적용한 결과를 $R(\phi)$ , $D$ , $R(\theta)R(\-phi)$ 순서로 나누어서 보여줍니다.
즉 affine transformation A 에서의 연산 순서는
- ① $\phi$ 만큼 회전합니다.
- ② $x, y$ 방향으로 각각 $\lambda_{1}, \lambda{2}$ 만큼 scaling을 조정합니다. ( $\lambda_{1}x_{1} + \lambda{2}x_{2}$ )
- ③ $-\phi$ 만큼 역회전 합니다. 즉, $\phi$ 만큼 회전한 영역에서 주성분 방향으로 scaling을 조정하고 다시 역회전하여 회전을 없앱니다.
- ④ 마지막으로 $\theta$ 만큼 회전합니다.
이와 같은 순서로 연산을 살펴보았을 때, similarity transformation에 비하여 추가된 개념은 non-isotropic scaling입니다. 즉, scaling 조정 방향을 지정하는 각도 $\phi$ 와 scaling 조정 비율인 $\lambda{1}, \lambda{2}$ 가 이에 해당합니다.
따라서 affine transformation에서는 특정 각도에 대하여 직교하는 방향으로 scaling을 조정하는 것이 중요합니다.

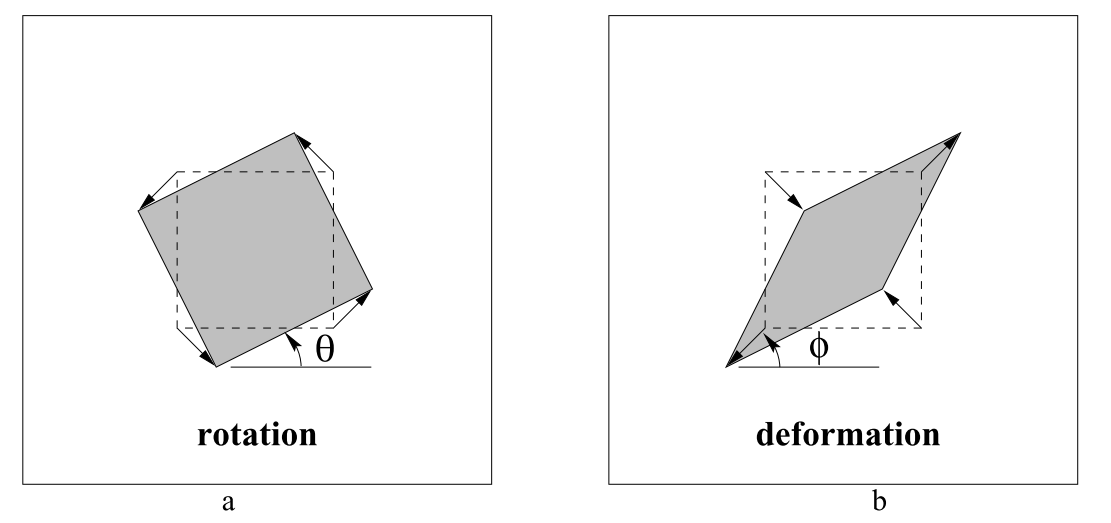
그림으로 나타내면 왼쪽 그림은 최종 $R(\theta)$ 에 의한 회전을 나타내고 오른쪽 그림은 $R(-\phi)DR(\phi)$ 에 의한 변형을 나타냅니다. scaling 방향으로 orthogonal 함을 유심히 살펴보면 이해하는 데 도움이 됩니다.

Multiple View Geometry 글 목차