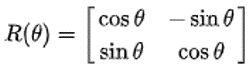
회전 변환 행렬 (2D, 3D)

선형대수학 글 목차

• 참조 : https://en.wikipedia.org/wiki/Rotation_matrix
• 참조 : https://ko.wikipedia.org/wiki/회전변환행렬

• 이번 글에서는 2D와 3D 상태에서의 좌표의 회전 변환하는 방법에 대하여 알아보도록 하겠습니다.

• 다른 방식의 회전 변환 개념은 아래 링크에서 확인하실 수 있습니다. 다음 내용은 본 글에서 다루는 euler rotation의 단점을 개선한 내용입니다.
  • 축각 회전 (로드리게스 회전)
  • 사원수를 이용한 회전 (quarternion)

목차

• 2D에서의 회전 변환

• 회전 변환 행렬 유도

• 임의의 점을 중심으로 회전 변환

• 3D에서의 회전 변환

• 회전 변환 행렬의 구성 요소

• 회전 변환 행렬의 직교성

• Roll, Pitch, Yaw와 Rotation 행렬의 변환

2D에서의 회전 변환

• 2D 좌표계에서 회전 변환을 할 때 사용하는 변환 행렬은 다음과 같습니다.

• $$R(\theta) = \begin{bmatrix} \text{cos}\theta & -\text{sin}\theta \\ \text{sin}\theta & \text{cos}\theta \end{bmatrix}$$

• 여기서 $\theta$는 각도에 해당합니다. 반시계 방향으로 회전하는 방향이 + 각도가 됩니다.
• 위 회전 행렬을 이용하여 $(x, y)$ 좌표를 회전 변환을 하면 다음과 같습니다.

• $$\begin{bmatrix} \text{cos}\theta & -\text{sin}\theta \\ \text{sin}\theta & \text{cos}\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \text{cos}\theta - y \text{sin}\theta \\ x \text{sin}\theta + y \text{cos}\theta \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix}$$

• 위 식을 이용하여 회전 변환한 좌표를 구하면 다음과 같습니다.

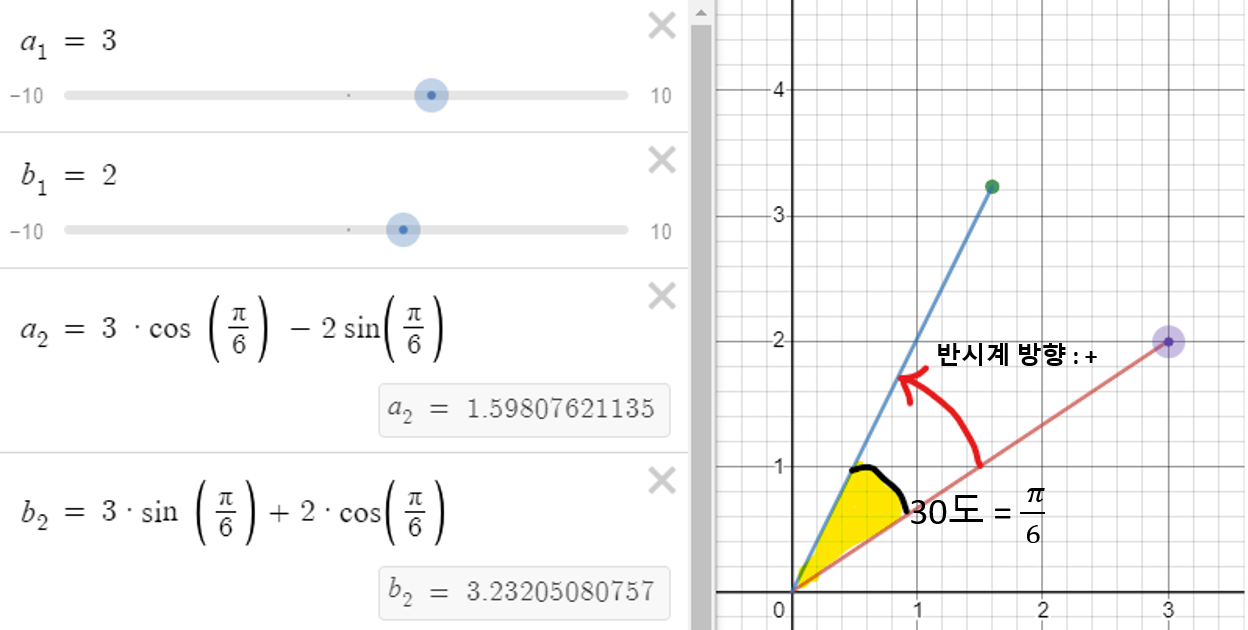
• 자주 사용하는 회전인 90도 회전 / 180도 회전 / 270도 회전은 다음과 같습니다.

• $$R(\frac{\pi}{2}) = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$$
• $$R(\frac{\pi}{2}) = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$$
• $$R(\frac{3\pi}{2}) = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}$$

회전 변환 행렬 유도

• 회전 변환을 다루는 방법에 대해서는 위 글에서 다루었습니다. 그러면 왜 저런 형태의 행렬식이 유도되었는 지에 대하여 다루어 보겠습니다.

• 먼저 앞에서 다룬 회전 변환은 원점을 기준으로 회전을 하게 됩니다. 따라서 위 그림에서도 원점을 중심으로 P가 P'로 어떻게 변환되는 지 다루어 보도록 하겠습니다.
• 아래 식에서 $P, \overline{OP}, \text{cos}(\alpha), \text{sin}(\alpha)$를 정의해 보겠습니다.

• $$P = (x, y)$$
• $$\overline{OP} = l = \sqrt{(x - 0)^{2} + (y - 0)^{2})} = \sqrt{x^{2} + y^{2}}$$
• $$\text{cos}(\alpha) = \frac{x}{\overline{OP}} = \frac{x}{\sqrt{x^{2} + y^{2}}}$$
• $$\text{sin}(\alpha) = \frac{y}{\overline{OP}} = \frac{y}{\sqrt{x^{2} + y^{2}}}$$

• 위 식을 그대로 이용하여 $P'$에 적용해 보도록 하겠습니다. $P' = (x', y')$는 $P = (x, y)$를 $+\theta$ 만큼 회전 시킨 것이므로 회전 각도 만큼 반영해여 식을 적어보겠습니다.

• $$x' = \sqrt{x^{2} + y^{2}} \text{cos}(\alpha + \theta)$$
• $$y' = \sqrt{x^{2} + y^{2}} \text{sin}(\alpha + \theta)$$

• 삼각함수의 덧셈 정리를 이용하여 식을 풀어보도록 하겠습니다.

• $$x' = \sqrt{x^{2} + y^{2}}(\text{cos}(\alpha)\text{cos}(\theta) -\text{sin}(\alpha)\text{sin}(\theta)) = \Biggl(\sqrt{x^{2} + y^{2}}\frac{x}{\sqrt{x^{2} + y^{2}}}\text{cos}(\theta) - \sqrt{x^{2} + y^{2}}\frac{y}{\sqrt{x^{2} + y^{2}}}\text{sin}(\theta) \Biggr) = x\text{cos}(\theta) - y\text{sin}(\theta)$$

• $$y' = \sqrt{x^{2} + y^{2}}\text{sin}(\alpha + \theta) = \sqrt{x^{2} + y^{2}}(\text{sin}(\alpha)\text{cos}(\theta) + \text{cos}(\alpha)\text{sin}(\theta)) = \Biggl(\sqrt{x^{2} + y^{2}}\frac{y}{\sqrt{x^{2} + y^{2}}}\text{cos}(\theta) + \sqrt{x^{2} + y^{2}}\frac{x}{\sqrt{x^{2} + y^{2}}}\text{sin}(\theta) \Biggr) = y\text{cos}(\theta) + x\text{sin}(\theta)$$

• 위에서 유도한 식을 정리하면 다음과 같습니다.

• $$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \text{cos}\theta & -\text{sin}\theta \\ \text{sin}\theta & \text{cos}\theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$

임의의 점을 중심으로 회전 변환

• 앞에서 다룬 내용은 모두 원점을 기준으로 회전한 것입니다. 좀 더 일반적인 케이스를 적용하기 위해 기준이 원점이 아니라 특정 좌표를 기준으로 회전 시켜보도록 하겠습니다.

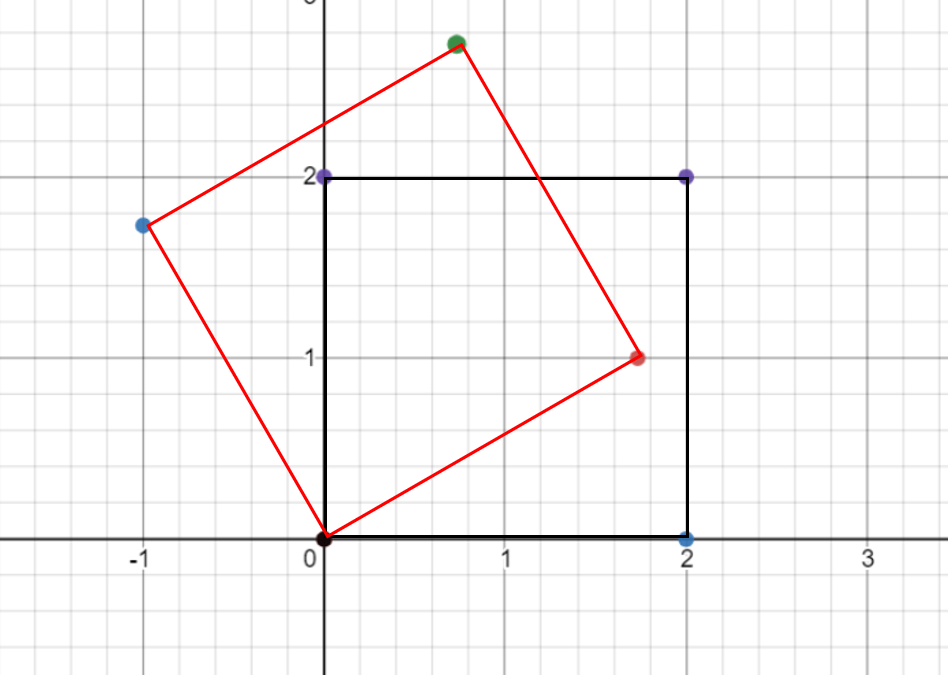
• 위 그림을 보면 원점을 기준으로 30도 회전한 것을 알 수 있습니다.

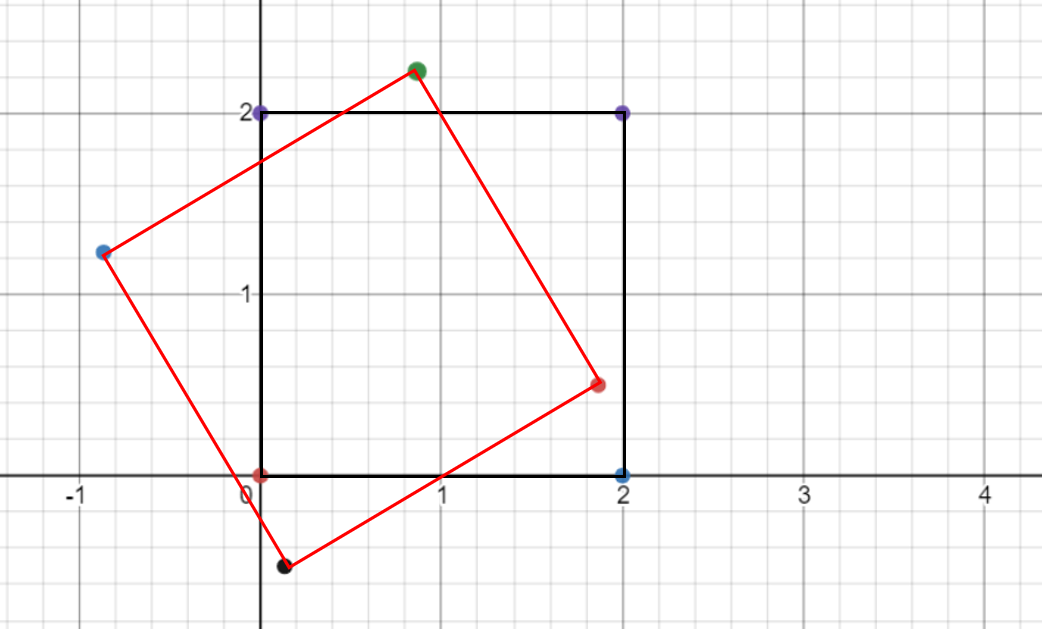
• 반면에 위 그림에서는 회전한 기준을 보면 (1, 0)임을 알 수 있습니다.

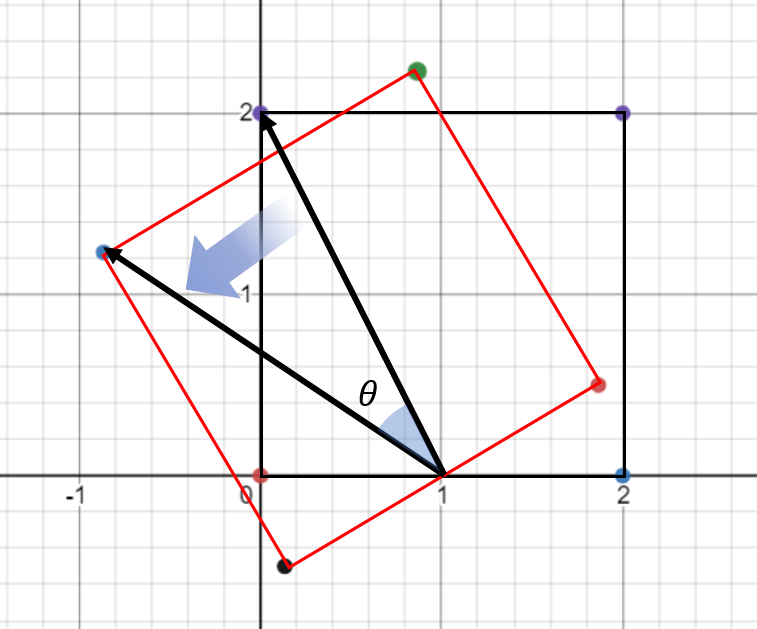
• 지금부터 해야할 작업은 위 그림 처럼 기준점에서 각 점 방향으로의 벡터를 회전하는 것입니다. (물론 반시계 방향 회전이 + 회전 각도 입니다.)

• ① 기준점을 $v_{0} = (x_{base}, y_{base})$ 이라고 하면 각 점 방향으로의 벡터는 $v_{i} - v_{0} = (x_{i} - x_{base}, y_{i} - y_{base})$이 됩니다.
• ② 이 벡터를 앞에서 알아본 변환 행렬을 이용하여 회전 시키면 됩니다.

• $$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \text{cos}\theta & -\text{sin}\theta \\ \text{sin}\theta & \text{cos}\theta \end{pmatrix} \begin{pmatrix} x - x_{base} \\ y - y_{base} \end{pmatrix}$$

• 여기 까지 계산 하면 ($(0, 0)$ → $(x - x_{base}, y - y_{base})$) 방향과 크기의 벡터가 $\theta$ 만큼 회전하여 $(x', y')$가 되었습니다.
• ③ 벡터의 시작점을 회전 기준인 $(x_{base}, y_{base})$으로 옮겨줍니다.
• ①, ②, ③ 과정을 식으로 옮기면 다음과 같습니다.

• $$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \text{cos}\theta & -\text{sin}\theta \\ \text{sin}\theta & \text{cos}\theta \end{pmatrix} \begin{pmatrix} x - x_{base} \\ y - y_{base} \end{pmatrix} + \begin{pmatrix} x_{base} \\ y_{base} \end{pmatrix}$$

3D에서의 회전 변환

• 3D에서의 회전 변환은 2차원에서 사용한 회전 변환 행렬을 유사하게 사용합니다. 다만 이 때, 3차원에 맞춰서 행렬의 차원이 늘어나게 되고 각 차원별로 회전을 고려해 주어야 합니다.
• 예를 들어서 $R_{x}(\theta)$는 x축을 중심으로 회전하는 행렬 변환이고 $R_{y}(\theta)$는 y축을 중심으로 $R_{z}(\theta)$는 z축을 중심으로 회전하는 행렬 변환입니다.

• $$R_{x}(\theta) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \text{cos}\theta & -\text{sin}\theta \\ 0 & \text{sin}\theta & \text{cos}\theta \end{bmatrix}$$
• $$R_{y}(\theta) = \begin{bmatrix} \text{cos}\theta & 0 & \text{sin}\theta \\ 0 & 1 & 0 \\ -\text{sin}\theta & 0 & \text{cos}\theta \end{bmatrix}$$
• $$R_{z}(\theta) = \begin{bmatrix} \text{cos}\theta & -\text{sin}\theta & 0 \\ \text{sin}\theta & \text{cos}\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

• 이 행렬을 정리해 보려고 하는데, 그 전에 roll, yaw, pitch에 대하여 알아보겠습니다.

• 위 회전축 기준으로 roll은 x축을 기준으로 회전한 양을 뜻하고 pitch는 y축을 기준으로 회전한 양 그리고 yaw는 z축을 기준으로 회전한 양을 뜻합니다. 위 그림처럼 생각하시면 됩니다.
  • 예를 들어 자동차가 좌회전 또는 우회전을 한다면 z축을 기준으로 회전을 하는 것이므로 yaw의 변화가 있게 됩니다.
• 그러면 $R_{x}(\theta)$, $R_{y}(\theta)$ 그리고 $R_{z}(\theta)$ 각각 x축, y축, z축을 기준으로 회전하는 회전 변환 행렬이 됩니다.
• x축을 기준으로 회전한 roll angle을 $\alpha$, y축을 기준으로 회전한 pitch angle을 $\beta$ 마지막으로 z축을 기준으로 회전한 yaw angle을 $\gamma$로 두겠습니다.

• $$R = R_{z}(\gamma)R_{y}(\beta)R_{x}(\alpha) = \begin{bmatrix} \text{cos}\gamma & -\text{sin}\gamma & 0 \\ \text{sin}\gamma & \text{cos}\gamma & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \text{cos}\beta & 0 & \text{sin}\beta \\ 0 & 1 & 0 \\ -\text{sin}\beta & 0 & \text{cos}\beta \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \text{cos}\alpha & -\text{sin}\alpha \\ 0 & \text{sin}\alpha & \text{cos}\alpha \end{bmatrix}$$

• 위 변환 행렬을 모두 곱하면 roll, pitch, yaw angle을 모두 고려한 회전을 나타낼 수 있습니다.
• 위 식을 풀어서 나타내면 다음과 같습니다.

• $$R = \begin{bmatrix} \text{cos}\gamma \ \text{cos}\beta & \text{cos}\gamma \ \text{sin}\beta \ \text{sin}\alpha - \text{sin}\gamma \ \text{cos}\alpha & \text{cos}\gamma \ \text{sin}\beta \ \text{cos}\alpha + \text{sin}\gamma \ \text{sin}\alpha \\ \text{sin}\gamma \ \text{cos}\beta & \text{sin}\gamma \ \text{sin}\beta \ \text{sin}\alpha + \text{cos}\gamma \ \text{cos}\alpha & \text{sin}\gamma \ \text{sin}\beta \ \text{cos}\alpha - \text{cos}\gamma \ \text{sin}\alpha \\ -\text{sin}\beta & \text{cos}\beta \ \text{sin} \alpha & \text{cos}\beta \ \text{cos} \alpha \\ \end{bmatrix}$$

• 위 식을 파이썬 코드로 나타내면 다음과 같습니다.

import numpy as np

def euler_to_rotation_matrix(roll, pitch, yaw):
    # Convert angles to radians
    roll = np.radians(roll)
    pitch = np.radians(pitch)
    yaw = np.radians(yaw)

    # Define individual rotation matrices
    Rx = np.array([[1, 0, 0],
                   [0, np.cos(roll), -np.sin(roll)],
                   [0, np.sin(roll), np.cos(roll)]])
    
    Ry = np.array([[np.cos(pitch), 0, np.sin(pitch)],
                   [0, 1, 0],
                   [-np.sin(pitch), 0, np.cos(pitch)]])
    
    Rz = np.array([[np.cos(yaw), -np.sin(yaw), 0],
                   [np.sin(yaw), np.cos(yaw), 0],
                   [0, 0, 1]])

    # Combine the rotations
    R = np.dot(Rz, np.dot(Ry, Rx))
    return R

회전 변환 행렬의 구성 요소

• 회전 변환 행렬의 경우 각 열의 성분이 각 축의 기저 벡터 (basis vector)가 회전 되었을 때의 벡터를 의미합니다. 3차원 행렬의 경우 $X, Y, Z$ 순서로 축의 의미를 가진다면 회전 변환 행렬의 첫번째 열은 $X$ 축의 기저 벡터를 회전 변환하였을 때의 벡터, 두번째 열은 $Y$ 축의 기저 벡터를 회전 변환하였을 때의 벡터, 세번째 열은 $Z$ 축의 기저 벡터를 회전 변환하였을 때의 벡터를 의미합니다.
• 각 축의 기저 벡터를 회전하는 예시를 확인하면 그 뜻을 쉽게 알 수 있습니다.

• $$\begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} R_{11} \\ R_{21} \\ R_{31} \end{bmatrix}$$
• $$\begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} R_{12} \\ R_{22} \\ R_{32} \end{bmatrix}$$
• $$\begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} R_{13} \\ R_{23} \\ R_{33} \end{bmatrix}$$

• 첫번째 예시인 $X$ 축의 예시를 살펴보면 기저 벡터가 $[1, 0, 0]^{T} \to [R_{11}, R_{21}, R_{31}]^{T}$ 로 변환된 것을 알 수 있습니다. 두번째, 세번째 예시를 통하여 $Y, Z$ 축이 어떻게 변하는 지 또한 확인할 수 있습니다.

• 다음 예시를 통하여 간단하게 회전 변환의 역할에 대하여 알아보도록 하겠습니다.

• $$\begin{bmatrix} 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 & 0 \end{bmatrix}$$

• 먼저 첫번째 열인 $[0, 0, 1]^{T}$ 을 통해 $X$ 축의 기저 벡터에 회전 변환 행렬을 적용하면 $[1, 0, 0] \to [0, 0, 1]^{T}$ 이 된 것을 알 수 있습니다. 즉, $Z$ 축의 기저 벡터 처럼 변경 되었습니다.
• 두번째 열인 $[-1, 0, 0]^{T}$ 을 통해 $Y$ 축의 기저 벡터에 회전 변환 행렬을 적용하면 $[0, 1, 0] \to [-1, 0, 0]^{T}$ 이 된 것을 알 수 있습니다. 즉, 음의 방향의 $X$ 축 기저 벡터 처럼 변경 되었습니다.
• 세번째 열인 $[0, -1, 0]^{T}$ 을 통해 $Z$ 축의 기저 벡터에 회전 변환 행렬을 적용하면 $[0, 0, 1] \to [0, -1, 0]^{T}$ 이 된 것을 알 수 있습니다. 즉, 음의 방향의 $Y$ 축 기저 벡터 처럼 변경 되었습니다.
• 따라서 R[:, 0], R[:, 1], R[:, 2] 성분을 이용하면 기저 벡터가 어떻게 회전 변환 되는 지 알 수 있습니다.

• 임의의 회전 행렬을 적용하였을 때, 현재 좌표축 기준으로 변환된 좌표축에서의 기저 벡터를 구하고 싶다면 각 열에서 절대값이 가장 큰 축을 기저 벡터로 간주하여 기저 벡터를 구성하면 됩니다. 이 때, 부호 또한 반영하면 현재 기저 벡터 기준으로 축의 방향 또한 고려하여 확인할 수 있습니다.

R = np.array([
    0.00463, -0.99998, 0.00385, 
    -0.01405, -0.00391, -0.99989, 
    0.99989, 0.00457, -0.01407]
).reshape(3, 3)

basis_rotation = np.zeros((3, 3), dtype=np.float32)
for i in range(3):
    axis = np.argmax(np.abs(R[:, i]))
    if R[axis, i] > 0:
        basis_rotation[axis, i] = 1.0
    elif R[axis, i] < 0:
        basis_rotation[axis, i] = -1.0
    else:
        basis_rotation[axis, i] = 0.0

print(basis_rotation)
# [[ 0. -1.  0.]
#  [ 0.  0. -1.]
#  [ 1.  0.  0.]]

• basis_rotation이 앞에서 해석한 내용과 동일한 값을 가집니다. 이와 같은 방법으로 현재 좌표계 기준의 기저 벡터가 회전 변환을 거쳤을 때, 어떻게 바뀌는 지 확인할 수 있습니다.

회전 변환 행렬의 직교성

• 지금까지 살펴본 rotation 행렬은 orthogonal 행렬이며 다음과 같은 성질을 따릅니다.

• $$R^{T} = R^{-1}$$
• $$R^{T} R = I$$

• orthogonal 또는 orthonormal인 행렬 $Q$ 가 있을 때, $QQ^{T} = Q^{T}Q = I$ 임은 필요충분 조건임이 알려져 있습니다.
• 앞에서 살펴본 2D, 3D 회전 변환 행렬의 경우도 $RR^{T} = R^{T}R = I$ 를 만족하며 일반적으로 orthogonal 형태이므로 orthogonal 하다고 말할 수 있습니다.
• 또한 orthogonal한 경우 determinant가 1을 만족하는데 이 조건에도 만족하게 됩니다.

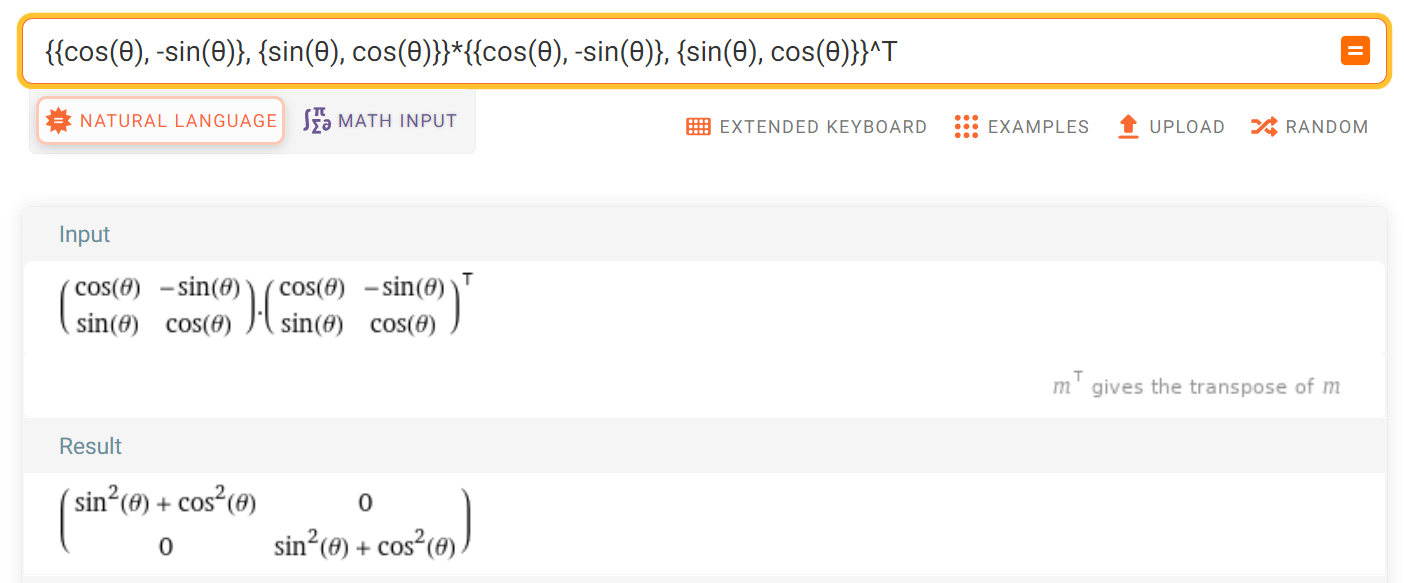
• 위 계산 결과와 같이 2D 회전 변환 행렬 $R$ 의 $RR^{T} = I$ 임을 확인할 수 있습니다.

• 3D 회전 변환 행렬의 경우 간단히 det(R) = I 임을 통해 orthogonal임을 확인해 보겠습니다.

• 아래 식과 같이

• $$R = R_z(\alpha)\,R_y(\beta)\,R_x(\gamma)$$
• $$R^T\,R=(R_z\,R_y\,R_x)^T\,(R_z\,R_y\,R_x)=R_x^T\,R_y^T\,R_z^T\,R_z\,R_y\,R_x$$
• $$R_{x}^{T}R_{X} = I$$
• $$R_{y}^{T}R_{y} = I$$
• $$R_{z}^{T}R_{z} = I$$
• $$\therefore R^{T}R = I$$
• $$\text{plus, } \det(R)=\det(R_z)\,\det(R_y)\,\det(R_x)=1\times 1\times 1=1$$

• 아래와 같이 3D 회전 변환 행렬의 각 방향의 $R_{x}, R_{y}, R_{z}$ 의 determinant는 1임을 확인할 수 있습니다.

Roll, Pitch, Yaw와 Rotation 행렬의 변환

• 참조 : https://eecs.qmul.ac.uk/~gslabaugh/publications/euler.pdf
• 참조 : atan과 atan2 비교

• 지금까지 살펴본 방식은 Roll, Pitch, Yaw를 이용하여 Rotation 행렬을 구하는 방법에 대하여 살펴보았습니다.
• 이번에는 임의의 Rotation 행렬이 주어졌을 때, 이 행렬을 Roll, Pitch, Yaw로 분해하는 방법을 알아보도록 하겠습니다. 3차원 좌표축의 기준은 앞에서 다룬바와 같이 $X$ 축이 전방, $Y$ 축이 왼쪽, $Z$ 축이 위로 향하는 Forward-Left-Up 순서의 좌표축을 의미합니다. 만약 다른 좌표축 기준에서 Roll, Pitch, Yaw 성분을 분해하려면 아래 내용을 이해한 다음에 분해 순서 및 방식을 일부 수정하여 적용해야 합니다.

• 앞에서 Roll, Pitch, Yaw 각각은 다음과 같은 형태로 표현할 수 있었습니다. 아래 식에서 $\psi$ 는 $x$ 축의 회전인 Roll 의 각도를 의미하며 $\theta$ 는 $y$ 축의 회전인 Pitch의 각도를 의미하고 마지막으로 $\phi$ 는 $z$ 축의 회전인 Yaw의 각도를 의미합니다.

• $$R_{x}(\psi) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\psi} & -\sin{\psi} \\ 0 & \sin{\psi} & \cos{\psi} \end{bmatrix}$$
• $$R_{y}(\theta) = \begin{bmatrix} \cos{\theta} & 0 & \sin{\theta} \\ 0 & 1 & 0 \\ -\sin{\theta} & 0 & \cos{\theta} \end{bmatrix}$$
• $$R_{z}(\phi) = \begin{bmatrix} \cos{\phi} & -\sin{\phi} & 0 \\ \sin{\phi} & \cos{\phi} & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

• 앞에서 다룬 바와 같이 Rotation 행렬은 다음과 같이 Roll, Pitch, Yaw를 이용하여 표현할 수 있었습니다. 회전 순서는 $R_{x}, R_{y}, R_{z}$ 순서로 곱해지기 때문에 Roll, Pitch, Yaw 순서로 회전 됩니다.

• $$\begin{align} R &= R_{z}(\phi)R_{y}(\theta)R_{x}(\psi) \\ &= \begin{bmatrix} \cos{\theta}\cos{\phi} & \sin{\psi}\sin{\theta}\cos{\phi}-\cos{\psi}\sin{\phi} & \cos{\psi}\sin{\theta}\cos{\phi} + \sin{\psi}\sin{\phi} \\ \cos{\theta}\sin{\phi} & \sin{\psi}\sin{\theta}\sin{\phi} + \cos{\psi}\cos{\phi} & \cos{\psi}\sin{\theta}\sin{\phi}-\sin{\psi}\cos{\phi} \\ -\sin{\theta} & \sin{\psi}\cos{\theta} & \cos{\psi}\cos{\theta} \end{bmatrix} \\ &= \begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33}\end{bmatrix} \end{align}$$

• 현재 알고 싶은 정보는 위 Rotation 행렬 $R$ 을 이용하여 $\psi, \theta, \phi$ 를 구하고 싶은 것입니다.

• 2개의 $\theta$ 구하기

• 앞에서 $R$ 을 구하였을 때, $R_{31}$ 은 다음과 같습니다.

• $$R_{31} = -\sin{(\theta)}$$

• 따라서 $\theta$ 를 쉽게 구할 수 있습니다.

• $$\theta = \sin^{-1}{(-R_{31})} = -\sin^{-1}{(R_{31})}$$

• 추가적으로 $\sin{(\pi - \theta)} = \sin{\theta}$ 를 만족하므로 다음과 같이 2개의 식을 만족하는 $\theta$ 를 구할 수 있습니다. 단, $R_{31} \ne \pm 1$ 인 경우를 가정하며 이유는 글의 뒷부분에서 이어서 설명하도록 하겠습니다.

• $$\theta_{1} = -\sin^{-1}{(R_{31})}$$
• $$\theta_{2} = \pi - \theta_{1} = \pi + \sin^{-1}{(R_{31})}$$

• 위 식의 전개와 같이 $\theta$ 가 2 종류가 나오기 때문에 최종 해 또한 2 종류로 도출됩니다.

• 대응되는 $\psi$ 구하기

• 위 식에서 $R_{32}, R_{33}$ 을 이용하면 $\psi$ 를 구할 수 있습니다.

• $$\frac{R_{32}}{R_{33}} = \frac{\sin{(\psi)}\cos{(\theta)}}{\cos{(\psi)}\cos{(\theta)}} = \frac{\sin{(\psi)}}{\cos{(\psi)}} = \tan{(\psi)}$$
• $$\psi = \text{atan2}(R_{32}, R_{33})$$

• 위 식의 $\text{atan2}$ 는 수치적 안정성을 위해 사용합니다. 일반적인 $\text{atan}$ 은 1사분면과 4사분면만 표현할 수 있습니다. 즉, 분자, 분모가 모두 양수이거나 모두 음수인 경우만 $\text{atan}$ 을 연산할 수 있습니다. 반면에 4개의 사분면에서 모두 $\text{atan}$ 을 적용하기 위해 함수화한 것이 $\text{atan2}$ 라고 말할 수 있습니다. 상세 내용은 아래 링크를 참조하시기 바랍니다.
  • 참조 : atan과 atan2 비교

• 따라서 $\text{atan2}$ 를 적용할 때에는 부호를 잘 고려해서 함수에 적용하면 위 링크에서 예외 처리한 내용을 고민하지 않고 계산할 수 있습니다.
• 따라서 앞선 식 $\frac{R_{32}}{R_{33}} = \frac{\sin{(\psi)}\cos{(\theta)}}{\cos{(\psi)}\cos{(\theta)}} = \frac{\sin{(\psi)}}{\cos{(\psi)}}$ 에서 단순히 $\cos{(\theta)}$ 를 소거하지 않고 다음과 같이 연산해 줍니다. 다음과 같이 연산하면 $\cos{(\theta)} \ne 0$ 일 때에 연산이 모두 유효합니다.

• $$\psi = \text{atan2}(\frac{R_{32}}{\cos{(\theta)}}, \frac{R_{33}}{\cos{(\theta)}})$$

• 위 식에서 $\cos{(\theta)}$ 는 $\theta$ 의 값이 1, 4 사분면에 있으면 양수이고 2, 3 사분면에 있으면 음수이기 때문에 위 식과 같이 부호를 고려한다면 $\theta$ 의 값에 따라 $\psi$ 를 구할 수 있습니다.
• 앞선 식에서 $\theta$ 의 후보로 $\theta_{1}, \theta_{2}$ 가 있었기 때문에 다음과 같이 2개의 $\psi_{1}, \psi_{2}$ 를 구할 수 있습니다. $\cos{(\theta)} = 0$ 인 경우는 글 뒷부분에서 한번에 예외처리 하도록 하겠습니다.

• $$\psi_{1} = \text{atan2}(\frac{R_{32}}{\cos{(\theta_{1})}}, \frac{R_{33}}{\cos{(\theta_{1})}})$$
• $$\psi_{2} = \text{atan2}(\frac{R_{32}}{\cos{(\theta_{2})}}, \frac{R_{33}}{\cos{(\theta_{2})}})$$

• 대응되는 $\phi$ 구하기

• 앞에서 $\psi_{1}, \psi_{2}$ 를 구할 때에는 $R_{32}, R_{33}$ 을 이용하였습니다. $\phi$ 를 구할 때에는 $R_{21}, R_{11}$ 을 이용해 보도록 하겠습니다. 방식은 완전히 동일합니다.

• $$\phi = \text{atan2}(\frac{R_{21}}{\cos{(\theta)}}, \frac{R_{11}}{\cos{(\theta)}})$$

• 이 경우에도 $\cos{(\theta)} \ne 0$ 일 때, 계산이 모두 유효하며 아래와 같이 2개의 $\phi_{1}, \phi_{2}$ 를 구할 수 있습니다.

• $$\phi_{1} = \text{atan2}(\frac{R_{21}}{\cos{(\theta_{1})}}, \frac{R_{11}}{\cos{(\theta_{1})}})$$
• $$\phi_{2} = \text{atan2}(\frac{R_{21}}{\cos{(\theta_{2})}}, \frac{R_{11}}{\cos{(\theta_{2})}})$$

• $\cos{(\theta)} \ne 0$ 일 때의 Euler Angles

• 지금까지 살펴본 방법으로 $\cos{(\theta)} \ne 0$ 일 때, 다음과 같이 2가지 Euler Angles를 구할 수 있습니다.

• $$(\psi_{1}, \theta_{1}, \phi_{1}) = (\text{Roll}_{1}, \text{Pitch}_{1}, \text{Yaw}_{1})$$
• $$(\psi_{2}, \theta_{2}, \phi_{2}) = (\text{Roll}_{2}, \text{Pitch}_{2}, \text{Yaw}_{2})$$

• $\cos{(\theta)} = 0$ 일 때의 Euler Angles

• 다음과 같이 $\cos{(\theta)} = 0$ 인 경우는 $\theta = \frac{\pi}{2}$ 또는 $\theta = -\frac{\pi}{2}$ 입니다. 그리고 $R_{31} = \sin{(\theta)} = \pm 1$ 인 경우를 의미하기도 합니다.
• 이 경우에도 앞에서 살펴본 방식과 동일하게 수식을 전개한다면 $R_{11}, R_{12}, R_{32}, R_{33}$ 이 0이기 때문에 다음과 같은 문제가 발생합니다.

• $$\psi = \text{atan2}(\frac{0}{0}, \frac{0}{0})$$
• $$\phi = \text{atan2}(\frac{0}{0}, \frac{0}{0})$$

• 즉, $\psi, \phi$ 의 값을 정할 수 없게 됩니다. 이와 같은 현상을 Gimbal Lock이라고 하며 다음 링크에서 그 현상의 기하학적인 의미를 살펴볼 수 있습니다.
  • 링크 : https://gaussian37.github.io/vision-concept-axis_angle_rotation/
• 이러한 문제를 회피하여 Euler Angles를 구하기 위해 다음과 같이 식을 전개해 보도록 하겠습니다.

• 먼저 $\theta = \frac{\pi}{2}$ 인 경우 부터 살펴보도록 하겠습니다. $\cos{(\theta)} \ne 0$ 일 때에는 $R_{32}, R_{33}$ 을 이용하여 $\psi$ 를 구하고 $R_{11}, R_{21}$ 을 이용하여 $\phi$ 를 구하였습니다. 반면 $\cos{(\theta)} = 0$ 와 같은 예외 상황을 처리하기 위해서는 $R_{12}, R_{13}, R_{22}, R_{23}$ 을 이용합니다.

• 삼각함수의 덧셈 공식을 이용하면 다음과 같이 식을 전개할 수 있습니다.

$\text{Case 1: } \theta = \frac{\pi}{2}$

• $$R_{12} = \sin{(\psi)}\cos{(\phi)} - \cos{(\psi)}\sin{(\phi)} = \sin{(\psi - \phi)}$$
• $$R_{13} = \cos{(\psi)}\cos{(\phi)} + \sin{(\psi)}\sin{(\phi)} = \cos{(\psi - \phi)}$$
• $$R_{22} = \sin{(\psi)}\sin{(\phi)} - \cos{(\psi)}\cos{(\phi)} = \cos{(\psi - \phi)} = R_{13}$$
• $$R_{23} = \cos{(\psi)}\sin{(\phi)} - \sin{(\psi)}\cos{(\phi)} = -\sin{(\psi - \phi)} = -R_{12}$$

• $$\frac{R_{12}}{R_{13}} = \frac{ \sin{(\psi - \phi)} }{ \cos{(\psi - \phi)} } = \tan{(\psi - \phi)}$$
• $$(\psi - \phi) = \text{atan2}(R_{12}, R_{13})$$
• $$\psi = \phi + \text{atan2}(R_{12}, R_{13})$$

$\text{Case 2: } \theta = -\frac{\pi}{2}$

• $$R_{12} = -\sin{(\psi)}\cos{(\phi)} - \cos{(\psi)}\sin{(\phi)} = -\sin{(\psi + \phi)}$$
• $$R_{13} = -\cos{(\psi)}\cos{(\phi)} + \sin{(\psi)}\sin{(\phi)} = -\cos{(\psi + \phi)}$$
• $$R_{22} = -\sin{(\psi)}\sin{(\phi)} + \cos{(\psi)}\cos{(\phi)} = \cos{(\psi + \phi)} = -R_{13}$$
• $$R_{23} = -\cos{(\psi)}\sin{(\phi)} - \sin{(\psi)}\cos{(\phi)} = -\sin{(\psi + \phi)} = R_{12}$$

• $$\frac{-R_{12}}{-R_{13}} = \frac{ \sin{(\psi + \phi)} }{ \cos{(\psi + \phi)} } = \tan{(\psi + \phi)}$$
• $$(\psi + \phi) = \text{atan2}(-R_{12}, -R_{13})$$
• $$\psi = -\phi + \text{atan2}(-R_{12}, -R_{13})$$

• 지금까지 내용을 살펴보면 $\theta = \pm \frac{\pi}{2}$ 인 Gimbal Lock 상황에서는 $\psi$ 와 $\phi$ 가 서로 연결되어 있어 특정 해를 구할 수 없습니다. 따라서 특정 해를 지정하고 싶으면 $\phi = 0$ 과 같이 임의의 값을 지정해 주어야 합니다.

• 이 조건들을 모두 이용하면 다음과 같이 의사 코드를 작성할 수 있습니다.

• 첫 조건문의 $R_{31} \ne \pm 1$ 은 $\theta \ne \pm\frac{\pi}{2}$ 을 의미합니다.
• 첫 조건문에서 else로 분기되면 $\phi$ 는 어떤 값이 되어도 되므로 임의로 0으로 지정할 수 있습니다.

• 정리하면 임의의 Rotation 행렬을 Euler Angle의 Roll, Pitch, Yaw로 분해할 수 있습니다.
• 이 때, 특정 한 축의 회전각이 $\pm\frac{\pi}{2}$ 인 경우가 아니라면 2개의 해를 가지게 되고 회전 각도의 범위를 고려하여 1개의 해를 선택하여 사용할 수 있습니다. 반면 한 축의 회전각이 $\pm\frac{\pi}{2}$ 인 경우에는 무한히 많은 해를 가지게 되며 Gimbal Lock 현상이 발생합니다.

python code

• 먼저 앞에서 설명한 기호를 이용하여 코드를 작성하면 다음과 같습니다.

import numpy as np

# Define the conversion function
def rotation_matrix_to_euler_angles(R):
    assert(R.shape == (3, 3))

    if R[2, 0] != 1 and R[2, 0] != -1:
        theta1 = -np.arcsin(R[2, 0])
        theta2 = np.pi - theta1
        psi1 = np.arctan2(R[2, 1] / np.cos(theta1), R[2, 2] / np.cos(theta1))
        psi2 = np.arctan2(R[2, 1] / np.cos(theta2), R[2, 2] / np.cos(theta2))
        phi1 = np.arctan2(R[1, 0] / np.cos(theta1), R[0, 0] / np.cos(theta1))
        phi2 = np.arctan2(R[1, 0] / np.cos(theta2), R[0, 0] / np.cos(theta2))
        return (psi1, theta1, phi1), (psi2, theta2, phi2)
    else:
        phi = 0  # can set to anything, it's the gimbal lock case
        if R[2, 0] == -1:
            theta = np.pi / 2
            psi = phi + np.arctan2(R[0, 1], R[0, 2])
        else:
            theta = -np.pi / 2
            psi = -phi + np.arctan2(-R[0, 1], -R[0, 2])
        return (psi, theta, phi), (None, None, None)

# Example rotation matrix
R_example = np.array([
    [0.5, -0.1464, 0.8536],
    [0.5, 0.8536, -0.1464],
    [-0.7071, 0.5, 0.5]
])


# Get the Euler angles
euler_angles_set_1, euler_angles_set_2 = rotation_matrix_to_euler_angles(R_example)

print("euler_angles_set_1:")
print(f"psi: {euler_angles_set_1[0]} radian.({euler_angles_set_1[0] * 180 / np.pi} deg).")
print(f"theta: {euler_angles_set_1[1]} radian.({euler_angles_set_1[1] * 180 / np.pi} deg).")
print(f"phi: {euler_angles_set_1[2]} radian.({euler_angles_set_1[2] * 180 / np.pi} deg).")

print("\neuler_angles_set_2:")
print(f"psi: {euler_angles_set_2[0]} radian.({euler_angles_set_2[0] * 180 / np.pi} deg).")
print(f"theta: {euler_angles_set_2[1]} radian.({euler_angles_set_2[1] * 180 / np.pi} deg).")
print(f"phi: {euler_angles_set_2[2]} radian.({euler_angles_set_2[2] * 180 / np.pi} deg).")

# euler_angles_set_1:
# psi: 0.7853981633974483 radian.(45.0 deg).
# theta: 0.7853885733974476 radian.(44.99945053347443 deg).
# phi: 0.7853981633974483 radian.(45.0 deg).

# euler_angles_set_2:
# psi: -2.356194490192345 radian.(-135.0 deg).
# theta: 2.3562040801923456 radian.(135.00054946652557 deg).
# phi: -2.356194490192345 radian.(-135.0 deg).

• 먼저 첫번째 셋의 결과는 다음과 같습니다.
  • psi = 0.7853981633974483 radian.(45.0 deg).
  • theta = 0.7853885733974476 radian.(44.99945053347443 deg).
  • phi = 0.7853981633974483 radian.(45.0 deg).
• 두번째 셋의 결과는 다음과 같습니다.
  • psi = -2.356194490192345 radian.(-135.0 deg).
  • theta = 2.3562040801923456 radian.(135.00054946652557 deg).
  • phi = -2.356194490192345 radian.(-135.0 deg).
    
• 일반적으로 첫번째 셋의 결과를 사용하면 됩니다.

• 다음으로 많이 사용하는 roll, pitch, yaw로 바꾸어서 표현하면 다음과 같습니다. 구현 방법 및 결과는 동일합니다.

import numpy as np

# Redefine the conversion function using roll, pitch, and yaw after the code state reset
def rotation_matrix_to_euler_angles(R):
    assert(R.shape == (3, 3))

    if R[2, 0] != 1 and R[2, 0] != -1:
        pitch1 = -np.arcsin(R[2, 0])
        pitch2 = np.pi - pitch1
        roll1 = np.arctan2(R[2, 1] / np.cos(pitch1), R[2, 2] / np.cos(pitch1))
        roll2 = np.arctan2(R[2, 1] / np.cos(pitch2), R[2, 2] / np.cos(pitch2))
        yaw1 = np.arctan2(R[1, 0] / np.cos(pitch1), R[0, 0] / np.cos(pitch1))
        yaw2 = np.arctan2(R[1, 0] / np.cos(pitch2), R[0, 0] / np.cos(pitch2))
        return (roll1, pitch1, yaw1), (roll2, pitch2, yaw2)
    else:
        yaw = 0  # can set to anything, it's the gimbal lock case
        if R[2, 0] == -1:
            pitch = np.pi / 2
            roll = yaw + np.arctan2(R[0, 1], R[0, 2])
        else:
            pitch = -np.pi / 2
            roll = -yaw + np.arctan2(-R[0, 1], -R[0, 2])
        return (roll, pitch, yaw), (None, None, None)

# Example rotation matrix
R_example = np.array([
    [0.5, -0.1464, 0.8536],
    [0.5, 0.8536, -0.1464],
    [-0.7071, 0.5, 0.5]
])


# Get the Euler angles
euler_angles_set_1, euler_angles_set_2 = rotation_matrix_to_euler_angles(R_example)

print("euler_angles_set_1:")
print(f"Roll: {euler_angles_set_1[0]} radian.({euler_angles_set_1[0] * 180 / np.pi} deg).")
print(f"Pitch: {euler_angles_set_1[1]} radian.({euler_angles_set_1[1] * 180 / np.pi} deg).")
print(f"Yaw: {euler_angles_set_1[2]} radian.({euler_angles_set_1[2] * 180 / np.pi} deg).")

print("\neuler_angles_set_2:")
print(f"Roll: {euler_angles_set_2[0]} radian.({euler_angles_set_2[0] * 180 / np.pi} deg).")
print(f"Pitch: {euler_angles_set_2[1]} radian.({euler_angles_set_2[1] * 180 / np.pi} deg).")
print(f"Yaw: {euler_angles_set_2[2]} radian.({euler_angles_set_2[2] * 180 / np.pi} deg).")
# euler_angles_set_1:
# Roll: 0.7853981633974483 radian.(45.0 deg).
# Pitch: 0.7853885733974476 radian.(44.99945053347443 deg).
# Yaw: 0.7853981633974483 radian.(45.0 deg).

# euler_angles_set_2:
# Roll: -2.356194490192345 radian.(-135.0 deg).
# Pitch: 2.3562040801923456 radian.(135.00054946652557 deg).
# Yaw: -2.356194490192345 radian.(-135.0 deg).

• 위 코드의 결과를 수식을 통해 계산한 결과와 비교해 보도록 하겠습니다.

• $$R = \begin{bmatrix} 0.5 & -0.1464 & 0.8536 \\ 0.5 & 0.8536 & -0.1464 \\ -0.7071 & 0.5 & 0.5 \end{bmatrix}$$
• $$\theta_{1} = -\sin{(-0.7071)} = \frac{\pi}{4}$$
• $$\theta_{2} = \pi - \theta_{1} = \pi - \frac{\pi}{4} = \frac{3 \pi}{4}$$
• $$\psi_{1} = \text{atan2}(\frac{0.5}{\cos{(\pi/4)}}, \frac{0.5}{\cos{(\pi/4)}}) = \frac{\pi}{4}$$
• $$\psi_{2} = \text{atan2}(\frac{0.5}{\cos{(3\pi/4)}}, \frac{0.5}{\cos{(3\pi/4)}}) = -\frac{3\pi}{4}$$
• $$\phi_{1} = \text{atan2}(\frac{0.5}{\cos{(\pi/4)}}, \frac{0.5}{\cos{(\pi/4)}}) = \frac{\pi}{4}$$
• $$\psi_{2} = \text{atan2}(\frac{0.5}{\cos{(3\pi/4)}}, \frac{0.5}{\cos{(3\pi/4)}}) = -\frac{3\pi}{4}$$

• $$(\psi_{1}(\text{Roll}), \theta_{1}(\text{Pitch}), \phi_{1}(\text{Yaw})) = (\frac{\pi}{4}, \frac{\pi}{4}, \frac{\pi}{4})$$
• $$(\psi_{2}(\text{Roll}), \theta_{2}(\text{Pitch}), \phi_{2}(\text{Yaw})) = (-\frac{3\pi}{4}, \frac{3\pi}{4}, -\frac{3\pi}{4})$$

• 만약 Gimbal Lock과 같은 상황을 고려하지 않고 간단하게 Roll, Pitch, Yaw를 구하고 싶다면 다음과 같이 간단하게 사용할 수 있습니다.

def rotation_matrix_to_euler_angles(R):
    assert(R.shape == (3, 3))
    theta = -np.arcsin(R[2, 0])
    psi = np.arctan2(R[2, 1] / np.cos(theta), R[2, 2] / np.cos(theta))
    phi = np.arctan2(R[1, 0] / np.cos(theta), R[0, 0] / np.cos(theta))
    return np.array([psi, theta, phi]) # Roll, Pitch, Yaw

선형대수학 글 목차