(멀티플 뷰 지오메트리) Lecture 1. 2D and 1D projective geometry

Multiple View Geometry 글 목차

참조 : https://youtu.be/LAHQ_qIzNGU?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : https://youtu.be/gQ7IUS8NKCI?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : Multiple View Geometry in Computer Vision
참조 : https://www.cuemath.com/learn/mathematics/conics-in-real-life/

이번 글에서는 2D and 1D projective geometry 내용의 강의를 듣고 정리해 보도록 하겠습니다.

지금 부터는 2D and 1D projective geometry 강의의 후반부로 conics, dual conics와 관련된 내용과 transform 관련 내용에 대하여 다루어 보도록 하겠습니다.

projective plane이란 3차원 공간에서 원점을 지나는 모든 직선들의 모임으로 해석할 수 있습니다. 이 관점에서 projective plane의 point는 원점을 지나는 각각의 직선 (line)이고 line은 원점을 지나는 3차원 공간 속의 2차원 평면 (plane)으로 정의할 수 있습니다.
projective plane은 일반적인 plane과 유사하지만, point at infinity라는 무한대의 점이 존재하여 모든 두 직선이 항상 교차가 되는 특성이 있습니다. 모든 point at infinity 들이 지나는 직선을 line at infinity라고 합니다.

위 슬라이드의 $C$ 는 대칭 행렬 형태를 가지며 의미는 3개의 차원이 구성하는 관계를 수치로 나타낸 것을 의미합니다.
예를 들어 (1, 1) 위치는 $x_{1}, x_{1}$ 의 관계를 수치로 나타낸 것이고 (1, 2) 는 $x_{1}, x_{2}$ 의 관계를 수치로 나타낸 것입니다. 따라서 $(i, j)$ 와 $(j, i)$ 의 관계는 같기 때문에 대칭 행렬 형태를 가지게 됩니다.

\[a \cdot x_{1}^{2} + b \cdot x_{1}x_{2} + c \cdot x_{2}^{2} + d \cdot x_{1}x_{3} + e \cdot x_{2}x_{3} + f \cdot x_{3}^{2} = 0\]

위 슬라이드의 $C$ 또한 3개의 차원이 구성하는 관계를 수치로 나타낸 것이며 위 식에서 $X^{T} C X = 0$ 을 만족하도록 $C$ 를 구성한 것입니다.
이와 같은 행렬 $C$ 를 homogeneouse representation of conic이라고 합니다.
homogeneouse representation of conic $C$ 는 3개 차원의 경우의 수의 관계를 수치로 나타낸 것이므로 그 관계에 따라서 다양한 기하 형태가 나타납니다. 3개 차원의 경우의 수는 다음을 의미합니다. 아래 행렬에서 $x_{d}$ 는 $x$ 차원, $y_{d}$ 는 $y$ 차원, $h_{d}$ 는 homogeneous 차원을 의미합니다. $\text{rel}(a, b)$ 는 $a, b$ 의 관계를 의미합니다.

\[\begin{align} C &= \begin{bmatrix} \text{rel}(x_{d}, x_{d}) & \text{rel}(x_{d}, y_{d}) & \text{rel}(x_{d}, h_{d}) \\ \text{rel}(y_{d}, x_{d}) & \text{rel}(y_{d}, y_{d}) & \text{rel}(y_{d}, h_{d}) \\ \text{rel}(h_{d}, x_{d}) & \text{rel}(h_{d}, y_{d}) & \text{rel}(h_{d}, h_{d}) \end{bmatrix} \\ &= \begin{bmatrix} a & b/2 & d/2 \\ b/2 & c & e/2 \\ d/2 & e/2 & f \end{bmatrix} \end{align}\]

그 중 $C$ 의 $\text{rank}(C) = 3$ (full rank) 인 경우 원, 타원, 포물선, 쌍곡선 형태가 나타나는 반면 $C$ 의 $\text{rank}(C) \lt 3$ 인 경우 교차선, 평행선, 단일선, 점과 같은 degenerate conic 형태가 나타나기도 합니다. 이 부분은 차례대로 설명할 예정입니다.

따라서 지금부터 다룰 conic $C$ 는 가장 작은 형태인 point를 시작하여 line, circle, ellipse, hyperbola, parabola 등을 모두 포함하는 집합이기 때문에 Multiple View Geometry에서 가장 중요하게 다루는 개념 중 하나입니다.

위 슬라이드에서 $l$ 과 $m$ 은 line을 나타내므로 각각 다음과 같습니다.

\[l = \begin{bmatrix} l_{1} & l_{2} & l_{3} \end{bmatrix}^{T}\]
\[m = \begin{bmatrix} m_{1} & m_{2} & m_{3} \end{bmatrix}^{T}\]

2개의 선 $l, m$ 의 관계 또한 3개 차원의 경우의 수인 9개로 나타내기 위해 outer product를 한 것이고 대칭 행렬로 나타내고자 $lm^{T} + ml^{T}$ 형태로 나타내어 conic $C$ 를 구성합니다.
위 식의 $C = lm^{T} + ml^{T}$ 에서 $lm^{T}$ 와 $ml^{T}$ 각각의 outer product의 rank는 1이기 때문에 outer product의 결합으로 이루어진 $lm^{T} + ml^{T}$ 은 항상 degenerate conic 임을 만족합니다.
위 슬라이드에서는 $l$ 과 $m$ 이 independent 하여 $C = lm^{T} + ml^{T}$ 의 $\text{rank}(C) = 2$ 가 만족하는 degenerate conic 상황으로 가정합니다. 따라서 위 예시와 같이 교차하는 2개의 선으로 나타낼 수 있습니다.
슬라이드의 $C = lm^{T} + ml^{T}$ 를 좀더 자세하게 풀어 쓰면 다음과 같습니다.

\[l = \begin{bmatrix} l_{1} \\ l_{2} \\ l_{3} \end{bmatrix}\]
\[m = \begin{bmatrix} m_{1} \\ m_{2} \\ m_{3} \end{bmatrix}\]
\[lm^{T} = \begin{bmatrix} l_{1}m_{1} & l_{1}m_{2} & l_{1}m_{3} \\ l_{2}m_{1} & l_{2}m_{2} & l_{2}m_{3} \\ l_{3}m_{1} & l_{3}m_{2} & l_{3}m_{3}\end{bmatrix}\]
\[\begin{align} C = lm^{T} + ml^{T} &= \begin{bmatrix} l_{1}m_{1} & l_{1}m_{2} & l_{1}m_{3} \\ l_{2}m_{1} & l_{2}m_{2} & l_{2}m_{3} \\ l_{3}m_{1} & l_{3}m_{2} & l_{3}m_{3}\end{bmatrix} + \begin{bmatrix} m_{1}l_{1} & m_{1}l_{2} & m_{1}l_{3} \\ m_{2}l_{1} & m_{2}l_{2} & m_{2}l_{3} \\ m_{3}l_{1} & m_{3}l_{2} & m_{3}l_{3}\end{bmatrix} \\ &= \begin{bmatrix} l_{1}m_{1} + m_{1}l_{1} & l_{1}m_{2} + m_{1}l_{2} & l_{1}m_{3} + m_{1}l_{3} \\ l_{2}m_{1} + m_{2}l_{1} & l_{2}m_{2} + m_{2}l_{2} & l_{2}m_{3} + m_{2}l_{3} \\ l_{3}m_{1} + m_{3}l_{1} & l_{3}m_{2} + m_{3}l_{2} & l_{3}m_{3} + m_{3}l_{3}\end{bmatrix} \end{align}\]

위 식을 살펴 보면 $C = lm^{T} + ml^{T}$ 는 대칭행렬이 됨을 알 수 있습니다.

반면 위 슬라이드에서는 $l = m$ 으로 나타내었기 때문에 한 개의 선으로 표현합니다. 따라서 $\text{rank}(C) = 1$ 인 degenerate conic 상황으로 가정합니다. 따라서 위 예시와 같이 하나의 선으로 나타낼 수 있습니다.

\[x = \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix}\]
\[y = \begin{bmatrix} y_{1} \\ y_{2} \\ y_{3} \end{bmatrix}\]
\[xy^{T} = \begin{bmatrix} x_{1}y_{1} & x_{1}y_{2} & x_{1}y_{3} \\ x_{2}y_{1} & x_{2}y_{2} & x_{2}y_{3} \\ x_{3}y_{1} & x_{3}y_{2} & x_{3}y_{3}\end{bmatrix}\]
\[\begin{align} C^{*} = xy^{T} + yx^{T} &= \begin{bmatrix} x_{1}y_{1} & x_{1}y_{2} & x_{1}y_{3} \\ x_{2}y_{1} & x_{2}y_{2} & x_{2}y_{3} \\ x_{3}y_{1} & x_{3}y_{2} & x_{3}y_{3}\end{bmatrix} + \begin{bmatrix} y_{1}x_{1} & y_{1}x_{2} & y_{1}x_{3} \\ y_{2}x_{1} & y_{2}x_{2} & y_{2}x_{3} \\ y_{3}x_{1} & y_{3}x_{2} & y_{3}x_{3}\end{bmatrix} \\ &= \begin{bmatrix} x_{1}y_{1} + y_{1}x_{1} & x_{1}y_{2} + y_{1}x_{2} & x_{1}y_{3} + y_{1}x_{3} \\ x_{2}y_{1} + y_{2}x_{1} & x_{2}y_{2} + y_{2}x_{2} & x_{2}y_{3} + y_{2}x_{3} \\ x_{3}y_{1} + y_{3}x_{1} & x_{3}y_{2} + y_{3}x_{2} & x_{3}y_{3} + y_{3}x_{3}\end{bmatrix} \end{align}\]

지금까지 배운 내용 종합하면 Point, Line, Two Lines, Circle, Ellipse, Hyperbola, Parabola을 Conic을 이용하여 표현할 수 있음을 확인하였습니다. 이번에는 각 항목을 실제 예시를 들어서 어떻게 표현하는 지 살펴보도록 하겠습니다.

① Point
- Point는 $3 \times 1$ 크기의 벡터로 표현이 가능합니다. 예를 들어 inhomogeneous coordinate의 $(2, 3)$ Point는 homogeneous coordinate에서 $(2, 3, 1)$ 로 표현됩니다. 만약 conic을 이용하여 Point를 표현하려면 degenerate dual conic 형태를 이용해야 합니다. 왜냐하면 점을 표현하려면 2개의 선 (Two Lines)이 한 점을 통과하는 형태를 나타내어야 하기 때문입니다.
- 따라서 $(2, 3, 1)$ 을 지나는 두 개의 선 $l = (1, 0, -2)^{T}$ 와 $m = (0, 1, -3)^{T}$ 를 이용하여 degenerate dual conic을 나타내면 다음과 같습니다.
- \[\begin{align} C^{*} &= lm^{T} + ml^{T} \\ &= \begin{bmatrix} 1 \\ 0 \\ -2 \end{bmatrix} \begin{bmatrix} 0 & 1 & -3 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ -3 \end{bmatrix} \begin{bmatrix} 1 & 0 & -2 \end{bmatrix} \\ &= \begin{bmatrix} 0 & 1 & -3 \\ 1 & 0 & -2 \\ -3 & -2 & 12 \end{bmatrix} \end{align}\]
- 위 식의 $C^{*}$ 는 두 선의 교점을 나타내므로 두 선의 교점인 Point $x = (2, 3, 1)$ 는 다음식을 만족하여 $C^{*}$ 가 Point를 나타냄을 알 수 있습니다.
- \[x^{T} C^{*} x = \begin{bmatrix} 2 \\ 3 \\ 1 \end{bmatrix} \begin{bmatrix} 0 & 1 & -3 \\ 1 & 0 & -2 \\ -3 & -2 & 12 \end{bmatrix} \begin{bmatrix} 2 & 3 & 1 \end{bmatrix} = 0\]
② Line
- Line은 2개의 점을 이용하여 생성할 수 있습니다. 따라서 homogeneous coordiate의 2개의 점을 이용하여 $C$ 를 구성하면 degenerate conic으로 선을 표현할 수 있습니다.
- 아래 예제는 $l = x + 2y - 3 \to (1, 2, -3)$ 이라는 식을 표현하기 위하여 2개의 점 $a = (3, 0, 1)$ 과 $b = (0, 1.5, 1)$ 을 이용해 보겠습니다. 두 점은 $l$ 상에 존재합니다.
- \[\begin{align} C &= ab^{T} + ba^{T} \\ &= \begin{bmatrix} 3 \\ 0 \\ 1 \end{bmatrix} \begin{bmatrix} 0 & 1.5 & 1 \end{bmatrix} + \begin{bmatrix} 0 \\ 1.5 \\ 1 \end{bmatrix} \begin{bmatrix} 3 & 0 & 1 \end{bmatrix} \\ &= \begin{bmatrix} 0 & 4.5 & 3 \\ 4.5 & 0 & 1.5 \\ 3 & 1.5 & 2 \end{bmatrix} \end{align}\]
- 위 식의 $C$ 는 Line을 나타내므로 다음과 같이 확인해 볼 수 있습니다.
- \[l^{T} C l = \begin{bmatrix} 1 \\ 2 \\ -3 \end{bmatrix} \begin{bmatrix} 0 & 4.5 & 3 \\ 4.5 & 0 & 1.5 \\ 3 & 1.5 & 2 \end{bmatrix} \begin{bmatrix} 1 & 2 & -3 \end{bmatrix} = 0\]
③ Two Lines
- Two Lines를 나타내는 Conic은 앞에서 Point를 나타내는 Conic을 통해 다루었습니다. $l = (1, 2, -3)$ , $m = (2, -1, 4)$ 가 있을 때, 이 두 선을 나타내는 degenerate dual conic은 다음과 같습니다.
- \[\begin{align} C^{*} &= lm^{T} + ml^{T} \\ &= \begin{bmatrix} 1 \\ 2 \\ -3 \end{bmatrix} \begin{bmatrix} 2 & -1 & 4 \end{bmatrix} + \begin{bmatrix} 2 \\ -1 \\ 4 \end{bmatrix} \begin{bmatrix} 1 & 2 & -3 \end{bmatrix} \\ &= \begin{bmatrix} 4 & 3 & -2 \\ 3 & -4 & 11 \\ -2 & 11 & -24 \end{bmatrix} \end{align}\]
- 선 $l$ 상의 점 $x_{1} = (-1, 2, 1)$ 과 $m$ 상의 점 $x_{2} = (-2, 0, 1)$ 모두 다음과 같이 계산하면 $C^{*}$ 이 두 선을 나타냄을 알 수 있습니다.
- \[x_{1}^{T} C^{*} x_{1} = \begin{bmatrix} -1 \\ 2 \\ 1 \end{bmatrix} \begin{bmatrix} 4 & 3 & -2 \\ 3 & -4 & 11 \\ -2 & 11 & -24 \end{bmatrix} \begin{bmatrix} -1 & 2 & 1 \end{bmatrix} = 0\]
- \[x_{2}^{T} C^{*} x_{2} = \begin{bmatrix} -2 \\ 0 \\ 1 \end{bmatrix} \begin{bmatrix} 4 & 3 & -2 \\ 3 & -4 & 11 \\ -2 & 11 & -24 \end{bmatrix} \begin{bmatrix} -2 & 0 & 1 \end{bmatrix} = 0\]
④ Circle
- 앞에서 다룬 Conic 유도식의 $a \cdot x_{1}^{2} + b \cdot x_{1}x_{2} + c \cdot x_{2}^{2} + d \cdot x_{1}x_{3} + e \cdot x_{2}x_{3} + f \cdot x_{3}^{2} = 0$ 을 통하여 $(h, k)$ 를 원의 중심으로 가지는 반지름 $r$ 인 원은 다음과 같은 형태를 가짐을 알 수 있습니다.
- \[C = \begin{bmatrix} 1 & 0 & -h \\ 0 & 1 & -k \\ -h & -k & h^{2} + k^{2} -r^{2} \end{bmatrix}\]
- 예를 들어 원의 중심이 $(0, 0)$ 이고 반지름이 $1$ 인 원이라면 다음과 같이 표현할 수 있습니다.
- \[C = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{bmatrix}\]
⑤ Ellipse
- 타원 또한 위 식을 통하여 Conic을 유도하면 타원의 중심은 $(h, k)$ 이고 장축의 길이는 $a$ , 단축의 길이는 $b$ 일 경우 다음과 같이 정의할 수 있습니다.
- \[\frac{(x - h)^{2}}{a^{2}} + \frac{(y-k)^{2}}{b^{2}} = 1\]
- \[C = \begin{bmatrix} 1/a^{2} & 0 & -h/a^{2} \\ 0 & 1/b^{2} & -k/b^{2} \\ -h/a^{2} & -k/b^{2} & h^{2}/a^{2} + k^{2}/b^{2} - 1 \end{bmatrix}\]
- 예를 들어 타원의 중심이 $(2, 3)$ 이고 장축의 길이가 $4$ , 단축의 길이가 $2$ 라면 Conic은 다음과 같이 정의 됩니다.
- \[C = \begin{bmatrix} 1/16 & 0 & -1/8 \\ 0 & 1/4 & -3/4 \\ -1/8 & -3/4 & 7/16 \end{bmatrix}\]
⑥ Hyperbola
- 쌍곡선도 타원의 예시와 유사하게 다음과 같이 정의할 수 있습니다.
- \[\frac{(x - h)^{2}}{a^{2}} - \frac{(y-k)^{2}}{b^{2}} = 1\]
- \[C = \begin{bmatrix} 1/a^{2} & 0 & -h/a^{2} \\ 0 & -1/b^{2} & k/b^{2} \\ -h/a^{2} & k/b^{2} & h^{2}/a^{2} - k^{2}/b^{2} - 1 \end{bmatrix}\]
⑦ Parabola
- 마지막으로 포물선의 경우 포물선의 꼭지점이 $(h, k)$ 이고 width $a$ 는 다음과 같이 정의 할 수 있습니다.
- \[(y - k) = a(x - h)^{2}\]
- \[y - k - a(x-h)^{2} = 0\]
- $$ C = \begin{bmatrix} 0 & -a/2 & ah \ -a/2 & 1 & -k \ ah & -k & -h^{2} \end{bmatrix}
- 예를 들어 포물선의 꼭지점이 $(2, 3)$ 이고 $a = 1$ 이라면 다음과 같이 conic을 구성할 수 있습니다.
- \[C = \begin{bmatrix} 0 & -1/2 & 2 \\ -1/2 & 1 & -3 \\ 2 & -3 & -4 \end{bmatrix}\]
지금까지 살펴본 방식으로 기하학에서 흔히 다루는 7 가지 경우에 대하여 모두 conic으로 나타낼 수 있음을 확인하였습니다.

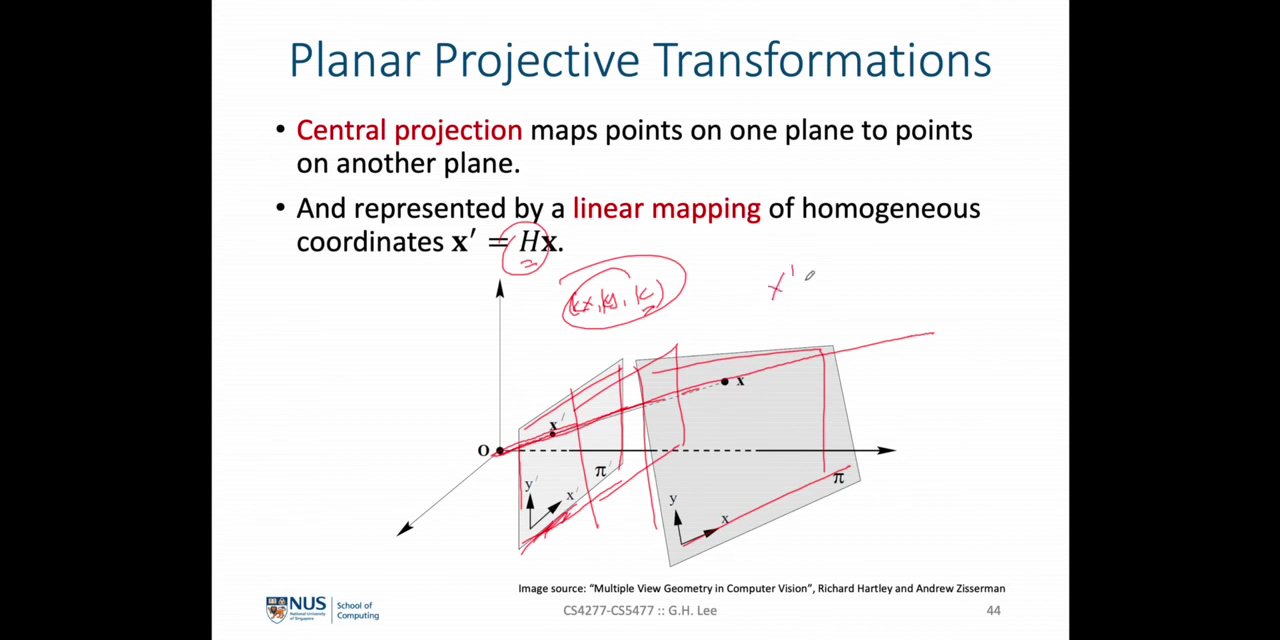
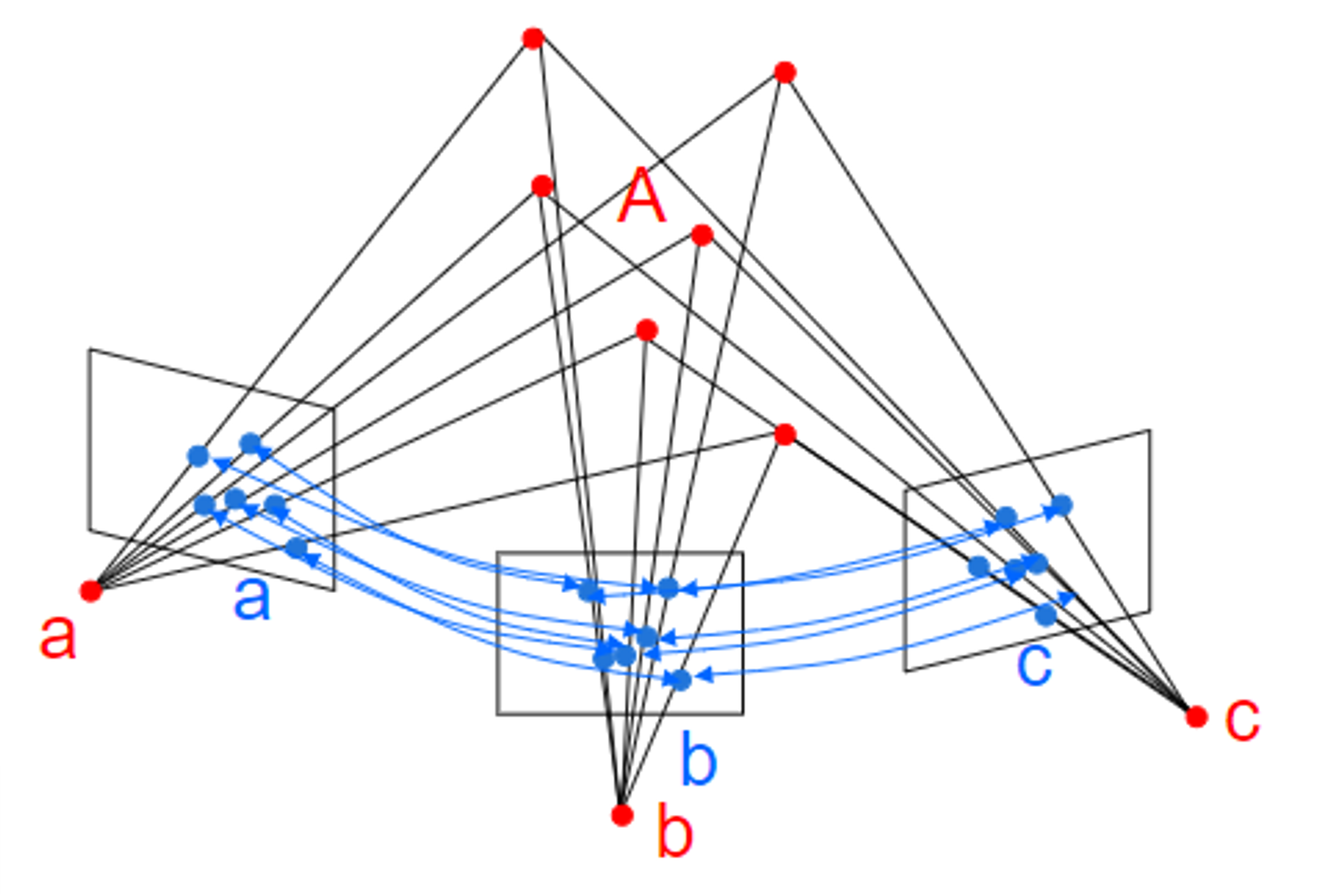
point $x_{i}$ 가 line $l$ 위에 있을 때, $l^{T} x_{i} = 0$ 으로 표현할 수 있습니다. 만약 transformed point (projective transformation) 인 $x_{i}' = H x_{i}$ 가 $l'$ 위에 있다면 ${l'}^{T} x_{i}' = 0$ 이 되고 $l$ 과 $l'$ 두 line의 관계로 나타내면 $l' = H^{-T} l$ 으로 표현할 수 있습니다. 수식 전개 과정은 아래와 같습니다.

\[x_{i}' = H x_{i}\]
\[{l'}^{T} x_{i}' = 0\]
\[\therefore \quad {l'}^{T} H x_{i} = 0\]
\[{l'}^{T} H x_{i} = l^{t} x_{i}\]
\[{l'}^{T} H = l^{t}\]
\[H^{T} l' = l\]
\[\therefore \quad l' = H^{-T} l\]

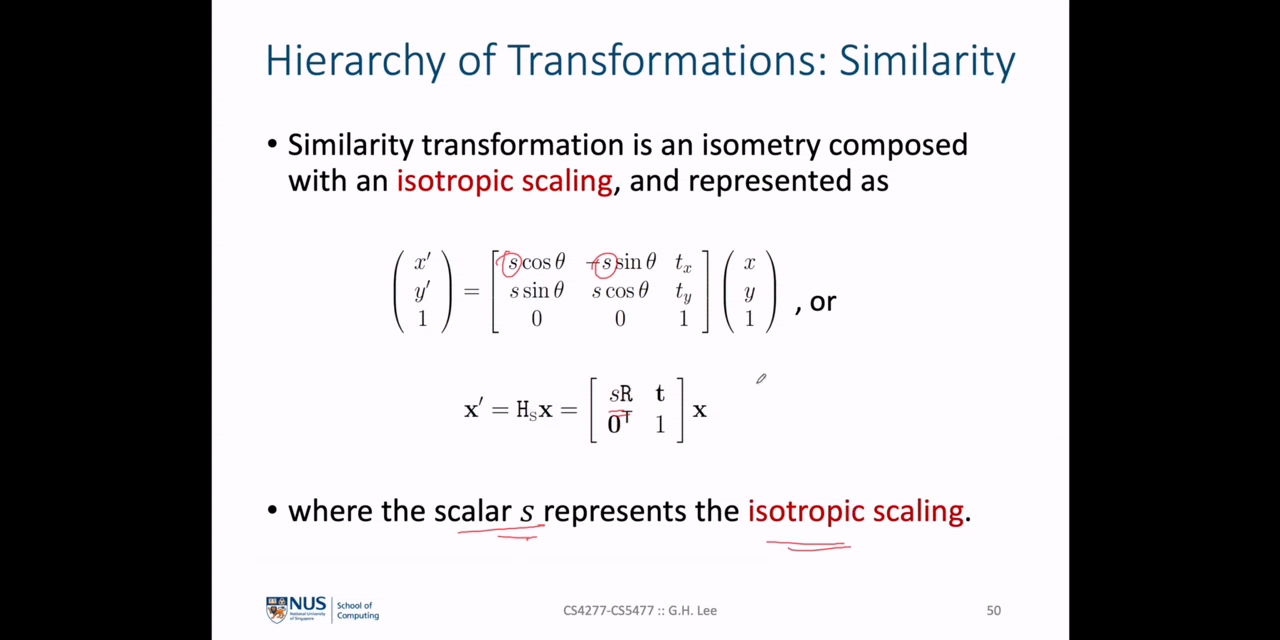
Similarity Transformation은 isotropic scaling 으로 구성되며 위 슬라이드의 식 처럼 표현됩니다.
isotropic이란 한글로 등방형이며 방향에 상관없이 일정하다는 뜻입니다. 즉, Similarity Transformation은 모든 방향에 동일한 효과를 적용합니다.
위 식에서 $s$ 는 isotropic scaling이라고 하며 Similarity Transformation 적용 시 변환의 크기를 조절합니다.

Similarity Transformation은 shape을 보존하기 때문에 equi-form transformation이라고도 합니다.
식에서 나타난 바와 같이 3개의 isometry DoF ( $\theta, t_{x}, t_{y}$ )와 isotropic scaling $s$ 를 가지므로 Similarity Transformation은 총 4 DoF를 가지며 DoF가 4개이므로 변환된 2개의 점을 알 때, 이 값들을 추정할 수 있습니다.
shape이 보존되기 때문에 Angle, ratio of two lengths, ratio of areas는 보존이되는 성질을 가집니다. 평행선은 평행선으로 유지되는 것 또한 중요한 성질입니다.

그 다음으로 Affinity에 대하여 다루어 보도록 하겠습니다.
위 슬라이드에서 설명하는 Affine Transformation 행렬은 non-singular linear transformation으로 간단히 말하면 역행렬이 존재하는 행렬이며 $A$ 부분의 2 X 2 행렬 또한 non-singular matrix로 역행렬이 존재합니다.
앞에서 살펴본 Similarity Transformation과 다르게 6 DoF로 DoF가 2개가 더 추가가 되었습니다. Similarity Transformation에서는 $\theta$ 가 정해지면 $H_{S}$ 가 정해졌으나 Affine Transformation에서는 4개의 각 성분이 모두 DoF를 가지기 때문에 DoF가 총 6개가 됩니다.
DoF가 6개이므로 기존의 3개의 점이 Affine Transformation 적용 시 어떻게 변환되는 지 관계를 알면 Affine Transformation을 구할 수 있습니다. (Similarity Transformation에서는 점 2개가 필요하였습니다.)
Affine Transformation을 적용하더라도 평행선은 그대로 유지되며 평행 선분의 길이 비율과 면적 비율은 유지됩니다. 반면 Similarity Transformation에서는 보존되었던 임의의 선의 길이 비율과 선 사이의 각도는 보존되지 않습니다. 그 이유에 대하여 Affine Transformation Matrix를 분해하여 살펴보도록 하겠습니다.

이번 슬라이드와 다음 슬라이드에서는 Affine Transformation을 SVD (Singular Value Decomposition)으로 분해하였을 때, 각 성분이 가지는 의미를 나타냅니다. 위 슬라이드에서는 먼저 어떻게 분해될 수 있는 지 설명합니다.

Affine Transformation의 의미를 기하학적으로 이해하기 위한 방법으로 rotation과 non-isotropic scaling 두 가지 선형 변환의 합성으로 생각하는 방법이 있습니다. 먼저 Affine Transformation은 아래와 같이 분해 됩니다.

\[A = R(\theta) R(-\phi) D R(\phi)\]
\[R(\theta), R(\phi) \text{ : rotation by} \theta, \phi \text{ respectively}\]
\[D = \begin{bmatrix} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{bmatrix} \text{ : diagonal matrix}\]

위 식과 같이 분해되는 이유는 아래와 같습니다. affine transformation matrix를 Singular Value Decomposition을 하고 SVD 결과의 $U, V$ 가 orthogonal matrix이므로 $U^{-1} = U^{T}$ , $V^임을{-1} = V^{T}$ 임을 이용하여 전개하였습니다.

\[A = U D V^{T} = U (V^{-1}V) D V^{T} = U (V^{T}V) D V^{T} = (U V^{T})V D V^{T}\]
\[= R(\theta)(R(-\phi) D R(\phi))\]

회전 행렬 관련 글에서 다룬 바와 같이 orthogonal matrix는 rotation 임을 만족하기 때문에 $U = R(\theta)$, $V = R(-\phi)$, $V^{T} = R(\phi)$ 로 표현할 수 있어서 위 식과 같이 전개됩니다.

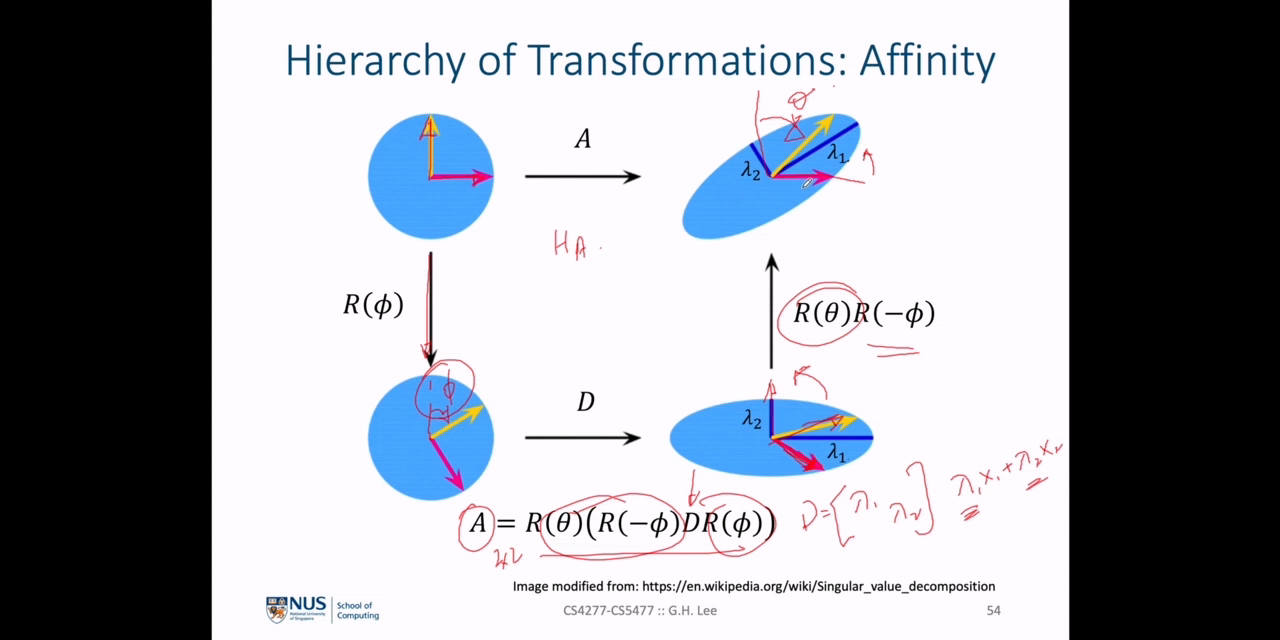
따라서 식을 위 슬라이드와 같이 시각적으로 나타낼 수 있습니다. 위 슬라이드는 affine transformation인 $A$ 를 바로 적용한 결과를 $R(\phi)$ , $D$ , $R(\theta)R(\-phi)$ 순서로 나누어서 보여줍니다.
즉 affine transformation $A$ 에서의 연산 순서는
- ① $\phi$ 만큼 회전합니다.
- ② $x, y$ 방향으로 각각 $\lambda_{1}, \lambda{2}$ 만큼 scaling을 조정합니다. ($\lambda_{1}x_{1} + \lambda{2}x_{2}$ )
- ③ $-\phi$ 만큼 역회전 합니다. 즉, $\phi$ 만큼 회전한 영역에서 주성분 방향으로 scaling을 조정하고 다시 역회전하여 회전을 없앱니다.
- ④ 마지막으로 $\theta$ 만큼 회전합니다.
이와 같은 순서로 연산을 살펴보았을 때, similarity transformation에 비하여 추가된 개념은 non-isotropic scaling입니다. 즉, scaling 조정 방향을 지정하는 각도 $\phi$ 와 scaling 조정 비율인 $\lambda{1}, \lambda{2}$ 가 이에 해당합니다.
따라서 affine transformation에서는 특정 각도에 대하여 직교하는 방향으로 scaling을 조정하는 것이 중요합니다.

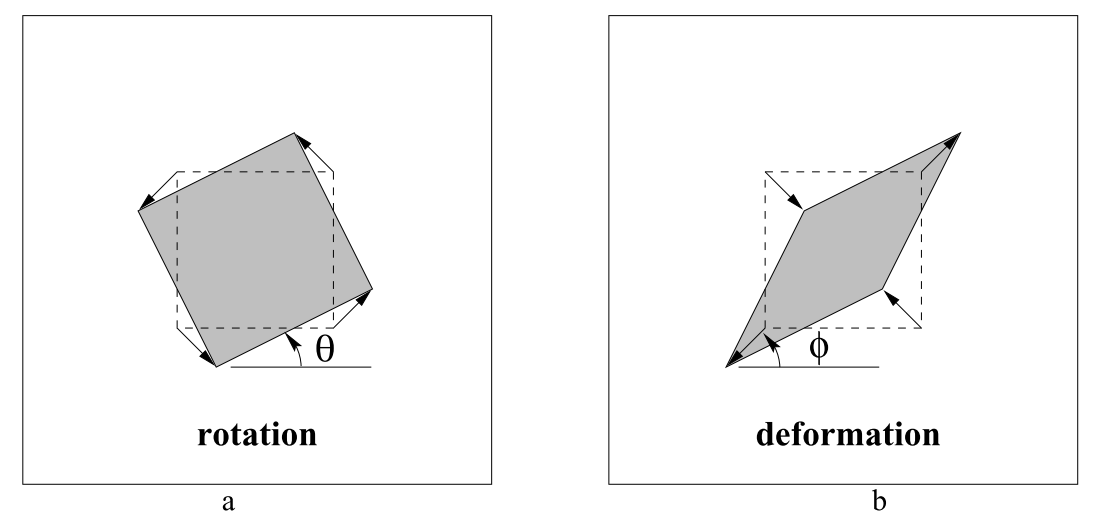
그림으로 나타내면 왼쪽 그림은 최종 $R(\theta)$ 에 의한 회전을 나타내고 오른쪽 그림은 $R(-\phi)DR(\phi)$ 에 의한 변형을 나타냅니다. scaling 방향으로 orthogonal 함을 유심히 살펴보면 이해하는 데 도움이 됩니다.

Multiple View Geometry 글 목차