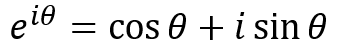
오일러 공식 (Euler formula)
2021, Mar 01
- 사전 지식 : 극좌표계
- 이번 글에서 다룰 오일러 공식은 다음 식과 같습니다.
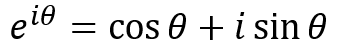
- 오일러 공식을 유도하는 다양한 방법 중 대표적으로
미분 방정식을 이용하여 유도하는 방법과테일러 급수를 이용하여 유도하는 방법에 대하여 이 글에서 다루어 보도록 하겠습니다.
미분 방정식을 이용한 오일러 공식 유도
- 오일러 공식을 사용할 때에는 수의 범위를 복소수의 범위에서 생각하겠습니다. 즉, 허수도 적용 가능한 공식임을 뜻합니다.

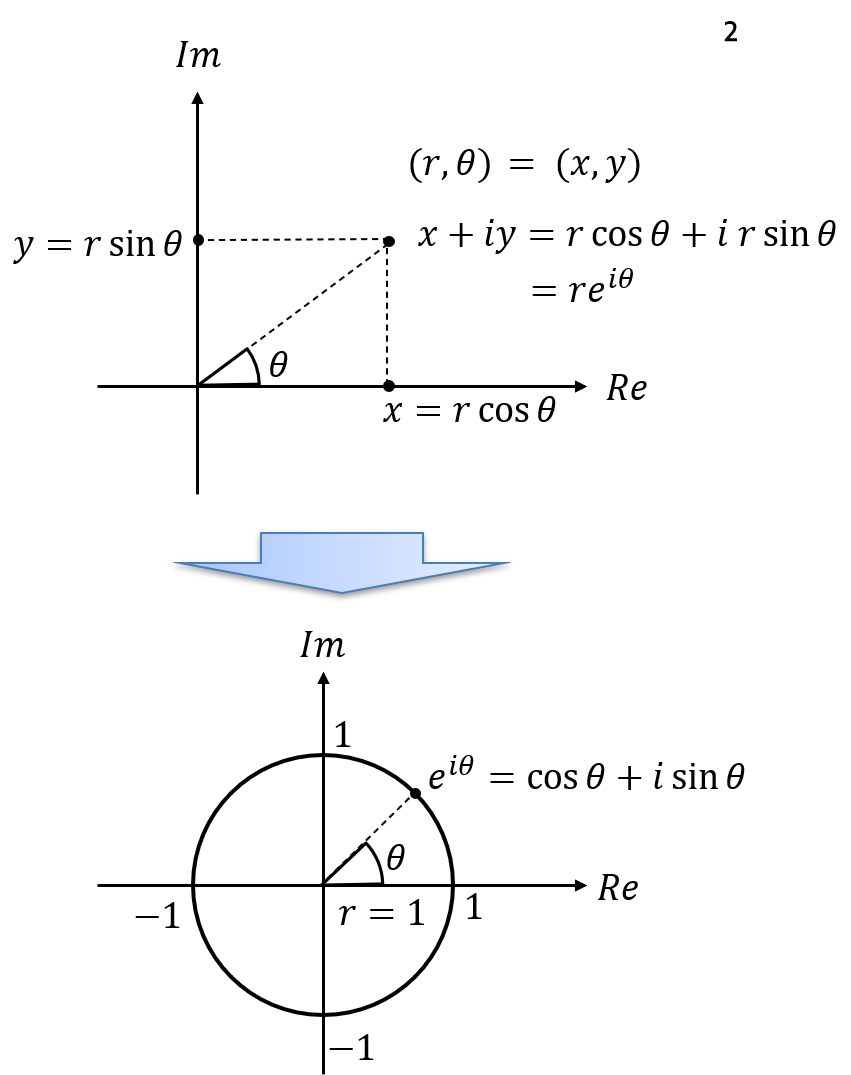
- 위 그래프는 복소 평면을 나타내며 복소 평면에서 복소수는 \(x + iy\) 형태의 한 점으로 나타낼 수 있습니다. 가로축은 실수(Real)을 뜻하고 세로축은 허수 (Imaginary)를 뜻합니다.
- 이 때, \(x + iy\)를 \((x, y)\)와 같이 직교 좌표계 형태로 나타낼 수 있는 반면
극 좌표계개념을 도입하여 \(x + iy = r\cos{\theta} + i r \sin{\theta}\) 형태로 나타낼 수 있습니다.
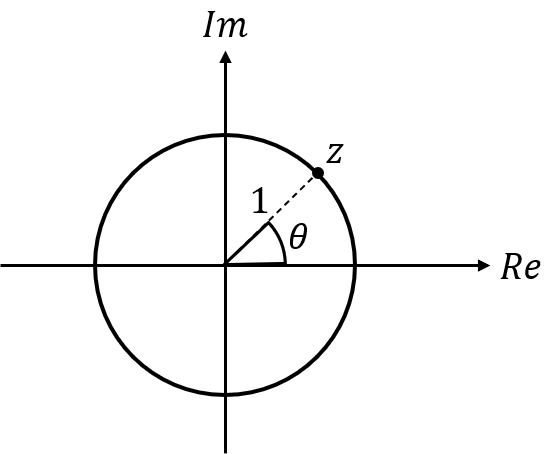
- 극 좌표계를 이용하여 위 그림과 같이 \(r = 1\)인 단위 원을 그리면 위 그래프와 같이 나타낼 수 있습니다. 이 경우 \(z = \cos{\theta} + i \sin{\theta}\)로 극 좌표 \(z\)를 나타낼 수 있습니다. 이 식과 미분 방정식을 이용하여 오일러 공식을 유도해 보겠습니다.
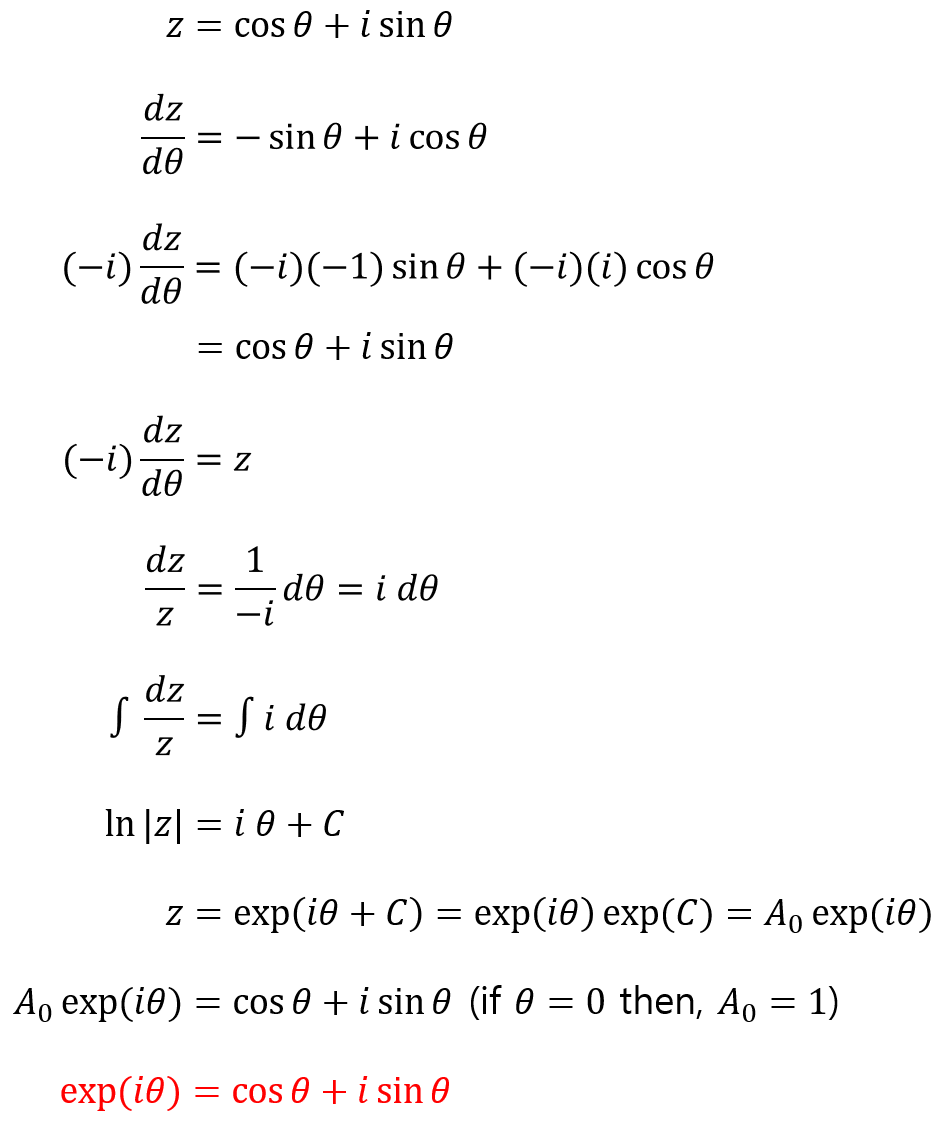
- 따라서 위 식에서 유도한 바와 같이 \(e^{i\theta} = \cos{\theta} + i\sin{\theta}\) 관계를 가지게 됩니다.

- 특히, \(\theta = \pi\)를 대입하면 \(e^{\pi i} + 1 = 0\)으로 정리할 수 있습니다. 이와 같이 대표적으로 나타내는 오일러 공식의 포맷을 정리할 수 있습니다.
- \[e^{i \theta} = \cos{\theta} + i\sin{\theta}\]
- \[e^{i \pi} +1 = 0\]
테일러 급수를 이용한 오일러 공식 유도
- 먼저 테일러 급수에 대한 개념은 다음 링크를 참조하시기 바랍니다. 테일러 급수의 내용을 이해하고 있다는 전제 하에 진행하겠습니다.
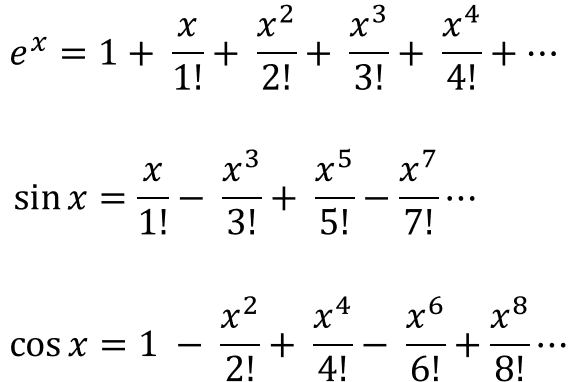
- 먼저 \(e^{x}, \sin{x}, \cos{x}\)를 각각 테일러 급수 형태로 나타내면 위 식과 같습니다. 이 식을 이용하여 오일러 공식을 유도해 보겠습니다.
- 먼저 \(e^{x}\)의 \(x\)에 \(ix\)를 대입해 보겠습니다.
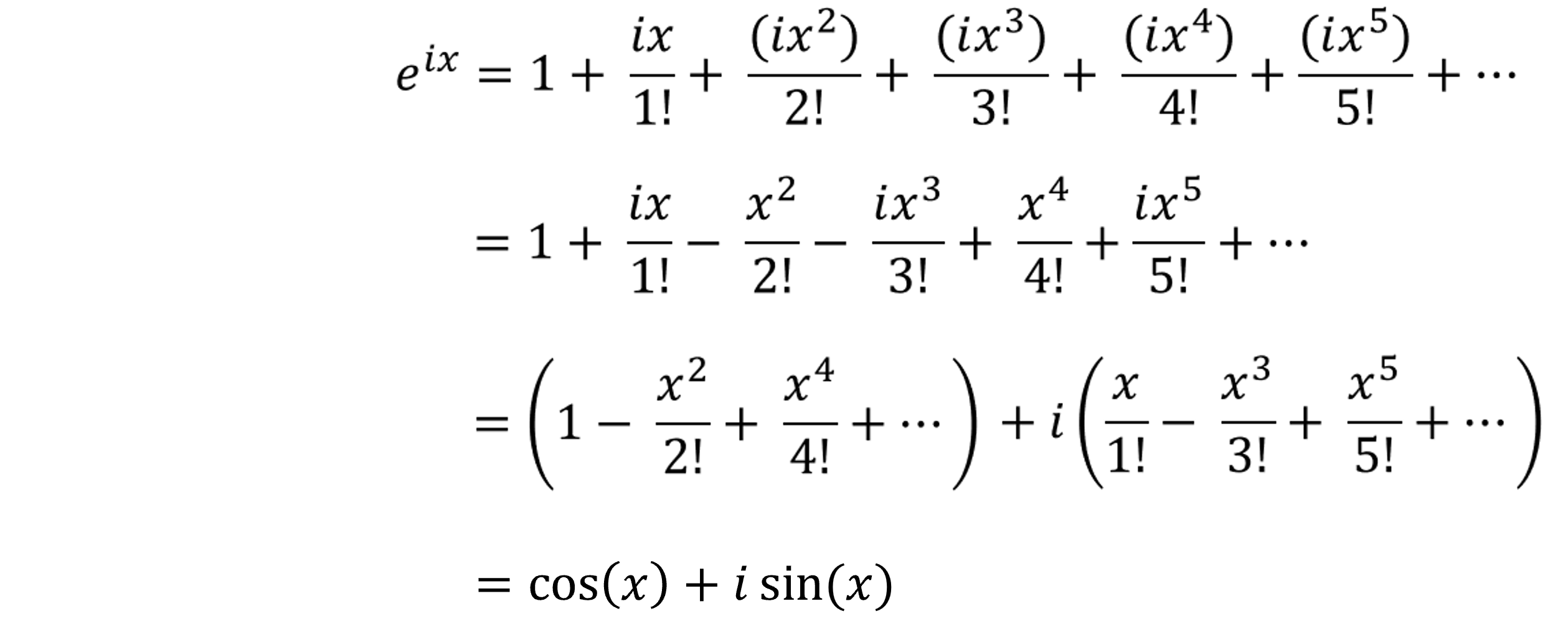
- 위 식의 전개를 살펴보면 자연 상수 \(e\)의 테일러 급수 표현과 \(\sin{x}, \cos{x}\) 각각의 테일러 급수 표현을 이용하여 오일러 공식을 유도하였습니다.
오일러 공식의 기하학적 의미
- 앞에서 다룬 내용과 다소 중복되지만 단순히 기하학적으로만 접근하여 오일러 공식을 유도하면 다음과 같습니다.
- 이와 같은 다양한 방법(
미분 방정식,테일러 급수,기하학적 접근)으로 오일러 공식을 유도할 수 있습니다.
오일러 공식의 응용
- 오일러 공식을 통하여 지수 함수를 삼각함수 형태로 나타내었습니다. 이 관계식을 이용하면 반대로 삼각함수를 지수 함수 형태로 나타낼 수 있습니다.
- \[\sin{(ix)} = \frac{e^{-x} - e^{x}}{2i}\]
- \[\cos{(ix)} = \frac{e^{x} + e^{-x}}{2}\]
- 위 식과 같이 유도하는 방법은 간단합니다.
- \[e^{ix} = \cos{(x)} + i \sin{(x)}\]
- \[e^{-ix} = \cos{(-x)} + i \sin{(-x)} = \cos{(x)} - i \sin{(x)}\]
- 위 두 식을 더한 뒤 양변을 정리하면 \(\cos{(ix)}\)에 대하여 정리가 가능하고 두 식을 뺀 뒤 양변을 정리하면 \(\sin{(ix)}\)에 대하여 식을 정리할 수 있습니다.