축각 회전 (Axis-Angle Rotation) 또는 로드리게스 회전 (Rodrigues Rotation)

Vision 관련 글 목차

참조 : 이득우의 게임 수학
참조 : https://mycom333.blogspot.com/2014/01/axis-angle-rotation.html

이번 글에서는 3차원 회전의 대표적인 방법 중 하나인 Axis-Angle Rotation에 대하여 다루어 보도록 하겠습니다. 이 방법은 방법론을 제시한 로드리게스의 이름을 따서 로드리게스 회전이라고도 불립니다. 본 글에서는 Axis-Angle Rotation으로 사용하겠습니다.

Axis-Angle Rotation의 필요성

Axis-Angle Rotation은 Euler Angle의 단점을 개선할 수 있는 3차원 회전 방법으로 사용 됩니다. Euler Angle을 이용한 3차원 회전은 직관적이며 단순하다는 장점이 있지만 크게 2가지 문제점이 있습니다. 바로 Gimbal Lock (짐벌 락) 현상과 Rotaional Interpolation (회전 보간)의 한계점 입니다.
- 이와 관련된 상세 내용은 아래 링크에서도 확인할 수 있습니다.
- 링크 : https://gaussian37.github.io/math-la-rotation_matrix/

① Gimbal Lock 현상은 X, Y, Z 축을 90도 회전 시키다 보면 어떤 2개의 축의 회전이 동일해져 버리는 현상을 말합니다. 세 개의 축으로 자유롭게 회전할 수 있었는데 두 개의 축만 회전할 수 있도록 어떤 축의 회전이 Lock이 걸려 버리기 때문에 Gimbal Lock이라고 표현합니다. 아래 영상을 참조하시면 바로 이해가 되실 겁니다.

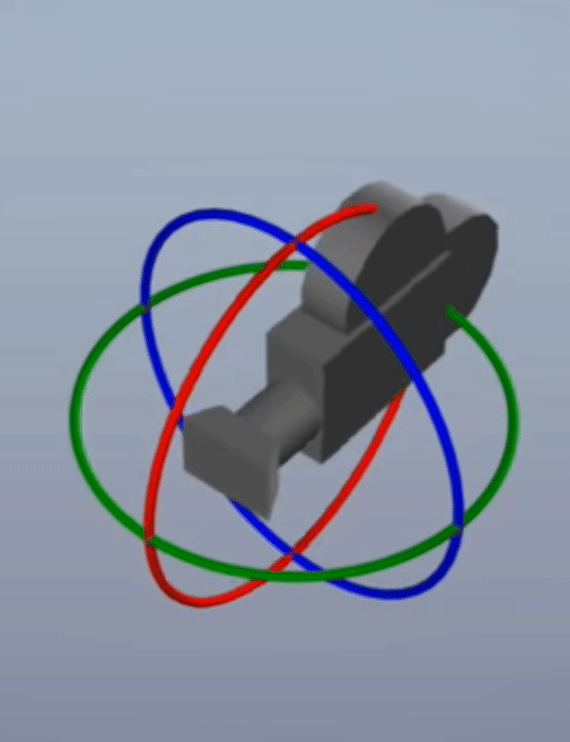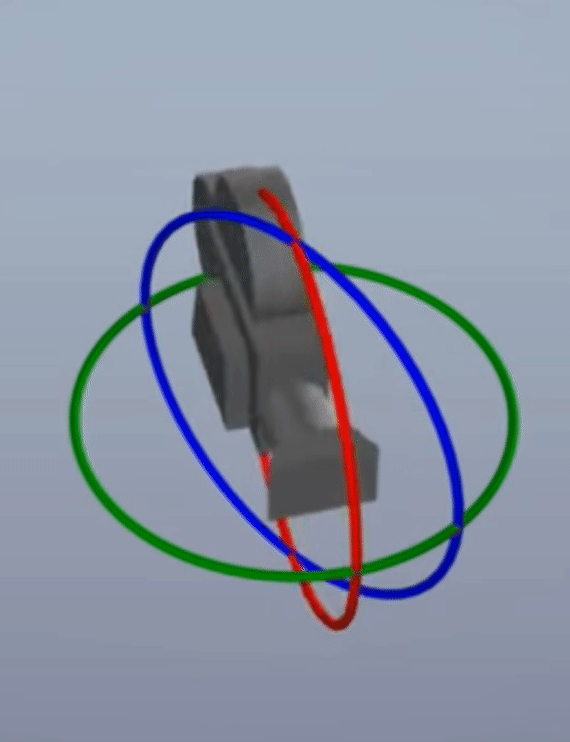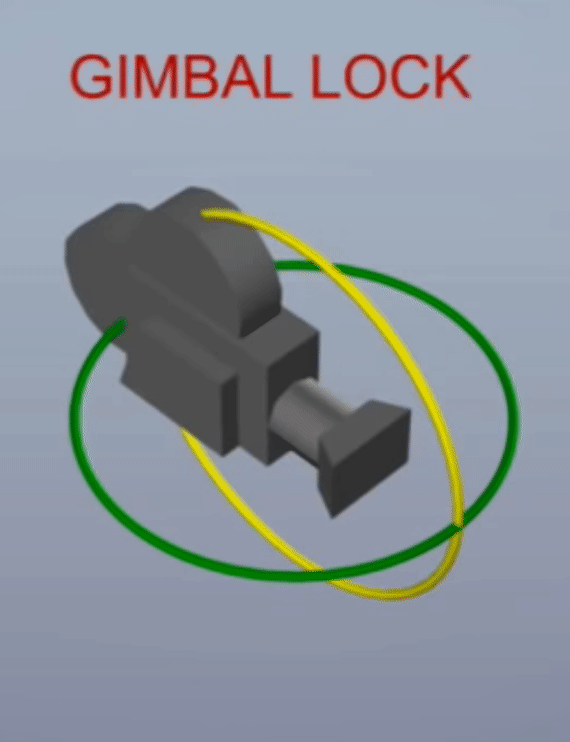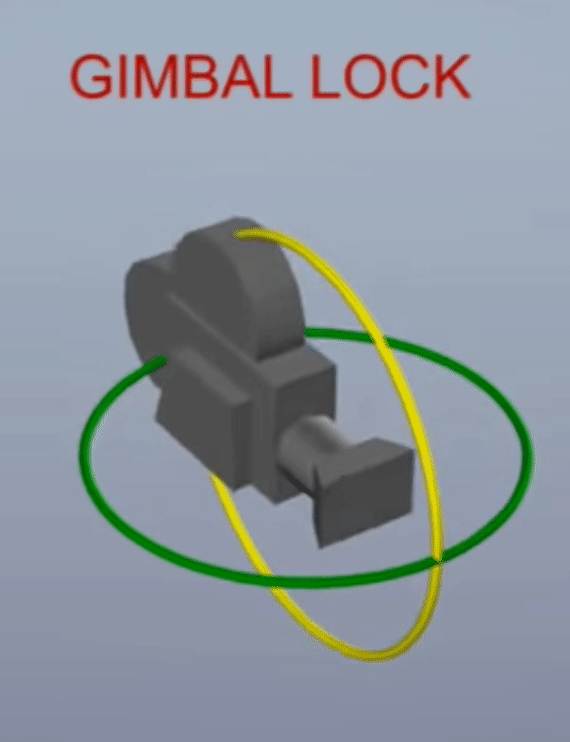
위 그림과 같이 90도 회전 시, 축이 사라지는 현상이 발생하는 것을 의미합니다.

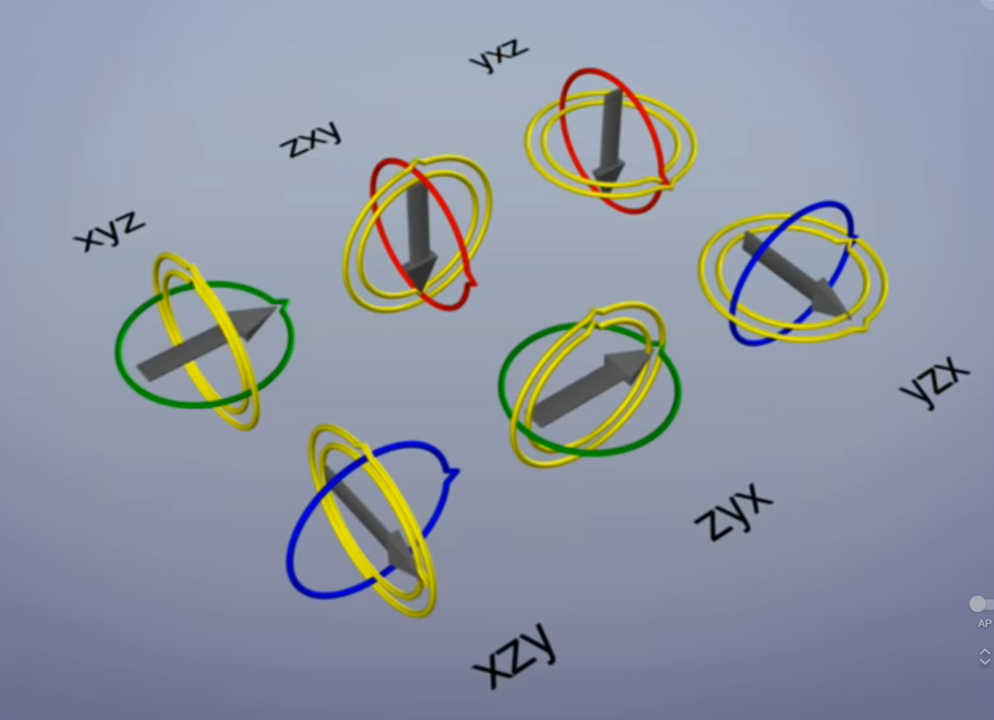
각 축으로 어떻게 90도 회전 하는 것에 따라서 위 그림 처럼 다양한 형태로 Gimbal Lock이 발생합니다.
물론 이와 같이 항상 축이 사라지지는 않으며 어떤 각도로 먼저 회전할 지에 따라서 문제가 되지 않을 수 있습니다. 따라서 Euler Angle에서의 Gimbal Lock 문제를 회피하기 위한 방법들이 존재 (위 링크 참조) 하지만, 근본적인 해결을 위해서는 다른 방법의 3차원 회전이 필요합니다.

② Rotaional Interpolation은 3차원 회전 시 시작 회전과 끝 회전을 지정하면 두 회전 사이를 부드럽게 전환할 수 있어야 함을 의미합니다. 파워포인트부터 다양한 3D 툴에서 회전량을 지정하면 애니매이션 효과를 줄 수 있는데, 이 때 사용되는 중간 중간의 움직임을 의미합니다.
이러한 동작을 구현하기 위해서는 경과된 시간에 따라 회전이 변화되도록 중간 회전값을 계산할 수 있어야 하는데 결과적으로 Euler Angle에서는 두 축 이상을 사용하는 Euler Angle의 linear interpolation을 사용할 수 없습니다. 1개의 축만 사용하여 회전할 때에는 문제가 없지만 2개의 축 이상을 사용할 때에는 이 부분이 문제가 발생합니다. 이 문제 또한 자세한 문제는 위 링크를 참조하시면 됩니다.

이와 같은 2가지 문제점을 해결하기 위하여 본 글에서는 다루는 Axis-Angle Rotation을 사용하거나 Quaternion을 사용하여 3차원 회전을 이용합니다. 이 2가지 해결책에도 각각 장단점이 있습니다.
본 글에서는 Axis-Angle Rotation을 알아볼 것입니다. Axis-Angle Rotation은 임의의 축에 직교하는 평면에 대한 임의의 회전을 할 수 있는 컨셉입니다. 따라서 Euler Angle 보다 더 유연하게 3차원 회전을 할 수 있습니다.

Axis-Angle Rotation 수식 설명

앞에서 언급한 바와 같이 Axis-Angle Rotation은 임의의 축에 대한 평면의 회전 방식을 이용합니다.

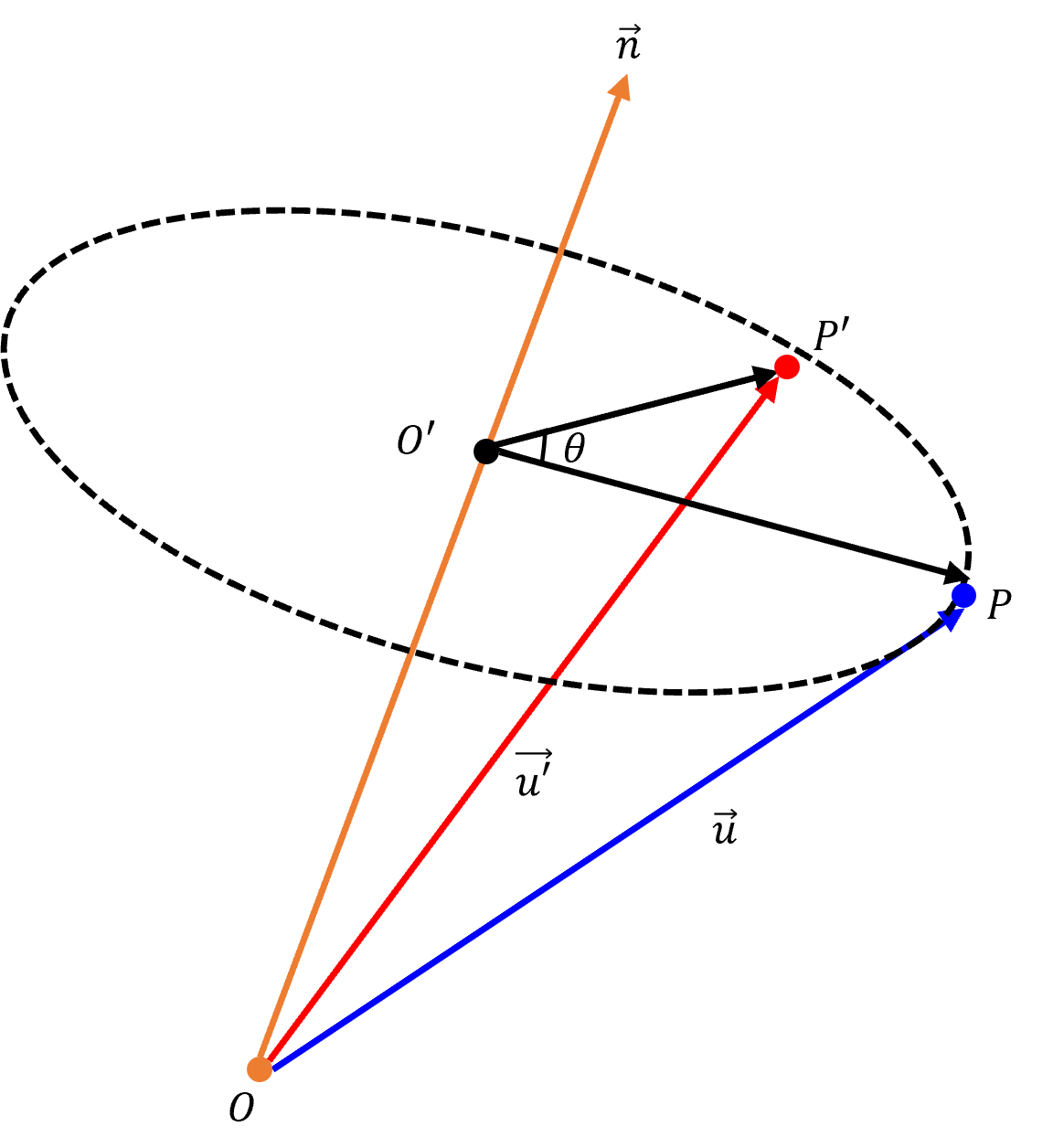
위 그림과 같이 3차원 공간에서 임의의 주황색 축을 이용하고 주황색 축에 직교 하는 검은색 점선 평면에서 회전을 하는 방식으로 3차원 회전을 합니다. 벡터의 내적과 외적 연산을 통하여 3차원 회전을 계산할 수 있으며 이 방법에 대하여 알아보도록 하겠습니다.
회전축이 되는 주황색 선을 $\vec{n}$ , 회전시킬 점을 $P$ , 회전할 각을 $\theta$ , 최종 회전한 점을 $P'$ , 월드 공간의 원점을 $O$ , 회전 평면의 중심을 $O'$ 로 정하겠습니다.
즉, 회전축은 월드 공간의 원점을 기점으로 뻗은 벡터이며 그 벡터 상의 특정 위치에 직교하는 평면이 생기고 그 평면을 기준으로 $\theta$ 만큼 회전하기 때문에 임의의 방향 및 크기대로 3차원 회전을 할 수 있는 원리 입니다.

지금부터 살펴볼 전개 방식은 위 그림에서 $\vec{OO'} + \vec{O'P'} = \vec{u'}$ 가 되는 구조로 먼저 $\vec{OO'} = \vec{v}$ 를 살펴보고 그 다음 $\vec{O'P'}$ 를 살펴보도록 하겠습니다.
이 과정을 통하여 최종적으로 구하고 싶은 $\vec{u'}$ 를 구할 수 있습니다.

① OO’ 벡터 구하기

위 그림에서 점 $P$ 의 좌표를 동차좌표계로 $P = (x, y, z, 1)$ 로 나타내 보겠습니다.

그러면 다음과 같이 간단하게 $\vec{u}$ 를 구할 수 있습니다.

$\vec{u} = P - O = (x, y, z, 0)$

최종적으로 구하고자 하는 벡터는 위 그림에서 $\vec{u'}$ 이고 이 값을 구하기 위해서는 $\vec{u}$ , $\vec{n}$ , $\theta$ 가 필요합니다.
임의의 축 $\vec{n}$ 에 대하여 $\vec{u}$ 를 각 $\theta$ 만큼 회전시켜 $\vec{u'}$ 를 계산하는 Axis-Angle Rotation의 식은 다음과 같습니다. 아래 식의 $\hat{n}$ 은 $\vec{n}$ 의 크기가 1인 벡터 입니다.

$\vec{u'} = \cos{(\theta)} \cdot \vec{u} + (1 - \cos{(\theta)}) \cdot (\vec{u} \cdot \hat{n}) \hat{n} + \sin{(\theta)} \cdot (\hat{n} \times \vec{u}) \tag{1}$

지금부터는 이 식의 유도 과정을 살펴보도록 하겠습니다.

먼저 위 그림과 같이 $O \to P$ 로 향하는 $\vec{u}$ 를 $O \to O'$ 로 향하는 $\vec{v}$ 로 만들기 위하여 다음과 같이 수식을 이용하여 만듭니다.

$\vec{OO'} = \vec{v} = (\vec{u} \cdot \hat{n}) \hat{n} \tag{2}$

식 (2)와 같이 전개되는 이유는 아래 링크를 참조하시기 바랍니다.
vector projection

따라서 $O' \to P$ 로 향하는 벡터는 $\vec{u}, \vec{v}$ 를 이용하여 $\vec{u} - \vec{v}$ 와 같이 구할 수 있습니다.

② O’P’ 벡터 구하기

앞에서 다룬 회전 평면을 위에서 아래로 내려다 보면서 회전 동작을 살펴보겠습니다.

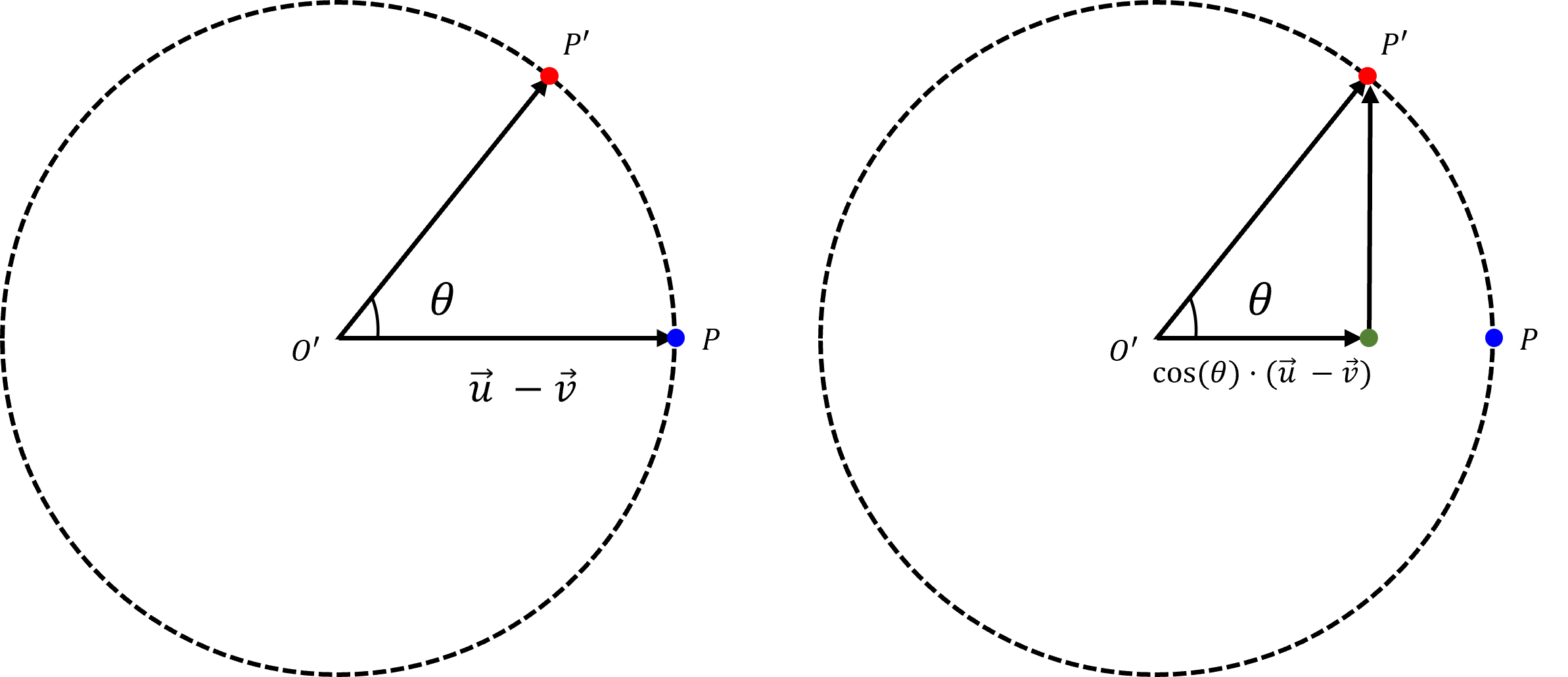
위 회전 평면에서 $\vec{O'P}$ 를 $\theta$ 만큼 회전 시킨 $\vec{O'P'}$ 를 구하는 것이 첫번째 목표입니다.
먼저 위 그림과 같이 $\vec{O'P'}$ 의 가로 성분은 $\cos{(\theta)} (\vec{u} - \vec{v})$ 와 같이 구할 수 있습니다.

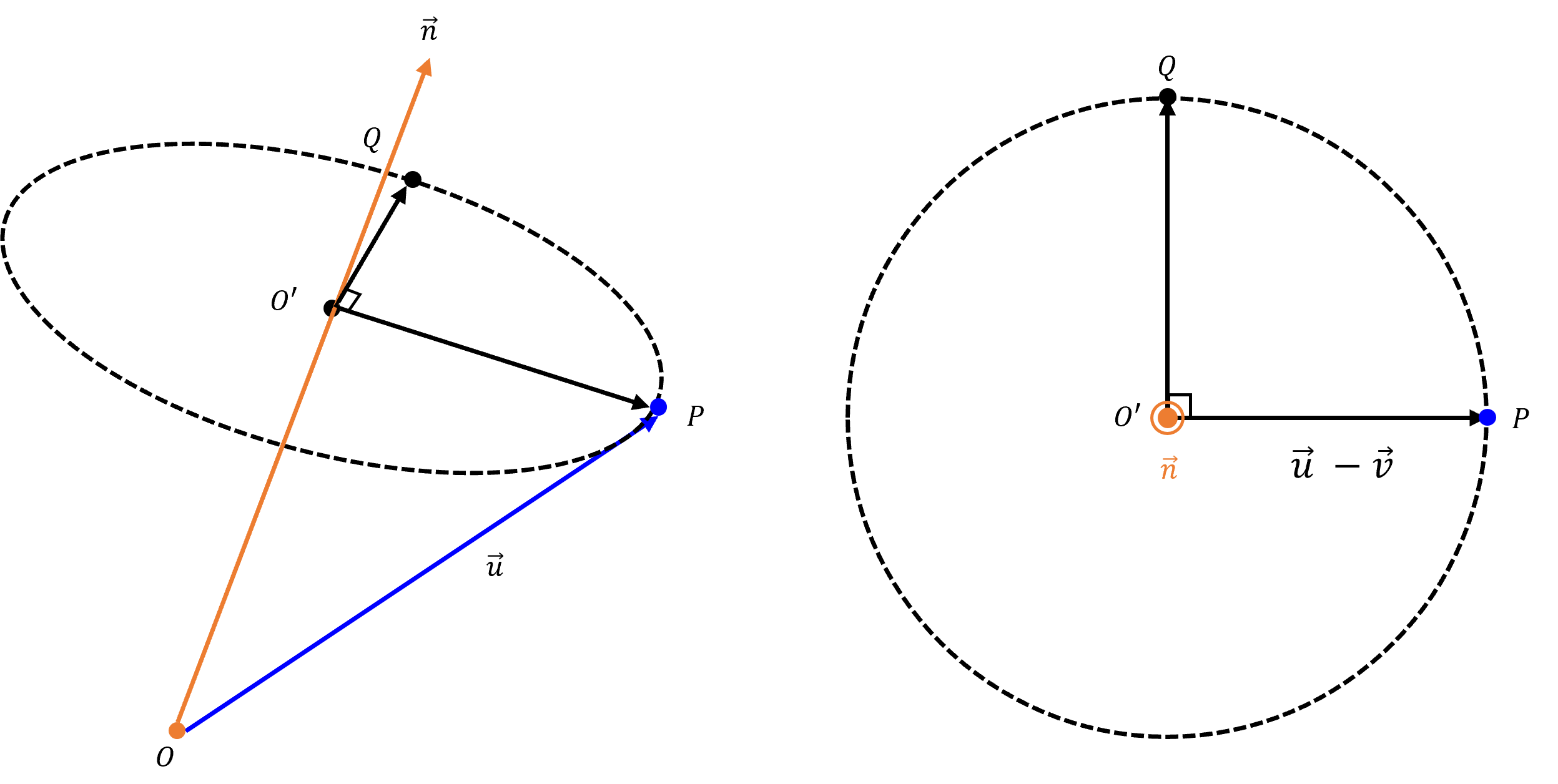
위 그림에서 $\vec{n}$ 과 $\vec{O'P'}$ 의 cross product를 통해 $\vec{O'Q}$ 를 구할 수 있습니다. 직교하는 성분이기 때문입니다.

$\vec{O'Q} = \hat{n} \times (\vec{u} - \vec{v}) \tag{3}$

지금 까지 확인한 내용을 이용하여 $\vec{O'Q}$ 의 값을 확인해 보도록 하겠습니다.

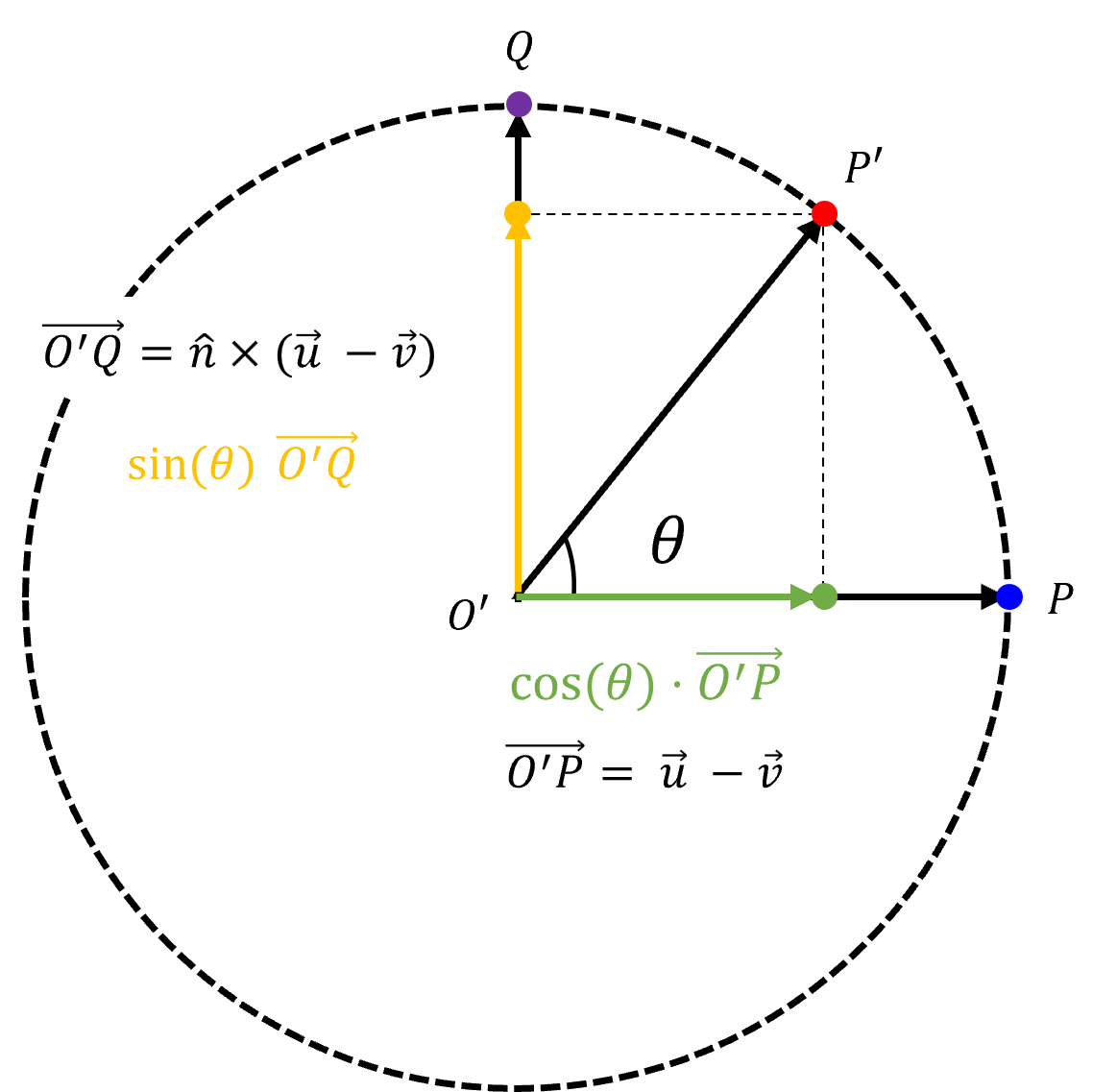
위 그림과 같이 수식을 전개하여 $\vec{O'P'}$ 를 구하면 다음과 같습니다.

$\begin{align}\vec{O'P'} &= \cos{(\theta)} \vec{O'P} + \sin{(\theta)} \vec{O'Q} \\ &= \cos{(\theta)} (\vec{u} - \vec{v}) + \sin{(\theta)} (\hat{n} \times (\vec{u} - \vec{v})) \\ &= \cos{(\theta)} (\vec{u} - \vec{v}) + \sin{(\theta)} (\hat{n} \times \vec{u} - \hat{n} \times \vec{v}) \\ &= \cos{(\theta)} (\vec{u} - \vec{v}) + \sin{(\theta)} (\hat{n} \times \vec{u}) \end{align} \tag{4}$

위 식에서 마지막의 $\hat{n} \times \vec{u}$ 가 소거된 이유는 두 벡터가 평행하기 때문에 cross product가 0이 되어서 소거하였습니다.
따라서 식을 정리하면 다음과 같습니다.

$\vec{O'P'} = \cos{(\theta)} (\vec{u} - \vec{v}) + \sin{(\theta)} (\hat{n} \times \vec{u}) \tag{5}$

③ OP’ 벡터 구하기

식 (2)의 벡터 $\vec{OO'}$ 와 식 (5)의 벡터 $\vec{O'P'}$ 를 더하면 최종적으로 구하고자 하는 벡터 $\vec{OP'}$ 를 구할 수 있습니다.

$\vec{OP'} = \vec{v} + \cos{(\theta)} (\vec{u} - \vec{v}) + \sin{(\theta)} (\hat{n} \times \vec{u}) \tag{6}$

마지막으로 $\vec{v} = (\vec{u} \cdot \hat{n}) \hat{n}$ 를 대입하면 최종적으로 다음과 같습니다.

$\vec{OP'} = \vec{u'} = \cos{(\theta)} \vec{u} + (1 - \cos{(\theta)})(\vec{u} \cdot \hat{n}) \hat{n} + \sin{(\theta)} (\hat{n} \times \vec{u}) \tag{7}$

위 수식의 의미를 다시 살펴보면 입력으로 들어오는 벡터는 $\vec{u}$ 이며 회전할 때 사용되는 값이 $\hat{n}$ 과 $\theta$ 입니다. 즉, $\hat{n}$ 과 $\theta$ 에 따라서 $\vec{u} \to \vec{u'}$ 가 되는 식으로 이해할 수 있습니다.
지금까지가 Axis-Angle Rotation을 수식적으로 살펴보았습니다. 이와 같은 회전 방식을 고안해 낸 로드리게스의 이름을 따서 로드리게스 회전 이라고도 부릅니다.

Axis-Angle Rotation의 행렬식 표현

지금까지 살펴본 공식을 통하여 3차원 공간에서 어떻게 임의의 축을 회전하여 3차원 회전하는 지 살펴보았습니다.
이번에는 Axis-Angle Rotation을 행렬로 나타내는 방법에 대하여 다루어 보도록 하겠습니다.

Axis-Angle Rotation을 행렬로 나타내기 위해서는 앞에서 다룬 식 (7)을 조금 변형해야 합니다.

$(\vec{u} \cdot \hat{n}) \hat{n} \to (\hat{n} \otimes \hat{n}^{T}) \cdot \vec{u} \tag{8}$

먼저 식 (7)의 $(\vec{u} \cdot \hat{n}) \hat{n}$ 부분을 위 식과 같이 변형하여 $\vec{u}$ 를 빼낼 수 있도록 만듭니다.
식 (8)의 우변의 $\otimes$ 는 outer product를 의미합니다. 좌/우변이 같음은 아래 결과를 참조하시면 됩니다.

따라서 식 (7)은 다음과 같이 다시 정리하여 쓸 수 있습니다.

$\vec{u'} = \cos{(\theta)} \vec{u} + (1 - \cos{(\theta)})(\hat{n} \otimes \hat{n}^{T}) \cdot \vec{u} + \sin{(\theta)} (\hat{n} \times \vec{u}) \tag{9}$

cross product 또한 행렬식으로 나타낼 수 있습니다.

$\hat{n} = \begin{bmatrix} \hat{n}_{x} & \hat{n}_{y} & \hat{n}_{z} \end{bmatrix}$
$\vec{u} = \begin{bmatrix} u_{x} & u_{y} & u_{z} \end{bmatrix}$

위 식과 같이 $\hat{n}, \vec{u}$ 를 정의하면 다음과 같이 cross product를 위한 행렬 식을 설정할 수 있습니다.

$\hat{n} \times \vec{u} = \begin{bmatrix} \hat{n}_{y}u_{z} - \hat{n}_{z}u_{y} \\ \hat{n}_{z}u_{x} - \hat{n}_{x}u_{z} \\ \hat{n}_{x}u_{y} - \hat{n}_{y}u_{x} \end{bmatrix} = \begin{bmatrix} 0 & -\hat{n}_{z} & \hat{n}_{y} \\ \hat{n}_{z} & 0 & -\hat{n}_{x} \\ -\hat{n}_{y} & \hat{n}_{x} & 0 \end{bmatrix} \begin{bmatrix} u_{x} \\ u_{y} \\ u_{z} \end{bmatrix} \tag{10}$

식 (10) 에서 $\hat{n}$ 으로 이루어진 행렬을 다음과 같이 $K$ 로 정의해 보겠습니다.

$K = \begin{bmatrix} 0 & -\hat{n}_{z} & \hat{n}_{y} \\ \hat{n}_{z} & 0 & -\hat{n}_{x} \\ -\hat{n}_{y} & \hat{n}_{x} & 0 \end{bmatrix}$

$\hat{n} \times \vec{u} = K\vec{u} \tag{11}$

이 때, $K^{2}$ 을 구해보면 다음과 같습니다.

$K^{2} = \begin{bmatrix} 0 & -\hat{n}_{z} & \hat{n}_{y} \\ \hat{n}_{z} & 0 & -\hat{n}_{x} \\ -\hat{n}_{y} & \hat{n}_{x} & 0 \end{bmatrix} \begin{bmatrix} 0 & -\hat{n}_{z} & \hat{n}_{y} \\ \hat{n}_{z} & 0 & -\hat{n}_{x} \\ -\hat{n}_{y} & \hat{n}_{x} & 0 \end{bmatrix} = \begin{bmatrix} -\hat{n}_{z}^{2}-\hat{n}_{y}^{2} & \hat{n}_{x}\hat{n}_{y} & \hat{n}_{z}\hat{n}_{x} \\ \hat{n}_{x}\hat{n}_{y} & -\hat{n}_{z}^{2}-\hat{n}_{x}^{2} & \hat{n}_{y}\hat{n}_{z} \\ \hat{n}_{x}\hat{n}_{z} & \hat{n}_{y}\hat{n}_{z} & -\hat{n}_{x}^{2}-\hat{n}_{y}^{2} \end{bmatrix} \tag{12}$

여기서 $\hat{n}$ 의 norm의 정의에 따라 $\hat{n}_{x}^{2} + \hat{n}_{y}^{2} + \hat{n}_{z}^{2} = 1$ 을 만족하므로 식 (12)의 우변을 다음과 같이 정리할 수 있습니다.

$\begin{bmatrix} -\hat{n}_{z}^{2}-\hat{n}_{y}^{2} & \hat{n}_{x}\hat{n}_{y} & \hat{n}_{z}\hat{n}_{x} \\ \hat{n}_{x}\hat{n}_{y} & -\hat{n}_{z}^{2}-\hat{n}_{x}^{2} & \hat{n}_{y}\hat{n}_{z} \\ \hat{n}_{x}\hat{n}_{z} & \hat{n}_{y}\hat{n}_{z} & -\hat{n}_{x}^{2}-\hat{n}_{y}^{2} \end{bmatrix} = \begin{bmatrix} \hat{n}_{x}^{2} - 1 & \hat{n}_{x}\hat{n}_{y} & \hat{n}_{z}\hat{n}_{x} \\ \hat{n}_{x}\hat{n}_{y} & \hat{n}_{y}^{2} - 1 & \hat{n}_{y}\hat{n}_{z} \\ \hat{n}_{x}\hat{n}_{z} & \hat{n}_{y}\hat{n}_{z} & \hat{n}_{z}^{2} - 1 \end{bmatrix} = \hat{n} \otimes \hat{n}^{T} - I \tag{13}$

$K^{2} = \hat{n} \otimes \hat{n}^{T} - I \tag{14}$
$\hat{n} \otimes \hat{n}^{T} = K^{2} + I \tag{15}$

식 (11)과 식 (15)를 이용하여 식 (9)를 전개해 보도록 하겠습니다.

$\begin{align} \vec{u'} &= \cos{(\theta)} \vec{u} + (1 - \cos{(\theta)})(\hat{n} \otimes \hat{n}^{T}) \cdot \vec{u} + \sin{(\theta)} (\hat{n} \times \vec{u}) \\ &= \cos{(\theta)} \vec{u} + (1 - \cos{(\theta)})(K^{2} + I)\vec{u} + \sin{(\theta)}K\vec{u} \\ &= (\cos{(\theta)}I + (1 - \cos{(\theta)})(K^{2} + I) + \sin{(\theta)}K)\vec{u} \\ &= R \vec{u} \end{align} \tag{16}$

$\begin{align} R &= \cos{(\theta)}I + (1 - \cos{(\theta)})(K^{2} + I) + \sin{(\theta)}K \\ &= \cos{(\theta)}\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} + (1 - \cos{(\theta)})\begin{bmatrix} \hat{n}_{x}^{2} & \hat{n}_{x}\hat{n}_{y} & \hat{n}_{z}\hat{n}_{x} \\ \hat{n}_{x}\hat{n}_{y} & \hat{n}_{y}^{2} & \hat{n}_{y}\hat{n}_{z} \\ \hat{n}_{x}\hat{n}_{z} & \hat{n}_{y}\hat{n}_{z} & \hat{n}_{z}^{2} \end{bmatrix} + \sin{(\theta)}\begin{bmatrix} 0 & -\hat{n}_{z} & \hat{n}_{y} \\ \hat{n}_{z} & 0 & -\hat{n}_{x} \\ -\hat{n}_{y} & \hat{n}_{x} & 0 \end{bmatrix} \end{align} \tag{17}$

$c : \cos{(\theta)}$
$s : \sin{(\theta)}$
$t : 1 - \cos{(\theta)}$

$R = \begin{bmatrix} t\hat{n}_{x}^{2} + c & t\hat{n}_{x}\hat{n}_{y} -s\hat{n}_{z} & t\hat{n}_{z}\hat{n}_{x} + s\hat{n}_{y} \\ t\hat{n}_{x}\hat{n}_{y} + s\hat{n}_{z} & t\hat{n}_{y}^{2} + c & t\hat{n}_{y}\hat{n}_{z} - s\hat{n}_{x} \\ t\hat{n}_{x}\hat{n}_{z} -s\hat{n}_{y} & t\hat{n}_{y}\hat{n}_{z} + s\hat{n}_{x}& t\hat{n}_{z}^{2} + c \end{bmatrix} \tag{18}$

풀어서 식을 쓰면 다음 식과 같습니다.

$R = \begin{bmatrix} (1 - \cos{(\theta)})\hat{n}_{x}^{2} + \cos{(\theta)} & (1 - \cos{(\theta)})\hat{n}_{x}\hat{n}_{y} -\sin{(\theta)}\hat{n}_{z} & (1 - \cos{(\theta)})\hat{n}_{z}\hat{n}_{x} + \sin{(\theta)}\hat{n}_{y} \\ (1 - \cos{(\theta)})\hat{n}_{x}\hat{n}_{y} + \sin{(\theta)}\hat{n}_{z} & (1 - \cos{(\theta)})\hat{n}_{y}^{2} + \cos{(\theta)} & (1 - \cos{(\theta)})\hat{n}_{y}\hat{n}_{z} - \sin{(\theta)}\hat{n}_{x} \\ (1 - \cos{(\theta)})\hat{n}_{x}\hat{n}_{z} -\sin{(\theta)}\hat{n}_{y} & (1 - \cos{(\theta)})\hat{n}_{y}\hat{n}_{z} + \sin{(\theta)}\hat{n}_{x}& (1 - \cos{(\theta)})\hat{n}_{z}^{2} + \cos{(\theta)} \end{bmatrix} \tag{19}$

Axis-Angle Rotation의 Python code

앞에서 다룬 내용을 이용하여 rotation 행렬을 axis-angle rotation으로 구현 방법은 다음과 같습니다.

def rot_from_axisangle(axis, theta):   
    axis = axis/np.linalg.norm(axis)
    c = np.cos(theta)
    s = np.sin(theta)
    t = 1 - c

    x = axis[0]
    y = axis[1]
    z = axis[2]

    rot = np.zeros((3, 3))
    
    rot[0, 0] = t * x * x + c
    rot[0, 1] = t * x * y - s * z
    rot[0, 2] = t * z * x + s * y
    rot[1, 0] = t * x * y + s * z
    rot[1, 1] = t * y * y + c
    rot[1, 2] = t * y * z - s * x
    rot[2, 0] = t * z * x - y * x
    rot[2, 1] = t * y * z + y * x
    rot[2, 2] = t * z * z + c
    return rot

위 코드를 3D Rotation Converter 예제를 이용하여 살펴보면 다음과 같습니다.
예를 들어 X, Y, Z 방향으로 각각 30도 회전한 경우를 살펴보도록 하겠습니다.

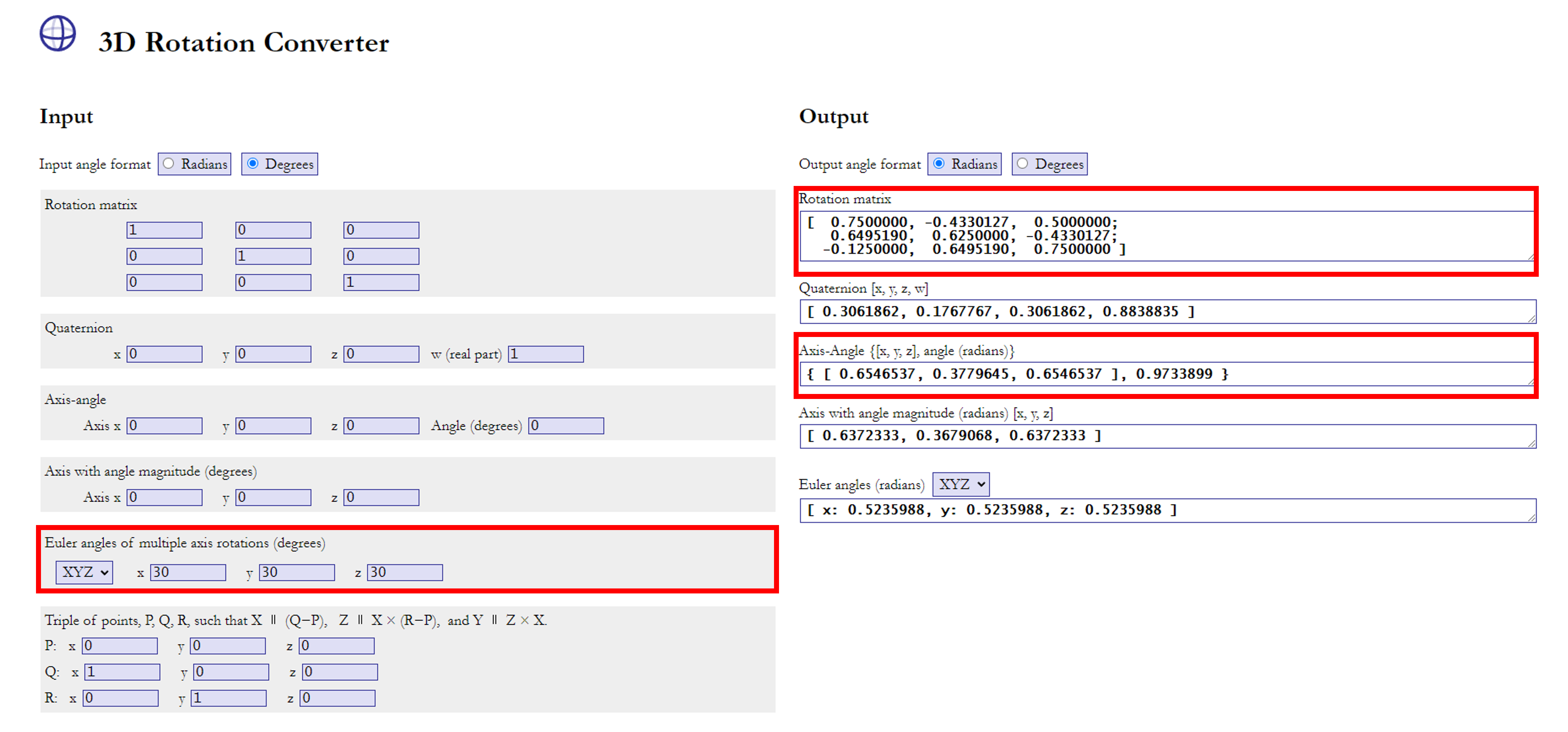
우측 Output에서의 Rotation matrix가 그 결과임을 알 수 있으며 이 때, Axis-Angle의 값 또한 알 수 있습니다.
위에 정의된 Python 코드를 이용하여 Axis-Angle을 구해보면 다음과 같습니다.

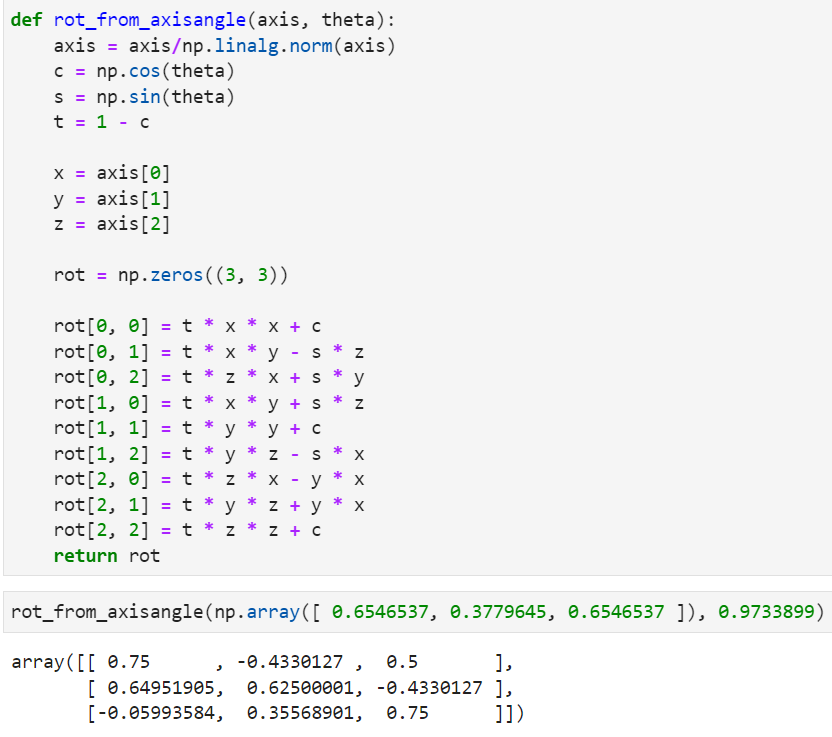
위 코드의 Rotation matrix의 결과 또한 같은 값임을 알 수 있습니다. 즉, Euler Angle Rotation이나 Axis-Angle Rotation이나 표현 방식이 다를 뿐 3차원 공간 상의 회전은 같음을 알 수 있습니다.

Axis-Angle Rotation의 단점

Axis-Angle Rotation은 Euler Angle Rotation의 2가지 문제 (Gimbal Lock, Rotaional Interpolation)를 해결하는 좋은 방법입니다. 하지만 Axis-Angle Rotation에서도 나타나는 몇가지 약점들이 있습니다.
먼저 연산량이 많다는 점입니다. 3D 회전이 많이 필요한 경우에 계속 누적된 Axis-Angle Rotation은 다른 Rotation 방법에 비해 상대적으로 연산량을 더 필요로 합니다.
그리고 Axis-Angle Rotation에서 회전 $\theta$ 가 0인 경우와 $2\pi$ 인 경우가 같다는 모호한 점도 있습니다.
마지막으로 회전이 계속 중첩되는 concatenation에서는 위 코드에서 다룬 바와 같이 Axis-Angle Rotation을 다른 형태의 행렬로 변환해서 사용해야 합니다. 즉, 단순히 수식으로만 사용하기에는 어려움이 있습니다.

Euler Angle Rotation 문제 뿐 아니라 Axis-Angle Rotation 문제도 해결하는 좋은 방법이 바로 quaternion 입니다.
quaternion은 다른 3차원 회전 방법에 대비하여 직관적이지 않다는 단점이 있지만 개념을 학습하고 익숙해져서 잘 사용하기만 하면 다른 회전 방법에서 발생하는 문제를 모두 개선할 수 있습니다.
아래 링크에서 quaternion의 개념을 익혀보시는 것을 추천 드립니다.
- 링크 : https://gaussian37.github.io/vision-concept-quaternion/

Vision 관련 글 목차