Fisheye Camera (어안 카메라) 관련 정리

Fisheye Camera (어안 카메라) 관련 정리

2023, Apr 26    


Vision 관련 글 목차



  • 참조 : https://arxiv.org/abs/2205.13281
  • 참조 : https://plaut.github.io/fisheye_tutorial/#pinhole-camera-distortion
  • 참조 : https://kr.mathworks.com/help/vision/ug/camera-calibration.html
  • 참조 : http://jinyongjeong.github.io/2020/06/19/SLAM-Opencv-Camera-model-%EC%A0%95%EB%A6%AC/
  • 참조 : http://jinyongjeong.github.io/2020/06/15/Camera_and_distortion_model/


  • 이번 글에서는 Fisheye Camera에 관한 전반적인 내용에 대하여 다루도록 하겠습니다. 글의 내용을 이해하려면 사전 지식에 해당하는 2개의 글을 반드시 읽고 오시길 권장 드립니다.
  • 글의 전반적인 내용은 Fisheye Camera가 가지는 의미나 필요했던 내용 그리고 Kumar의 survey 논문에 대한 내용을 다룹니다.
  • 본 글에서 다루는 데이터셋은 woodscape 데이터셋 이거나 개인적으로 구매한 Fisheye Camera를 이용하여 촬영한 데이터셋입니다. 제가 자체적으로 취득한 데이터셋들은 아래 링크에 공개하오니 자유롭게 쓰셔도 됩니다.
    • Woodscape (Public Dataset) : https://woodscape.valeo.com/dataset
    • Fisheye Mono Camera (Custom Dataset) : https://drive.google.com/drive/u/0/folders/16kPNXPaBFMogi8xt3fm6jhKp4jO6wB-H
    • Fisheye Stereo Camera (Custom Dataset) : https://drive.google.com/drive/u/0/folders/1Q4f8bAD0lypEXgqvqehrgbAtEGzC6jOX


  • Custom Dataset의 Fisheye Camera는 다음 링크에서 구매하였습니다.
    • Fisheye Mono Camera : https://ko.aliexpress.com/item/4000333240423.html
    • Fisheye Stereo Camera : https://astar.ai/collections/astar-products/products/stereo-camera


목차



Fisheye Camera의 특징과 Pinhole Camera와의 차이점


  • Pinhole Camera는 렌즈의 왜곡이 없는 이상적인 perspective view 형태의 카메라를 의미합니다.


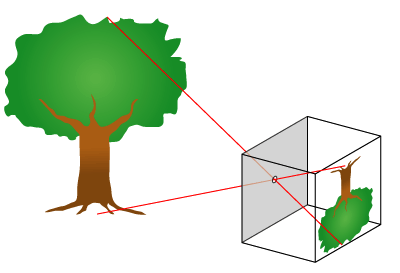
Drawing


  • Pinhole Camera는 위 그림과 같이 바늘 구멍으로 빛이 입사되어 실제 상에 해당하는 3D 공간 상의 점과 2D 이미지에 투영된 점이 직선으로 1대1 대응이 된 형태를 뜻합니다. 이와 같은 형태의 경우 빛이 직진하게 되므로 빛이 굴절되는 왜곡 현상은 나타나지 않고 이미지 내에서 물체들이 선형적인 관계를 가지기 때문에 선형 변환 등을 적용하여 알고리즘을 설계하기 용이합니다.
  • 하지만 카메라 렌즈가 없다면 빛을 효율적으로 모을 수 없기 때문에, 투영된 이미지가 매우 어둡고 볼 수 있는 영역도 매우 제한적이게 되어 사실상 사용할 수 없습니다.
  • 이와 같은 이유로 대부분의 카메라는 카메라 렌즈를 사용하게 되며 렌즈의 굴곡 정도에 따라서 원거리를 선명하게 볼 수 있으나 좁은 각도만 볼 수 있는 협각 카메라, 근거리만 선명하게 볼 수 있으나 넓은 영역을 볼 수 있는 광각 카메라와 같은 형태로 사용이 됩니다.
  • 본 글에서 다루는 카메라는 광각 카메라 중 180도 화각 정도를 다루는 Fisheye Camera에 대한 내용입니다.


Pinhole Camera의 Perspective Projection


  • Pinhoe Camera는 Perspective Projection이라는 성질을 따릅니다. Perspective Projection의 특징은 입사각 그대로 투영된다는 점입니다. 아래 그림을 살펴보도록 하겠습니다.


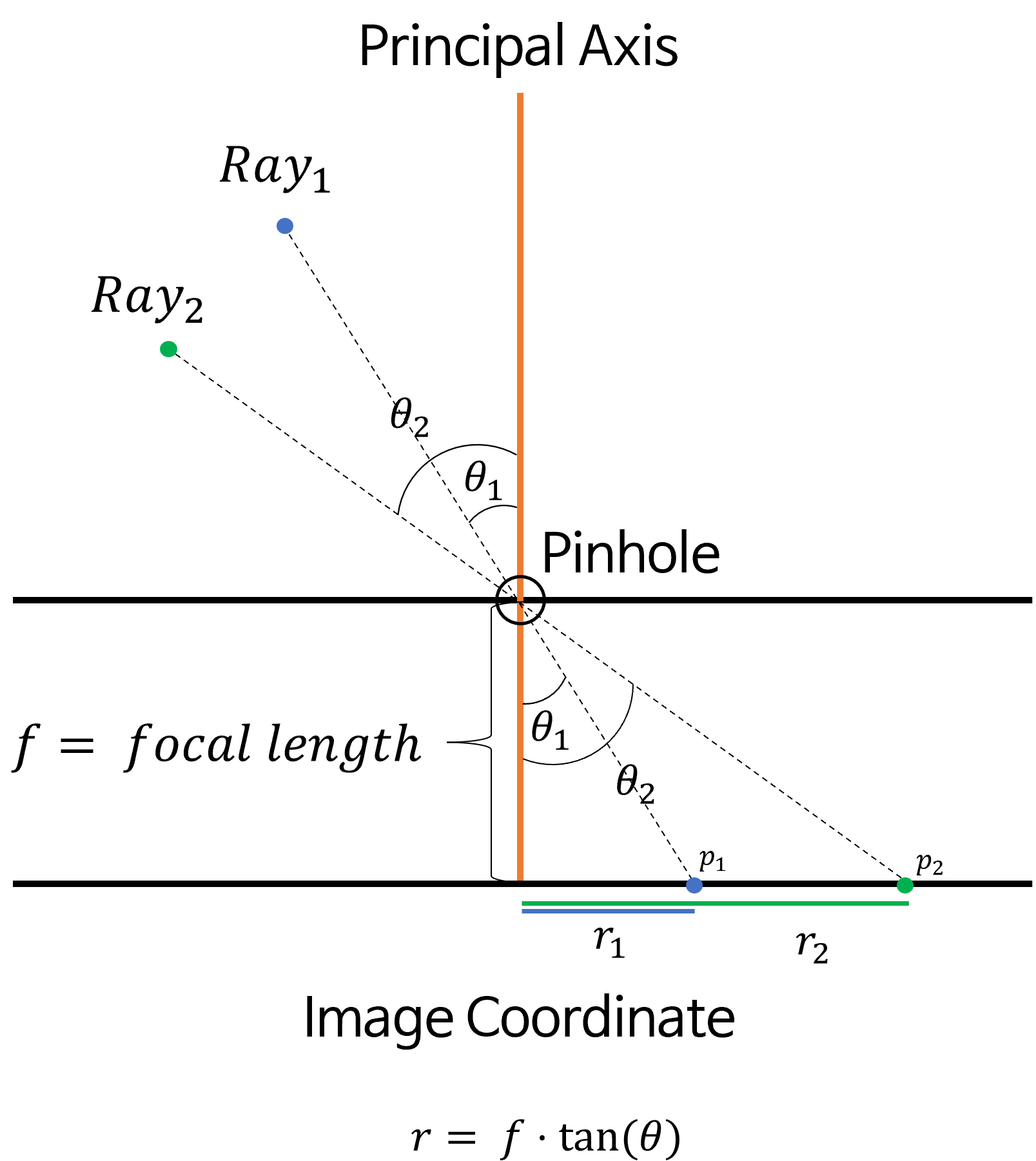
Drawing


  • Pinhole Camera의 경우 각 Ray는 Pinhole을 그대로 통과하여 Image Coordinate에 투영됩니다.
  • 위 그림에서 핵심은 Pinhole을 기점으로 \(\theta\) 가 그대로 유지된다는 점입니다. 따라서 Ray의 입사각이 결정되면 Image Coordinate에 투영되는 지점인 \(r\) 을 다음과 같이 계산할 수 있습니다.


  • \[r = f \cdot \tan{(\theta)}\]


  • 이와 같은 성질을 Perspective Projection이라고 합니다. 결국 Ray가 입사되는 각도 \(\theta\) 와 \(\tan{(\cdot)}\) 에 의해 투영되는 위치가 normalized된 좌표에서 결정된 후 \(f\) 만큼 비례하여 투영되면 최종적으로 Image Coordinate에 투영되게 됩니다.


Fisheye Camera의 Equidistance Projection


  • 반면 Fisheye Camera는 Equidistance Projection이라는 성질을 따르도록 카메라 모델링을 많이 합니다. Pinhole Camera의 경우 Perspective Projection을 따른다고 생각하면 되지만 Fisheye Camera는 Equidistance Projection을 따른다고 가정하고 모델링 합니다. 따라서 다른 Projection 모델을 사용할 수 도 있습니다. 하지만 대부분의 Fisheye Camera는 Equidistance Projection을 따라 모델링하므로 이 글에서도 Equidistance Projection만 다루고자 합니다.
  • Equidistance Projection의 특징은 Ray에 대하여 입사각 \(\theta\) 와 Image Coordinate에서의 Pinciple Axis와 투영된 점의 거리(Distance)가 같은 비율을 가진다는 점입니다.


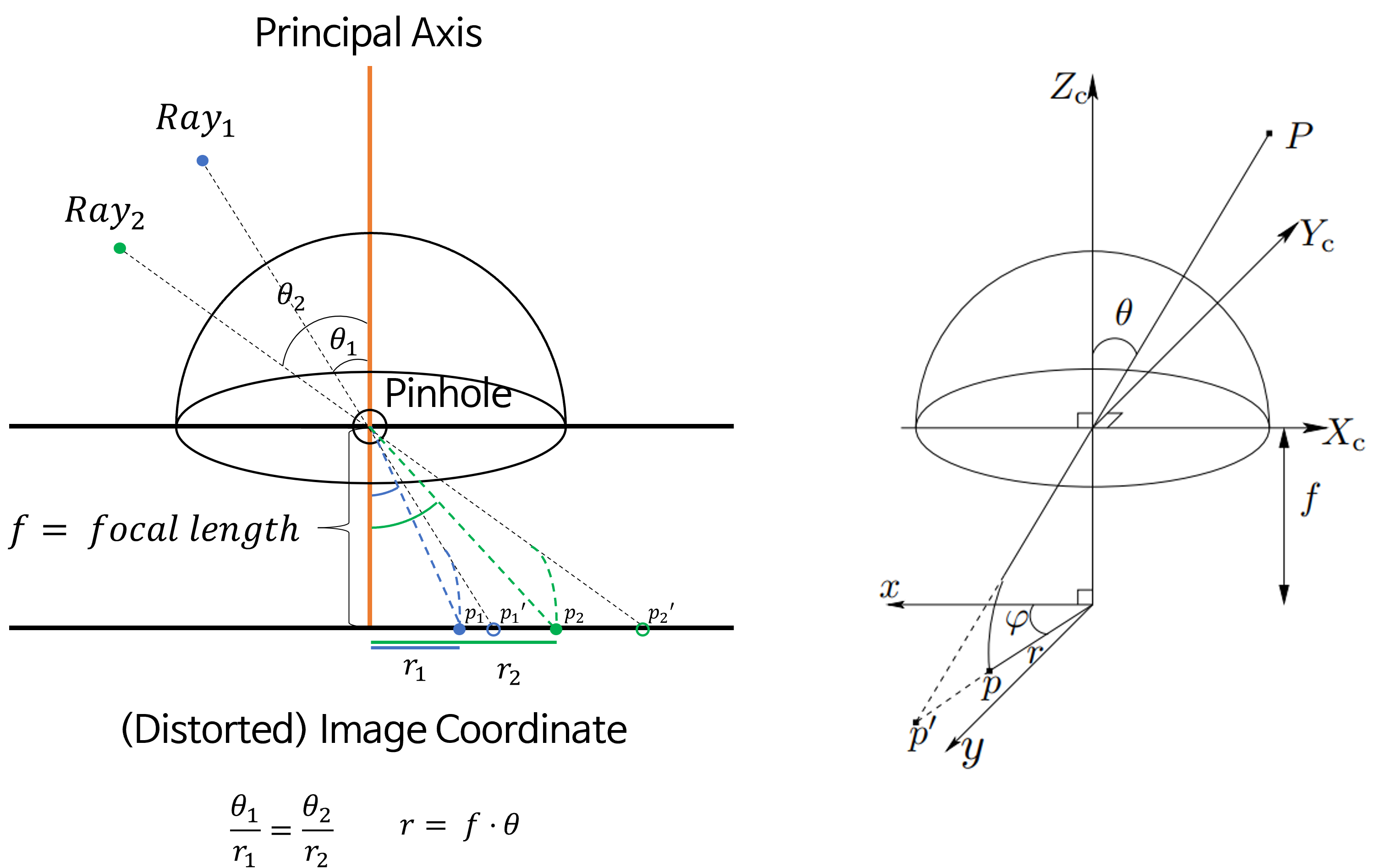
Drawing


  • 앞에서 설명한 Pinhole 모델과 다르게 Fisheye Camera에서는 Ray가 입사하면 Image Coordinate 에 그대로 입사각이 유지된 상태로 투영되는 것이 아니라 위 그림처럼 왜곡이 발생되어 Image Coordinate로 투영되게 됩니다. 왜곡이 되었기 때문에 Distorted 라는 단어를 추가하여 표현하기도 합니다.
  • Equidistance Projection에서의 가정은 \(\theta / r\) 의 비율이 일정하다는 것을 이용합니다. 따라서 \(\theta\) 가 정해지면 어떤 모델링된 식에 따라서 \(\theta / r\) 을 만족하도록 \(r\) 이 정해지게 됩니다. 이와 같은 가정을 Equidistance Projection 이라고 합니다. Equidistance Projection을 사용하는 모델링 식 중 보편적으로 사용 카메라 모델링 Generic Camera Model이며 아래 링크에서 내용을 참조할 수 있습니다.
  • 위 오른쪽 그림을 살펴보면 \(p\) 와 \(p'\) 가 하나의 ray 상에 존재하되 \(r\) 값이 조정되어 투영된 것으로 나타납니다. 기존에 Perspective Projection에서 \(r = f \cdot \tan{(\theta)}\) 을 만족하기 위해서는 \(p'\) 에 투영되는 것이 맞지만 \(\theta / r\) 을 만족하기 위해서는 \(r\) 값이 조정되어 \(p\) 에 투영되어야 한다는 것이 핵심입니다. 이러한 이유로 Projection의 이름이 Equidistance가 됩니다.


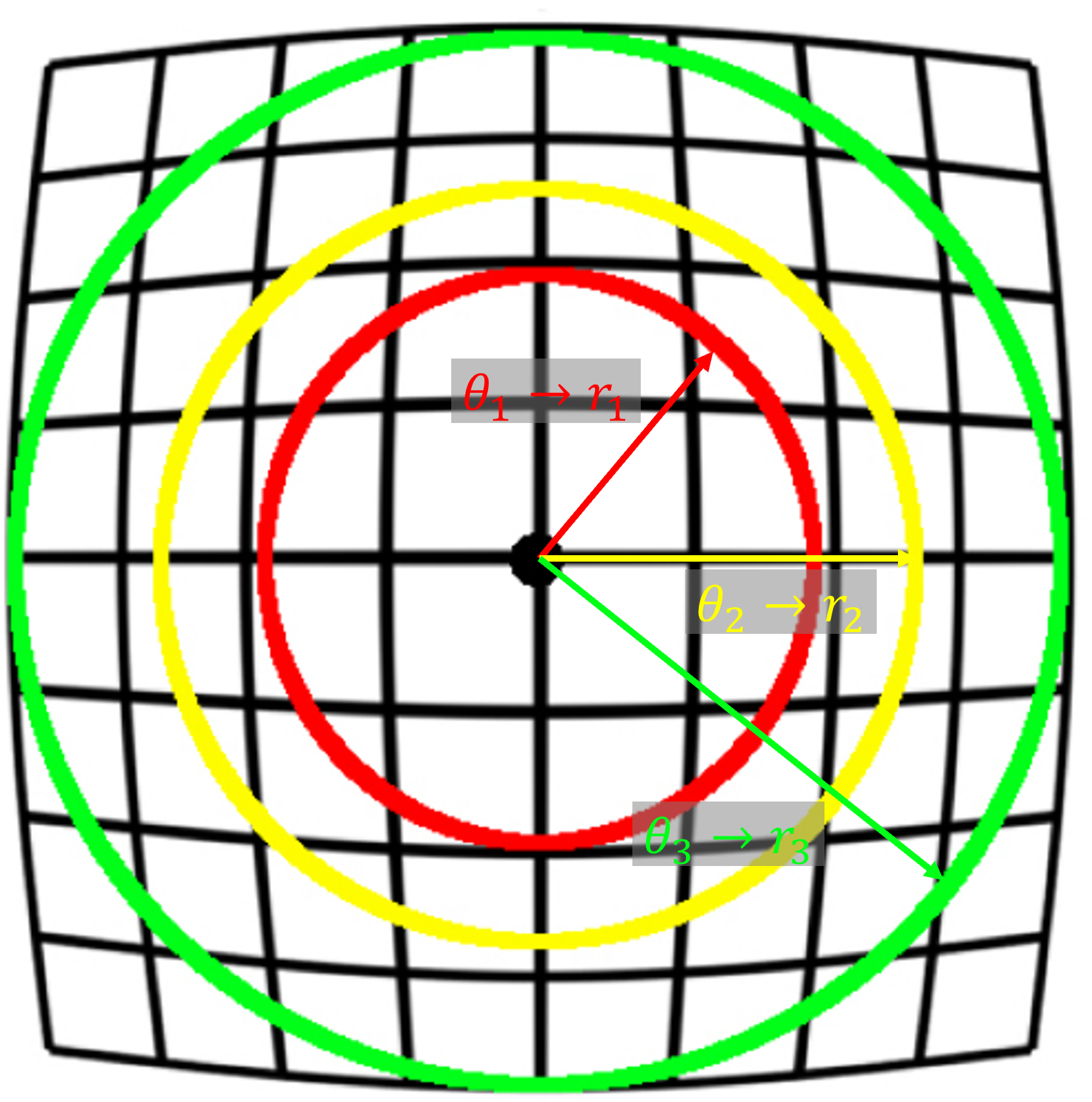
Drawing


  • 따라서 위 그림과 같이 입사각 \(\theta\) 에 의해 \(r\) 이 결정되고 각 방향에서 같은 입사각 \(\theta\) 에 대하여 같은 \(r\) 을 가지므로 위 그림과 같이 동심원을 그리는 형태로 \(r\) 이 형성됨을 알 수 있습니다. 이와 같은 형태의 렌즈 왜곡을 Barrel Distortion이라고 합니다.


Fisheye Camera의 Vignetting 영역 인식 방법


  • 아래는 Fisheye Camera의 vignetting 영역을 인식하는 방법입니다.
  • Vignetting 영역은 상이 맺히지 않아 일반적으로 검은색으로 나타나며 grayscale 형태로 이미지를 나타냈을 때, 0에 가까운 값을 가지게 됩니다.
  • 아래 코드는 이미지의 상단부터 하단 까지 좌/우 양끝에서 vignetting 영역이 아닌 픽셀 까지 찾은 다음에 least square를 통하여 circle을 찾습니다. circle은 center point와 radius를
  • 마지막으로 안전하게 radius 값을 margin 만큼 줄이면 안전하게 내부 영역을 찾을 수 있습니다.


from scipy.optimize import leastsq

# Function to calculate the residuals for least squares circle fit
def calculate_residuals(c, x, y):
    xi = c[0]
    yi = c[1]
    ri = c[2]
    return ((x-xi)**2 + (y-yi)**2 - ri**2)

# Initialize lists to store the coordinates of the first non-black pixels from left and right for each row
x_coords = []
y_coords = []

non_vignetting_threshold = 20
inner_circle_margin = 10

img = cv2.imread("image.png")
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Scan each row of the image
for i in range(img_gray.shape[0]):

    # Scan from the left
    for j in range(img_gray.shape[1]):
        if np.any(img_gray[i,j] > non_vignetting_threshold):
            x_coords.append(j)
            y_coords.append(i)
            break

    # Scan from the right
    for j in range(img_gray.shape[1]-1, -1, -1):
        if np.any(img_gray[i,j] > non_vignetting_threshold):
            x_coords.append(j)
            y_coords.append(i)
            break

# Convert the lists to numpy arrays
x = np.array(x_coords)
y = np.array(y_coords)

# Initial guess for circle parameters (center at middle of image, radius half the image width)
c0 = [img_gray.shape[1]/2, img_gray.shape[0]/2, img_gray.shape[1]/4]

# Perform least squares circle fit
c, _ = leastsq(calculate_residuals, c0, args=(x, y))

img_color = img.copy()
# Draw the circle on the original image
cv2.circle(img_color, (int(c[0]), int(c[1])), int(c[2])-10, (0, 255, 0), 2);

# Fill in the inside of the circle
mask_valid = np.zeros((img.shape[0], img.shape[1])).astype(np.uint8)
cv2.circle(mask_valid, (int(c[0]), int(c[1])), int(c[2])-inner_circle_margin, 1, -1);


Drawing


  • 위 그림과 같이 내부 circle을 찾을 수 있으며 circle 내부의 영역만 실제 유효한 RGB 값이 존재하는 영역임을 알 수 있습니다.


Drawing


  • circle 내부 영역을 표시하면 위 그림과 같습니다.


Generic Camera 모델의 Fisheye Camera의 유효 영역 확인 방법


  • 이 부분을 이해하기 위해서는 아래 글을 먼저 읽으시는 것을 권장드립니다.



  • 앞에서 살펴본 내용은 Fisheye Camera의 Vignetting 영역을 기준으로 영상의 유효한 영역과 유효하지 않은 영역을 나눈 예시였습니다.
  • Generic Camera Model을 이용한 카메라 캘리브레이션을 하면 카메라에 대하여 빛의 입사각(Angle of Incidence)에 따른 normalized camera coordinate에서의 왜곡 정도를 모델링 할 수 있습니다. 이 때, intrinsic 파라미터와 distortion coefficient를 얻을 수 있습니다.


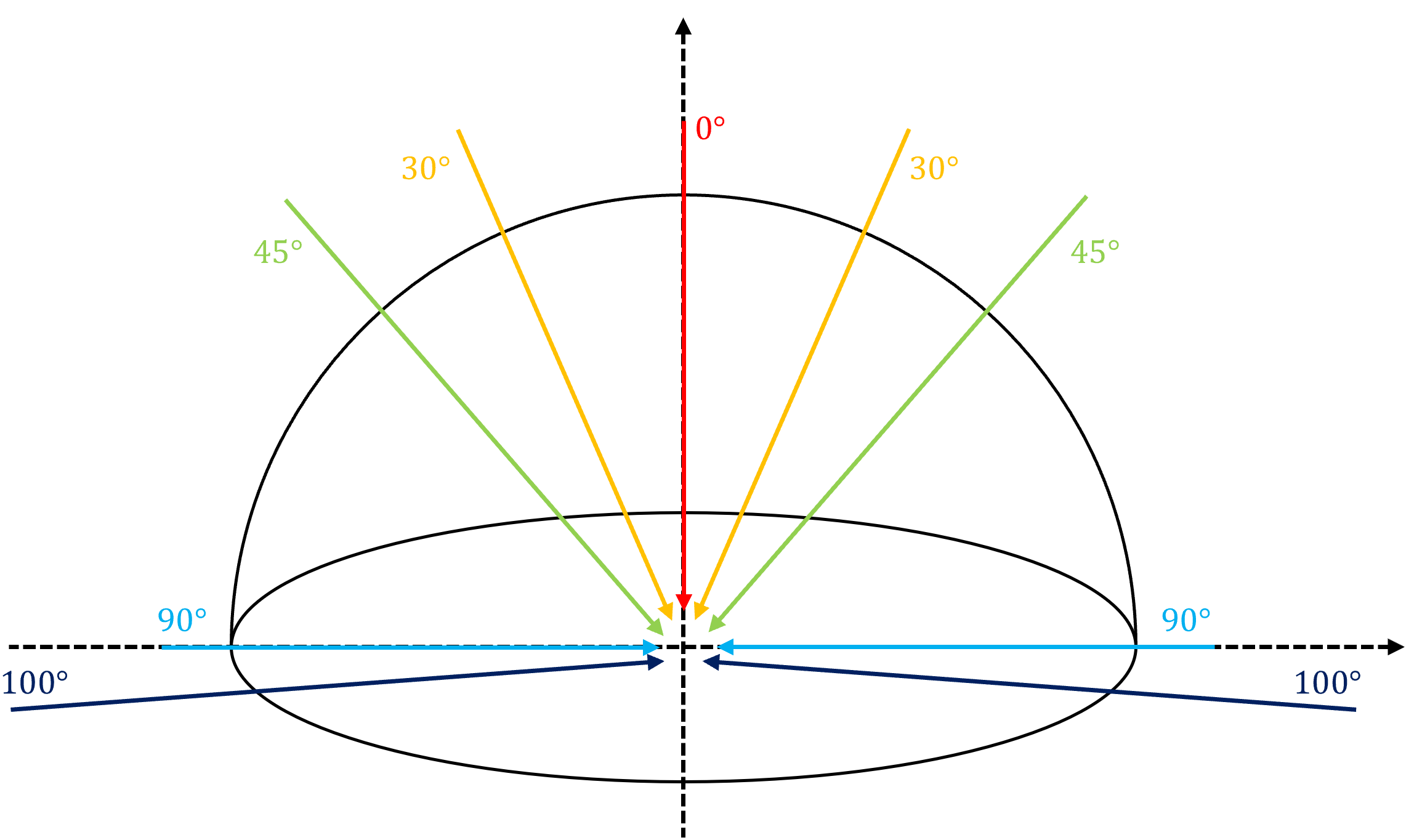
Drawing


  • 입사각은 위 그림과 같이 카메라 렌즈의 가장 바깥쪽 끝부분으로 빛이 수직 입사하는 경우의 입사각을 \(0 \deg\) 라고 하고 수평 입사하는 경우의 입사각을 \(90 \deg\) 이라고 합니다. 수평을 넘어서는 경우 \(90 \deg\) 를 넘게 됩니다.


  • distortion coefficient을 이용하면 입사각에 따라서 어떻게 영상이 왜곡이 되는 지 알 수 있기 때문에 렌즈 왜곡에 의해 발생한 영상을 모델링 할 수 있습니다.
  • 반대로 distortion coefficient을 이용하면 영상의 좌표들을 이용하여 입사각을 역방향으로 구할 수 있습니다. 이와 같이 입사각을 구하고자 하는 이유는 렌즈 왜곡이 방사형으로 발생하고 입사각이 커질수록 렌즈 왜곡이 심해지기 때문입니다. 따라서 영상의 유효한 영역을 입사각 기준으로 구분하게 되면 사용하기 유리한 영역을 선택할 수 있습니다.


  • 아래는 Generic Camera Model을 기준으로 카메라 캘리브레이션을 한 intrinsic과 distortion coefficient 계수 입니다.
  • 사용한 Fisheye 카메라는 USBFHD01M-L180 모델로 검색하면 상세한 스펙은 살펴볼 수 있습니다. 수평 화각 (Horizontal HOV)가 180도인 카메라이므로 스펙 상으로 최대 입사각 90도 까지 지원 가능한 카메라 입니다. 수평으로 양쪽 입사각 90도이면 전체가 180도가 되기 때문입니다.


fx = 567.85821196
skew = 0.
cx = 960.58762478

fy = 567.33818371
cy = 516.27957345

k0, k1, k2, k3, k4 = 1.0, -0.07908567, 0.03639387, -0.04227248, 0.01444498


  • Generic Camera Model에서는 위 계수 중 \(k_{0}, k_{1}, k_{2}, k_{3}, k_{4}\) 를 이용한 9차 기함수(odd function)를 이용하여 입사각에 따른 영상 왜곡을 모델링 합니다. 따라서 위 계수가 모델링 하는 비선형 식을 살펴보는 것이 중요합니다.


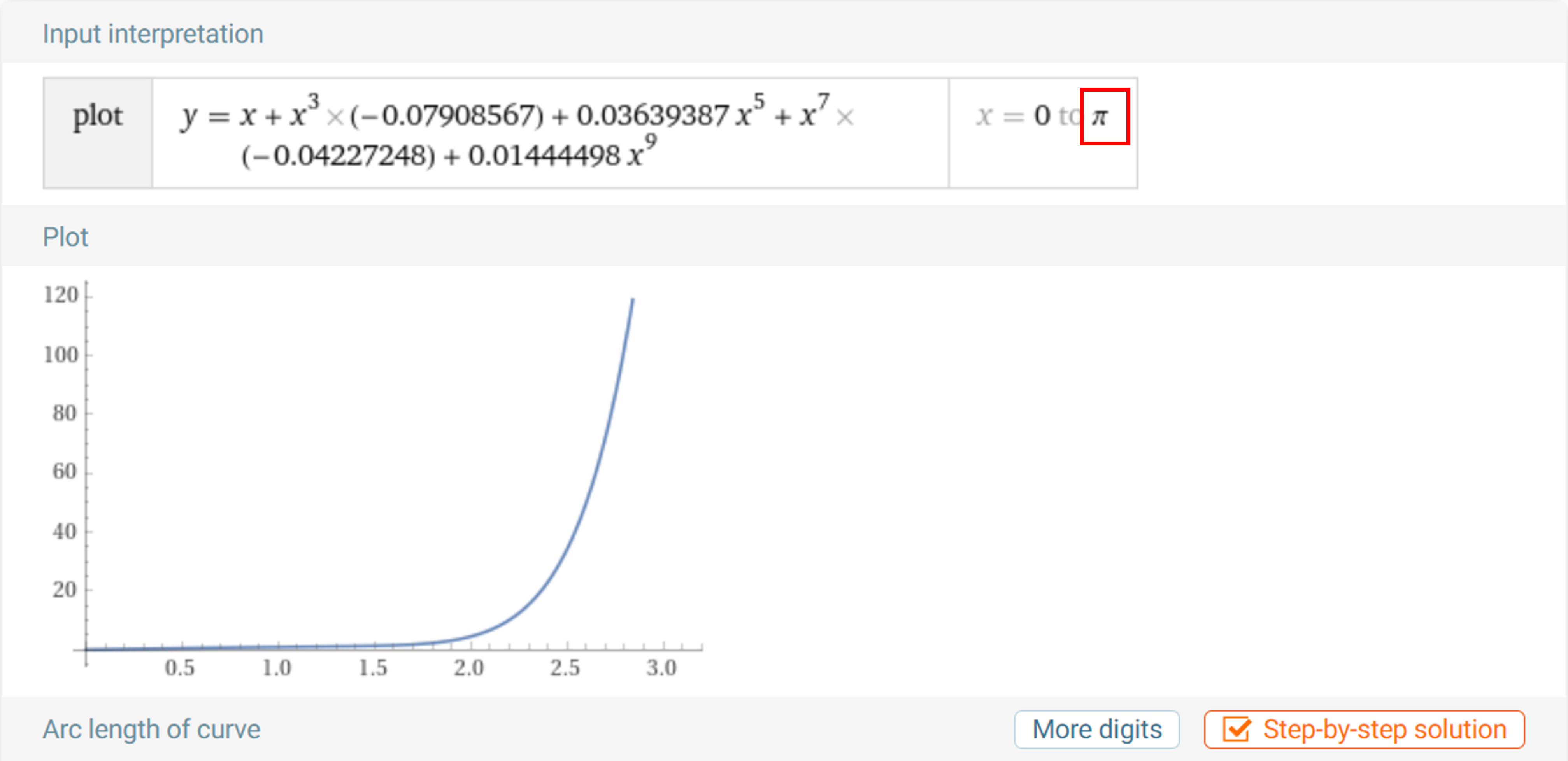
Drawing


  • 위 그래프는 \(0 ~ \pi\) 까지 모델링 해본 것입니다. 렌즈 입사각 \(0 ~ \pi\) 까지를 의미하므로 360도 전체를 모델링 한 것입니다.
  • 실제 카메라 캘리브레이션을 입사각 기준 \(0 ~ \frac{\pi}{2}\) 영역까지 밖에 하지 못하기 때문에 (카메라 스펙이 수평 화각이 180도 인 상태입니다.) \(\frac{\pi}{2}\) 가 넘어가는 영역에서 심하게 발산하게 됩니다.


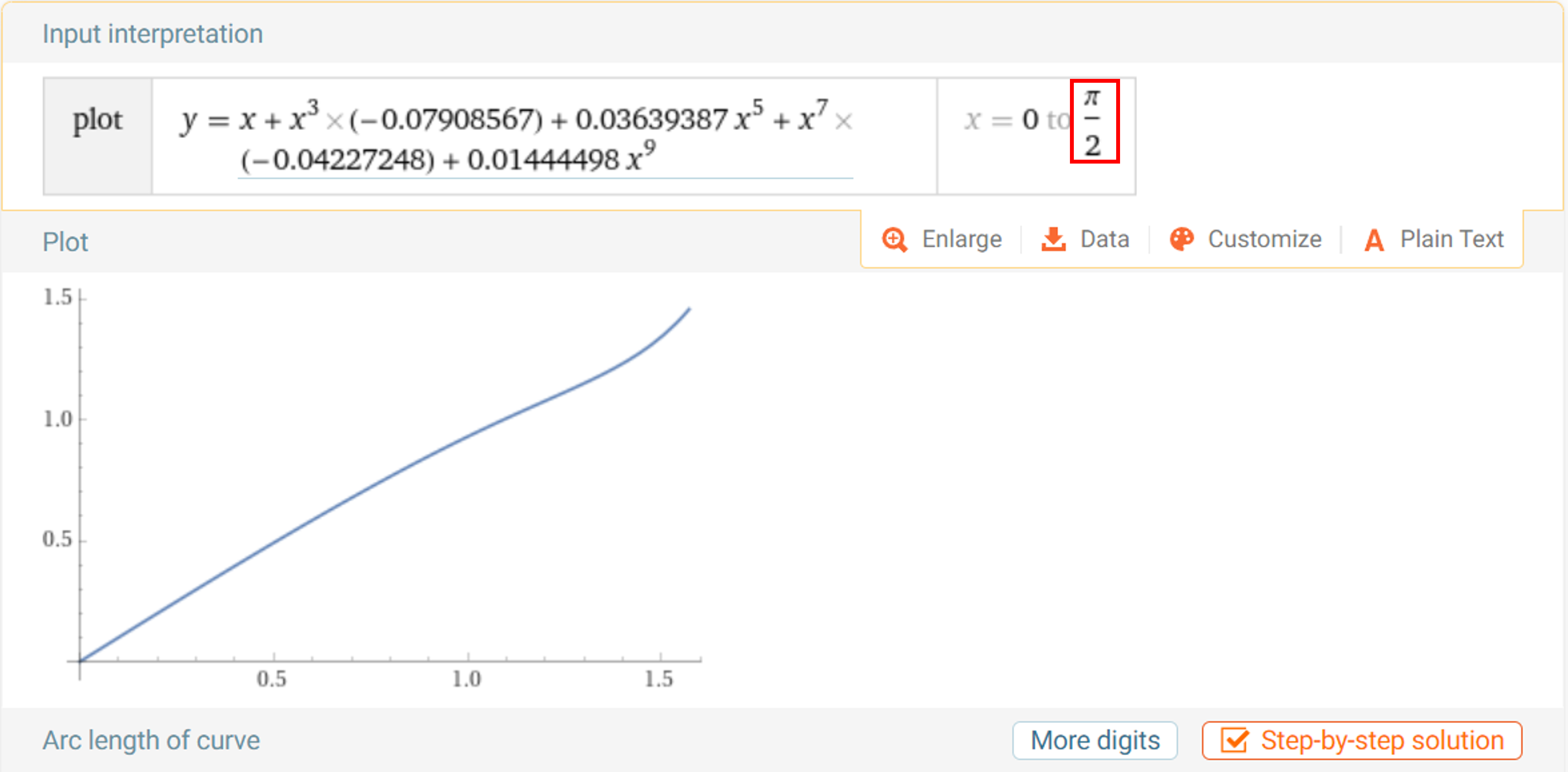
Drawing


  • 반면 \(\frac{\pi}{2}\) 영역 까지 그래프를 그려보면 꽤 안정적으로 \(x, y\) 축이 1:1 대응 관계로 모델링 된 것을 볼 수 있습니다. 1:1 대응 관계가 중요한 이유는 이미지 좌표 기준으로 입사각을 추정해야 하기 때문에 추정되는 입사각이 유일해야 하기 때문입니다.


  • 그러면 이미지 좌표를 통해 입사각을 추정하고 최종적으로 입사각 기반의 FOV를 확인하는 방법을 살펴보도록 하겠습니다. 관련 내용은 카메라 모델과 렌즈 왜곡 (lens distortion)에 자세히 설명되어 있습니다.


def f_theta_pred(theta_pred, r, k0, k1, k2, k3, k4):
    return k0*theta_pred + k1*theta_pred**3 + k2*theta_pred**5 + k3*theta_pred**7 + k4*theta_pred**9 - r

def f_theta_pred_prime(theta_pred, r, k0, k1, k2, k3, k4):
    return k0 + 3*k1*theta_pred**2 + 5*k2*theta_pred**4 + 7*k3*theta_pred**6 + 9*k4*theta_pred**8

def rdn2theta(x_dn, y_dn, k0, k1, k2, k3, k4):
    r_dn = np.sqrt(x_dn**2 + y_dn**2)
    theta_init = np.arctan(r_dn)

    # newton-method
    result = root_scalar(
        f_theta_pred, 
        args=(r_dn, k0, k1, k2, k3, k4), 
        method='newton', 
        x0=theta_init, 
        fprime=f_theta_pred_prime
    )
    
    theta_pred = result.root    
    r_un = np.tan(theta_pred)
    x_un = r_un * (x_dn / r_dn)
    y_un = r_un * (y_dn / r_dn)
    return x_un, y_un, r_dn, theta_pred

def get_fov_with_angle_of_incidience(
    height, width, degree, 
    fx, fy, skew, cx, cy, k0, k1, k2, k3, k4):
    
    board = np.zeros((height, width))
    for h in range(height):
        for w in range(width):
            y_dn = (h - cy) / fy
            x_dn = (w - cx - skew*y_dn) / fx
            
            _, _, _, theta_pred = rdn2theta(x_dn, y_dn, k0, k1, k2, k3, k4)
            
            if (theta_pred * 180 / np.pi) < degree:
                board[h][w] = 1
                
    return board

def bfs(board, h, w):
    rows, cols = board.shape
    visited = np.zeros(board.shape).astype(np.uint8)
    components = []
    
    queue = deque([(h, w)])
    
    while queue:
        y, x = queue.popleft()
        y = int(y)
        x = int(x)
        
        if y < 0 or y >= rows or x < 0 or x >= cols:
            continue
            
        if visited[y][x] or board[y][x] == 0:
            continue
            
        visited[y][x] = True
        components.append((y, x))
        
        for dx in [-1, 0, 1]:
            for dy in [-1, 0, 1]:
                queue.append((y + dy, x + dx))
                
    return components, visited


  • 위 코드는 다음 순서로 진행됩니다.
  • ① get_fov_with_angle_of_incidience 함수에서는 이미지 좌표계에서 모든 픽셀 좌표를 탐색하면서 픽셀 별 입사각을 역으로 계산합니다. 이 때, rdn2theta 함수를 이용하여 distorted normalized coordinate에서 undistorted normalized coordinate로 접근할 수 있도록 newton method를 이용하여 근사화합니다.
  • ② 픽셀 별 입사각을 계산하였을 때, degree 값 범위 이내로 입사각이 구해진 픽셀들을 유효한 픽셀로 표시합니다. degree 값은 일종의 threshold로 사용됩니다.
  • ③ 최종적으로 구한 유효한 픽셀에서 \((c_{x}, c_{y})\) 를 시작점으로 BFS를 하여 이어진 모든 픽셀을 유효한 영역으로 연결합니다. 왜냐하면 카메라 캘리브레이션 오차등으로 인하여 유효한 영역이 아님에도 유효한 영역으로 구분되는 영역이 가끔씩 존재하기 때문입니다.


img = cv2.cvtColor(cv2.imread('./fisheye_camera_calibration_test_10cm_01.png'), cv2.COLOR_BGR2RGB)
H, W = img.shape[:2]

board_90 = get_fov_with_angle_of_incidience(H, W, 90, fx, fy, skew, cx, cy, k0, k1, k2, k3, k4)
board_80 = get_fov_with_angle_of_incidience(H, W, 80, fx, fy, skew, cx, cy, k0, k1, k2, k3, k4)
board_70 = get_fov_with_angle_of_incidience(H, W, 70, fx, fy, skew, cx, cy, k0, k1, k2, k3, k4)
board_60 = get_fov_with_angle_of_incidience(H, W, 60, fx, fy, skew, cx, cy, k0, k1, k2, k3, k4)
board_50 = get_fov_with_angle_of_incidience(H, W, 50, fx, fy, skew, cx, cy, k0, k1, k2, k3, k4)

_, board_90_bfs = bfs(board_90, cy, cx)
_, board_80_bfs = bfs(board_80, cy, cx)
_, board_70_bfs = bfs(board_70, cy, cx)
_, board_60_bfs = bfs(board_60, cy, cx)
_, board_50_bfs = bfs(board_50, cy, cx)


  • 위 코드를 차례 대로 실행하면 다음과 같습니다.


Drawing


  • 입사각이 90도에서 50도로 줄어들수록 \((c_{x}, c_{y})\) 중심점 방향으로 유효한 영역이 좁아지는 것을 확인할 수 있습니다.


Fisheye Camera 왜곡 보정 방법 : Perspective Images


Perspective Image 왜곡 보정 방법


World to Perspective Image


Perspective Image to World


Fisheye Camera 왜곡 보정 방법 : Cylindrical Images


  • 참조 : https://plaut.github.io/fisheye_tutorial
  • 참조 : https://arxiv.org/pdf/2003.03759.pdf


Cylindrical Image 왜곡 보정 방법


World to Cylindrical Image


Cylindrical Image to World



Fisheye Camera 왜곡 보정 방법 : Spherical Images


  • 참조 : https://paulbourke.net/dome/fish2/
  • 참조 : https://paulbourke.net/dome/dualfish2sphere/


Spherical Image 왜곡 보정 방법


World to Spherical Image


Spherical Image to World




Surround-view Fisheye Camera Perception for Automated Driving 리뷰


Abstract



1. Introduction



2. Fisheye Camera Models



3. Surround View Camera System



4. Perception Tasks



5. Public Datasets And Research Directions




Vision 관련 글 목차


Twitter Facebook Google+
# fisheye camera # 어안 카메라 # lens distortion # 카메라 모델 # 렌즈 왜곡