(멀티플 뷰 지오메트리) Lecture 3. Circular points and Absolute conic

Multiple View Geometry 글 목차

참조 : https://youtu.be/T-p6d7av32Y?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : https://youtu.be/tsO6VO1s_x8?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : https://youtu.be/k63Bi74Meyc?list=PLxg0CGqViygP47ERvqHw_v7FVnUovJeaz
참조 : Multiple View Geometry in Computer Vision

이번 글에서는 Circular points and Absolute conic 내용의 강의를 듣고 정리해 보도록 하겠습니다.

이번 강의에서는 크게 위 3가지 내용을 배울 예정입니다.
① line at infinity 와 circular points 개념을 배우고 이 개념을 이용하여 affine 또는 projective distortion을 제거하는 방법에 대하여 배워보도록 하겠습니다.
② 개념을 확장하여 plane at infinity를 배우고 affine transformation에서 불변한 성질에 대하여 배워보도록 하곘습니다.
③ absolute conic과 absolute dual quadrics를 배우고 similarity transformation에서 불변한 성질에 대하여 배워보도록 하겠습니다.

Recovery of Affine Properties from Images

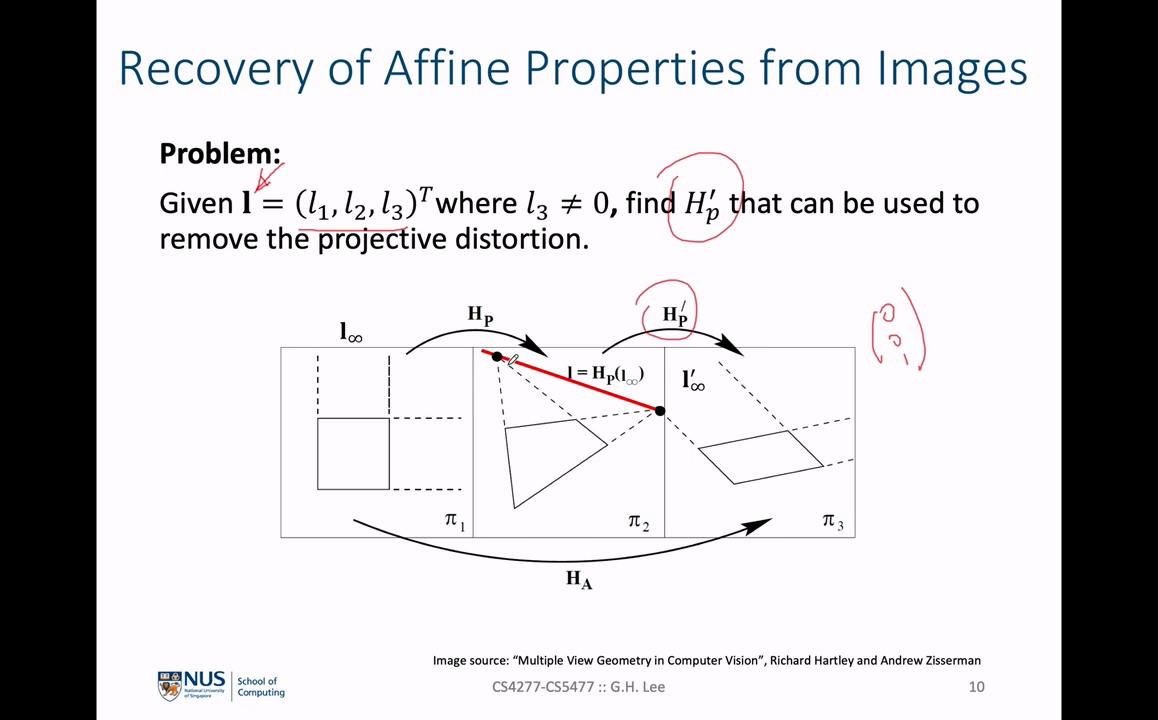
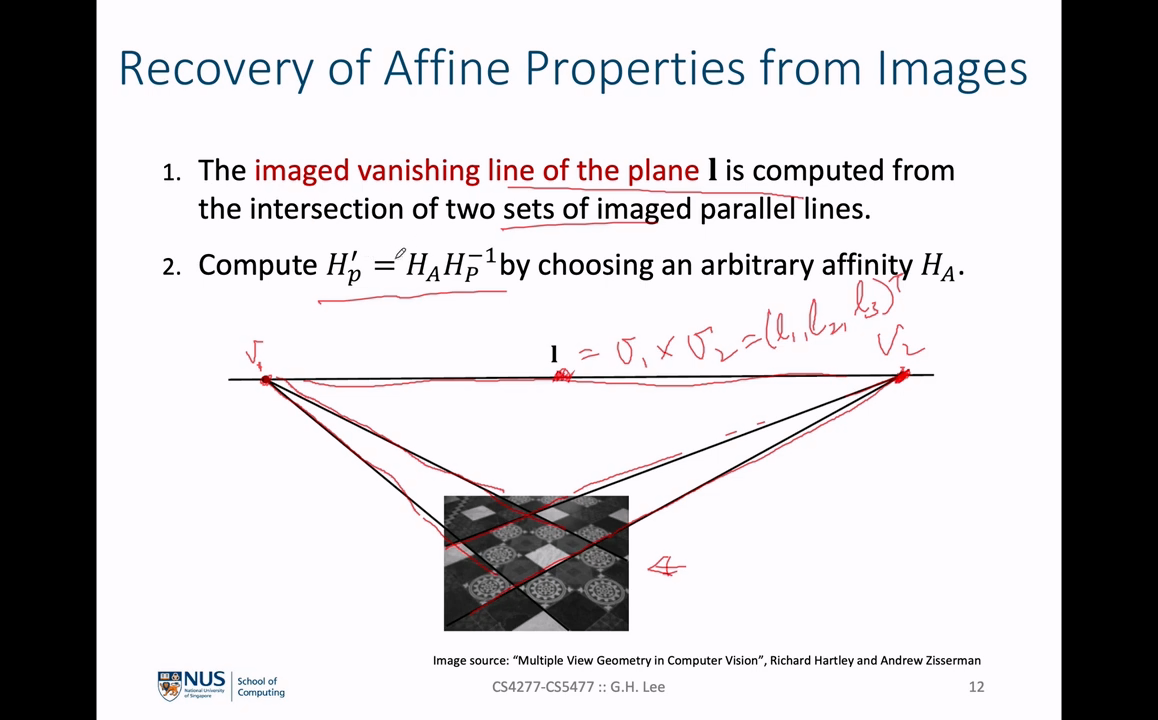
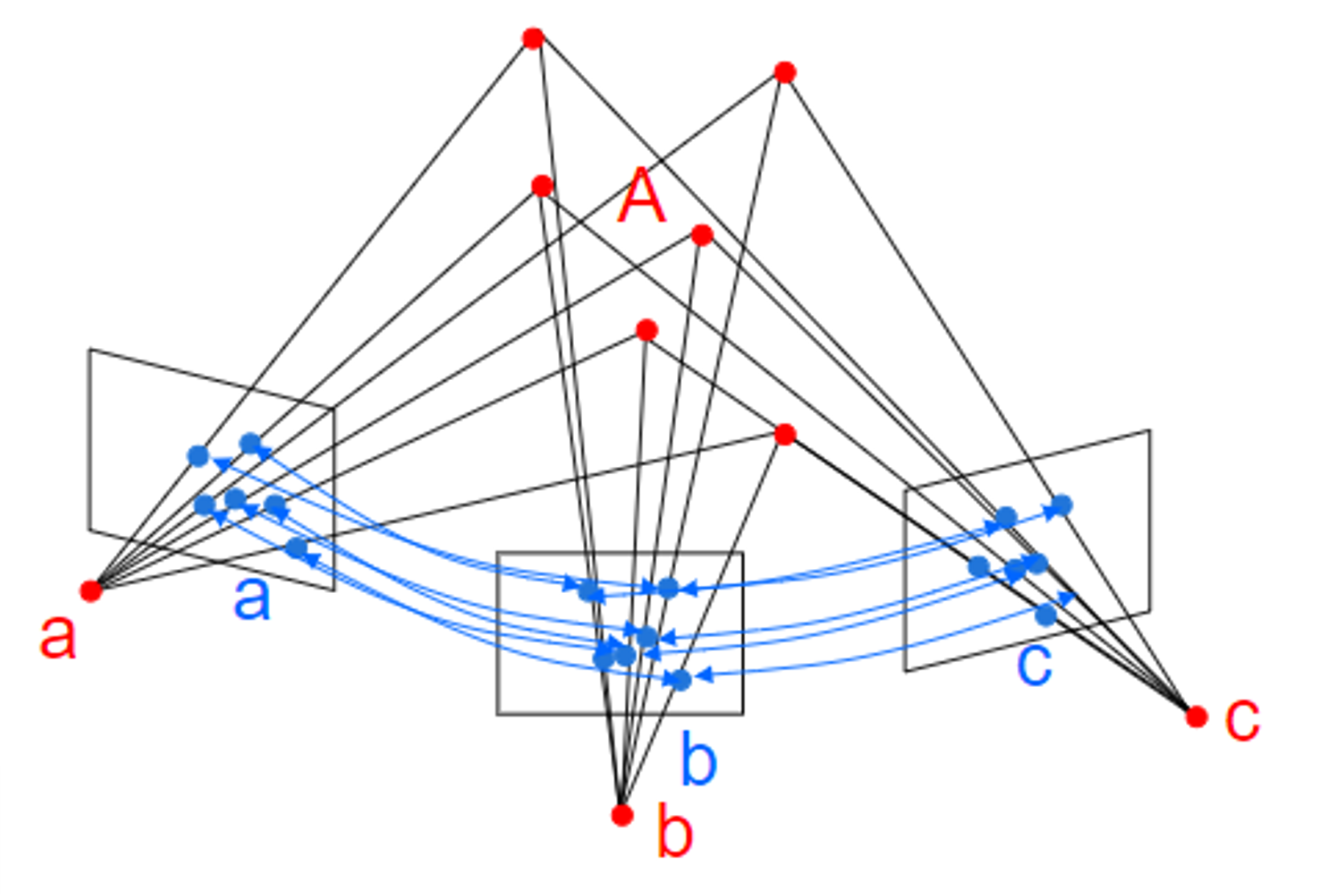
위 슬라이드에서 \(v_{1}, v_{2}\) 2개의 점의 cross product를 이용하여 \(l\) 을 구하는 방법은 다음과 같습니다.

위 그림과 같은 선 \(l\), \(v_{1}, v_{2}\) 점의 관계에서 두 점이 선 \(l\) 위에 있으므로 아래 식을 만족합니다.

\[l \cdot v_{1} = 0\]
\[l \cdot v_{2} = 0\]

벡터 \((a, b, c)\) 는 \((x_{1}, y_{1}, z_{1})\) 과 \((x_{2}, y_{2}, z_{2})\) 에 모두 수직인 벡터입니다. 따라서 \(v_{1}\) 과 \(v_{2}\) 모두에 수직인 벡터를 구하는 방법이 cross product이므로 다음과 같이 \(l\) 을 구할 수 있습니다.

\[l = v_{1} \times v_{2}\]

Computing a Vanishing Point from a Length Ratio

이번에는 Vanishing Point를 어떻게 계산하는 지 살펴보도록 하겠습니다.

vanishing point를 계산하기 위하여 이미지 상에서 동일선(collinear) 상에 있는 점들 \(a, b, c\) 를 가정하겠습니다. 상세 내용은 다음 슬라이드에서 설명하겠습니다.

위 그림과 같이 1차원 선 \(\mathbb{P}^{1}\) 상에서 \(a = (0, 1)^{T}, b = (a, 1)^{T}, c = (a + b, 1)^{T}\) 를 나타내며 그 사이의 거리는 각각 \(a, b\) 가 됩니다.
이와 같은 방식으로 정한 점 \(a, b, c\) 를 Perspective 성질이 포함된 이미지 (실제 촬영된 이미지)와 Perspective 성질이 제거된 이미지 각각에서 점을 구해볼 수 있습니다.

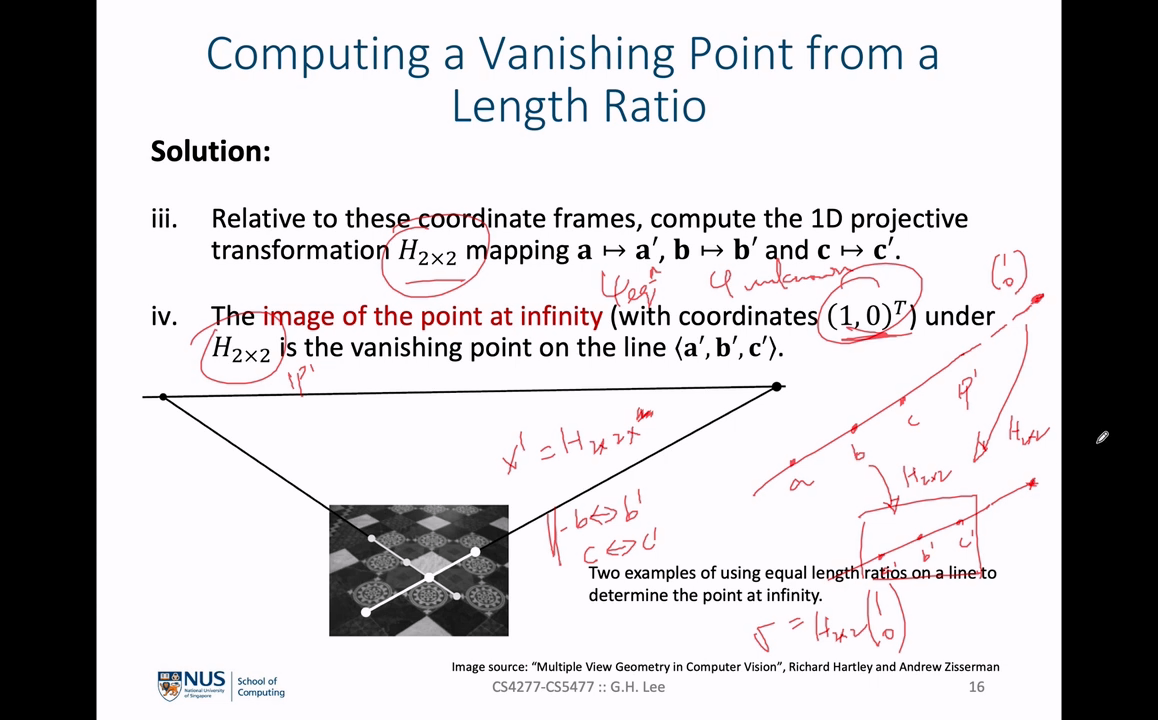
Vanishing Point를 찾기 위하여 Perspective 성질이 제거된 오른쪽 이미지에서 왼쪽 이미지로 같은 선상의 점들의 이동 관계를 나타내는 \(H_{2\times2}\) 행렬을 찾습니다. 그러면 \(a \to a', b \to b' , c \to c'\) 로 변환할 수 있습니다.
마지막으로 구하고자 하는 소실점은 오른쪽의 이미지에서는 point at infinity인 \((1, 0)\) 에 존재합니다. 이 점을 왼쪽의 perspective 왜곡이 적용된 이미지로 반영하기 위해서는 \(H_{2\times2}\) 로 변환해 줍니다.

\[x' = H_{2\times2}x = H_{2\times2} \begin{bmatrix} 1 \\ 0 \end{bmatrix}\]

위 식과 같이 Vanishing Point인 \(x'\) 를 구할 수 있습니다.

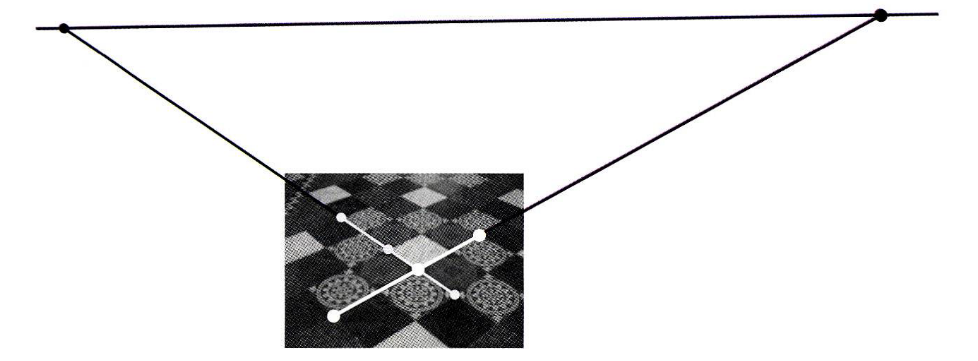
위 그림에서는 point at infinity 를 결정하기 위하여 선분의 동일한 길이 비율을 사용합니다. 선분 간격은 가는 흰색 선을 이용하였고 점은 두꺼운 흰색 선으로 표시하였습니다.
검은색 선은 line at infinity이며 검은색 두개의 점은 point at infinity입니다. 이 점은 앞에서 다룬 변환과 마찬가지로 Perspective 왜곡이 없는 이미지의 point at infinity에 \(H_{2\times2}\) 를 적용하여 Perspective 왜곡이 있는 이미지에서 point at infinity를 구할 수 있습니다.

Circular Points and Their Dual

circular points의 개념을 배우기 전에 아래 링크에서 Affine and Euclidean Geometry 개념에 대하여 숙지하고 오면 도움이 됩니다.
- 링크 : https://gaussian37.github.io/vision-mvg-nus_lec0/#affine-and-euclidean-geometry-1

어떤 두 개의 점이 \(l_{\infty}\) (line at infinity) 상에서 similarity transformation에 대하여 fixed point 라고 생각해 보겠습니다.
먼저 fixed point라고 하면 정의역과 공역이 공간 \(X\) 인 함수 \(f : X \to X\) 에 대하여 \(x_{0} \in X\) 가 \(f(x_{0}) = x_{0}\) 을 만족할 때, 이 점 \(x_{0}\) 를 fixed points라고 합니다.
이 때, \(l_{\infty}\) 상에 존재하는 fixed points인 두 개의 점을 circular (absolute) points 라고 하며 아래와 같이 복소수 형태로 나타냅니다. (이름의 의미는 이후 슬라이드에서 설명합니다.)
아래 \(I, J\) 는 표준 좌표의 형태이며 다르게 변형될 수 있습니다.

\[I = \begin{pmatrix} 1 \\ i \\ 0 \end{pmatrix}\]
\[J = \begin{pmatrix} 1 \\ -i \\ 0 \end{pmatrix}\]

위 표준 좌표인 두 점 \(I, J\) 는 \(l_{\infty}\) 상에 있으므로 마지막 차원은 0인 ideal points 형태를 만족합니다.

위 슬라이드에서는 circular points인 \(I, J\) 가 fixed point 일 때, projective transformation \(H\) 는 similarity transformation임이 필요 충분 조건임을 설명합니다.
따라서 위 슬라이드 조건과 앞에서 설명한 fixed point의 정의와 같이 \(I' = H_{x}I = I\) 임을 통하여 정의역 \(I\) 가 \(H_{x}\) 를 거치더라도 \(I\) 됨을 통하여 fixed point 임을 보입니다.

위 식에서 \(H_{s}\) 는 similarity transformation 행렬로 아래 식을 따릅니다.

\[H_{s} = \begin{bmatrix} s\cos{(\theta)} & -s\sin{(\theta)} & t_{x} \\ s\sin{(\theta)} & s\cos{(\theta)} & t_{y} \\ 0 & 0 & 1 \end{bmatrix}\]

따라서 위 식과 슬라이드의 오일러 공식을 이용하면 다음과 같이 정리할 수 있습니다.

\[I' = H_{s}I = \begin{bmatrix} s\cos{(\theta)} & -s\sin{(\theta)} & t_{x} \\ s\sin{(\theta)} & s\cos{(\theta)} & t_{y} \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ i \\ 0 \end{bmatrix}\]
\[= \begin{bmatrix} s \cdot \cos{(\theta)} - s \cdot i \cdot \sin{(\theta)} \\ s \cdot \sin{(\theta)} + s \cdot i \cdot \cos{(\theta)} \end{bmatrix}\]
\[= s \begin{bmatrix} \cos{(\theta)} - i \cdot \sin{(\theta)} \\ \sin{(\theta)} + i \cdot \cos{(\theta)} \\ 0 \end{bmatrix}\]
\[= s \begin{bmatrix} e^{-i\theta} \\ i(\cos{(\theta)} - i\sin{(\theta)}) \\ 0 \end{bmatrix}\]
\[= s \begin{bmatrix} e^{-i\theta} \\ i(e^{-i\theta}) \\ 0 \end{bmatrix}\]
\[= s e^{-i\theta} \begin{bmatrix} 1 \\ i \\ 0 \end{bmatrix}\]

마지막 식이 \(I\) 가 되면 fixed points 임을 만족하며 \(l_{\infty}\) 상에서는 스케일 변환이 허용되기 때문에 아래와 최종 식은 \(I\) 와 동일함을 알 수 있습니다.

\[I' = H_{x}I = s e^{-i\theta} \begin{bmatrix} 1 \\ i \\ 0 \end{bmatrix} = I\]

위 식의 뜻은 similarity transformation에 의해서는 \(l_{\infty}\) 에 있는 ideal point가 변하지 않음을 나타냅니다.

위 식과 같은 전개 과정을 \(J\) 에 대하여 적용하면 유사하게 유도할 수 있습니다.
따라서 circular points가 fixed points이면 이 때 사용된 transformation matrix는 similarity transformation임을 확인할 수 있었습니다.

이번 슬라이드에서는 circular points의 의미에 대하여 설명합니다.
이전 강의에서 배운 conics 관련 식은 아래와 같습니다.

circular points를 살펴보기 위하여 위 슬라이드의 conics 식에서 a = c = s (ex. 1), b = 0 으로 두겠습니다. a와 c를 1로 둔 것은 편의를 위함이고 scale 값인 임의의 s를 적용해도 무관합니다.

\[x_{1}^{2} + x_{2}^{2} + dx_{1}x_{3} + ex_{1}x_{3} + fx_{3}^{2} = 0\]

위 식은 homogeneous coordinate에서의 원의 방정식에 해당합니다. 즉, conics → circle으로 구성하였습니다.
여기서 \(l_{\infty}\) 와 conic이 교차하는 지점의 ideal points는 슬라이드와 같이 \(I, J\) 에서 만나게 됨을 알 수 있으며 이 때 ideal points의 좌표가 앞에서 다룬 \(I, J\) 가 됩니다.
이 때 ideal points는 \(x_{3} = 0\) 조건과 \(x_{1}^{2} + x_{2}^{2} = 0\) 이 되어야 식을 만족할 수 있습니다. 따라서 \(I = (1, i, 0)^{T}, J = (1, -i , 0)^{T}\) 의 복소수 해를 구할 수 있습니다.
위 과정을 통해 circular points의 각 요소는 복소수로 확장됨을 확인할 수 있으며 모든 circle은 circular points에서 \(l_{\infty}\) 와 교차하는 것을 확인할 수 있습니다.

위 연산 과정을 통하여 circular points을 확인할 수 있으면 추후에 알아볼 similarity 복원 시 circular points를 활용할 수 있습니다.
circular points를 분해하여 살펴보면 euclidean geometry에서의 orthogonal인 \((1, 0, 0)^{T}\) 와 \((0, 1, 0)^{T}\) 이며 한 개의 켤레 복소수가 합쳐진 것임을 알 수 있습니다.

\[I = (1, 0, 0)^{T} + i (0, 1, 0)^{T}\]
\[J = (1, 0, 0)^{T} + i (0, -1, 0)^{T}\]

따라서 circular points가 확인되면 orthogonal과 metric 속성이 결정됩니다.

일반적으로 degenerate line conic 은 \(C^{*} = xy^{T} + yx^{T}\) 와 같이 정의되며 conic 상의 2개의 점 x, y를 통하여 만들 수 있습니다.
- https://gaussian37.github.io/vision-mvg-nus_lec1/에서 degenereate conic 부분을 참조하시면 됩니다.
2개의 점 x, y를 circular points인 I, J를 이용하여 표현하면 \(l_{\infty}\) 가 관통하는 degenerate line conic을 만들 수 있고 \(C^{*}_{\infty}\) 라고 표현합니다. line은 \(l_{\infty}\) 가 되며 I와 J를 각각 통과하는 직선이 됩니다.
그리고 \(C^{*}_{\infty}\) 을 풀어 쓰면 degenerate line conic with circular points가 되며 degenerate가 되었으므로 Rank가 2이면 두 점, Rank가 1이면 중복된 1개의 점이 conic 상에 있는 것을 알 수 있습니다.
위 슬라이드에서는 Rank 2를 가정하였으므로 I, J 두 점에서 각각 통과하는 직선들로 구성되는 것을 그림으로 나타내었습니다.
추가적으로 표준 좌표를 이용하여 \(C^{*}_{\infty}\) 를 수식으로 나타내면 Rank가 2인 행렬이 되는 것을 슬라이드를 통해 확인할 수 있습니다.
마지막 부분의 계산에서 \(IJ^{T} + JI^{T}\) 계산 결과가 등호가 성립하는 이유는 \(l_{\infty}\) 상에서는 스케일 변환이 허용되기 때문입니다.

위 슬라이드에서는 앞선 슬라이드에서 보여준 것 처럼 \(C^{*}_{\infty}\) 에서 또한 similarity transformation을 적용하면 fixed가 됨을 보여줍니다.
식 전개에서 \(C^{*}_{\infty} {'} = H_{S} C^{*}_{\infty} H_{S}^{T}\) 가 됨은 이전 글에서 다루었던 내용입니다. 간략히 정리하면 다음과 같습니다.

점 변환 \(x' = Hx\) 에 대하여 다음과 같이 변환 됩니다.

\[x = H^{-1}x'\]
\[x^{T}C x = (H^{-1}x')^{T} C H^{-1}x' = x'^{T} H^{-T} C H^{-1}x' = x'^{T}(H^{-T} C H^{-1})x'\]
\[\therefore \quad C' = H^{-T} C H^{-1}\]

즉, 점 변환을 위한 행렬 \(H\) 가 있을 때, 이 행렬을 통해 conic \(C \to C'\) 로 변환하려면 다음 식을 따릅니다.

\[C' = H^{-T} C H^{-1}\]

그리고 \(l^{T}C^{*}l = 0\) 과 \(x^{T}Cx = 0\) 에서의 \(C^{*}\) 와 \(C\) 의 관계는 이전 글에서 \(C^{*} = C^{-1}\) 임을 확인하였으므로 다음과 같이 표현할 수 있습니다. 따라서 양변에 역행렬을 적용하여 구하면 다음과 같습니다.

\[C'^{-1} = (H^{-T} C H^{-1})^{-1}\]
\[C^{*}{'} = H C^{*} H^{T}\]
따라서 위 슬라이드에서 \(C^{*}_{\infty}\) 또한 다음과 같은 식을 따릅니다.

\[C^{*}_{\infty}{'} = H_{S} C^{*}_{\infty} H_{S}^{T}\]

위 식의 최종 전개에서도 \(l_{\infty}\) 상에서는 스케일 변환이 허용되기 때문에 \(s\) 는 무시하여 등호가 성립하다고 말할 수 있습니다.

위 슬라이드에서는 지금까지 살펴본 \(C^{*}_{\infty}\) 내용을 통해 2가지 특성에 대하여 설명합니다.

① \(C^{*}_{\infty}\) 은 4 DoF (Degree of Freedom)을 가집니다. 원래 \(C^{*}_{\infty}\) 는 3 X 3 대칭 행렬이고 (3, 3) 위치의 스케일 값을 무시한다고 하면 5개의 자유도를 가집니다. 하지만 \(\text{det}(C^{*}_{\infty}) = 0\) 이고 자유 변수가 1개 생기므로 DoF는 4개로 줄어듭니다.
여기서 의문인 점이 있습니다. 4 DoF는 \(C^{*}_{\infty}\) 를 만들 때, a, b, c, d, e, f에서 d, e, f는 소거되어 의미가 없고 b = 0으로 정해집니다. 의미있는 변수인 a = c는 같고 어떤 scale 값 s로 정해져야 하므로 1 DoF가 됩니다. 따라서 나머지 3 DoF는 어떻게 정해져야 하는 지 정확히 이해가 안된 상태입니다.
개인적으로 conic을 정할 때, 3 x 3 대칭 행렬에서 성분 a, b, c, d, e, f 를 정해야 하는데 b = 0으로 정해지고, a = c가 되어서 남은 DoF가 a=c, d, e, f로 4 DoF 아닐까 추정합니다. (틀릴 수 있습니다.)

② \(l_{\infty}\) 는 \(C^{*}_{\infty}\) 의 null vector 를 의미합니다. 즉, \(C^{*}_{\infty}\) 을 만족하는 점들 (circular points) 들이 \(l_{\infty}\) 에 존재한다는 의미이며 슬라이드의 식과 같이 간단히 수식으로 전개 됩니다.

지금 부터는 Circular points and Absolute conic 강의의 중반부 내용을 살펴보도록 하겠습니다.

두 벡터의 내적을 이용하여 두 벡터 사이의 각도 \(\theta\) 를 계산하는 방법을 익히 알고 있고 각 선의 식을 이용하여 각 선의 normal vector를 구할 수 있으므로 두 선의 각 normal vector 간의 사이각을 통해 두 선의 사이각을 구할 수 있습니다.

\[l = (l_{1}, l_{2}, l_{3})^{T}\]
\[m = (m_{1}, m_{2}, m_{3})^{T}\]

\[\text{normal vector of } l \text{ : } (l_{1}, l_{2})^{T}\]
\[\text{normal vector of } m \text{ : } (m_{1}, m_{2})^{T}\]

따라서 두 normal vector의 내적을 통하여 사이각을 구하면 아래와 같습니다.

\[\cos{(\theta)} = \frac{l_{1}m_{1} + l_{2}m_{2}}{\sqrt{(l_{1}^{2} + l_{2}^{2}) + (m_{1}^{2} + m_{2}^{2})}}\]

※ 참고로 line을 이용하여 normal vector를 구하는 방법은 다음과 같습니다.

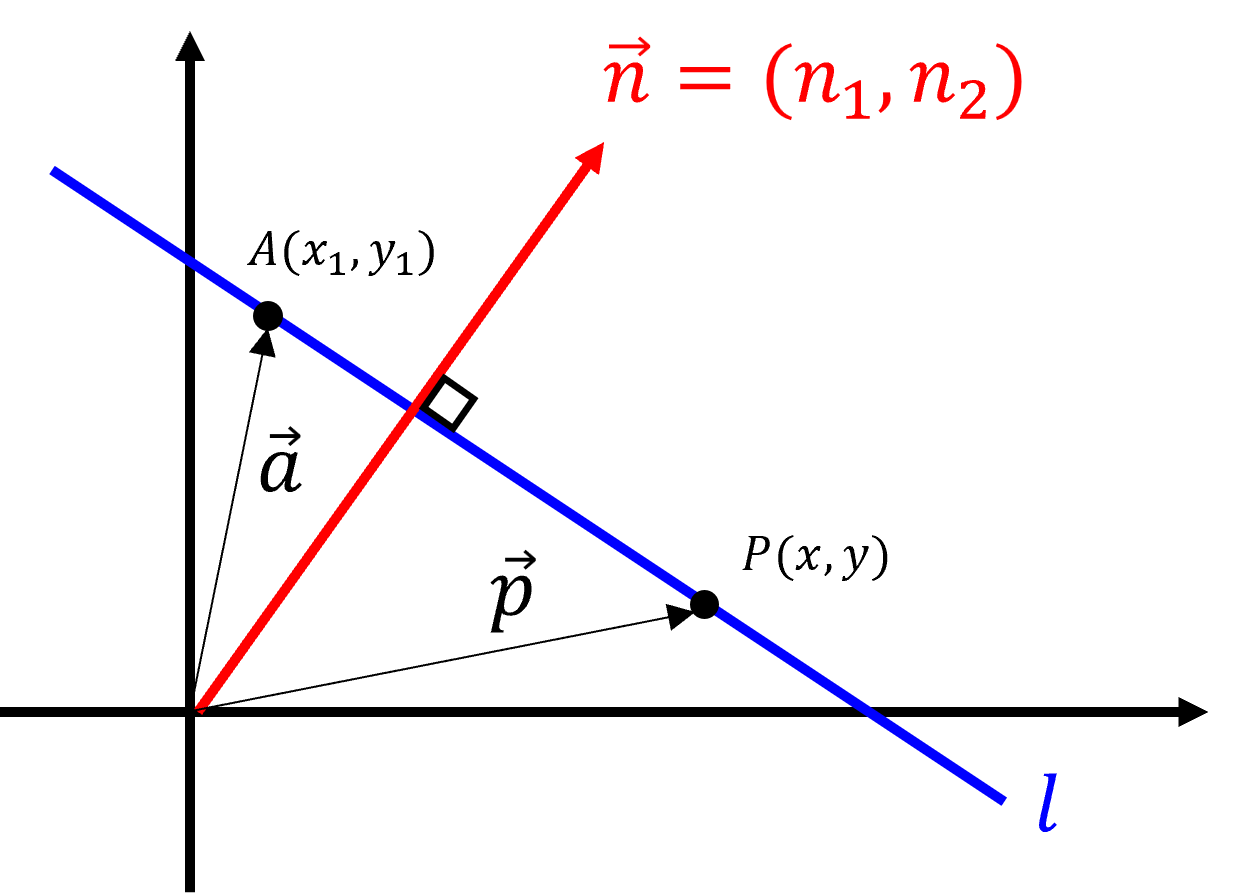
\[\vec{AP} \perp \vec{n}\]
\[\vec{AP} \cdot \vec{n} = 0\]
\[(\vec{p} - \vec{a}) \cdot \vec{n} = 0\]
\[((x, y) - (x_{1}, y_{1})) \cdot (n_{1}, n_{2}) = 0\]
\[(x - x_{1}, y - y_{1}) \cdot (n_{1}, n_{2}) = 0\]
\[n_{1}(x - x_{1}) + n_{2}(y - y_{1}) = 0\]
\[n_{1}x + n_{2}y - (n_{1}x_{1} + n_{2}y_{1}) = 0\]

따라서 \(l = (l_{1}, l_{2}, l_{3})\) 에서 \((l_{1}, l_{2}) = (n_{1}, n_{2})\) 가 되어 normal vector 를 line을 이용하여 만들 수 있습니다.
최종적으로 두 벡터의 내적을 통해 다음과 같이 사잇각을 구할 수 있습니다.

\[\begin{bmatrix} l_{1} \\ l_{2} \end{bmatrix}^{T} \begin{bmatrix} m_{1} \\ m_{2} \end{bmatrix} = \Vert \begin{bmatrix} l_{1} & l_{2} \end{bmatrix}^{T} \Vert \Vert \begin{bmatrix} m_{1} & m_{2} \end{bmatrix}^{T} \Vert \cos{(\theta)}\]
\[\cos{(\theta)} = \frac{l_{1}m_{1} + l_{2}m_{2}}{\sqrt{(l_{1}^{2} + l_{2}^{2}) + (m_{1}^{2} + m_{2}^{2})}}\]

이와 같은 방식으로 두 선 사이의 각을 구할 수 있으나 affine/projective transformation이 적용되었을 때에는 angle이 유지되지 않기 때문에 \(l, m\) line의 사이각을 \(l'= H^{-T}l, m' = H^{-T}m\) 에서 적용할 수 없습니다.

앞의 슬라이드와 유사한 수식 표현이 위 슬라이드에 나타나 있습니다. 위 슬라이드에서는 \(C^{*}_{\infty}\) 개념을 도입하여 projective transformation을 적용하더라도 사이 각을 구할 수 있는 방법을 제시합니다.

\[H = H_{P}H_{A}H_{S} = \begin{bmatrix} I & 0 \\ v^{T} & 1 \end{bmatrix} \begin{bmatrix} K & 0 \\ 0^{T} & 1 \end{bmatrix} \begin{bmatrix} sR & t \\ 0^{T} & 1 \end{bmatrix}\]

강의에서는 제외되었지만 책에는 존재하는 conic의 추가 속성에 대하여 다루어 보도록 하겠습니다.

마지막으로 Circular points and Absolute conic 강의의 후반부 내용을 살펴보도록 하겠습니다.

이번에는 absolute conic이라는 개념에 대하여 다루어 보도록 하겠습니다.
앞에서 line at infinity와 plane at infinity를 다룬 것 처럼 conic의 경우에도 infinity 측면에서의 정의를 내릴 때 absolute conic이라는 개념을 사용합니다.
위 슬라이드에서 정의한 바와 같이 absolute coninc은 \(\Omega_{\infty}\) 기호를 통해 나타내며 \(\pi_{\infty}\) (plane at infinity) 상의 (point) conic으로 정의 됩니다.

absolute conic의 개념을 배우기 전에 이 개념이 중요한 이유를 살펴보도록 하겠습니다.
Lecture 6. Single view metrology 에서 다룰 내용이지만 absolute coninc은 카메라의 위치에 상관 없이 카메라 파라미터 intrinsic \(K\) 에만 영향을 받습니다. 따라서 \(K\) 만 정해지면 카메라의 위치 이동 (extrinsic)과 무관하게 이미지 내에서 얻을 수 있는 정보를 추출할 수 있습니다.
예를 들어 point의 경우 vanishing point, line의 경우 vanishing line과 같은 특성이 있는데 conic의 경우 absolute conic이 이와 같은 개념에 해당합니다.
따라서 카메라 위치에 변하지 않는 특성을 찾기 위해 ( \(K\) 에만 관련있는 ) absolute conic 개념이 필요합니다.

absolute conic은 \(\pi_{\infty}\) 에 존재하는 conic이고 카메라의 위치 이동에 상관 없이 고정값이 됩니다. 정확하지는 않지만 비유를 한다면 하늘에 있는 달이 absolute conic이 될 수 있습니다. 왜냐하면 나의 위치가 변하더라도 달의 크기와 위치는 변하지 않고 고정이기 때문입니다. 달의 크기와 위치가 변하지 않고 고정인 이유는 내가 바라보는 달의 위치가 \(\pi_{\infty}\) 에 존재한다고 가정할 수 있기 때문입니다. (물론 비유한 것이지 달은 유한한 거리에 있습니다.)

absolute conic 또한 conic의 한 종류 이므로 \(3 \times 3\) 크기의 행렬을 가집니다. absolue conic은 아래 2가지 정의에 따라 결론적으로 항등 행렬 \(I\) 와 같은 형태가 됩니다.

\[X_{1}^{2} + X_{2}^{2} + X_{3}^{2} = 0\]
\[X_{4} = 0\]

위 조건의 이유와 absolute conic이 \(I\) 형태인 이유를 앞에서 배운 circular points와 비교해서 설명하겠습니다.

circular points : line at infinity가 통과하는 circle에서 생기는 점
absolute conic : plane at infinity에서 sphere가 만나서 생기는 선

먼저 앞에서 다룬 circular points 정의를 다시 정리하여 나열해 보겠습니다.

\[x_{1}^{2} + x_{2}^{2} = 0\]
\[x_{3} = 0\]

circular points에서 \(x_{1}^{2} + x_{2}^{2} = 0\) 를 만족해야 하는 이유는 \(x_{3} = 0\) 이기 때문에 conic을 표현하는 2차식에서 \(x_{3}\) 가 사용된 항은 모두 소거되기 때문이고 \(x_{1}^{2}, x_{2}^{2}\) 의 계수가 1인 이유는 circle을 가정했기 때문입니다.
따라서 circular points를 정의하는 행렬은 다음과 같습니다. \((x_{1}, x_{2}, x_{3})\) 는 homogeneous 에서의 point를 의미합니다.

\[\begin{bmatrix} x_{1} & x_{2} & x_{3} \end{bmatrix} C \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} = 0\]
\[\Rightarrow x_{1}^{2} + x_{2}^{2} = 0\]
\[\therefore C = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}\]

따라서 \(C\) 가 위 식과 같이 정의될 때 \(x_{1}^{2} + x_{2}^{2} = 0\), \(x_{3} = 0\) 을 만족하는 \((x_{1}, x_{2}, x_{3})\) 는 circle 상에 있음을 알 수 있습니다.

이번에는 absolute conic의 정의에 대하여 유사한 방식으로 나열해 보겠습니다. absolute conic은 circular points에 비해 차원이 하나 추가된 것으로 이해하면 쉽게 이해할 수 있습니다.

\[x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = 0\]
\[x_{4} = 0\]

absolute coninc에서 \(x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = 0\) 를 만족해야 하는 이유는 \(x_{4} = 0\) 이기 때문에 conic을 표현하는 2차식에서 \(x_{4}\) 가 사용된 항은 모두 소거되기 때문이고 \(x_{1}^{2}, x_{2}^{2}, x_{3}^{2}\) 의 계수가 1인 이유는 sphere를 가정했기 때문입니다.
따라서 absolute coninc를 정의하는 행렬은 다음과 같습니다. \((x_{1}, x_{2}, x_{3})\) 는 homogeneous 에서의 point를 의미합니다.

\[\begin{bmatrix} x_{1} & x_{2} & x_{3} \end{bmatrix} C \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} = 0\]
\[\Rightarrow x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = 0\]
\[\therefore C = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

따라서 \(C\) 가 위 식과 같이 정의될 때 \(x_{1}^{2} + x_{2}^{2} + x_{3}^{2} = 0\), \(x_{4} = 0\) 을 만족하는 \((x_{1}, x_{2}, x_{3})\) 는 absolute conic 상에 있음을 알 수 있습니다.

Multiple View Geometry 글 목차