
IPM(Inverse Perspective Mapping)을 이용한 BEV(Bird Eye View) 변환
2022, Jan 29
- 참조 : https://towardsdatascience.com/a-hands-on-application-of-homography-ipm-18d9e47c152f
- 참조 : https://github.com/darylclimb/cvml_project
- 참조 : https://csyhhu.github.io/2015/07/09/IPM/
- 참조 : https://kr.mathworks.com/help/driving/ref/birdseyeview.imagetovehicle.html
- 사전 지식 : Homogeneous Coordinate (동차좌표계)
- 사전 지식 : 카메라 캘리브레이션
- 사전 지식 : 포인트 클라우드와 뎁스 맵의 변환 관계 정리
- 이번 글에서 다룰 내용은 위 그림과 같이 흔히 보는 왼쪽 그림과 같은
perspective view형태의 이미지를Bird Eye View형태로 변환하는 방법에 대하여 알아보도록 하겠습니다.
목차
-
IPM의 사용 배경
-
IPM을 위한 배경 설명
-
IPM 적용 방법
-
Cityscapes 데이터셋 IPM 적용 예시
-
렌즈 왜곡을 반영한 IPM 적용 방법
-
Custom 데이터를 이용한 IPM 적용 예시
-
IPM을 이용한 3차원 공간 채우기
-
IPM 적용 application 사례
IPM의 사용 배경
IPM은Inverse Perspective Mapping의 줄임말이며 그 역할은 2D 이미지를BEV(Bird Eye View)방식의 3D로 변환하는 것입니다.BEV로 나타내기 때문에 최종 표현되는 결과는 2D 이며 따라서 2D 이미지로 표현 가능합니다.

- 위 그림에서 좌측이
2D 이미지이고 우측이BEV입니다. 우측의BEV의 하단 부분에서 상단 부분으로 갈수록 RGB 영역이 점점 커지는 이유는 실제 카메라가 촬영하는 화각에 의해 반영되는 것입니다. 빛이 카메라 렌즈로 입사할 때, 실제 이미지로 투영되는 영역이 위에 보이는 화각 영역 정도라고 생각하시면 됩니다.
IPM의 이름을 살펴보면Inverse,Perspective Mapping2가지 의미로 나뉘게 됩니다.- 먼저
Perspective Mapping은Perspective Projection을 의미합니다.Perspective Projection은 3D Scene을 2D image plane으로 투영하는 작업 방식 중에 하나이며Perspective Projection을 하면 일반적으로 보는 사진과 같이 원근감이 있도록 2D 이미지가 생성 됩니다. 같은 크기의 물체임에도 불구하고 가까우면 크게 보이고 멀리 있으면 작게 보이는 것이Perspective Projection에 나타나는 왜곡의 형태 (Perspective Distortion) 입니다. Inverse는Perspective Projection의 과정을 역으로 진행하면서 앞에서 설명한원근감 (Perspective)에 의한 왜곡을 제거하는 것을 의미합니다. 따라서IPM의 과정은Perspective Distortion을 제거하여 전체 3D Scene에 대하여 카메라와의 거리에 상관 없이 일관성 있게 표현하는 것을 목표로 하며 표현 방식은BEV형식으로 표현하게 됩니다.- 여기서
BEV로 표현하는 이유는BEV로 보았을 때, 카메라와의 원근에 상관 없이 동일한 크기로 표현할 수 있다는 점을 이용하는 것과 3D 상의 실제 물체의Depth는 알 수 없으므로 모든 물체는 높이가 없이 지면(ground)에 붙어 있는 것을 가정해야 하기 때문입니다. 2D 이미지의 정보를 3D 로 변환하기 위해서는Depth를 통하여 물체의 높이 정보를 알 수 있는데 (포인트 클라우드와 뎁스 맵의 변환 관계 정리 참조) 이 정보를 알 수 없으니 모든 물체의 높이를 무시할 수 있는 방법인BEV를 선택한 것입니다. 하늘에서 땅을 정면으로 바라보았을 때, 높이는 알 수 없는 형태의 시점으로 밖에 볼 수 없는데 그 점을 이용한 것입니다.
- 정리하면
IPM, Inverse Perspective Mapping은 2D 이미지를 3D 공간으로 변환하는데,Perspective Distortion을 제거하기 위함과Depth값의 부재로 인하여BEV형태로 변환하는 과정을 의미합니다. - 이와 같은 가정을 전제 조건으로 두고
IPM을 진행하기 때문에 아래 그림과 같이 한계 상황들이 이미 발생합니다.

- 전제 조건인 모든 물체의 높이는 0이다 라는 가정 즉, 모든 물체는 높이가 없이 지면에 붙어 있다는 가정으로 인하여 실제 지면에 있는 정보들 (도로, 차선 풀 등)은
Perspective Distortion없이 정상적으로 보이지만 자동차와 같이 높이가 있는 물체는 이상하게 보입니다. 즉, 전제 조건에 위배하기 때문에 정상적으로 나타낼 수 없습니다. - 또한 도로 자체가 오르막길이거나 내리막길이면 발생하면 모든 물체의 높이는 0이다라는 가정에 위배되기 때문에 이상한 형상이 발생합니다. 아래 영상의 39초 정도에 그 현상을 살펴볼 수 있습니다.
- 이와 같은 단점에도 불구하고 이상적인 평지 (flat ground) 환경에서는 지면의 정보를 인식하는 데에는
Perspective Distortion이 없다는 장점이 있기 때문에 상황에 따라서 사용하기도 합니다. - 아래는
KITTI데이터 셋의 이미지를IPM을 통하여BEV로 생성한 데모이며KITTI데이터셋 에서는 지면의 높낮이가 적은 평지이기 때문에 이상적으로 잘 보이는 것을 알 수 있습니다.
- 그러면 지금부터는 실제
IPM을 적용하는 방법에 대하여 살펴보도록 하겠습니다.
IPM을 위한 배경 설명
- 지금부터 살펴볼 방법은 front view 이미지를
BEV이미지로 변경하는 방법입니다.IPM은 이러한 처리를 카메라의원근 효과(perspective effect)를 제거하고 top-view 기반의 2D 도메인 상에 다시 매핑하는 방법을 사용합니다. 즉,BEV이미지는 원근 효과를 보정하여 거리와 평행선을 유지하는 성질을 가지고 있습니다.
- 만들고자 하는
BEV이미지는perspective view이미지의 도로를 평평한 2차원 평면으로 변환하여 생성합니다. 따라서 ( \(X, Y, Z = 0\) ) 과 같이 모델링 하여 높이 정보가 없는 2차원 평면으로 간주합니다.
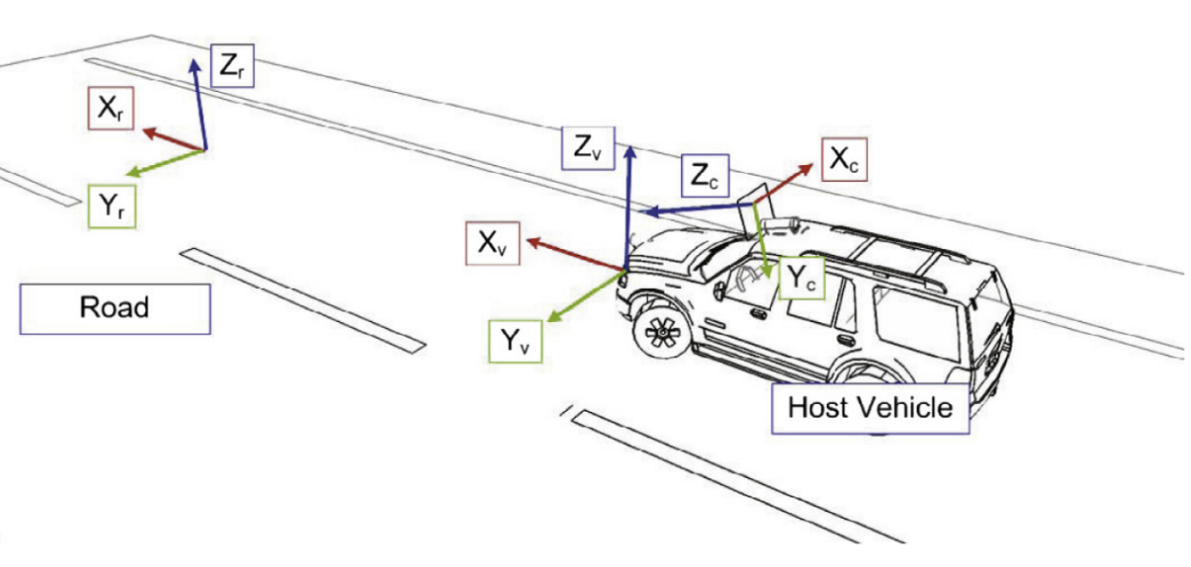
- 위 그림과 같이 어떤 좌표계를 사용하는 지에 따라서 같은 물체를 서로 다른 위치로 표현할 수 있습니다. 위 그림에서는
Road,Vehicle,Camera3개의 다른 좌표계가 있고 일반적으로IPM을 적용하기 위해서는Camera와Vehicle간의 관계를 알아야 하기 때문에 두 좌표계를 변환할 수 있는 정보를calibration을 통해 얻고 이 값을 통하여Vehicle좌표계의 3D Scene을 2D 이미지로projection하게 됩니다. - 위
calibration내용에서vehicle과camera간의 위치 관계를 표현하는 것은extrinsic파라미터이고camera의 위치를 원점으로 두었을 때, 카메라 기준의 3차원 정보와 이미지의 픽셀 관계를 표현하는 것을intrinsic파라미터라고 합니다. 이 내용은 카메라 캘리브레이션 내용을 참조해 주시기 바랍니다.
Perspective projection
Perspective projection은 3D 공간을 2D 평면에 매핑하는 것입니다. 매핑 과정 중, 3D 공간 상의 평행한 2개의 선이 2D 평면에 표현될 때, 평행한 선이 어떤 특정점에서 만나게 되는 현상이 나타납니다.
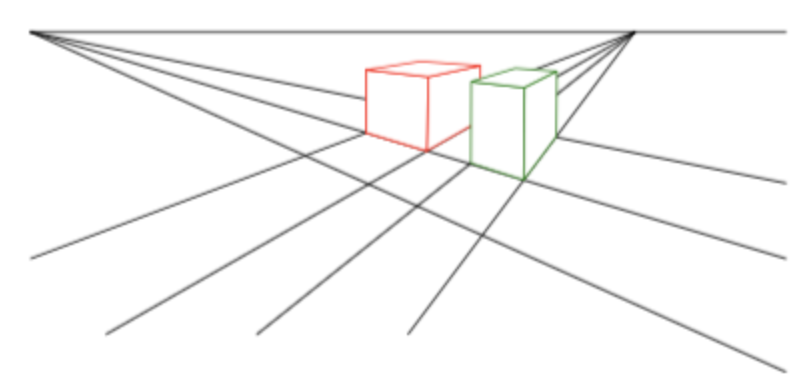
- 위 그림의 선을 보면 3D 공간 상에서는 평행한 선이지만 2D 공간에서는 선이 만나는 것을 볼 수 있습니다.
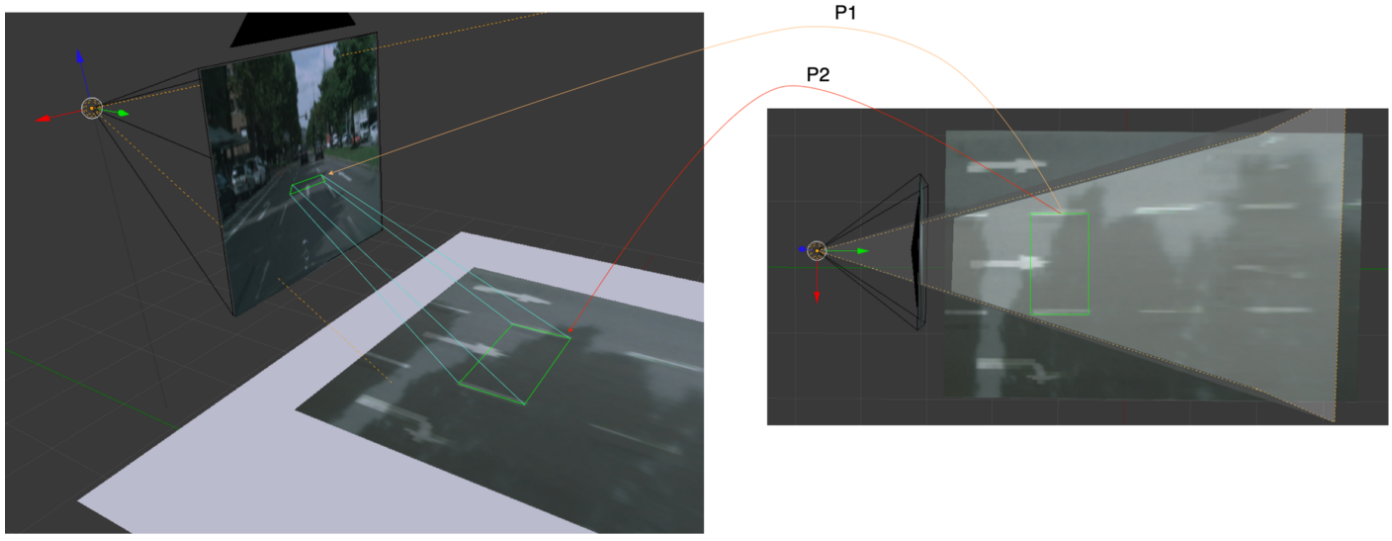
- 위 그림의 왼쪽 그림은 차량의 윗부분에 위치하는 카메라를 통해 도로를 본 관점 (view) 이고 오른쪽 그림은 BEV로 본 주변 환경 입니다.
viewpoint가perspective view로 보는 지 또는BEV로 보는 지에 따라서 관측되는 장면이 달라집니다. - 두 view의 차이점 중 중요한 점은 왼쪽과 같이
projective transformation을 적용하게 되면 평행선이 더 이상 보존되지 않는 다는 점입니다. 반면BEV의 경우 평행선이 그대로 유지되는 것을 볼 수 있습니다. 앞에서 설명한Perspective Distortion이 제거된 것입니다. - 본 글에서 설명하는
IPM은 평행 성분을 그대로 평행 선으로 유지하는 것에 장점이 있습니다.
Camera Projective Geometry
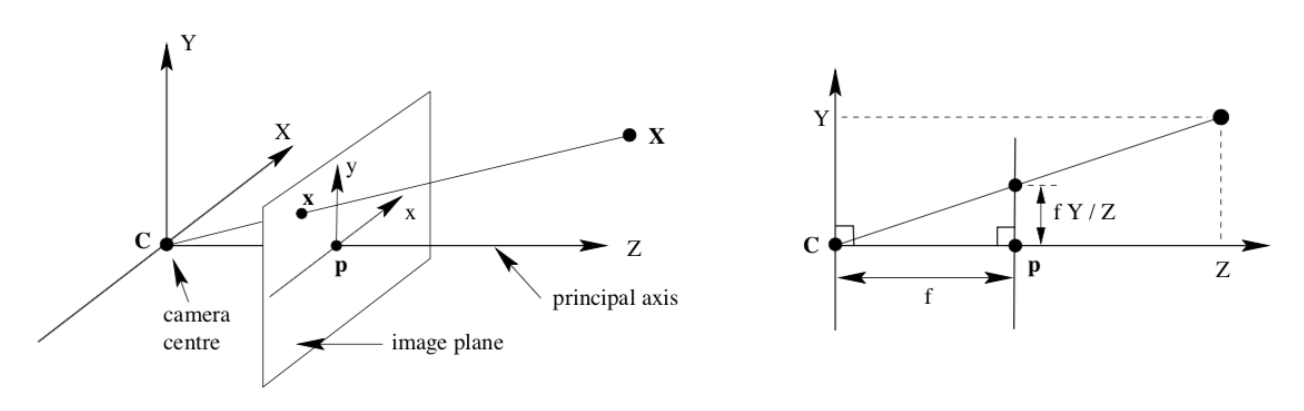
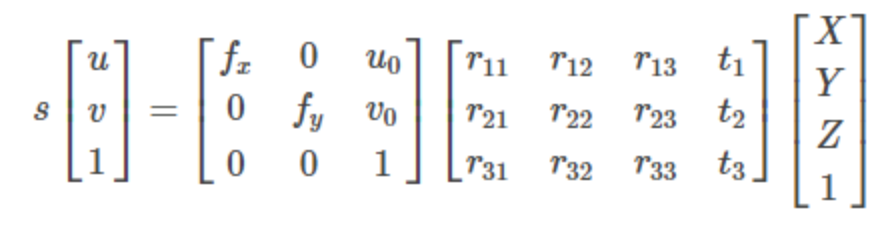
- 카메라 모델은 3D scene 에서 2D 이미지로
perspective projection을 하며 2D 이미지를 만들 때,calibration을 통해 구한intrinsic과extrinsic값에 따라 원하는 2D 이미지가 만들어 집니다. extrinsic\([R \vert t]\) 는world와camera간의 상태 위치 및 방향을 나타내어world coordinate를camera coordinate로 변환하는 역할을 합니다.intrinsic\(K\) 는camera coordinate기준으로 3D scene이 어떻게 2D 이미지 상의image coordinate로 변환되는 지와 연관되어 있으며 \(K\) 는 카메라의 구성 성분인focal length와camera center성분 값을 가집니다. (가장 간단한 핀홀 카메라 케이스에 해당하며pixel skew,lens distortion등은 생략하였습니다.)
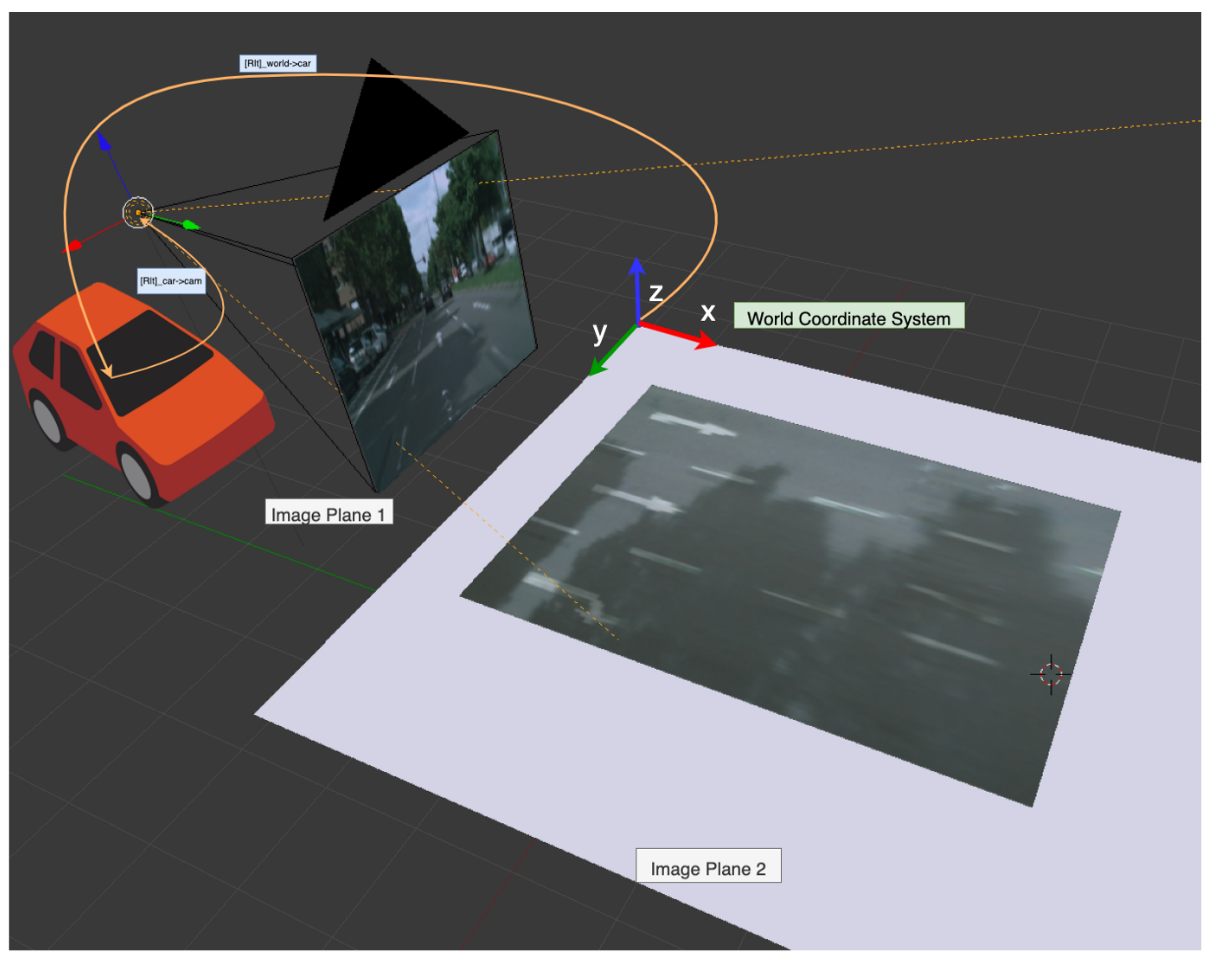
- 위 그림을 통해
IPM의 과정을 참조한다고 하면 실제 카메라를 통해 취득되는 이미지는카메라 좌표계의image plane1 (perspective view)과 같은 형태이고IPM을 통하여 만들고자 하는 것은world 좌표계의image plane2 (Bird Eye View)와 같은 형태입니다. (참고로 위 그림의world 좌표계의 \(y\) 축이 반대로 표현되어 있습니다. 앞으로 살펴볼 설명 및 코드는 오른손 좌표계를 그대로 사용할 예정입니다.)
- 앞으로 설명할 방식은 위 그림과 같은 오른쪽 좌표계 이므로
XZ평면의 왼쪽 방향이 \(y\) 축의 양의 방향이 됩니다.
- 앞에서 언급 하였듯이,
IPM을 적용하기 위해서는 도로가 지면에 평평하다고 가정했습니다. 따라서 도로에 있는 모든 점에 대해world 좌표계의 \(Z = 0\) 을 만족해야 합니다. - 따라서 만약 도로가 평지가 아니라면 \(Z = 0\) 이라는 전제 조건을 만족하지 못하기 때문에
IPM의 결과가 왜곡이 되어 보일 것입니다. 예를 들어 도로가 휘어지거나, 차선이 직선이 아닌 형태로 나타나는 경우가 발생하는데 도로가 지면에 평평하지 않기 때문에 발생할 수 있습니다. - 뿐만 아니라 앞으로 살펴볼
extrinsic이 올바르지 못하면 \(Z = 0\) 을 만족시키지 못하기 때문에 같은 이유로 왜곡이 발생해서 보일 수 있습니다. - 마지막으로
intrinsic이 올바르지 못하면image plane1의 정확한 RGB 값을 가져와서image plane2에 대응시키지 못하기 때문에 왜곡이 발생할 수 있습니다.
- 따라서 ①
flat ground, ②extrinsic정확성, ③intrinsic정확성의 3가지 모두를 만족한다면IPM을 이용하여BEV이미지를 만들 수 있습니다.
IPM 적용 방법
- 지금까지는
IPM적용을 위한 배경 지식을 살펴보았고 실제로IPM을 적용하기 위한 프로세스를 살펴보겠습니다. IPM을 적용하기 위해서는 크게 아래 4가지 과정이 필요합니다.
- ①
calibraition정보 읽기 - ②
BEV이미지와world좌표간의 관계 정하기 - ③
BEV이미지와Image좌표간의 LUT (Look Up Table) 구하기 - ④
backward방식으로IPM처리하여BEV이미지 생성하기
① calibraition 정보 읽기
- 본 글에서는
calibration을 하는 방법에 대해서는 다르지 않지만 아래 글에서 참조하실 수 있습니다. - 다루어 보는 데이터는
cityscapes의 데이터 셋으로 아래의calibration정보를 이용하실 수 있습니다. cityscapes에서 제공하는 데이터 취득 차량의calibration정보는 다음과 같습니다.
{
"baseline": 0.21409619719999115,
"pitch": 0.03842560000000292,
"roll": 0.0,
"x": 1.7,
"y": 0.026239999999999368,
"yaw": -0.009726800000000934,
"z": 1.212400000000026,
"fx": 2263.54773399985,
"fy": 2250.3728170599807,
"u0": 1079.0175620000632,
"v0": 515.0066006000195
}
- 위 정보 중,
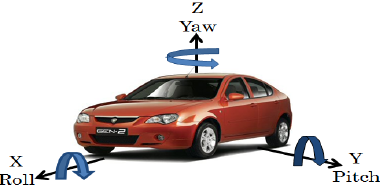
roll,pitch,yaw를 이용하여Vehicle → Camera로 변환하는Rotation값을 추출하고x,y,z를 이용하여Vehicle → Camera로 변환하는Translation값을 추출합니다.
roll,pitch,yaw를 이용하여Vehicle → Camera로 변환하는Rotation값을 추출하는 방식은 아래 내용을 참조하시면 됩니다.cityscapes에서roll,pitch,yaw와x,y,z는 모두Camera → Vehicle로의 관계로 정의되어 있기 때문에 반대 방향으로의extrinsic을 구해주면 됩니다.Rotation의 경우Transpose를 취해주면Inverse가 되기 때문에 아래 코드와 같이Inverse를 취해주면 되고Translation의 경우 음의 방향으로 이동하면 되기 때문에 음수를 적용해 줍니다.- 계산의 편의를 위하여 homogeneous coordinate를 사용하여 표현하였습니다.
def rotation_from_euler(roll=1., pitch=1., yaw=1.):
"""
Get rotation matrix
Args:
roll, pitch, yaw: In radians
Returns:
R: [4, 4]
"""
si, sj, sk = np.sin(roll), np.sin(pitch), np.sin(yaw)
ci, cj, ck = np.cos(roll), np.cos(pitch), np.cos(yaw)
cc, cs = ci * ck, ci * sk
sc, ss = si * ck, si * sk
R = np.identity(4)
R[0, 0] = cj * ck
R[0, 1] = sj * sc - cs
R[0, 2] = sj * cc + ss
R[1, 0] = cj * sk
R[1, 1] = sj * ss + cc
R[1, 2] = sj * cs - sc
R[2, 0] = -sj
R[2, 1] = cj * si
R[2, 2] = cj * ci
return R
def translation_matrix(vector):
"""
Translation matrix
Args:
vector list[float]: (x, y, z)
Returns:
T: [4, 4]
"""
M = np.identity(4)
M[:3, 3] = vector[:3]
return M
def load_camera_params():
"""
Get the intrinsic and extrinsic parameters
Returns:
Camera extrinsic and intrinsic matrices
"""
p = {}
p["roll"] = 0.0
p["pitch"] = 0.03842560000000292
p["yaw"] = -0.009726800000000934
p["x"] = 1.7
p["y"] = 0.026239999999999368
p["z"] = 1.212400000000026
p["fx"] = 2263.54773399985
p["fy"] = 2250.3728170599807
p["u0"] = 1079.0175620000632
p["v0"] = 515.006600600019
fx, fy = p['fx'], p['fy']
u0, v0 = p['u0'], p['v0']
pitch, roll, yaw = p['pitch'], p['roll'], p['yaw']
x, y, z = p['x'], p['y'], p['z']
# Intrinsic
K = np.array([[fx, 0, u0, 0],
[0, fy, v0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]])
# Extrinsic
R_veh2cam = np.transpose(rotation_from_euler(roll, pitch, yaw))
T_veh2cam = translation_matrix((-x, -y, -z))
# Rotate to camera coordinates
R = np.array([[0., -1., 0., 0.],
[0., 0., -1., 0.],
[1., 0., 0., 0.],
[0., 0., 0., 1.]])
RT = R @ R_veh2cam @ T_veh2cam
return RT, K
load_camera_params의 마지막에 \(R\) 행렬을 곱하는 이유는Vehicle → Camera로 좌표계의 방향이 바뀌기 때문에 적용해 준 것입니다. 살펴보면 다음과 같습니다.Camera X←World -YCamera Y←World -ZCamera Z←World X
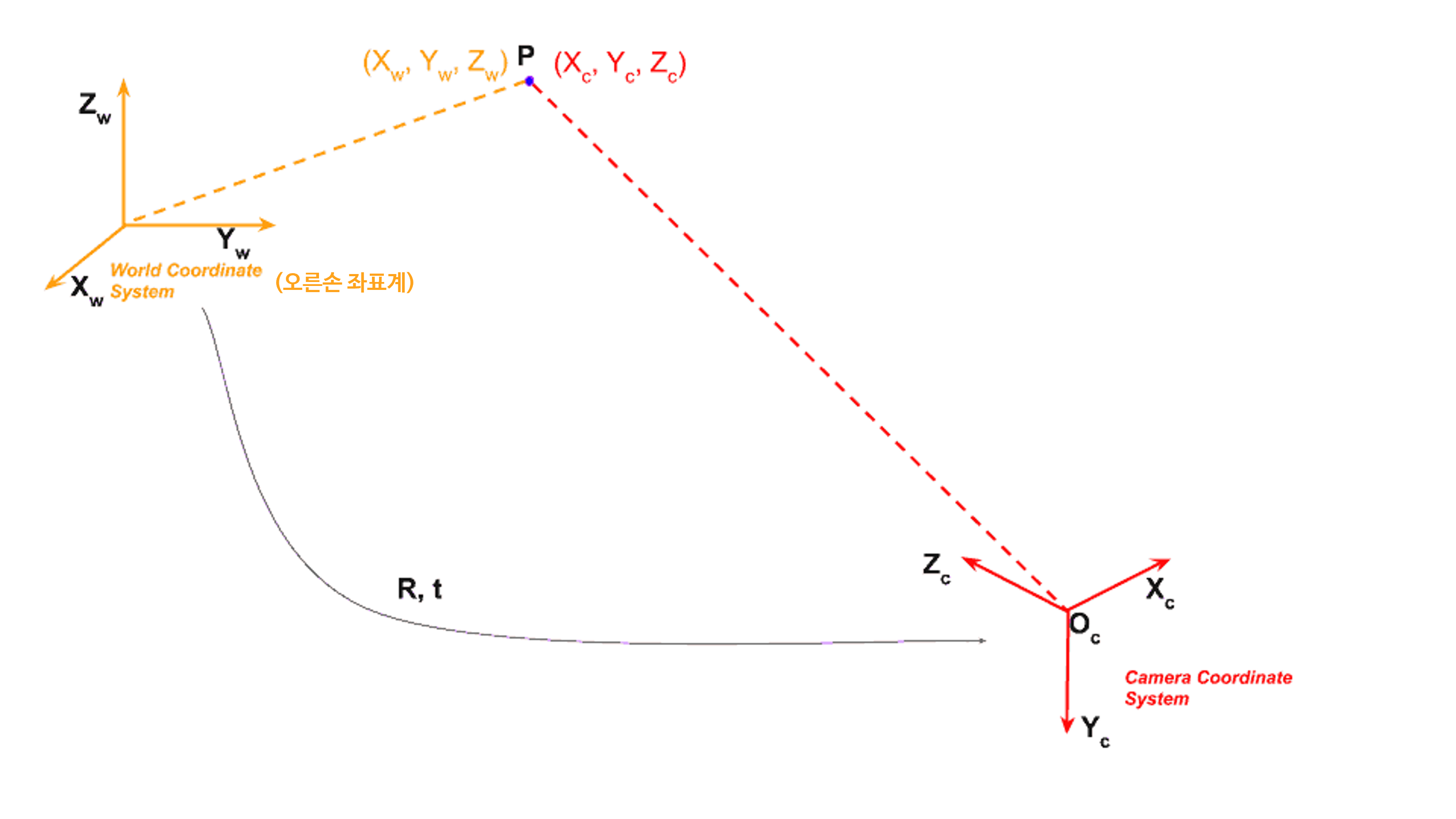
- 위 그림과 같이 \(X, Y, Z\) 축의 방향이 바뀌기 때문에 \(R\) 행렬을 곱해줍니다.
② BEV 이미지와 world 좌표간의 관계 정하기
BEV이미지의 장점은perspective distortion이 제거된 것도 있지만 이미지 자체에world 좌표계의 정보를 그대로 담고 있다는 것입니다.- 즉,
BEV이미지의 각 픽셀 좌표가world 좌표계에서 위치 정보를 포함하고 있다는 점입니다. 예를 들어BEV이미지의 \((u_{\text{BEV}}, v_{\text{BEV}})\) 는world 좌표계에서 \(X, Y, Z=0\) 에 해당하는 것을 바로 알 수 있다는 뜻입니다. - 이 관계는 사용자가 어떻게 설계하여
BEV이미지를 생성하는 것에 따라 달려 있습니다. 살펴 볼 예제에서는world 좌표계기준으로 \(X\) 방향으로의최댓값과최솟값을 정하고 \(Y\) 방향으로의최댓값과최솟값을 정하여BEV이미지의 전체 영역을 설계합니다. 또한BEV이미지에서의 행방향으로의 간격이 실제world 좌표계에서 몇 m를 의미하는지, 열방향으로의 간격이 실제world 좌표계에서 몇 m를 의미하는 지 설계해주면BEV이미지의 전체 사이즈를 결정할 수 있습니다. - 예를 들어
BEV이미지에서 행 방향으로 1 픽셀 만큼 증감하면world 좌표계에서 \(X\) 방향으로 0.05 (m) 만큼 증감하도록 하고BEV이미지에서 열 방향 1 픽셀 만큼 증가하면world 좌표계에서 \(Y\) 방향으로 0.025 (m) 만큼 증감하도록 만들 수 있습니다.
world_x_max = 50
world_x_min = 7
world_y_max = 10
world_y_min = -10
world_x_interval = 0.05
world_y_interval = 0.025
# Calculate the number of rows and columns in the output image
output_width = int(np.ceil((world_y_max - world_y_min) / world_y_interval))
output_height = int(np.ceil((world_x_max - world_x_min) / world_x_interval))
print("(width, height) :", "(", output_width, ",", output_height, ")")
# (width, height) : ( 800 , 860 )
- 위 값은
Vehicle좌표계 기준으로 \(X\) 축 방향으로 7 ~ 50 m, \(Y\) 축 방향으로 -10 ~ 10 m 영역을BEV이미지로 만들겠다는 의미입니다.BEV이미지의 행 방향이World 좌표계의 \(X\) 축과 대응되므로 행 방향으로 1픽셀씩 이동할수록 0.05 m 만큼 증감하게 되고 같은 논리로 열방향으로는 0.025 m 만큼 증감하게 된다는 것을 의미합니다. - 이와 같이 설계하였을 때,
BEV이미지 사이즈는width는 800 사이즈를 가지고height는 860 사이즈를 가지게 됩니다.
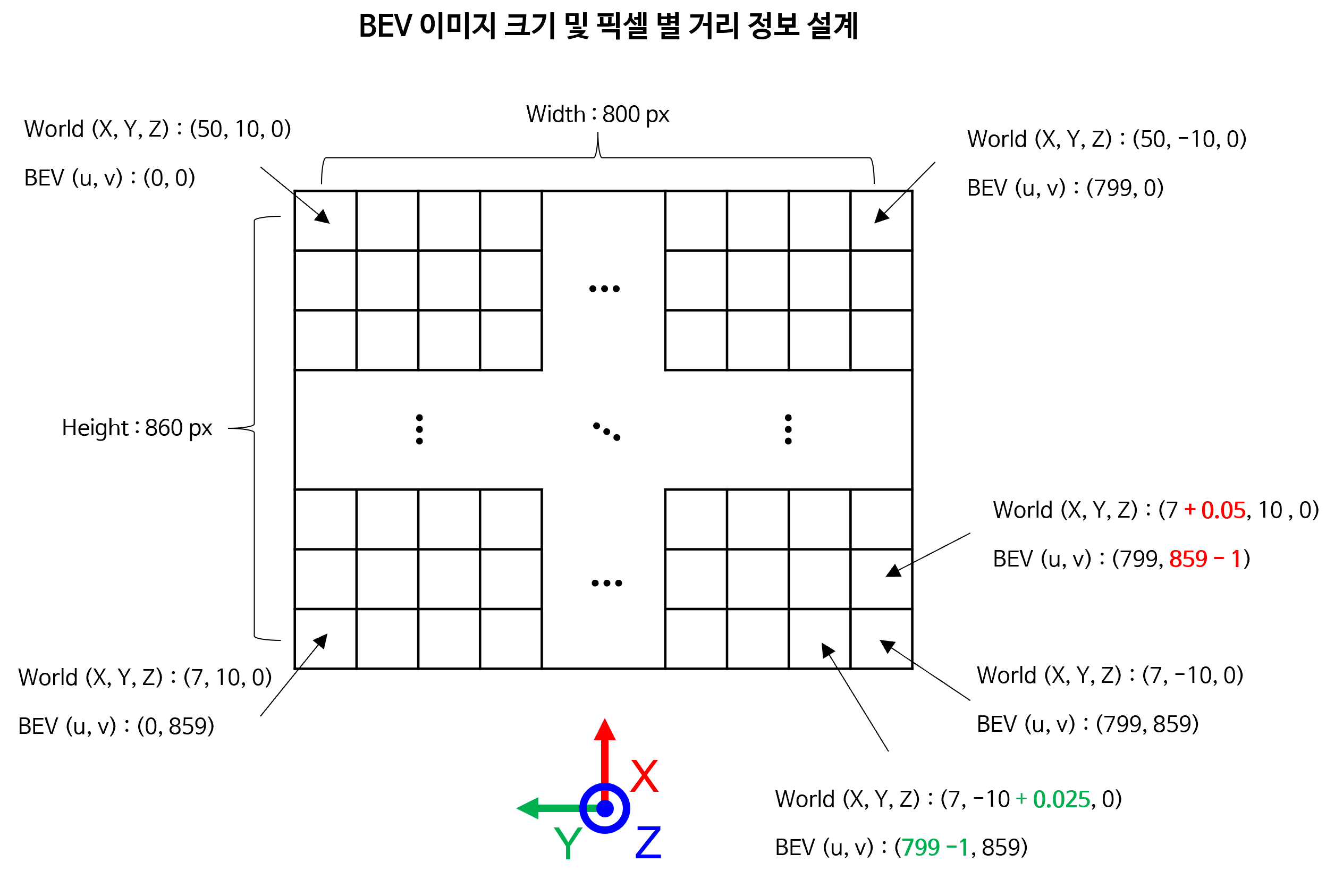
- 앞에 설명을 위 그림에 대응하여 이해하면 쉽게 이해하실 수 있을 것입니다.
- 이와 같은 방법으로
World 좌표계의 임의의 \(X, Y, Z=0\) 의 점을 이미지 좌표계에 대응하였을 때, 어떻게 대응되는 지 살펴보도록 하겠습니다. - 아래 예제 점들은 이해를 돕기 위하여 선정한 샘플 점들입니다.
points = np.array([
[world_x_max, world_y_max, 0, 1],
[world_x_max, world_y_min, 0, 1],
[world_x_min, world_y_min, 0, 1],
[world_x_min, world_y_max, 0, 1],
[10, -3, 0, 1],
[10, 3, 0, 1],
[6, 0, 0, 1],
[7, 0, 0, 1],
[8, 0, 0, 1],
[9, 0, 0, 1],
[10, 0, 0, 1],
[11, 0, 0, 1],
[12, 0, 0, 1],
[13, 0, 0, 1],
[14, 0, 0, 1],
[15, 0, 0, 1],
[16, 0, 0, 1],
[17, 0, 0, 1],
[18, 0, 0, 1],
[19, 0, 0, 1],
[20, 0, 0, 1],
[21, 0, 0, 1],
[22, 0, 0, 1],
[23, 0, 0, 1],
[24, 0, 0, 1],
[25, 0, 0, 1],
], dtype=np.float32)
image_coords = intrinsic @ extrinsic @ points.T
image_coords /= image_coords[2]
uv = image_coords[:2, :]
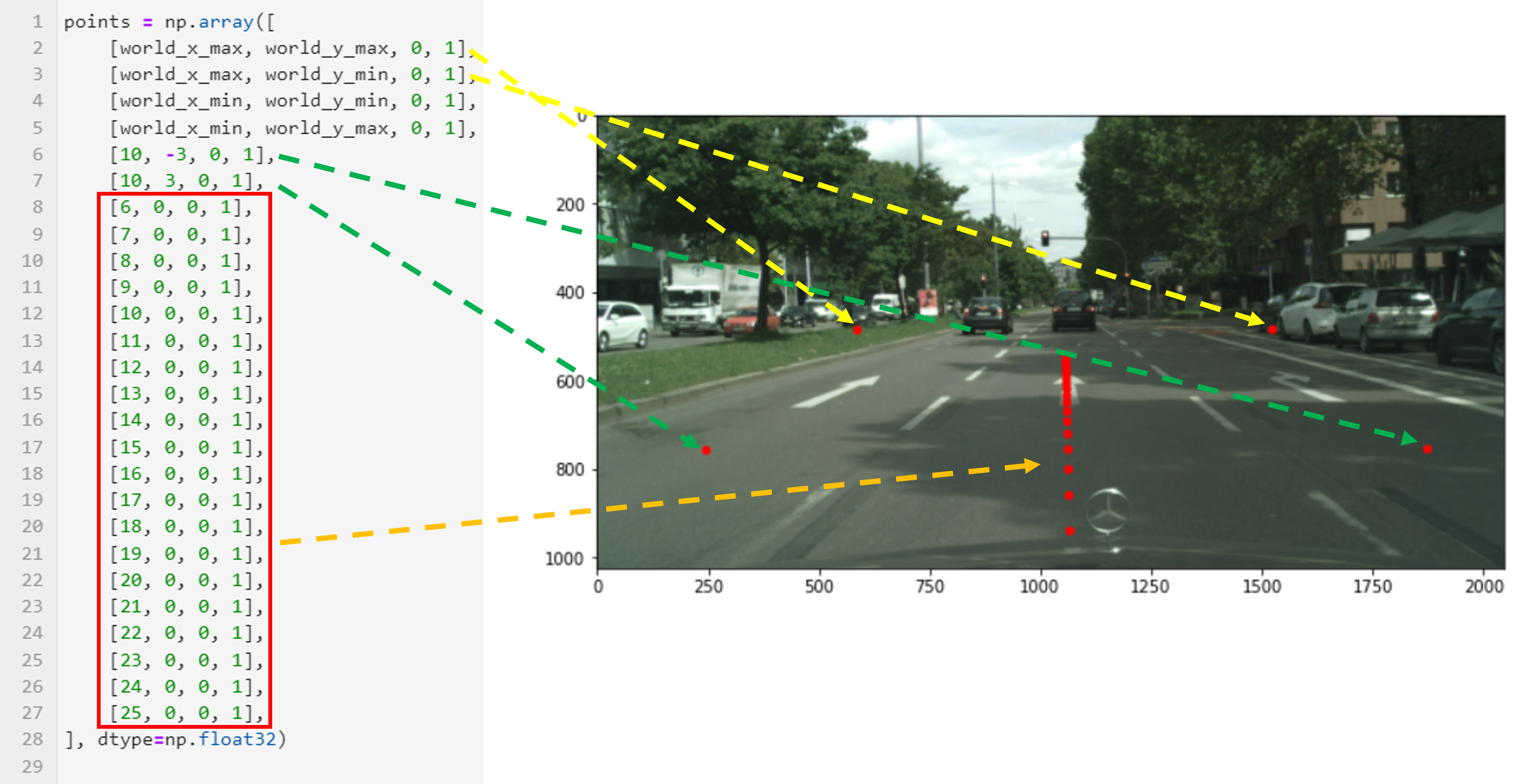
- ① 위 코드에서 2, 3번째 행의
world 좌표계의 점은 노란색 점선에 해당하는 위치의 원본 이미지 좌표에 해당합니다. - ② 4, 5번째 행의
world 좌표계의 점은 실제 원본 이미지에 대응되지 않는 점입니다. 즉, 이미지에서 보이지 않는 영역으로 이해할 수 있습니다. - ③ 6, 7번째 행의
world 좌표계의 점은 근거리 영역의 점입니다. 2, 3번째 행의 좌표와 비교해 보면world 좌표계에서의 좌표값은 종방향, 횡방향 모두 많은 차이가 있는 반면에 이미지에서는 횡방향에서 큰 차이가 없는 것 처럼 보입니다. 이러한 점들이 원근감이 반영된perspective distortion의 영향이며 위치를 짐작하는 데 왜곡을 발생시킵니다. - ④ 8번째 행부터 끝까지는 6 m에서 25 m 까지
world 좌표계의 \(X\) 축으로 1 m 씩 증가시키면서 점들의 위치를 이미지에서 확인해 본 것입니다. 몇가지 내용을 확인할 수 있는데, 첫째, 6 m 부터 이미지 상에서 점들이 확인이 가능했다는 점입니다. 즉 6m 이내의 점들은 이미지 상에 들어오지 않았습니다. 둘째,world 좌표계가 차량의 중심에 있는 것으로 유추할 수 있는점입니다. \(Y\) 축이 이미지의 한가운데 근처에 있는 것으로 보입니다. 마지막으로 원근감에 의하여world 좌표계의 원점과 멀리 떨어져 있는 점들은 비슷한 픽셀에 모여 있을 가능성이 높아집니다. 즉, 멀리 있는 픽셀 하나가 넓은 공간을 모두 대변하고 있으며 그만큼 해상도가 줄어들 것입니다.
③ BEV 이미지와 Image 좌표간의 LUT (Look Up Table) 구하기
- 지금까지 내용을 살펴보면
world 좌표계의 임의의 점 \((X, Y, Z=0)\) 가 이미지 좌표계의 어떤 픽셀에 해당하는 지 관계만 알 수 있으면BEV이미지를 생성할 수 있음을 확인하였습니다.
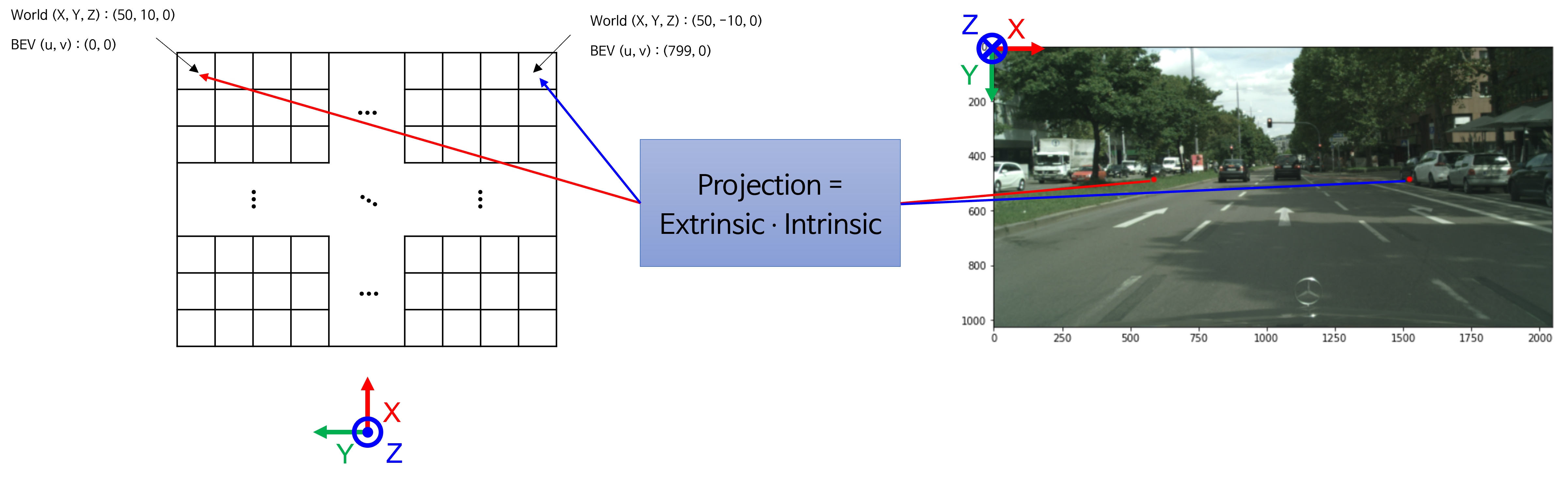
- 예를 들어 위 그림의 예시와 같이
world 좌표계의 정보를 이용하여 설정한BEV이미지에서 임의의 픽셀을extrinsic과intrinsic을 이용하여 원본 이미지의 픽셀 어디와 대응되는 지 알 수 있습니다. - 모든
BEV이미지의 모든 픽셀에 대하여 이 대응되는 정보를 가지고 있을 수 있다면 매번BEV이미지를 만들어 낼 수 있으므로 이 대응되는 정보를 구하는 것이BEV이미지를 만드는 핵심입니다. 이 대응 관계를 나타내는LUT(Look Up Table)를 구하는 방법을 살펴보겠습니다.
- 아래 코드를 이용하면 원하는
world_x_max,world_x_min,world_y_max,world_y_min,world_x_interval,world_y_interval을 만족하는LUT인map_x,map_y를 구할 수 있습니다. BEV이미지의(u, v)좌표의 값은dst[v][u] = src[ map_y[v][u] ][ map_x[v][u] ]와 같은 방법으로 인덱스 참조하여 구할 수 있는 것이map_x,map_y의 정보 입니다.
def generate_direct_backward_mapping(
world_x_min, world_x_max, world_x_interval,
world_y_min, world_y_max, world_y_interval, extrinsic, intrinsic):
print("world_x_min : ", world_x_min)
print("world_x_max : ", world_x_max)
print("world_x_interval (m) : ", world_x_interval)
print()
print("world_y_min : ", world_y_min)
print("world_y_max : ", world_y_max)
print("world_y_interval (m) : ", world_y_interval)
world_x_coords = np.arange(world_x_max, world_x_min, -world_x_interval)
world_y_coords = np.arange(world_y_max, world_y_min, -world_y_interval)
output_height = len(world_x_coords)
output_width = len(world_y_coords)
map_x = np.zeros((output_height, output_width)).astype(np.float32)
map_y = np.zeros((output_height, output_width)).astype(np.float32)
world_z = 0
for i, world_x in enumerate(world_x_coords):
for j, world_y in enumerate(world_y_coords):
# world_coord : [world_x, world_y, 0, 1]
# uv_coord : [u, v, 1]
world_coord = [world_x, world_y, world_z, 1]
camera_coord = extrinsic[:3, :] @ world_coord
uv_coord = intrinsic[:3, :3] @ camera_coord
uv_coord /= uv_coord[2]
# map_x : (H, W)
# map_y : (H, W)
# dst[i][j] = src[ map_y[i][j] ][ map_x[i][j] ]
map_x[i][j] = uv_coord[0]
map_y[i][j] = uv_coord[1]
return map_x, map_y
map_x, map_y = generate_direct_backward_mapping(world_x_min, world_x_max, world_x_interval, world_y_min, world_y_max, world_y_interval, extrinsic, intrinsic)
# world_x_min : 7
# world_x_max : 50
# world_x_interval (m) : 0.05
# world_y_min : -10
# world_y_max : 10
# world_y_interval (m) : 0.025
- 생성된
map_x,map_y의 크기는BEV이미지의 크기와 동일합니다. 따라서 위 예제에서는 (w=800, h=860) 크기의map_x,map_y를 가지게 되므로 모든 인덱스에dst[v][u] = src[ map_y[v][u] ][ map_x[v][u] ]를 적용할 수 있습니다.
④ backward 방식으로 IPM 처리하여 BEV 이미지 생성하기
- 앞에서 생성한
map_x,map_y가 핵심이며 이제backward방식으로BEV이미지를 생성하면 됩니다. backward방식이란 만들고자 하는target이미지의 픽셀에서 부터 거꾸로source이미지의 픽셀에 접근하여 원하는 RGB 값을 가져오는 방식을 의미합니다.- 이와 같은 방식을 사용하는 이유는
source이미지에서target이미지로 값을 대응시켜 보낼 경우 모든 픽셀에 값을 대응시키기 어려워target이미지에서 픽셀이 대응되지 않아hole이 발생하기 때문입니다. 예를 들어 앞에서 살펴본 바와 같이 카메라와 먼 영역에서는 한 픽셀에 대응되는BEV이미지의 픽셀이 여러개가 될 수 있습니다.
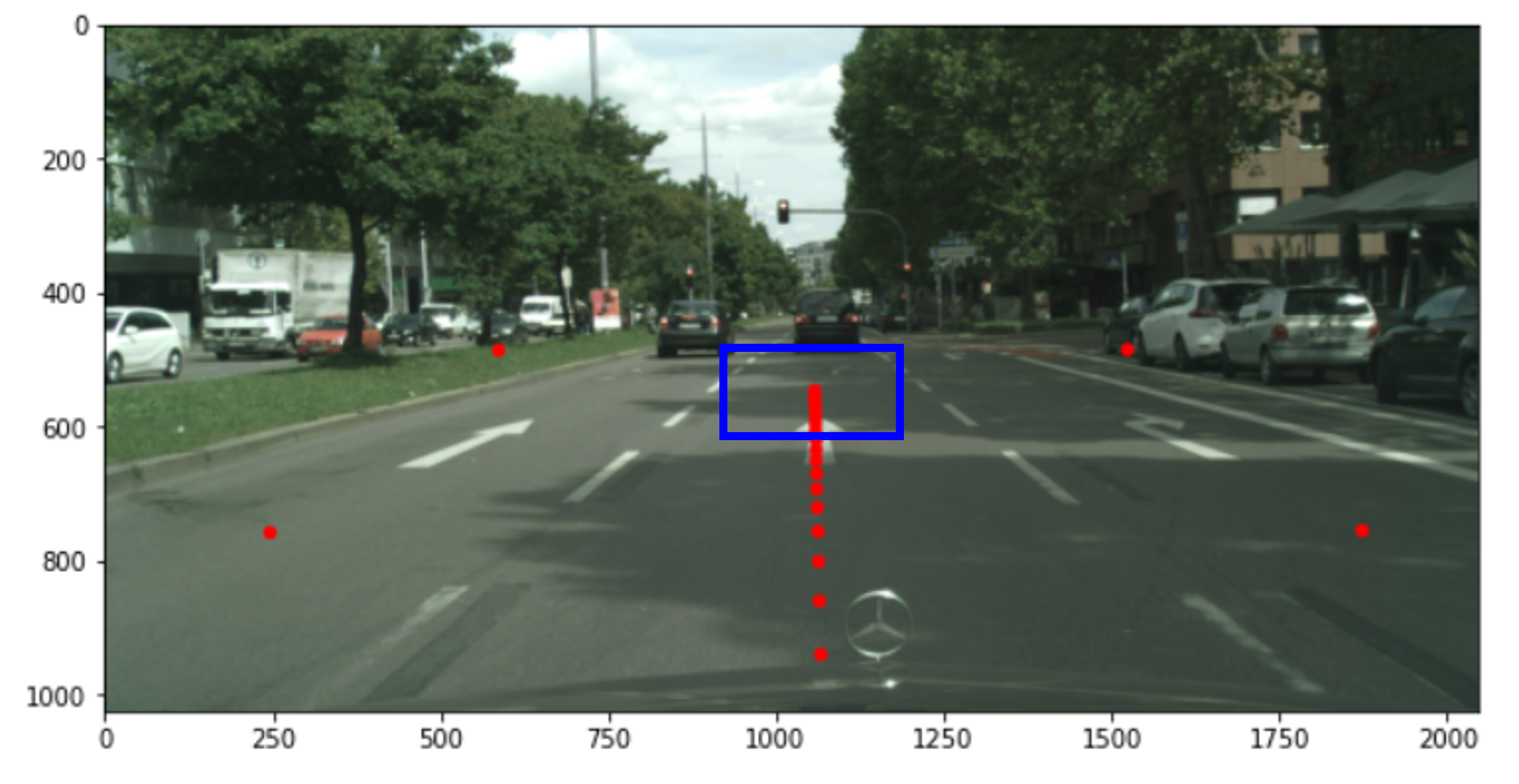
- 위 그림에서 파란색 영역을 보면 점들이 겹치기 시작합니다. 원거리 영역에서 이런 경우가 더 많이 발생합니다.
src → target(BEV)으로 점을 한개씩 보내면BEV이미지에 대응되지 않는 점이 많아질 것입니다. - 따라서
target → src방향으로 참조해야 할 픽셀의 관계를 정하는 것이BEV이미지를 모두 채울 수 있는 방법이며 이와 같은 방식을backward mapping이라고 합니다. 아래 코드에서는remap으로 명명하겠습니다.
- 아래는 가장 간단한
remap방식입니다.map_x,map_y가float값으로 되어 있기 때문에round처리하여 가장 가까운 픽셀을 가져오도록 한 것입니다.
def remap_nearest(src, map_x, map_y):
src_height = src.shape[0]
src_width = src.shape[1]
dst_height = map_x.shape[0]
dst_width = map_x.shape[1]
dst = np.zeros((dst_height, dst_width, 3)).astype(np.uint8)
for i in range(dst_height):
for j in range(dst_width):
src_y = int(np.round(map_y[i][j]))
src_x = int(np.round(map_x[i][j]))
if 0 <= src_y and src_y < src_height and 0 <= src_x and src_x < src_width:
dst[i][j] = src[src_y, src_x, :]
return dst
output_image_nearest = remap_nearest(image, map_x, map_y)
output_image = cv2.remap(image, map_x, map_y, cv2.INTER_NEAREST, borderMode=cv2.BORDER_CONSTANT)
mask = (output_image > [0, 0, 0])
output_image = output_image.astype(np.float32)
output_image_nearest = output_image_nearest.astype(np.float32)
print("L1 Loss of opencv remap Vs. custom remap nearest : ", np.mean(np.abs(output_image[mask]-output_image_nearest[mask])))
print("L2 Loss of opencv remap Vs. custom remap nearest : ", np.mean((output_image[mask]-output_image_nearest[mask])**2))
# L1 Loss of opencv remap Vs. custom remap nearest : 0.0
# L2 Loss of opencv remap Vs. custom remap nearest : 0.0
remap_nearest는round방식으로src이미지에 접근하여backward mapping한 방식이며 편하게 사용하기 위해서는cv2.remap함수를 사용하면 됩니다. 대신에 옵션으로cv2.INTER_NEAREST을 주면 같은round방식이 됩니다.- 마지막에
remap_nearest와cv2.remap의 차이를 보면 차이가 없는 것을 확인할 수 있습니다. - 생성된
BEV이미지를 보면 아래와 같습니다.

- 하지만 이와 같은
round연산은 카메라와 멀어질수록 참조하는 픽셀이 같아지도로고 만들면서 위 그림의 이미지 상단과 같이 해상도가 떨어져 보이는artifact가 발생하게 됩니다. - 이와 같은 문제를 개선하기 위하여 일반적으로
round연산으로 소수점을 처리하지 않고bilinear interpolation을 많이 사용합니다. - 다음 링크를 참조하시면 됩니다. (https://en.wikipedia.org/wiki/Bilinear_interpolation).
round방식으로 값을 선택하지 않고 다음 그림과 같이 주변 4개의 점과 사용해야 할float점 값의 관계를 이용하여interpolation을 하는 방법입니다.
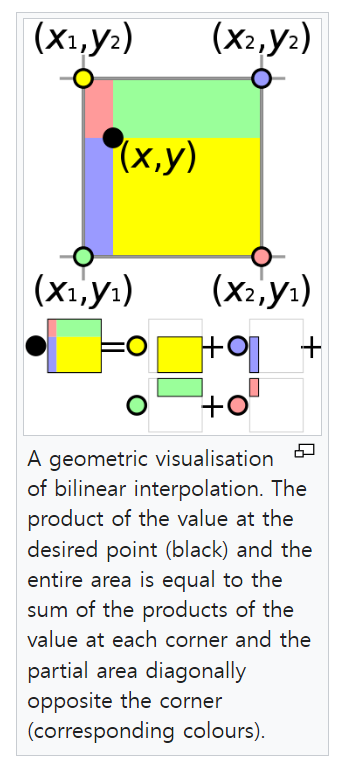
- 이와 같은 방법을 사용하려면 아래 코드를 사용하여 구현할 수 있습니다.
def bilinear_sampler(imgs, pix_coords):
"""
Construct a new image by bilinear sampling from the input image.
Args:
imgs: [H, W, C]
pix_coords: [h, w, 2]
:return:
sampled image [h, w, c]
"""
img_h, img_w, img_c = imgs.shape
pix_h, pix_w, pix_c = pix_coords.shape
out_shape = (pix_h, pix_w, img_c)
pix_x, pix_y = np.split(pix_coords, [1], axis=-1) # [pix_h, pix_w, 1]
pix_x = pix_x.astype(np.float32)
pix_y = pix_y.astype(np.float32)
# Rounding
pix_x0 = np.floor(pix_x)
pix_x1 = pix_x0 + 1
pix_y0 = np.floor(pix_y)
pix_y1 = pix_y0 + 1
# Clip within image boundary
y_max = (img_h - 1)
x_max = (img_w - 1)
zero = np.zeros([1])
pix_x0 = np.clip(pix_x0, zero, x_max)
pix_y0 = np.clip(pix_y0, zero, y_max)
pix_x1 = np.clip(pix_x1, zero, x_max)
pix_y1 = np.clip(pix_y1, zero, y_max)
# Weights [pix_h, pix_w, 1]
wt_x0 = pix_x1 - pix_x
wt_x1 = pix_x - pix_x0
wt_y0 = pix_y1 - pix_y
wt_y1 = pix_y - pix_y0
# indices in the image to sample from
dim = img_w
# Apply the lower and upper bound pix coord
base_y0 = pix_y0 * dim
base_y1 = pix_y1 * dim
# 4 corner vertices
idx00 = (pix_x0 + base_y0).flatten().astype(np.int32)
idx01 = (pix_x0 + base_y1).astype(np.int32)
idx10 = (pix_x1 + base_y0).astype(np.int32)
idx11 = (pix_x1 + base_y1).astype(np.int32)
# Gather pixels from image using vertices
imgs_flat = imgs.reshape([-1, img_c]).astype(np.float32)
im00 = imgs_flat[idx00].reshape(out_shape)
im01 = imgs_flat[idx01].reshape(out_shape)
im10 = imgs_flat[idx10].reshape(out_shape)
im11 = imgs_flat[idx11].reshape(out_shape)
# Apply weights [pix_h, pix_w, 1]
w00 = wt_x0 * wt_y0
w01 = wt_x0 * wt_y1
w10 = wt_x1 * wt_y0
w11 = wt_x1 * wt_y1
output = w00 * im00 + w01 * im01 + w10 * im10 + w11 * im11
return output
def remap_bilinear(image, map_x, map_y):
pix_coords = np.concatenate([np.expand_dims(map_x, -1), np.expand_dims(map_y, -1)], axis=-1)
bilinear_output = bilinear_sampler(image, pix_coords)
output = np.round(bilinear_output).astype(np.int32)
return output
output_image_bilinear = remap_bilinear(image, map_x, map_y)
output_image = cv2.remap(image, map_x, map_y, cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT)
mask = (output_image > [0, 0, 0])
output_image = output_image.astype(np.float32)
output_image_bilinear = output_image_bilinear.astype(np.float32)
print("L1 Loss of opencv remap Vs. custom remap bilinear : ", np.mean(np.abs(output_image[mask]-output_image_bilinear[mask])))
print("L2 Loss of opencv remap Vs. custom remap bilinear : ", np.mean((output_image[mask]-output_image_bilinear[mask])**2))
# L1 Loss of opencv remap Vs. custom remap bilinear : 0.045081623
# L2 Loss of opencv remap Vs. custom remap bilinear : 0.66912574

- 위 그림과 같이
bilinear interpolation을 적용하면artifact현상이 개선된 것을 볼 수 있습니다. 따라서 연산은 추가되지만artifact가 사라지는bilinear interpolation을 사용하는 것을 권장 드립니다. - 위 코드의 결과와 같이
bilinear interpolation은 구현 방법에 따라 값의 차이가 발생하는 것을 볼 수 있습니다.nearest케이스와는 다르게remap_bilinear와cv2.remap의 결과가 완전 동일하지는 않습니다. (차이 수준은 무시할만한 수준입니다.)
Cityscapes 데이터셋 IPM 적용 예시
- 아래 영상은
Cityscapes데이터에IPM을 적용한 예시입니다.BEV이미지를 생성한 방법은 다음과 같습니다.
world_x_max = 50
world_x_min = 7
world_y_max = 10
world_y_min = -10
world_x_interval = 0.05
world_y_interval = 0.025
- 다음은 2번째 예시 입니다. 좁은 영역을 조금 더 자세하게 보기 위한 예시입니다.
world_x_max = 30
world_x_min = 7
world_y_max = 5
world_y_min = -5
world_x_interval = 0.02
world_y_interval = 0.01
렌즈 왜곡을 반영한 IPM 적용 방법
- 지금까지 살펴본
Cityscapes의 예제는 왜곡이 보정된 영상입니다. 영상을 참조하였을 때에도 영상에 왜곡이 없는 것을 확인할 수 있으며 위 코드의load_camera_params()함수를 이용하여 카메라 파라미터를 불러올 때에도 왜곡 계수가 없는 것을 알 수 있습니다. - 실제 카메라를 사용할 때에는 카메라 렌즈 왜곡을 이용하여 왜곡 보정을 하여 사용하거나 아니면 영상에 왜곡이 존재하는 상태로 사용해야 합니다. 왜곡 보정이나 카메라 렌즈 왜곡과 관련된 내용은 카메라 모델과 렌즈 왜곡 (lens distortion)을 참조하면 알 수 있습니다.
- 만약 실제 사용하는 영상을 왜곡 보정하여 사용한다면 본 글에서 다룬
Cityscapes의 예제와 같이 동일한 방식으로 사용할 수 있습니다. 하지만 왜곡 보정을 하지 않고 원래 영상에서 그대로 사용한다면렌즈 왜곡을 반영하여 사용해야 합니다.
- 카메라 모델과 렌즈 왜곡과 Generic Camera Model을 참조하면
Distortion Coefficient를 어떻게 이용해야 하는 지 확인할 수 있습니다. 이번 글에서도Generic Camera Model을 이용하여 영상의 왜곡을 반영하는 함수를 간략히 소개하겠습니다.
def generate_direct_backward_mapping(
world_x_min, world_x_max, world_x_interval,
world_y_min, world_y_max, world_y_interval, R, t, K, D, hfov=180):
world_x_coords = np.arange(world_x_max, world_x_min, -world_x_interval)
world_y_coords = np.arange(world_y_max, world_y_min, -world_y_interval)
output_height = len(world_x_coords)
output_width = len(world_y_coords)
map_x = np.ones((output_height, output_width)).astype(np.float32) * -1
map_y = np.ones((output_height, output_width)).astype(np.float32) * -1
if len(D) == 5:
k1, k2, k3, k4 = D[1:]
elif len(D) == 4:
k1, k2, k3, k4 = D
else:
print("Wrong Distortion.")
exit()
fx = K[0][0]
fy = K[1][1]
skew = K[0][1]
cx = K[0][2]
cy = K[1][2]
world_z = 0
for i, world_x in enumerate(world_x_coords):
for j, world_y in enumerate(world_y_coords):
world_coord = [world_x, world_y, world_z]
camera_coord = R @ world_coord + t
#################### undistorted normalized coordinate ######################
x_un = camera_coord[0] / camera_coord[2]
y_un = camera_coord[1] / camera_coord[2]
#################### distorted normalized coordinate ########################
r_un = np.sqrt(x_un**2 + y_un**2)
theta = np.arctan(r_un)
r_dn = 1*theta + k1*theta**3 + k2*theta**5 + k3*theta**7 + k4*theta**9
x_dn = r_dn * (x_un/r_un)
y_dn = r_dn * (y_un/r_un)
################################ image plane ###############################
u = np.round(fx*x_dn + skew*y_dn + cx)
v = np.round(fy*y_dn + cy)
#############################################################################
if (np.rad2deg(theta) < (hfov/2)) and (camera_coord[2] > 0):
# map_x : (H, W)
# map_y : (H, W)
# dst[i][j] = src[ map_y[i][j] ][ map_x[i][j] ]
map_x[i][j] = u
map_y[i][j] = v
return map_x, map_y
- 변경된
generate_direct_backward_mapping함수를 살펴보면 함수의 인자로distortion이라는 것을 받습니다.Generic Camera Model의 정의에 의하여 9차 기함수(odd function)를 이용하여 렌즈 왜곡을 추정하기 때문에distortion은 9차 방정식의 홀수 차수의 계수를 저장합니다.distortion의 값이 4개이면 3, 5, 7, 9차 항의 계수를 의미하고distortion이 5개이면 1차 항의 계수 까지 포함합니다. (opencv의 캘리브레이션 함수에서 1차 항의 계수는 1로 고정하기 때문에 이와 같은 표현법이 사용됩니다.) undistorted normalized coordinate→distorted normalized coordinate→image plane변환의 의미는 카메라 모델과 렌즈 왜곡에 자세하게 설명되어 있으니 참조 부탁드립니다.- 함수의 인자 중
R,t,K,D는 각각Rotation,translation,intrinsic,distortion을 뜻합니다. hfov는IPM적용 시 사용할 카메라 화각을 의미합니다. 예를 들어hfov= 150 으로 적용하면 카메라 수평 화각이 150도를 넘는다고 하더라도 렌즈 중심으로부터 좌우 75도만 사용하여 최대 150도 화각만 사용한다는 것을 의미합니다. 위 코드에서(np.rad2deg(theta) < (hfov/2))부분에 해당하며 이 조건을 통하여 원하는 화각 영역만IPM을 적용할 수 있습니다.- 코드에서
(camera_coord[2] > 0)조건은 카메라 기준depth가 양수인 영역만IPM을 적용한다는 뜻으로 카메라 뒤 영역은IPM적용에서 제외한다는 의미입니다.
Custom 데이터를 이용한 IPM 적용 예시
- 이번 예제는 화각이 180도 이상인
fisheye camera4대를 이용하여 카메라 캘리브레이션을 한 데이터를 이용하여IPM을 적용해 보도록 하겠습니다.
- 사용한 카메라: ELP-USB16MP01-BL180
- 데이터셋 링크: https://drive.google.com/drive/folders/15cnXNjEaztZl0CBT25oCaJ9-8qyfRYAw?usp=drive_link
camera_calibration.jsonfront_fisheye_camera.pngrear_fisheye_camera.pngleft_fisheye_camera.pngright_fisheye_camera.png
- 캘리브레이션 환경은 아래 그림과 같습니다.
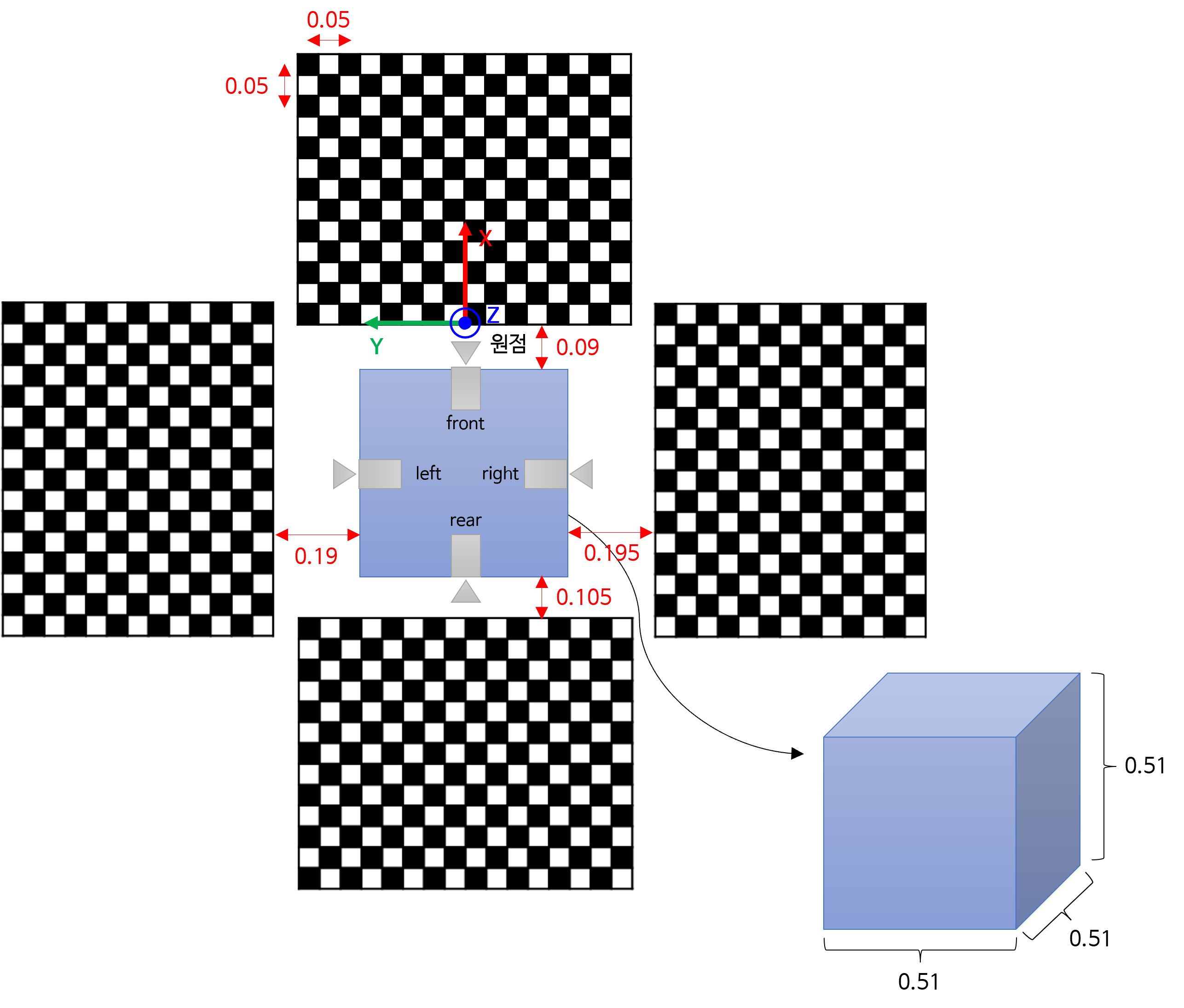
- 4개의 카메라 이미지는 다음과 같습니다

- 원점과 X, Y, Z 축을 고려하여 각 카메라의 위치를 카메라 캘리브레이션 결과를 통해 확인하면 아래와 같습니다. 카메라 아랫면에서 렌즈부 까지의 길이는 약 0.02 ~ 0.03 m 정도입니다. 렌즈부가 돌출된 형태도 대략 0.02 ~ 0.03 m 정도입니다.
front_fisheye_camera: (X = -0.06803, Y = -0.00688, Z = 0.53321)rear_fisheye_camera: (X = -0.62111, Y = -0.00121, Z = 0.55104)left_fisheye_camera: (X = -0.33217, Y = 0.26681, Z = 0.53275)right_fisheye_camera: (X = -0.34385, Y = -0.28677, Z = 0.54694)
- 아래 코드를 이용하여 4개의 이미지를 읽어서
IPM을 적용하여 시각화 해보겠습니다. 먼저 편의상front_fisheye_camera와rear_fisheye_camera를 묶어서IPM결과를 시각화하고left_fisheye_camera와right_fisheye_camera를 묶어서IPM결과를 시각화 해보겠습니다.
import json
import numpy as np
import cv2
import matplotlib.pyplot as plt
import os
def generate_direct_backward_mapping(
world_x_min, world_x_max, world_x_interval,
world_y_min, world_y_max, world_y_interval, R, t, K, D, hfov=180):
world_x_coords = np.arange(world_x_max, world_x_min, -world_x_interval)
world_y_coords = np.arange(world_y_max, world_y_min, -world_y_interval)
output_height = len(world_x_coords)
output_width = len(world_y_coords)
map_x = np.ones((output_height, output_width)).astype(np.float32) * -1
map_y = np.ones((output_height, output_width)).astype(np.float32) * -1
if len(D) == 5:
k1, k2, k3, k4 = D[1:]
elif len(D) == 4:
k1, k2, k3, k4 = D
else:
print("Wrong Distortion.")
exit()
fx = K[0][0]
fy = K[1][1]
skew = K[0][1]
cx = K[0][2]
cy = K[1][2]
world_z = 0
for i, world_x in enumerate(world_x_coords):
for j, world_y in enumerate(world_y_coords):
world_coord = [world_x, world_y, world_z]
camera_coord = R @ world_coord + t
#################### undistorted normalized coordinate ######################
x_un = camera_coord[0] / camera_coord[2]
y_un = camera_coord[1] / camera_coord[2]
#################### distorted normalized coordinate ########################
r_un = np.sqrt(x_un**2 + y_un**2)
theta = np.arctan(r_un)
r_dn = 1*theta + k1*theta**3 + k2*theta**5 + k3*theta**7 + k4*theta**9
x_dn = r_dn * (x_un/r_un)
y_dn = r_dn * (y_un/r_un)
################################ image plane ###############################
u = np.round(fx*x_dn + skew*y_dn + cx)
v = np.round(fy*y_dn + cy)
#############################################################################
if (np.rad2deg(theta) < (hfov/2)) and (camera_coord[2] > 0):
# map_x : (H, W)
# map_y : (H, W)
# dst[i][j] = src[ map_y[i][j] ][ map_x[i][j] ]
map_x[i][j] = u
map_y[i][j] = v
return map_x, map_y
world_x_max = 2
world_x_min = -2.5
world_y_max = 2
world_y_min = -2
world_x_interval = 0.01
world_y_interval = 0.01
path = "path/to/the/calibration_and_image/"
camera_calib = json.load(open(path + os.sep + "camera_calibration.json", "r"))
bev_image_dict = {}
camera_names = ['front_fisheye_camera', 'rear_fisheye_camera', 'left_fisheye_camera', 'right_fisheye_camera']
for camera_name in camera_names:
image_path = path + os.sep + camera_name + ".png"
image = cv2.cvtColor(cv2.imread(image_path), cv2.COLOR_BGR2RGB)
R = np.array(camera_calib[camera_name]['Extrinsic']['World']['Camera']['R']).reshape(3, 3)
t = np.array(camera_calib[camera_name]['Extrinsic']['World']['Camera']['t'])
K = np.array(camera_calib[camera_name]['Intrinsic']["K"]).reshape(3, 3)
D = np.array(camera_calib[camera_name]['Intrinsic']["D"])
map_x, map_y = generate_direct_backward_mapping(
world_x_min,
world_x_max,
world_x_interval,
world_y_min,
world_y_max,
world_y_interval,
R, t, K, D, 180
)
output_image = cv2.remap(image, map_x, map_y, cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT)
bev_image_dict[camera_name] = output_image
plt.imshow(bev_image_dict['front_fisheye_camera'] + bev_image_dict['rear_fisheye_camera'])
plt.imshow(bev_image_dict['left_fisheye_camera'] + bev_image_dict['right_fisheye_camera'])
- 아래 코드를 이용하여 4개의 이미지의 중첩 영역을 간단하게 오버랩하여 시각화 하면 아래와 같습니다.
imgs = [
bev_image_dict['front_fisheye_camera'],
bev_image_dict['rear_fisheye_camera'],
bev_image_dict['left_fisheye_camera'],
bev_image_dict['right_fisheye_camera']
]
# Stack into a single array of shape (4, H, W, 3)
stack = np.stack(imgs, axis=0) # dtype=uint8
# Build a mask: True where any channel is nonzero
# shape (4, H, W); dtype=float32 for later arithmetic
mask = (stack != 0).any(axis=-1).astype(np.float32)
# Multiply each pixel by its mask
# shape broadcast to (4, H, W, 1) then multiplied
masked = stack.astype(np.float32) * mask[..., None]
# Sum the colors and sum the masks
sum_colors = masked.sum(axis=0) # shape (H, W, 3)
count = mask.sum(axis=0)[..., None] # shape (H, W, 1)
# Avoid division by zero: wherever count==0, set to 1
count_safe = np.where(count==0, 1.0, count)
# Compute the average and convert back to uint8
ipm_result = (sum_colors / count_safe).astype(np.uint8)
plt.imshow(ipm_result)
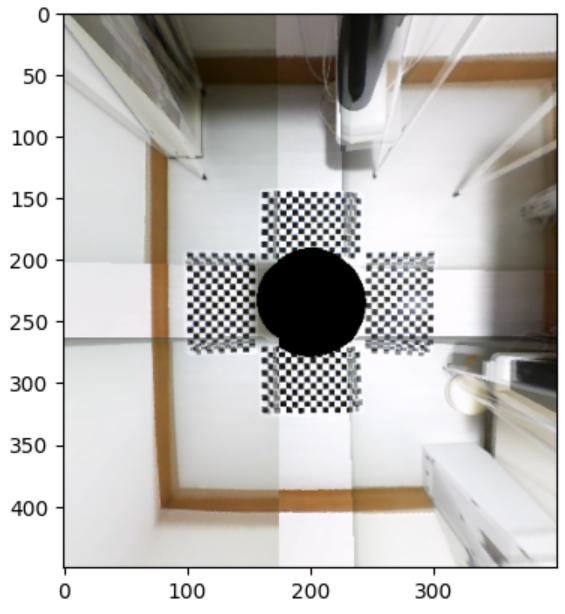
IPM을 이용한 3차원 공간 채우기
IPM 적용 application 사례
- 아래 영상은
RidgeRun이라는 곳에서IPM을 이용하여 application을 적용한 사례를 보여줍니다.
- 영상을 살펴보면 4개의
fisheye camera를 이용하여 전방/좌측/우측/후방을 잘 조합하여 하나의BEV이미지를 만들어 냅니다.
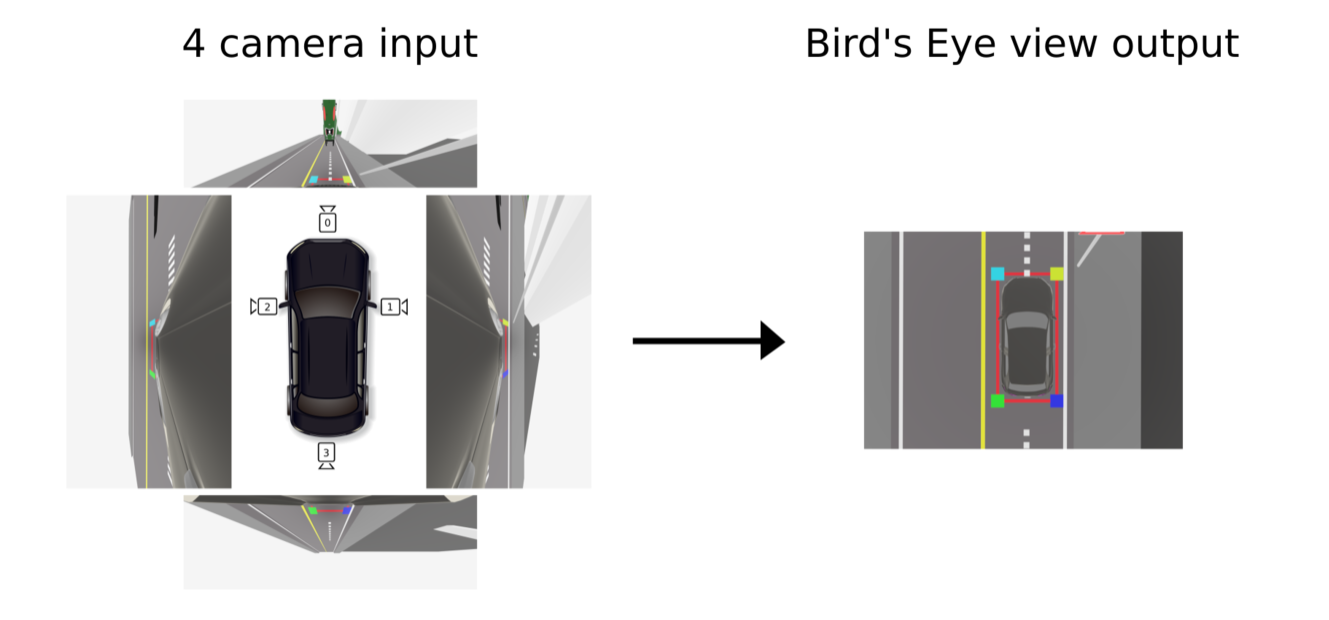
- 4개의
fisheye camera에서 동시에 취득한 이미지에 모두IPM을 적용하여 360도를BEV이미지에 mapping 하여 볼 수 있도록 하였습니다.- 상세 내용 링크 : https://developer.ridgerun.com/wiki/index.php/Birds_Eye_View
- 앞에서 설명하였듯이
flat ground조건을 만족하기 위해서는 실제 ground가 flat 해야 하기도 하지만extrinsic이 정확히 잘 맞아야 합니다. 4개의 카메라가 모두 정확한extrinsic을 구할 수 있도록 위 영상과 같이calibration환경을 구성하였다는 점을 참조할 수 있습니다. 전/후/좌/우 4개의 선이 어긋남 없이 연결되는 것을 영상을 통해 확인할 수 있습니다.
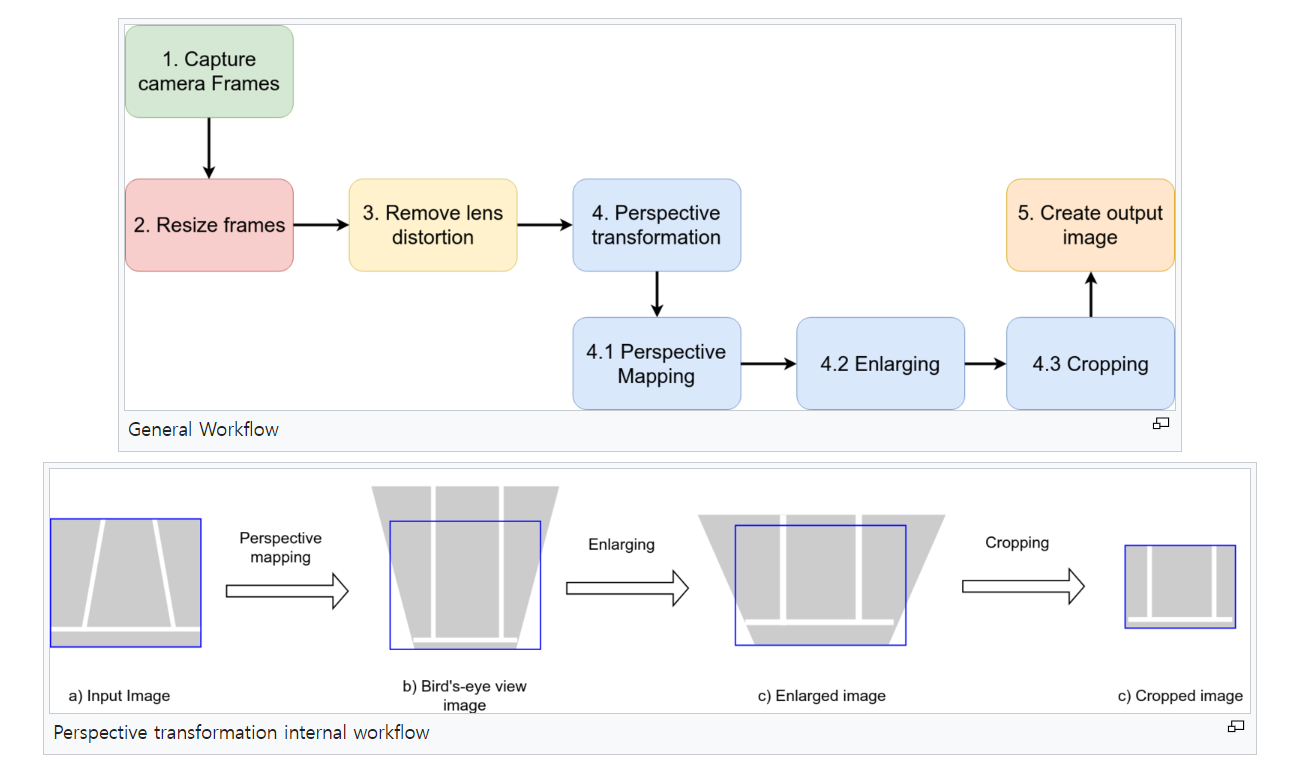
IPM을 적용하여BEV이미지를 만드는 전체 프로세스를 위 flow와 같이 제시하였습니다.- 상세 내용 링크 : https://developer.ridgerun.com/wiki/index.php?title=Birds_Eye_View/Introduction/Research
- 위 flow와 같이
perspective mapping을 이용하여도 구현할 수 있으며 본 글에서 제시한 방식과 유사합니다. - 다만 위 flow와 같이 진행하려면
Remove lens distortion작업이 반드시 필요하나 본 글에서 제시한 방식으로 할 경우 이 과정이 필요 없습니다. - 또한 이미지가 생성되지 않는 검은색 영역을 제거하기 위하여 필요한 영역만
crop한 것은 실제 application을 사용할 때 필요한 작업임을 확인하는 것도 도움이 됩니다. - 위 링크를 통하여
fisheye camera에서 어떻게IPM을 적용하는 지 쉽게 설명이 되어있으니 참조하기 좋아 정리해 두었습니다.