사원수(Quaternion)와 회전 (Rotation)

2022, May 10    

Vision 관련 글 목차

• 참조 : 이득우의 게임 수학
• 참조 : 수학과 OpenGL 프로그래밍
• 참조 : https://www.youtube.com/watch?v=zjMuIxRvygQ&t=226s
• 참조 : https://ghebook.blogspot.com/2010/07/quaternion.html

• 사전 지식 ① : Euler Angle Rotation
• 사전 지식 ② : Axis-Angle Rotation
• 사전 지식 ③ : 복소수와 복소 평면
• 사전 지식 ④ : 벡터의 내적
• 사전 지식 ⑤ : 벡터의 외적

목차

• 사원수의 사용 이유

• 사원수의 정의

• 사원수의 연산

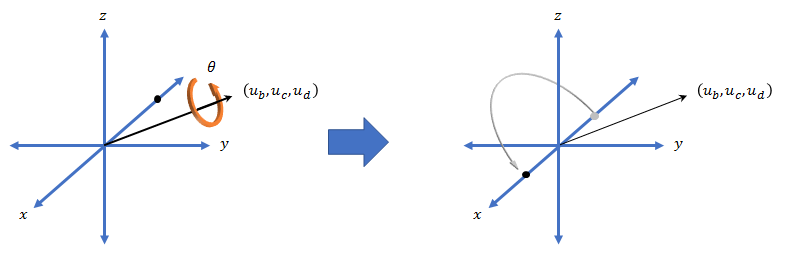
• 사원수와 회전의 관계

• 사원수의 보간

• pyquaternion 사용법

사원수의 사용 이유

사원수의 정의

• 사원수는 스칼라 값과 3차원 벡터를 묶어 구성한 복소수입니다. 3차원 벡터 $v = (a, b, c)$ 를 각각의 축 방향 단위 벡터인 기저 $i, j, k$ 로 표현하면 $ai + bj + ck$ 가 됩니다. 사원수는 여기에 스칼라 값 $d$ 가 추가된 $d + ai + bj + ck$ 가 됩니다.
• 만약 기저를 제외하고 표현하면 $(d, (a, b, c))$ 와 같이 표현할 수 있고 벡터 기호로 표현하면 이는 $(d, v)$ 로 표현할 수 있습니다.
• 스칼라 값은 기저가 실수의 단위 값인 1이라고 이해하면 사원수는 $1, i, j, k$ 를 기저로 하는 벡터라고 할 수 있습니다. 이 사원수는 로보틱스와 컴퓨터 그래픽스 분야에서 회전을 다루는 데에 빈번히 이용됩니다.

• 먼저 사원수의 기본적인 성질에 대하여 살펴보도록 하겠습니다.

• $$i^{2} = -1 \tag{1}$$
• $$i^{2} = j^{2} = k^{2} = ijk = -1 \tag{2}$$

• 식 (1)은 복소수에 대한 정의라면 식 (2)는 사원수에 대한 정의입니다. 식 (2)를 이용하면 사원수의 각 축간의 관계를 정의할 수 있습니다.

• $$ijk \cdot k = (-1) \cdot k \quad \Rightarrow \quad ij = k \tag{3}$$
• $$i \cdot ijk = i \cdot (-1) \quad \Rightarrow \quad jk = i \tag{4}$$

• 식 (3), (4)를 통해 $ij = k, jk = i$ 임을 확인하였습니다. 뒤에 알아보겠지만 사원수는 교환법칙이 성립하지 않으므로 식 (3), (4)를 다음 식을 유도해 보겠습니다.

• $$jk \cdot i = i \cdot i \quad \Rightarrow \quad j \cdot jki = j \cdot (-1) \tag{5}$$
• $$\therefore ki = j \tag{6}$$

• 따라서 식 (6)과 같이 관계를 정리할 수 있습니다.
• 식 (4), (5), (6) 의 관계를 이용하면 사원수 체계에는 교환 법칙이 성립하지 않음을 알 수 있습니다.
• 아래 식은 사원수에서 결합 법칙이 성립함을 전제로 진행됩니다. 본 글에서 자세한 유도는 생략하겠습니다만 사원수에서 결합 법칙과 분배 법칙은 성립합니다.

• $$j \cdot ij \cdot j = j \cdot k \cdot j \quad \Rightarrow \quad -ji = ij \tag{7}$$
• $$k \cdot jk \cdot k = k \cdot i \cdot k \quad \Rightarrow \quad -kj = jk \tag{8}$$
• $$i \cdot ki \cdot i = i \cdot j \cdot i \quad \Rightarrow \quad -ik = ki \tag{9}$$

• 따라서 위 식과 같이 사원수에서 교환법칙은 성립하지 않으며 식 (7), (8), (9)와 같은 관계를 가집니다.

사원수의 연산

• 지금까지 다룬 사원수에서의 성질을 이용하여 사원수의 덧셈, 뺄셈 곱셈에 대하여 다루어 보겠습니다.
• 사원수는 단순한 4차원 벡터와 유사한 성격을 갖습니다. 따라서 연산 역시 벡터의 연산과 유사한 것이 많습니다.

사원수의 덧셈과 뺼셈

• 우선 사원수의 덧셈을 살펴보도록 하겠습니다. 벡터의 덧셈은 대응되는 성분별로 더하면 됩니다. 두 개의 사원수 $\hat{p}$ 와 $\hat{q}$ 가 각각 $(s_{p}, v_{p})$ 와 $(s_{p}, v_{p})$ 라고 하면 두 사원수의 합은 다음과 같습니다.

• $$\hat{p} + \hat{q} = (s_{p} + s_{q}, v_{p} + v_{q}) \tag{10}$$

• 만약 두 사원수를 $\hat{p} = (a_{p}, b_{p}, c_{p}, d_{p} )$ 와 $\hat{q} = (a_{q}, b_{q}, c_{q}, d_{q} )$ 로 표현한다면 두 사원수의 합은 간단히 다음과 같이 표현할 수 있습니다.

• $$\hat{p} + \hat{q} = (a_{p} + a_{q}, b_{p} + b_{q}, c_{p} + c_{q}, d_{p} + d_{q}) \tag{11}$$

• 뺄셈 또한 덧셈과 같이 성분 별로 이루어집니다.

• $$\hat{p} - \hat{q} = (a_{p} - a_{q}, b_{p} - b_{q}, c_{p} - c_{q}, d_{p} - d_{q}) \tag{12}$$

• 스칼라와 벡터로 나누어 표현하면 다음과 같습니다.

• $$\hat{p} = (s_{p}, v_{p}), \hat{q} = (s_{q}, v_{q}) \tag{13}$$
• $$\hat{p} + \hat{q} = (s_{p} - s_{q}, v_{p} - v_{q}) \tag{14}$$

사원수의 곱셈

• 사원수와 어떤 스칼라 $\lambda$ 를 곱사는 것은 매우 간단합니다. 사원수의 모든 성분에 이 스칼라 값을 곱하면 됩니다. 따라서 사원수의 스칼라 곱은 다음과 같이 표현할 수 있습니다.

• $$\lambda \hat{p} = (\lambda s_{p}, \lambda v_{p}) = (\lambda a_{p}, \lambda b_{p}, \lambda c_{p}, \lambda d_{p}) \tag{15}$$

• 두 사원수 $\hat{p}$ 와 $\hat{q}$ 를 곱하려면 어떻게 해야 할까요? 앞서 말한 바와 같이 사원수는 각각의 기저를 서로 다른 허수 $i, j, k$ 로 보고 벡터 부분의 각 성분은 이 허수에 곱해진 값과 스칼라 부분이 더해져서 얻어지는 복소수로 정의할 수 있습니다.

• $$\hat{p} = d_{p} + a_{p} i + b_{p}j + c_{p}k \tag{16}$$
• $$\hat{q} = d_{q} + a_{q} i + b_{q}j + c_{q}k \tag{17}$$
• $$\hat{p}\hat{q} = (d_{p} + a_{p} i + b_{p}j + c_{p}k)(d_{q} + a_{q} i + b_{q}j + c_{q}k) \tag{18}$$

• 식 (18)을 정리하면 다음과 같습니다.

• 위 식에서 각 단계별 정리 내용은 다음과 같습니다.
• ① → ② : 각 허수 단위 순서로 재배열
• ② → ③ : 두 허수의 곱을 하나의 허수로 표현 (ex. $ij = k$)
• ③ → ④ → ⑤ : 기저 역할의 허수 별로 다시 모아서 정리
• ⑤ → ⑥ : 벡터의 내적과 외적을 이용하여 정리

• 따라서 식 (18)을 정리하면 다음과 같습니다.

• $$\hat{p}\hat{q} = (d_{p}, v_{p})(d_{q}, v_{q}) = (d_{p}d_{q} - v_{p} \cdot v_{q}, d_{p}v_{q} + d_{q}v_{p} + v_{p} \times v_{q}) \tag{19}$$

• 식 (19)의 의미를 이해하기 위해 스칼라와 벡터의 곱으로 내용을 설명해 보도록 하겠습니다.
• 사원수는 스칼라와 벡터로 구성되며 스칼라와 벡터로 이루어진 사원수 둘을 곱하면 역시 스칼라와 벡터로 구성된 새로운 사원수가 나타난다는 것입니다.
• 이렇게 얻은 사원수의 스칼라 부분은 두 사원수가 가진 스칼라 값을 서로 곱한 값에서 두 사원수가 가진 벡터를 내적한 결과를 빼준 것입니다. 내적 결과가 스칼라이므로 이 값은 어려움 없이 구할 수 있습니다.
• 반면 곱셈의 결과로 얻어지는 사원수의 벡터 부분은 두 사원수가 가진 스칼라와 벡터를 이용하여 만들수 있는 벡터들이 합산됩니다. 즉, 각 사원수가 가진 스칼라 값을 상태편의 벡터 부분에 곱하면 두 개의 벡터를 얻을 수 있고 여기에 두 사원수가 가진 벡터를 서로 외적하여 얻는 벡터를 추가로 더하면 됩니다.

사원수의 연산 규칙

사원수와 회전의 관계

사원수의 보간

Vision 관련 글 목차