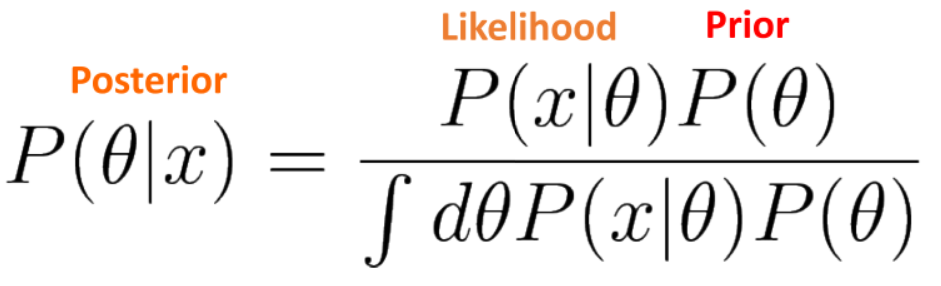
기초 베이지안 이론 (Basic Bayesian Theory)

2020, Aug 09    

머신 러닝 관련 글 목록

• 사전 지식 1 : https://gaussian37.github.io/ml-concept-mle-and-map/
• 사전 지식 2 : https://gaussian37.github.io/ml-concept-mlemap
• 사전 지식 3 : https://gaussian37.github.io/ml-concept-probability_model/
• 사전 지식 4 : https://gaussian37.github.io/ml-concept-basic_information_theory/
• 사전 지식 5 : https://gaussian37.github.io/ml-concept-infomation_theory/

목차

• 베르누이 분포

• 베르누이 분포와 MLE

• MLE의 가정과 문제점

• 베이지안 이론

• Conjugate Prior

• 베이즈 갱신 (Bayes Update)

• 이번 글에서는 동전 던지기 실행을 통해 베이지안 이론을 접근을 하려고 합니다. 동전 던지기 실험을 알아보기 위하여 먼저 베르누이 분포에 대하여 알아보도록 하겠습니다.

베르누이 분포

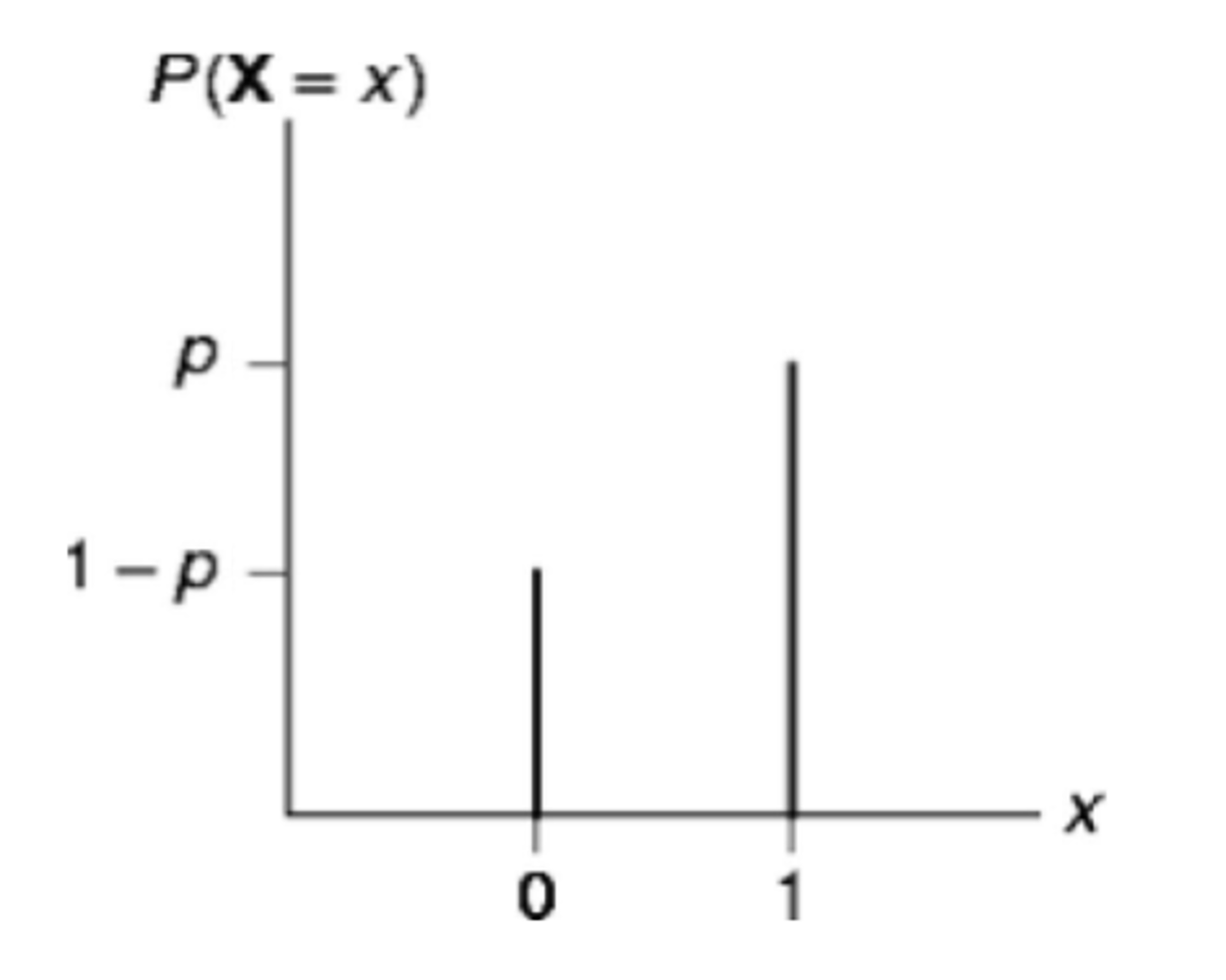
• 베르누이 분포란 확률 이론 및 통계학에서 자주 사용되는 분포로서 동전 전지기의 앞면 또는 뒷면, 입시의 합격과 불합격, 사업의 성공과 실패, 수술 후 환자의 치유 여부 등, 어던 실험이 두 가지 가능한 결과만을 가질 경우 이를 표현하는 확률 모형입니다.

• $$\text{Bernoulli Random Variable : } X \in \{0, 1 \} \tag{1}$$
• $$P(X = 1) = p \tag{2}$$
• $$f(x) = p^{x}(1-p)^{1-x} \tag{3}$$

베르누이 분포와 MLE

• 동전 던지기 실험을 하였을 때, 위 그림처럼 앞/뒤/뒤/뒤/뒤 와 같은 결과를 얻었다고 가정하겠습니다.
• 관측된 데이터로부터, 같은 동전을 던질 때, 앞면이 나타날 확률은 Likelihood를 이용하여 계산합니다.

• $$P(x \vert \theta) = \prod_{i=1}^{5} P(x_{i} \vert \theta) = \theta \cdot (1 - \theta) \cdot (1 - \theta) \cdot (1 - \theta) \cdot (1 - \theta) \tag{4}$$
• $$P(x \vert \theta) : \text{Likelihood}$$
• $$\theta : \text{Parameter}$$

• 식 (4)를 likelihood 즉, $\theta$ 에 대한 함수로 보며 관측된 데이터를 가장 잘 설명하는 파라미터 $\theta$ 를 찾기 위한 MLE(Maximum Likelihood Estimation)을 수행하면 다음과 같습니다. MLE`는 데이터는 고정이고 파라미터만 변경하여 최적의 파라미터를 찾는 문제입니다.
• 아래 식은 MLE를 통해 log-likelihood를 최대화화는 $\theta$ 를 찾는 방법입니다.

• $$\theta_{\text{ML}} = \operatorname*{argmax}_\theta l(\theta) \tag{5}$$
• $$\frac{\partial l(\theta)}{\partial \theta} = \frac{\partial}{\partial \theta}\sum_{i=1}^{5} \log{P(x_{i} ]vert \theta)} \tag{6}$$
• $$= \frac{\partial}{\partial \theta} \log{\theta \cdot (1 - \theta) \cdot (1 - \theta) \cdot (1 - \theta) \cdot (1 - \theta)} \tag{7}$$
• $$= \frac{\partial}{\partial \theta} (\log{\theta} + 4\log{(1 - \theta)}) \tag{8}$$
• $$= \frac{1}{\theta} - \frac{4}{1 - \theta} \tag{9}$$

• 미분한 결과를 정리한 식 (9)가 0이되는 변곡점에서 식의 최댓값을 가지는 $\theta$를 찾을 수 있습니다.

• $$\frac{1}{\theta} - \frac{4}{1 - \theta} = 0 \tag{10}$$

• 식 (10)을 풀면 다음과 같습니다.

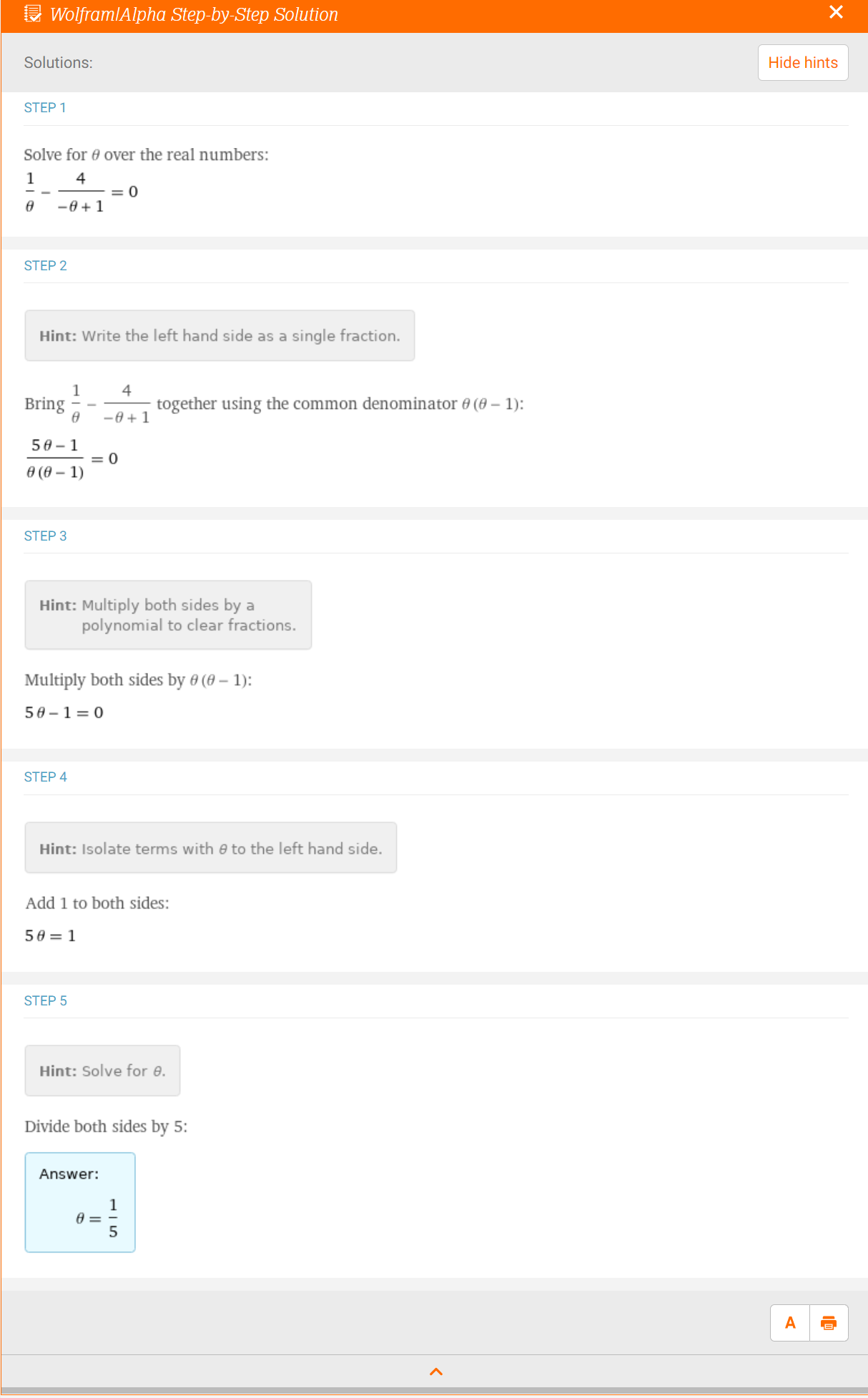
• 즉, 5번 동전을 던졌을 때, 1번 앞면이 나왔으니 앞면이 나올 확률은 1/5일 것이다와 같은 직관적인 생각과 같은 결과가 도출되었습니다.
• 그런데 일반적으로 동전 던지기는 1/2의 확률을 가진다고 알고 있습니다. 5번의 실험을 통해서 관측한 결과와 흔히 알고 있는 동전 던지기를 한 결과의 확률 차이가 크게 나는데 왜 그럴까요?

MLE의 가정과 문제점

• MLE는 asymptotically unbiased 즉, 점진적으로 bias가 없어지는 성질을 가집니다. 여기서 점진적이라는 말의 뜻은 데이터가 점점 더 관측이 된다는 뜻을 말합니다.
• 만약 무한대의 관측 데이터가 주어질 경우 MLE로 예측한 파라미터는 실제 파라미터로 수렴하게 됩니다.
• 하지만 현실적으로 무한대의 관측 데이터를 찾기 어렵고, 제한된 수량의 관측 데이터만 주어진다면 bias한 결과를 얻게 됩니다.

• 앞에서 다룬 동전 던지기 예제에서 과연 5번의 시도만으로 앞면의 확률이 1/5이라고 단정지을 수 있을까요?
• 이 예제에 따르면 MLE는 초기 관측에 쉽게 overfitting하게 됩니다. 극단적으로 동전 던지기를 1번 해서 앞면이 나오면 앞면의 확률이 1이라고 단정지을 수 있을까요?
• 이러한 문제를 개선하기 위하여 베이지안 방식으로 접근할 수 있습니다.

베이지안 이론

• 앞에서 살펴본 MLE에서는 관측된 데이터에 한정하여 Maximum Likelihood를 추정하므로 극단적으로 동전을 던졌을 때, 계속 앞면이 나오면 앞면이 나올 확률을 1로 단정지어 버리는 문제가 발생하였습니다.
• 하지만 우리는 일반적인 동전 던지기의 확률은 0.5인 것을 알고 있습니다. 이러한 사전 정보를 사용하여 확률을 구하고자 하는 것이 베이지안 접근 방식입니다.

• 즉, 경험적으로 동전 던지기에서 앞/뒷면이 나올 확률이 반반인 동전이 많은 것을 알고 있고 파라미터 $\theta$ 에 대해 우리의 경험을 바탕으로한 확률적인 가정 $\theta = 1/2$ 을 더하는 것이 베이지안 접근 방식입니다.
• 베이지안 접근 방식을 사용하면 궁극적으로 알고 싶은 사후 정보를 MLE에서 구하는 Likelihood와 사전 정보인 Prior를 통해 구할 수 있으므로 단순히 Likelihood만을 이용하였을 때, 발생하는 overfitting문제를 개선할 수 있습니다.

Conjugate Prior

• 동전 던지기 문제에 베이지안 접근 방식을 도입하려면, Likelihood, Prior, Posterior를 정의해야 합니다.
• 결론적으로 살펴보면 Likelihood는 Bernoulli distribution이 되고, Prior와 Posterior는 Beta distribution이 됩니다.

• 만약 Bernoulli distribution을 Likelihood로 사용하였을 때, 베이지안 식에서 Prior와 Posterior에 사용될 수 있는 분포는 Beta distribution가 됩니다. 식은 다음과 같습니다.

• $$P(\theta \vert \alpha, \beta) = \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{B(\alpha, \beta)} \tag{11}$$

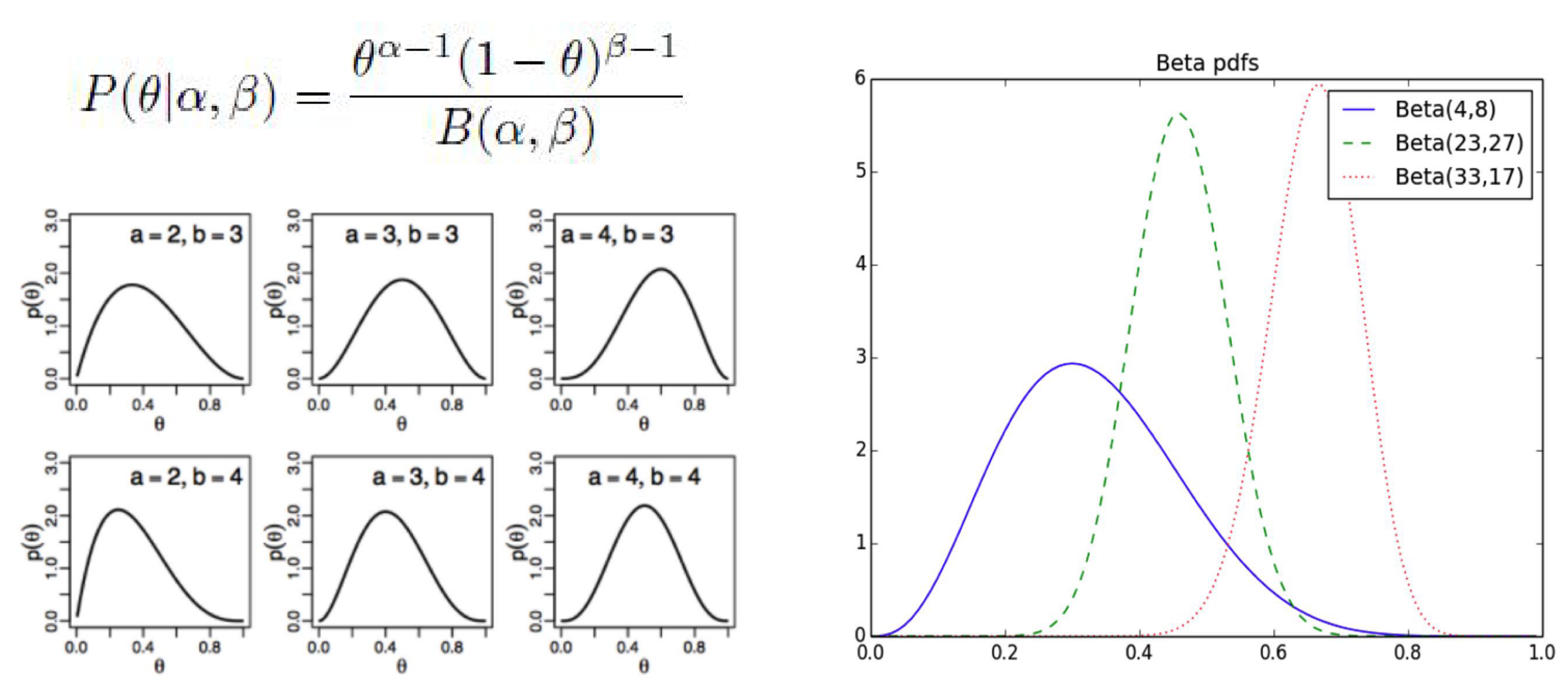
• Beta distribution의 자세한 내용은 다음 링크를 참조해 주시기 바랍니다.
  • 링크 : https://gaussian37.github.io/math-pb-beta-distribution/

• 여기서 Likelihood가 Bernoulli distribution일 때, Prior와 Posterior는 Beta distribution이라고 설명하였습니다.
• 즉, Prior와 Posterior가 Beta distribution이라는 같은 분포를 가진다는 뜻입니다. 이와 같이 Prior와 Posterior가 같은 형태의 분포를 가지는 경우는 특수한 형태이며 이와 같은 쌍을 가질 때, Conjugate Prior라고 부릅니다.
• 이와 같은 Conjugate Prior 관계를 가지는 Prior와 Posterior를 사용하여 식을 전개할 때, 직관적이며 편리한점이 생깁니다.
• 예를 들면 식을 해설할 때, Prior가 Likelihood를 이용하여 확률값을 업데이트하면 Posterior가 되는데, 그 확률 분포의 형태는 같고 파라미터값만 변경되므로 관측값에 따라 확률 분포가 업데이트 되는 것 처럼 해석할 수 있습니다.

• 정리하면, Conjugate prior는 베이즈 룰에 의해 식을 유도하였을 떄, Posterior가 Prior와 같은 distribution 형태를 갖게 하는 prior입니다.

• $$\text{Bayes Theorem : } P(\theta \vert x) = \frac{P(x \vert \theta)P(\theta)}{P(x)} \tag{12}$$
• $$\text{Bernoulli Likelihood : } P(x \vert \theta) = \theta^{x} (1 - \theta)^{1-x} \tag{13}$$
• $$\text{Beta Prior : } P(\theta \vert \alpha, \beta) = \frac{\theta^{\alpha -1}(1 - \theta)^{\beta - 1}}{B(\alpha, \beta)} \tag{14}$$
• $$\text{Posterior : } P(\theta \vert x) = \frac{\theta^{x} (1 - \theta)^{1-x} \theta^{\alpha -1}(1 - \theta)^{\beta - 1}}{P(x)B(\alpha, \beta)} \propto \theta^{\alpha + x -1}(1 - \theta)^{\beta +(1-x)-1} = \text{Beta}(\hat{\alpha}, \hat{\beta}) \tag{15}$$

• 식 (15)를 보면 결국 Prior와 Posterior는 같은 Beta distribution이 되었고 Posterior는 파라미터가 업데이트된 상태가 됩니다.

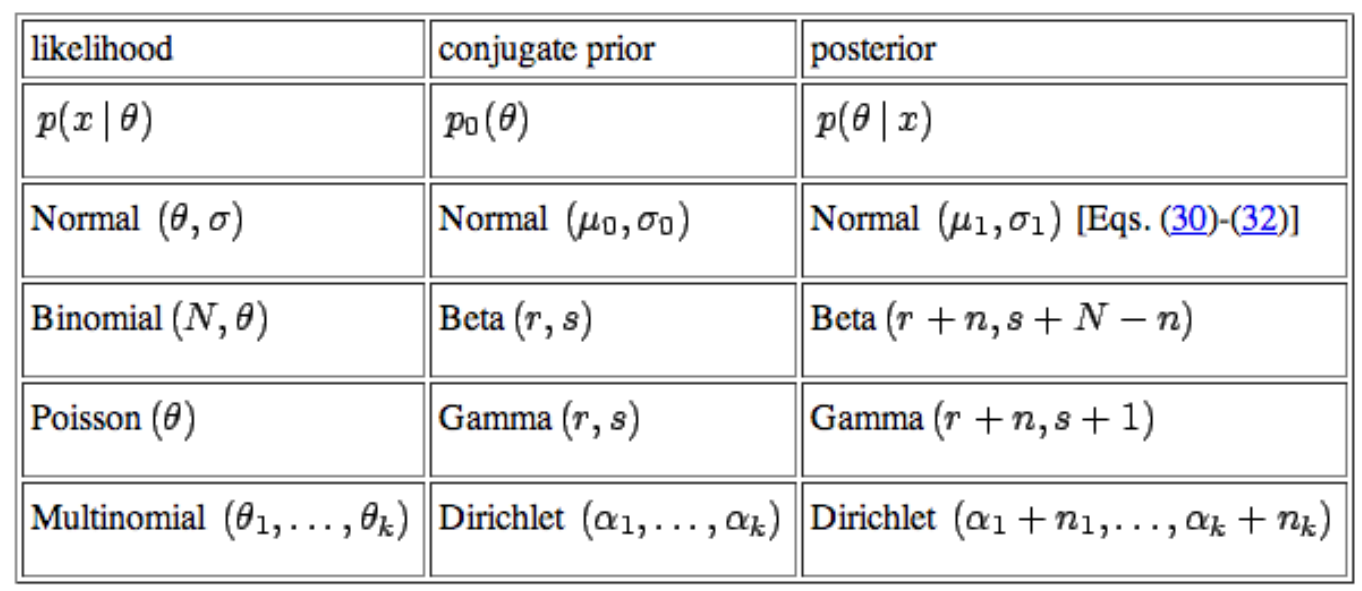
• 흔히 베이지안 룰에서 많이 사용하느 Conjugate prior는 위 식과 같습니다.
• Normal distribution, Binomial distribution, Poisson distribution, Multinomial distribution은 많이 들어본 확률 분포 입니다. 이와 같은 분포는 Prior와 Posterior의 형태가 같은 대표적인 케이습니다.
• 전통적인 베이지안에서는 이와 같은 Conjugate 관계를 중요시하며 이 관계를 통해 recursive하게 Prior와 Posterior를 업데이트 합니다.
• 지금까지 살펴본 케이스는 Bernoulli distribution이었고 이 분포는 Binomial distribution의 형태로 확장될 수 있기 때문에 Binomial과 Beta가 한 쌍을 으루고 있습니다.

• 위 표에서 Bernoulli distribution 대신 표현된 Binomial distribution에 대하여 간략하게 알아보겠습니다. Bernoulli distribution는 어떤 실험이 두 가지 가능한 결과만을 가질 경우 이를 표현하는 확률 모형이었습니다.
• 만약 Random Variable $X$ 가 n번의 연속적인 베르누이 시행이라면 어떻게 표현될 수 있을까요?

• $$X \in \{0, n \}$$
• $$f(x) = P(X = x) = \begin{pmatrix} n \\ x \end{pmatrix} p^{x}(1-p)^{n-x} = \frac{n!}{x!(n-x)!} p^{x}(1-p)^{n-x} \tag{16}$$

• 식 (11)과 같이 연속적인 베르누이 분포를 가지는 확률 분포를 Binomial distribution (이항 분포) 라고 합니다.
• 베르누이 분포와의 차이는 여러번 시행하는 횟수의 차이이므로 Binomial distribution의 최적의 파라미터를 구하는 문제 또한 Likelihood를 구하는 문제가 됩니다. 즉, Likelihood로 사용할 수 있습니다.

베이즈 갱신 (Bayes Update)

• 지금까지 살펴본 개념을 이용하여 Bayes Update를 진행해 보도록 하겠습니다.
• 가장 오른쪽 Prior 그래프는 베타 분포의 예시를 나타냅니다. 초기 Prior는 사전에 가지고 있는 데이터나 주관적인 믿음의 분포를 나타내며 Likelihood를 통해 그 믿음이 update되는 결과가 Posterior가 됩니다.
• 동전 던지기를 할 때, 일반적으로 가지고 있는 Prior는 동전이 앞면이 나올 확률이 1/2 이므로 $theta = 1/2$ 로 정의 됩니다.
• 앞에서 살펴본 바와 같이 실제 5번 동전을 던져서 1번 앞면이 나왔다고 하였을 때, MLE를 구하면 $theta = 1/5$ 가 됩니다.
• 즉, Prior : $theta = 1/2$ 가 MLE : $\theta = 1/5$ 에 의해 업데이트되어 MAP $\1/5 \lt \theta \lt 1/2$ 가 됩니다. MAP (Maximum a Posterior)는 Posterior가 최대인 지점을 의미합니다. MAP의 수식적인 의미를 살펴보면 다음과 같습니다.

• $$\hat{\theta}_{\text{MAP}} = \operatorname*{argmax}_\theta P(\theta \vert X) \tag{17}$$
• $$= \operatorname*{argmax}_\theta \frac{P(X \vert \theta) P(\theta)}{P(X)} \tag{18}$$
• $$= \operatorname*{argmax}_\theta \log{P(X \vert \theta)} + \log{P(\theta)} - \log{P(X)} \tag{19}$$
• $$= \operatorname*{argmax}_\theta \log{P(X \vert \theta)} + \log{P(\theta)} - \require{cancel} \cancel{\log{P(X)}} \tag{20}$$

• 식 (20) 에서 마지막 항은 $\theta$ 가 없으므로 argmax 과정과 무관하여 소거되며 regularization의 의미를 가집니다.
• 정리하면 Posterior는 likelihood를 통해서 Data를 관측하고 정보가 업데이트된 Prior 이며 이를 식으로 나타내면 다음과 같습니다.

• $$P(z) \tag{16}$$
• $$P(z \vert x_{1}) = \frac{}{P(x_{1})} \tag{17}$$
• $$P(z \vert x_{1}, x_{2}) = \frac{P(x_{2} \vert z, x_{1})P(z \vert x_{1})}{P(x_{2} \vert x_{1})} = \frac{ P(x_{2} \vert z) P(z \vert x_{1})}{P(x_{2})} \tag{17}$$
• $$P(z \vert x_{1}, x_{2}, x_{3}) = \frac{P(x_{3} \vert z) P(z \vert x_{1}, x_{2})}{P(x_{3})} \tag{18}$$
• $$P(z \vert X) \tag{19}$$

• 위 식과 같이 step이 진행될수록 $t - 1$ 번째의 Posterior가 $t$ 번째의 Prior가 되며 데이터가 많이 쌓일 수록 Posterior는 정확해 집니다.

• 이번 글에서 알아본 내용을 정리하면 다음과 같습니다.
• 관측된 데이터를 가장 잘 설명하는 파라미터 $\theta$ 즉, 분포를 찾기 위하여 MLE를 사용하였습니다.
• 하지만 제한된 데이터에서는 MLE로는 overfitting이 발생하는 것을 확인하였고 이를 개선하기 위하여 베이지안 룰을 사용하였습니다. 베이즈를 이용하면 prior를 적용할 수 있고 제한된 데이터에서 overfitting을 개선할 수 있으며 데이터가 많아질수록 MLE는 수렴하게됩니다.
• 베이지안 접근법은 파라미터에 확률 분포를 추가적으로 가정한 후 Posterior를 통해서 Optimal Parameter $\theta$ 를 추정하는 MAP 과정을 의미합니다.
• Posterior는 likelihood를 통해서 데이터를 관측하고 정보가 업데이트된 Prior를 의미하며 이 Prior는 재귀적으로 계속 사용이 되어집니다.

머신 러닝 관련 글 목록