이미지의 구면 좌표계 투영법 (Spherical Projection)

Vision 관련 글 목차

• 참조 : https://plaut.github.io/fisheye_tutorial/
• 사전 지식 : 직교 좌표계, 원통 좌표계 및 구면 좌표계
• 사전 지식 : 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습
• 사전 지식 : 카메라 모델과 렌즈 왜곡 (lens distortion)

• 이번 글에서는 구면 좌표계를 이용하여 이미지를 구면 투영법에 적용하는 방법에 대하여 알아보도록 하겠습니다.
• 앞으로 다루는 내용은 직교 좌표계, 원통 좌표계 및 구면 좌표계, 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습, 카메라 모델과 렌즈 왜곡 (lens distortion) 에서 다룬 내용을 기반으로 설명할 예정입니다. 따라서 생략된 용어에 대한 설명은 각 링크를 통해 참조해 주시면 됩니다.
• 최종 코드는 회전을 고려한 World 기준 구면 투영법에서 완성한 코드를 참조하시면 됩니다.

목차

• 구면 투영법 사용 이유

• 카메라 기준 구면 투영법

• 회전을 고려한 카메라 기준 구면 투영법

• 회전을 고려한 World 기준 구면 투영법

• 회전을 고려한 World 기준 구면 투영법의 World-to-Image, Image-to-World

• 회전을 고려한 World 기준 구면 투영법의 기본적인 사용 방법

• 회전을 고려한 World 기준 구면 파노라마 투영법

구면 투영법 사용 이유

• 카메라를 통하여 이미지 데이터를 취득하였을 때, 일반적으로 사용할 수 있는 2가지 방법은 원본 이미지를 사용하는 것과 원근 투영법(Perspective Projection)을 사용하는 것입니다. 이번 글에서 소개하고자 하는 방법은 구면 투영법(Spherical Projection)입니다. 각각의 투영법에 대한 정의와 장단점 및 특성등을 정의해 보면 다음과 같습니다.

• 구면 투영 이미지는 오른쪽 그림과 같은 형태로 투영되며 세계 지도와 같이 구(Sphere) 형태에서 azimuth, elevation의 각도를 격자 단위로 나누고 각 격자를 이미지의 픽셀로 나타낸 것 표현 방식을 의미합니다.

각 투영법의 정의

• ① 원본 이미지
  • ⓐ 정의: 카메라를 통하여 취득한 원본 이미지를 뜻합니다. 원본 이미지에는 카메라 렌즈에 의하여 발생된 왜곡이 영상에 그대로 반영되어 있습니다.
  • ⓑ 각 픽셀의 의미 : 각 픽셀은 렌즈를 통과하는 ray의 비선형 매핑에 해당합니다. 정확한 ray의 방향을 확인하기 위해서는 카메라 캘리브레이션이 필요합니다.
  • ⓒ 장점 : 원본 이미지이므로 영상의 artifact가 존재하지 않으며 fisheye 카메라와 같은 경우에는 넓은 화각 영역을 커버할 수 있는 장점이 있습니다.
  • ⓓ 단점 : 카메라 렌즈에 의해 발생한 왜곡으로 인하여 직선이 곡선으로 나타나는 현상이 발생합니다.
• ② 원근 투영법 (Perspective Projection)
  • ⓐ 정의: 핀홀 카메라 모델을 의미합니다. 핀홀 카메라 모델에서는 직선은 직선 그대로 모양을 가지는 특성이 있습니다.
  • ⓑ 각 픽셀의 의미 : 각 픽셀은 카메라 핀홀에 의해 투사된 ray에 의해 대응되며 원본 이미지와는 다르게 ray의 선형 매핑에 해당합니다.
  • ⓒ 장점 : 실제 직선이 이미지 상에서 그대로 직선 형태로 나타나며 픽셀 매핑 시 선형식을 통한 매핑이 가능하다는 단순함이 있습니다.
  • ⓓ 단점 : 원본 이미지를 원근 투영법 반영 시 이미지의 FOV가 제한적으로 표현됩니다. 특히 넓은 화각을 위한 카메라의 경우 FOV의 손실이 크게 발생할 수 있습니다.
• ③ 구면 투영법 (Spherical Projection)
  • ⓐ 정의: 수평 화각은 최대 360도, 수직 화각은 최대 180도의 구(sphere)에 매핑이 되는 투영법입니다.
  • ⓑ 각 픽셀의 의미 : 각 픽셀은 구에서 각 위치를 나타내는 방법과 동일합니다. 따라서 각 픽셀은 azimuth angle과 elevation angle을 의미합니다.
  • ⓒ 장점 : 실제 3D 공간이 구 형태로 되어 있으므로 실제 3D 환경을 표현하기에 용이 합니다. 따라서 VR 등에서도 구면 투영법을 통한 영상 투영을 사용하기도 합니다.
  • ⓓ 단점 : 구의 양쪽 극단에서 왜곡이 발생할 수 있습니다.
• ④ 원통 투영법 (Cylindrical Projection)
  • ⓐ 정의: 수직 원통에 이미지가 투영된 다음에 원통의 옆면이 펴진 형태의 투영법입니다.
  • ⓑ 각 픽셀의 의미 : 각 픽셀은 azimuth angle과 원통의 높이에 대응됩니다. 원본 이미지나 원근 투영법에서는 각 픽셀이 ray에 대응된 반면 원통 투영법에는 각 픽셀이 실제 원통을 구성하는 azimuth angle과 높이에 대응된다는 차이가 있습니다.
  • ⓒ 장점 : 최대 360도 까지의 수평 화각을 커버할 수 있도록 설계할 수 있습니다. 원통 기둥을 생각해 보면 이 점을 이해할 수 있을 것입니다. 원통을 모델링하여 표현하기 때문에 수직 방향으로는 왜곡이 보정이 되는 장점도 존재합니다. 따라서 수직 방향의 직선은 직선 형태로 나타내어 집니다.
  • ⓓ 단점 : 수직 화각을 표현하는 데 제한이 생기고 원통의 수직 방향으로 양쪽 끝지점에서 왜곡이 생기거나 불균일하게 샘플링 됩니다.

• 이번 글에서는 구면 투영법을 적용하는 방법을 단계적으로 살펴보고 그 성질에 대하여 살펴보도록 하겠습니다. 구면 투영법을 사용하는 근본적인 이유는 다음 4가지 효과를 얻기 위해서 입니다.
• ① azimuth, elevation (+ distance)로 좌표를 나타내었을 때, 효과를 얻을 수 있는 상황에서 이미지 데이터를 이용하기 위함입니다.
• ② 멀티 카메라 환경에서 특정 구(sphere)를 기준으로 영상을 생성하기 위함입니다. 기준이 되는 구가 존재하고 그 구를 기준으로 원본 영상이 구에 투영되기 때문에 멀티 카메라 환경을 구성하기 유리합니다. 예를 들어 각 나라별 이미지 사진들을 여러개 보는 것 보다 구글 어스를 이용하는 것이 더 효과적인 것과 유사합니다.
• ③ 다양한 스펙의 카메라 영상을 하나의 기준으로 생성할 수 있기 때문에 카메라 간 영상의 차이를 줄일 수 있습니다. 이 부분은 ②와도 연관되어 있습니다. 구면 투영법에서는 ⓐ 카메라 수직/수평 화각, ⓑ 픽셀 증가에 따른 azimuth, elevation의 변화량 \(\Delta\phi, \Delta\theta\) ⓒ 카메라 포즈 등이 정해지면 그 기준에 맞춰서 영상을 생성할 수 있습니다. 만약 카메라 왜곡 보정 시, 정보의 손실이나 다른 문제가 발생한다면 구면 투영법을 고려해 보는것도 좋은 방법일 수 있습니다. 카메라 스펙이 다르더라도 최종 생성된 이미지 픽셀의 의미가 같다면 영상이 매우 유사해지고 카메라의 포즈를 맞춘다면 카메라 장착 시 발생할 수 있는 카메라 장착 차이도 개선할 수 있기 때문입니다.
• ④ 영상 내의 소실선(vanishing line)은 카메라의 방향에 영향을 받습니다. 카메라 장착 시 달라질 수 있는 Rotation을 항상 일관성 있게 맞춘다면 영상 내의 소실선을 같은 방향으로 유지할 수 있습니다. How Do Neural Networks See Depth in Single Images의 연구 결과 및 알려진 바와 같이 단안 카메라에서의 뎁스 추정은 지면과의 관계가 중요하기 때문에 지면의 위치와 관련 있는 소실점 및 소실선의 위치를 고정하는 것은 뎁스 추정에 도움이 될 수 있습니다.

• 구면 투영법은 ① 카메라 좌표계 기준에서 투영하는 방법과 ② World 좌표계 기준에서 투영하는 방법이 존재합니다.
• 카메라 좌표계 기준 구면 투영법은 기본적으로 카메라가 바라보는 방향과 3차원 좌표계의 좌표축이 동일하다는 관점에서 구면 투영법을 진행합니다. 반면 World 좌표계 기준 구면 투영법은 World 좌표계의 좌표축을 기준으로 구면 투영법을 진행하기 때문에 카메라와 World 좌표계 간의 Extrinsic 중 Rotation의 관계를 고려해야 합니다. 즉, 이 방법을 이용하면 한 개의 World 좌표계 기준으로 여러개의 카메라를 구면 투영할 수 있고 각 카메라의 기준이 동일한 World 좌표계이기 때문에 파노라마 뷰를 생성할 수 있습니다. 따라서 카메라 좌표계 기준 구면 투영법은 카메라의 Intrinsic만 사용하는 반면 World 좌표계 기준 구면 투영법은 카메라의 Intrinsic, 과 Extrinsic의 Rotation을 사용합니다.

• 먼저 아래 그림들을 통하여 카메라 좌표계 기준과 World 좌표계 기준의 차이를 살펴보도록 하겠습니다.

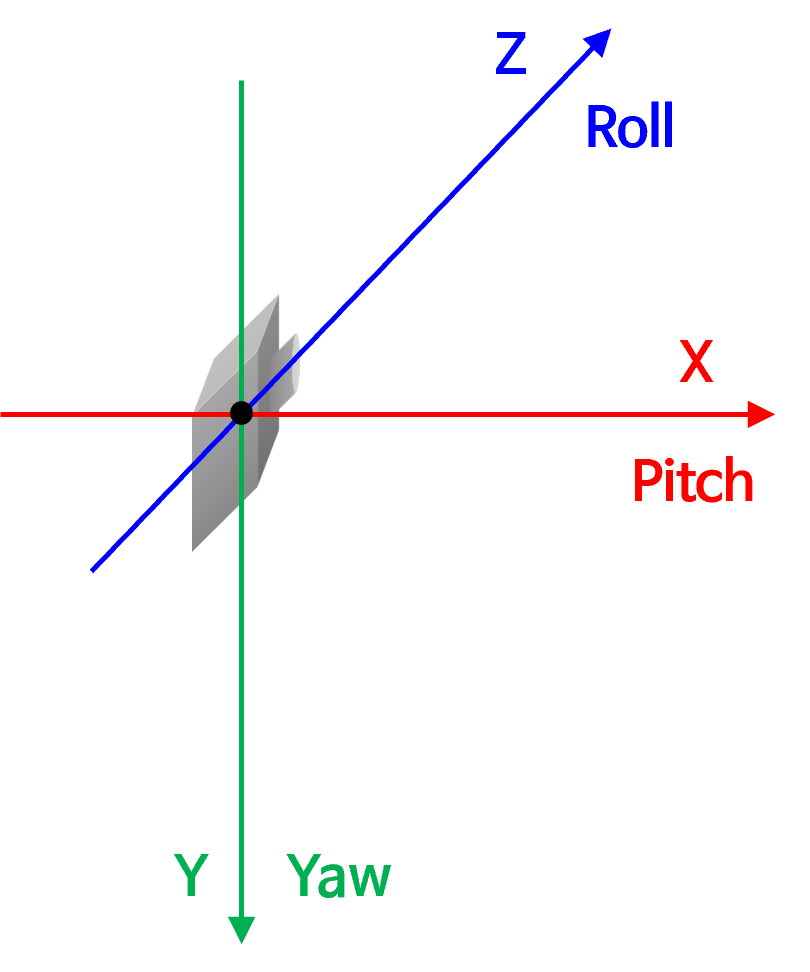
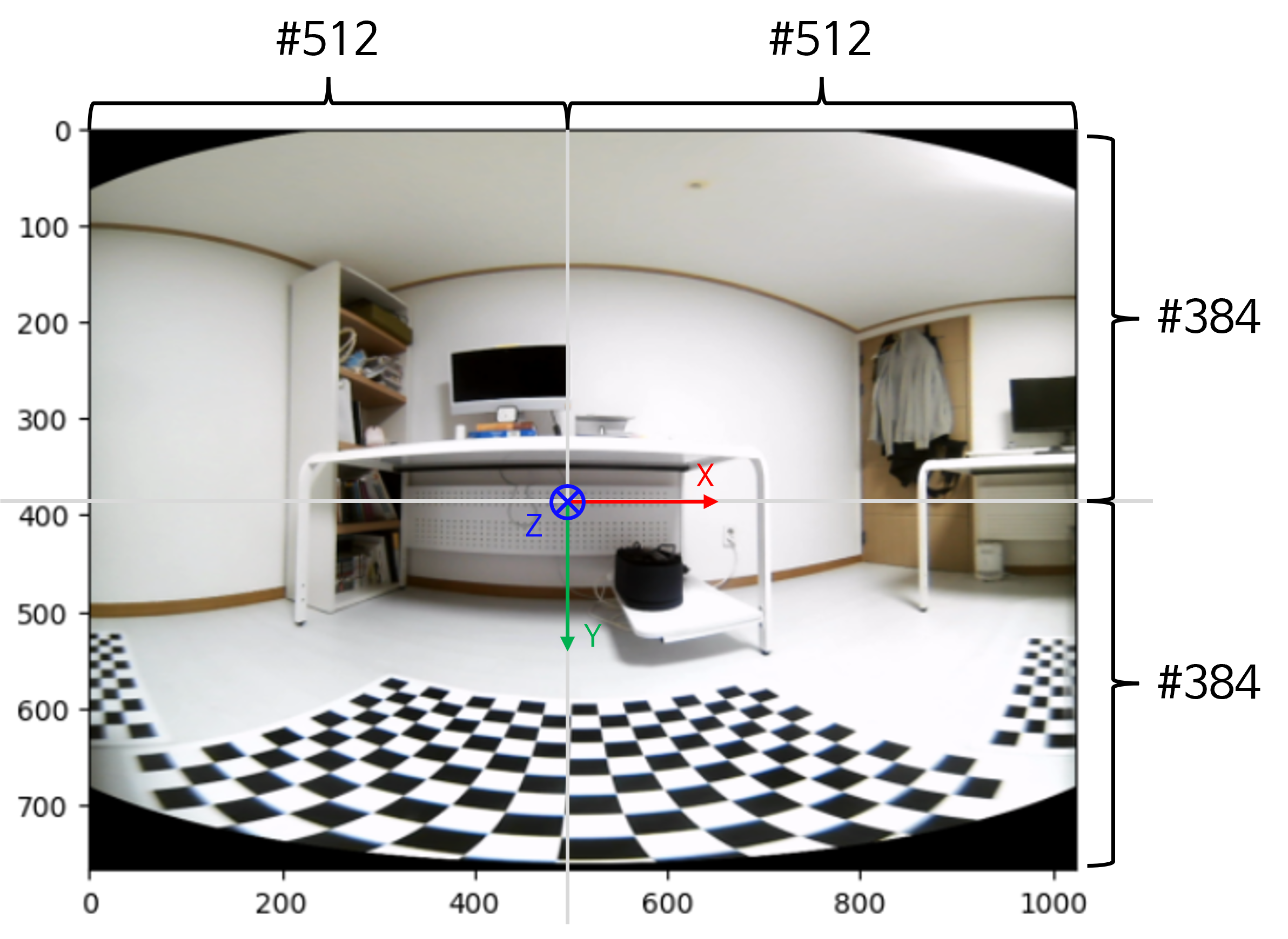
• 위 그림은 카메라 좌표계 기준의 그림을 나타냅니다. 카메라 좌표계에서 사용하는 RDF(Right-Down-Forward)축과 카메라가 바라보는 방향이 일치하는 것을 알 수 있습니다. 일반적으로 카메라 좌표계에서 \(X\) 축은 Right, \(Y\) 축은 Down 그리고 \(Z\) 축은 Forward를 나타내기 때문입니다.

• 반면 World 좌표계 기준 구면 투영법을 적용할 때에는 3차원 좌표축이 카메라 좌표축과는 별개로 존재합니다. 먼저 현재 사용되는 카메라가 사전에 계산된 Rotation(Extrinsic)을 통하여 좌표축과 어떤 관계에 있는 지 계산한 뒤 구면 투영을 한다는 점에서 차이가 있습니다. 따라서 World 좌표계 기준 구면 투영에서는 카메라의 Extrinsic 중 Rotation과 카메라 Intrinsic을 필요로 합니다.

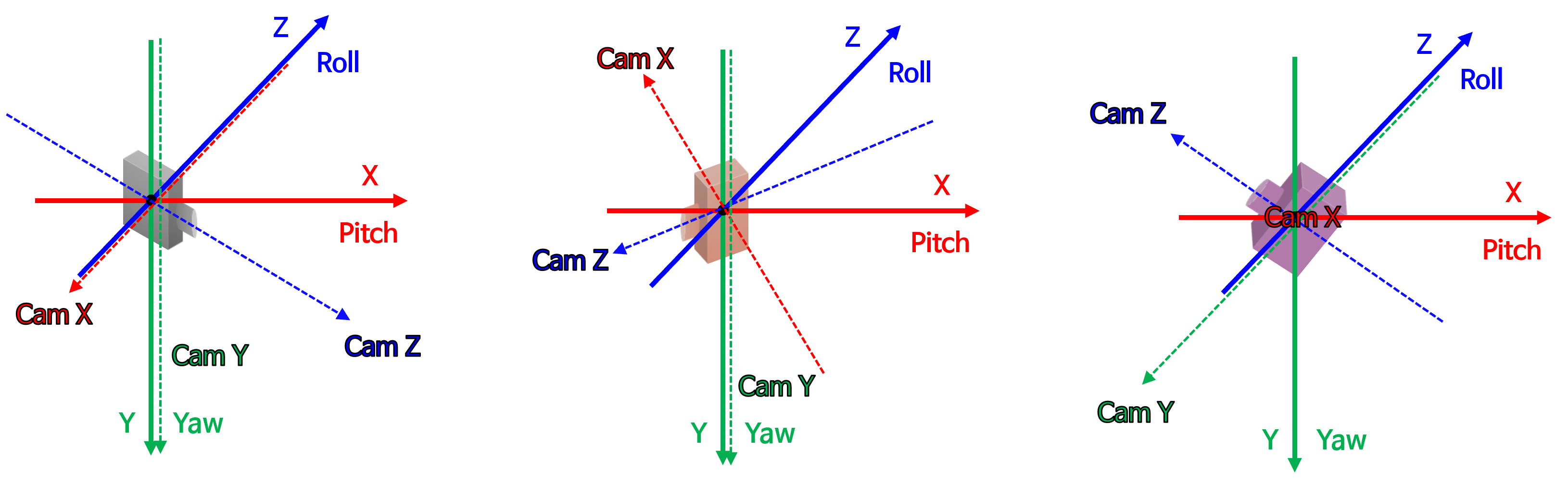
• 위 그림에는 3개의 카메라가 존재합니다. 각 카메라는 서로 다른 방향을 바라보고 있습니다. 반면 실선 화살표로 표시된 좌표축은 동일한 방향을 가리킵니다. 이 실선 화살표는 World 기준의 좌표축을 의미합니다. 반면 점선 화살표는 각 카메라 좌표계를 나타냅니다.
• World 기준의 구면 투영법을 사용하는 이유는 다수의 카메라 영상을 동일한 좌표축 기준으로 영상을 생성할 수 있다는 장점이 있기 때문입니다. 이와 같은 사용법은 멀티 카메라 환경에서 이미지를 사용하거나 생성할 때 도움이 됩니다. 각 카메라의 영상을 구면 투영할 때, 하나의 좌표축 기준으로 생성할 수 있으므로 실제 카메라가 장착된 각도를 고려하여 영상을 투영할 수 있고 더 나아가 360도 환경의 파노라마 이미지를 고려할 수 있기 때문입니다.

• 위 내용을 고려하여 본 글에서는 다음 순서로 구면 투영하는 방법을 살펴볼 예정입니다.
• ① 카메라 기준 구면 투영법: 이미지를 단순히 구면 좌표계로 투영하는 방법을 의미합니다. 이 과정에서 구면 좌표계로 영상을 투영하는 원리를 이해할 수 있 습니다. 이 단계에서 카메라 중심축과 구면 좌표계 중심축의 방향이 일치합니다.
• ② 회전을 고려한 카메라 기준 구면 투영법: 카메라가 바라보는 방향이 roll, pitch, yaw 각 방향으로 회전이 발생한 상황을 고려합니다. 이와 같이 카메라 자세에 회전이 발생하였을 때 구면 좌표계로 투영하는 방법을 이해해 보려고 합니다. 이 방법을 이용하면 임의의 방향으로 카메라가 회전하였을 때 영상을 만들어낼 수 있습니다.
• ③ 회전을 고려한 World 기준 구면 투영법: 구면 좌표계의 roll, pitch, yaw의 기준이 카메라 중심축이 아닌 외부의 World 좌표가 기준이 된다는 점에서 ②와 차이점이 있습니다.
• ④ 앞에서 다룬 내용을 이용하여 회전을 고려한 World 기준 구면 투영법에서 Image-to-World와 World-to-Image에 대하여 다루어 보고 멀티 카메라 이미지를 이용하여 Topivew 생성을 통해 World 좌표계와 구면 좌표계 간의 관계를 명확히 이해해보도록 하겠습니다.
• ⑤ 회전을 고려한 World 기준 구면 파노라마 투영법: ③의 개념을 확장하여 복수개의 카메라를 하나의 구면 좌표 공간으로 투영하는 방법을 다루어 보겠습니다.

카메라 기준 구면 투영법

• 본 글을 이해하기 위해서는 아래 사전 지식의 직교 좌표계와 구면 좌표계의 관계에 대한 명확한 이해가 필요합니다. 아래 글을 먼저 읽고 본문 내용을 읽어 보시는 것을 추천드립니다.
• 사전 지식 : 직교 좌표계, 원통 좌표계 및 구면 좌표계

• 본 글에서 사용할 샘플 데이터의 링크 및 설명은 아래를 참조하시면 됩니다.
  • 데이터셋 링크: https://drive.google.com/drive/folders/15cnXNjEaztZl0CBT25oCaJ9-8qyfRYAw?usp=drive_link
  • 데이터 관련 설명: 링크

• 카메라 기준 구면 투영법은 이미지를 단순히 구면 좌표계로 투영하는 방법을 의미합니다. 따라서 카메라 중심축과 구면 좌표계의 중심축 방향이 일치합니다. 아래 구면 좌표계를 참조하시면 됩니다.

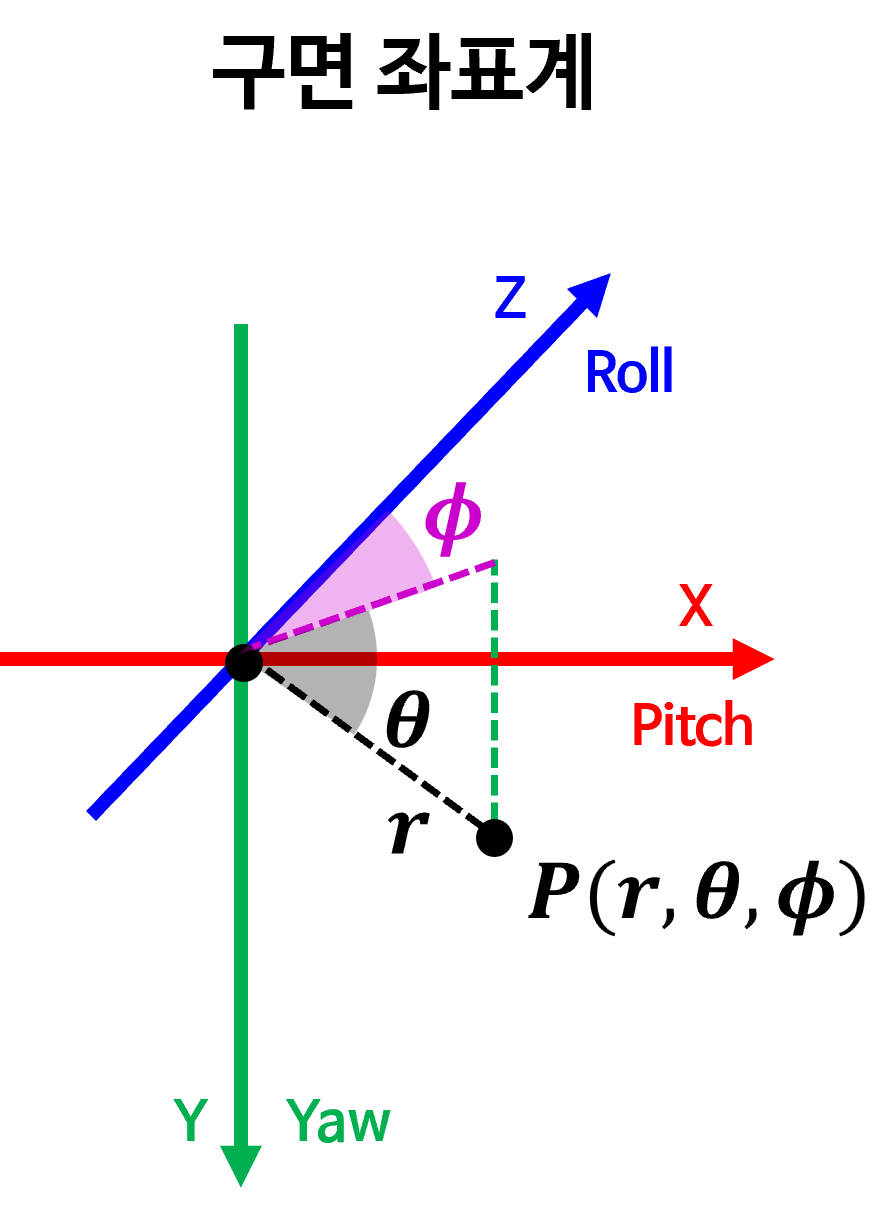
• 위 구면 좌표계는 RDF(Right-Down-Forward) 좌표축으로 정의되었으며 카메라 좌표계와 축의 방향을 일치시키기 위함입니다.

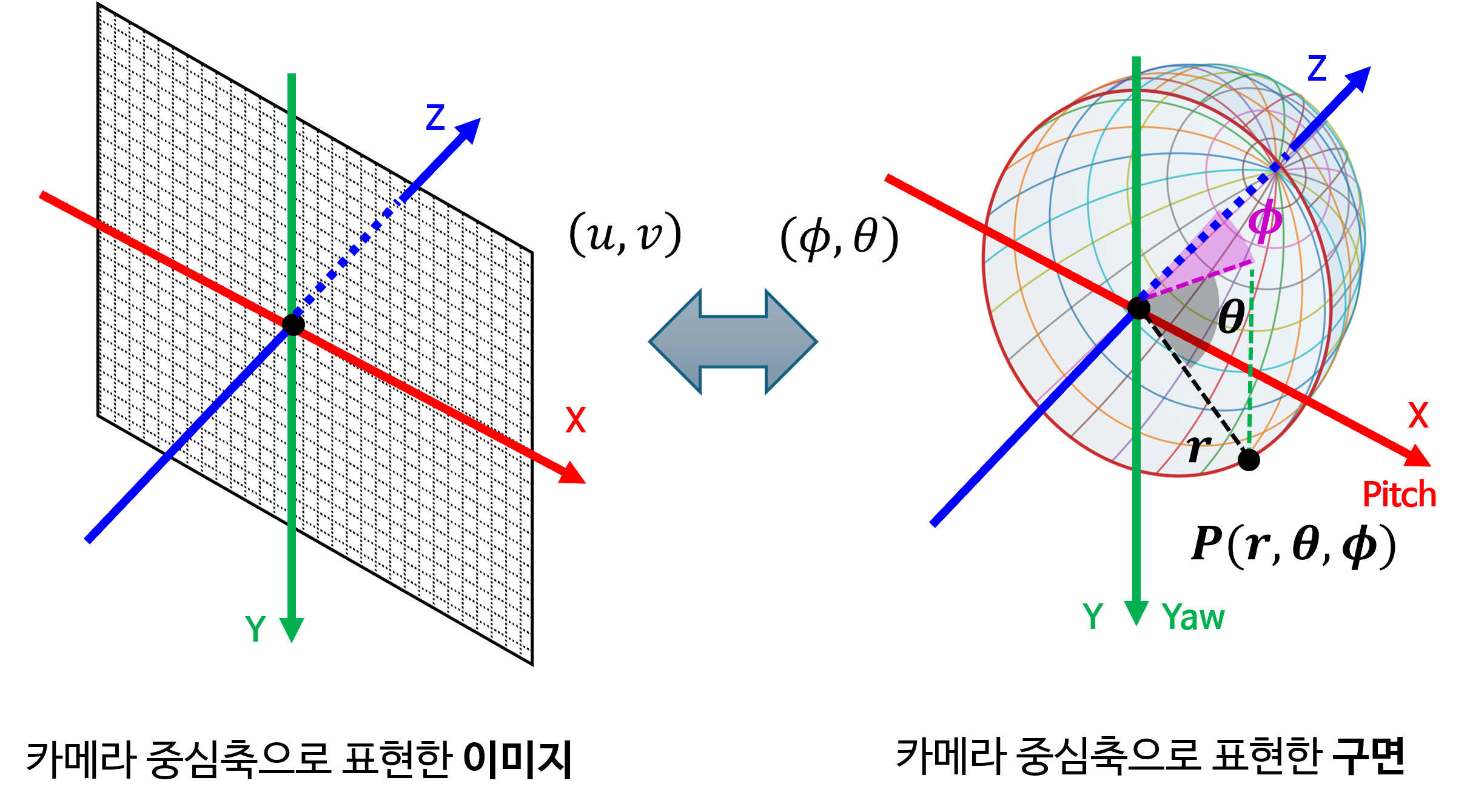
• 위 그림의 왼쪽은 카메라 중심축 기준으로 표현한 직교 좌표계 상의 이미지이고 오른쪽은 구면 좌표계 상에 존재하는 구면을 표현한 것입니다.
• 구면 투영을 위하여 필요한 정보는 왼쪽 이미지의 \((u, v)\) 좌표와 오른쪽 구면에 존재하는 \((\phi, \theta)\) 좌표를 대응 시키는 방법입니다.

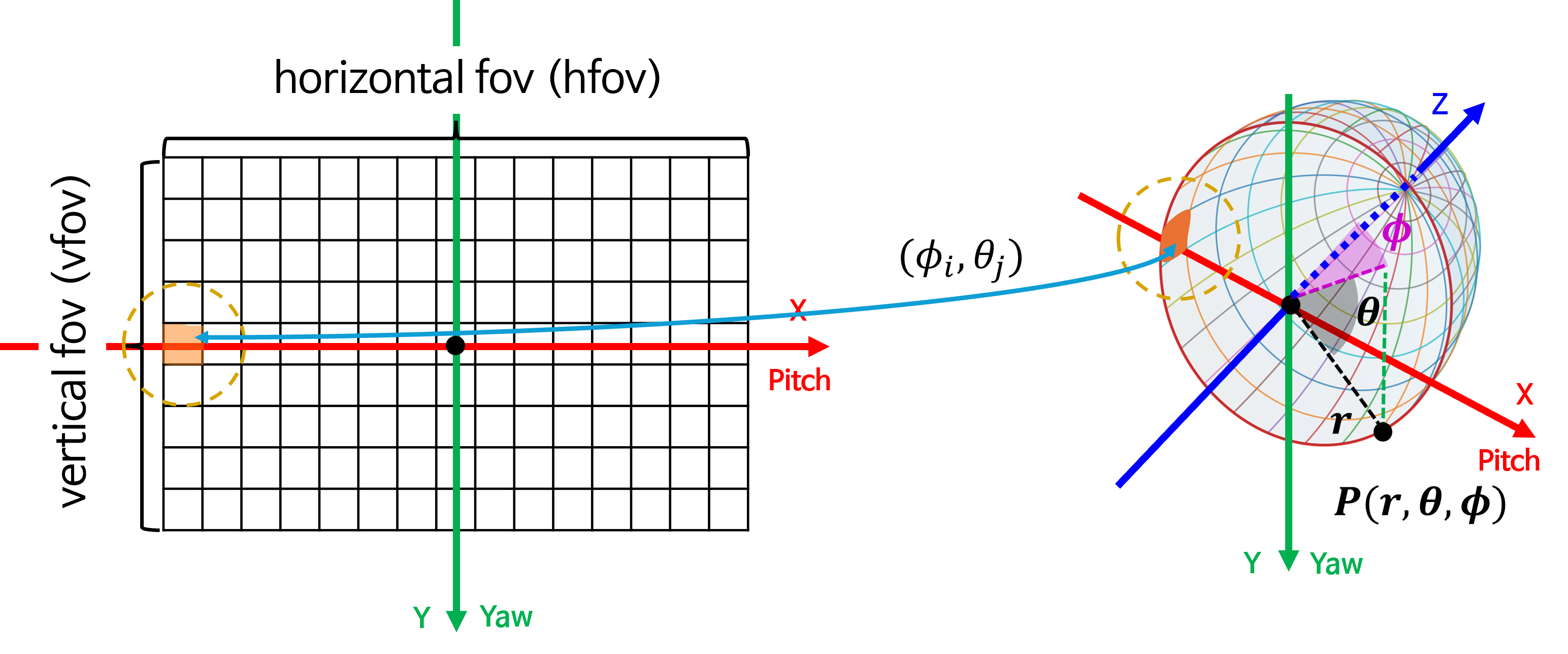
• 실제 의미는 구면을 다루는 것이지만 이미지 데이터나 구면 좌표로 투영된 이미지를 다룰 때에는 행렬로 나타내어야 하기 때문에 평면 이미지를 다루게 됩니다. 따라서 앞으로 생성할 이미지는 비록 직사각형의 이미지이지만 의미론적으로는 구면을 생각해 주시면 됩니다.
• 위 그림을 살펴보겠습니다. 왼쪽 그림의 이미지 각 픽셀은 구면 좌표계에서 azimuth와 elevation을 뜻하는 \((\phi_{i}, \theta_{j})\) 입니다. 따라서 의미적으로는 오른쪽 그림에서의 각 분할된 면과 대응될 수 있습니다. 위 그림에서 주황색으로 표시된 픽셀 및 작은 면적이 의미적으로 대응된다는 것을 이해하면 됩니다.
• 따라서 구면 투영을 거쳐 원본 이미지의 \((u, v)\) 좌표가 구면 투영 이미지의 \((\phi, \theta)\) 좌표에 대응되면 아래 그림과 같은 관계를 가집니다.

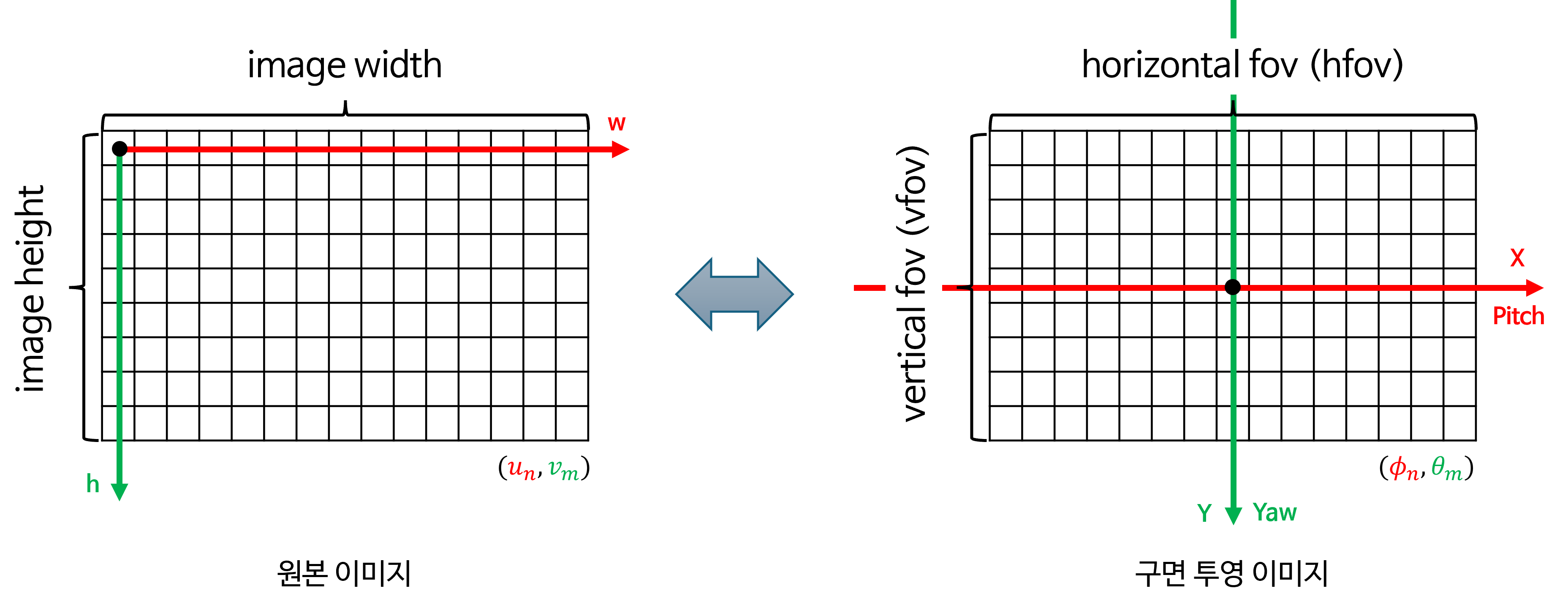
• 즉, 구면 투영법의 핵심은 원본 이미지의 임의의 픽셀 좌표 \((u_{n}, v_{m})\) 과 구면 투영 이미지의 픽셀 좌표 \((\phi_{i}, \theta_{j})\) 의 1:1 매핑 방법입니다.
• 원본 이미지 또는 구면 투영 이미지에서 이미지 생성 직전 단계인 normalized 좌표에서 두 이미지의 차이를 살펴보겠습니다.

• 위 예시에서는 카메라 중심축과 구면 좌표계 중심축 방향이 일치하기 때문에 구면 투영 이미지의 중점에서 \(\phi = 0, \theta = 0\) 임을 알 수 있습니다. 구면 투영 이미지 및 구면 좌표계에서 오른쪽 방향으로 \(\phi\) (azimuth)가 증가하고 아래쪽 방향으로 \(\theta\) (elevation)이 증가합니다.
• 원본 이미지는 기존에 많이 사용하는 직교 좌표계를 이용하고 본 글에서 다루는 구면 투영 이미지는 구면 좌표계를 사용하기 때문에 위 그림과 같이 \(X, Y\) 좌표축의 방향은 같더라도 각 좌표가 의미하는 값은 달라지게 됩니다.

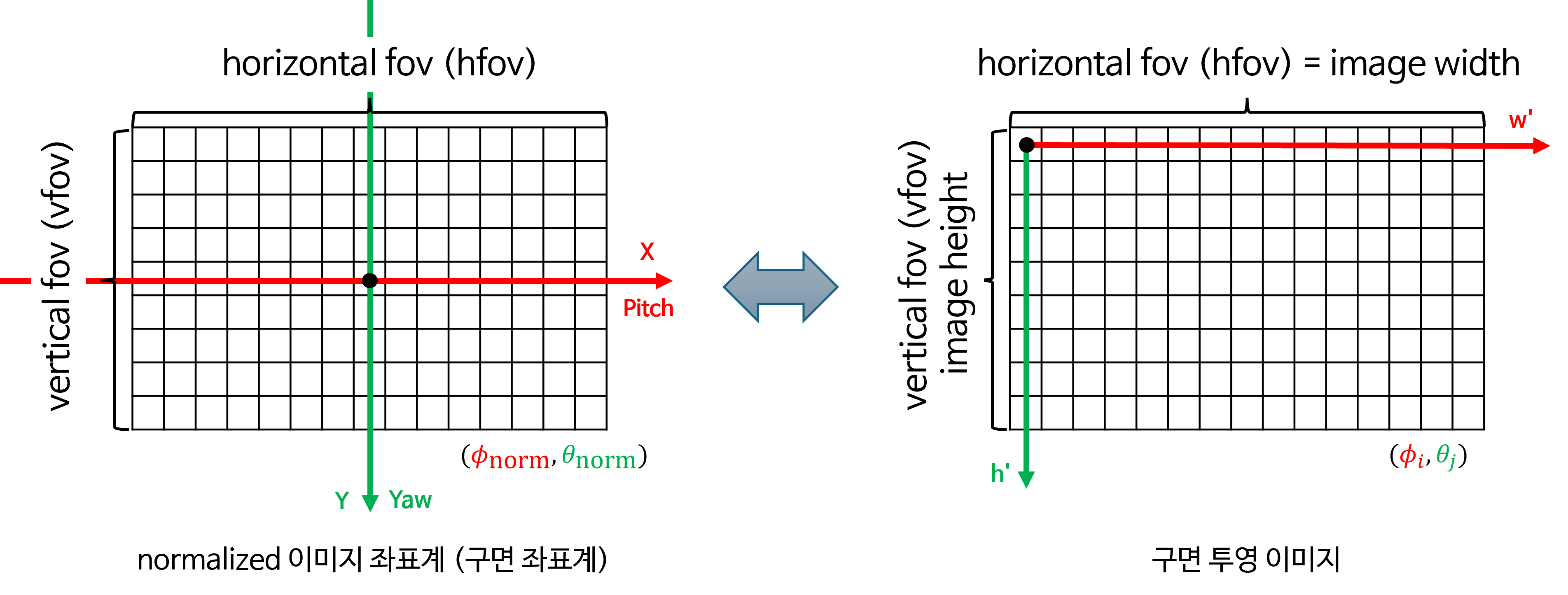
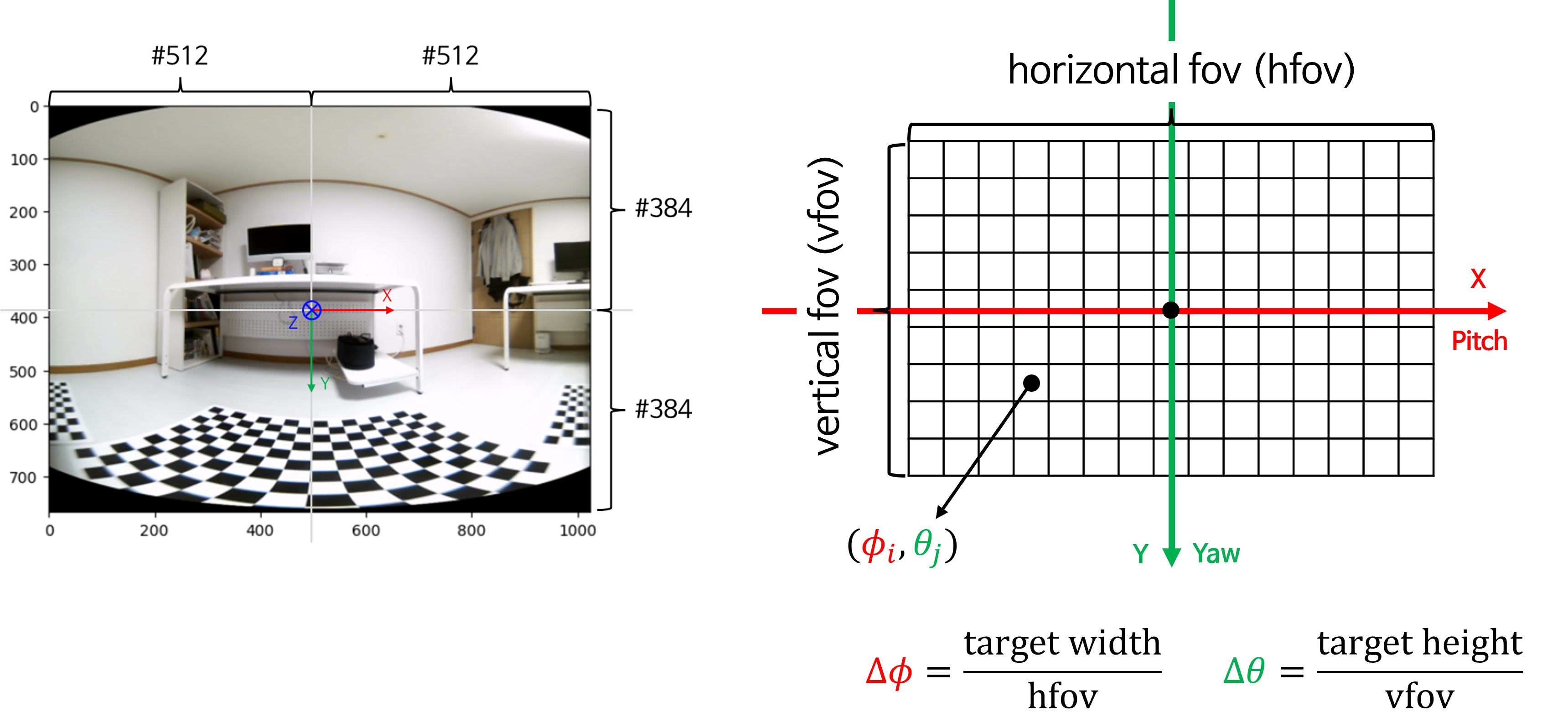
• 위 그림에서 hfov(horizontal fov)는 구면 투영 이미지의 수평 화각입니다. hfov는 원점을 중심으로 좌우 대칭으로 화각을 설정할 때, 최대 몇 화각까지 볼 지 결정합니다. 예를들어 hfov가 120도이면 구면 좌표계 중심 기준 좌/우 각각 60도씩 수평 화각을 가집니다. 이와 같은 논리로 vfov(vertical fov) 또한 존재합니다. (좌/우 또는 상/하를 비대칭으로 설계할 수도 있지만 본 글에서는 대칭 화각으로 설계할 예정입니다.)
• 구면 투영 이미지에서 가로축인 hfov를 구성하는 픽셀이 W개이면 가로축으로 1픽셀 증가(우측으로 한 칸)할 때 마다 hfov / W 만큼 화각이 증가합니다. 같은 논리로 세로축인 vfov를 구성하는 픽셀이 H개이면 세로축으로 1픽셀 증가(아래쪽으로 한 칸)할 때 마다 vfov / H 만큼 화각이 증가합니다.
• 앞에서 살펴본 구면 투영법 사용 이유에서 카메라 화각과 \(\Delta \phi, \Delta \theta\) 에 맞추어서 영상이 생성된다는 것이 위 내용에 대응됩니다.

• 지금부터 살펴볼 모든 내용은 구면 투영 이미지에서 표현해야 할 모든 \((\phi_{i}, \theta_{j})\) 위치에 대한 색상 정보를 원본 이미지의 어떤 픽셀 좌표 \((u_{n}, v_{m})\) 에서 가져와야 할 지 찾는 과정입니다. 이 과정을 통해 LUT(Look Up Table)를 만들고 LUT를 통해 원본 이미지를 구면 투영 이미지로 쉽게 변환하는 과정을 코드로 살펴보려고 합니다.

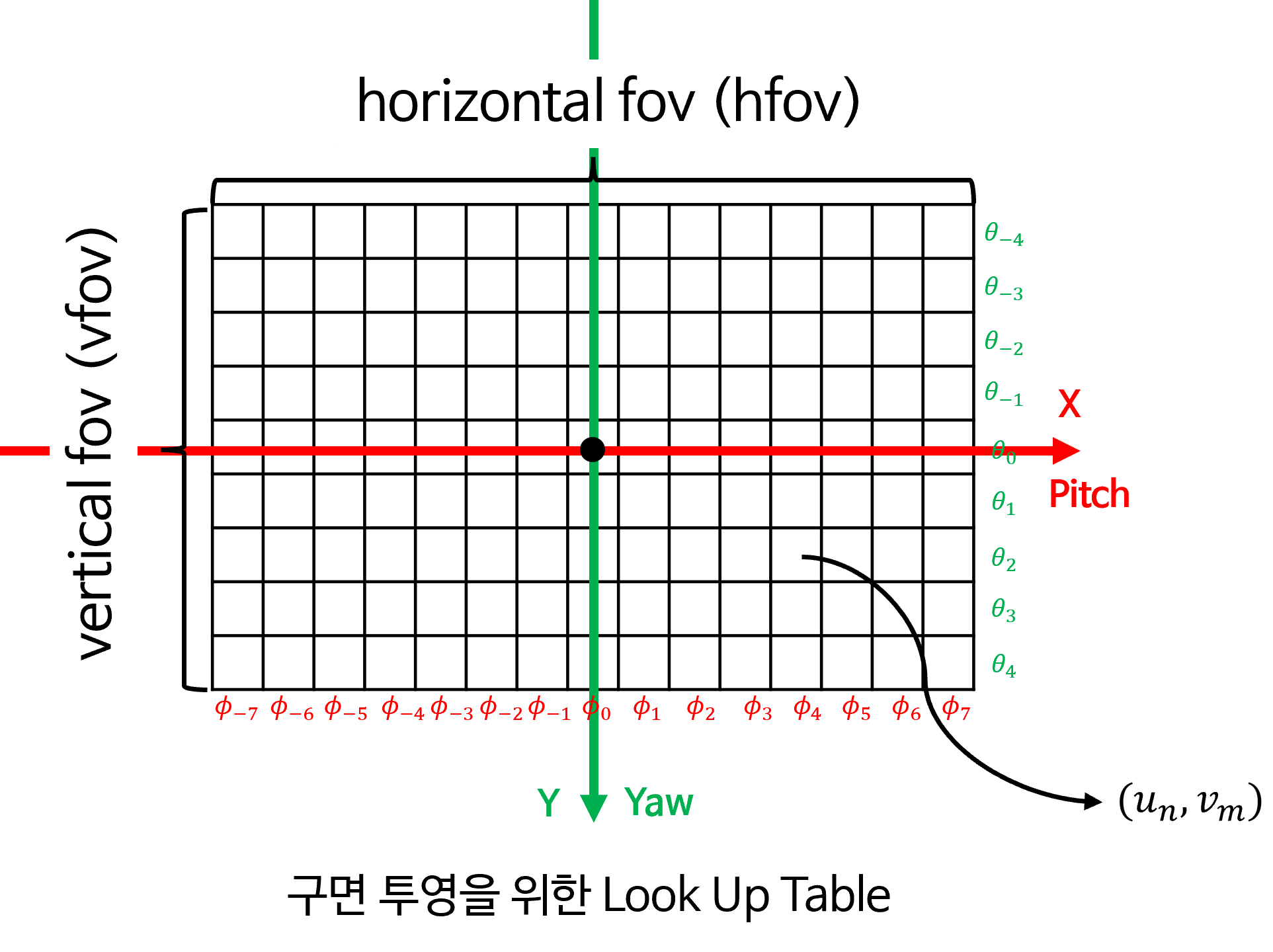
• 따라서 LUT는 위 그림과 같이 모든 \((\phi_{i}, \theta_{j})\) 픽셀에 대하여 대응되는 원본 이미지의 좌표 \((u_{n}, v_{m})\) 의 값을 저장해야 합니다.
• 즉, \((\phi_{i}, \theta_{j})\) 와 일대일 대응이 되는 \((u_{n}, v_{m})\) 을 찾아야 하므로 다음과 같은 순서로 접근을 해야 합니다. 전체적인 순서는 backward mapping으로 최종 생성하고자 하는 구면 투영 이미지의 좌표값인 \((\phi_{i}, \theta_{j})\) 에서 부터 원본 이미지의 좌표값인 \((u_{n}, v_{m})\) 로 접근하는 과정을 아래에 차례대로 소개합니다.
  • ① 구면 투영 이미지: 최종적으로 생성하고자 하는 구면으로 정의된 이미지의 픽셀 좌표를 의미합니다.
  • ② normalized 구면 좌표: 구면 투영 이미지 각 픽셀 좌표값을 normalized 공간으로 변환한 값을 의미합니다. 원본 이미지에 접근 하기 위한 중간 과정이며 구면 좌표계를 사용합니다.
  • ③ normalized 직교 좌표: 원본 이미지 각 픽셀 좌표값의 normalized 공간을 의미합니다. 직교 좌표계를 사용합니다.
  • ④ 원본 이미지: 원본 이미지를 의미하며 구면 투영 이미지에서 사용할 RGB 값을 가져올 때 사용 됩니다.

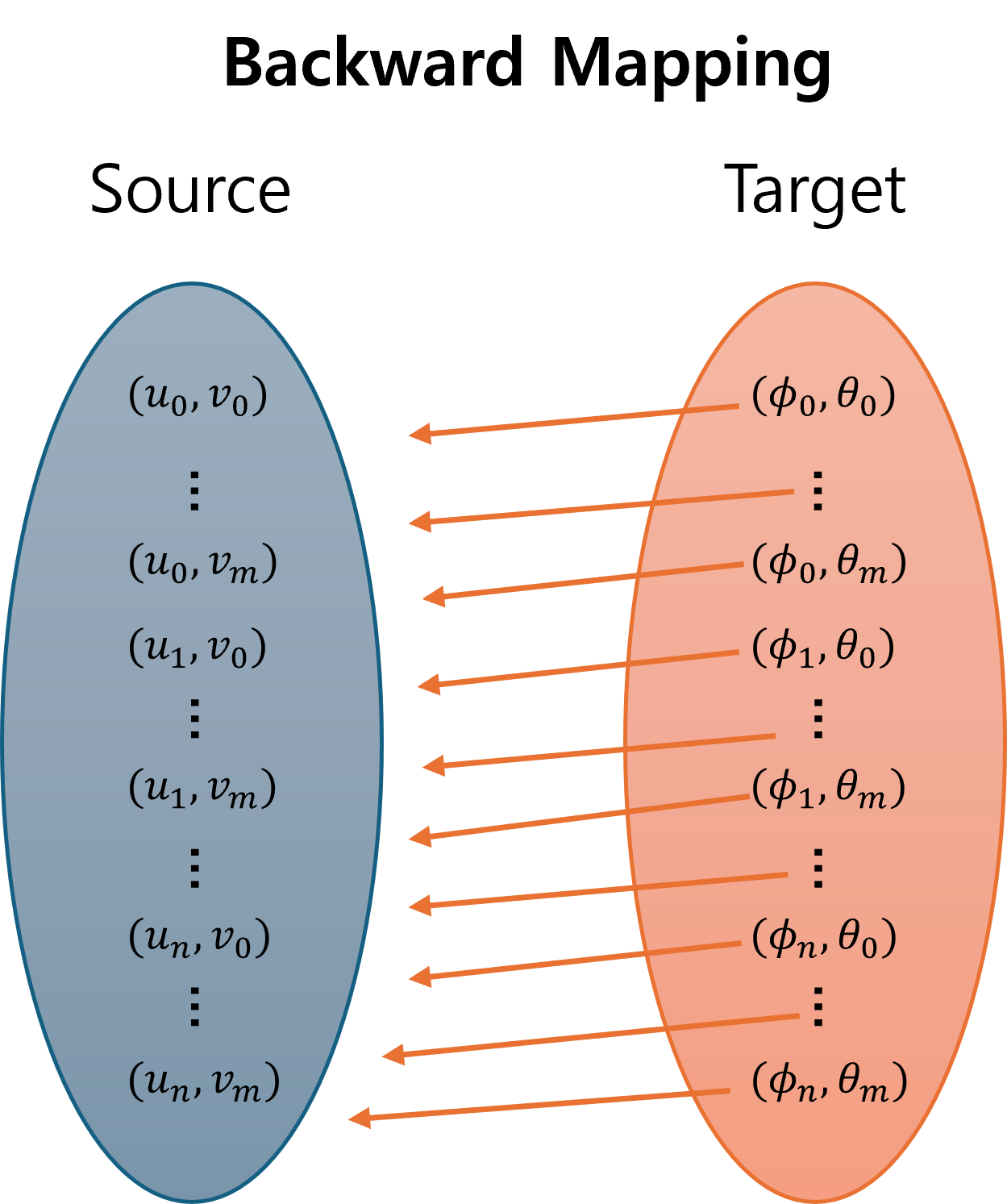
• 위 그림과 같이 backward mapping 방법은 최종 생성하고자 하는 target 공간을(위 예시에서는 구면 투영 이미지) 정의하고 target 공간에서 부터 역으로 참조하고자 하는 source 공간까지 차례대로 접근하여 target을 채우기 위해서 source의 어디를 접근하면 되는 지 매핑하는 과정을 의미합니다. 이와 같은 방법을 사용하면 target 공간을 빈틈없이 채울 수 있는 장점이 존재하여 이미지 생성 시 주로 사용하고 있습니다. 반대로 forward mapping을 이용하면 source 공간에서 시작하여 target 공간까지 접근하게 되므로 target 공간에 매핑이 되지 않는 좌표들이 발생할 수 있는 문제가 발생하므로 이미지 생성때에는 사용하지 않습니다.
• 위 그림에서 target의 모든 좌표 위치에서 화살표가 source로 향하기 때문에 target의 모든 값은 source에 접근하여 매핑이 가능한 상태입니다. 어떤 source값은 중복되어 선택될 수도 있습니다. target과 source가 일대일 대응이 아닌 target → source로의 일대일 함수이기 때문에 backward mapping을 사용합니다.

• 각 단계 별로 더 자세하게 살펴보도록 하겠습니다.
• ① 구면 투영 이미지에서 최종 생성해야 하는 이미지의 공간을 정의해 놓고 이 이미지의 \((\phi_{i}, \theta_{j})\) 와 대응되는 ④ 이미지의 \((u_{n}, v_{m})\) 를 매핑 시키는 작업을 해야 합니다. ②, ③ 은 중간 과정으로 거쳐야 하는 공간입니다.
• normalized 공간에 대한 정의는 아래 글에서 확인해 보시기 바랍니다.
  • 사전 지식 : 카메라 모델 및 카메라 캘리브레이션의 이해와 Python 실습
  • 사전 지식 : 카메라 모델과 렌즈 왜곡 (lens distortion)

• LUT를 만들기 위한 시작은 가상의 이미지 공간 생성입니다. 위 그림과 같은 LUT 사이즈의 이미지를 생성한다고 가정해 보겠습니다.

• 생성할 구면 투영 이미지의 가로 사이즈를 target_width, 세로 사이즈를 target_height로 정의하고 생성할 이미지의 라디안 단위의 가로 화각을 hfov, 세로 화각을 vfov라고 정의한다면 생성할 이미지의 각 픽셀 한 칸의 의미는 다음과 같습니다.

• \[\Delta \phi_{\text{pixel}} = \frac{\text{target width}}{\text{hfov}}\]
• \[\Delta \theta_{\text{pixel}} = \frac{\text{target height}}{\text{vfov}}\]

• ② normalized 구면 투영 이미지 → ① 구면 투영 이미지 로 변환하기 위한 intrinsic 행렬은 다음과 같이 정의할 수 있습니다.

• \[\text{new K} = \begin{bmatrix} f_{x} & \text{skew} & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} \frac{\text{target width}}{\text{hfov}} & 0 & \frac{\text{target width}}{2} \\ 0 & \frac{\text{target height}}{\text{vfov}} & \frac{\text{target height}}{2} \\ 0 & 0 & 1 \end{bmatrix}\]

• 각 픽셀 당 \(\Delta \phi_{\text{pixel}}, \quad \Delta \theta_{\text{pixel}}\) 의 비율 만큼 증가하므로 intrinsic에서 사용되는 \(f_{x} = \Delta \phi_{\text{pixel}}, \quad f_{y} = \Delta \theta_{\text{pixel}}\) 에 대응됩니다. 그리고 principal point은 \(c_{x} = \frac{\text{target width}}{2}, \quad c_{y} = \frac{\text{target height}}{2}\) 에 대응됩니다. 즉, \(c_{x} = \frac{\text{target width}}{2}, \quad c_{y} = \frac{\text{target height}}{2}\) 를 통해 생성하고자 하는 가상 이미지의 중심에 해당하는 \(\phi, \theta\) 가 정해지면 좌/우, 상/하 화각이 대칭이 되도록 배치합니다.
• 새롭게 생성되는 구면 투영 이미지의 intrinsic인 \(\text{new K}\) 는 이와 같은 방법으로 생성됩니다.

• 가상의 구면 투영 이미지의 픽셀 좌표는 다음과 같이 생성합니다.

# xv : (target_height, target_width), yv : (target_height, target_width)
xv, yv = np.meshgrid(range(target_width), range(target_height), indexing='xy')

# p.shape : (3, #target_height, #target_width)
p = np.stack([xv, yv, np.ones_like(xv)])  # pixel homogeneous coordinates
# p.shape : (#target_height, #target_width, 3, 1)
p = p.transpose(1, 2, 0)[:, :, :, np.newaxis] # [u, v, 1]
'''
- p[:, : 0, :] : 0, 1, 2, ..., W-1
- p[:, : 1, :] : 0, 1, 2, ..., H-1    
- p[:, : 2, :] : 1, 1, 1, ..., 1
'''

• 위 과정을 통하여 ① 구면 투영 이미지의 모든 좌표들을 생성합니다.

• 다음 과정을 통하여 ① 구면 투영 이미지의 모든 좌표값들을 ② normalized 구면 좌표로 변경합니다.

# hfov_deg: 0 ~ 360
# vfov_deg: 0 ~ 180
# 구면 투영 시 생성할 azimuth/elevation 각도 범위
# hfov: azimuth
# vfov: elevation
hfov=np.deg2rad(hfov_deg)
vfov=np.deg2rad(vfov_deg)
    
# 구면 투영 시, normalized → image 로 적용하기 위한 intrinsic 행렬
new_K = np.array([
    [target_width/hfov,       0,                     target_width/2],
    [0,                       target_height/vfov,    target_height/2],
    [0,                       0,                     1]
], dtype=np.float32)

new_K_inv = np.linalg.inv(new_K)

# p_norm.shape : (#target_height, #target_width, 3, 1)
p_norm = new_K_inv @ p  # r is in normalized coordinate

'''
p_norm[:, :, 0, :]. phi (azimuthal angle. horizontal) : -hfov/2 ~ hov/2
p_norm[:, :, 1, :]. theta (elevation angla. vertical) : -vfov/2 ~ vfov/2
p_norm[:, :, 2, :]. 1.    
'''

• 다음으로 ② normalized 구면 좌표 → ③ normalized 직교 좌표로 변경합니다. \(\phi, \theta\) 를 이용하여 \(x, y, z\) 의 직교 좌표계로 변경하는 과정에 해당합니다.
• 다음 과정은 아래 링크의 내용을 사전에 이해해야 합니다.
  • 사전 지식 : 직교 좌표계, 원통 좌표계 및 구면 좌표계

# azimuthal angle
phi = p_norm[:, :, 0]
# elevation angle
theta = p_norm[:, :, 1]   

RDF_cartesian = np.zeros(p_norm.shape).astype(np.float32)

# x, y, z : cartesian coordinate in camera coordinate system (RDF, Right-Down-Forward)
# hemisphere
x =np.cos(theta)*np.sin(phi) # -1 ~ 1
y =np.sin(theta) # -1 ~ 1
z =np.cos(theta)*np.cos(phi) # 0 ~ 1

RDF_cartesian[:,:,0,:]=x
RDF_cartesian[:,:,1,:]=y
RDF_cartesian[:,:,2,:]=z    

# x_un, y_un, z_un: (target_height, target_width)
x_un = RDF_cartesian[:, :, 0, 0]
y_un = RDF_cartesian[:, :, 1, 0]
z_un = RDF_cartesian[:, :, 2, 0]

• 마지막으로 ③ normalized 직교 좌표 → ④ 원본 이미지로 변경하는 과정입니다. 이 과정을 통하여 ① 에서 정의한 구면 투영 이미지의 좌표를 원본 이미지의 좌표들과 대응시킬 수 있으므로 LUT를 생성할 수 있습니다. 여기서 사용하는 LUT는 구면 투영 이미지에서 원본 이미지의 색상 정보를 접근하기 위한 backward 매핑을 의미합니다.
• 아래 코드에서 카메라 모델을 이용한 렌즈 왜곡을 반영한 부분은 아래 링크를 참조하시기 바랍니다.
  • 링크: https://gaussian37.github.io/vision-concept-lens_distortion/

theta = np.arccos(z_un / np.sqrt(x_un**2 + y_un**2 + z_un**2))
mask = theta > np.pi/2

# project the ray onto the fisheye image according to the fisheye model and intrinsic calibration
r_dn = D[0]*theta + D[1]*theta**3 + D[2]*theta**5 + D[3]*theta**7 + D[4]*theta**9

r_un = np.sqrt(x_un**2 + y_un**2)

x_dn = r_dn * x_un / (r_un + 1e-6) # horizontal
y_dn = r_dn * y_un / (r_un + 1e-6) # vertical    

map_x_origin2new = K[0][0]*x_dn + K[0][1]*y_dn + K[0][2]
map_y_origin2new = K[1][1]*y_dn + K[1][2]

map_x_origin2new[mask] = DEFAULT_OUT_VALUE
map_y_origin2new[mask] = DEFAULT_OUT_VALUE

map_x_origin2new = map_x_origin2new.astype(np.float32)
map_y_origin2new = map_y_origin2new.astype(np.float32)

import json
import cv2
import numpy as np
import matplotlib.pyplot as plt

def get_camera_spherical_lut(
    K, D, origin_width, origin_height, target_width, target_height, hfov_deg, vfov_deg, DEFAULT_OUT_VALUE=-1):
    
    '''
    - K : (3, 3) intrinsic matrix
    - D : (5, ) distortion coefficient
    - origin_width, origin_height: input image size
    - target_width, target_height: output image size
    - hfov_deg: 0 ~ 360
    - vfov_deg: 0 ~ 180
    '''

    # 구면 투영 시 생성할 azimuth/elevation 각도 범위
    # hfov: azimuth
    # vfov: elevation
    hfov=np.deg2rad(hfov_deg)
    vfov=np.deg2rad(vfov_deg)
    
    # 구면 투영 시, normalized → image 로 적용하기 위한 intrinsic 행렬
    new_K = np.array([
        [target_width/hfov,       0,                     target_width/2],
        [0,                       target_height/vfov,    target_height/2],
        [0,                       0,                     1]
    ], dtype=np.float32)
    
    new_K_inv = np.linalg.inv(new_K)
    
    # Create pixel grid and compute a ray for every pixel
    # xv : (target_height, target_width), yv : (target_height, target_width)
    xv, yv = np.meshgrid(range(target_width), range(target_height), indexing='xy')
    
    # p.shape : (3, #target_height, #target_width)
    p = np.stack([xv, yv, np.ones_like(xv)])  # pixel homogeneous coordinates    
    # p.shape : (#target_height, #target_width, 3, 1)    
    p = p.transpose(1, 2, 0)[:, :, :, np.newaxis] # [u, v, 1]
    '''
    p.shape : (H, W, 3, 1)
    p[:, : 0, :] : 0, 1, 2, ..., W-1
    p[:, : 1, :] : 0, 1, 2, ..., H-1    
    p[:, : 2, :] : 1, 1, 1, ..., 1
    '''
    # p_norm.shape : (#target_height, #target_width, 3, 1)
    p_norm = new_K_inv @ p  # r is in normalized coordinate
    
    '''
    p_norm[:, :, 0, :]. phi (azimuthal angle. horizontal) : -hfov/2 ~ hov/2
    p_norm[:, :, 1, :]. theta (elevation angla. vertical) : -vfov/2 ~ vfov/2
    p_norm[:, :, 2, :]. 1.    
    '''
    # azimuthal angle
    phi = p_norm[:, :, 0]
    # elevation angle
    theta = p_norm[:, :, 1]   
    
    RDF_cartesian = np.zeros(p_norm.shape).astype(np.float32)
    
    # x, y, z : cartesian coordinate in camera coordinate system (RDF, Right-Down-Forward)
    # hemisphere
    x =np.cos(theta)*np.sin(phi) # -1 ~ 1
    y =np.sin(theta) # -1 ~ 1
    z =np.cos(theta)*np.cos(phi) # 0 ~ 1
    
    RDF_cartesian[:,:,0,:]=x
    RDF_cartesian[:,:,1,:]=y
    RDF_cartesian[:,:,2,:]=z    
    
    # x_un, y_un, z_un: (target_height, target_width)
    x_un = RDF_cartesian[:, :, 0, 0]
    y_un = RDF_cartesian[:, :, 1, 0]
    z_un = RDF_cartesian[:, :, 2, 0]
    
    theta = np.arccos(z_un / np.sqrt(x_un**2 + y_un**2 + z_un**2))
    
    mask = theta > np.pi/2

    # project the ray onto the fisheye image according to the fisheye model and intrinsic calibration
    r_dn = D[0]*theta + D[1]*theta**3 + D[2]*theta**5 + D[3]*theta**7 + D[4]*theta**9
    
    r_un = np.sqrt(x_un**2 + y_un**2)
    
    x_dn = r_dn * x_un / (r_un + 1e-6) # horizontal
    y_dn = r_dn * y_un / (r_un + 1e-6) # vertical    
    
    map_x_origin2new = K[0][0]*x_dn + K[0][1]*y_dn + K[0][2]
    map_y_origin2new = K[1][1]*y_dn + K[1][2]
    
    map_x_origin2new[mask] = DEFAULT_OUT_VALUE
    map_y_origin2new[mask] = DEFAULT_OUT_VALUE
    
    map_x_origin2new = map_x_origin2new.astype(np.float32)
    map_y_origin2new = map_y_origin2new.astype(np.float32)
    
    return map_x_origin2new, map_y_origin2new

calib = json.load(open("camera_calibration.json", "r"))
image = cv2.cvtColor(cv2.imread("front_fisheye_camera.png", -1), cv2.COLOR_BGR2RGB)

origin_height, origin_width, _ = image.shape
target_height, target_width  = origin_height//2, origin_width//2
hfov_deg = 180
vfov_deg = 150

K = np.array(calib['front_fisheye_camera']['Intrinsic']['K']).reshape(3, 3)
D = np.array(calib['front_fisheye_camera']['Intrinsic']['D'])

map_x, map_y = get_camera_spherical_lut(K, D, origin_width, origin_height, target_width, target_height, hfov_deg=hfov_deg, vfov_deg=vfov_deg)
new_image = cv2.remap(image, map_x, map_y, interpolation=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=(0, 0, 0))
plt.imshow(new_image)

• 위 코드를 통하여 왼쪽의 원본 이미지를 오른쪽의 구면 투영 이미지와 같이 변경할 수 있습니다. 구면 투영 이미지는 원본 이미지의 절반 사이즈로 생성하였습니다.

• 앞에서 설명한 바와 같이 \(\color{red}{X}\) 가 증가하는 방향으로 \(\phi\) (azimuth)가 증가합니다. normalized 구면 좌표관점에서 생각하면 \(\phi\) 는 우측 방향으로 최대 \(\text{hfov} / 2\) 만큼 커지고 좌측 방향으로 최소 \(-\text{hfov} / 2\) 만큼 작아집니다.
• 마찬가지로 \(\color{green}{Y}\) 가 증가하는 방향으로 \(\theta\) (elevation)이 증가합니다. normalized 구면 좌표관점에서 생각하면 아래 방향으로 최대 \(\text{vfov} / 2\) 만큼 커지고 윗 방향으로 최소 \(-\text{vfov} / 2\) 만큼 작아집니다.
• new_K를 생성하였을 때, 정의한 \(c_{x}, c_{y}\) 로 인하여 \(\phi, \theta\) 에 대한 배치가 좌/우, 상/하 대칭이 되도록 이미지를 생성하였습니다.

• 내용을 정리하면 위 그림과 같습니다. 직교 좌표계에 정의된 원본 이미지를 구면 좌표계로 변환하기 위해서는 \(\text{target height}, \text{target width}, \text{hfov}, \text{vfov}\) 가 정의 되어야 합니다. 그리고 각 이미지 픽셀 \(\phi_{i}, \theta{j}\) 의 의미는 구면 좌표계에서 정의된 azimuth, elevation를 뜻합니다.
• 지금까지 모든 과정을 다시 정리하면 ① 의 좌표에서 시작하여 ④ 까지 차례대로 변환하여 LUT를 만들었습니다.
  • ① 구면 투영 이미지
  • ② normalized 구면 좌표
  • ③ normalized 직교 좌표
  • ④ 원본 이미지

회전을 고려한 카메라 기준 구면 투영법

• 앞에서 살펴본 내용에서는 구면 좌표 축에 회전이 없는 상태로 구면 투영 이미지를 생성하였습니다. 앞에서 살펴본 4가지 단계를 차례대로 보면 좌표계 변환만 있었을 뿐, 추가적인 회전을 적용하는 단계가 없었습니다.
• 만약 Roll, Pitch, Yaw 축의 각 방향에 Rotation을 적용하여 구면 투영 이미지를 생성한다면 어떻게 생성할 수 있을까요? 이와 같이 이미지를 생성한다면 카메라의 장착이 회전되었을 때를 고려하여 이미지를 생성할 수 있습니다. 이 방법에 대하여 살펴보도록 하겠습니다.

• 먼저 카메라 좌표계 기준에서 roll, pitch, yaw를 변환하는 방법은 아래와 같습니다.
• 카메라 좌표계 또는 RDF 좌표계에서는 \(X\) 축 회전이 pitch 회전에 대응되고, \(Y\) 축 회전이 yaw 회전, \(Z\) 축 회전이 roll 회전에 대응됩니다. 각 좌표축에서 양의 방향으로 회전 시 축의 방향이 반시계 방향으로 회전하도록 설정하겠습니다.

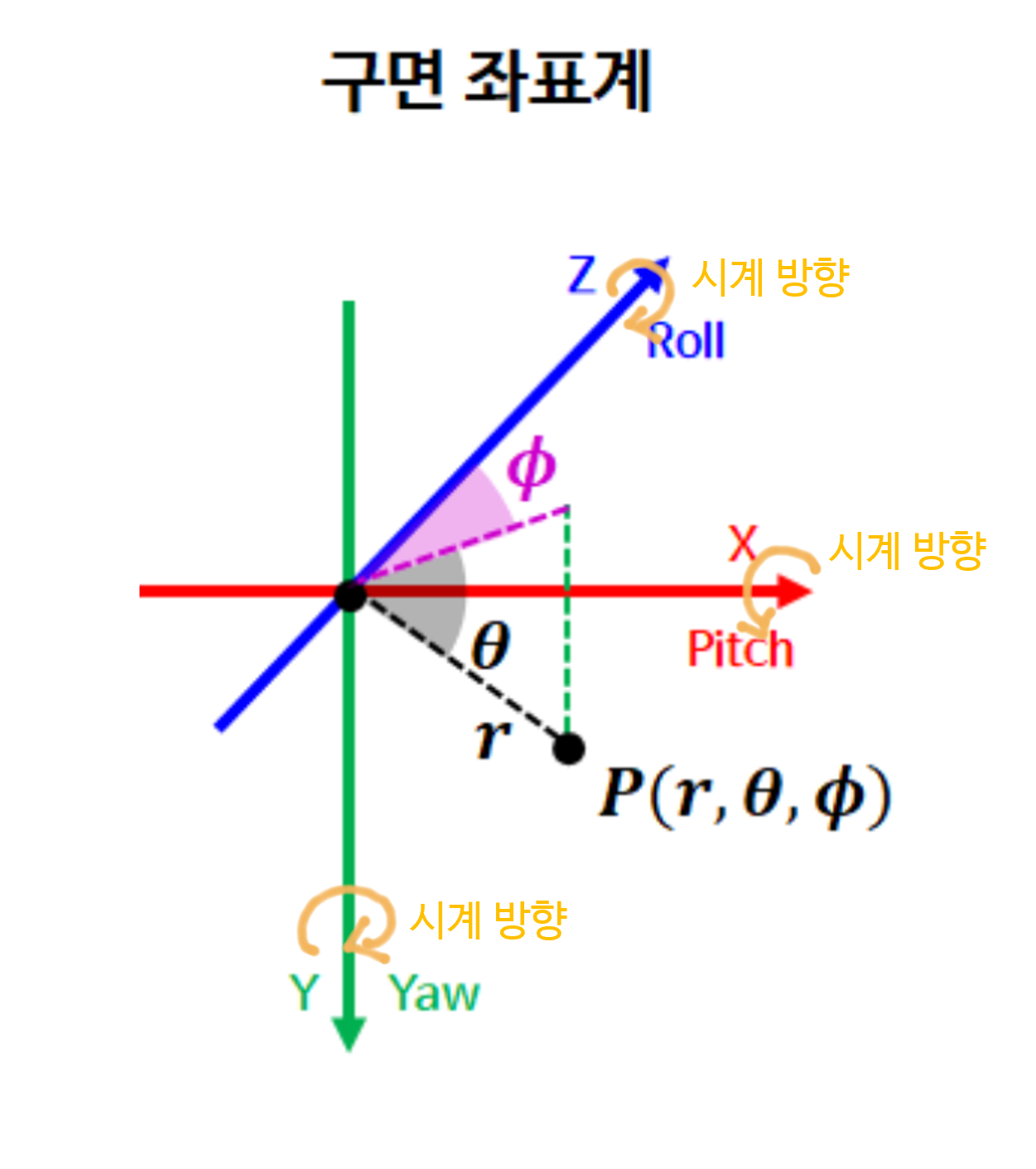
• 따라서 위 그림의 주황색 회전 방향과 같이 RDF 좌표계에서는 양의 방향으로 회전 시 반시계 방향으로 회전하도록 회전을 설계해 볼 예정입니다. 모든 회전은 원점 기준에서 관측하는 것을 전제로 합니다.
• 예를 들어 \(X\) 축 즉, pitch 방향으로 +30도 회전하게 되면 카메라는 아래쪽을 바라보도록 회전합니다. \(Y\) 축 즉, yaw 방향으로 +30도 회전하게 되면 카메라는 왼쪽을 바라보도록 회전합니다. 마지막으로 \(Z\) 축 즉, roll 방향으로 +30도 회전하게 되면 카메라는 광축을 기준으로 +30도 반시계 방향으로 회전합니다. 이 내용을 그림으로 살펴보면 다음과 같습니다.

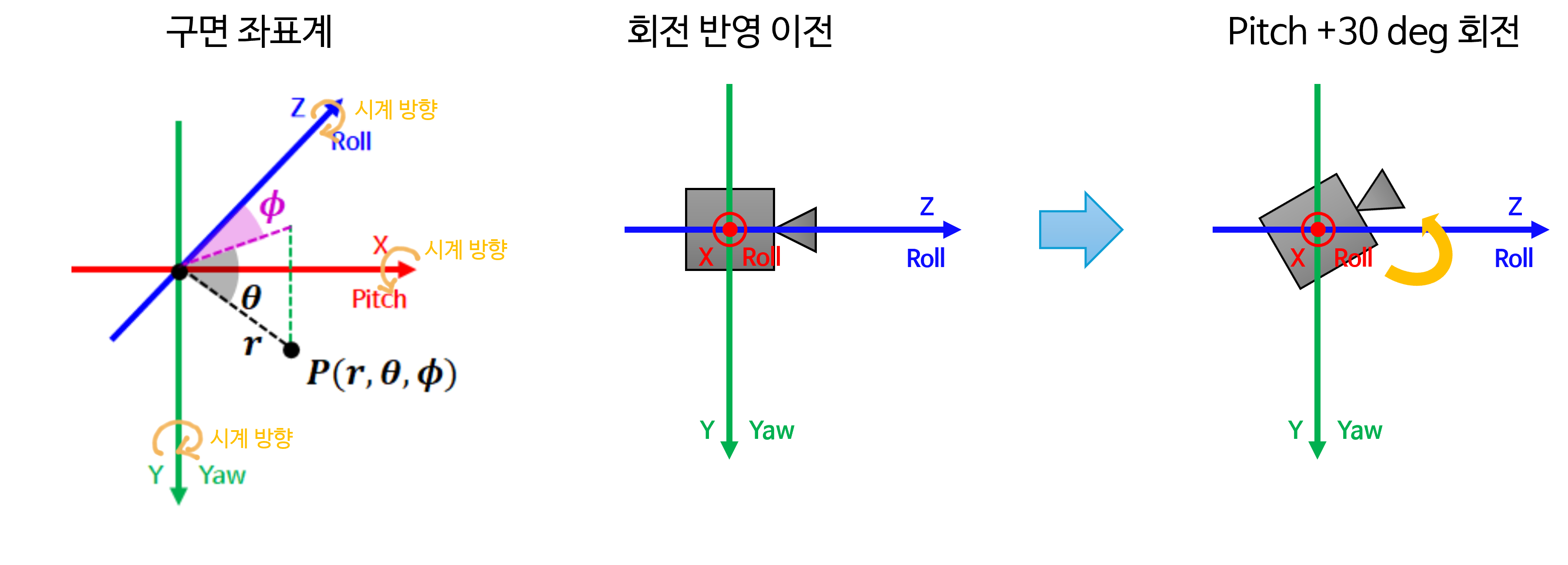
• 먼저 pitch 기준의 회전을 살펴보면 위 그림과 같습니다. \(X\) 축을 기준으로 반시계 방향으로 회전한 것을 볼 수 있습니다. (위 그림에서는 그림 상 축 외부에서 회전을 표시할 수 밖에 없어서 시계 방향으로 회전한 것처럼 보이지만 원점에서 바라보면 반시계 방향으로 회전한 것을 알 수 있습니다.)

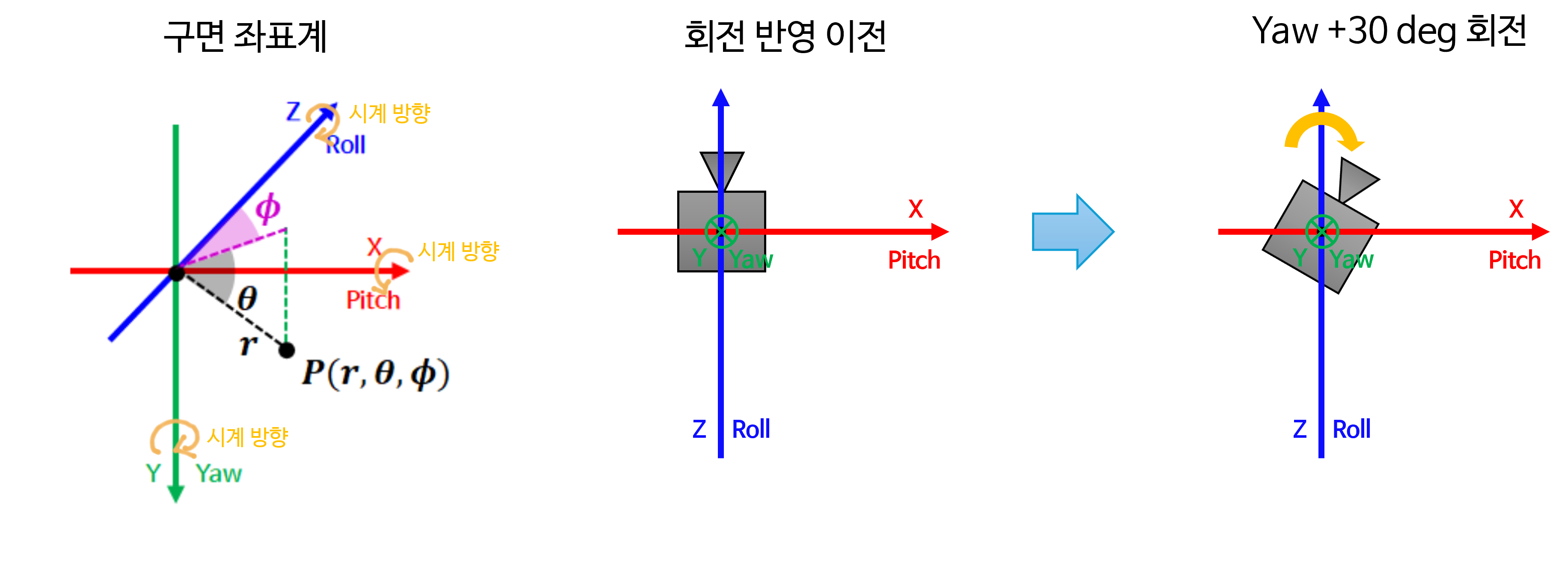
• 다음은 yaw 기준의 회전을 살펴보겠습니다. \(Y\) 축을 기준으로 반시계 방향으로 회전한 것을 볼 수 있습니다.

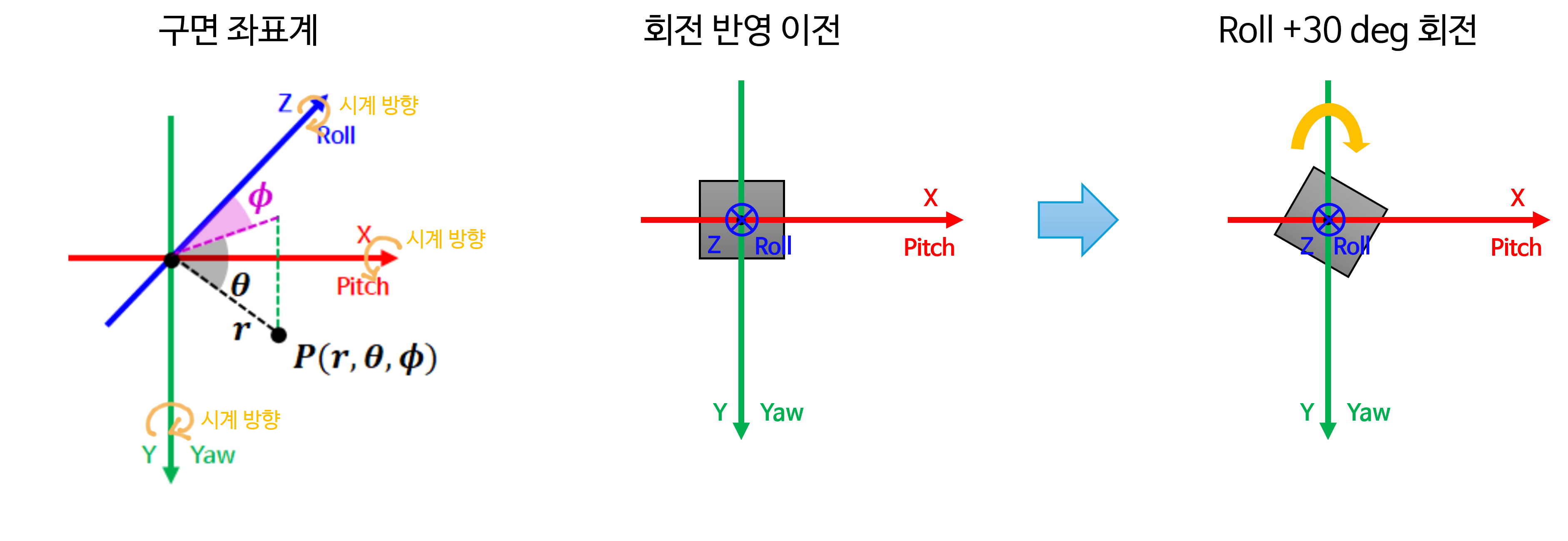
• 다음은 roll 기준의 회전을 살펴보겠습니다. \(Z\) 축을 기준으로 반시계 방향으로 회전한 것을 볼 수 있습니다.

• 이와 같이 roll, pitch, yaw 각 방향으로 회전을 하였을 때, 카메라는 각 축을 기준으로 반시계 방향 회전을 하게 됩니다.
• 카메라의 회전을 반영하는 방법은 2가지 방법이 있습니다. 첫번째로 카메라 축을 회전하는 방법이 있고 두번째로 앞의 코드에서 RDF_cartesian인 좌표값을 회전하는 방법이 있습니다. 이번 글에서는 두번째 방법인 좌표값을 회전하는 방법을 기준으로 설명을 진행하려고 합니다.
• 좌표값 회전 방법을 사용하는 이유는 ① 궁극적으로 회전을 해야 하는 것은 구면 좌표계에서부터 정의되어 직교 좌표계로 변환된 RDF_cartesian이기 때문입니다. 그리고 ② 회전해야 할 포인트들을 직접 회전시키는 것이 더 이해하기도 쉽고 설명하기도 쉽기 때문입니다.
• 카메라 축 회전과 포인트 자체를 회전하는 것을 각각 Passive Transformtation, Active Transformation이라고 합니다. 즉, 본 글에서는 Active Transformation을 사용하여 내용을 전개할 예정입니다. 이와 관련된 내용은 아래 링크를 참조해 보시기 바랍니다.
  • 링크: https://gaussian37.github.io/vision-concept-calibration/ (글 내부에서 Active/Passive Transformation을 확인)
• 핵심적으로 이해해야 할 것은 Active Transformation과 Passive Transformation은 같은 회전을 다루는 것이지만 객체(ex. 포인트)를 중심으로 회전할 지, 좌표축을 기준으로 회전할 지에 따라 관점이 반대라는 것이고 실제 두 회전 행렬은 역행렬 관계라는 점입니다. 이 내용은 글 전체에 설명에 사용됩니다.
• 따라서 본 글에서 정의하는 기준인 좌표축은 반시계 방향으로 회전하고 좌표값은 그 반대인 시계 방향으로 움직인 다는 것을 이해하고 기억해 주시기 바랍니다.

• 앞에서 다룬 이 그림을 다시 한번 살펴보도록 하겠습니다. 카메라의 회전을 반영하기 위하여 왼쪽 이미지의 각 픽셀 (\(\phi_{i}, \theta_{j})\) 들을 Active Transformation을 적용하여 회전하도록 하겠습니다. 즉, 구면 투영 이미지의 각 픽셀들이 회전한다고 볼 수 있습니다. 위 그림에서 주황색이 픽셀을 의미하며 이 픽셀이 회전을 한다고 생각해야 합니다.

• 먼저 앞에서 알아본 바와 마찬가지로 backward mapping의 접근 프로세스를 먼저 알아보도록 하겠습니다.
  • ① 구면 투영 이미지: 최종적으로 생성하고자 하는 구면으로 정의된 이미지 공간 입니다.
  • ② normalized 구면 좌표 (c_rotated): 회전이 반영된 normalized 구면 좌표계에서의 좌표값입니다. 이 단계에서 회전이 반영되었기 때문에 구면 투영 이미지 또한 회전이 반영된 상태로 이미지가 형성된 것입니다.
  • ③ normalized 구면 좌표 (c): 회전이 반영되지 않은 원래 상태의 normalized 구면 좌표계에서의 좌표값입니다.
  • ④ normalized 직교 좌표: 원본 이미지의 normalized 직교 좌표계에서의 좌표값입니다.
  • ⑤ 원본 이미지: 원본 이미지를 의미하며 구면 투영 이미지에서 사용할 RGB 값을 가져올 때 사용 됩니다.
• 프로세스 상 ② ~ ③ 단계에서 Rotation을 적용하였다는 점에서 앞에서 살펴본 카메라 기준 구면 투영법과의 차이점이 존재합니다.

• 회전을 고려한 카메라 기준 구면 투영법에서 다루고자 하는 최종 결과를 먼저 살펴보면서 어떤 개념을 다루는 지 간단히 살펴보겠습니다.

• 위 그림 예시는 카메라를 Yaw 방향으로 +30도 회전한 결과 입니다. 사용해야 할 좌표축이 반시계 방향으로 회전하였으니 기존 영상에서 상이 맺히지 않은 영역을 바라보게 되어 위 그림과 같이 빈 공간이 생성될 수 있습니다. 여기서 중요한 것은 카메라가 Yaw 방향으로 회전하였을 때, 회전된 좌표값들이 기존 좌표값과 어떻게 대응되는 지 이해하는 것입니다. 이 좌표값들은 (\(\phi_{i}, \theta_{j}\)) 로 표기합니다.

• 위 그림은 카메라를 Pitch 방향으로 +30도 회전한 결과입니다. 카메라가 \(X\) 축의 반시계 방향으로 회전하기 때문에 카메라는 아래를 바라보게 되고 각 좌표값들은 위쪽으로 회전한 것 처럼 보이게 됩니다.

• 위 그림은 카메라를 Roll 방향으로 +30도 회전한 결과입니다. 카메라가 \(Z\) 축의 반시계 방향으로 회전하기 때문에 각 좌표값들은 오른쪽으로 회전한 것 처럼 보이게 됩니다.

• 앞에서 설명한 것과 같이 카메라 회전과 좌표값 회전 중 Active Transform인 좌표값 회전을 통하여 회전을 나타내 보려고 합니다. Roll, Pitch, Yaw 방향의 회전을 반영한 Active Transformation 행렬은 다음 코드를 통하여 만들 수 있습니다.
• 아래 코드는 ② normalized 구면 좌표 (c_rotated) → ③ normalized 구면 좌표 (c) 로 좌표값 회전을 적용하는 회전 행렬을 구하는 과정입니다.

x_c_to_c_ratated_radian = np.radians(pitch_degree)
y_c_to_c_ratated_radian = np.radians(yaw_degree)
z_c_to_c_ratated_radian = np.radians(roll_degree)

# X축(Pitch) Active Transform 회전 행렬
Rx_c_to_c_rotated = np.array([
    [1, 0, 0],
    [0, np.cos(x_c_to_c_ratated_radian),  -np.sin(x_c_to_c_ratated_radian)],   
    [0, np.sin(x_c_to_c_ratated_radian), np.cos(x_c_to_c_ratated_radian)]])

# Y축(Yaw) Active Transform 회전 행렬
Ry_c_to_c_rotated = np.array([
    [np.cos(y_c_to_c_ratated_radian), 0, np.sin(y_c_to_c_ratated_radian)],
    [0, 1, 0],
    [-np.sin(y_c_to_c_ratated_radian), 0, np.cos(y_c_to_c_ratated_radian)]])

# Z축(Roll) Active Transform 회전 행렬
Rz_c_to_c_rotated = np.array([
    [np.cos(z_c_to_c_ratated_radian),  -np.sin(z_c_to_c_ratated_radian), 0],
    [np.sin(z_c_to_c_ratated_radian), np.cos(z_c_to_c_ratated_radian), 0],
    [0, 0, 1]])

# Roll @ Pitch @ Yaw
R_c_to_c_rotated = Rz_c_to_c_rotated @ Rx_c_to_c_rotated @ Ry_c_to_c_rotated
R_c_rotated_to_c = R_c_to_c_rotated.T

• R_c_rotated_to_c 행렬이 의미하는 것은 회전이 적용된 좌표값 → 회전이 적용되지 않은 좌표값으로 회전하기 위한 행렬을 의미합니다. 이 행렬을 이용하여 ② → ③ 과정으로 변환할 수 있습니다.

RDF_rotated_cartesian = np.zeros(p_norm.shape).astype(np.float32)
RDF_rotated_cartesian[:,:,0,:]=x
RDF_rotated_cartesian[:,:,1,:]=y
RDF_rotated_cartesian[:,:,2,:]=z

RDF_cartesian = R_c_rotated_to_c @ RDF_rotated_cartesian

• 앞에서 다룬 카메라 기준 구면 투영법에서는 RDF_cartesian를 바로 구면 좌표계에서의 최종 좌표값으로 사용하였지만 이번 파트에서는 RDF_rotated_cartesian을 먼저 선언하고 이 좌표값을 R_c_rotated_to_c를 이용하여 RDF_cartesian으로 변환하여 사용합니다. 즉, 원본 이미지의 좌표값에 접근하기 위해 역회전을 적용한 것이라고 보면 됩니다.
• 위 과정을 거치면 앞에서 다룬 것 처럼 ③ normalized 구면 좌표 (c) → ④ normalized 직교 좌표 → ⑤ 원본 이미지 로 차례대로 접근할 수 있습니다.
• 추가된 Rotation 부분을 포함하여 전체 코드를 작성하면 다음과 같습니다.

def get_camera_rotation_spherical_lut(
    K, D, origin_width, origin_height, target_width, target_height, hfov_deg, vfov_deg, roll_degree, pitch_degree, yaw_degree, DEFAULT_OUT_VALUE=-8):
    '''
    - K : (3, 3) intrinsic matrix
    - D : (5, ) distortion coefficient
    - origin_width, origin_height: input image size
    - target_width, target_height: output image size
    - hfov_deg: 0 ~ 360
    - vfov_deg: 0 ~ 180
    - roll_degree: 0 ~ 360
    - pitch_degree: 0 ~ 360
    - yaw_degree: 0 ~ 360
    '''

    # 구면 투영 시 생성할 azimuth/elevetion 각도 범위
    hfov=np.deg2rad(hfov_deg)
    vfov=np.deg2rad(vfov_deg)
    
    x_c_to_c_ratated_radian = np.radians(pitch_degree)
    y_c_to_c_ratated_radian = np.radians(yaw_degree)
    z_c_to_c_ratated_radian = np.radians(roll_degree)
    
    # X축(Pitch) Active Transform 회전 행렬
    Rx_c_to_c_rotated = np.array([
        [1, 0, 0],
        [0, np.cos(x_c_to_c_ratated_radian),  -np.sin(x_c_to_c_ratated_radian)],   
        [0, np.sin(x_c_to_c_ratated_radian), np.cos(x_c_to_c_ratated_radian)]])
    
    # Y축(Yaw) Active Transform 회전 행렬
    Ry_c_to_c_rotated = np.array([
        [np.cos(y_c_to_c_ratated_radian), 0, np.sin(y_c_to_c_ratated_radian)],
        [0, 1, 0],
        [-np.sin(y_c_to_c_ratated_radian), 0, np.cos(y_c_to_c_ratated_radian)]])
    
    # Z축(Roll) Active Transform 회전 행렬
    Rz_c_to_c_rotated = np.array([
        [np.cos(z_c_to_c_ratated_radian),  -np.sin(z_c_to_c_ratated_radian), 0],
        [np.sin(z_c_to_c_ratated_radian), np.cos(z_c_to_c_ratated_radian), 0],
        [0, 0, 1]])
    
    # Roll @ Pitch @ Yaw
    R_c_to_c_rotated = Rz_c_to_c_rotated @ Rx_c_to_c_rotated @ Ry_c_to_c_rotated
    R_c_rotated_to_c = R_c_to_c_rotated.T
    ##############################################################################################################
    
    # 구면 투영 시, normalized → image 로 적용하기 위한 intrinsic 행렬
    new_K = np.array([
        [target_width/hfov,       0,                     target_width/2],
        [0,                       target_height/vfov,    target_height/2],
        [0,                       0,                     1]
    ], dtype=np.float32)
    
    new_K_inv = np.linalg.inv(new_K)
    
    # Create pixel grid and compute a ray for every pixel
    # xv : (target_height, target_width), yv : (target_height, target_width)
    xv, yv = np.meshgrid(range(target_width), range(target_height), indexing='xy')
    
    # p.shape : (3, #target_height, #target_width)
    p = np.stack([xv, yv, np.ones_like(xv)])  # pixel homogeneous coordinates    
    # p.shape : (#target_height, #target_width, 3, 1)    
    p = p.transpose(1, 2, 0)[:, :, :, np.newaxis] # [u, v, 1]
    '''
    p.shape : (H, W, 3, 1)
    p[:, : 0, :] : 0, 1, 2, ..., W-1
    p[:, : 1, :] : 0, 1, 2, ..., H-1    
    p[:, : 2, :] : 1, 1, 1, ..., 1
    '''
    # p_norm.shape : (#target_height, #target_width, 3, 1)
    p_norm = new_K_inv @ p  # r is in normalized coordinate
    
    '''
    p_norm[:, :, 0, :]. phi (azimuthal angle. horizontal) : -hfov/2 ~ hov/2
    p_norm[:, :, 1, :]. theta (elevation angla. vertical) : -vfov/2 ~ vfov/2
    p_norm[:, :, 2, :]. 1.    
    '''
    # x, y, z : cartesian coordinate in camera coordinate system (RDF, Right-Down-Front)
    # azimuthal angle
    phi = p_norm[:, :, 0, :]
    # elevation angle
    theta = p_norm[:, :, 1, :] 
    
    x =np.cos(theta)*np.sin(phi) # -1 ~ 1
    y =np.sin(theta) # -1 ~ 1
    z =np.cos(theta)*np.cos(phi) # 0 ~ 1
    
    RDF_rotated_cartesian = np.zeros(p_norm.shape).astype(np.float32)
    RDF_rotated_cartesian[:,:,0,:]=x
    RDF_rotated_cartesian[:,:,1,:]=y
    RDF_rotated_cartesian[:,:,2,:]=z
    
    RDF_cartesian = R_c_rotated_to_c @ RDF_rotated_cartesian
            
    # compute incidence angle
    # x_un, y_un, z_un: (target_height, target_width)
    x_un = RDF_cartesian[:, :, 0, 0]
    y_un = RDF_cartesian[:, :, 1, 0]
    z_un = RDF_cartesian[:, :, 2, 0]
    theta = np.arccos(z_un / np.sqrt(x_un**2 + y_un**2 + z_un**2))
    
    mask = theta > np.pi/2
    # project the ray onto the fisheye image according to the fisheye model and intrinsic calibration
    r_dn = D[0]*theta + D[1]*theta**3 + D[2]*theta**5 + D[3]*theta**7 + D[4]*theta**9
    
    r_un = np.sqrt(x_un**2 + y_un**2)
    
    x_dn = r_dn * x_un / (r_un + 1e-6) # horizontal
    y_dn = r_dn * y_un / (r_un + 1e-6) # vertical    
    
    map_x_origin2new = K[0][0]*x_dn + K[0][1]*y_dn + K[0][2]
    map_y_origin2new = K[1][1]*y_dn + K[1][2]
    
    map_x_origin2new[mask] = DEFAULT_OUT_VALUE
    map_y_origin2new[mask] = DEFAULT_OUT_VALUE
    
    map_x_origin2new = map_x_origin2new.astype(np.float32)
    map_y_origin2new = map_y_origin2new.astype(np.float32)
    
    return map_x_origin2new, map_y_origin2new

camera_name = "front_fisheye_camera"
calib = json.load(open("camera_calibration.json", "r"))
image = cv2.cvtColor(cv2.imread(f"{camera_name}.png", -1), cv2.COLOR_BGR2RGB)

origin_height, origin_width, _ = image.shape
target_height, target_width  = origin_height//2, origin_width//2
hfov_deg = 180
vfov_deg = 150

K = np.array(calib[camera_name]['Intrinsic']['K']).reshape(3, 3)
D = np.array(calib[camera_name]['Intrinsic']['D'])

roll_degree = 0 # roll 회전 행렬 입력
pitch_degree = 0 # pitch 회전 행렬 입력
yaw_degree = 0 # yaw 회전 행렬 입력
map_x, map_y = get_camera_rotation_spherical_lut(
    K, D, origin_width, origin_height, target_width, target_height, 
    hfov_deg=hfov_deg, vfov_deg=vfov_deg, 
    roll_degree=roll_degree, pitch_degree=pitch_degree, yaw_degree=yaw_degree
)
new_image = cv2.remap(image, map_x, map_y, interpolation=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=(0, 0, 0))
plt.imshow(new_image)

print("new_K: \n", new_K)
print("new_R: \n", new_R)

• 다음은 위 코드를 활용하여 roll, pitch, yaw를 각 360도 회전하였을 때, 어떻게 회전하는 지 살펴볼 수 있도록 만든 동영상 입니다.
• 먼저 yaw 회전의 예시 입니다. 회전 각도가 증가함에 따라서 영상이 어떻게 변화하는 지 살펴보시면 됩니다.

• 다음은 pitch 회전의 예시 입니다. 회전 각도가 증가함에 따라서 영상이 어떻게 변화하는 지 살펴보시면 됩니다.

• 다음은 roll 회전의 예시 입니다. 회전 각도가 증가함에 따라서 영상이 어떻게 변화하는 지 살펴보시면 됩니다.

• 다음은 roll, pitch, yaw를 동시에 변화하여 360도 회전하는 영상 샘플입니다.

• 지금까지 특정 카메라 기준에서 회전을 고려한 구면 투영법에 대하여 알아보았습니다.

회전을 고려한 World 기준 구면 투영법

• 구면 투영법 사용 이유 에서 다룬 바와 같이 구면 투영법을 사용해야 하는 이유 중 멀티 카메라 환경에서 영상들을 동일한 구면에 투영할 수 있다는 장점을 간단히 언급하였었습니다.
• 회전을 고려한 카메라 기준 구면 투영법에서는 특정 카메라를 기준으로 Roll, Pitch, Yaw의 회전을 고려하였으나 멀티 카메라 환경을 고려하기 위해서는 특정 기준이 필요합니다. 이번에 다룰 내용은 멀티 카메라 환경을 고려하기 위하여 카메라 외부의 World 좌표계를 정해놓고 그 기준에 맞춰서 Roll, Pitch, Yaw 회전을 반영하는 방법에 대하여 알아보도록 하겠습니다. 사용할 데이터는 동일합니다.
• 데이터셋 링크: https://drive.google.com/drive/folders/15cnXNjEaztZl0CBT25oCaJ9-8qyfRYAw?usp=drive_link
• 데이터 관련 설명: 링크

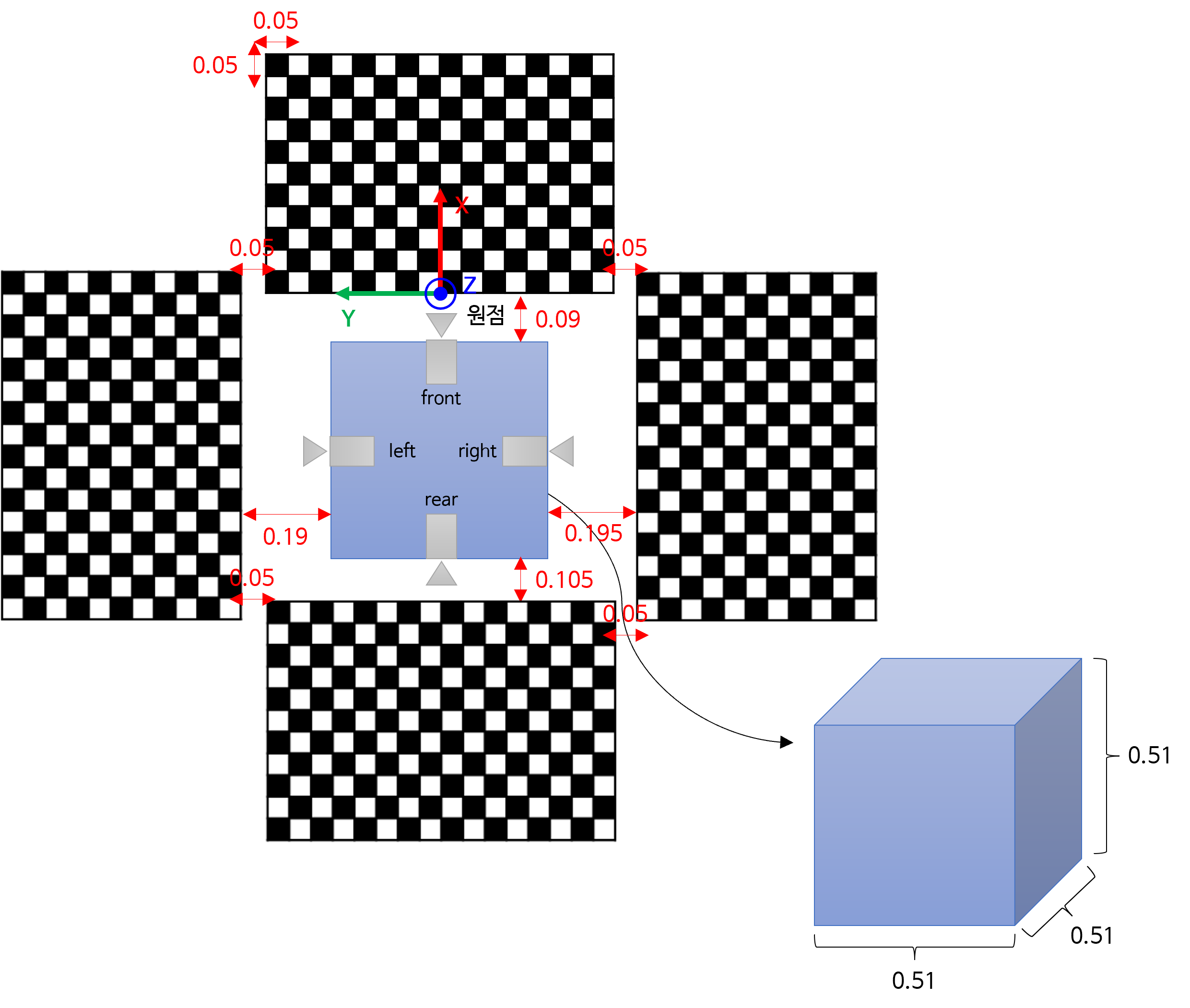
• 데이터 셋 설명을 기준으로 나타내면 World 좌표계는 원점으로 정의해 놓은 위치입니다. World 좌표계에서 관심있는 부분은 각 카메라와 World 좌표계 간의 Rotation 관계입니다. 회전을 고려한 카메라 기준 구면 투영법에서는 카메라의 회전 각도 사양을 정의할 때, 카메라 기준의 Roll, Pitch, Yaw를 정의하고 그 사양에 맞추어 LUT를 생성하였습니다. World 기준 구면 투영법에서는 World 원점을 기준으로 Roll, Pitch, Yaw를 정의하고 그 사양에 맞추어 LUT를 생성합니다.

• 먼저 앞에서 알아본 바와 마찬가지로 backward mapping의 접근 프로세스를 먼저 알아보도록 하겠습니다. c_rotated는 최종적으로 회전하고자 하는 카메라의 방향이며 c_calib는 캘리브레이션의 Rotation에 반영된 Roll, Pitch, Yaw 만큼 회전이 반영된 카메라의 방향을 의미합니다.
  • ① 구면 투영 이미지: 최종적으로 생성하고자 하는 구면으로 정의된 이미지 공간 입니다.
  • ② normalized 구면 좌표 (c_rotated): 회전이 반영된 normalized 구면 좌표계에서의 좌표값입니다. 이 단계에서 회전이 반영되었기 때문에 구면 투영 이미지 또한 회전이 반영된 상태로 이미지가 형성된 것입니다.
  • ③ normalized 구면 좌표 (world) : c_rotated → c_calib 로 회전하기 위해 (의미상) 중간 단계로 거쳐가는 구간입니다. World 좌표계가 기준이 되기 때문에 c_rotated → world로 먼저 회전을 하여 World 좌표계 상에서는 회전이 없는 상태를 임시적으로 만듭니다. 따라서 이 단계에서는 c_rotated에서 회전된 양만큼 회전이 제거된 normalized 구면 좌표계에서의 좌표값을 가집니다.
  • ④ normalized 구면 좌표 (c_calib): world → c_calib로 회전을 반영합니다. 따라서 이 단계에서는 World 좌표계 기준으로 보았을 때, 캘리브레이션의 Rotation에 반영된 회전만큼 좌표값의 회전을 반영합니다. ② → ③ → ④ 과정을 통하여 c_rotated 카메라 방향 → c_calib 카메라 방향으로 회전을 할 수 있습니다. 다시 정리하면 c_rotated는 최종 회전이 반영된 카메라의 방향이고 c_calib는 원본 이미지가 취득된 카메라의 방향이므로 원본 이미지에 접근하기 위해 이와 같이 카메라 회전 방향을 변경합니다.
  • ⑤ normalized 직교 좌표: 원본 이미지의 normalized 직교 좌표계에서의 좌표값입니다.
  • ⑥ 원본 이미지: 원본 이미지를 의미하며 구면 투영 이미지에서 사용할 RGB 값을 가져올 때 사용 됩니다.

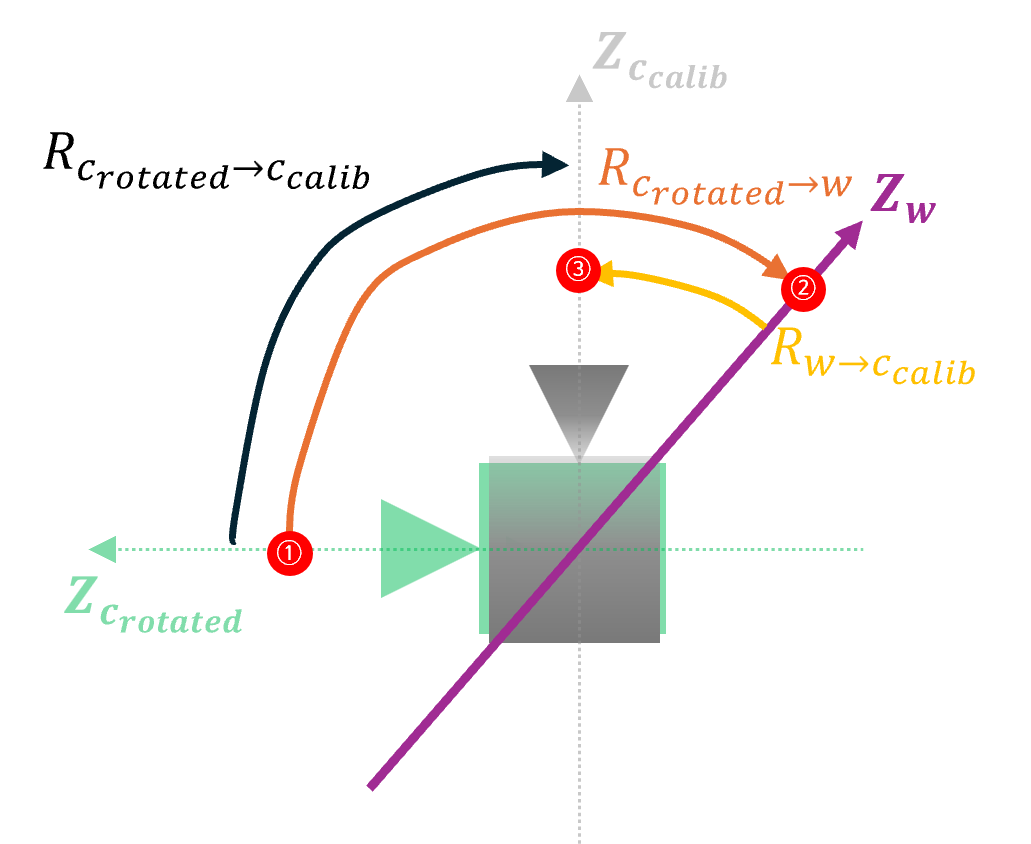
• 설명을 위해 \(Z\) 축 관점에서만 다루어 보겠습니다. 위 그림에서 빨간색 점이 실제 회전을 해야 할 포인트 (좌표) 입니다. 실제 존재하는 좌표축은 \(Z_{w}\) 이고 투명하게 표시한 \(Z_{c_{\text{rotated}}}\) 와 \(Z_{c_{\text{calib}}}\) 그리고 카메라 모양은 이해를 돕기 위한 가상의 그림이니 무시하셔도 됩니다. 빨간색 점이 어떻게 이동하는 지 이해하는 것이 핵심입니다.
• 위 그림과 같이 \(Z_{w}\) 축 상의 빨간색 점 ①이 ②로 위치를 회전하였다가 ③으로 다시 회전할 수 있도록 회전 행렬을 만들어 보려고 합니다.
• 점 ① 은 위치 상 최종 회전이 반영된 카메라 방향에 위치합니다. 따라서 이 점이 world 기준에서 어떻게 이동하는 지 살펴보도록 하겠습니다.

• \[R_{c_{\text{rotated}} \to w} = \text{Activation Transformation(Rotation) from rotated camera to world.}\]
• \[R_{w \to c_{\text{calib}}} = \text{Activation Transformation(Rotation) from world to calibrated camera.}\]
• \[R_{c_{\text{rotated}} \to c_{\text{calib}}} = \text{Activation Transformation(Rotation) from rotated camera to calibrated camera.}\]

• 위 그림과 같이 ① → ② → ③ 순서로 회전해야 하므로 다음과 같이 행렬을 구성할 수 있습니다.

• \[R_{c_{\text{rotated}} \to c_{\text{calib}}} = R_{w \to c_{\text{calib}}} R_{c_{\text{rotated}} \to w}\]

• 위 행렬에서 회전의 방향을 \(world \to\) 로 일관성있게 정리하면 다음과 같습니다.

• \[R_{c_{\text{rotated}} \to c_{\text{calib}}} = R_{w \to c_{\text{calib}}} R_{c_{\text{rotated}} \to w} = R_{w \to c_{\text{calib}}} R_{w \to c_{\text{rotated}}}^{-1} = R_{w \to c_{\text{calib}}} R_{w \to c_{\text{rotated}}}^{T}\]
• \[\therefore R_{c_{\text{rotated}} \to c_{\text{calib}}} = R_{w \to c_{\text{calib}}} R_{w \to c_{\text{rotated}}}^{T}\]

• 코드 상에서는 \(R_{w \to c_{\text{calib}}}\) 는 캘리브레이션을 통해 얻은 Rotation 을 사용하고 \(R_{w\ to c_{\text{rotated}}}\) 는 사용자가 사양을 정의해서 사용할 예정입니다.

• 먼저 \(R_{w \to c_{\text{calib}}}\) 을 구하는 방법을 알아보도록 하겠습니다. 이 행렬은 현재 데이터셋의 Rotation에 따른 것이니 데이터셋의 정의에 맞게 적용해야 합니다.
• 캘리브레이션에 정의된 Rotation은 \(R_{w_{FLU} \to c_{calib, RDF}}\) 로 회전 변환 적용 전과 후의 축의 기준이 다릅니다. 따라서 이번 글에서 주로 다루는 카메라 좌표계인 RDF 좌표계로 바꾸는 과정을 통해 \(R_{w_{RDF} \to c_{calib, RDF}}\) 행렬을 만들어야 합니다. 왜냐하면 \(R_{w \to c_{\text{calib}}}\) 행렬 변환 적용 전/후 모두 RDF 좌표값을 다루기 때문입니다.

• \[R_{w \to c_{\text{calib}}} = R_{w_{RDF} \to c_{calib, RDF}} = R_{w_{FLU} \to c_{calib, RDF}} R_{RDF \to FLU}\]
• \[R_{FLU \to RDF} = \begin{bmatrix} 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 & 0 \end{bmatrix}\]
• \[R_{RDF \to FLU} = R_{FLU \to RDF}^{T} = \begin{bmatrix} 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 & 0 \end{bmatrix}^{T}\]

• 행렬 \(R_{w \to c_{\text{calib}}} = R_{w_{FLU} \to c_{calib, RDF}} R_{RDF \to FLU}\) 을 살펴보면 \(R_{w \to c_{\text{calib}}} \cdot P_{RDF}\) 와 같이 사용하였을 때 RDF 좌표계의 좌표값을 입력으로 받아 \(R_{w \to c_{\text{calib}}}\) 내부적으로 RDF → FLU로 한번 변환하는 과정을 겁치다. 따라서 \(R_{w \to c_{\text{calib}}}\) 는 RDF 좌표계의 좌표값을 회전하여 입/출력 모두 RDF 좌표계의 좌표값을 사용하게 됩니다.
• 이 과정을 코드로 나타내면 다음과 같습니다.

R_flu_to_rdf = np.array(
        [[0, -1, 0],
         [0, 0, -1],
         [1, 0, 0]], dtype=np.float32
    )

R_rdf_to_flu = R_flu_to_rdf.T
R_w_rdf_to_c_calib_rdf = R_w_flu_to_c_calib_rdf @ R_rdf_to_flu

• 이 과정을 통해서 R_w_rdf_to_c_calib_rdf 즉, \(R_{w \to c_{\text{calib}}}\) 를 구할 수 있습니다.

• 다음으로 \(R_{w \to c_{\text{rotated}}}\) 를 구해보도록 하겠습니다. 이 행렬을 만들기 위해서는 최종 회전을 반영하기 위해 사용자가 회전의 사양을 정의해 주어야 합니다. 예를 들어 Roll 0도, Pitch 0도, Yaw 60도 와 같이 최종 생성하고자 하는 각 축의 회전 각도를 정해야 \(c_{\text{rotated}}\) 를 구할 수 있습니다. 만약 특정 각도를 지정하지 않는다면 캘리브레이션의 Rotation 값을 기본값으로 지정할 수 있도록 반영해 보겠습니다. 캘리브레이션 값을 기본값으로 사용하면 카메라가 장착된 방향을 기본값으로 사용할 수 있습니다.

• 아래는 먼저 캘리브레이션 Rotation에서 Roll, Pitch, Yaw를 추출하는 방식 및 코드입니다. 데이터 셋에 맞춰서 사용하면 되며 현재 사용하는 데이터 셋이 \(R_{w_{\text{FLU}} \to c_{\text{RDF}}}\) 이므로 다음 방법으로 Roll, Pitch, Yaw를 구하였습니다.

• \[R_{w_{\text{FLU}} \to c_{\text{RDF}}}^{\text{passive}} R_{\text{RDF} \to \text{FLU}}^{\text{passive}} = R_{w_{\text{FLU}} \to c_{\text{FLU}}}^{\text{passive}}\]

• Roll, Pitch, Yaw와 Rotation의 변환 의 설명에 따라 \(R_{w_{\text{FLU}} \to c_{\text{FLU}}}^{\text{passive}}\) 를 rotation_matrix_to_euler_angles 함수에 넣으면 Roll, Pitch, Yaw로 분해할 수 있습니다. 코드는 다음과 같습니다.

def rotation_matrix_to_euler_angles(R):
    assert(R.shape == (3, 3))

    theta = -np.arcsin(R[2, 0])
    psi = np.arctan2(R[2, 1] / np.cos(theta), R[2, 2] / np.cos(theta))
    phi = np.arctan2(R[1, 0] / np.cos(theta), R[0, 0] / np.cos(theta))
    return np.array([psi, theta, phi])

# FLU: Forward-Left-Up
# RDF: Right-Down-Forward
R_w_flu_to_c_calib_rdf = R.copy()
R_w_flu_to_c_calib_rdf_passive = R_w_flu_to_c_calib_rdf.T

R_flu_to_rdf = np.array(
    [[0, -1, 0],
        [0, 0, -1],
        [1, 0, 0]], dtype=np.float32
)

R_rdf_to_flu = R_flu_to_rdf.T
R_flu_to_rdf_passive = R_flu_to_rdf.T
R_rdf_to_flu_passive = R_flu_to_rdf_passive.T

RPY_FLU_TO_FLU_PASSIVE = R_w_flu_to_c_calib_rdf_passive @ R_rdf_to_flu_passive
ROLL_PITCH_YAW = np.rad2deg(rotation_matrix_to_euler_angles(RPY_FLU_TO_FLU_PASSIVE)) # FLU based Roll, Pitch, Yaw

calib_roll_degree = ROLL_PITCH_YAW[0]
calib_pitch_degree = ROLL_PITCH_YAW[1]
calib_yaw_degree = ROLL_PITCH_YAW[2]

# 사양이 정해지지 않으면 캘리브레이션 값을 이용하여 카메라 장착 위치로 맞춤
if pitch_degree is None:
    x_w_to_c_rotated_degree = calib_pitch_degree
else:
    x_w_to_c_rotated_degree = pitch_degree
    
if yaw_degree is None:
    y_w_to_c_rotated_degree = calib_yaw_degree
else:
    y_w_to_c_rotated_degree = yaw_degree
    
if roll_degree is None:
    z_w_to_c_rotated_degree = calib_roll_degree
else:
    z_w_to_c_rotated_degree = roll_degree

x_w_to_c_rotated_radian = np.radians(x_w_to_c_rotated_degree)
y_w_to_c_rotated_radian = np.radians(y_w_to_c_rotated_degree)
z_w_to_c_rotated_radian = np.radians(z_w_to_c_rotated_degree)

• 위 코드상에서 구한 calib_roll/pitch/yaw_degree를 기본 회전값으로 사용하면 사용자가 회전 각도를 특별히 지정해 주지 않았을 때, 카메라가 장착된 방향으로 회전을 적용합니다.
• 최종 정의된 x/y/z_w_to_c_rotated_radian를 이용하여 R_w_rdf_to_c_calib_rdf 즉, \(R_{w \to c_{\text{calib}}}\), R_w_rdf_to_c_rotated_rdf 즉, \(R_{w \to c_{\text{rotated}}}\), R_c_rotated_rdf_to_c_calib_rdf 즉, \(R_{c_{\text{rotated}} \to c_{\text{calib}}}\) 를 구하면 아래 코드와 같습니다.

# X축(Pitch) 회전 행렬
Rx_w_to_c_rotated = np.array([
    [1, 0, 0],
    [0, np.cos(x_w_to_c_rotated_radian), -np.sin(x_w_to_c_rotated_radian)],   
    [0, np.sin(x_w_to_c_rotated_radian), np.cos(x_w_to_c_rotated_radian)]])

# Y축(Yaw) 회전 행렬
Ry_w_to_c_rotated = np.array([
    [np.cos(y_w_to_c_rotated_radian), 0, np.sin(y_w_to_c_rotated_radian)],
    [0, 1, 0],
    [-np.sin(y_w_to_c_rotated_radian), 0,  np.cos(y_w_to_c_rotated_radian)]])

# Z축(Roll) 회전 행렬
Rz_w_to_c_rotated = np.array([
    [np.cos(z_w_to_c_rotated_radian), -np.sin(z_w_to_c_rotated_radian), 0],
    [np.sin(z_w_to_c_rotated_radian), np.cos(z_w_to_c_rotated_radian), 0],
    [0, 0, 1]])

R_w_rdf_to_c_calib_rdf = R_w_flu_to_c_calib_rdf @ R_rdf_to_flu
R_w_rdf_to_c_rotated_rdf = Rz_w_to_c_rotated @ Rx_w_to_c_rotated @ Ry_w_to_c_rotated
R_c_rotated_rdf_to_c_calib_rdf = R_w_rdf_to_c_calib_rdf @ R_w_rdf_to_c_rotated_rdf.T    

• 앞에서 다룬 바와 같이 R_c_rotated_rdf_to_c_calib_rdf를 이용하여 RDF_rotated_cartesian → RDF_cartesian 로 변환하여 ② normalized 구면 좌표 (c_rotated) → ③ normalized 구면 좌표 (world) → ④ normalized 구면 좌표 (c_calib) 순서로 좌표를 회전 변환 합니다. 코드 상으로 다음과 같습니다.

RDF_cartesian = R_c_rotated_rdf_to_c_calib_rdf @ RDF_rotated_cartesian

• 지금까지 살펴본 내용을 하나의 코드로 합쳐서 정리하면 다음과 같습니다.
• 함수 인자에 roll_degree, pitch_degree, yaw_degree의 기본값이 None으로 되어 있습니다. 만약 None인 경우에는 캘리브레이션 Rotation의 Roll, Pitch, Yaw를 사용합니다.
• 함수 마지막의 new_R과 new_t는 회전을 고려한 World 기준 구면 투영법의 World-to-Image, Image-to-World에서 사용할 예정입니다. 관련 내용도 다음 챕터에서 설명하도록 하겠습니다.

import json
import cv2
import numpy as np
import matplotlib.pyplot as plt
np.set_printoptions(suppress=True)

def rotation_matrix_to_euler_angles(R):
    assert(R.shape == (3, 3))

    theta = -np.arcsin(R[2, 0])
    psi = np.arctan2(R[2, 1] / np.cos(theta), R[2, 2] / np.cos(theta))
    phi = np.arctan2(R[1, 0] / np.cos(theta), R[0, 0] / np.cos(theta))
    return np.array([psi, theta, phi])

def get_world_camera_rotation_spherical_lut(
    R, t, K, D, origin_width, origin_height, target_width, target_height, hfov_deg, vfov_deg, 
    roll_degree=None, pitch_degree=None, yaw_degree=None, DEFAULT_OUT_VALUE=-8):
    '''
    - R : (3, 3) rotation matrix (World → Camera, active transformation)
    - K : (3, 3) intrinsic matrix
    - D : (5, ) distortion coefficient
    - origin_width, origin_height: input image size
    - target_width, target_height: output image size
    - hfov_deg: 0 ~ 360
    - vfov_deg: 0 ~ 180
    - roll_degree: 0 ~ 360
    - pitch_degree: 0 ~ 360
    - yaw_degree: 0 ~ 360
    '''
    
    hfov=np.deg2rad(hfov_deg)
    vfov=np.deg2rad(vfov_deg)
    
    # FLU: Forward-Left-Up
    # RDF: Right-Down-Forward
    R_w_flu_to_c_calib_rdf = R.copy()
    R_w_flu_to_c_calib_rdf_passive = R_w_flu_to_c_calib_rdf.T

    R_flu_to_rdf = np.array(
        [[0, -1, 0],
         [0, 0, -1],
         [1, 0, 0]], dtype=np.float32
    )
    
    R_rdf_to_flu = R_flu_to_rdf.T
    R_flu_to_rdf_passive = R_flu_to_rdf.T
    R_rdf_to_flu_passive = R_flu_to_rdf_passive.T

    RPY_FLU_TO_FLU_PASSIVE = R_w_flu_to_c_calib_rdf_passive @ R_rdf_to_flu_passive
    ROLL_PITCH_YAW = np.rad2deg(rotation_matrix_to_euler_angles(RPY_FLU_TO_FLU_PASSIVE)) # FLU based Roll, Pitch, Yaw

    calib_roll_degree = ROLL_PITCH_YAW[0]
    calib_pitch_degree = ROLL_PITCH_YAW[1]
    calib_yaw_degree = ROLL_PITCH_YAW[2]

    # From here, all coordinate systems are based on RDF(Right-Down-Forward).
    # From here, all rotation matrices are active transformation.

    # 사양이 정해지지 않으면 캘리브레이션 값을 이용하여 카메라 장착 위치로 맞춤
    if pitch_degree is None:
        x_w_to_c_rotated_degree = calib_pitch_degree
    else:
        x_w_to_c_rotated_degree = pitch_degree
        
    if yaw_degree is None:
        y_w_to_c_rotated_degree = calib_yaw_degree
    else:
        y_w_to_c_rotated_degree = yaw_degree
        
    if roll_degree is None:
        z_w_to_c_rotated_degree = calib_roll_degree
    else:
        z_w_to_c_rotated_degree = roll_degree

    x_w_to_c_rotated_radian = np.radians(x_w_to_c_rotated_degree)
    y_w_to_c_rotated_radian = np.radians(y_w_to_c_rotated_degree)
    z_w_to_c_rotated_radian = np.radians(z_w_to_c_rotated_degree)
        
    # X축(Pitch) 회전 행렬
    Rx_w_to_c_rotated = np.array([
        [1, 0, 0],
        [0, np.cos(x_w_to_c_rotated_radian), -np.sin(x_w_to_c_rotated_radian)],   
        [0, np.sin(x_w_to_c_rotated_radian), np.cos(x_w_to_c_rotated_radian)]])

    # Y축(Yaw) 회전 행렬
    Ry_w_to_c_rotated = np.array([
        [np.cos(y_w_to_c_rotated_radian), 0, np.sin(y_w_to_c_rotated_radian)],
        [0, 1, 0],
        [-np.sin(y_w_to_c_rotated_radian), 0,  np.cos(y_w_to_c_rotated_radian)]])

    # Z축(Roll) 회전 행렬
    Rz_w_to_c_rotated = np.array([
        [np.cos(z_w_to_c_rotated_radian), -np.sin(z_w_to_c_rotated_radian), 0],
        [np.sin(z_w_to_c_rotated_radian), np.cos(z_w_to_c_rotated_radian), 0],
        [0, 0, 1]])

    R_w_rdf_to_c_calib_rdf = R_w_flu_to_c_calib_rdf @ R_rdf_to_flu
    R_w_rdf_to_c_rotated_rdf = Rz_w_to_c_rotated @ Rx_w_to_c_rotated @ Ry_w_to_c_rotated
    R_c_rotated_rdf_to_c_calib_rdf = R_w_rdf_to_c_calib_rdf @ R_w_rdf_to_c_rotated_rdf.T    
    ##############################################################################################################
    new_K = np.array([
        [target_width/hfov,       0,                     target_width/2],
        [0,                       target_height/vfov,    target_height/2],
        [0,                       0,                     1]], dtype=np.float32)
    new_K_inv = np.linalg.inv(new_K)

    # Create pixel grid and compute a ray for every pixel
    # xv : (target_height, target_width), yv : (target_height, target_width)
    xv, yv = np.meshgrid(range(target_width), range(target_height), indexing='xy')

    # p.shape : (3, #target_height, #target_width)
    p = np.stack([xv, yv, np.ones_like(xv)])  # pixel homogeneous coordinates    
    # p.shape : (#target_height, #target_width, 3, 1)    
    p = p.transpose(1, 2, 0)[:, :, :, np.newaxis] # [u, v, 1]
    '''
    p.shape : (H, W, 3, 1)
    p[:, : 0, :] : 0, 1, 2, ..., W-1
    p[:, : 1, :] : 0, 1, 2, ..., H-1    
    p[:, : 2, :] : 1, 1, 1, ..., 1
    '''
    # p_norm.shape : (#target_height, #target_width, 3, 1)
    p_norm = new_K_inv @ p  # r is in normalized coordinate

    '''
    p_norm[:, :, 0, :]. phi (azimuthal angle. horizontal) : -hfov/2 ~ hov/2
    p_norm[:, :, 1, :]. theta (elevation angla. vertical) : -vfov/2 ~ vfov/2
    p_norm[:, :, 2, :]. 1.    
    '''
    # azimuthal angle
    phi = p_norm[:, :, 0, :]
    # elevation angle
    theta = p_norm[:, :, 1, :]   

    # x, y, z : cartesian coordinate in camera coordinate system (RDF, Right-Down-Forward)
    # hemisphere
    x = np.cos(theta)*np.sin(phi) # -1 ~ 1
    y = np.sin(theta) # -1 ~ 1
    z = np.cos(theta)*np.cos(phi) # 0 ~ 1

    ####################
    RDF_rotated_cartesian = np.zeros(p_norm.shape).astype(np.float32)
    RDF_rotated_cartesian = np.zeros(p_norm.shape).astype(np.float32)
    RDF_rotated_cartesian[:,:,0,:]=x
    RDF_rotated_cartesian[:,:,1,:]=y
    RDF_rotated_cartesian[:,:,2,:]=z
    
    RDF_cartesian = R_c_rotated_rdf_to_c_calib_rdf @ RDF_rotated_cartesian
            
    # compute incidence angle
    # x_un, y_un, z_un: (target_height, target_width)
    x_un = RDF_cartesian[:, :, 0, 0]
    y_un = RDF_cartesian[:, :, 1, 0]
    z_un = RDF_cartesian[:, :, 2, 0]
    ################
    
    # theta = np.arccos(RDF_rotated_cartesian[:, :, [2], :] / np.linalg.norm(RDF_rotated_cartesian, axis=2, keepdims=True))
    theta = np.arccos(z_un / np.sqrt(x_un**2 + y_un**2 + z_un**2))

    mask = theta > np.pi/2
    # project the ray onto the fisheye image according to the fisheye model and intrinsic calibration
    r_dn = D[0]*theta + D[1]*theta**3 + D[2]*theta**5 + D[3]*theta**7 + D[4]*theta**9

    r_un = np.sqrt(x_un**2 + y_un**2)

    x_dn = r_dn * x_un / (r_un + 1e-6) # horizontal
    y_dn = r_dn * y_un / (r_un + 1e-6) # vertical    

    map_x_origin2new = K[0][0]*x_dn + K[0][1]*y_dn + K[0][2]
    map_y_origin2new = K[1][1]*y_dn + K[1][2]

    map_x_origin2new[mask] = DEFAULT_OUT_VALUE
    map_y_origin2new[mask] = DEFAULT_OUT_VALUE

    map_x_origin2new = map_x_origin2new.astype(np.float32)
    map_y_origin2new = map_y_origin2new.astype(np.float32)
    
    # new_R: R_w2c_rotated
    # new_t: t_w2c_rotated
    new_R = Rz_w_to_c_rotated @ Rx_w_to_c_rotated @ Ry_w_to_c_rotated @ R_flu_to_rdf
    new_t = new_R @ R.T @ t

    return map_x_origin2new, map_y_origin2new, new_K, new_R, new_t
    
camera_name = 'front_fisheye_camera'
calib = json.load(open("camera_calibration.json", "r"))
image = cv2.cvtColor(cv2.imread(f"{camera_name}.png", -1), cv2.COLOR_BGR2RGB)

origin_height, origin_width, _ = image.shape
target_height, target_width  = origin_height//2, origin_width//2

# example case
roll_degree = 0
pitch_degree = 0
yaw_degree = 0

hfov_deg = 180
vfov_deg = 150

K = np.array(calib[camera_name]['Intrinsic']['K']).reshape(3, 3)
D = np.array(calib[camera_name]['Intrinsic']['D'])
R = np.array(calib[camera_name]['Extrinsic']['World']['Camera']['R']).reshape(3, 3)
t = np.array(calib[camera_name]['Extrinsic']['World']['Camera']['t']).reshape(3, 1)

map_x, map_y, new_K, new_R, new_t = get_world_camera_rotation_spherical_lut(
    R, t, K, D, 
    origin_width, origin_height, target_width, target_height, 
    hfov_deg=hfov_deg, vfov_deg=vfov_deg, 
    roll_degree=roll_degree, pitch_degree=pitch_degree, yaw_degree=yaw_degree)
new_image = cv2.remap(image, map_x, map_y, interpolation=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=(0, 0, 0))
plt.imshow(new_image)    

• 데이터 셋 설명을 보면 왼쪽 이미지는 대략 Yaw가 90도 회전되어 있는 상태입니다. 따라서 위 그림과 같이 회전 각도를 설정하였습니다. 추가적으로 pitch에 따라서 어떻게 달라지는 지 또한 확인하였습니다.

• 먼저 위 코드를 이용하여 front, left, rear, right 카메라의 이미지 순서로 Yaw는 고정한 상태로 Roll, Pitch를 변화하였을 때 어떻게 변화하는 지 살펴보도록 하겠습니다.

• 먼저 위 영상은 front 카메라 영상입니다. pitch와 roll 각각을 회전하였을 때, 어떻게 영상이 생성되는 지 확인해 보겠습니다. Yaw 값은 0도로 고정하였습니다.

• 다음으로 위 영상은 left 카메라 영상입니다. Yaw 값은 90도로 고정하였습니다. Yaw 값이 90도 부근일 때, 왼쪽 카메라 영상이 생성되는 것을 확인할 수 있습니다.

• 다음으로 위 영상은 rear 카메라 영상입니다. Yaw 값은 180도로 고정하였습니다.

• 마지막으로 위 영상은 right 카메라 영상입니다. Yaw 값은 270도로 고정하였습니다.

• 다음은 모든 카메라의 Roll과 Pitch는 0으로 고정한 상태로 Yaw만 변화하여 멀티 카메라 환경을 고려해 보겠습니다. 이 방법을 통하여 Yaw의 회전에 따라서 멀티 카메라 환경에서 영상이 어떻게 형성되는 지 알 수 있습니다.

• 위 영상의 가운데 화살표는 현재 Yaw의 회전을 나타내면 카메라가 바라보는 방향입니다. 12시 방향 0도일 때 부터 시작하여 반시계 방향으로 한 바퀴 회전할 때, 멀티 카메라에서 보이는 영상을 확인할 수 있습니다.

회전을 고려한 World 기준 구면 투영법의 World-to-Image, Image-to-World

World-to-Image

• 지금까지 살펴본 내용은 World 좌표계 환경에서 멀티 카메라 기반 구면 투영 이미지를 생성하였을 때, 영상이 어떻게 형성되는 지 살펴보았습니다.
• 이 내용들을 이용하여 추가적으로 World-to-Image, Image-to-World 접근 방법을 살펴보도록 하겠습니다. 구면 투영법을 통해 new_K, new_R이 생성되었기 때문에 이 값들을 이용하여 이미지와 World 간의 대응이 이루어져야 합니다.
• 원본 이미지에 대한 World-to-Image, Image-to-World 방법은 아래 링크를 참조해 주시기 바랍니다.
  • 링크: World-to-Image, Image-to-World
• 먼저 new_R과 new_K가 어떻게 생성되었는 지 살펴보도록 하겠습니다. 앞의 코드에서 이 두 변수는 다음과 같이 정의되었습니다.

new_R = Rz_w_to_c_rotated @ Rx_w_to_c_rotated @ Ry_w_to_c_rotated @ R_flu_to_rdf
new_t = new_R @ R.T @ t

• 먼저 Rotation과 Translation은 c_rotated 기준으로 정의되어야 합니다. 구면 좌표 이미지로 생성된 영상이 \(R_{w \to c_{\text{rotated}}}\) 로 반영되어 있기 때문입니다. 다음과 같이 기존 Rotation, Translation을 분해해 보겠습니다.

• \[\begin{align} P_{c} &= \color{blue}{R_{w \to c_{\text{calib}}}}P_{w} + t_{w \to c_{\text{calib}}} \\ &= \color{blue}{R_{w \to c_{\text{calib}}}}(P_{w} + \color{blue}{R_{w \to c_{\text{calib}}}}^{-1} t_{w \to c_{\text{calib}}}) \end{align} \\ \Rightarrow\]
• \[\begin{align} P'_{c} &= \color{red}{R_{w \to c_{\text{rotated}}}}(P_{w} + \color{blue}{R_{w \to c_{\text{calib}}}}^{-1} t_{w \to c_{\text{calib}}}) \\ &= \color{red}{R_{w \to c_{\text{rotated}}}}P_{w} + \color{red}{R_{w \to c_{\text{rotated}}}}\color{blue}{R_{w \to c_{\text{calib}}}}^{-1} t_{w \to c_{\text{calib}}} \\ &= \color{red}{R_{w \to c_{\text{rotated}}}}P_{w} + \color{red}{R_{w \to c_{\text{rotated}}}}\color{blue}{R_{w \to c_{\text{calib}}}}^{T} t_{w \to c_{\text{calib}}} \end{align}\]

• 새롭게 정의된 Rotation인 new_R과 Translation인 new_t는 다음과 같습니다. 특히 Rotation의 경우 앞에서 다룬 바와 같이 World 좌표계의 좌표축은 FLU 기준이기 때문에 행렬 내부적으로 FLU → RDF 축 변환 작업이 필요하여 위 식과 같이 행렬이 정의됩니다. (위에 정의된 R, t 모두 RDF → RDF 축으로 정의됨)

• \[\text{new_R} = R_{w \to c_{\text{rotated}}} R_{\text{FLU} \to \text{RDF}}\]
• \[\text{new_t} = R_{w \to c_{\text{rotated}}}R_{w \to c_{\text{calib}}}^{T}t_{w \to c_{\text{calib}}}\]

• World-to-Image를 구현할 때, 다음 순서를 통해 World에서 Image까지 접근하게 됩니다.
  • ① World 좌표 → 카메라 좌표
  • ② 카메라 좌표 → \(\phi, \theta\)
  • ③ \(\phi, \theta\) → 구면 이미지 좌표

• 먼저 ① World 좌표 → 카메라 좌표 과정은 다음과 같이 변환됩니다. 이 때 사용되는 Rotation, Translation은 앞에서 정의된 new_R, new_t 입니다.

world_data = np.array(world_data)
cam_data = (new_R @ world_data.T) + new_t
x_c, y_c, z_c = cam_data[0], cam_data[1], cam_data[2]

• 다음으로 ② 카메라 좌표 → \(\phi, \theta\) 과정을 위해 직교 좌표계 → 구면 좌표계로의 변환이 필요합니다.

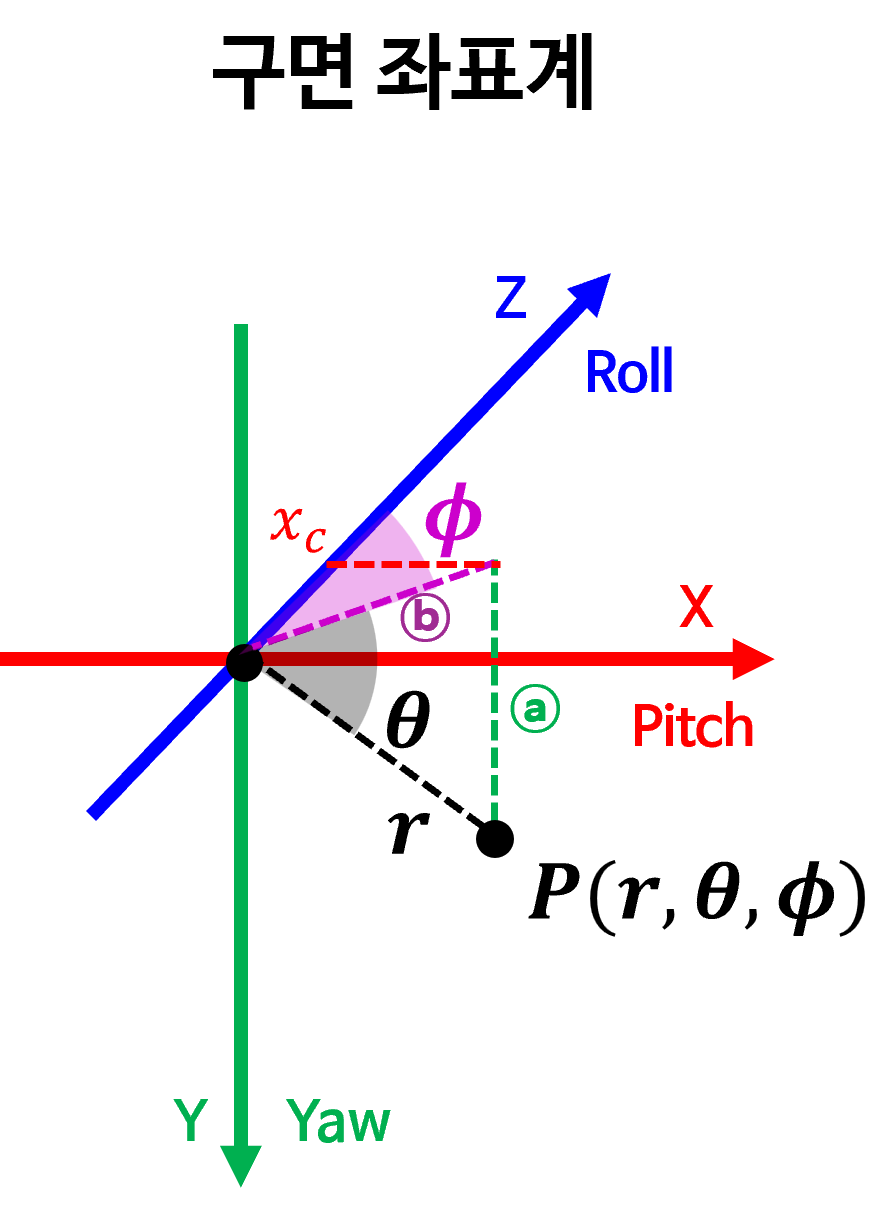
• 위 그림에서 \(r\) 은 다음과 같이 쉽게 구해집니다.

• \[r = \sqrt{x_{c}^{2} + y_{c}^{2} + z_{c}^{2}}\]

• 그 다음 \(\theta\) 는 다음과 같이 구할 수 있습니다. 위 그림에서 ⓐ가 \(y_{c}\) 에 해당합니다.

• \[\frac{y_{c}}{r} = \sin{(\theta)}\]
• \[\therefore \theta = \sin^{-1}{\left(\frac{y_{c}}{r}\right)}\]

• 마지막으로 \(\phi\) 는 다음과 같이 구할 수 있습니다. 위 그림에서 ⓑ 가 \(r \cos{(\theta)}\) 에 해당합니다.

• \[\sin{(\phi)} = \frac{x_{c}}{r\cos{(\theta)}}\]
• \[\therefore \phi = \sin^{-1}{\left(\frac{x_{c}}{r\cos{(\theta)}}\right)}\]

• 따라서 코드로 표현하면 다음과 같습니다.

r = np.sqrt(x_c**2 + y_c**2 + z_c**2)
theta = np.arcsin(y_c/r)
phi = np.arcsin(x_c/(r*np.cos(theta)))

• 마지막으로 ③ \(\phi, \theta\) → 구면 이미지 좌표 단계를 진행하면 아래와 같습니다. 앞에서 구한 new_K를 사용하여 이미지 좌표로 변경합니다.

phi_theta = np.stack([phi, theta, np.ones_like(theta)]) # (3, N)
phi_theta_coord= new_K @ phi_theta
phi_theta_coord = np.round(phi_theta_coord)

• World-to-Image를 위한 전체 코드는 아래와 같습니다. 중간 중간에 존재하는 코드는 불필요한 영역에 대한 마스킹 처리 등을 한 것이므로 코드의 주석을 참조하시기 바랍니다.

world_data = [
    ##### ① #####
    [0.0, 0.0, 0.0],
    [0.1, 0.0, 0.0],
    [0.2, 0.0, 0.0],
    [0.3, 0.0, 0.0],
    [0.4, 0.0, 0.0],
    [0.5, 0.0, 0.0],
    
    ##### ② #####
    [0.0, 0.4, 0.0],
    [0.1, 0.4, 0.0],
    [0.2, 0.4, 0.0],
    [0.3, 0.4, 0.0],
    [0.4, 0.4, 0.0],
    [0.5, 0.4, 0.0],

    ##### ③ ##### 
    [0.0, 0.45, 0.0],
    [0.0, 0.55, 0.0],
    [0.0, 0.65, 0.0],
    [0.0, 0.75, 0.0],
    [0.0, 0.85, 0.0],
    [0.0, 0.95, 0.0],
    
    ##### ④ ##### 
    [-0.35, 0.45, 0.0],
    [-0.35, 0.55, 0.0],
    [-0.35, 0.65, 0.0],
    [-0.35, 0.75, 0.0],
    [-0.35, 0.85, 0.0],
    [-0.35, 0.95, 0.0],

    ##### ⑤ #####
    [-0.7, 0.45, 0.0],
    [-0.7, 0.55, 0.0],
    [-0.7, 0.65, 0.0],
    [-0.7, 0.75, 0.0],
    [-0.7, 0.85, 0.0],
    [-0.7, 0.95, 0.0],

    ##### ⑥ #####
    [-0.7, 0.4, 0.0],
    [-0.8, 0.4, 0.0],
    [-0.9, 0.4, 0.0],
    [-1.0, 0.4, 0.0],
    [-1.1, 0.4, 0.0],
    [-1.2, 0.4, 0.0],
    
    ##### ⑦ #####
    [-0.7, 0.0, 0.0],
    [-0.8, 0.0, 0.0],
    [-0.9, 0.0, 0.0],
    [-1.0, 0.0, 0.0],
    [-1.1, 0.0, 0.0],
    [-1.2, 0.0, 0.0],

    ##### ⑧ #####
    [-0.7, -0.4, 0.0],
    [-0.8, -0.4, 0.0],
    [-0.9, -0.4, 0.0],
    [-1.0, -0.4, 0.0],
    [-1.1, -0.4, 0.0],
    [-1.2, -0.4, 0.0],

    ##### ⑨ #####
    [-0.7, -0.45, 0.0],
    [-0.7, -0.55, 0.0],
    [-0.7, -0.65, 0.0],
    [-0.7, -0.75, 0.0],
    [-0.7, -0.85, 0.0],
    [-0.7, -0.95, 0.0],
    
    ##### ⑩ #####
    [-0.35, -0.45, 0.0],
    [-0.35, -0.55, 0.0],
    [-0.35, -0.65, 0.0],
    [-0.35, -0.75, 0.0],
    [-0.35, -0.85, 0.0],
    [-0.35, -0.95, 0.0],

    ##### ⑪ #####
    [0.0, -0.45, 0.0],
    [0.0, -0.55, 0.0],
    [0.0, -0.65, 0.0],
    [0.0, -0.75, 0.0],
    [0.0, -0.85, 0.0],
    [0.0, -0.95, 0.0],

    ##### ⑫ #####
    [0.0, -0.4, 0.0],
    [0.1, -0.4, 0.0],
    [0.2, -0.4, 0.0],
    [0.3, -0.4, 0.0],
    [0.4, -0.4, 0.0],
    [0.5, -0.4, 0.0],
]

camera_name = 'front_fisheye_camera'
calib = json.load(open("camera_calibration.json", "r"))
image = cv2.imread(f"{camera_name}.png", -1)

origin_height, origin_width, _ = image.shape
target_height, target_width  = origin_height//2, origin_width//2

# example case
roll_degree = None
pitch_degree = None
yaw_degree = None

hfov_deg = 180
vfov_deg = 150

K = np.array(calib[camera_name]['Intrinsic']['K']).reshape(3, 3)
D = np.array(calib[camera_name]['Intrinsic']['D'])
R = np.array(calib[camera_name]['Extrinsic']['World']['Camera']['R']).reshape(3, 3)
t = np.array(calib[camera_name]['Extrinsic']['World']['Camera']['t']).reshape(3, 1)

map_x, map_y, new_K, new_R, new_t = get_world_camera_rotation_spherical_lut(
    R, t, K, D, 
    origin_width, origin_height, target_width, target_height, 
    hfov_deg=hfov_deg, vfov_deg=vfov_deg, 
    roll_degree=roll_degree, pitch_degree=pitch_degree, yaw_degree=yaw_degree)
new_image = cv2.remap(image, map_x, map_y, interpolation=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT, borderValue=(0, 0, 0))

# ① World 좌표 → 카메라 좌표
world_data = np.array(world_data)
cam_data = (new_R @ world_data.T) + new_t
x_c, y_c, z_c = cam_data[0], cam_data[1], cam_data[2]

# ② `카메라 좌표` → phi, theta    
r = np.sqrt(x_c**2 + y_c**2 + z_c**2)
theta = np.arcsin(y_c/r)
phi = np.arcsin(x_c/(r*np.cos(theta)))

hfov = np.deg2rad(hfov_deg)
vfov = np.deg2rad(vfov_deg)
fov_mask = (-hfov/2 < phi) & (phi < hfov/2) & (-vfov/2 < theta) & (theta < vfov/2) & (cam_data[2] > 0)

r = r[fov_mask]
phi = phi[fov_mask]
theta = theta[fov_mask]

# phi, theta → 구면 이미지 좌표
phi_theta = np.stack([phi, theta, np.ones_like(theta)]) # (3, N)
phi_theta_coord= new_K @ phi_theta
phi_theta_coord = np.round(phi_theta_coord)

# phi_coord, theta_coord, r
phi_theta_coord_r = np.concatenate([
    np.expand_dims(phi_theta_coord[0], -1),
    np.expand_dims(phi_theta_coord[1], -1),
    np.expand_dims(r, -1)
], axis=1) # (N, 3)

phi_coord = np.clip(np.round(phi_theta_coord_r[:, 0]).astype(np.int32), 0, target_width-1)
theta_coord = np.clip(np.round(phi_theta_coord_r[:, 1]).astype(np.int32), 0, target_height-1)

for phi_i, theta_i in zip(phi_coord, theta_coord):    
    cv2.circle(new_image, (phi_i, theta_i), 5, (0, 0, 255), -1)
    
mask = (map_x > 0) & (map_y > 0) & (map_x < origin_width) & (map_y < origin_height)
new_image = new_image * np.expand_dims(mask, -1)

• 위 그림의 왼쪽 열은 일반적인 상황에서의 구면 투영 이미지 입니다. Roll, Pitch의 회전은 없고 Yaw는 카메라 장착 위치와 유사한 0/90/180/270으로 설정하였습니다. 반면 오른쪽 열은 임의의 회전을 모두 적용하였습니다. 위 예시를 통하여 World-to-Image로 원하는 좌표 투영 시, 회전을 반영하여 정확히 투영되는 것을 확인할 수 있습니다.

Image-to-World

• Image-to-World로 좌표를 변환하기 위해서는 다음 과정을 통해 변환을 해야 합니다. 앞의 World-to-Image의 변환 순서와 반대이나 추가 작업이 필요합니다. 왜냐하면 ② 과정에서 주어진 \(Z_{w}\) 를 이용하여 \(r\) 값을 복원하는 과정이 필요하기 때문입니다.
  • ① 구면 이미지 좌표 → \(\phi, \theta\)
  • ② \(\phi, \theta\) → 카메라 좌표
  • ③ 카메라 좌표 → World 좌표

• 먼저 ① 구면 이미지 좌표 → \(\phi, \theta\) 의 변환은 다음과 같이 쉽게 변환할 수 있습니다.

phi_coord = 501 # 임의의 값
theta_coord = 711 # 임의의 값
p = np.array([phi_coord, theta_coord, 1]).reshape(3, 1)
phi, theta, r_norm = new_K_inv @ p

• 그 다음으로 ② \(\phi, \theta\) → 카메라 좌표계 의 과정 또한 앞에서 다룬 바와 같이 변환할 수 있습니다. 다만 실제 \(r\) 값을 알아야 정확한 \(x_{c}, y_{c}, z_{c}\) 를 구할 수 있습니다.

• \[X_{c} = r \sin{(\phi)}\cos{(\theta)}\]
• \[Y_{c} = r \sin{(\theta)}\]
• \[Z_{c} = r \cos{(\phi)}\cos{(\theta)}\]

• 위 식에서 \(r\) 값만 유추하는 방법을 확인해 보겠습니다. \(r\) 값을 유추하기 위해서는 변수를 줄여야 합니다. World 좌표에서 Image로 투영 시, \(Z\) 값이 사라졌기 때문에 사라진 \(Z\) 값을 복원할 수 없습니다. 따라서 \(Z\) 값을 상수로 고정해야 \(r\) 을 구할 수 있습니다. 예를 들어 \(Z_{w} = 0\) 이라는 가정을 둔다면 \(r\) 을 복원할 수 있습니다. 이와 관련된 내용은 아래 링크를 참조해 보셔도 됩니다.
  • 링크: 이미지의 Image-to-World 방법
• 이번 예제에서도 \(Z_{w} = 0\) 이라는 가정을 통하여 \(r\) 을 복원하는 과정을 살펴보도록 하겠습니다. 즉, 이미지의 모든 픽셀에 대응되는 \(Z_{w} = 0\) 이라는 가정을 통하여 \(X_{w}, Y_{w}\) 만 구하면 되는 상황입니다.

• \[\begin{align} P_{\text{world}} = \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \end{bmatrix} &= R^{-1}(P_{\text{camera}} - t) = R^{T}(P_{\text{camera}} - t) \\ &= \begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix}^{T} \begin{bmatrix} X_{c} - t_{1} \\ Y_{c} - t_{2} \\ Z_{c} - t_{3} \end{bmatrix} \\ &= \begin{bmatrix} R_{11} & R_{21} & R_{31} \\ R_{12} & R_{22} & R_{32} \\ R_{13} & R_{23} & R_{33} \end{bmatrix} \begin{bmatrix} X_{c} - t_{1} \\ Y_{c} - t_{2} \\ Z_{c} - t_{3} \end{bmatrix} \end{align}\]
• \[\Rightarrow \begin{bmatrix} R_{13} & R_{23} & R_{33} \end{bmatrix} \begin{bmatrix} X_{c} - t_{1} \\ Y_{c} - t_{2} \\ Z_{c} - t_{3} \end{bmatrix} = Z_{w} \quad \text{(Used Thrid Row)}\]
• \[\Rightarrow R_{13}(X_{c} - t_{1}) + R_{23}(Y_{c} - t_{2}) + R_{33}(Z_{c} - t_{3}) = Z_{w}\]

• 위 식에서 \(X_{c}, Y_{c}, Z_{c}\) 대신 다음 값으로 식을 대체해 보겠습니다.

• \[X_{c} = r \sin{(\phi)}\cos{(\theta)}\]
• \[\Rightarrow X_{c, \text{norm}} = \sin{(\phi)}\cos{(\theta)}\]

• \[Y_{c} = r \sin{(\theta)}\]
• \[\Rightarrow Y_{c, \text{norm}} = \sin{(\theta)}\]

• \[Z_{c} = r \cos{(\phi)}\cos{(\theta)}\]
• \[\Rightarrow Z_{c, \text{norm}} = \cos{(\phi)}\cos{(\theta)}\]

• \[R_{13}(X_{c} - t_{1}) + R_{23}(Y_{c} - t_{2}) + R_{33}(Z_{c} - t_{3}) = Z_{w}\]
• \[R_{13}(r\cdot X_{c, \text{norm}} - t_{1}) + R_{23}(r \cdot Y_{c, \text{norm}} - t_{2}) + R_{33}(r \cdot Z_{c, \text{norm}} - t_{3}) = Z_{w}\]
• \[r \left(R_{13}X_{c, \text{norm}} + R_{23}Y_{c, \text{norm}} + R_{33}Z_{c, \text{norm}} \right) = Z_{w} + R_{13}t_{1} + R_{23}t_{2} + R_{33}t_{3}\]
• \[\therefore r = \frac{Z_{w} + R_{13}t_{1} + R_{23}t_{2} + R_{33}t_{3}}{R_{13}X_{c, \text{norm}} + R_{23}Y_{c, \text{norm}} + R_{33}Z_{c, \text{norm}}}\]

• 따라서 위에서 구한 \(r\) 을 이용하여 \(X_{c, \text{norm}}, Y_{c, \text{norm}}, Z_{c, \text{norm}}\) 를 \(X_{c}, Y_{c}, Z_{c}\) 로 변환할 수 있습니다.
• 코드로 나타내면 다음과 같습니다.

x_norm = np.cos(theta)*np.sin(phi) # -1 ~ 1
y_norm = np.sin(theta) # -1 ~ 1
z_norm = np.cos(theta)*np.cos(phi) # 0 ~ 1

Z_w = 0
new_r = (Z_w + new_R[0, 2]*new_t[0] + new_R[1, 2]*t[1] + new_R[2, 2]*new_t[2]) / (new_R[0, 2]*x_norm + new_R[1,2]*y_norm + new_R[2, 2]*z_norm)

x_c = new_r*x_norm
y_c = new_r*y_norm
z_c = new_r*z_norm

• 마지막으로 ③ 카메라 좌표 → World 좌표 변환은 다음과 같이 적용할 수 있습니다.

• \[P_{w} = R^{T}(P_{c} - t) \quad (\because P_{c} = R P_{w} + t)\]

• 이 모든 과정을 코드로 정리하면 다음과 같습니다.

phi_coord = 504 # example
theta_coord = 708 # example
Z_w = 0

p = np.array([phi_coord, theta_coord, 1]).reshape(3, 1)
new_K_inv = np.linalg.inv(new_K)
phi, theta, r_norm = new_K_inv @ p

x_norm = np.cos(theta)*np.sin(phi) # -1 ~ 1
y_norm = np.sin(theta) # -1 ~ 1
z_norm = np.cos(theta)*np.cos(phi) # 0 ~ 1
new_r = (Z_w + new_R[0, 2]*new_t[0] + new_R[1, 2]*new_t[1] + new_R[2, 2]*new_t[2]) / (new_R[0, 2]*x_norm + new_R[1,2]*y_norm + new_R[2, 2]*z_norm)
x_c = new_r*x_norm
y_c = new_r*y_norm
z_c = new_r*z_norm

P_c = np.array([x_c, y_c, z_c]).reshape(3, 1)
P_w = np.round(new_R.T@(P_c - new_t), 2)

• 아래는 \(Z_{w} = 0\) 으로 가정하였을 때, phi_coord, theta_coord에 따른 World 좌표 추정 결과 예시입니다.

• 왼쪽 열은 yaw의 회전만 반영한 결과이고 오른쪽 열은 임의의 roll, pitch, yaw 회전을 모두 반영한 결과 입니다.
• 임의의 회전을 적용하더라도 의미상 같은 위치의 픽셀을 Image-to-World를 하였을 때, 같은 World 좌표가 도출되는 것을 볼 수 있습니다.

회전을 고려한 World 기준 구면 투영법의 기본적인 사용 방법

• 회전을 고려한 World 기준 구면 투영법을 사용하기 위한 가장 일반적인 방법은 Roll = 0, Pitch = 0, YaW = 카메라 장착 위치 입니다.
• 멀티 카메라 환경에서 카메라들이 장착된 위치 및 자세에 따라 다양한 형태의 이미지가 형성이 될 수 있으나 위 방식을 따르면 Roll, Pitch가 모두 0으로 고정되어 카메라가 바라보는 방향을 평평한 바닥과 수평이 될 수 있도록 고정할 수 있기 때문입니다. Roll, Pitch 모두 0이면 이미지의 소실선 또한 이미지 세로 방향의 한 가운데에 생성할 수 있어서 카메라들의 자세를 통일 시킬 수 있습니다. Yaw의 경우 카메라의 장착 방향이 다양하기 때문에 실제 카메라가 장착된 방향을 그대로 사용하면 가로 방향의 이미지 한 가운데 기준으로 대칭으로 이미지를 만들 수 있습니다. (만약 특정 각도로만 Yaw를 지정하고 싶은 경우에 Yaw를 지정할 수도 있습니다.)

• 위 그림의 경우 Roll = 0, Pitch = 0, YaW = 카메라 장착 위치를 따라 이미지를 생성하였을 때, 결과를 보여줍니다. Roll, Pitch가 모두 0이므로 소실선은 한 가운데 생성됩니다. 실내에서 촬영한 영상이라 소실선이 보이지 않으나 가로 점선 기준으로 소실선이 형성됩니다. 각 이미지의 세로 점선이 각 카메라 장착 위치의 Yaw값에 해당합니다. 따라서 모든 이미지가 좌우 대칭하여 생성되고 검은색 빈 영역도 최소화 되는 것을 볼 수 있습니다.

회전을 고려한 World 기준 구면 파노라마 투영법

Vision 관련 글 목차